Compact LWFA-Based Extreme Ultraviolet Free Electron Laser: Design Constraints
Abstract
:1. Introduction
2. Main Constraints for a Compact FEL
3. Laser–Plasma Acceleration for EUV-FEL
4. Electron Beam Transport for EUV-FEL
5. EUV-FEL Regime
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pellegrini, C. The development of XFELs. Nat. Rev. Phys. 2020, 2, 330–331. [Google Scholar] [CrossRef]
- XFEL: The European X-Ray Free-Electron Laser. Technical Design Report; DESY: Hamburg, Germany, 2006. [Google Scholar] [CrossRef]
- Milne, C.J.; Schietinger, T.; Aiba, M.; Alarcon, A.; Alex, J.; Anghel, A.; Arsov, V.; Beard, C.; Beaud, P.; Bettoni, S.; et al. SwissFEL: The Swiss X-ray Free Electron Laser. Appl. Sci. 2017, 7, 720. [Google Scholar] [CrossRef]
- Huang, Z.; Lindau, I. SACLA hard-X-ray compact FEL. Nat. Photonics 2012, 6, 505–506. [Google Scholar] [CrossRef]
- Gruner, F.; Becker, S.; Schramm, U.; Eichner, T.; Fuchs, M.; Weingartner, R.; Habs, D.; Meyer-ter-Vehn, J.; Geissler, M.; Ferrario, M.; et al. Design considerations for table-top, laser-based VUV and X-ray free electron lasers. Appl. Phys. B 2007, 86, 431–435. [Google Scholar] [CrossRef] [Green Version]
- Mourou, G.; Tajima, T. The Extreme Light Infrastructure: Optics’ Next Horizon. Opt. Photon. News 2011, 22, 47–51. [Google Scholar] [CrossRef]
- Gonsalves, A.; Nakamura, K.; Daniels, J.; Benedetti, C.; Pieronek, C.; de Raadt, T.; Steinke, S.; Bin, J.; Bulanov, S.; van Tilborg, J.; et al. Petawatt Laser Guiding and Electron Beam Acceleration to 8 GeV in a Laser-Heated Capillary Discharge Waveguide. Phys. Rev. Lett. 2019, 122, 084801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jalas, S.; Kirchen, M.; Messner, P.; Winkler, P.; Hübner, L.; Dirkwinkel, J.; Schnepp, M.; Lehe, R.; Maier, A.R. Bayesian Optimization of a Laser-Plasma Accelerator. Phy. Rev. Lett. 2021, 126, 505–506. [Google Scholar] [CrossRef]
- Schlenvoigt, H.P.; Haupt, K.; Debus, A.; Budde, F.; Jäckel, O.; Pfotenhauer, S.; Schwoerer, H.; Rohwer, E.; Gallacher, J.G.; Brunetti, E.; et al. A compact synchrotron radiation source driven by a laser-plasma wakefield accelerator. Nat. Phys. 2008, 4, 130–133. [Google Scholar] [CrossRef]
- Fuchs, M.; Weingartner, R.; Popp, A.; Major, Z.; Becker, S.; Osterhoff, J.; Cortrie, I.; Zeitler, B.; Hörlein, R.; Tsakiris, G.D.; et al. Laser-driven soft-X-ray undulator source. Nat. Phys. 2009, 5, 826–829. [Google Scholar] [CrossRef] [Green Version]
- André, T.; Andriyash, I.A.; Loulergue, A.; Labat, M.; Roussel, E.; Ghaith, A.; Khojoyan, M.; Thaury, C.; Valléau, M.; Briquez, F.; et al. Control of laser plasma accelerated electrons for light sources. Nat. Commun. 2018, 9, 1334. [Google Scholar] [CrossRef]
- Delbos, N.; Werle, C.; Dornmair, I.; Eichner, T.; Hübner, L.; Jalas, S.; Jolly, S.; Kirchen, M.; Leroux, V.; Messner, P.; et al. Lux—A laser-plasma driven undulator beamline. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2018, 909, 318–322. [Google Scholar] [CrossRef]
- Maier, A.R.; Kajumba, N.; Guggenmos, A.; Werle, C.; Wenz, J.; Delbos, N.; Zeitler, B.; Dornmair, I.; Schmidt, J.; Gullikson, E.M.; et al. Water-Window X-Ray Pulses from a Laser-Plasma Driven Undulator. Sci. Rep. 2020, 10, 5634. [Google Scholar] [CrossRef]
- Assmann, R.W.; Weikum, M.K.; Akhter, T.; Alesini, D.; Alexandrova, A.S.; Anania, M.P.; Andreev, N.E.; Andriyash, I.; Artioli, M.; Aschikhin, A.; et al. EuPRAXIA Conceptual Design Report. Eur. Phys. J. Spec. Top. 2020, 229, 3675–4284. [Google Scholar] [CrossRef]
- Ghaith, A.; Couprie, M.E.; Oumbarek-Espinos, D.; Andriyash, I.; Massimo, F.; Clarke, J.; Courthold, M.; Bayliss, V.; Bernhard, A.; Trunk, M.; et al. Undulator design for a laser-plasma-based free-electron-laser. Phys. Rep. 2021, 937, 1–73. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, W.; Liu, J.; Wang, W.; Yu, C.; Tian, Y.; Nakajima, K.; Deng, A.; Qi, R.; Wang, C.; et al. Energy spread minimization in a cascaded laser wakefield accelerator via velocity bunching. Phys. Plasmas 2016, 23, 053106. [Google Scholar] [CrossRef]
- Maier, A.R.; Meseck, A.; Reiche, S.; Schroeder, C.B.; Seggebrock, T.; Gruener, F. Demonstration Scheme for a Laser-Plasma-Driven Free-Electron Laser. Phys. Rev. X 2012, 2, 031019. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Feng, K.; Ke, L.; Yu, C.; Xu, Y.; Qi, R.; Chen, Y.; Qin, Z.; Zhang, Z.; Fang, M.; et al. Free-electron lasing at 27 nanometres based on a laser wakefield accelerator. Nature 2021, 595, 516–520. [Google Scholar] [CrossRef]
- Faatz, B.; Braune, M.; Hensler, O.; Honkavaara, K.; Kammering, R.; Kuhlmann, M.; Ploenjes, E.; Roensch-Schulenburg, J.; Schneidmiller, E.; Schreiber, S.; et al. The FLASH Facility: Advanced Options for FLASH2 and Future Perspectives. Appl. Sci. 2017, 7, 1114. [Google Scholar] [CrossRef]
- Bocchetta, C.; Abrami, A.; Allaria, E.; Andrian, I.; Bacescu, D.; Badano, L.; Banchi, L.; Bulfone, D.; Bonțoiu, C.; Bracco, R.; et al. Conceptual Design Report for the FERMI@Elettra Project ST/F-TN-07/12; Elettra Sincrotrone Trieste: Basovizza Italy, 2007. [Google Scholar]
- Schmidt, T.; Böhler, P.; Brügger, M.; Calvi, M.; Danner, S.; Huber, P.; Imhof, A.; Jöhri, H.; Keller, A.; Locher, M.; et al. SwissFEL U15 prototype design and first results. In Proceedings of the Free Electron Laser Conference (IBIC’12); JACoW Publishing: Geneva, Switzerland, 2012; pp. 666–669. [Google Scholar]
- Xie, M. Exact and variational solutions of 3D eigenmodes in high gain FELs. Nucl. Instrum. Methods Phys. Res. A 2000, 445, 59–66. [Google Scholar] [CrossRef] [Green Version]
- Huang, Z.; Kim, K.J. Review of x-ray free-electron laser theory. Phys. Rev. ST Accel. Beams 2007, 10, 034801. [Google Scholar] [CrossRef]
- Maier, A.R.; Delbos, N.M.; Eichner, T.; Hübner, L.; Jalas, S.; Jeppe, L.; Jolly, S.W.; Kirchen, M.; Leroux, V.; Messner, P.; et al. Decoding Sources of Energy Variability in a Laser-Plasma Accelerator. Phys. Rev. X 2020, 10, 031039. [Google Scholar] [CrossRef]
- Green, T.; Antipenkov, R.; Bakule, P. L2-DUHA 100TW High Repetition Rate Laser System at ELI-Beamlines: Key Design Considerations. Rev. Laser Eng. 2021, 49, 106–109. [Google Scholar]
- Malka, V.; Fritzler, S.; Lefebvre, E.; Aleonard, M.-M.; Burgy, F.; Chambaret, J.-P.; Chemin, J.-F.; Krushelnick, K.; Malka, G.; Dangor, A.E.; et al. Electron Acceleration by a Wake Field Forced by an Intense Ultrashort Laser Pulse. Science 2002, 298, 1596–1600. [Google Scholar] [CrossRef] [PubMed]
- Hafz, N.A.M.; Jeong, T.M.; Choi, I.W.; Lee, S.K.; Pae, K.H.; Kulagin, V.V.; Sung, J.H.; Yu, T.J.; Hong, K.-H.; Hosokai, T.; et al. Electron stable generation of GeV-class electron beams from self-guided laser-plasma channels. Nature 2008, 2, 571–577. [Google Scholar] [CrossRef]
- Hofmann, I. Halo coupling and cleaning by a space charge resonance in high intensity beams. Phys. Rev. ST Accel. Beams 2013, 16, 084201. [Google Scholar] [CrossRef] [Green Version]
- Loulergue; Labat, A.; Evain, M.; Benabderrahmane, C.; Malka, C.; Couprie, E.M. Beam manipulation for compact laser wakefield accelerator based free-electron lasers. New J. Phys. 2015, 17, 023028. [Google Scholar] [CrossRef]
- Migliorati, M.; Bacci, A.; Benedetti, C.; Chiadroni, E.; Ferrario, M.; Mostacci, A.; Palumbo, L.; Rossi, A.R.; Serafini, L.; Antici, P. Intrinsic normalized emittance growth in laser-driven electron accelerators. Phys. Rev. ST Accel. Beams 2013, 16, 011302. [Google Scholar] [CrossRef] [Green Version]
- Halbach, K. Design of permanent multipole magnets with oriented rare earth cobalt material. Nucl. Instrum. Methods 1980, 169, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Panofsky, W.K.H.; Baker, W.R. A Focusing Device for the External 350-MeV Proton Beam of the 184-inch Cyclotron at Berkeley. Rev. Sci. Instrum. 1950, 21, 445–447. [Google Scholar] [CrossRef]
- Chiadroni, E.; Anania, M.; Bellaveglia, M.; Biagioni, A.; Bisesto, F.; Brentegani, E.; Cardelli, F.; Cianchi, A.; Costa, G.; Di Giovenale, D.; et al. Overview of plasma lens experiments and recent results at SPARC_LAB. Nucl. Instrum. Methods Phys. Res. A 2018, 909, 16–20. [Google Scholar] [CrossRef]
- van Tilborg, J.; Barber, S.K.; Benedetti, C.; Schroeder, C.B.; Isono, F.; Tsai, H.E.; Geddes, C.G.R.; Leemans, W.P. Comparative study of active plasma lenses in high-quality electron accelerator transport lines. Phys. Plasmas 2018, 25, 056702. [Google Scholar] [CrossRef] [Green Version]
- Lindstrøm, C.; Sjobak, K.; Adli, E.; Röckemann, J.H.; Schaper, L.; Osterhoff, J.; Dyson, A.; Hooker, S.; Farabolini, W.; Gamba, D.; et al. Overview of the CLEAR plasma lens experiment. Nucl. Instrum. Methods Phys. Res. A 2018, 909, 379–382. [Google Scholar] [CrossRef]
- Molodozhentsev, A.; Korn, G.; Maier, A.; Pribyl, L. “LWFA-driven” Free Electron Laser for ELI-Beamlines. In Proceedings of the 60th ICFA Advanced Beam Dynamics Workshop (FLS’18), Shanghai, China, 5–9 March 2018; JACoW Publishing: Geneva, Switzerland, 2018; pp. 62–67. [Google Scholar] [CrossRef]
- Molodozhentsev, A.; Kruchinin, K.; Pribyl, L. Degradation of Electron Beam Quality for a Compact Laser-Based FEL. In Proceedings of the 9th International Particle Accelerator Conference (IPAC’18), Vancouver, BC, Canada, 29 April–4 May 2018; JACoW Publishing: Geneva, Switzerland, 2018; pp. 3029–3031. [Google Scholar] [CrossRef]
- Kruchinin, K.; Kocon, D.; Lyapin, A. Electron Beam Diagnostics Concept for the LWFA Driven FEL at ELI-Beamlines. Proc. IBIC 2019, 19, 184–187. [Google Scholar] [CrossRef]
- Uriot, D.; Pichoff, N. Status of TraceWin Code. In Proceedings of the 6th International Particle Accelerator Conference (IPAC’15), Richmond, VA, USA, 3–8 May 2015; JACoW: Geneva, Switzerland, 2015; pp. 92–94. [Google Scholar] [CrossRef]
- Tanaka, T. SIMPLEX: Simulator and postprocessor for free-electron laser experiments. J. Synchrotron Radiat. 2015, 22, 1319–1326. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reiche, S. Overview of seeding methods for FELs. In Proceedings of the 4th International Particle Accelerator Conference (IPAC’13), Shanghai, China, 12–17 May 2013; JACoW Publishing: Geneva, Switzerland; pp. 2063–2067. [Google Scholar]

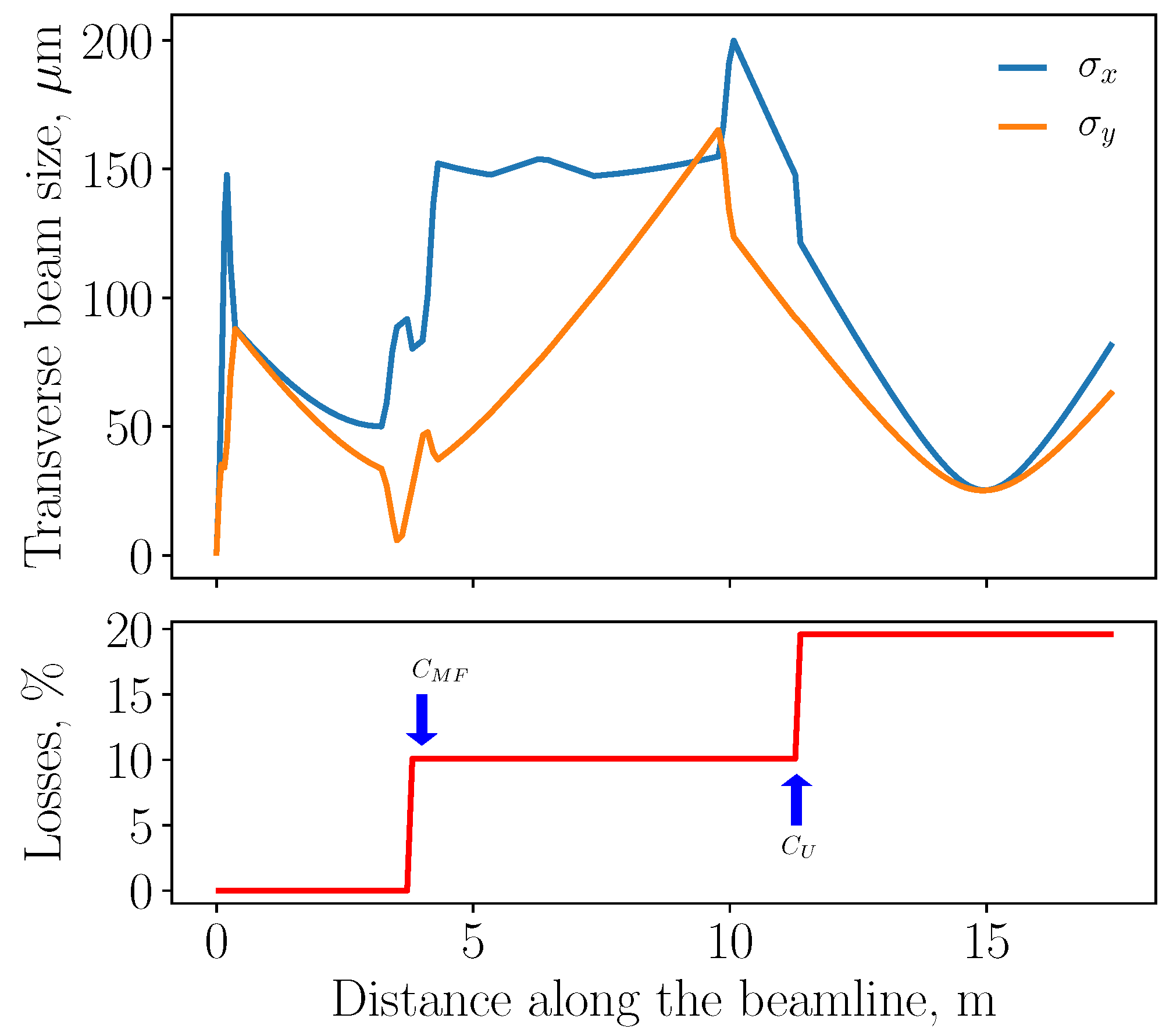

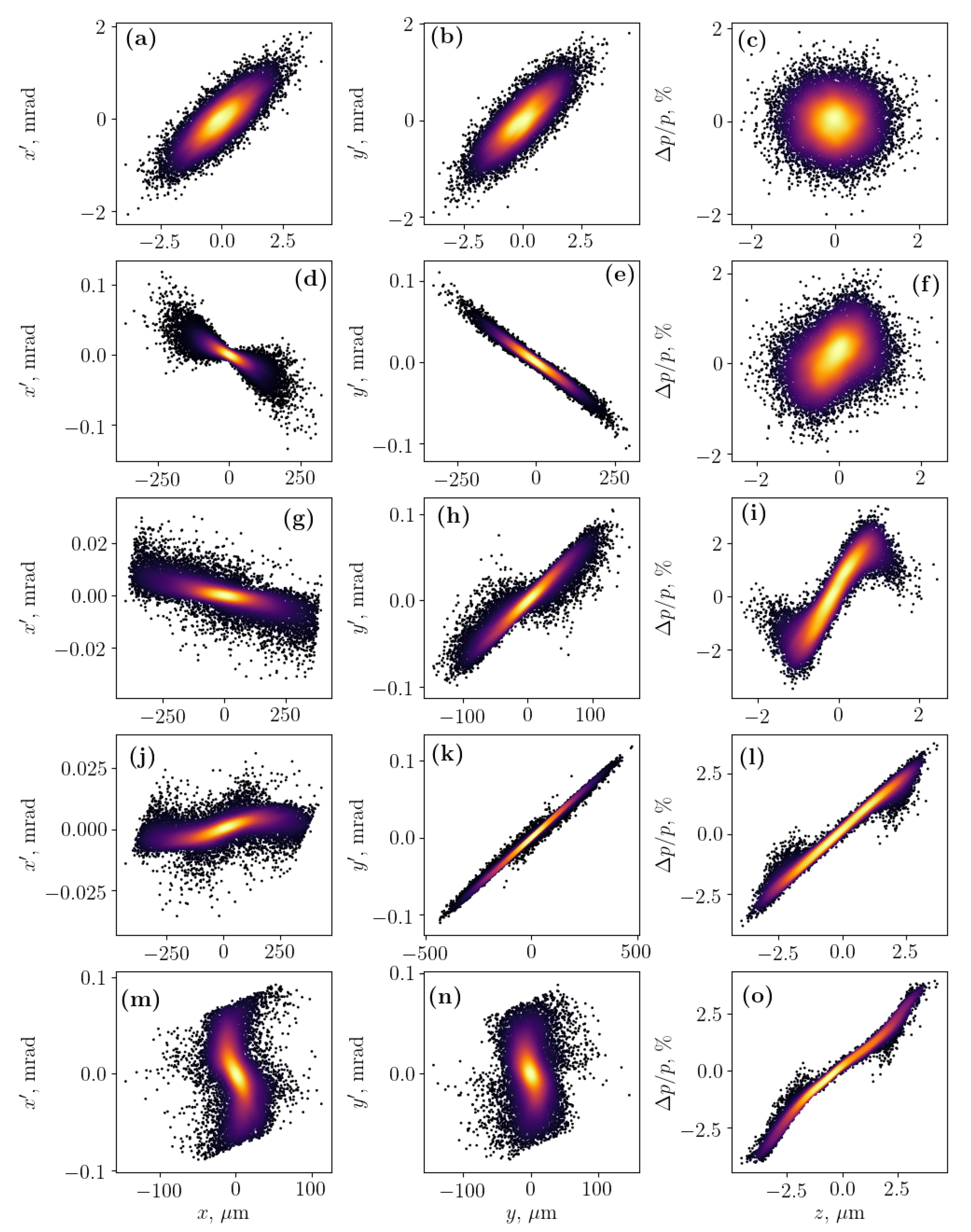

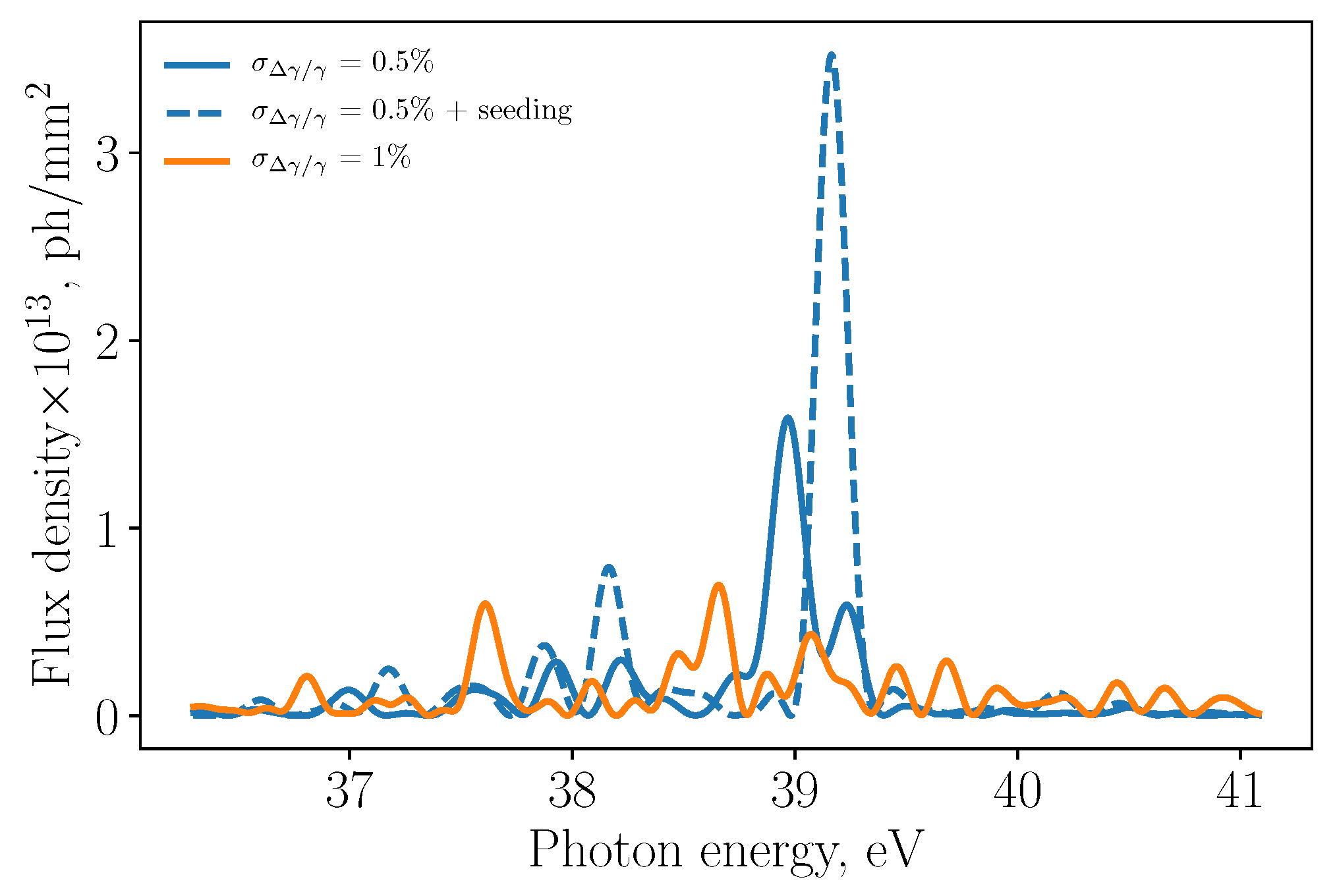
| Parameter | Symbol | Units | Value | |
|---|---|---|---|---|
| Undulator parameters | ||||
| Period | mm | 15 | 15 | |
| Gap | mm | 4 | 7 | |
| Peak magnetic field | T | 1 | 0.54 | |
| Undulator parameter | – | 1.4 | 0.75 | |
| LWFA-based electron beam parameters | ||||
| Energy | MeV | 350 | 350 | |
| RMS emittance (slice) | mm mrad | < | < | |
| RMS beam size in undulator | <> | m | ∼25 | ∼20 |
| Energy spread (slice) | % | 0.25 | 0.25 | |
| RMS bunch length | m | 1 | 1 | |
| Total bunch charge | Q | pC | 25 | 35 |
| Peak current | kA | 3 | 4.2 | |
| LWFA-based FEL parameters | ||||
| Photon radiation wavelength | nm | 31.6 | 20.4 | |
| Photon radiation energy | eV | 39 | 60.5 | |
| Coherent RMS emittance | mm mrad | 1.7 | 1.2 | |
| 1D Pierce parameter | – | 0.0058 | 0.0065 | |
| 1D gain length | m | 0.12 | 0.1 | |
| 1D coherence length | m | 0.4 | 0.25 | |
| Total number of photons at saturation | – | 6.2 × 10 | 3.3 × 10 | |
| Relative FWHM frequency bandwidth | % | 1.2 | 1.3 | |
| Photon peak brilliance (0.1%BW) | ph/pulse/mm/mrad | 2.6 × 10 | 3.4 × 10 | |
| 1D peak power at saturation | GW | 5.4 | 5.2 | |
| 3D gain length | m | 0.18 | 0.18 | |
| 3D total saturation length | m | ∼3.5 | ∼3.5 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molodozhentsev, A.Y.; Kruchinin, K.O. Compact LWFA-Based Extreme Ultraviolet Free Electron Laser: Design Constraints. Instruments 2022, 6, 4. https://doi.org/10.3390/instruments6010004
Molodozhentsev AY, Kruchinin KO. Compact LWFA-Based Extreme Ultraviolet Free Electron Laser: Design Constraints. Instruments. 2022; 6(1):4. https://doi.org/10.3390/instruments6010004
Chicago/Turabian StyleMolodozhentsev, Alexander Yu., and Konstantin O. Kruchinin. 2022. "Compact LWFA-Based Extreme Ultraviolet Free Electron Laser: Design Constraints" Instruments 6, no. 1: 4. https://doi.org/10.3390/instruments6010004
APA StyleMolodozhentsev, A. Y., & Kruchinin, K. O. (2022). Compact LWFA-Based Extreme Ultraviolet Free Electron Laser: Design Constraints. Instruments, 6(1), 4. https://doi.org/10.3390/instruments6010004






