2.1. Vortex Target Design
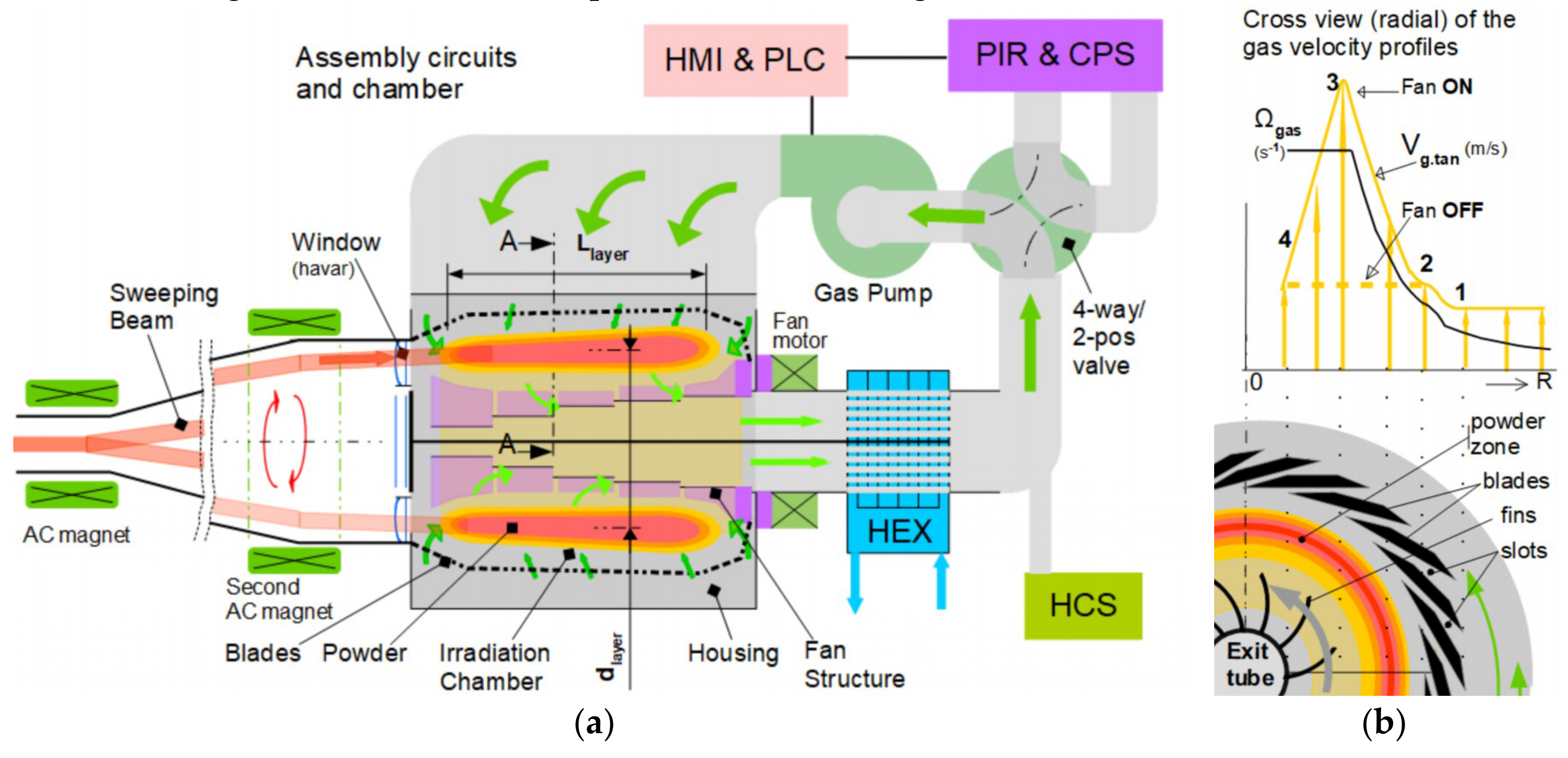
The assembly design proposed here is based on an inert gas closed-loop circuit for removing the heat induced by the hitting beam to a secondary cooling water circuit. Micrometer-sized powder particles injected into such a gas circuit accumulate inside the circular arranged blade configuration, as indicated by the orange/red zone in
Figure 1a. The purpose of the blades and the fan structure is to control the cylindrical-shaped area, where both the centrifugal and inward-directed drag and buoyant forces on the powder are balanced. The blade’s front and end (
Figure 1a) are conical and inwardly directed to establish small inward axial-directed particle drift. Thus, the conical sections prevent powder accumulation outside the orange/red zone.
Figure 1b shows a radial cross-sectional view (A–A) half-way through the powder layer. The corresponding radial profile diagram indicates the angular and tangential gas velocities (
Ωgas and
vg.tan). The tangential gas velocity
vg.tan increased from radial point 1 to a maximum indicated value at radial point 3, which is close to the fin tips of the elongated centered fan structure. The enforced gas spinning (region inside radial points 2 and 3,
Figure 1b) and subsequently enhanced centrifugal force lead to the continued accumulation of powder particles in the indicated cylindrical orange/red zone with a length denoted by L
layer. The product of the dispersed powder density and length L
layer is equal to the powder-in-gas mass thickness (i.e., g/cm
2) and must correspond to the thick target values.
Figure 1a shows the gas circuit components and equipment for process control, including the central parts: cochlea (housing); window section; irradiation chamber with the blades’ configuration; and elongated fan structure, which is driven by a magnet-coupled fan motor. The gas pump, shown in green in
Figure 1a, generates an inert gas flow that passes the blades and spirals strongly inward to the centered exit tube inside the fan structure.
Other equipment labeled in the figure include:
Heat exchanger (HEX) for heat removal by the secondary cooling water circuit;
Helium control system (HCS) for the regulation of the circuit pressure and gas temperatures;
Four-way/two-position valve for loading and emptying the irradiation chamber;
Powder injection and recovery (PIR) system and Chemical Processing System (CPS); and
Process control (PLC) and operator panel (HMI).
Prior to the operation, residual gasses in the target chamber are evacuated. Subsequently, the chamber and circuit are helium pressurized, and the gas pump and the central fan structure are turned on. As a result of the 4w-valve operation, the injected powder is dispersed into the circuit and accumulates in the (indicated orange/red) cylindrical zone.
Subsequently after irradiation, the powder circulating in the irradiation chamber can be scavenged in the PIR system using the 4w-valve operation and reduction of the fan’s spinning structure while the gas pump continues inert gas circulation. Reducing the fan’s spinning frequency leads to a reduction in centrifugal forces operating on the powder’s particles, resulting in a further inward and exiting powder transfer. The decrease in the tangential gas velocity is indicated in
Figure 1b by the shift of point 3 to the dashed line level.
2.2. Principle of the Vortex
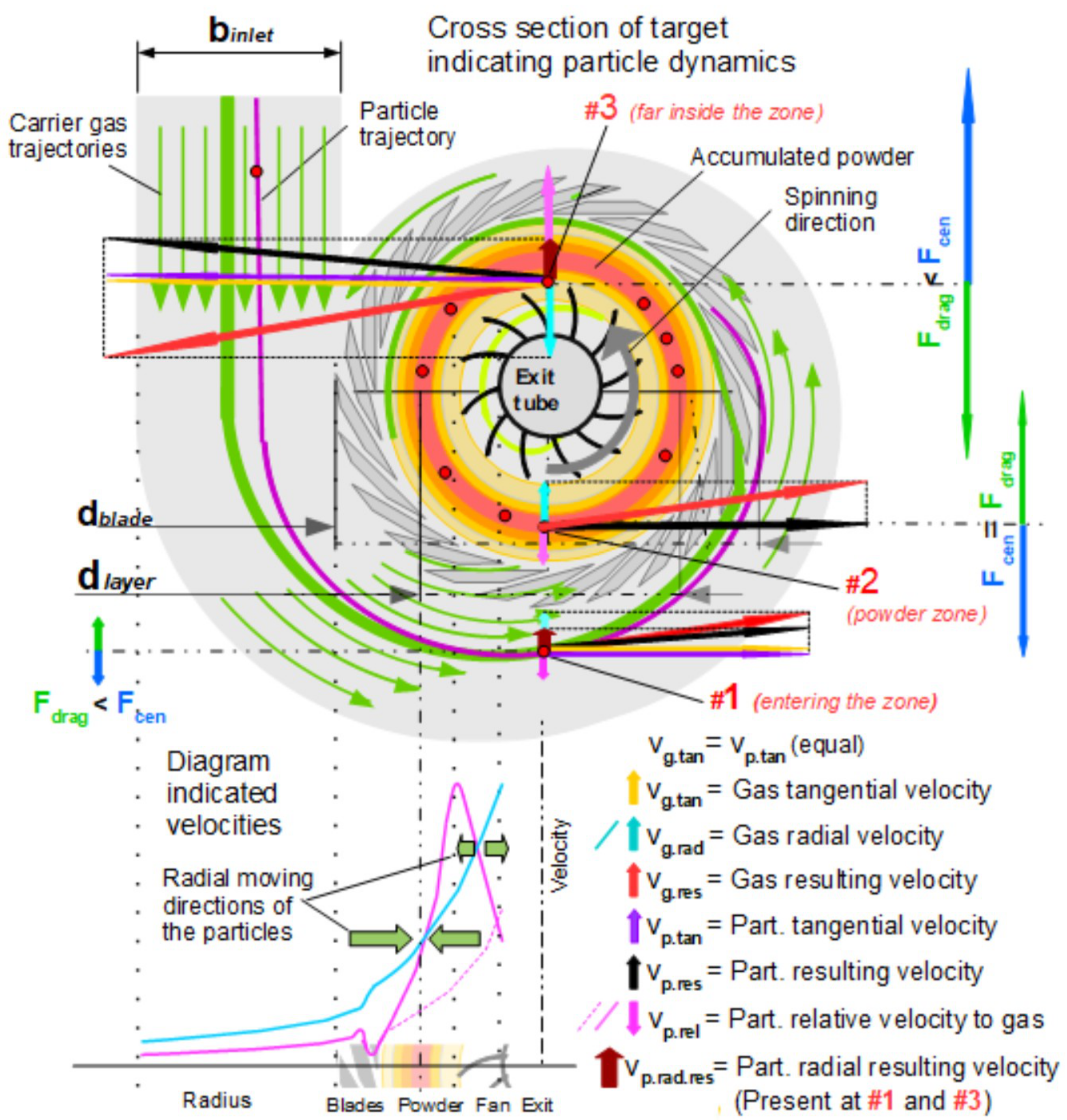
When the operation begins, the powder is dispersed and brought by the carrier gas into the indicated orange/red zone. In this zone, a balance of all forces in the radial direction must be achieved. The carrier gas rotation induces a centrifugal, a buoyant, and a drag force on the particles. The drag force is related to the particle’s drift velocity relative to the gas.
For the particles present in the balanced zone, as illustrated in
Figure 2, radial forces are expressed by Equation (1):
where
Fcen is the centrifugal force,
Fdrag is the drag force, and
Fbuo is the buoyant force.
The main expression for
Fcen is:
where
is the particle’s mass (kg),
is the average powder layer diameter, and
vg.tan is the entering gas velocity equal to the quotient of gas volume flow rate and cross-section of gas inlet.
Calculating drag force
Fdrag—on the expected micrometer-sized particles moving in viscous gas—can be described by Stokes’ law, which is accurate in a gaseous environment with a Reynolds number of Re ≤ 0.1. For particles having Reynolds numbers of Re ≤ 1.0, Stokes’ law remains a proper approximation [
6]. Preliminary calculations showed that the range of interest for the particle’s size was smaller than 10 μm, while the differential or relative velocities to the carrier gas were expected to be ~1.0 m/s. The Reynolds number verification was carried out for circulating helium gas in the irradiation chamber at a gas density of
ρg = 1.25 kg/m
3 (≈ 7E + 05 Pa, 300 K) and a dynamic viscosity of μ = 2.1E − 05 Pa·s. Particle calculations in the expected ranges of size and velocity (
dp < 10 μm,
vp.rel ≈ 1.0 m/s) by Equation (3),
resulted in Reynolds numbers of
Rep < 0.5. Herein,
μ is the dynamic viscosity of the carrier gas,
dp is the particle diameter (m),
ρg is the gas density (kg/m
3), and
vp.rel is the differential velocity of the particles relative to the gas. The dynamic viscosity’s temperature dependency was investigated and determined to be of minor significance for this study.
The drag formula for low differential velocities is expressed by:
where
feff is a factor for irregular particle surface condition.
The next equation shows the balance of buoyant force
Fbuo and drag force
Fdrag equal to the centrifugal force
Fcen by:
where
dlayer is the average diameter of the intended powder zone inside the blades, and
vg.tan is the tangential gas velocity. The expressions
fp and
feff are correction factors for the particle’s density and surface roughness, respectively. The variables
ρg and
ρp are the densities (kg/m
3) of gas and particles, respectively.
The extraction of the particle’s velocity relative to the gas results in Equation (6):
Of course, Equation (6) can be used for areas other than the balanced zone by redefining the quantity dlayer by a new expression for the diameter or twice the radius.
Particles not exceeding a certain size or diameter will be transferred inward by the carrier gas, as indicated by the small brown radial resulting velocity vector
vp.rad.res (
Figure 2, #1).
The inward-spiraling carrier gas has a radial velocity component
vg.rad (light blue arrow) that is related to gas velocity
vg.tan, quotient of the indicated housing dimensions
binlet, and the circumference of the blade’s configuration in the cochlea (
Figure 2, #1). Position #2 indicates the location of equal forces without the presence of a brown radial resulting velocity vector
vp.rad.res. Enhanced gas spinning far inside the zone (position #3) results in a velocity vector
vp.rad.res directed outward. Green block arrows in the diagram show the particles’ radial moving directions.
Density of the powder material is related to its porosity. Therefore, the factor fp is defined and estimated to be between 0.5 and 0.9. The shape and (irregular) surface finish correction factor feff represents the multiplying factor for the diameter dp. The factor feff varies from 1.0 for a smooth surface to higher values for irregular surfaces. The size, density, and surface finish are surely affected by the preparation of the powder. A preparation procedure must be developed to determine the optimal range of the powder’s size that can be applied for injection.
The purpose of carrier gas circuits is to transfer the dissipated heat induced by the beam outside the target system. When the maximum allowed temperature rise, ΔTgas, and circuit pressure of the carrier gas are defined for an expected beam power load tot (Watt), the mass flow rate ṁg (kg/s) and volume flow rate fl (m3/s) of the gas cooling can be calculated.
2.3. Stopping Power, Ranges, and Beam Features
To model the system, two radionuclide production routes,
68Zn(p,n)
68Ga and
100Mo(p,2n)
99mTc, were taken into consideration. For determining the design, the significant factors are the accelerated ion energy at the entrance, the projected ranges related to the electronic and nuclear (minor) stopping powers, and the lower threshold energy for the considered nuclear reaction [
7,
8].
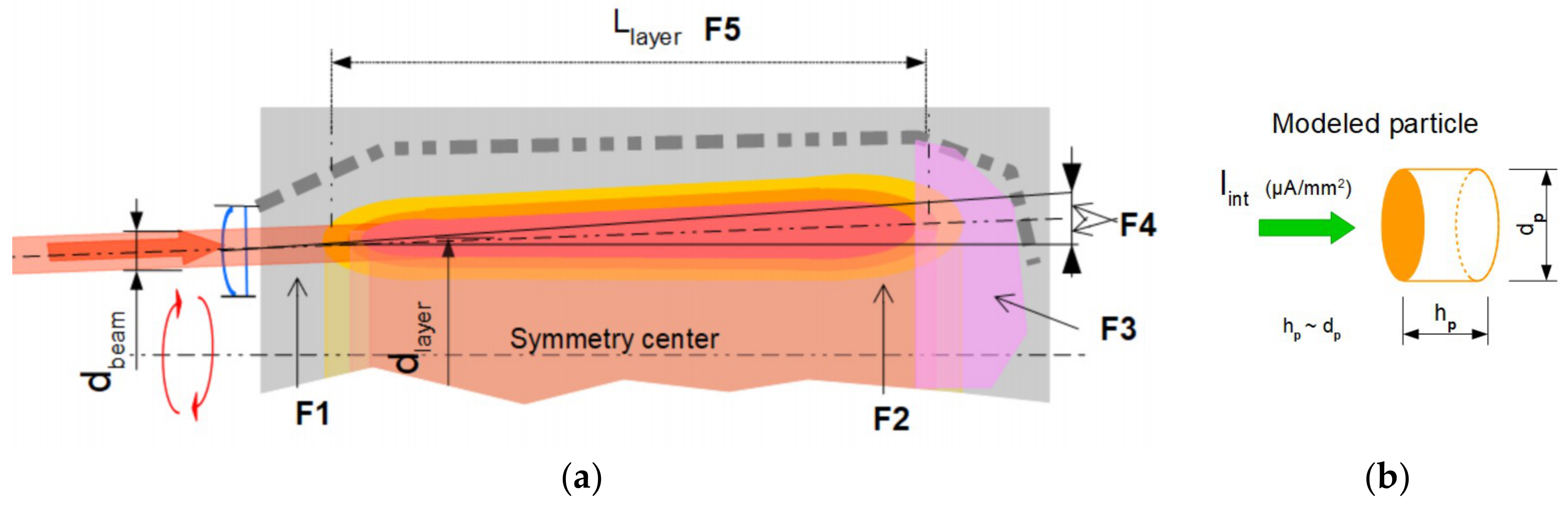
The ion beam, which enters the assembly nearly parallel to the central assembly’s symmetry axis, is intended to pass the full length L
layer of the mixed powder-in-gas layer. The powder-in-gas mass thickness (i.e., g/cm
2) should correspond closely to the values of known thick targets. The rest of the energy from the ion beam, assumed to be less than the specific nuclear reaction threshold energy, dissipates at the end section of the blades. The ion energy losses due to scattering at the entrance window, the carrier gas, mixed powder-in-gas layer, and blades are defined by Equation (7):
where ΔE
havar and ΔE
gas.1 are the energy losses in the window and the first section of the carrier gas, respectively. Generally, beam scattering and energy loss ΔE
gas.1 in the carrier gas are expected to be minor. The expression (ΔE
mat + ΔE
gas.2)
mixed is the ion beam energy loss due to both dispersed powder ΔE
mat and carrier gas ΔE
gas.2 in the same volumetric region. The relative contribution of the latter is much lower than the former.
For a technical assessment of the concept, the maximum temperature rise of the powder particles was estimated. Temperature rise depends on the energy level of the local proton beam hitting the particles. For a particle at the start of the layer near the target’s entrance, energy loss will be significantly lower than that for a particle at the end of the passed powder-in-gas layer (L
layer). Otherwise, beam intensity (μA/mm
2) at the entrance is significantly higher compared to when it is further “away” inside the irradiation chamber. To account for worst-case scenario, we calculated the temperature rise of a cylindrical-shaped particle (
Figure 3b), with an energy loss at the maximum stopping power at the top of the Bragg peak. Therefore, the beam intensity was calculated at the end of the powder-in-gas layer and supported by ion range and scattering (SRIM) calculations [
7,
8,
9].
A particle’s passage (in a static beam) driven by the tangential velocity
vg.tan occurs in a few milliseconds, while particle heating occurs instantly in tens of microseconds. The heating and convective cooling of a particle reach equilibrium at a differential temperature Δ
Ttr relative to the gas. The maximum dissipated ion energy ΔE
max in MeV per powder particle (1 eV = 1.602E − 19 J), with the diameter
dp and density
ρp, is by approximation:
where
SPmax is the maximum mass stopping power at the Bragg peak in MeV·cm
2/gr. The dissipated beam power
in a powder particle is:
where
Iint.static is the beam intensity in μA/mm
2 (or μC/(s·mm
2)), which corresponds to the accelerated ion particle’s ‘flow rate’ per square millimeter.
The maximum powder particle differential temperature Δ
Ttr.staic relative to the gas is then:
where
Ap is the cylindrical particle surface divided by two, given the assumption that only the front-half of the particle’s surface is cooled.
Otherwise, when the maximum for the differential temperature Δ
Ttr.max is set for the worst-case scenario of energy loss due to the mass stopping power
SPmax at the “Bragg peak” for a known particle diameter
dp and density
ρp, the maximum allowed beam intensity can be calculated by the following formula:
where
Iint.static.max is the maximum for the static flat-top beam profile, and
hHe is the heat transfer coefficient (W/m
2·K), which is determined by gas flow data and explained in the discussion.
The flat-top beam profile reduces the damaging effects of hotspots on the (2 × 15 μm Havar) windows and allows a higher beam power while keeping the maximum allowed peak current density noted in the introduction (5 μA/mm
2) unchanged. Further decrease in beam intensity or a higher allowed total beam power can be established by sweeping the flat-top beam around the assembly’s symmetrical center. Sweeping around the center further reduces the window’s heat stress as well as the particle heating. Preliminary calculations showed that due to the instantaneous heating of powder particles, a beam sweeping frequency of 1 kHz results in a significant reduction in the particle’s differential temperature Δ
Ttr.
Figure 3a shows an impression: