Abstract
In this work, we report on tests performed with an experimental apparatus prototype based on a broad-energy germanium detector aimed at investigating topical, foundational issues in quantum mechanics: i.e., possible violations of the spin-statistics connection and models of dynamical wave function collapse. Our recent phenomenological analyses demonstrated the importance of pushing the research of new physics signal, predicted in these fields, to an energy range below 10 keV. We describe the development of the dedicated data acquisition system and of the pulse shape discrimination algorithm, which have already allowed us to get a factor two improvement in the lower energy threshold. Future plans are discussed to further improve the lower energy threshold to the level of a few keV.
1. Scientific Motivation
The VIP-2 (VIolation of the Pauli exclusion principle-2) collaboration is performing high-sensitivity experiments in the extremely low background environment of the Gran Sasso underground laboratories of INFN (LNGS), with the aim of testing foundational issues in quantum gravity and quantum mechanics. In particular, VIP-2 is testing the spin-statistics connection for electrons and models of dynamical wave function collapse. Recent phenomenological investigations of these models pointed to the need to perform surveys in the X-ray domain and to search for a signal related to new physics in the energy range below 10 keV, as described in the following sections.
1.1. Spin-Statistics Violation and Quantum Gravity Models
The Pauli Exclusion Principle (PEP), which forbids fermions to occupy the same quantum state, is one of the main pillars of science. The PEP is a consequence of the Spin-Statistics Theorem (SST) [1], and since the SST is based on the assumption of Lorentz invariance, it is related to the fundamental symmetries and structure of space–time. Several quantum gravity frameworks foresee non-commutativity of the space–time coordinates close to the Planck scale, thus deforming the Lorentz algebra at the very fundamental level. The connection of Non-Commutative Quantum Gravity (NCQG) models with both string theory and loop quantum gravity has been extensively studied in the literature (see, e.g., refs. [2,3]). In this framework, it has been recently demonstrated that NCQG models predict violations of PEP that depend on the energy scales peculiar to the models under scrutiny [4].
The VIP-2 collaboration is performing extreme-sensitivity searches of PEP-violating atomic transitions, which has proven to test NCQG models at unexpectedly high non-commutativity energy scales [5,6]. In particular, the most commonly adopted model, -Poincaré [4], was excluded by our collaboration up to one-tenth of the Planck scale [5]. The result was achieved by searching for signals of atomic Kα and Kβ PEP-violating transitions in an ultra-radio-pure Roman lead target surrounding a High-Purity Germanium detector (HPGe).
Our aim is to test the -Poincaré model up to the Planck scale by improving the sensitivity by at least one order of magnitude with respect to our previous measurement. The strategy is to use a Broad-Energy Germanium detector (BEGe) as an active target. The peculiar electric field configuration of the BEGe, coupled to an innovative pulse shape discrimination technique, will allow us to reject electronic noise and multi-site background events (energetic photons releasing energy over a broad region of the crystal), pushing the lower energy detection limit to a few keV. We will search for Kα and Kβ PEP-violating transitions in the Ge crystal itself, thus exploiting a gain of about four orders of magnitude in the detection efficiency. Considered that the standard Kα transitions in Ge are located around 9.9 keV and the corresponding PEP-violating transitions are shifted downwards in energy by about 0.3 keV, a lower energy threshold of about 6 keV is needed. Moreover, performing a scan of the (limits of the) spin-statistics violation probability over the periodic table is an important task in general [7], not only for testing predictions in the quantum gravity framework (where the probability explicitly depends on the energy of the atomic transition under test) but also for testing other types of PEP violations. A discussion of other PEP violation models and related experimental tests is given in ref. [8]. Important recent research in these directions has been performed (see, e.g., [9,10,11]), and new research is under development [12].
1.2. Spontaneous Radiation from Wave Function Collapse Search in the Few-keV Regime
The reason why quantum properties, most notably the superposition principle, do not extend to the macroscopic world has been debated since the birth of quantum theory (QT) [13]. Dynamical collapse models address the spontaneous disappearance of the superposition—with the increasing mass of the object—as due to the friction between the linearity and unitarity of the Schrödinger equation and the non-linear and stochastic nature of the wave–packet reduction principle [14]. Accordingly, an intense theoretical effort was devoted to develop consistent non-linear and stochastic modifications of the Schrödinger dynamics, such as solving the measurement problem while preserving the quantum mechanical predictions for microscopic objects. The two major approaches are Continuous Spontaneous Localization models (CSLs) [15,16,17,18,19] and the Diósi–Penrose model (DP) [20,21,22,23,24]. An unavoidable effect related to spontaneous collapse consists of a faint electromagnetic radiation emission, called spontaneous radiation, which is not predicted by the standard QT. Spontaneous radiation is a consequence of the intrinsic randomness of the dynamical collapse and is rooted in the necessity to avoid faster-than-light signaling [25]; quantum systems are subject to diffusive motion, which corresponds to the emission of radiation from their charged constituents [26].
The experimental study of the spontaneous radiation phenomenon produced severe constraints on both CSL and DP (see, e.g., the recent works [27,28,29,30]) by setting the strongest limits on their characteristic parameters over broad ranges of the parameter spaces. In particular, the simplest (Markovian) formulations of the models, which assume a white correlation function for the stochastic noise inducing the collapse, are close to being ruled out when combining the experimental bounds with theoretical considerations. Refined dynamical reduction models embedding dissipative and non-Markovian effects are being developed [31,32,33,34,35,36,37]. In particular, non-Markovian models require the introduction of a cutoff frequency in the noise spectrum; hence, their investigation requires a systematic scan of the spontaneous radiation as a function of the decreasing energy. A survey in the energy range (1–3.8) MeV was performed to test Markovian collapse models in refs. [27,28,30], in which the expected spontaneous radiation rate by atomic systems was derived by assuming spontaneous photons were emitted in the -ray regime, and the emission spectra were then compared to the radiation spectrum measured by a High-Purity Germanium detector (HPGe). Markovian models were also experimentally tested in the lower-energy X-ray domain (few tens of keV) in [38] and, more recently, in [29], where the adopted spontaneous radiation rate was approximated.
The general expression of the spontaneous radiation rate for both white and non-Markovian collapse models and also valid in the X-ray domain was recently derived in [39], wherein new features were predicted:
- The general spontaneous emission rate differs from the approximated one in the range (1–100) keV;
- In the same energy range, the spontaneous radiation energy spectra also depend on the atomic structure of the emitter;
- The CSL and the DP rates significantly differ (relative difference of more than 10%) in the range (1–10) keV.
The importance of testing non-Markovian dynamical collapse at lower energies and the prediction of a rich phenomenology associated with the spontaneous radiation in the X-ray energy domain motivate optimization, in the view of a dedicated measurement, of a setup based on a BEGe detector, which is described in this work.
2. The Experimental Setup
The setup is based on a cylindrical BEGe (model BE3830 Canberra, 71 mm diameter, 30 mm thickness, active area 3800 mm2). A section of the detector is schematically represented in Figure 4, top left. The acquisition and elaboration of the signals generated by the BEGe detector are performed by means of a CAEN Flash-ADC (FADC), model DT 5743, with the following main features: resolution of 12 bits, maximum sampling rate of 3.2 GS/s, analog input impedance of 50 Ω, and a 2.55 Vpp dynamic range.
After a preliminary configuration realized at the Laboratori Nazionali di Frascati (LNF) of INFN, the BEGe front-end system (i.e., the FADC and a PC for data acquisition and elaboration using the CAEN’s dedicated software “WaveCatcher” (https://www.caen.it/products/wavecatcher/, accessed on 2 January 2024)) was delivered and installed at LNGS in September 2020.
In order to enhance the spectroscopic capability of the BEGe detector, the device is cooled down to 80 K by means of liquid N2 (cryostat model: 7915-30-CD-ULB Canberra), contained in a dedicated dewar, and is surrounded by two layers of Cu and Pb shielding, which suppress the residual background. A Canberra preamplifier (model 2002C) provides polarization of the device through a dedicated HV line. The detector is characterized by P-I-N doping. The charge-sensitive circuit has RC feedback, and the bias voltage is +4500 V. The detector is operated above the depletion voltage: that is +4000 V. The current signals are read directly from the p+ contact side of the detector. The front-end circuitry and readouts are all commercial. The signals associated with the electrons collected at the detector anode are sent to the dedicated timing output, which has 50 impedance, after a pre-amplification stage equivalent to 500 mV/MeV. At this stage, the signals provided by the preamplifier are directly fed to the 50 impedance input of the FADC through a 50 cm cable in order to avoid a processing stage that alters signal integrity.
A first data-taking period was performed in order to test the stability of the system and the background conditions during the last months of 2020. The LabVIEW 2023 software was employed for the first raw noise rejection. The fast ADC starts an acquisition when a voltage signal that exceeds the voltage trigger threshold is present at its input. Raw data from the digitizer are stored on the disk. Then, pulse shape analysis is performed offline on the files saved on disk using a Python package with the NumPy library. After successful characterization/configuration activity, a data-taking campaign of about three months was performed during the period of July–October 2021 in order to collect enough statistics for a preliminary evaluation of the system’s spectroscopic response.
2.1. Pulse Shape Discrimination Analysis
Events selection is based on a dedicated pulse shape discrimination algorithm. Pulse shape discrimination allows us to select analog signals from germanium detectors that did not originate from electronic noise or multi-site events. Electronic noise together with the microphonic background (see Section 2.3) are the dominant sources of background in the range of a few tens of keV; multi-site background events are dominant in the -ray range. Dedicated algorithms typically require extensive fine tuning and calibration; moreover, different detectors exhibit different characteristics. The software that we optimized is based on both amplitude and shape analysis and performs a three-step selection:
- first, a comparison of the fluctuations mean values at pulse beginning and end is performed (i.e., the mean value of the first and the last 100 points of the pulse). Moreover, the maximum pulse height is compared with the mean value at the end of the pulse.
- The second step consists of discrimination, with respect to linear behavior, at the end of the pulse.
- As a third step, pulse derivative selection is performed, which rejects multi-site events based on both the width and discrimination (using the error function template).
Electronic noise is an important source of distortion in BEGe pulses and is increasingly relevant for low-energy events. To allow robust rejection of noise events, in Step 1, we also compare the maximum pulse height with the mean value at the end of the pulse. Since the pulse decay time is typically much slower than the rise time for the candidate events, we expect the maximum pulse height to be close to the height at the end. In noise events for which there is no real energy deposit, this is not the case. Step 2 allows discrimination of noise events that, by chance, passed the first step. In Step 3, we discriminate between single- and multi-site events. While the former arise from the photon’s interaction and energy deposit inside the active volume of the detector, the latter originates from multiple-particle interactions, which are associated mainly with background events. These can be discriminated due to the presence of a time-distance between single components. In our discrimination strategy, a single-site event presents a pulse for which the derivative is compatible with a Gaussian peak; in cases with more components, more than one peak will be present.
As an example, in the top panel of Figure 1 is represented a typical multi-site event that passes the second condition but is cut by the third one. A signal event that is selected by the algorithm is shown in the bottom panel of Figure 1.
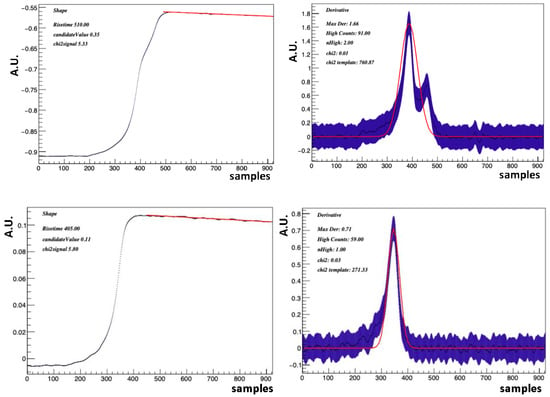
Figure 1.
Top panel: a typical multi-site event that would survive selection cut 2 but not selection cut 3. Bottom panel: a signal event that has been selected by the algorithm. Figures on the right correspond to the derivatives of the corresponding curves on the left. The full acquisition time window is 2560 ns, one acquisition corresponds to 1024 samples, and the sampling rate is 400 MHz, so one sample corresponds to 2.5 ns.
We are currently developing and testing an improved pulse shape discrimination procedure, based on convolutional neural networks, trained on a dataset of simulated pulse shapes from single site and multi-site events.
The calibrated energy spectrum for the selected data sample is shown in Figure 2 right. The calibration was performed using the peaks present in the spectrum; these originated from the decay chains of 238U and 232Th and are 210Pb at 46 keV, 212Pb at 239 keV, 214Pb at 295 keV, and 352 keV, 214Bi at 609 keV. The calibration line is shown in Figure 2 left. The energy resolution was determined to be 2.2 keV (FWHM) at the 210Pb peak.
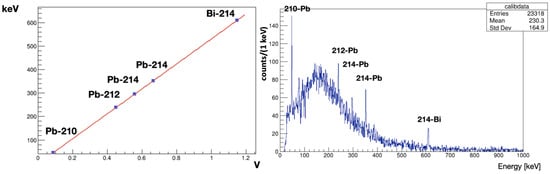
Figure 2.
Left: the obtained energy calibration line. Right: the energy-calibrated spectrum.
The analysis of the data acquired in 2021 revealed an intrinsic low energy threshold of about 25 keV (see Figure 2). This is caused both by external disturbances on the system and by the intrinsic electronic noise of the digitizer front-end, that behaves as a voltage noise generator of about 4mV pp, at the input of the digitizer itself. An exemplifying event is shown in Figure 3, where a peak-to-peak noise amplitude of about 4 mV is evident over a signal of about 18 mV. Considered that the investigation of an eventual PEP-violating Kα transition in Ge requires a lower energy threshold of at least 6 keV (corresponding to about 3 mV), the Data Acquisition (DAQ) system was improved as described in Section 2.2.
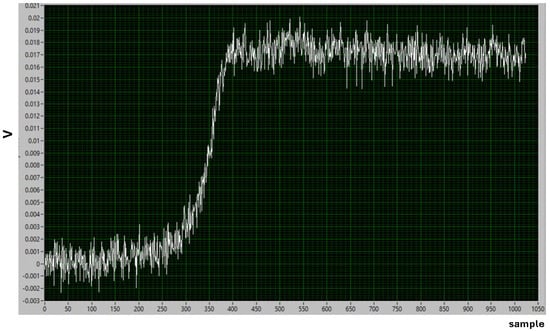
Figure 3.
An event corresponding to the data-taking period of July–September 2021 is shown, in which the intrinsic noise of the digitizer at 4 mV is evident.
2.2. Upgrade of the the Data Acquisition System
Further improvement to the experimental apparatus was addressed to solve the aforementioned problems and aimed to reach a lower energy threshold of a few keV. In order to improve the signal-to-noise ratio of BEGe electrical impulses, which correspond to photons of a few keV, the DAQ system was upgraded as described below:
- A careful analysis of the sources of electrical noise highlighted that the connection via USB cable between the computer and Fast ADC is the main origin. To address this problem, we decided to replace the USB cable connection with a fiber optic connection. Moreover, in order to further reduce the noise coming from the power supplies, the power supplies provided with the instrumentation (Fast ADC and preamplifier) were replaced with special power supplies with very low residual noise. And finally, careful distribution of the electrical grounding was also studied.
- A second step was the installation of a very-low-noise broadband amplifier (CAEN A1423B) with a voltage gain of 10 at the input of the Fast ADC to further improve the overall behavior of the DAQ system.
After completion of the DAQ system upgrade (which is schematically represented in Figure 4), two data-taking runs were performed during the periods of February–October 2022 and February–June 2023.
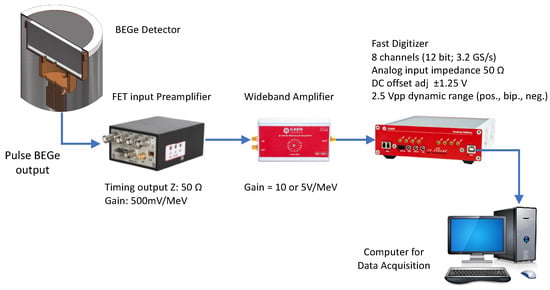
Figure 4.
Block diagram of the upgraded BEGe DAQ system.
The effect of the wide-band amplifier is to increase the amplitude of the BEGe signals corresponding to photons of a few keV. As a consequence, the ratio of the signal over the intrinsic electronic noise of the digitizer was greatly improved. The reduction in the noise induced on the germanium sensor is clearly visible in Figure 5, which represents an event collected during the 2022 data-taking run and has an amplitude comparable to that of the signal shown in Figure 3. The peak-to-peak noise is now reduced to the level of about 0.5 mV. The different shape of the event is caused by the shaping time introduced by the amplifier. The effect of the amplification stage on the improved, CNN-based, pulse shape discrimination is currently under testing.The analysis of the 2022 data also revealed a further - external -background source, which was magnified by the amplification stage: namely, a microphonic background, which is described in Section 2.3
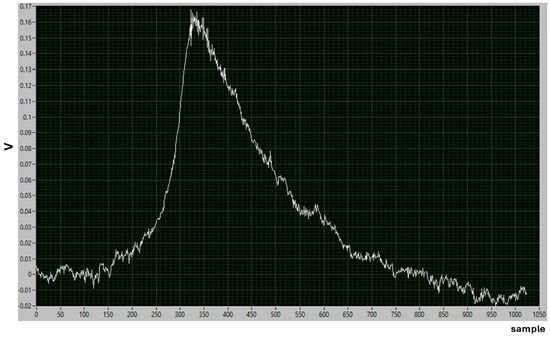
Figure 5.
An event acquired during the 2022 data-taking period is shown: the peak-to-peak electronic noise corresponds to about 0.5 mV.
2.3. Analysis of the Microphonic Background
The analysis of the 2022/2023 dataset demonstrated a further reduction in the energy threshold to 13 keV. Lower energies are not accessible, as the system is affected by an overwhelming microphonic noise due to flooring vibrations, sound, and other environmental noise. This is caused by the fact that the germanium crystal is a resonant system, and it responds to external mechanical solicitations with an electric signal at the exit of the preamplifier characterized by a resonance frequency of 6 MHz. The amplitude of the electric signal is roughly linear with the intensity of the mechanical solicitation. A typical microphonic noise event is shown in Figure 6 left; on the right of the same figure, a signal event is represented with the microphonic background superimposed.
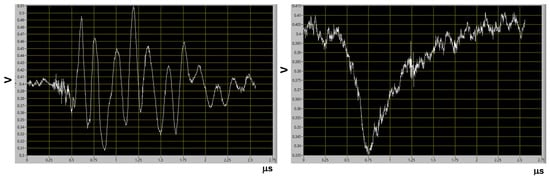
Figure 6.
Left: a microphonic noise event is shown. Right: a signal event is represented with the microphonic background superimposed.
A trigger threshold of 13 keV was fine-tuned to reject most of the environmental background events. In order to access lower energies, the amplitudes of the mechanical and sound solicitations need to be reduced. With the aim of optimizing the characteristics of an isolation system for the experimental setup, accurate measurement of the microphonic background in the LNGS laboratory was performed during the period of 28–30 June 2023. The setup consisted of two geophones (model CMG-40T) and two accelerometers (model PCB-393B12), which allowed us to measure the vertical GM from 0.1 Hz to 100 Hz and the horizontal GM from 0.1 Hz to 50 Hz. An NI PXI-4472B 8-channel dynamical signal acquisition system was used, characterized by 24-bit resolution and a 102.4 kS/s maximum shaping rate.
The results from a measurement of about three hours is shown in Figure 7 and represents the displacement power spectral density of one accelerometer. This confirms that the floor of the laboratory is very noisy and evidences, in particular, a floating floor with prominent peaks at frequencies of about 50 Hz, 100 Hz, and 180 Hz.
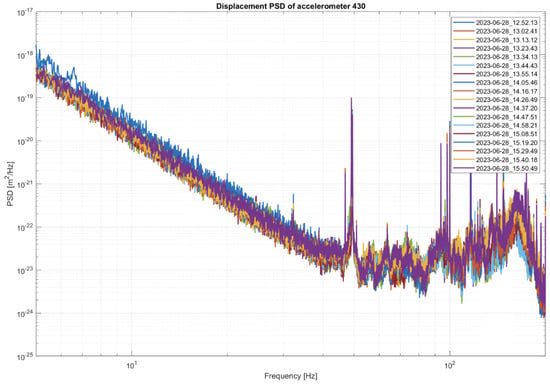
Figure 7.
The results of a long-term measurement of the environmental noise in the laboratory is shown. The plot reports multiple measurements performed with one accelerometer and taken at consecutive times.
Based on the results of these measurements, an isolation system was designed to decouple the detector from the environmental vibrations. The setup will be held on an aluminum slab that is sustained by pneumatic isolators and will be surrounded by a soundproof box that will also act as a Faraday cage. The pneumatic spring is equipped with level adjustment and is characterized by a low natural frequency of 1.5 Hz and high damping. The characteristic attenuation curve of the system in dB is represented in Figure 8 as a function of the ratio between the mechanical excitation frequency and the resonance frequency of the attenuation system which is 1.5 Hz. The plot shows that for a dominant frequency of the mechanical background that is greater than about 4.5 Hz (which is the case for our laboratory), the system provides attenuation that is greater than 20 dB, corresponding to a reduction in the mechanical background by a factor greater than 10. The improvement in the signal-over-microphonic-background ratio will allow us to reduce the trigger threshold by a factor greater than 10 and, hence, achieve a lower energy threshold in the order of 1 keV.
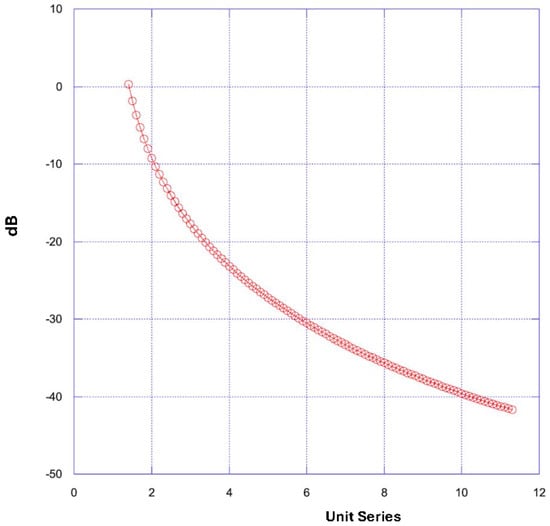
Figure 8.
The attenuation curve of the optimized isolation system is shown in dB and is a function of the ratio between the mechanical excitation frequency and the resonance frequency of the system which is 1.5 Hz. The curve is theoretical and is taken from an application note present in the Angst + Pfister pneumatic suspension catalog.
3. Conclusions and Perspectives
The VIP-2 collaboration is developing an experimental apparatus devoted to testing foundational issues in Quantum Mechanics: in particular, spin-statistics violations for electrons, connected with space-time non-commutativity in Quantum Gravity, and the spontaneous wave function collapse. A characteristic electromagnetic radiation signature is expected for both of the aforementioned models in the energy range of a few keV. This work describes our ongoing activity that aims to optimize a test setup based on a broad-energy germanium detector to be capable of reaching a lower energy threshold of the order of keV. We already obtained a lower energy threshold of 13 keV, and the corresponding datasets, which were collected in 2022 and 2023, are currently being analyzed to set preliminary constraints on new features predicted in models of dynamical wave function collapse and to optimize the sensitivity of the final setup. A further upgrade of the experimental setup is being performed and aims to reduce prohibitive microphonic noise in the range of a few keV, which will allow us to reach the goal.
Author Contributions
Conceptualization, C.C., A.C., M.L., K.P. and F.N.; methodology, C.C., A.C., M.L., M.M., K.P., F.N. and S.T.; software, M.M., F.N., A.P., N.B., R.D.G. and S.M.; validation, A.C., D.L.S., S.T., M.L. and F.N.; formal analysis, N.B., A.P., A.C., L.D.P., R.D.G., M.I., F.N., A.S., D.L.S., F.S. (Florin Sirghi), K.P. and C.C.; investigation K.P., M.B. (Massimiliano Bazzi), M.B. (Mario Bragadireanu), M.C., A.C., L.D.P., R.D.G., C.G., M.I., M.L., S.M., J.M., M.M., F.N., A.S., F.S. (Francesco Sgaramella), D.L.S., F.S. (Florin Sirghi), O.V.D., J.Z. and C.C.; data curation, M.L., A.C., M.M., F.N., K.P., R.D.G. and C.C.; writing—original draft preparation, K.P., D.L.S., A.C. and C.C.; writing—review and editing, K.P., M.B. (Massimiliano Bazzi), M.B. (Mario Bragadireanu), M.C., A.C., L.D.P., R.D.G., C.G., M.I., M.L., S.M., J.M., M.M., F.N., A.P., A.S., F.S. (Francesco Sgaramella), D.L.S., F.S. (Florin Sirghi), S.T., O.V.D., J.Z. and C.C.; visualization, A.C., F.N., D.L.S. and S.T.; supervision, C.C., A.C., M.L., K.P. and F.N.; project administration, C.C.; funding acquisition, C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This publication was made possible through the support of the INFN institute and Centro Ricerche Enrico Fermi—Museo Storico della Fisica e Centro Studi e Ricerche “Enrico Fermi” Institute. We acknowledge the support of grant 62099 from the John Templeton Foundation. The opinions expressed in this publication are those of the authors and do not necessarily reflect the views of the John Templeton Foundation. We acknowledge support from the Foundational Questions Institute and the Fetzer Franklin Fund, a donor-advised fund of the Silicon Valley Community Foundation (grant Nos. FQXi-RFP-CPW-2008 and FQXi-MGB-2011), and from the H2020 FET TEQ (grant No. 766900). We thank the Austrian Science Foundation (FWF), which supports the VIP2 project with grants P25529-N20, project P 30635-N36 and W1252-N27 (doctoral college particles and interactions).
Data Availability Statement
The datasets presented in this article are not readily available because the data are part of an ongoing study.
Acknowledgments
We thank: the Gran Sasso underground laboratory of INFN, INFN-LNGS, and its Director, Ezio Previtali; the LNGS staff; and the Low Radioactivity laboratory for the experimental activities dedicated to high-sensitivity tests of the Pauli exclusion principle and wave function collapse.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pauli, W. The connection between spin and statistics. Phys. Rev. 1940, 58, 716. [Google Scholar] [CrossRef]
- Seiberg, N.; Witten, E. String theory and noncommutative geometry. J. High Energy Phys. 1999, 1999, 032. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Smolin, L.; Starodubtsev, A. Quantum symmetry, the cosmological constant and Planck-scale phenomenology. Class. Quantum Gravity 2004, 21, 3095. [Google Scholar] [CrossRef]
- Addazi, A.; Marcianò, A. A modern guide to θ-Poincaré. Int. J. Mod. Phys. A 2020, 35, 2042003. [Google Scholar] [CrossRef]
- Piscicchia, K.; Addazi, A.; Marcianò, A.; Bazzi, M.; Cargnelli, M.; Clozza, A.; De Paolis, L.; Del Grande, R.; Guaraldo, C.; Iliescu, M.A.; et al. Strongest Atomic Physics Bounds on Noncommutative Quantum Gravity Models. Phys. Rev. Lett. 2022, 129, 131301. [Google Scholar] [CrossRef] [PubMed]
- Piscicchia, K.; Marcianò, A.; Addazi, A.; Sirghi, D.L.; Bazzi, M.; Bortolotti, N.; Bragadireanu, M.; Cargnelli, M.; Clozza, A.; De Paolis, L.; et al. First Experimental Survey of a Whole Class of Non-Commutative Quantum Gravity Models in the VIP-2 Lead Underground Experiment. Universe 2023, 9, 321. [Google Scholar] [CrossRef]
- Okun, L. Possible violation of the Pauli principle in atoms. JETP Lett. 1987, 46, 529532. [Google Scholar]
- Elliott, S.; LaRoque, B.; Gehman, V.; Kidd, M.; Chen, M. An improved limit on Pauli-exclusion-principle forbidden atomic transitions. Found. Phys. 2012, 42, 1015–1030. [Google Scholar] [CrossRef]
- Arnquist, I.; Avignone, F., III; Barabash, A.; Barton, C.; Bhimani, K.; Blalock, E.; Bos, B.; Busch, M.; Buuck, M.; Caldwell, T.; et al. Search for charge nonconservation and Pauli exclusion principle violation with the Majorana Demonstrator. arXiv 2022, arXiv:2203.02033. [Google Scholar]
- Abgrall, N.; Arnquist, I.; Avignone, F., III; Barabash, A.; Bertrand, F.; Bradley, A.; Brudanin, V.; Busch, M.; Buuck, M.; Caldwell, T.; et al. New limits on bosonic dark matter, solar axions, pauli exclusion principle violation, and electron decay from the Majorana demonstrator. Phys. Rev. Lett. 2017, 118, 161801. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Cappella, F.; Cerulli, R.; Dai, C.; d’Angelo, A.; He, H.; Incicchitti, A.; Kuang, H.; Ma, X.; et al. New search for processes violating the Pauli exclusion principle in sodium and in iodine. Eur. Phys. J. C 2009, 62, 327–332. [Google Scholar] [CrossRef]
- Piscicchia, K.; Bartalucci, S.; Bertolucci, S.; Bazzi, M.; Borghi, G.; Bragadireanu, M.; Capoccia, C.; Cargnelli, M.; Clozza, A.; Del Grande, R.; et al. High Sensitivity Pauli Exclusion Principle Tests by the VIP Experiment: Status and Perspectives. Acta Phys. Pol. A 2022, 142, 361–366. [Google Scholar] [CrossRef]
- Schrodinger, E. Die gegenwartige Situation in der Quantenmechanik. Naturwissenschaften 1935, 23, 807–812. [Google Scholar] [CrossRef]
- Bassi, A.; Ghirardi, G. Dynamical reduction models. Phys. Rep. 2003, 379, 257–426. [Google Scholar] [CrossRef]
- Ghirardi, G.C.; Rimini, A.; Weber, T. Unified dynamics for microscopic and macroscopic systems. Phys. Rev. D 1986, 34, 470. [Google Scholar] [CrossRef]
- Pearle, P. Reduction of the state vector by a nonlinear Schrödinger equation. Phys. Rev. D 1976, 13, 857. [Google Scholar] [CrossRef]
- Pearle, P. Toward explaining why events occur. Int. J. Theor. Phys. 1979, 18, 489–518. [Google Scholar] [CrossRef]
- Pearle, P. Combining stochastic dynamical state-vector reduction with spontaneous localization. Phys. Rev. A 1989, 39, 2277. [Google Scholar] [CrossRef]
- Ghirardi, G.C.; Pearle, P.; Rimini, A. Markov processes in Hilbert space and continuous spontaneous localization of systems of identical particles. Phys. Rev. A 1990, 42, 78. [Google Scholar] [CrossRef]
- Diósi, L. Gravitation and quantum-mechanical localization of macro-objects. Phys. Lett. A 1984, 105, 199–202. [Google Scholar] [CrossRef]
- Diósi, L. A universal master equation for the gravitational violation of quantum mechanics. Phys. Lett. A 1987, 120, 377–381. [Google Scholar] [CrossRef]
- Diósi, L. Models for universal reduction of macroscopic quantum fluctuations. Phys. Rev. A 1989, 40, 1165. [Google Scholar] [CrossRef] [PubMed]
- Penrose, R. On gravity’s role in quantum state reduction. Gen. Rel. Grav. 1996, 28, 581–600. [Google Scholar] [CrossRef]
- Penrose, R. On the Gravitization of Quantum Mechanics 1: Quantum State Reduction. Found. Phys. 2014, 44, 557–575. [Google Scholar] [CrossRef]
- Gisin, N. Stochastic quantum dynamics and relativity. Helv. Phys. Acta 1989, 62, 363–371. [Google Scholar]
- Donadi, S.; Ferialdi, L.; Bassi, A. Collapse dynamics are diffusive. Phys. Rev. Lett. 2023, 130, 230202. [Google Scholar] [CrossRef] [PubMed]
- Donadi, S.; Piscicchia, K.; Del Grande, R.; Curceanu, C.; Laubenstein, M.; Bassi, A. Novel CSL bounds from the noise-induced radiation emission from atoms. Eur. Phys. J. C 2021, 81, 773. [Google Scholar] [CrossRef]
- Donadi, S.; Piscicchia, K.; Curceanu, C.; Diósi, L.; Laubenstein, M.; Bassi, A. Underground test of gravity-related wave function collapse. Nat. Phys. 2021, 17, 74–78. [Google Scholar] [CrossRef]
- Arnquist, I.J.; Avignone, F.T.; Barabash, A.S.; Barton, C.J.; Bhimani, K.H.; Blalock, E.; Bos, B.; Busch, M.; Buuck, M.; Caldwell, T.S.; et al. Search for Spontaneous Radiation from Wave Function Collapse in the Majorana Demonstrator. Phys. Rev. Lett. 2022, 129, 080401. [Google Scholar] [CrossRef]
- Piscicchia, K.; Porcelli, A.; Bassi, A.; Bazzi, M.; Bragadireanu, M.; Cargnelli, M.; Clozza, A.; De Paolis, L.; Del Grande, R.; Derakhshani, M.; et al. A Novel Approach to Parameter Determination of the Continuous Spontaneous Localization Collapse Model. Entropy 2023, 25, 295. [Google Scholar] [CrossRef]
- Smirne, A.; Bassi, A. Dissipative continuous spontaneous localization (CSL) model. Sci. Rep. 2015, 5, 12518. [Google Scholar] [CrossRef] [PubMed]
- Di Bartolomeo, G.; Carlesso, M.; Piscicchia, K.; Curceanu, C.; Derakhshani, M.; Diósi, L. Linear-friction many-body equation for dissipative spontaneous wave-function collapse. Phys. Rev. A 2023, 108, 012202. [Google Scholar] [CrossRef]
- Adler, S.L.; Ramazanoğlu, F.M. Photon-emission rate from atomic systems in the CSL model. J. Phys. A Math. Theor. 2007, 40, 13395. [Google Scholar] [CrossRef]
- Bassi, A.; Dürr, D. On the electromagnetic properties of matter in collapse models. J. Phys. A Math. Theor. 2009, 42, 485302. [Google Scholar] [CrossRef]
- Adler, S.L.; Bassi, A.; Donadi, S. On spontaneous photon emission in collapse models. J. Phys. A Math. Theor. 2013, 46, 245304. [Google Scholar] [CrossRef]
- Bassi, A.; Donadi, S. Spontaneous photon emission from a non-relativistic free charged particle in collapse models: A case study. Phys. Lett. A 2014, 378, 761–765. [Google Scholar] [CrossRef]
- Donadi, S.; Deckert, D.A.; Bassi, A. On the spontaneous emission of electromagnetic radiation in the CSL model. Ann. Phys. 2014, 340, 70–86. [Google Scholar] [CrossRef]
- Piscicchia, K.; Bassi, A.; Curceanu, C.; Grande, R.D.; Donadi, S.; Hiesmayr, B.C.; Pichler, A. CSL collapse model mapped with the spontaneous radiation. Entropy 2017, 19, 319. [Google Scholar] [CrossRef]
- Piscicchia, K.; Donadi, S.; Manti, S.; Bassi, A.; Derakhshani, M.; Curceanu, C. Surprising results of a refined dynamical collapse spontaneous radiation study: CSL and gravity related collapse have distinctive features at atomic orbits wavelength scale. arXiv 2023, arXiv:2301.09920. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).