Superconductors without Symmetry Breaking
Abstract
1. Introduction
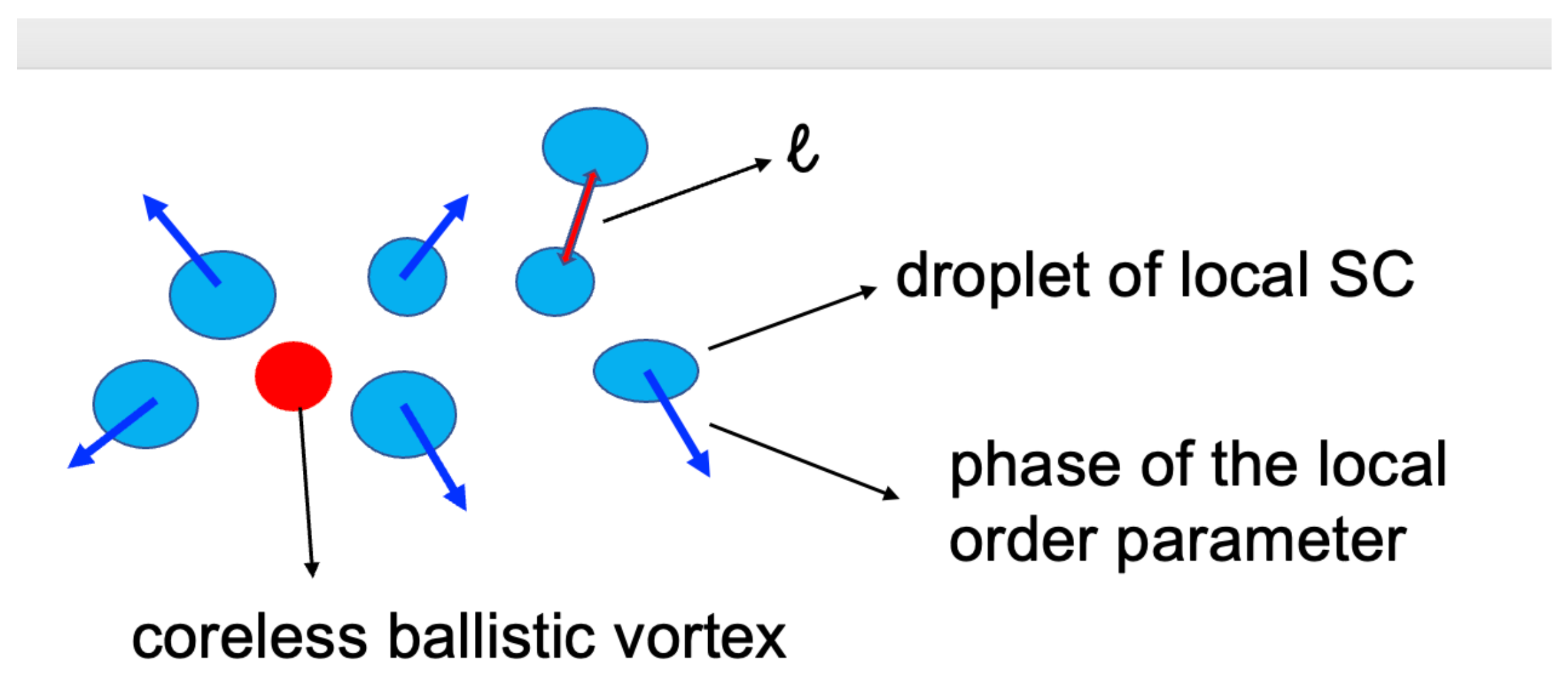
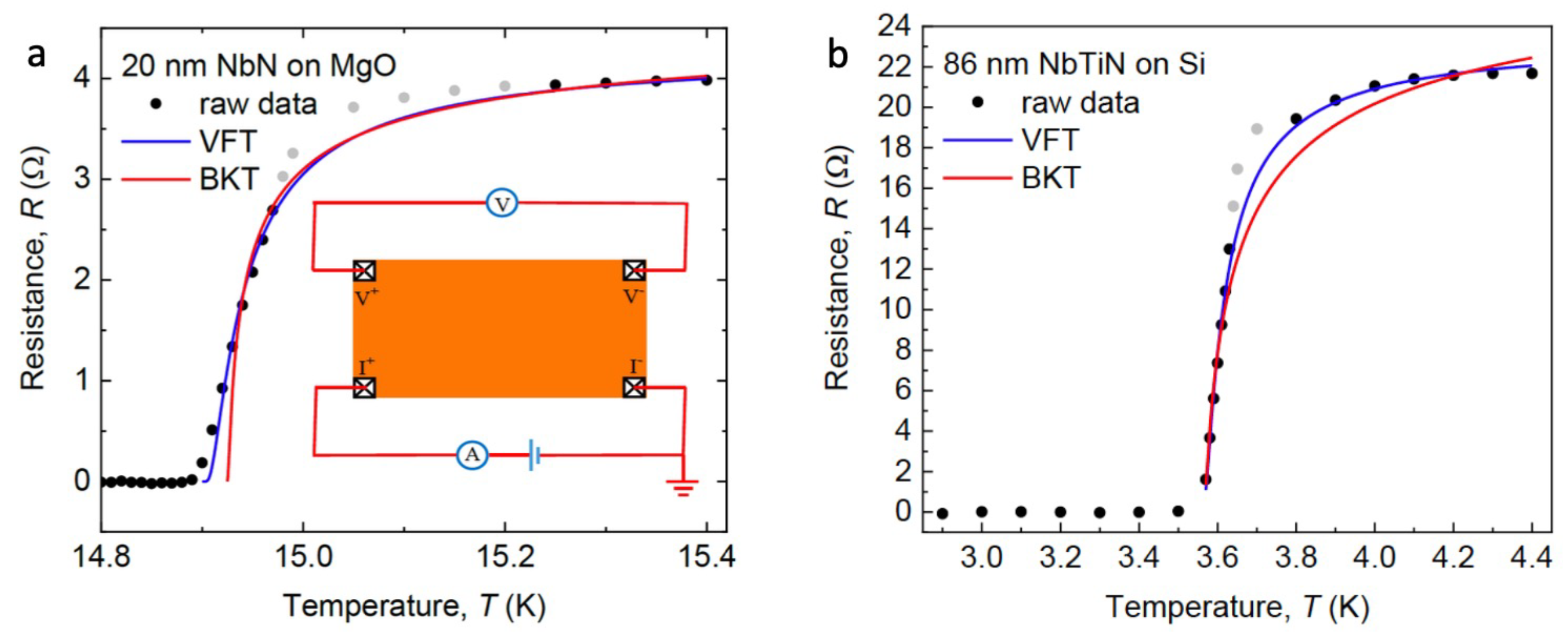
2. Vortices in Type-III Superconductors
3. Effective Gauge Theory Description of Type-III Superconductors
Funding
Conflicts of Interest
References
- Tinkham, M. Introduction to Superconductivity; Dover Publications: New York, NY, USA, 1996. [Google Scholar]
- Shimano, R.; Tsuji, N. Higgs Mode in Superconductors. Annu. Rev. Condens. Matter Phys. 2020, 11, 103–124. [Google Scholar] [CrossRef]
- Volkov, A.F.; Kogan, S.M. Collisionless relaxation of the energy gap in superconductors. Zh. Eksp. Teor. Fiz. 1973, 65, 2038–2046. [Google Scholar]
- Littlewood, P.B.; Varma, C.M. Amplitude collective modes in superconductors and their coupling to charge-density waves. Phys. Rev. B 1982, 26, 4883–4893. [Google Scholar] [CrossRef]
- Matsunaga, R.; Hamada, Y.I.; Makise, K.; Uzawa, Y.; Terai, H.; Wang, Z.; Shimano, R. Higgs Amplitude Mode in the BCS Superconductors Nb1-x Tix N induced by terahertz pulse excitation. Phys. Rev. Lett. 2013, 111, 057002. [Google Scholar] [CrossRef] [PubMed]
- Saipuddin, S.F.; Hashim, A.; Suhaimi, N.E. Type I and Type II Superconductivity. In Superconducting Materials; Slimani, Y., Hannachi, E., Eds.; Springer: Singapore, 2022. [Google Scholar]
- Onnes, H.K. The resistance of pure mercury at helium temperatures. Comm. Leiden. 1911, 28, 120. [Google Scholar]
- Abrikosov, A. The magnetic properties of superconducting alloys. J. Phys. Chem. Solids 1957, 2, 199–208. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. Am. Phys. Soc. 1957, 108, 1175–1204. [Google Scholar] [CrossRef]
- Diamantini, M.C.; Sodano, P.; Trugenberger, C.A. Superconductors with topological order. Eur. Phys. J. B 2006, 53, 19–22. [Google Scholar] [CrossRef]
- Diamantini, M.C.; Trugenberger, C.A. Higgsless superconductivity from topological defects in compact BF terms. Nucl. Phys. B 2015, 891, 401–419. [Google Scholar] [CrossRef]
- Diamantini, M.C.; Trugenberger, C.A.; Chen, S.Z.; Lu, Y.J.; Liang, C.T.; Vinokur, V.M. Type-III superconductivity. Adv. Sci. 2023, 1, 2206523. [Google Scholar] [CrossRef]
- Berezinskii, V.L. Destruction of long-range order in one-dimensional and two-dimensional systems having a continuous symmetry group. I. Classical systems. Sov. Phys. JETP 1970, 32, 493–500. [Google Scholar]
- Kosterlitz, J.M.; Thouless, D.J. Long range order and metastability in two dimensional solids and superfluids. (Application of dislocation theory). J. Phys. C Solid State Phys. 1972, 5, L124–L126. [Google Scholar] [CrossRef]
- Goldman, A.M. The Berezinskii-Kosterlitz-Thouless Transition in Superconductors. In 40 Years of Berezinskii-Kosterlitzthouless Theory; Jorge, J., Ed.; World Scientific Publishing Co.: Singapore, 2013; pp. 135–160. [Google Scholar]
- Minnhagen, P. The two-dimensional Coulomb gas, vortex un- binding and superfluid-superconducting films. Rev. Mod. Phys. 1987, 59, 1001–1066. [Google Scholar] [CrossRef]
- Diamantini, M.C.; Trugenberger, C.A.; Vinokur, V.M. How planar superconductors cure their infrared divergences. J. High Energy Phys. 2022, 2022, 1–10. [Google Scholar] [CrossRef]
- Diamantini, M.C.; Gammaitoni, L.; Trugenberger, C.A.; Vinokur, V.M. Vogel-Fulcher-Tamman criticality of 3D superinsulators. Sci. Rep. 2018, 8, 15718. [Google Scholar] [CrossRef] [PubMed]
- Deser, S.; Jackiw, R.; Templeton, S. Three-Dimensional Massive Gauge Theories. Phys. Rev. Lett. 1982, 48, 975–978. [Google Scholar] [CrossRef]
- Allen, T.J.; Bowick, M.J.; Lahiri, A. Topological mass generation in 3+ 1 dimensions. Mod. Phys. Lett. 1991, A6, 559. [Google Scholar] [CrossRef]
- Trugenberger, C.A. Superinsulators, Bose Metals and High-Tc Superconductors: The Quantum Physics of Emergent Magnetic Monopoles; World Scientific: Singapore, 2022. [Google Scholar]
- Diamantini, M.C.; Trugenberger, C.A.; Vinokur, V.M. Confinement and asymptotic freedom with Cooper pairs. Commun. Phys. 2018, 1, 77. [Google Scholar] [CrossRef]
- Diamantini, M.C.; Gammaitoni, L.; Trugenberger, C.A.; Vinokur, V.M. The Superconductor-Superinsulator Transition: S-duality and the QCD on the Desktop. J. Supercond. Nov. Magn. 2018, 32, 47–51. [Google Scholar] [CrossRef]
- Diamantini, M.; Mironov, A.; Postolova, S.; Liu, X.; Hao, Z.; Silevitch, D.; Kopelevich, Y.; Kim, P.; Trugenberger, C.; Vinokur, V. Bosonic topological insulator intermediate state in the superconductor-insulator transition. Phys. Lett. A 2020, 384, 126570. [Google Scholar] [CrossRef]
- Wen, X.-G. Quantum order: A quantum entanglement of many particles. Phys. Lett. A 2002, 300, 175–181. [Google Scholar] [CrossRef]
- Chen, X.; Liu, Z.-X.; Wen, X.-G. Two-dimensional symmetry-protected topological orders and their protected gapless edge excitations. Phys. Rev. B 2011, 84, 235141. [Google Scholar] [CrossRef]
- Diamantini, M.; Sodano, P.; Trugenberger, C. Gauge theories of Josephson junction arrays. Nucl. Phys. B 1996, 474, 641–677. [Google Scholar] [CrossRef]
- Cho, G.Y.; Moore, J.E. Topological BF field theory description of topological insulators. Ann. Phys. 2011, 326, 1515–1535. [Google Scholar] [CrossRef]
- Jackiw, R.; Templeton, S. How super-renormalizable interactions cure their infrared divergences. Phys. Rev. D 1981, 23, 2291–2304. [Google Scholar] [CrossRef]
- Jaeger, H.M.; Haviland, D.B.; Orr, B.G.; Goldman, A.M. Onset of superconductivity in ultrathin granular metal films. Phys. Rev. B 1989, 40, 182–196. [Google Scholar] [CrossRef] [PubMed]
- Hebard, A.F.; Paalanen, M.A. Magnetic-field-tuned superconductor-insulator transition in two-dimensional films. Phys. Rev. Lett. 1990, 65, 927–930. [Google Scholar] [CrossRef] [PubMed]
- Goldman, A.M. Superconductor-insulator transitions. Int. J. Mod. Phys. B 2010, 24, 4081–4101. [Google Scholar] [CrossRef]
- Sacepe, B.; Chapelier, C.; Baturina, T.I.; Vinokur, V.M.; Baklanov, M.R.; Sanquer, M. Disorder-Induced Inhomogeneities of the Superconducting State Close to the Superconductor-Insulator Transition. Phys. Rev. Lett. 2008, 101, 157006. [Google Scholar] [CrossRef] [PubMed]
- Sacepe, B.; Dubouchet, T.; Chapelier, C.; Sanquer, M.; Ovadia, M.; Shahar, D.; Feigel’man, M.; Ioffe, L. Localization of preformed Cooper pairs in disordered superconductors. Nat. Phys. 2011, 7, 239–244. [Google Scholar] [CrossRef]
- Kowal, D.; Ovadyahu, Z. Disorder induced granularity in an amorphous superconductor. Solid State Commun. 1994, 90, 783–786. [Google Scholar] [CrossRef]
- Fazio, R.; Schön, G. Charge and vortex dynamics in arrays of tunnel junctions. Phys. Rev. B 1991, 43, 5307–5320. [Google Scholar] [CrossRef] [PubMed]
- Fazio, R.; Van Der Zant, H. Quantum phase transitions and vortex dynamics in superconducting netrworks. Phys. Rep. 2001, 355, 235–334. [Google Scholar] [CrossRef]
- Zhang, X.; Palevski, A.; Kapitulnik, A. Anomalous metals: From “failed superconductor” to “failed insulator”. Proc. Natl. Acad. Sci. USA 2022, 119, e2202496119. [Google Scholar] [CrossRef] [PubMed]
- Parra, C.; Niestemski, F.C.; Contryman, A.W.; Giraldo-Gallo, P.; Geballe, T.H.; Fisher, I.R.; Manoharan, H.C. Signatures of two-dimensional superconductivity emerging within a three-dimensional host superconductor. Proc. Natl. Acad. Sci. USA 2021, 118, e2017810118. [Google Scholar] [CrossRef] [PubMed]
- Pelc, D.; Vučković, M.; Grbić, M.S.; Požek, M.; Yu, G.; Sasagawa, T.; Greven, M.; Barišić, N. Emergence of superconductivity in the cuprates via a universal percolation process. Nat. Commun. 2018, 9, 4327. [Google Scholar] [CrossRef] [PubMed]
- Likharev, K.K. Superconducting weak links. Rev. Mod. Phys. 1979, 51, 101. [Google Scholar] [CrossRef]
- Kunchur, M.N.; Liang, M.; Gurevich, A. The vortex explosion transition. AIP Conf. Proc. 2013, 19, 1512. [Google Scholar]
- Trugenberger, C.A. Gauge Theories of Josephson Junction Arrays: Why Disorder Is Irrelevant for the Electric Response of Disordered Superconducting Films. Condens. Matter 2023, 8, 85. [Google Scholar] [CrossRef]
- Golubev, D.S.; Zaikin, A.D. Quantum tunneling of the order parameter in superconducting nanowires. Phys. Rev. B 2001, 64, 014504. [Google Scholar] [CrossRef]
- Golubev, D.S.; Zaikin, A.D. Fluctuations and Superconductivity in One Dimension. Phys. Rep. 2008, 464, 84–102. [Google Scholar]
- Ioffe, L.B.; Narozhny, B.N. Resistance of Josephson-junction arrays at low temperatures. Phys. Rev. B 1998, 58, 11449–11457. [Google Scholar] [CrossRef]
- Bottcher, C.G.L.; Nichele, F.; Shabani, J.; Palmstrom, C.J.; Marcus, C. MDynamical vortex transitions in a gate-tunable Josephson junction array. arXiv 2022, arXiv:2212.08651. [Google Scholar]
- Diamantini, M.C.; Trugenberger, C.A.; Vinokur, V.M. Superconductor-insulator transition in the absence of disorder. Phys. Rev. B 2021, 103, 174516. [Google Scholar] [CrossRef]
- Wilczek, F. Disassembling anyons. Phys. Rev. Lett. 1992, 69, 132–135. [Google Scholar] [CrossRef] [PubMed]
- Aharonov, Y.; Bohm, D. Significance of Electromagnetic Potentials in the Quantum Theory. Phys. Rev. B 1959, 115, 485–491. [Google Scholar] [CrossRef]
- Aharonov, Y.; Casher, A. Topological Quantum Effects for Neutral Particles. Phys. Rev. Lett. 1984, 53, 319–321. [Google Scholar] [CrossRef]
- Diamantini, M.C.; Trugenberger, C.A.; Vinokur, V.M. Quantum magnetic monopole condensate. Commun. Phys. 2021, 4, 25. [Google Scholar] [CrossRef]
- Trugenberger, C.; Diamantini, M.C.; Poccia, N.; Nogueira, F.S.; Vinokur, V.M. Magnetic Monopoles and Superinsulation in Josephson Junction Arrays. Quantum Rep. 2020, 2, 388–399. [Google Scholar] [CrossRef]
- Kaufmann, L.H. Formal Knot Theory; Princeton University Press: Princeton, NJ, USA, 1983. [Google Scholar]
- Bergeron, M.; Semenoff, G.W.; Szabo, R.J. Canonical BF-type topological field theory and fractional statistics of strings. Nucl. Phys. B 1995, 437, 695–721. [Google Scholar] [CrossRef][Green Version]
- Wilczek, F. Fractional Statistics and Anyon Superconductivity; World Scientific: Singapore, 1990. [Google Scholar]
- Dunne, G.V.; Jackiw, R.; Trugenberger, C.A. “Topological” (Chern-Simons) quantum mechanics. Phys. Rev. D 1990, 41, 661–666. [Google Scholar] [CrossRef]
- Julia, B.; Toulouse, G. The many-defect problem: Gauge-like variables for ordered media containing defects. Phys. Lett. 1979, 40, 396. [Google Scholar] [CrossRef]
- Brezin, E.; Zinn-Justin, J. Fields, Strings and Critical Phenomena; North-Holland: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Quevedo, F.; Trugenberger, C.A. Phases of antisymmetric tensor field theories. Nucl. Phys. B 1997, 501, 143–172. [Google Scholar] [CrossRef]
- Diamantini, M.C.; Trugenberger, C.A.; Vinokur, V.M. Topological Nature of High Temperature Superconductivity. Adv. Quantum Technol. 2021, 4, 135. [Google Scholar] [CrossRef]
- Diamantini, M.C.; Trugenberger, C.A.; Vinokur, V.M. Effective magnetic monopole mechanism for localized electron pairing in HTS. Front. Phys. 2022, 10, 909310. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diamantini, M.C. Superconductors without Symmetry Breaking. Condens. Matter 2024, 9, 21. https://doi.org/10.3390/condmat9020021
Diamantini MC. Superconductors without Symmetry Breaking. Condensed Matter. 2024; 9(2):21. https://doi.org/10.3390/condmat9020021
Chicago/Turabian StyleDiamantini, Maria Cristina. 2024. "Superconductors without Symmetry Breaking" Condensed Matter 9, no. 2: 21. https://doi.org/10.3390/condmat9020021
APA StyleDiamantini, M. C. (2024). Superconductors without Symmetry Breaking. Condensed Matter, 9(2), 21. https://doi.org/10.3390/condmat9020021





