Enhancing Spectroscopic Experiment Calibration through Differentiable Programming
Abstract
1. Introduction
2. Methods
2.1. Differentiable Programming
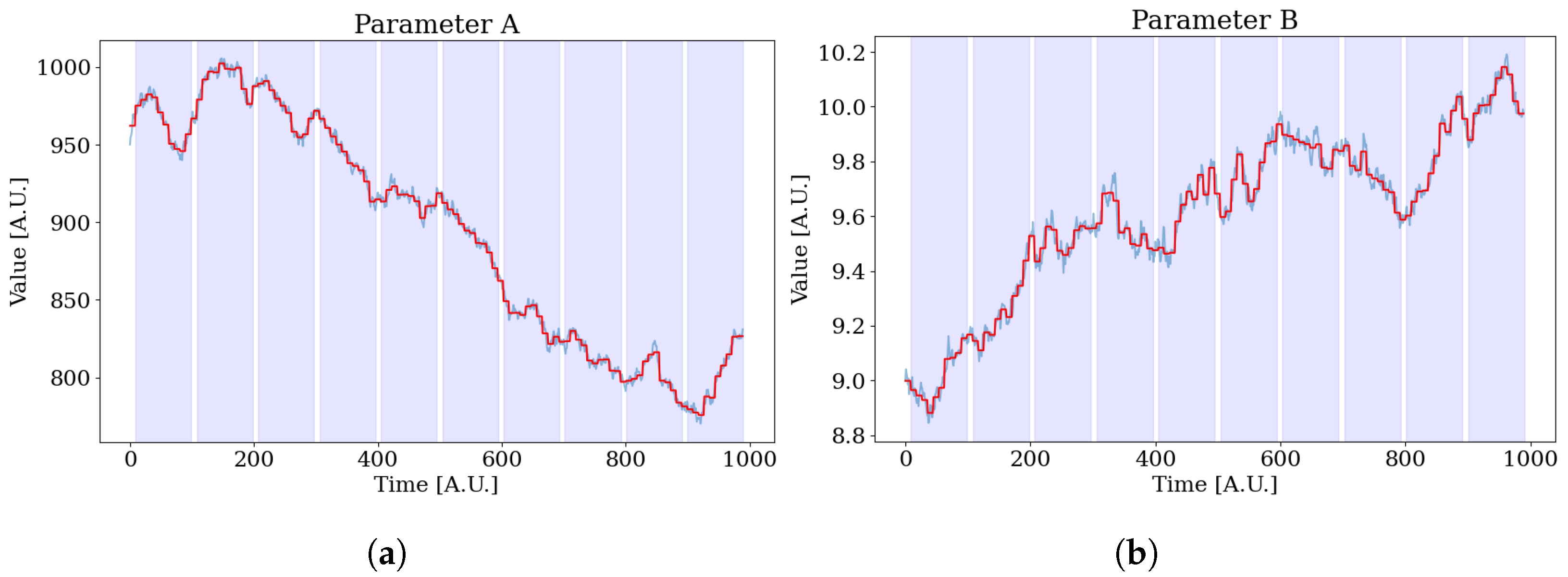
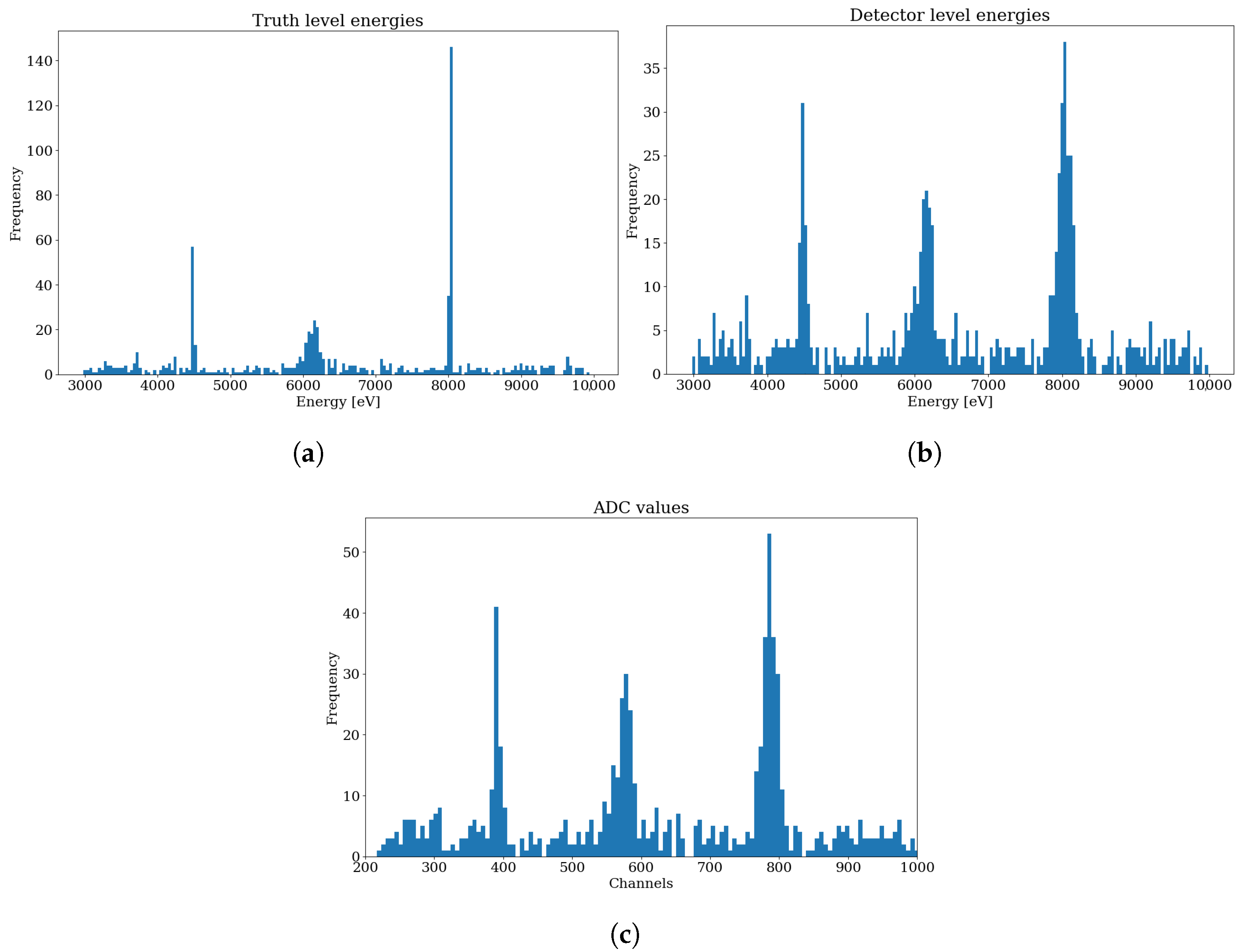
2.2. Toy Setup
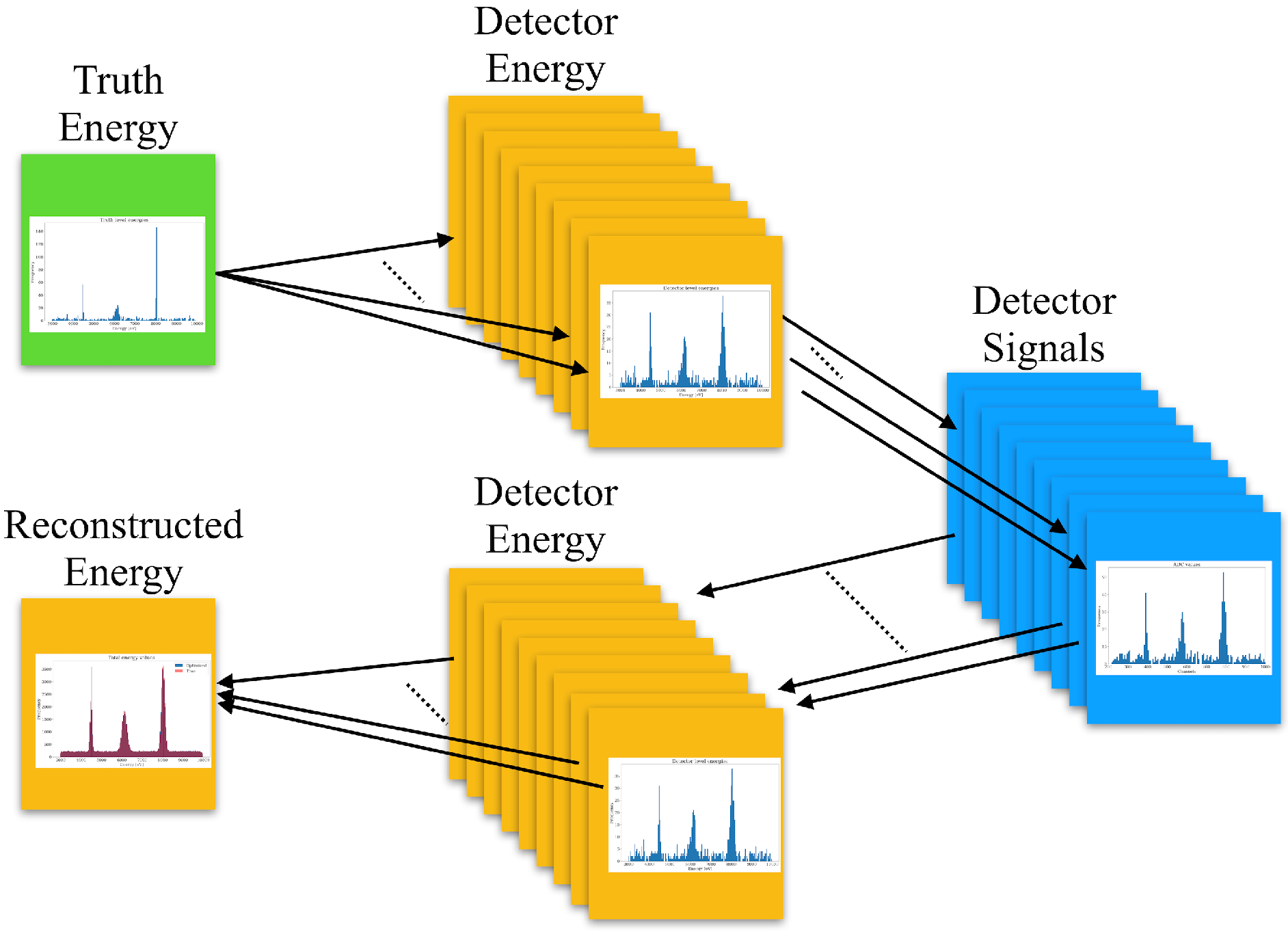
- Use the calibration constants: From known spectroscopic lines, the calibration constants , are derived in the calibration runs. These are then applied to the subsequent physics runs, until a new calibration is performed.
- Calibrating detector data: Using and , we apply the calibration to the entire dataset. This process corrects the recorded detector ADCs for each batch, ensuring that they are accurately aligned with the true energy values of the emitted lines.
- Combining the data: Finally, we combine the calibrated data from each batch together. This results in a fully calibrated dataset where the detector signals are corrected to reflect the actual energy values of the emitted lines.
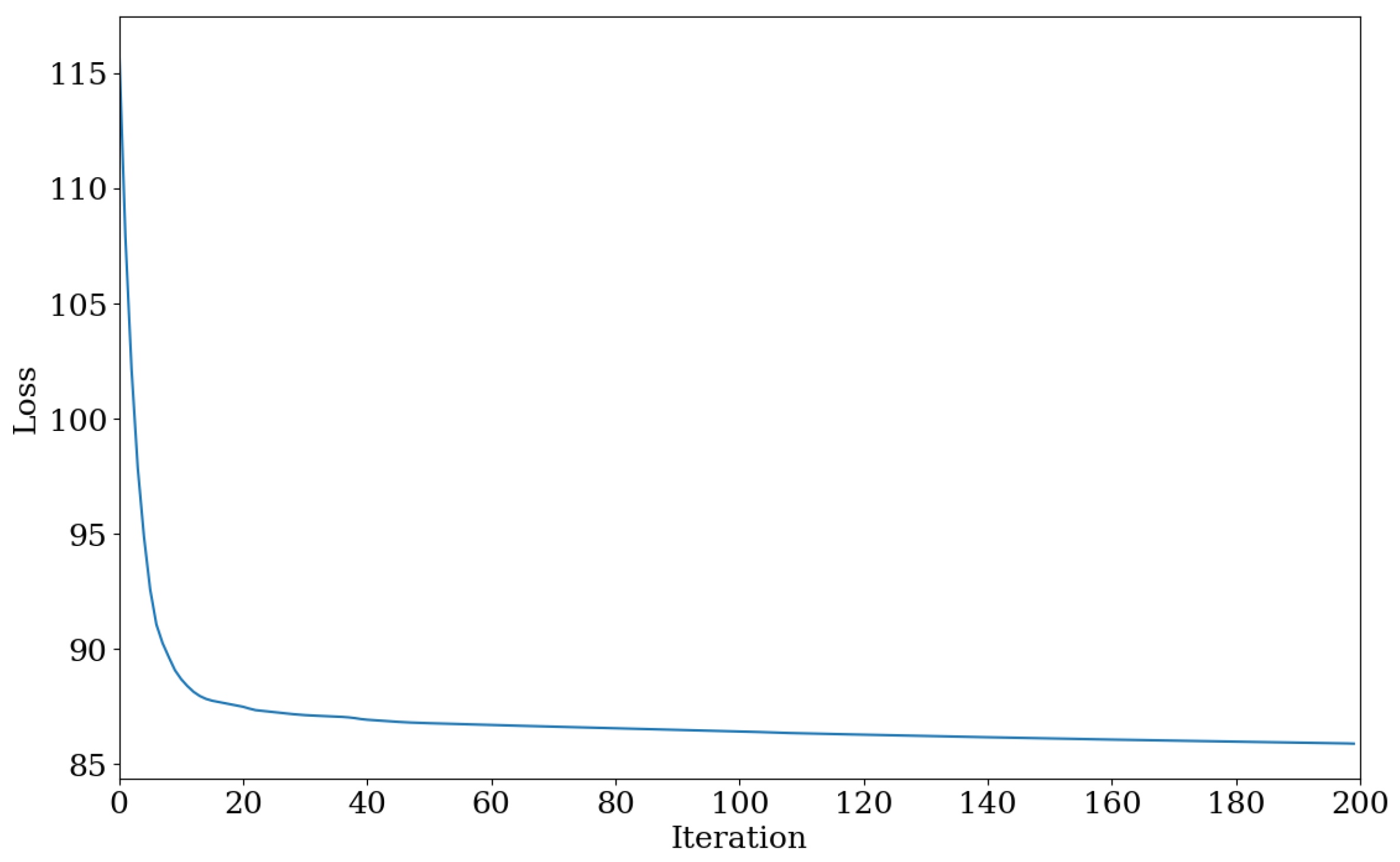
2.3. Gradient-Based Optimization
3. Results
4. Discussion
5. Conclusions
- The previous unbinned likelihood-based loss function, , which was suited to rare event searches in underground laboratories, is now replaced by a global -based loss function. This allows for a wealth of different shapes to be taken into account, and the method can be applied to a broader range of spectroscopic experiments.
- Unlike previous methods, the -based loss function allows the use of KDE as a representation of the underlying PDF, providing a fully differentiable model, which can be used in gradient-based optimization. The KDE can be trivially implemented as a binned KDE, reducing the computational overhead, and allowing the method to be used with high statistics data.
- In the case of precision measurements or characterization of spectroscopic lines, the global loss function ensures a much more contained degree of distortion of the calibration parameters, making the calibration more robust and reliable, and enabling a more accurate estimation of the associated systematic uncertainties.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lechner, P.; Eckbauer, S.; Hartmann, R.; Krisch, S.; Hauff, D.; Richter, R.; Soltau, H.; Strüder, L.; Fiorini, C.; Gatti, E.; et al. Silicon drift detectors for high resolution room temperature X-ray spectroscopy. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1996, 377, 346–351. [Google Scholar] [CrossRef]
- Lechner, P.; Fiorini, C.; Hartmann, R.; Kemmer, J.; Krause, N.; Leutenegger, P.; Longoni, A.; Soltau, H.; Stötter, D.; Stötter, R.; et al. Silicon drift detectors for high count rate X-ray spectroscopy at room temperature. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2001, 458, 281–287. [Google Scholar] [CrossRef]
- Bazzi, M.; Beer, G.; Bombelli, L.; Bragadireanu, A.; Cargnelli, M.; Corradi, G.; Curceanu, C.; d’Uffizi, A.; Fiorini, C.; Frizzi, T.; et al. First measurement of kaonic helium-3 X-rays. Phys. Lett. B 2011, 697, 199–202. [Google Scholar] [CrossRef] [PubMed]
- Tatsuno, H.; Doriese, W.B.; Bennett, D.A.; Curceanu, C.; Fowler, J.W.; Gard, J.; Gustafsson, F.P.; Hashimoto, T.; Hayano, R.S.; Hays-Wehle, J.P.; et al. Absolute Energy Calibration of X-ray TESs with 0.04 eV Uncertainty at 6.4 keV in a Hadron-Beam Environment. J. Low Temp. Phys. 2016, 184, 930–937. [Google Scholar] [CrossRef]
- Hashimoto, T.; Aikawa, S.; Akaishi, T.; Asano, H.; Bazzi, M.; Bennett, D.; Berger, M.; Bosnar, D.; Butt, A.; Curceanu, C.; et al. Measurements of Strong-Interaction Effects in Kaonic-Helium Isotopes at Sub-eV Precision with X-ray Microcalorimeters. Phys. Rev. Lett. 2022, 128, 112503. [Google Scholar] [CrossRef] [PubMed]
- Fowler, J.W.; O’Neil, G.C.; Alpert, B.K.; Bennett, D.A.; Denison, E.V.; Doriese, W.; Hilton, G.C.; Hudson, L.T.; Joe, Y.I.; Morgan, K.M.; et al. Absolute energies and emission line shapes of the L x-ray transitions of lanthanide metals. Metrologia 2021, 58, 015016. [Google Scholar] [CrossRef] [PubMed]
- Fowler, J.; Alpert, B.; Bennett, D.; Doriese, W.; Gard, J.; Hilton, G.; Hudson, L.; Joe, Y.; Morgan, K.; O’Neil, G.; et al. A reassessment of absolute energies of the X-ray L lines of lanthanide metals. Metrologia 2017, 54, 494. [Google Scholar] [CrossRef]
- Almazán, H.; Bernard, L.; Blanchet, A.; Bonhomme, A.; Buck, C.; Chalil, A.; del Amo Sanchez, P.; El Atmani, I.; Labit, L.; Lamblin, J.; et al. STEREO neutrino spectrum of 235U fission rejects sterile neutrino hypothesis. Nature 2023, 613, 257–261. [Google Scholar] [CrossRef]
- Napolitano, F.; Bazzi, M.; Bragadireanu, M.; Cargnelli, M.; Clozza, A.; De Paolis, L.; Del Grande, R.; Fiorini, C.; Guaraldo, C.; Iliescu, M.; et al. Novel machine learning and differentiable programming techniques applied to the VIP-2 underground experiment. Meas. Sci. Technol. 2023, 35, 025501. [Google Scholar] [CrossRef]
- De Castro, P.; Dorigo, T. INFERNO: Inference-aware neural optimisation. Comput. Phys. Commun. 2019, 244, 170–179. [Google Scholar] [CrossRef]
- Dorigo, T.; Giammanco, A.; Vischia, P.; Aehle, M.; Bawaj, M.; Boldyrev, A.; Manzano, P.d.C.; Derkach, D.; Donini, J.; Edelen, A.; et al. Toward the End-to-End Optimization of Particle Physics Instruments with Differentiable Programming: A White Paper. arXiv 2022. [Google Scholar] [CrossRef]
- Simpson, N.; Heinrich, L. neos: End-to-end-optimised summary statistics for high energy physics. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2023; Volume 2438, p. 012105. [Google Scholar]
- Bradbury, J.; Frostig, R.; Hawkins, P.; Johnson, M.J.; Leary, C.; Maclaurin, D.; Necula, G.; Paszke, A.; VanderPlas, J.; Wanderman-Milne, S.; et al. JAX: Composable Transformations of Python+NumPy Programs. 2018. Available online: http://github.com/google/jax (accessed on 31 May 2024).
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Shumway, R.H.; Stoffer, D.S.; Stoffer, D.S. Time Series Analysis and Its Applications; Springer: Berlin/Heidelberg, Germany, 2000; Volume 3. [Google Scholar]
- Miliucci, M.; Iliescu, M.; Amirkhani, A.; Bazzi, M.; Curceanu, C.; Fiorini, C.; Scordo, A.; Sirghi, F.; Zmeskal, J. Energy Response of Silicon Drift Detectors for Kaonic Atom Precision Measurements. Condens. Matter 2019, 4, 31. [Google Scholar] [CrossRef]
- James, F.; Roos, M. Minuit: A System for Function Minimization and Analysis of the Parameter Errors and Correlations. Comput. Phys. Commun. 1975, 10, 343–367. [Google Scholar] [CrossRef]
- Dembinski, H.; Ongmongkolkul, P.; Deil, C.; Schreiner, H.; Feickert, M.; Burr, C.; Watson, J.; Rost, F.; Pearce, A.; Geiger, L.; et al. scikit-hep/iminuit. Available online: https://zenodo.org/records/10638795 (accessed on 31 May 2024).
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Routledge: London, UK, 2018. [Google Scholar]
- Sirghi, F.; Sgaramella, F.; Abbene, L.; Amsler, C.; Bazzi, M.; Borghi, G.; Bosnar, D.; Bragadireanu, M.; Buttacavoli, A.; Carminati, M.; et al. SIDDHARTA-2 apparatus for kaonic atoms research on the DAΦNE collider. arXiv 2023, arXiv:2311.16144. [Google Scholar] [CrossRef]
- Sirghi, D.; Sirghi, F.; Sgaramella, F.; Bazzi, M.; Bosnar, D.; Bragadireanu, M.; Carminati, M.; Cargnelli, M.; Clozza, A.; Deda, G.; et al. A new kaonic helium measurement in gas by SIDDHARTINO at the DAΦNE collider. J. Phys. Nucl. Part. Phys. 2022, 49, 055106. [Google Scholar] [CrossRef]
- Bosnar, D.; Bazzi, M.; Cargnelli, M.; Clozza, A.; Curceanu, C.; Del Grande, R.; Guaraldo, C.; Iliescu, M.; Makek, M.; Marton, J.; et al. Revisiting the Charged Kaon Mass. Acta Phys. Pol. B 2020, 51, 115. [Google Scholar] [CrossRef]
- Heinonen, J.; Modanese, C.; Haarahiltunen, A.; Kettunen, H.; Rossi, M.; Jaatinen, J.; Juntunen, M. Results on radiation hardness of black silicon induced junction photodetectors from proton and electron radiation. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2020, 977, 164294. [Google Scholar] [CrossRef]
- Heinonen, J.; Haarahiltunen, A.; Kettunen, H.; Jaatinen, J.; Rossi, M.; Heino, J.; Savin, H.; Juntunen, M.A. Improved stability of black silicon detectors using aluminum oxide surface passivation. In Proceedings of the International Conference on Space Optics—ICSO, Virtual Conference, 30 March–2 April 2021; Sodnik, Z., Cugny, B., Karafolas, N., Eds.; The International Society for Optics and Photonics (SPIE): Bellingham, WA, USA, 2021. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, Z.; Jing, J.; Gao, R.; Liao, Z.; Zhang, W.; Liu, G.; Wang, Y.; Wang, K.; Xue, C. Black silicon for near-infrared and ultraviolet photodetection: A review. APL Mater. 2023, 11, 20. [Google Scholar] [CrossRef]
- Jouskari, E. Characterization and Application of Black Silicon Drift Detector to X-ray Measurements. Available online: https://lutpub.lut.fi/handle/10024/167422 (accessed on 31 May 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Napolitano, F. Enhancing Spectroscopic Experiment Calibration through Differentiable Programming. Condens. Matter 2024, 9, 26. https://doi.org/10.3390/condmat9020026
Napolitano F. Enhancing Spectroscopic Experiment Calibration through Differentiable Programming. Condensed Matter. 2024; 9(2):26. https://doi.org/10.3390/condmat9020026
Chicago/Turabian StyleNapolitano, Fabrizio. 2024. "Enhancing Spectroscopic Experiment Calibration through Differentiable Programming" Condensed Matter 9, no. 2: 26. https://doi.org/10.3390/condmat9020026
APA StyleNapolitano, F. (2024). Enhancing Spectroscopic Experiment Calibration through Differentiable Programming. Condensed Matter, 9(2), 26. https://doi.org/10.3390/condmat9020026





