Characterization of the SIDDHARTA-2 Setup via the Kaonic Helium Measurement

Abstract

The aim of the SIDDHARTA-2 experiment is to perform the first measurement ever of the width and shift induced by the strong interaction to the $2p\to 1s$ energy transition of kaonic deuterium. This ambitious goal implies a challenging task due to the very low X-ray yield of kaonic deuterium, which is why an accurate and thorough characterization of the experimental apparatus is mandatory before starting the data-taking campaign. Helium-4 is an excellent candidate for this characterization since it exhibits a high yield in particular for the $3d\to 2p$ transition, roughly 100 times greater than that of the kaonic deuterium. The ultimate goal of the work reported in this paper is to study the performances of the full experimental setup in view of the kaonic deuterium measurement. This is carried out by measuring the values of the shift and the width for the $3d\to 2p$ energy transition of kaonic helium-4, induced by the strong interaction. The values obtained for these quantities, for a total integrated luminosity of ∼31/$\mathrm{p}$$\mathrm{b}$, are ${\epsilon }_{2p}=2.0\pm 1.2\left(\mathrm{stat}\right)\pm 1.5\left(\mathrm{syst}\right)\mathrm{eV}$ and ${\mathrm{\Gamma }}_{2p}=1.9\pm 5.7\left(\mathrm{stat}\right)\pm 0.7\left(\mathrm{syst}\right)\mathrm{eV}$. The results, compared to the value of the shift measured by the SIDDHARTA experiment ${\epsilon }_{2p}=0\pm 6\left(\mathrm{stat}\right)\pm 2\left(\mathrm{syst}\right)\mathrm{eV}$, show a net enhancement of the resolution of the apparatus, providing strong evidence of the potential to perform the challenging measurement of the kaonic deuterium.

1. Introduction

An exotic atom [1] is an atomic system in which an electron is replaced by a negatively charged particle bound into an atomic orbit by its electromagnetic interaction with the nucleus. Quantum Electrodynamics (QED) provides an accurate prediction of the energy levels of the electromagnetic interaction between the negatively charged particle and the nucleus. When present, small deviations in the binding energy levels with respect to the QED-calculated ones, detected by X-ray spectroscopy, contain additional information on the interaction between the particle and the nucleus. In particular, among the exotic atoms, the hadronic ones play a crucial role, and studying them allows the experimental investigation of the strong interaction, manifested in the lowest atomic states before nuclear absorption occurs. In the specific case of radiative transitions to these levels, the strong interaction is measured at the threshold, given that the relative energy between the captured hadron and the nucleus is only the binding energy of the system, on the order of O( 10 $\mathrm{k}$$\mathrm{e}\mathrm{V}$). In this framework, the kaonic atoms play an important role, allowing us to directly probe the strong interaction of particles with strangeness in the non-perturbative regime.

From the measurement of the shift and the broadening induced by the strong interaction on the $1s$ level of the kaonic hydrogen and kaonic deuterium, the isospin-dependent antikaon–nucleon (antiK–N) scattering lengths can be obtained [2,3,4,5,6]. Moreover, the kaonic deuterium measurement will provide crucial information about the anti-K–N interaction, which unobtainable from the two-body data. The results of kaonic deuterium measurement will therefore contribute to the efforts to understand the anti-K–N interaction in the non-perturbative regime and will be a test bench for the different theoretical models based on dimensional regularization [7,8,9], off-shell form factors [10,11], effective field theory [12], and three-body calculation [13].

The SIDDHARTA experiment [14] successfully measured the kaonic hydrogen in 2009, while the kaonic deuterium measurement is still to be performed, and it presents itself as a very challenging task due to the yield of the X-ray transitions to the first level, which are expected to be about one order of magnitude lower than that of kaonic hydrogen. The SIDDHARTA-2 experiment aims at performing this measurement, for which it is of key importance that the experimental apparatus is thoroughly characterized using a high X-ray yield gaseous target. Helium-4 is an excellent candidate for this purpose since the $3d\to 2p$ transition has a yield roughly 100 times larger than that of kaonic deuterium. The measurement has already been performed by the SIDDHARTA collaboration [15] in 2009, resulting in a value of the shift of the $2p$ level of ${\epsilon }_{2p}=0\pm 6\left(\mathrm{stat}\right)\pm 2\left(\mathrm{syst}\right)\mathrm{eV}$. The new kaonic helium measurement presented in this work proves the excellent performance of the new apparatus, which qualifies as the state-of-the-art instrument for the challenging measurement of kaonic deuterium.

In Section 2 the experimental apparatus is illustrated. The calibration procedure and the data selection are reported in Section 3, together with the experimental fine-tuning of the degrader; Section 4 presents the results of the kaonic helium-4 shift and width measurements. Finally, a discussion of the obtained results are included in Section 5.

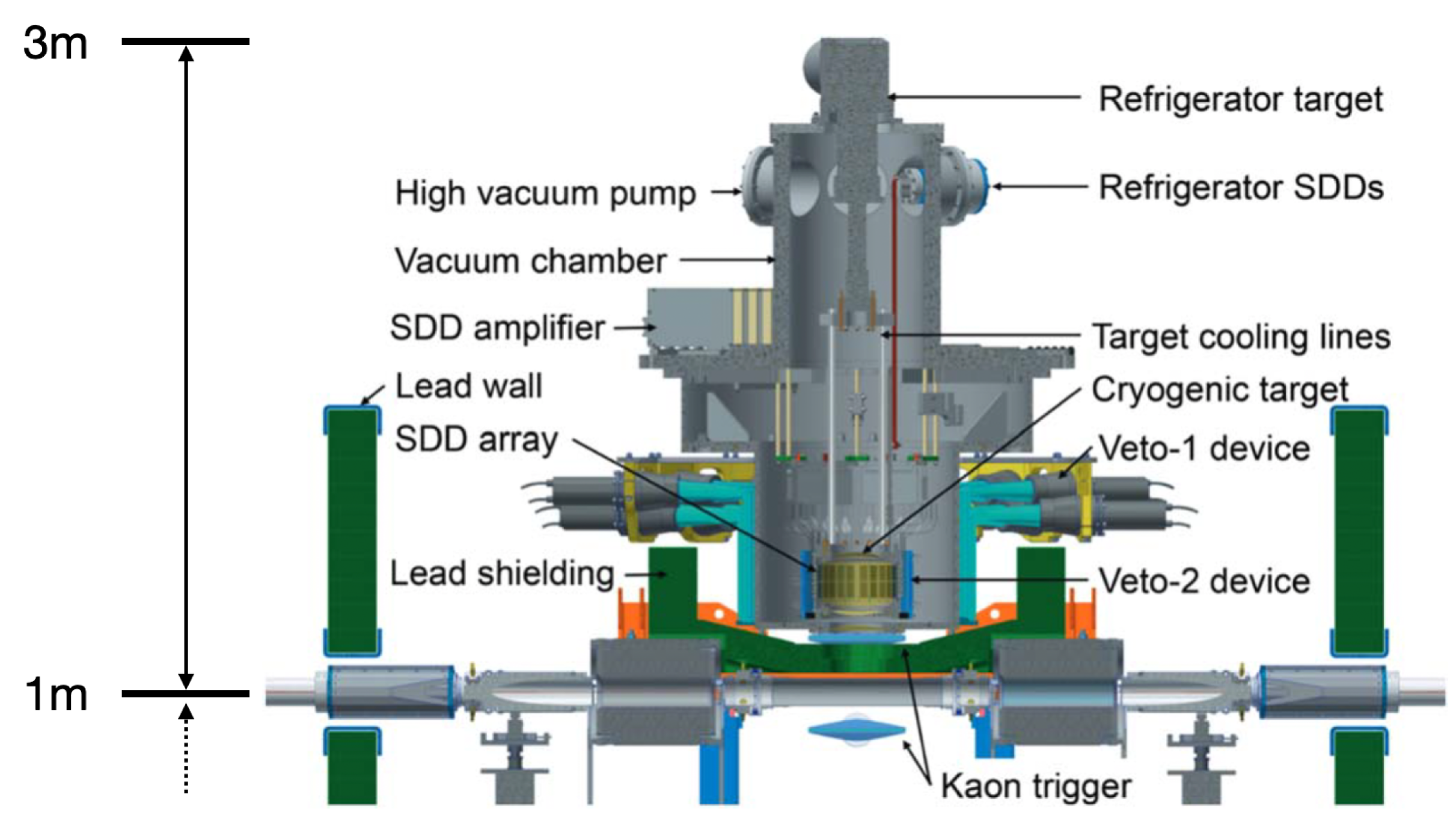
2. The SIDDHARTA-2 Setup on DAΦNE

DAΦNE is an electron-positron collider at the Frascati National Laboratory of INFN (INFN-LNF) [16] working at the center of mass energy of the $\varphi$ resonance (1.02 GeV), providing, via its decay, charged $K^{+}$/$K^{-}$ and neutral $K_L^0$/$K_S^0$ pairs with a branching ratio of $48.9\%$ and $34.2\%$, respectively. The produced charged kaons have a momentum of 127 MeV/c, and a momentum spread of $\mathsf{\Delta }p/p<0.1\%$. Therefore, the kaons produced by DAΦNE have much lower energy and are cleaner from background particles with respect to the ones obtained by proton collisions on a fixed target. The crossing angle between the two beams in the interaction point is ∼50 $\mathrm{m}$$\mathrm{rad}$. This relatively high crossing angle causes the $\varphi$ resonances to be boosted toward the center of the collider.

The SIDDHARTA-2 experiment is currently installed at the interaction point (IP) of the DAΦNE collider. The setup is shown in Figure 1 [17]. The key elements of the setup are the beam pipe, the kaon trigger, the Mylar degrader, the luminosity monitor, a cylindrical vacuum chamber housing the cryogenic target, and the X-ray detectors, encircled by a specialized veto system. Above and below the IP, a pair of plastic scintillators, read by two Photo-Multiplier Tubes (PMTs) each, act as a kaon trigger using the specific time of flight (TOF) of the slow kaons. The kaon trigger selects the kaons emitted back-to-back from the $\varphi$ decay in the IP and directed toward the target. The vacuum chamber is located above the IP and contains the cryogenic target cell. For thermal insulation, it is evacuated to a pressure below ${10}^{-6}$ mbar. The charged kaons travel through the vacuum chamber window, then enter the target cell and interact with the gas, forming kaonic atoms and subsequently emitting X-rays. Twelve plastic scintillators read by pairs of PMTs are placed around the cryogenic target outside the vacuum chamber, forming the Veto-1 system [18]. Inside the vacuum chamber, surrounding the target, smaller scintillators read by Silicon Photo-Multipliers (SiPMs) are used as an additional Veto-2 system [19,20]. The goal of these two detectors is to suppress the synchronous background originating from the nuclear absorption of the $K^{-}$ and to limit the fake signals induced by the Minimum Ionizing Particles (MIPs) on the X-ray detectors. The asynchronous background, related to particle losses from the $e^{+}$$e^{-}$ beams due to the Touschek effect and beam–gas interactions, is suppressed by the trigger system. Shielding is placed around and below the vacuum chamber to protect the apparatus from electromagnetic cascades coming from the $e^{+}$$e^{-}$ rings lost particles. The cryogenic target cell is a cylindrical volume with a diameter of 144 mm and a height of 125 mm. The side walls are made of two layers of 75 μm Kapton, a polyimide film (${\mathrm{C}}_{22}$${\mathrm{H}}_{10}$${\mathrm{N}}_2$${\mathrm{O}}_5$) that remains stable for a wide range of temperatures, with a reinforcement structure made out of high-purity aluminum. The target cell has a 125 μm thick Kapton entrance window for the kaons and a 100 μm thick titanium top roof, used for calibration purposes together with the high purity titanium–copper strips placed on dedicated holders on the target cell walls. The dimensions of the target cell were optimized with a Monte Carlo simulation to maximize the number of kaons stopped inside the gas while minimizing the number of detected background events. Surrounding the target, silicon drift detectors (SDDs) [21,22,23,24,25,26] are used to detect the X-rays coming from the cascade process of the kaonic atoms. A system made of two X-ray tubes is employed for the in situ calibration of the SDDs, using the X-ray fluorescence excitation of high-purity titanium and copper foils mounted on the target. A mylar degrader is placed between the target and the IP to optimize the stopping range of the kaons inside the gaseous target. Another pair of plastic scintillators read by PMTs is placed on the horizontal plane, near the IP, providing luminosity feedback to DAΦNE (SIDDHARTA-2 Luminosity Monitor (Luminometer) [27]) by measuring the kaon rates and evaluates the background. The geometry of the full setup was optimized with a GEANT4 simulation to maximize the signal for the given machine conditions. The simulation also provided the step-geometry of the degrader for slowing down the kaons to the best momentum for gas stopping and for compensating for the Φ boost. More details on the setup can be found in [28].

3. Calibration Procedure and Data Analysis

The characterization of the experimental setup was carried out using a helium-4 gaseous target at $1.5\%$ of liquid helium-4 density. During the characterization run, a total of 31 ${\mathrm{pb}}^{-1}$ of integrated luminosity was collected with different degrader thicknesses to maximize the number of kaons stopped in the target cell. The inclusive spectrum for the collected data has been analyzed to extract the shift and width induced by the strong interaction to the $2p$ level of helium.

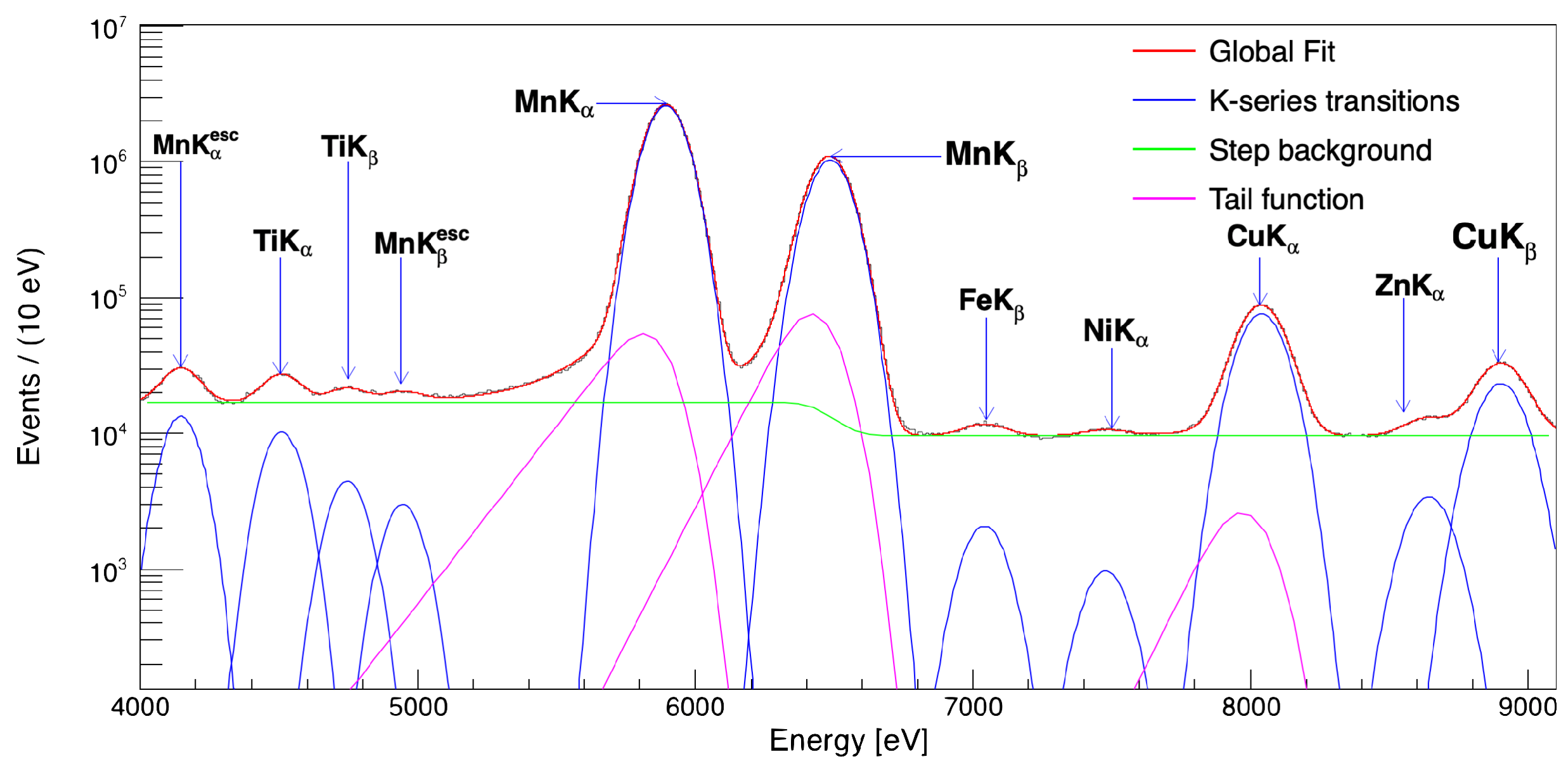
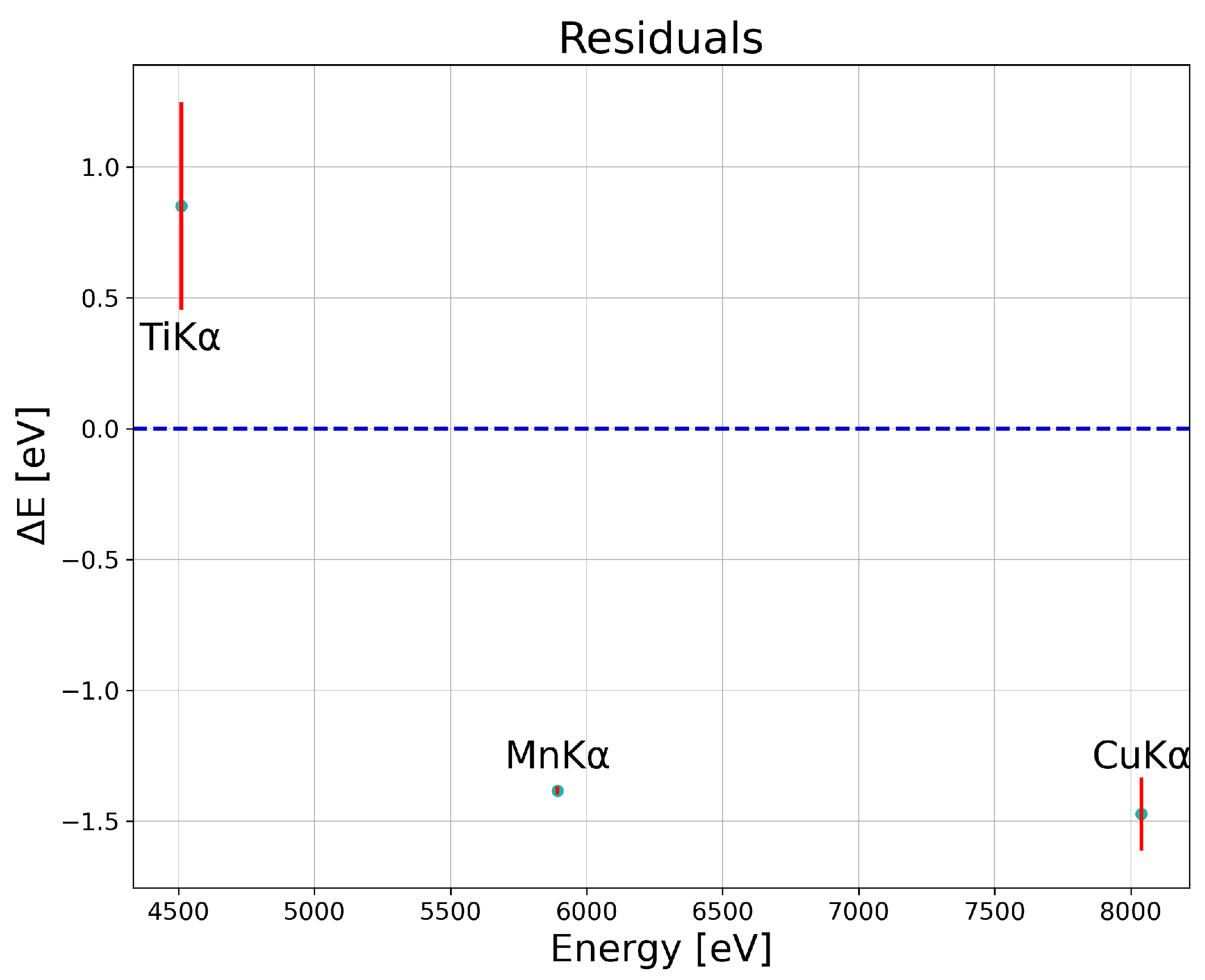
3.1. SDDs Calibration in DAΦNE

The characterization of the energy response of the setup in the actual experimental environment is mandatory for a precision experiment. Therefore, the energy calibration of the detectors inside the DAΦNE hall is one of the most critical aspects of the data analysis procedure. Given the slight differences between the SDDs and their front-end electronics, resulting in different charge collection and voltage conversion features, individual calibrations of the SDDs system are required before merging all the measured spectra. The calibration has been performed with two X-ray tubes and a ⁵⁵Fe source. The X-ray tubes are used to induce the characteristic fluorescence emission lines of the high-purity titanium and copper strips placed on the target cell walls; the ⁵⁵Fe decays via electron capture to an excited state of ⁵⁵Mn, which then emits an X-ray in the de-excitation process. Hence, we identified in the spectrum the peaks associated with the ${\mathrm{TiK}}_{\alpha }$, the ${\mathrm{CuK}}_{\alpha }$, and the ${\mathrm{MnK}}_{\alpha }$ X-ray emissions. Each peak is described by a Gaussian function:

$$G\left(E\right)=\frac{Gain}{\sqrt{2\pi }{\sigma }_i}{e}^{\frac{-{(E-E_0)}^2}{2{\sigma }^2}},$$

(1)

where $\sigma$ is the width of the Gaussian and represents the energy resolution of the SDDs, summed up to a tail component to account for the low energy contributions due to incomplete charge collection [29]:

$$T\left(E\right)=\frac{Gain}{2\beta \sigma }{e}^{\frac{(E-E_0)}{\beta \sigma }+\frac{1}{2{\beta }^2}}\mathrm{erfc}\left(\frac{E-E_0}{\sqrt{2}\sigma }+\frac{1}{\sqrt{2}\beta }\right),$$

(2)

where $\beta$ is the slope parameter of the tail function. Moreover, when considering an actual detector, the energy resolution ($\sigma$) of each detector will depend on the electronic and thermal noise ($Noise$) and on the intrinsic detector resolution related to the e-h generation statistics in the detector material, namely the Fano Factor ($FF$) [29]:

$$\sigma =\sqrt{{\left(\frac{Noise}{2\sqrt{2\ln 2}}\right)}^2+\epsilon ·FF·E},$$

(3)

where $\epsilon$ is the typical work function of the detector material, in our case the energy needed to create an e-h pair in silicon.

When the individual SDD calibration is completed, the spectra are summed up in a final spectrum, shown in Figure 2, which is then analyzed. Apart from the calibration lines, some contaminants appear in the spectrum. These are due to accidental excitations of certain materials that the experimental apparatus is made of, namely ${\mathrm{FeK}}_{\alpha }$, ${\mathrm{NiK}}_{\alpha }$ and ${\mathrm{ZnK}}_{\alpha }$ and to the escape peaks of the Mn K-series lines.

By analyzing the distribution of the residuals of the ${\mathrm{TiK}}_{\alpha }$, ${\mathrm{CuK}}_{\alpha }$, and ${\mathrm{MnK}}_{\alpha }$ peaks, shown in Figure 3, one obtains an estimate of the calibration accuracy, which is in the order of $1.5$ at ∼ 6 keV. The fit also provides a good estimate of the energy resolution of the apparatus at ∼ 6 keV (the closest energy to the ${\mathrm{L}}_{\alpha }$ line of kaonic helium) from the FWHM of the ${\mathrm{MnK}}_{\alpha }$ peak, yielding a value of $170.97\pm 0.69)\mathrm{eV}$ FWHM.

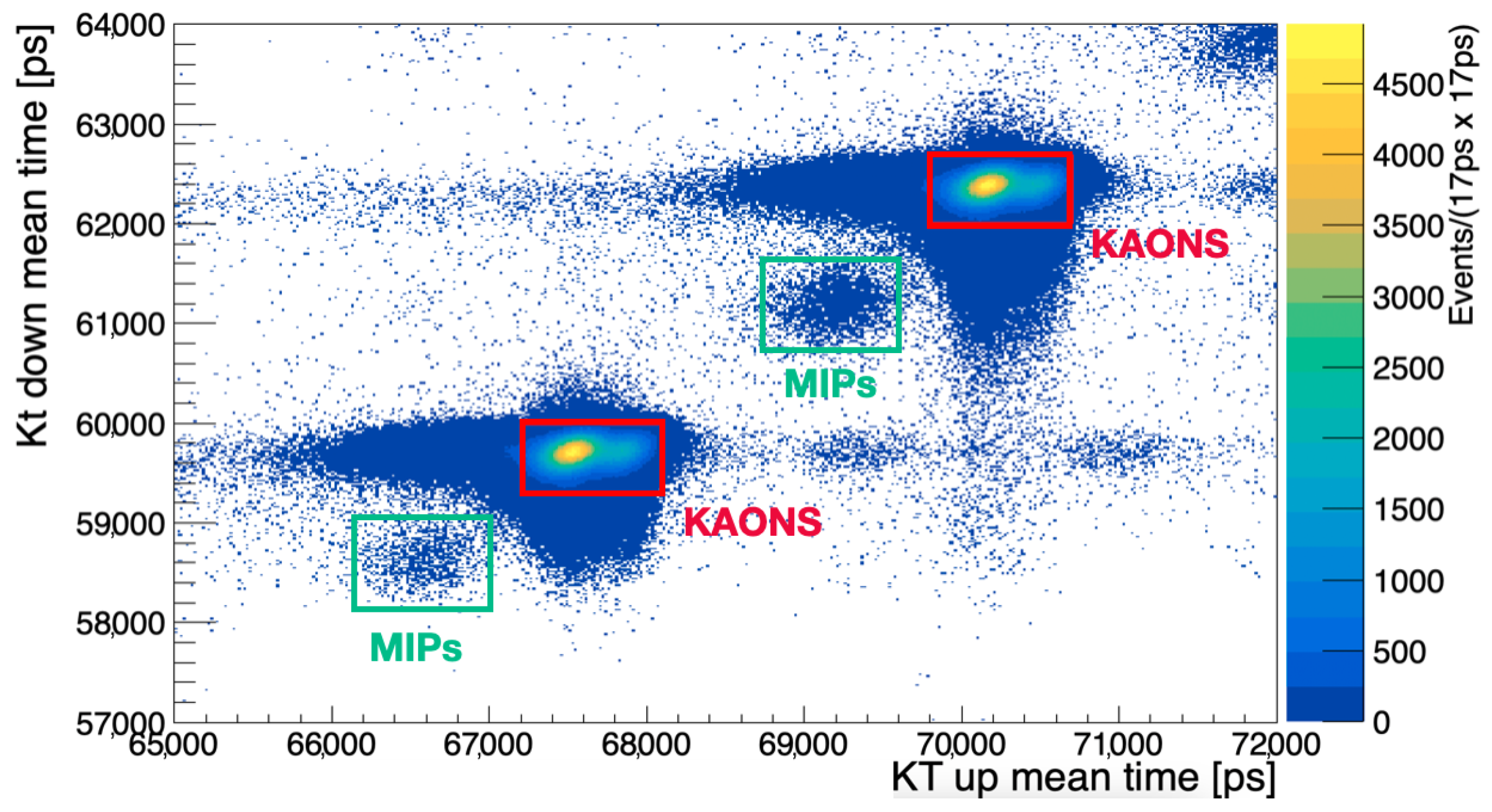
3.2. Data Selection

Figure 4 shows the inclusive energy spectrum acquired by the SDDs during the SIDDHARTA-2 helium-4 run, for a total integrated luminosity of ∼ 31 ${\mathrm{pb}}^{-1}$. The fluorescence peaks corresponding to the X-ray emission of the materials surrounding the SDDs are present. In particular, the titanium and the copper lines come from the setup materials inside the vacuum chamber, and the bismuth comes from the alumina ceramic carriers on which the SDDs are mounted.

The high continuous background hinders the direct observation of the kaonic helium lines; therefore, background rejection cuts need to be applied to the experimental data. The asynchronous component of the background, produced by DAΦNE due to particles lost from the two $e^{-}$$e^{+}$ rings, can be heavily suppressed by the kaon trigger (KT). A first hardware selection marks a 5 μs time window in coincidence with the KT signal, thus rejecting a substantial portion of the background. This selection by itself is not enough; MIPs, generated by the beam–beam and beam–gas interactions resulting in particle losses, can produce a trigger signal when extended EM showers simultaneously cross both KT scintillators. To discriminate between the triggers induced by $K^{+}$$K^{-}$ pairs and those induced by MIPs, the TOF signature is used by measuring the time difference between the trigger signal and the DAΦNE radio-frequency (RF), which provides a collision time reference. The signals produced by the two KT scintillators are read by two PMTs each and processed by a Constant Fraction Discriminator (CFD). The hits are recorded when the corresponding signals are above the CFD threshold, thus rejecting a fraction of MIPs. By computing the mean time of the PMTs signal of the upper scintillator and that of the lower one, the timing information of the trigger is extracted and referenced to the RF. Figure 5 shows the time distributions measured by the two KT scintillators and the TOF cut used to reject the MIPs-induced triggers. One can clearly distinguish between the coinciding events related to kaons (high intensity) from those induced by MIPs (low intensity).

To further strengthen the background rejection, the time difference between the X-ray detection and the KT signal is evaluated; since the charge collection inside the SDDs under cryogenic regime lasts less than the hardware time window of 5 μs, the coincident events will display the drift time distribution inside the silicon, as shown in Figure 6. The cut performed is marked by the two red lines. The events between the lines are related to hits on the SDDs coinciding with the KT signals, while the flat distribution on the sides comes from uncorrelated events, which are therefore rejected. The drift time distribution is fitted with a Gaussian curve to extract the time resolution of the SDDs system, which is $(507.60\pm 0.47)\mathrm{ns}\mathrm{FWHM}$.

After all the cuts, a total rejection factor of the order of ∼${10}^3$ is obtained. The obtained final spectrum is shown in Figure 7.

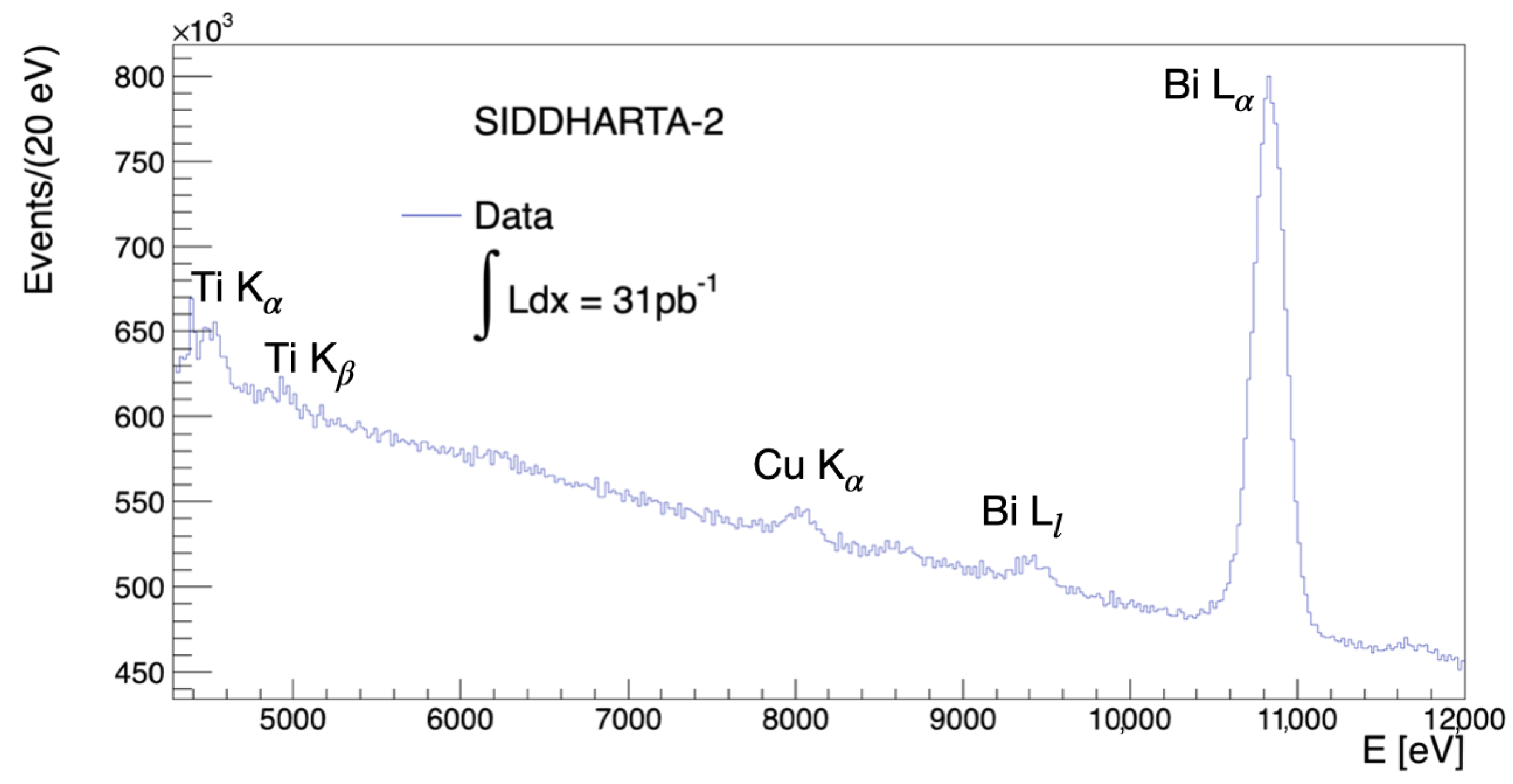
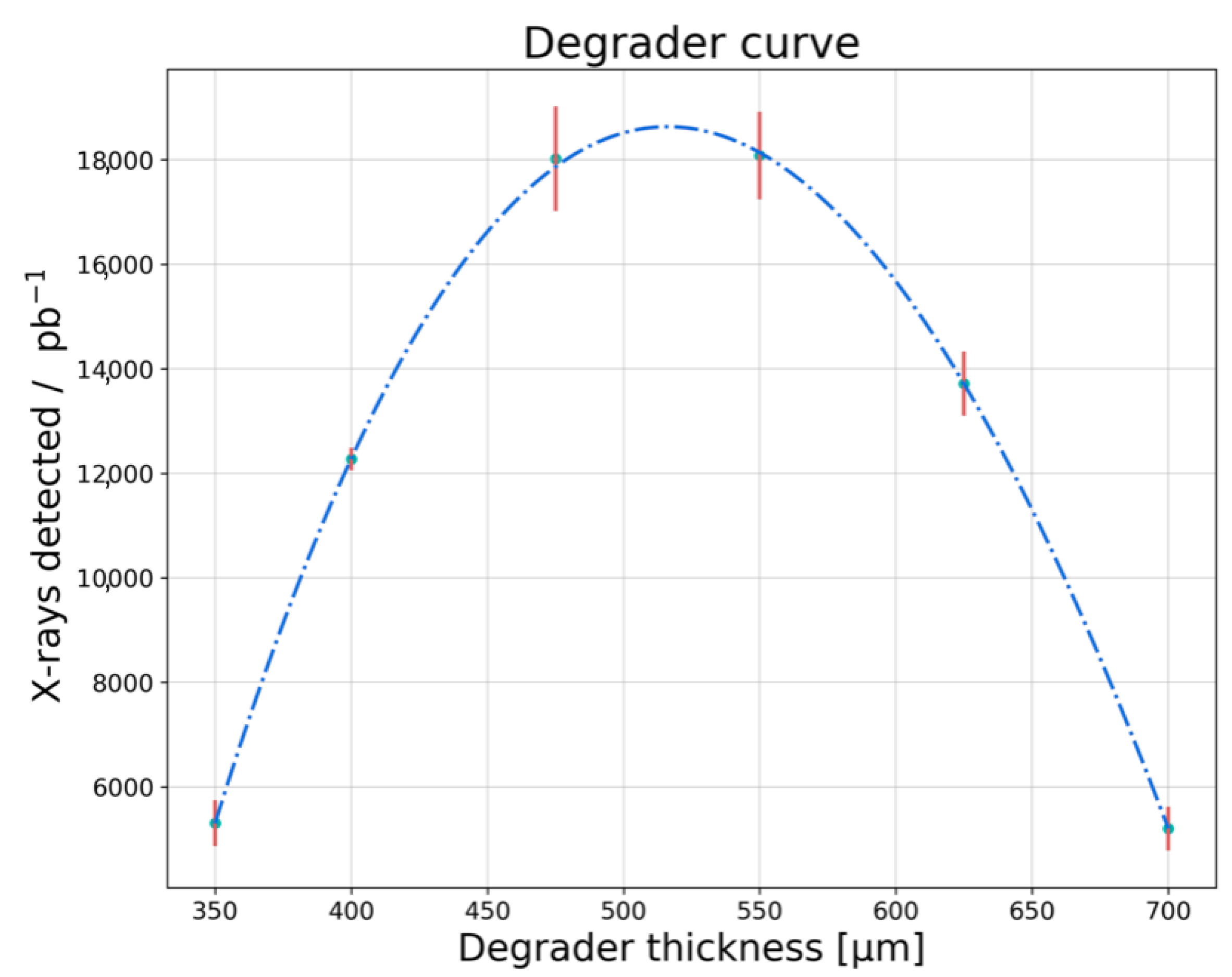
3.3. Degrader Optimization

Before entering the target cell, the kaons need to be slowed down for the atomic capture to happen. Moreover, the momentum distribution of the produced kaons is not uniform over the acceptance solid angle, due to the fact that the $e^{+}$$e^{-}$ collisions are not head-on, the collision angle of 50 $\mathrm{m}$$\mathrm{rad}$ inducing a boost towards the center of the collider. Thus, an eight-step degrader has been designed, both for slowing down the kaons and for making the kaon momentum distribution as uniform as possible in the solid angle used. The Monte Carlo simulation was used to optimize the number of steps of the degrader and their preliminary thickness. The final degrader thickness has been finely tuned experimentally to have most of the $K^{-}$ stopped at the center of the target cell. The number of kaonic helium-4 ${\mathrm{L}}_{\alpha }$ events was measured for six different degrader thicknesses ( 350 μm, 400 μm, 475 μm, 550 μm, 625 μm, and 700 μm in the middle) and normalized to the integrated luminosity of each data collection. The results of this experimental fine tuning are shown in Figure 8. The points have been fitted with a third-order polynomial to evaluate the optimal degrader thickness corresponding to the maximum of the X-ray yield distribution, resulting in a value of ∼ 516 μm for the given target density. The study shows that a difference of only 150–160 μm in the degrader thickness with respect to the optimal value will cause a reduction of a factor if ∼3 in the X-ray yield of the gaseous target, thus indicating the critical role of the degrader optimization for the success of the SIDDHARTA-2 experiment.

The helium gas in the target cell was stored at $1.5\%$ of the liquid helium-4 density (namely $1.88$ g ${\mathrm{L}}^{-1}$), which is also the same as the chosen deuterium density for the data-taking campaign of SIDDHARTA-2. The optimization of the degrader thickness for the kaonic helium was a fundamental step in the view of the kaonic deuterium measurement since this kind of study cannot be performed with a deuterium gaseous target as it would require a totally unrealistic amount of time due to its low X-ray yield.

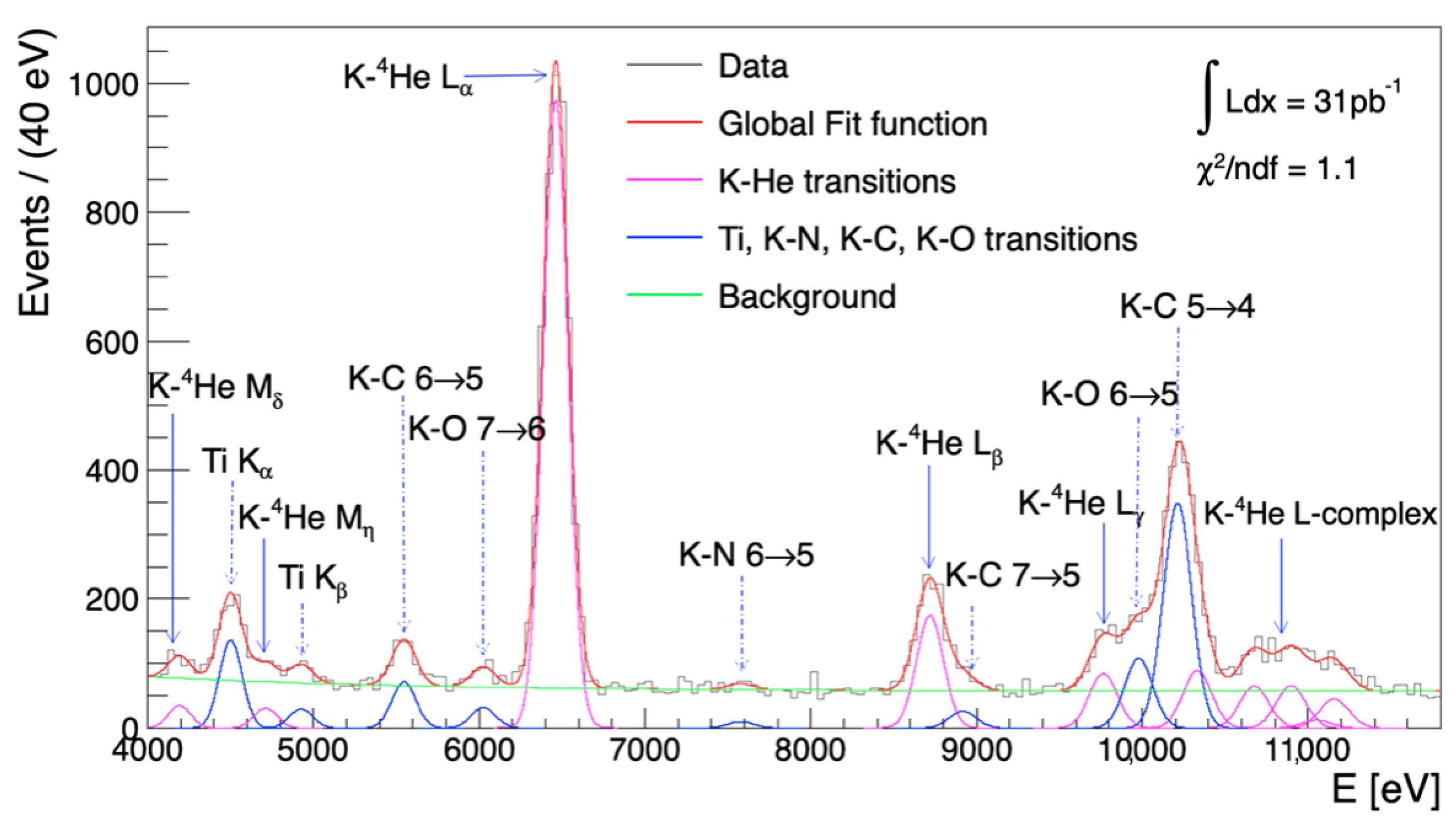
4. The Kaonic Helium-4 Energy Shift and Width

The fit to the final spectrum is shown in Figure 9. After the data selection, the kaonic helium-4 L-series lines are clearly visible, together with the ${\mathrm{M}}_{\delta }$ and ${\mathrm{M}}_{\eta }$ lines. The additional transition lines are the result of kaons stopped in the materials of the experimental apparatus: the kaonic carbon, oxygen, and nitrogen transitions arise from kaons stopped in the Kapton walls (${\mathrm{C}}_{22}$${\mathrm{H}}_{10}$${\mathrm{N}}_2$${\mathrm{O}}_5$). The kaonic helium-4 peaks are fitted to extract their energies. To account for the intrinsic line width (Γ) induced by the strong interaction, the kaonic helium peaks are fitted with a Lorentzian function:

$$L\left(E\right)=\frac{1}{\pi }\frac{\frac{1}{2}\mathrm{\Gamma }}{{(E-E_0)}^2+{\left(\frac{1}{2}\mathrm{\Gamma }\right)}^2},$$

(4)

convoluted with a Gaussian function. The other kaonic peaks are fitted with a Gaussian only, since the broadening of the energy level due to the strong interaction can be neglected. For the background, an exponential function was chosen:

$$bkg\left(E\right)=k+A·e^{-\lambda E},$$

(5)

where k is a constant offset and A and $\lambda$ are the amplitude and the scale of the exponential function, respectively. The global fit properly reproduces the energy distribution measured by the SDDs in the $4÷12$ keV range with a ${\chi }^2/ndf=181.4/160\simeq 1.1$.

From the fit, one can extract the value of the $3d\to 2p$ transition energy and its intrinsic width; the measured value is $E_{3d\to 2p}^{meas}=6461.3\pm 1.2\mathrm{eV}$, to be compared to the QED nominal value $E_{3d\to 2p}^{QED}=6463.3\mathrm{eV}$. The extracted value of the shift of the $2p$ level and its measured intrinsic width induced by the strong interaction are then

$${\epsilon }_{2p}=2.0\pm 1.2\left(\mathrm{stat}\right)\pm 1.5\left(\mathrm{syst}\right)\mathrm{eV},$$

$${\mathrm{\Gamma }}_{2p}=1.9\pm 5.7\left(\mathrm{stat}\right)\pm 0.7\left(\mathrm{syst}\right)\mathrm{eV}.$$

The systematic uncertainties of these quantities come from the calibration process of the SDDs in DAΦNE (see Section 3.1). Both the shift and the width induced by the strong interaction are compatible with the hypothesis of null values inside the error bars, in agreement with the theoretical models and with the previous results obtained by E570 [30] and by SIDDHARTA [15]. The new measurement of the kaonic helium ${\mathrm{L}}_{\alpha }$ transition, compared to the value of the shift measured by SIDDHARTA ${\epsilon }_{2p}=0\pm 6\left(\mathrm{stat}\right)\pm 2\left(\mathrm{syst}\right)\mathrm{eV}$, shows an improved accuracy, with a statistical uncertainty six times smaller than the SIDDHARTA one.

5. Conclusions

The purpose of the SIDDHARTA-2 experiment running at the DAΦNE collider of INFN-LNF is to perform the pioneering measurement of the shift and broadening induced by the strong interaction to the $1s$ atomic level of kaonic deuterium.

The current work presents the characterization of the SIDDHARTA-2 experimental setup, together with an experimental fine tuning aiming at the optimization of the degrader used by the experiment. The latter is crucial for the success of the measurement due to the extremely low X-ray yield of the kaonic deuterium transition to the fundamental level. A degrader with an inappropriate thickness would drastically reduce the already low signal yield. The run used a gaseous helium-4 target, which features an X-ray yield nearly 100 times higher than that expected from kaonic deuterium, operating at a density of $1.5\%$ of the liquid helium-4 density. A new measurement of the L-series lines of the kaonic helium-4 was used to study the performance of the new apparatus. A total of 31 ${\mathrm{pb}}^{-1}$ were collected.

The analysis of the collected data yielded a shift and a width of the $2p$ level of kaonic helium-4 of ${\mathsf{\epsilon }}_{2p}=2.0\pm 1.2\left(\mathrm{stat}\right)\pm 1.5\left(\mathrm{syst}\right)\mathrm{eV}$ and ${\mathrm{\Gamma }}_{2p}=1.9\pm 5.7\left(\mathrm{stat}\right)\pm 0.7\left(\mathrm{syst}\right)\mathrm{eV}$, thus excluding the hypothesis of a large shift, in good agreement with the theoretical models and with the previous experimental results. The new result exhibits an enhanced precision with respect to the measurement performed by SIDDHARTA [15] and highlights the excellent performance of the SIDDHARTA-2 apparatus, thus confirming it as the leading experiment for the challenging measurement of kaonic deuterium.