Topological Phase Diagram of an Interacting Kitaev Chain: Mean Field versus DMRG Study
Abstract
1. Introduction
2. Theoretical Model
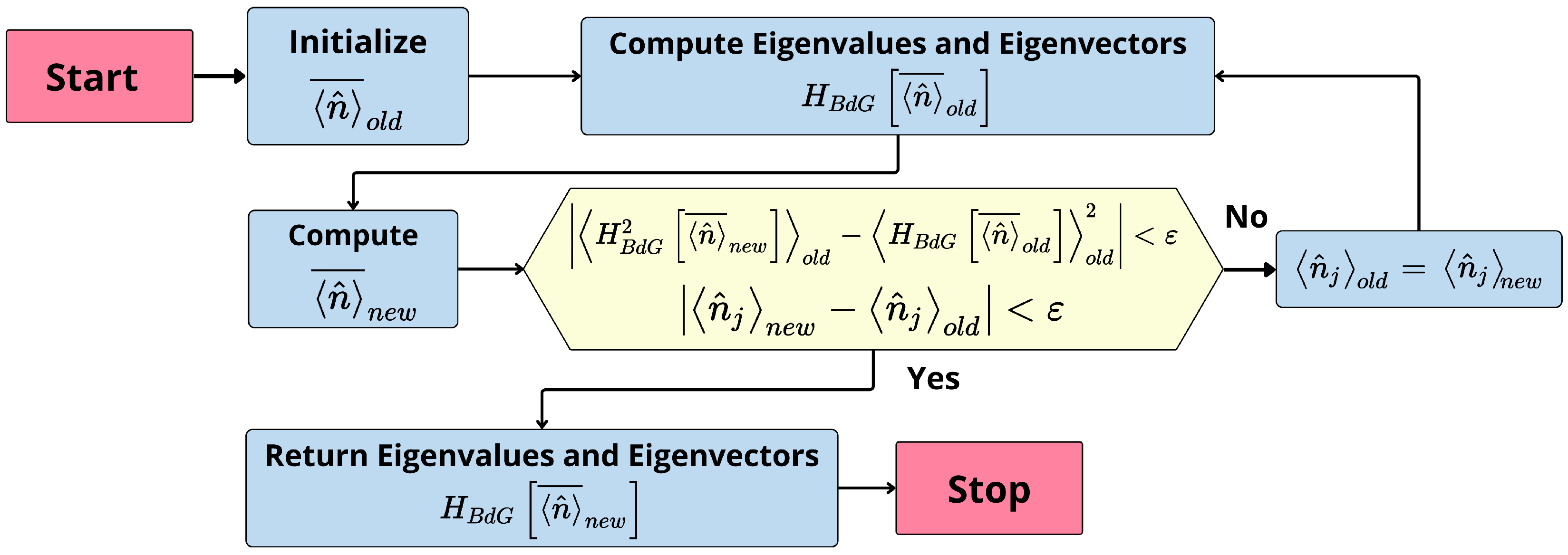
2.1. Mean-Field Approximation
2.1.1. Zero-Temperature Case
2.1.2. Finite-Temperature Case
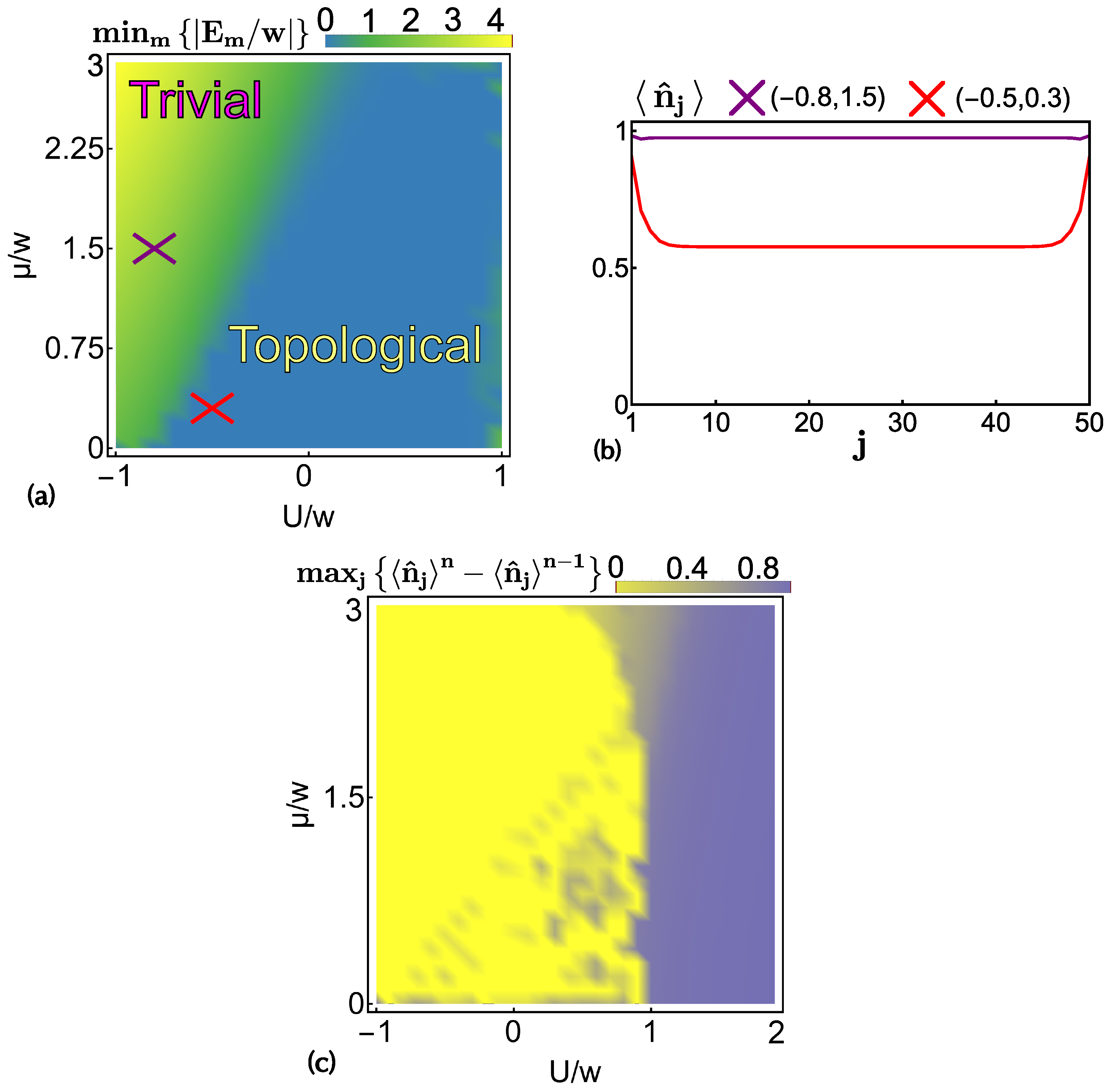
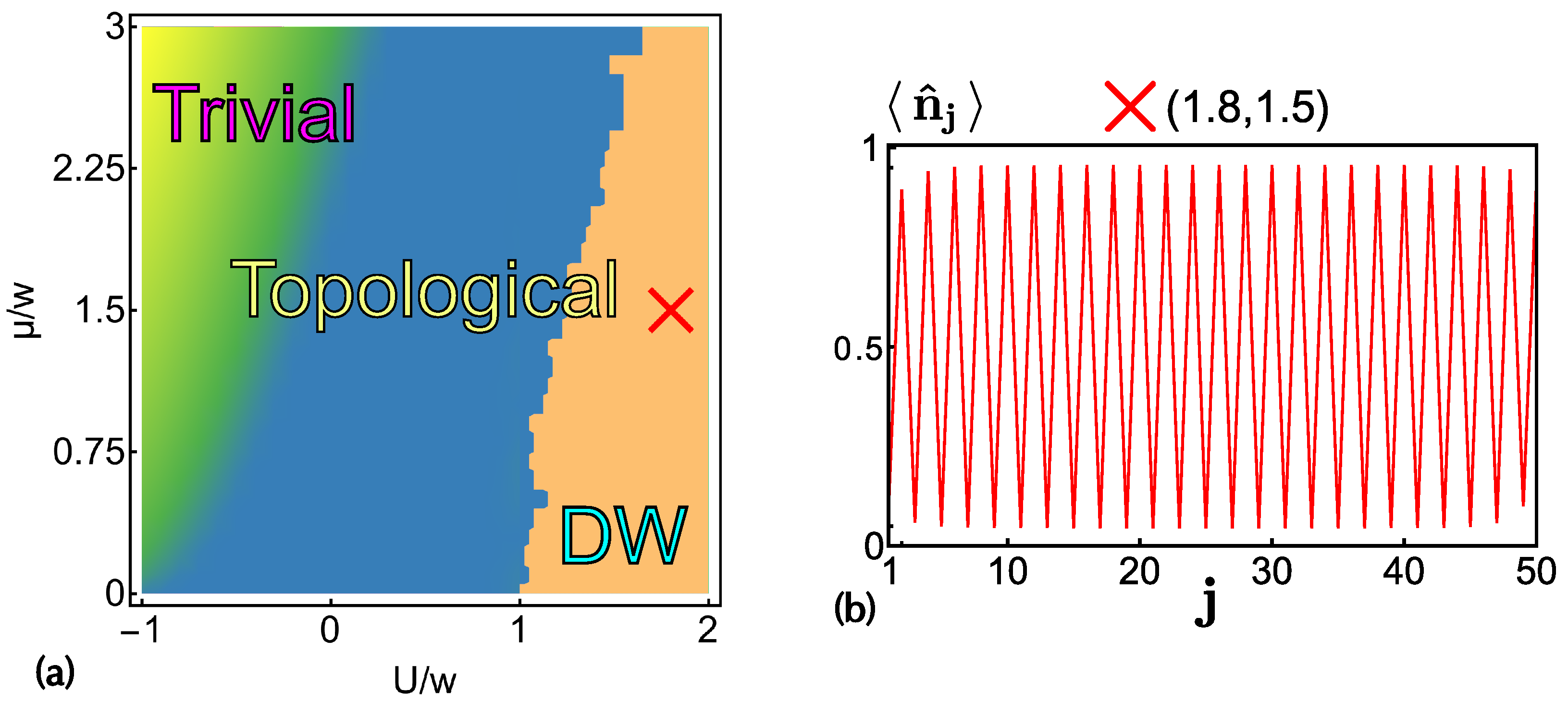
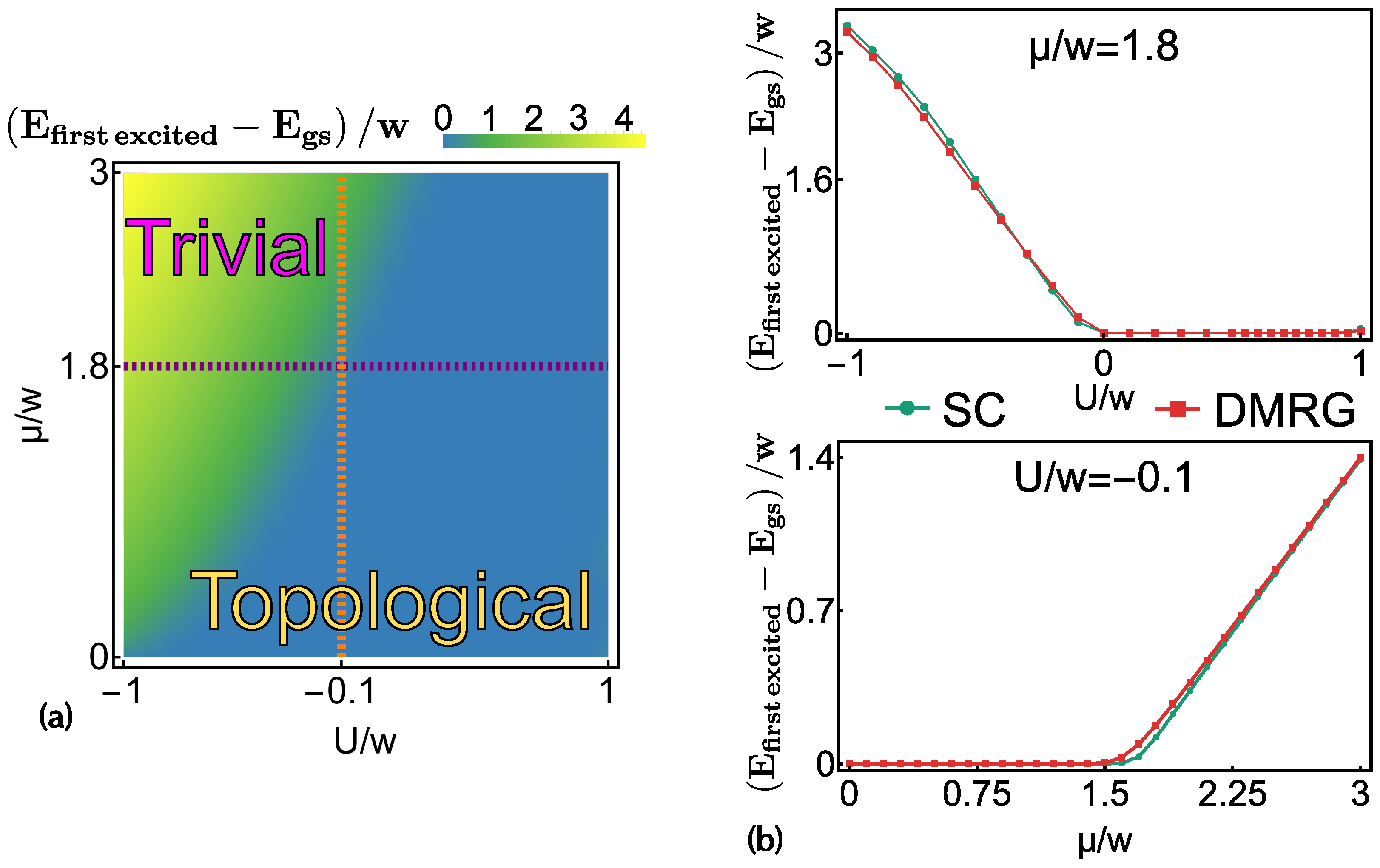
3. Numerical Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Read, N.; Green, D. Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries and the fractional quantum Hall effect. Phys. Rev. B 2000, 61, 10267–10297. [Google Scholar] [CrossRef]
- Maiellaro, A.; Romeo, F.; Citro, R. Topological phase diagram of a Kitaev ladder. Eur. Phys. J. Spec. Top. 2018, 227, 1397–1404. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
- Maiellaro, A.; Romeo, F.; Perroni, C.A.; Cataudella, V.; Citro, R. Unveiling Signatures of Topological Phases in Open Kitaev Chains and Ladders. Nanomaterials 2019, 9, 894. [Google Scholar] [CrossRef] [PubMed]
- Choy, T.P.; Edge, J.M.; Akhmerov, A.R.; Beenakker, C.W.J. Majorana fermions emerging from magnetic nanoparticles on a superconductor without spin-orbit coupling. Phys. Rev. B 2011, 84, 195442. [Google Scholar] [CrossRef]
- Tauber, C.; Delplace, P.; Venaille, A. Anomalous bulk-edge correspondence in continuous media. Phys. Rev. Res. 2020, 2, 013147. [Google Scholar] [CrossRef]
- Maiellaro, A.; Romeo, F.; Illuminati, F.; Citro, R. Resilience of topological superconductivity under particle current. Phys. Rev. B 2023, 107, 064505. [Google Scholar] [CrossRef]
- Maiellaro, A.; Romeo, F.; Illuminati, F. Edge states, Majorana fermions, and topological order in superconducting wires with generalized boundary conditions. Phys. Rev. B 2022, 106, 155407. [Google Scholar] [CrossRef]
- Brouwer, P.W.; Duckheim, M.; Romito, A.; von Oppen, F. Topological superconducting phases in disordered quantum wires with strong spin-orbit coupling. Phys. Rev. B 2011, 84, 144526. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Unpaired Majorana fermions in quantum wires. Phys.-Uspekhi 2001, 44, 131–136. [Google Scholar] [CrossRef]
- Chen, X.; Gu, Z.C.; Wen, X.G. Local unitary transformation, long-range quantum entanglement, wave function renormalization, and topological order. Phys. Rev. B 2010, 82, 155138. [Google Scholar] [CrossRef]
- Maiellaro, A.; Citro, R. Topological Edge States of a Majorana BBH Model. Condens. Matter 2021, 6, 15. [Google Scholar] [CrossRef]
- Ludwig, A.W.W. Topological phases: Classification of topological insulators and superconductors of non-interacting fermions, and beyond. Phys. Scr. 2015, T168, 014001. [Google Scholar] [CrossRef]
- Maiellaro, A.; Illuminati, F.; Citro, R. Topological Phases of an Interacting Majorana Benalcazar-Bernevig-Hughes Model. Condens. Matter 2022, 7, 26. [Google Scholar] [CrossRef]
- Chiu, C.K.; Teo, J.C.Y.; Schnyder, A.P.; Ryu, S. Classification of topological quantum matter with symmetries. Rev. Mod. Phys. 2016, 88, 035005. [Google Scholar] [CrossRef]
- Maiellaro, A.; Romeo, F.; Citro, R. Topological phase diagram of coupled spinless p-wave superconductors. J. Phys. Conf. Ser. 2019, 1226, 012015. [Google Scholar] [CrossRef]
- Pachos, J.K. Topological Quantum Computation; Springer: Berlin/Heidelberg, Germany, 2013; pp. 150–179. [Google Scholar] [CrossRef]
- Sarma, S.D.; Freedman, M.; Nayak, C. Majorana zero modes and topological quantum computation. NPJ Quantum Inf. 2015, 1, 15001. [Google Scholar] [CrossRef]
- Lahtinen, V.; Pachos, J.K. A Short Introduction to Topological Quantum Computation. SciPost Phys. 2017, 3, 021. [Google Scholar] [CrossRef]
- Kraus, C.V.; Zoller, P.; Baranov, M.A. Braiding of Atomic Majorana Fermions in Wire Networks and Implementation of the Deutsch-Jozsa Algorithm. Phys. Rev. Lett. 2013, 111, 203001. [Google Scholar] [CrossRef]
- Maiellaro, A.; Citro, R. Non-Hermitian topological phases in an extended Kitaev model. J. Phys. Conf. Ser. 2020, 1548, 012026. [Google Scholar] [CrossRef]
- Maiellaro, A.; Romeo, F.; Citro, R. Effects of geometric frustration in Kitaev chains. Eur. Phys. J. Plus 2021, 136, 627. [Google Scholar] [CrossRef]
- Beenakker, C. Search for Majorana Fermions in Superconductors. Annu. Rev. Condens. Matter Phys. 2013, 4, 113–136. [Google Scholar] [CrossRef]
- Rao, S. Introduction to abelian and non-abelian anyons. arXiv 2016, arXiv:1610.09260. [Google Scholar] [CrossRef]
- Chakhalian, J.; Millis, A.J.; Rondinelli, J. Whither the oxide interface. Nat. Mater. 2012, 11, 92–94. [Google Scholar] [CrossRef] [PubMed]
- Scheurer, M.S.; Schmalian, J. Topological superconductivity and unconventional pairing in oxide interfaces. Nat. Commun. 2015, 6, 6005. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, M.; Rao, M.; Venkatesan, T.; Fortunato, E.; Barquinha, P.; Branquinho, R.; Salgueiro, D.; Martins, R.; Carlos, E.; Liu, A.; et al. The 2016 oxide electronic materials and oxide interfaces roadmap. J. Phys. D Appl. Phys. 2016, 49. [Google Scholar] [CrossRef]
- Perroni, C.A.; Cataudella, V.; Salluzzo, M.; Cuoco, M.; Citro, R. Evolution of topological superconductivity by orbital-selective confinement in oxide nanowires. Phys. Rev. B 2019, 100, 094526. [Google Scholar] [CrossRef]
- Guarcello, C.; Citro, R. Progresses on topological phenomena, time-driven phase transitions, and unconventional superconductivity. Europhys. Lett. 2020, 132, 60003. [Google Scholar] [CrossRef]
- Barthelemy, A.; Bergeal, N.; Bibes, M.; Caviglia, A.; Citro, R.; Cuoco, M.; Kalaboukhov, A.; Kalisky, B.; Perroni, C.A.; Santamaria, J.; et al. Quasi-two-dimensional electron gas at the oxide interfaces for topological quantum physics. EPL (Europhys. Lett.) 2021, 133, 17001. [Google Scholar] [CrossRef]
- Trier, F.; Noël, P.; Kim, J.V.; Attané, J.P.; Vila, L.; Bibes, M. Oxide spin-orbitronics: Spin–charge interconversion and topological spin textures. Nat. Rev. Mater. 2021, 7, 258–274. [Google Scholar] [CrossRef]
- Maiellaro, A.; Settino, J.; Guarcello, C.; Romeo, F.; Citro, R. Hallmarks of orbital-flavored Majorana states in Josephson junctions based on oxide nanochannels. Phys. Rev. B 2023, 107, l201405. [Google Scholar] [CrossRef]
- Ohtomo, A.; Hwang, H.Y. A high-mobility electron gas at the LaAlO3/SrTiO3 heterointerface. Nature 2004, 427, 423–426. [Google Scholar] [CrossRef] [PubMed]
- Bristowe, N.C.; Ghosez, P.; Littlewood, P.B.; Artacho, E. The origin of two-dimensional electron gases at oxide interfaces: Insights from theory. J. Phys. Condens. Matter 2014, 26, 143201. [Google Scholar] [CrossRef] [PubMed]
- Caviglia, A.D.; Gabay, M.; Gariglio, S.; Reyren, N.; Cancellieri, C.; Triscone, J.M. Tunable Rashba Spin-Orbit Interaction at Oxide Interfaces. Phys. Rev. Lett. 2010, 104, 126803. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Z.; Tóth, A.; Held, K. Theory of spin-orbit coupling at LaAlO3/SrTiO3 interfaces and SrTiO3 surfaces. Phys. Rev. B 2013, 87, 161102. [Google Scholar] [CrossRef]
- Reyren, N.; Thiel, S.; Caviglia, A.D.; Kourkoutis, L.F.; Hammerl, G.; Richter, C.; Schneider, C.W.; Kopp, T.; Ruetschi, A.S.; Jaccard, D.; et al. Superconducting Interfaces between Insulating Oxides. Science 2007, 317, 1196–1199. [Google Scholar] [CrossRef] [PubMed]
- Caviglia, A.D.; Gariglio, S.; Reyren, N.; Jaccard, D.; Schneider, T.; Gabay, M.; Thiel, S.; Hammerl, G.; Mannhart, J.; Triscone, J.M. Electric field control of the LaAlO3/SrTiO3 interface ground state. Nature 2008, 456, 624–627. [Google Scholar] [CrossRef] [PubMed]
- Lutchyn, R.M.; Sau, J.D.; Sarma, S.D. Majorana Fermions and a Topological Phase Transition in Semiconductor-Superconductor Heterostructures. Phys. Rev. Lett. 2010, 105, 077001. [Google Scholar] [CrossRef]
- Oreg, Y.; Refael, G.; von Oppen, F. Helical Liquids and Majorana Bound States in Quantum Wires. Phys. Rev. Lett. 2010, 105, 177002. [Google Scholar] [CrossRef]
- Maiellaro, A.; Romeo, F.; Citro, R.; Illuminati, F. Squashed entanglement in one-dimensional quantum matter. Phys. Rev. B 2023, 107, 115160. [Google Scholar] [CrossRef]
- Jünemann, J.; Piga, A.; Ran, S.J.; Lewenstein, M.; Rizzi, M.; Bermudez, A. Exploring Interacting Topological Insulators with Ultracold Atoms: The Synthetic Creutz-Hubbard Model. Phys. Rev. X 2017, 7, 031057. [Google Scholar] [CrossRef]
- Maiellaro, A.; Marino, A.; Illuminati, F. Topological squashed entanglement: Nonlocal order parameter for one-dimensional topological superconductors. Phys. Rev. Res. 2022, 4, 033088. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, S.C. Simplified Topological Invariants for Interacting Insulators. Phys. Rev. X 2012, 2, 031008. [Google Scholar] [CrossRef]
- Schollwöck, U. The density-matrix renormalization group. Rev. Mod. Phys. 2005, 77, 259–315. [Google Scholar] [CrossRef]
- Schollwöck, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 2011, 326, 96–192. [Google Scholar] [CrossRef]
- Fröwis, F.; Nebendahl, V.; Dür, W. Tensor operators: Constructions and applications for long-range interaction systems. Phys. Rev. A 2010, 81, 062337. [Google Scholar] [CrossRef]
- Hassler, F.; Schuricht, D. Strongly interacting Majorana modes in an array of Josephson junctions. New J. Phys. 2012, 14, 125018. [Google Scholar] [CrossRef]
- Thomale, R.; Rachel, S.; Schmitteckert, P. Tunneling spectra simulation of interacting Majorana wires. Phys. Rev. B 2013, 88, 161103. [Google Scholar] [CrossRef]
- Milsted, A.; Seabra, L.; Fulga, I.C.; Beenakker, C.W.J.; Cobanera, E. Statistical translation invariance protects a topological insulator from interactions. Phys. Rev. B 2015, 92, 085139. [Google Scholar] [CrossRef]
- Kells, G.; Moran, N.; Meidan, D. Localization enhanced and degraded topological order in interacting p-wave wires. Phys. Rev. B 2018, 97, 085425. [Google Scholar] [CrossRef]
- Miao, J.J.; Jin, H.K.; Zhang, F.C.; Zhou, Y. Majorana zero modes and long range edge correlation in interacting Kitaev chains: Analytic solutions and density-matrix-renormalization-group study. Sci. Rep. 2018, 8, 488. [Google Scholar] [CrossRef] [PubMed]
- Katsura, H.; Schuricht, D.; Takahashi, M. Exact ground states and topological order in interacting Kitaev/Majorana chains. Phys. Rev. B 2015, 92, 115137. [Google Scholar] [CrossRef]
- Miao, J.J.; Jin, H.K.; Zhang, F.C.; Zhou, Y. Exact Solution for the Interacting Kitaev Chain at the Symmetric Point. Phys. Rev. Lett. 2017, 118, 267701. [Google Scholar] [CrossRef] [PubMed]
- Gangadharaiah, S.; Braunecker, B.; Simon, P.; Loss, D. Majorana Edge States in Interacting One-Dimensional Systems. Phys. Rev. Lett. 2011, 107, 036801. [Google Scholar] [CrossRef] [PubMed]
- Rahmani, A.; Zhu, X.; Franz, M.; Affleck, I. Phase diagram of the interacting Majorana chain model. Phys. Rev. B 2015, 92, 235123. [Google Scholar] [CrossRef]
- Sela, E.; Altland, A.; Rosch, A. Majorana fermions in strongly interacting helical liquids. Phys. Rev. B 2011, 84, 085114. [Google Scholar] [CrossRef]
- Stoudenmire, E.M.; Alicea, J.; Starykh, O.A.; Fisher, M.P. Interaction effects in topological superconducting wires supporting Majorana fermions. Phys. Rev. B 2011, 84, 014503. [Google Scholar] [CrossRef]
- Gergs, N.M.; Fritz, L.; Schuricht, D. Topological order in the Kitaev/Majorana chain in the presence of disorder and interactions. Phys. Rev. B 2016, 93, 075129. [Google Scholar] [CrossRef]
- Fishman, M.; White, S.; Stoudenmire, E. The ITensor Software Library for Tensor Network Calculations. SciPost Phys. Codebases 2022. [Google Scholar] [CrossRef]
- Vionnet, G.; Kumar, B.; Mila, F. Level crossings induced by a longitudinal coupling in the transverse field Ising chain. Phys. Rev. B 2017, 95, 174404. [Google Scholar] [CrossRef]
- Gennes, P.G. Superconductivity of Metals and Alloys; Nobel Laureate Pierre-Gilles de Gennes’s lecture note volume; CRC Press; Taylor & Francis Group: Boca Raton, FL, USA, 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nunziante, G.; Maiellaro, A.; Guarcello, C.; Citro, R. Topological Phase Diagram of an Interacting Kitaev Chain: Mean Field versus DMRG Study. Condens. Matter 2024, 9, 20. https://doi.org/10.3390/condmat9010020
Nunziante G, Maiellaro A, Guarcello C, Citro R. Topological Phase Diagram of an Interacting Kitaev Chain: Mean Field versus DMRG Study. Condensed Matter. 2024; 9(1):20. https://doi.org/10.3390/condmat9010020
Chicago/Turabian StyleNunziante, Giovanni, Alfonso Maiellaro, Claudio Guarcello, and Roberta Citro. 2024. "Topological Phase Diagram of an Interacting Kitaev Chain: Mean Field versus DMRG Study" Condensed Matter 9, no. 1: 20. https://doi.org/10.3390/condmat9010020
APA StyleNunziante, G., Maiellaro, A., Guarcello, C., & Citro, R. (2024). Topological Phase Diagram of an Interacting Kitaev Chain: Mean Field versus DMRG Study. Condensed Matter, 9(1), 20. https://doi.org/10.3390/condmat9010020





