Next Article in Journal
The Effect of Acyl Chain Position on the 2D Monolayer Formation of Monoacyl-sn-Glycerol at the Air/Water Interface: Quantum Chemical Modeling
Previous Article in Journal
Tc Saturation and Possible Electronic Phase Separation in Strongly Overdoped Cuprates
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Condensed Matter
Volume 8
Issue 3
10.3390/condmat8030057
condensedmatter-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Tensile Microstrain Fluctuations in the BaPbO Units in Superconducting BaPb1−xBixO3 by Scanning Dispersive Micro-XANES

by
Ruben Albertini
1,
Salvatore Macis
1,2,*,
Andrei A. Ivanov
3,
Alexey P. Menushenkov
3,
Alessandro Puri
4,
Virginia Monteseguro
5,
Boby Joseph
6,
Wei Xu
1,7,
Augusto Marcelli
1,8,
Paula Giraldo-Gallo
9,
Ian Randal Fisher
10,11,12,
Antonio Bianconi
1,13,* and
Gaetano Campi
1,13,*
1
RICMASS Rome International Centre Materials Science Superstripes Via dei Sabelli 119A, 00185 Rome, Italy
2
Department of Physics, Sapienza University Rome, P.le Aldo Moro 2, 00185 Rome, Italy
3
Department of Solid State Physics and Nanostructures, National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), 115409 Moscow, Russia
4
CNR-IOM-OGG c/o ESRF-The European Synchrotron, 71 Avenue des Martyrs, 38000 Grenoble, France
5
Condensed Matter Physics Department, MALTA Consolider Team, Facultad de Ciencias, University of Cantabria, 39005 Santander, Spain
6
Elettra-Sincrotrone Trieste, Basovizza, 34149 Trieste, Italy
7
Institute of High Energy Physics (IHEP), Chinese Academy of Sciences, Beijing 100039, China
8
INFN—Laboratori Nazionali di Frascati, 00044 Frascati, Italy
9
Department of Physics, Universidad de Los Andes, Bogotá 111711, Colombia
10
Department of Applied Physics, Stanford University, Stanford, CA 94305, USA
11
Geballe Laboratory for Advanced Materials, Stanford University, Stanford, CA 94305, USA
12
Stanford Institute for Materials and Energy Sciences, SLAC National Accelerator Laboratory, 2575 Sand Hill Road, Menlo Park, CA 94025, USA
13
Institute of Crystallography, National Research Council of Italy, Via Salaria Km 29.300, Monterotondo Stazione, 00015 Rome, Italy
 
add Show full affiliation list
 
remove Hide full affiliation list
*
Authors to whom correspondence should be addressed.
Condens. Matter 2023, 8(3), 57; https://doi.org/10.3390/condmat8030057
Submission received: 4 May 2023 / Revised: 6 July 2023 / Accepted: 7 July 2023 / Published: 11 July 2023
(This article belongs to the Section Superconductivity)
Browse Figures
Review Reports Versions Notes

Abstract

:
BaPb1−xBixO3 (BPBO) bismuthate, showing high TC superconductivity for 0.05 < x < 0.35, is an archetypal system for studying the complex inhomogeneity of perovskite lattice favoring the emergence of quantum coherence, called the superstripes phase. Local lattice fluctuations, detected by EXAFS; nanoscale stripes, detected by electron microscopy; and two competing crystalline structures, detected by diffraction, are known to characterize the superconducting phase. At nanoscale [BaBiO3] centered nanoscale units (BBO) coexist with BaPbO3 centered (BPO) units in the BPBO perovskite; therefore, we expect a tensile microstrain in BPO units due the misfit strain between the two different lattices. Here, we report the measurement of the spatial micro-fluctuations of the local tensile microstrain ε in the BaPO units in superconducting Ba(Pb1−xBix)O3 crystals with x1 = 0.19 an x2 = 0.28. We show here the feasibility of applying the scanning dispersive micro-X-ray absorption near edge structure (SdμXANES) technique, using focused synchrotron radiation, to probe the microscale spatial fluctuations of the microstrain in BPO units. This unconventional real-space SdμXANES microscopy at the Pb L3 edge has been collected in the dispersive mode. Our experimental method allows us to measure either the local Bi chemical concentration x and the local lattice microstrain of local BBO and BPO units. The 5 × 5 micron-size spots from the focused X-ray beam allowed us to obtain maps of 1600 points covering an area of 200 × 200 microns. The mapping shows a substantial difference between the spatial fluctuations of the microstrain ε and the chemical inhomogeneity x. Moreover, we show the different relations ε(x) in samples with lower (x1 = 0.19) and higher (x2 = 0.28) doping respect to the optimum doping (x = 0.25).

1. Introduction

The critical temperature of the superconducting transition and electronic structure at the Fermi level in quantum complex matter and high temperature superconductors is governed not only by doping, but also by the lattice strain in nickelates, iron-based superconductors, and heterostructures [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24] controlling the complex landscape generated by nanoscale phase separation [24,25,26,27,28,29] near the superconductor–insulator transition [30], as it was first shown in cuprates and diborides [18,19,20,21,22,23]. In this work we apply scanning μ-X-ray absorption near edge structure (SµXANES) to unveil the spatial heterogeneity of local lattice fluctuations [31,32,33,34,35] in a selected nanocluster related to the strain at specific sites, namely, microstrain spatial fluctuations near the metal to insulator transition in BaPb1−xBixO3. [36,37,38,39].
The dimorphic crystal structure of BaPb1−xBixO3 superconducting compounds is a distorted perovskite (ABO3) for the highest Bi concentrations and contains two Bi sites with different Bi-O bond lengths [40,41,42,43,44,45,46,47,48,49,50,51,52]. BaPb1−xBixO3 can be described as a composite heterostructure made of p-n junctions formed by a low charge carrier density (1021 cm−3) metallic BaPbO nanoscale units, and a charge density wave (CDW) of semiconducting BaBiO nanoscale units. With increasing Pb content, the insulating CDW phase disappears, giving rise to a metallic phase, where superconductivity appears at x > 0.05 and the metal insulator transition at x = 0.35. Recently, there has been increased interest in the artificial synthesis of thin film heterostructures providing the signature of 2D interface superconductivity in a landscape of nanoscale phase separation [53,54,55,56,57,58,59,60]. X-ray absorption near edge structure, called XANES spectroscopy, [61,62,63,64,65,66,67,68] provides a local and fast probe of the local lattice fluctuations probing nanoscale phase separation. It has been applied to investigate powder samples of BaPb1−xBixO3 [69,70,71] but its spatial inhomogeneities are unknown.
The BaPb1−xBixO3 structure [36,37,38,39], shown in Figure 1a, has a rich phase diagram due to the inter-relation between multiple perovskite structures as a function of temperature and doping [72,73,74,75]. In the region of 0.05 < x < 0.35, the diamagnetic signal increases and the material becomes superconducting. In this regime, its structure is polymorphic [36,37,38,39] with a fraction of its volume with orthorhombic Ibmm symmetry and the rest with tetragonal I4/mcm symmetry. The critical temperature TC as a function of the bismuth content x for the samples under study is presented in Figure 1b. For x values over the superconducting range until about x = 0.77, only the orthorhombic Ibmm symmetry is observed. In the BaBiO3 phase, the alternation of Bi3+ and Bi5+ leads to structural distortions involving both the so-called breathing distortions and the tilting of BiO6 octahedra, which lowers the crystal symmetry from a cubic to a monoclinic space group.
High-resolution transmission electron microscopy (HRTEM) has been used to unveil the emergence of structural stripes at the nanoscale in single crystals of BaPb1−xBixO3 [39]. The stripe-like morphology found in this study has a deep significance; it might provide a natural clue to understanding the characteristic behavior observed at the superconductor–insulator transition close to optimal doping in BaPb1−xBixO3, motivating a theoretical investigation of the percolation effects near the quantum phase transition in any material with a striped morphology.
While it is known that a misfit strain generates a complex nanoscale phase separation in cuprates [19,20,21,22,23,24,25,26,27,28] and iron-based superconductors with a percolative network, the misfit strain in Ba(Pb1−xBix)O3 has not yet been reported. In this work, we have used SµXANES to investigate the spatial distribution of microstrain in three BaPb1−xBixO3 samples with x = 0, 0.19 and 0.28 (full red circles in Figure 1b) to obtain a deeper insight into the relationship between local lattice inhomogeneity and superconductivity in this system.

2. Results

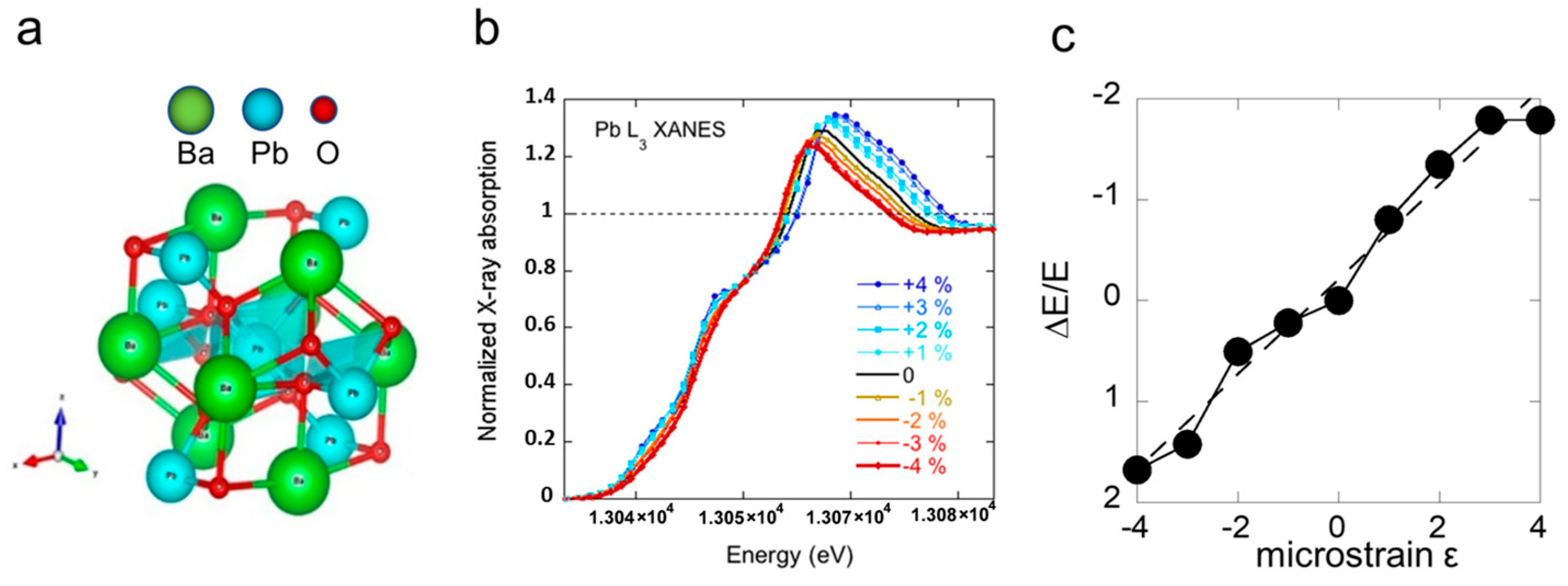
2.1. Variation of the Local Structure of BaPbO3 0.5 nm Nano Cluster Units in BaPb1−xBixO3

In intrinsically inhomogeneous composites, in nanoscale units, the microstrain is generated by the lattice misfit strain originating from the coexistence of different units with different lattice parameters occurring during the cubic-to-tetragonal and tetragonal-to-orthorhombic transitions. This mechanism results in a multi-domain microstructure with many incoherent boundaries, and originates the local lattice microstrain ε.
It has been proposed that the mobility of the charge carriers, moving through octahedra, may be favored by the tetragonal symmetry while carriers’ localization takes place when the symmetry decreases to the orthorhombic and then to the monoclinic phase with an increasing bismuth content; still, the spatial inhomogeneity of charge and lattice remains unknown.

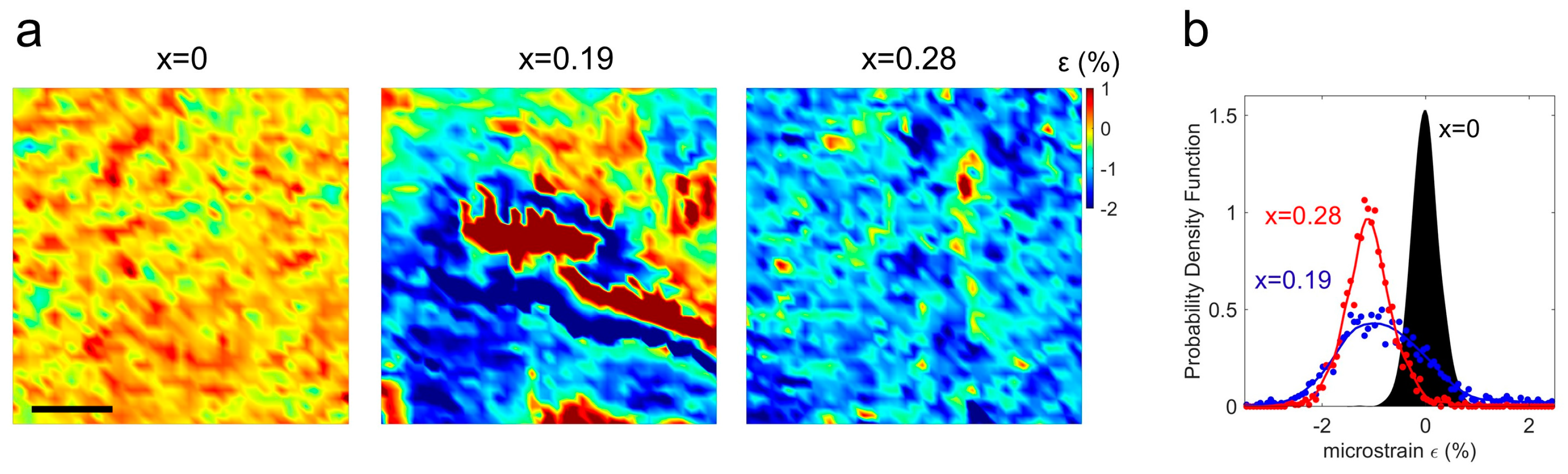
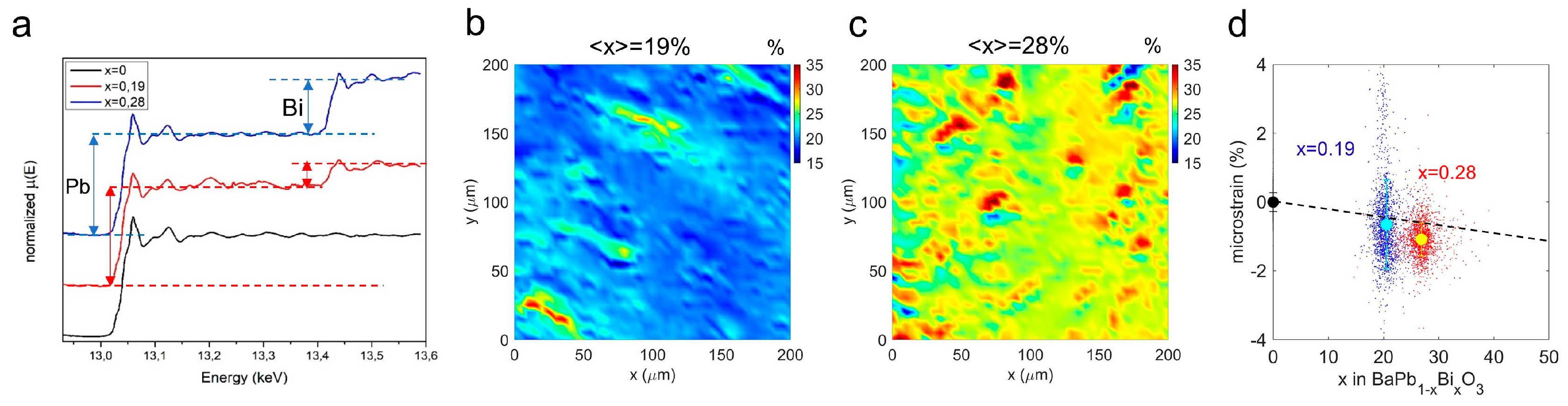
2.2. Scanning Micro XANES Microscopy: Microstrain Maps and Phase Separation

The SµXANES technique is a unique tool to investigate the local atomic lattice structure via multiple scattering resonances of the excited photoelectron probing the geometry of the local clusters surrounding selected atomic species. The local structure of the atomic cluster centered at the Pb-absorbing atom is shown in Figure 2a.
We have first calculated the XANES profiles at the Pb L3 edge for the cluster with the Pb ion at the center and different microstrain values using the full multiple-scattering approach. Calculated Pb L3 XANES are shown in Figure 2b, while the relative variation of the energy of the highest peak due to the multiple scattering resonance (MSR) as a function of the tensile or compressive microstrain is presented in Figure 2c.
The spatial distribution of the strain at different doping has been investigated by SµXANES using focused synchrotron radiation that allowed us to identify the spatial inhomogeneity at the micron scale related to incipient phase separation. Samples of superconducting BaPb1−xBixO3 single crystals with x = 0, 0.19 and 0.28 were scanned on a 200 × 200 µm2 area with a 5 µm step in both directions. Data have been collected at the ESRF beamline ID24 (Grenoble, France), which is equipped with an energy dispersive X-ray spectrometer and a unique setup for real-space scanning with variable temperature [7].
In Figure 3, we show XANES spectra at the Pb L3 edge, where the maximum absorption peak is due to the multiple scattering resonance (MSR) of the excited photoelectron, also called the Fano shape resonance in the continuum, at about 32 eV above the absorption threshold taken as zero energy. Alongside XANES spectra, we also show their first derivatives where we clearly recognize three peaks. The energy at 13027 eV has been chosen as the reference zero value for the energy scale while the energy of the multiple scattering resonance (EMSR) has been defined as the difference between the zero of the derivatives, E0, and the first derivative peak, P1:
E M S R = E 0 − P 1
MSR energy, EMSR, of the photoelectron confined in a nanoscale BPO cluster centered at the Pb-absorbing atom probes the variations of the average Pb–O bond length and its spatial variation. In this regard, EMSR is a sensitive measure of the local lattice strain at Pb sites. It is fundamental to remember that slight variations of the average bond distance (R) can be attributed to the dependence of phase shifts in the framework of the multiple scattering model [39].
It is known that the energy variation of the main multiple-scattering resonance in the XANES spectra is connected with Pb–O average distance in the cluster, R, by
E M S R ∝ R − 2
where the XANES microstrain can be calculated as
∆ R R = − 1 2 ∆ E M S R E M S R
where
∆ E M S R = E M S R − E M S R ¯
In the undoped (x = 0) BaPbO3 sample, the peak around its average value E M S R ¯ is relatively narrow and has been taken as reference for measuring the microstrain variation.
Measurements of single crystals of BaPb1−xBixO3 with different Bi compositions around the superconducting maximum [37] (referring to the diagram 1a) show signatures of granular and inhomogeneous superconductivity possibly associated with a nanoscale structural phase separation. Due to different values of Bi valence and the variation of Pb concentration, BaPb1−xBixO3 is polymorphic where different structural phases coexist. It is interesting to analyze how these phases appear in the lattice.
From Pb L3-edge XANES spectra, we obtained real space maps of the EMSR for different doping of BaPb1−xBixO3; then, we have calculated the microstrain referring to Equation (3). Here, we report the micro XANES data results for x = 0.19 and x = 0.28 crystalline samples collected at low temperatures of 50 ± 10 K. The spatial fluctuations of the slight energy shift of the multiple scattering resonance energy in the superconducting Bi-doped samples are compared to the data for the reference undoped BaPbO3 sample. The decreasing trend of the negative energy shift of the main multiple scattering resonance EMSR is attributed to a lattice expansion [39] of the Pb-centered nanoscale puddles increasing with the negative XANES tensile strain.
Figure 4a shows the microstrain maps at different Pb contents. Between the insulating (x = 0) and metallic (x = 0.28) phases, the sample with x = 0.19 presents a large inhomogeneity with a phase separation where microstrain assumes values of insulating and metallic phases in different spatial regions. This disorder behavior is measured by the probability distribution function (PDF), shown in Figure 4b, from which information about lattice strains can be obtained. Indeed, comparing the EMSR value of each point with the average value of the undoped sample, we obtained the local lattice strain for our differently doped compounds.
The extended X-ray absorption spectra of the BaPb1−xBixO3 at either the Pb L3 jump and the Bi L3 edge jump in the stoichiometric compounds at x = 0 and x = 1 allow the direct measure of the bismuth content x at each spot where the microstrain is measured (see Figure 5a).
In this way, we have obtained the maps of x content in the two samples with nominal content x = 0.19 and x = 0.28 shown Figure 5b,c, respectively.
In Figure 5d we visualize the microstrain in the BaPb1−xBixO3-doped samples vs. the Bi content x, where the x = 0.19 and x = 0.28 samples are represented with blue squares and red circles, respectively. The full circles represent the mean values of microstrain and x content in the x = 0.19 x = 0.28 samples, respectively.
The lattice tensile strain as a function of Bi content x measured by crystallography lattice parameters in BaPb1−xBixO3 going from x = 0 to x = 1 follows Vegard’s law represented by the dashed line ε = −2x [36] and the spatial average local microstrain in the Pb-centered clusters in the two BaPb1−xBixO3 samples is indicated by blue and yellow dots in Figure 5. In both samples, the average local tensile strain in Pb-centered clusters is larger than that measured in the average lattice crystal indicated by Vegard’s law.

3. Discussion

We reported local measurements of the lattice strain of BaPb1−xBixO3 for different values of doping. In complex perovskite materials, different structural phases are in competition, and their stability is tuned by the microstrain. These phases cause a local change in the atomic strain that can be observed in the MSR of XANES spectra. The BaPb1−xBixO3 superconductor shows a high-TC superconductivity for 0.05 < x < 0.35, becoming an archetypal system with competitions of different nanoscale units with local lattice symmetry [36,37,38,39,40] which favor the emergence of macroscopic quantum coherence in complex nanoscale phase separation [36,37,38,39,40]. This compound could be described as the complex solid solution of two nanoscale clusters, resulting from metallic [BaPbO3](1−x) and insulating [BaBiO3](x) perovskite units, which are expected to be strained due to the misfit between their different lattices. In the underdoped superconducting phase at x = 0.19 the Pb-centered nanocluster units probed by Pb L3 XANES spectroscopy shown in Figure 2a called BaPO unit shows large spatial tensile microstrain fluctuations in the range −0.1%<ε< −2%, while the Vegard’s law expected value is −0.38%.
In the overdoped regime at x = 0.28 the tensile microstrain fluctuations are strongly reduced and centered ε= −1% which is larger than the expected value of −0.5% predicted by the Vegard’s law as indicated in the figure. Therefore in the overdoped regime the deviation of the local microstrain ε in the probed [BPO] nanoscale cluster units from the average lattice strain measured by X-ray diffraction [36] indicates a nanoscale phase separation between first metallic units and insulating units, triggering high-temperature superconductivity, which is in agreement with high resolution electron diffraction [40].

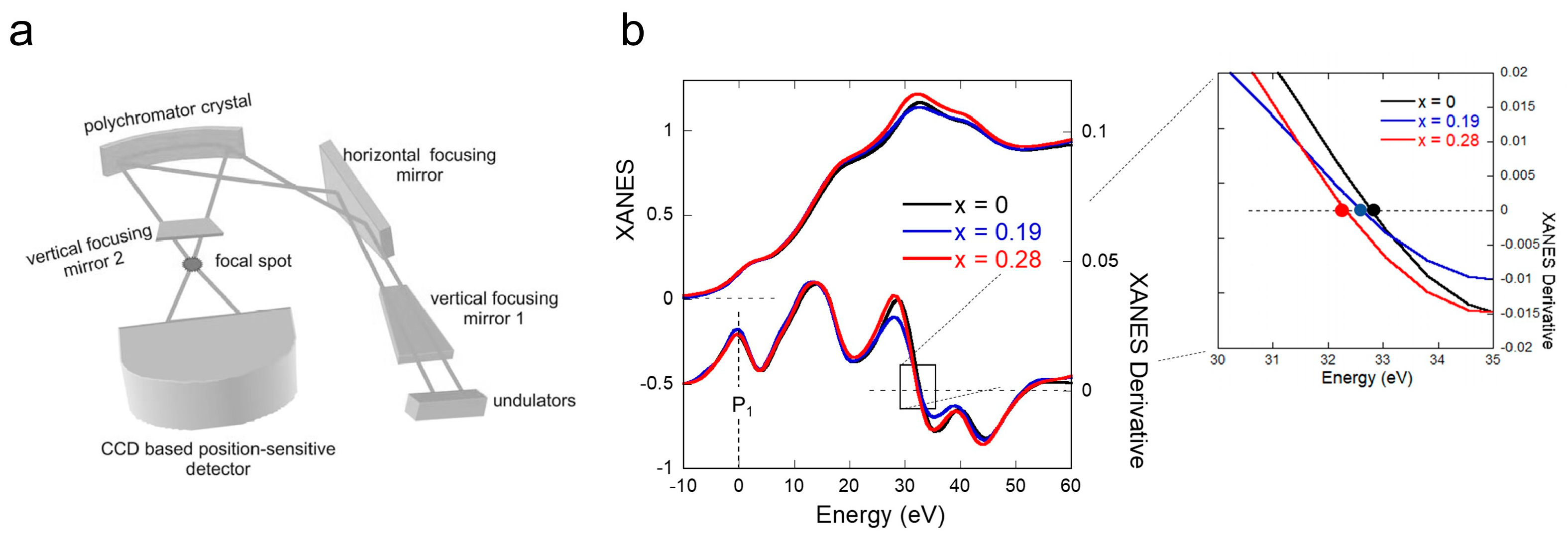
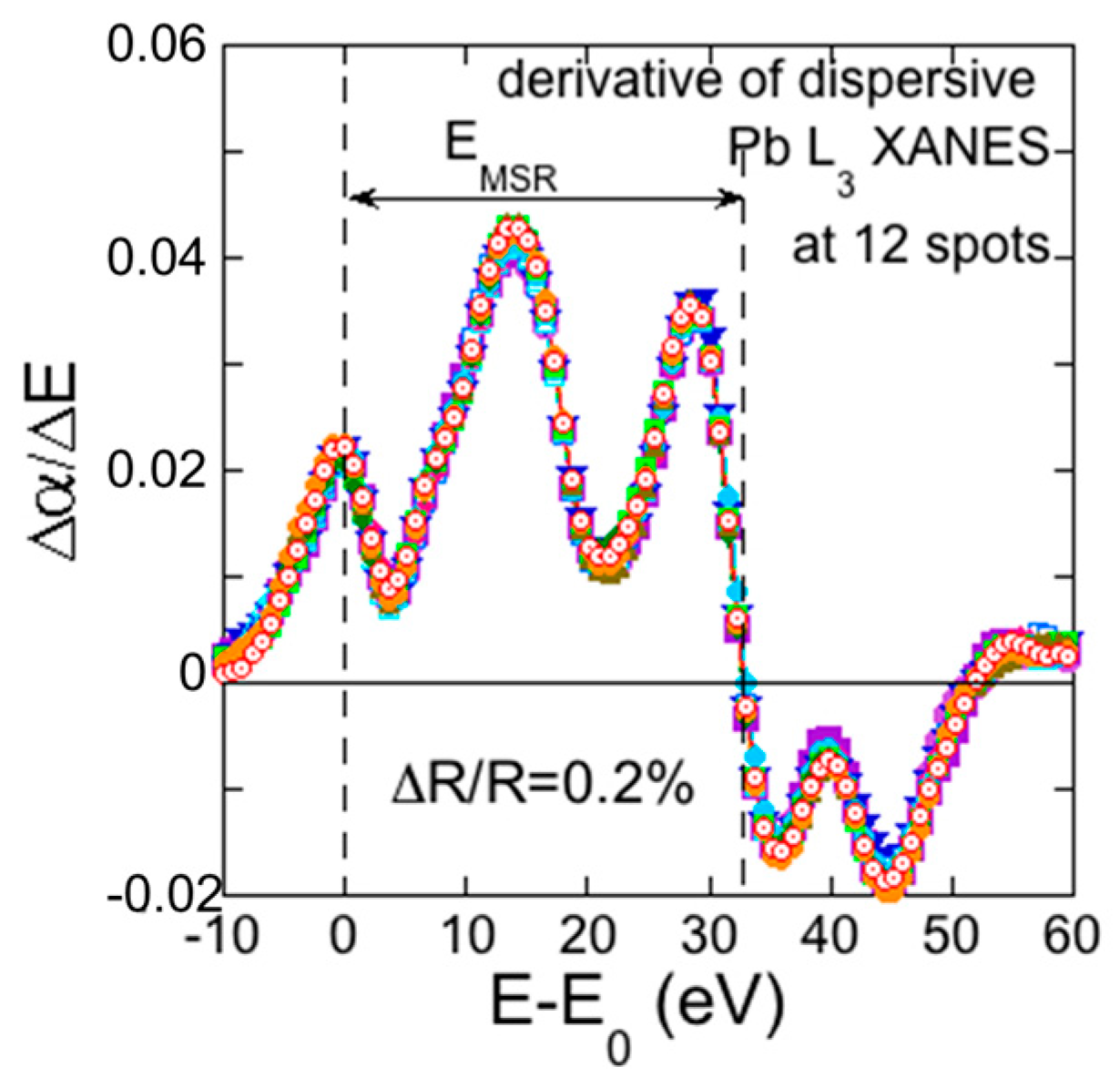
4. Materials and Methods

Single crystals of BaPb1−xBixO3 with Bi compositions x = 0, 0.19 and 0.28 were grown by slowly cooling a solution of BaCO3, PbO, and Bi2O3. The single crystals were polished in the Geballe Laboratory for Advanced Materials in Stanford to reach the optimal homogeneous hundred microns thickness for X-ray transmission experiments at the Pb L3 edge energy in the high X-ray energy range 13 KeV.
The in-depth comprehension of local structural phases requires tools not accessible in ordinary laboratories due to the need to probe micrometric areas without moving the sample, as well as short acquisition times. Given these non-trivial premises, the micro-XANES technique makes possible the detection of nanoscopic local lattice fluctuations in in-homogeneous systems. The energy dispersive technique, necessary for studying BaPb1−xBixO3 [76], has become available thanks to the dedicated synchrotron radiation beamline ID24 of the European Synchrotron Radiation Facility (ESRF) in Grenoble, France. The ID24, consists of a set of mirrors in a Kirkpatrick–Baez geometry (vertical and horizontal focusing mirrors) that focus the white beam on a polychromator crystal, which splits the beam. A second vertical mirror focuses the beam on the sample. A photon flux of ~1014 ph/s goes through the sample; the transmitted photons are detected by a Ge strip CCD equipped with an acquisition electronics with a readout time of 2.8 µs and minimum integration time of ∼80 ns. The particular setup of the beamline, and the lack of moving parts provide a small and stable focal spot (5 × 5 μm2 at Pb and Bi L3-edges) suitable for the scanning micro-XAS. [7]. The reported XANES data were collected at low temperatures of 50 ± 10 K.
In order to establish the actual limitation of the measure of the local cluster microstrain by scanning micro XANES in the dispersive mode, we present in Figure 6, the typical XANES spectra collected in 12 spots of the 1681 XANES spots collected in the area of 41 × 41 spots of the pure BaPbO3 sample shown in Figure 4. The energy of the multiple scattering resonance (EMSR) is given by the difference between the Fermi level at the maximum of first derivative peak and the zero of the XANES spectra derivative around 32.8 eV. The energy fluctuations of the multiple scattering resonance (EMSR) due to the noise level correspond to a noise fluctuation of the microstrain of the order of 0.12% in the undoped sample. Therefore, we can clearly measure microstrain spatial fluctuations larger than 0.12% in the doped superconducting samples.
Theoretical simulations of XANES spectra were performed in the framework of full multiple scattering theory for a finite atomic cluster centered at the absorbing Pb atom using the muffin-tin approximation [61,62,63,64] and self-consistent field using the implemented FEFF9.6 code, as described in reference [68]. The Hedin–Lundqvist exchange potential was adopted and the atomic potential was constructed in self-consistent field calculations. The full multiple scattering (MS) calculations were calculated increasing the atomic cluster radius centered at the Pb-absorbing atom. The calculated XANES spectra reproduced the experimental data for clusters with a radius larger than 5 Å , and remained invariant for larger clusters. This result shows that the experimental XANES spectrum probes only a BPO nanoscale cluster of 5 Å radius via multiple scattering. The instrumental and core–hole-induced broadening were consistently used for all simulated spectra to be comparable with experimental spectra.

5. Conclusions

We have measured the spatial distribution of microstrain of Pb-centered clusters with two different Bi contents (x) in BaPb1−xBixO3 using scanning dispersive μ-XANES (Sdµ-XANES). Our measurements reveal a relative variation of the Pb-O bond, as determined from the energy shift of the multiple scattering resonance EMSR. We have found that the largest inhomogeneity occurs in the under-doped regime with lower Bi dopant concentrations, with x = 0.19, close to the superconductor-to-metal transition (SMT) for the weak tensile microstrain. At variance, the sample with the higher Bi content x = 0.28, near the superconductor-to-insulator (SIT) transition shows a larger tensile strain in the Pb-centered nanoscale clusters probed by Pb L3-XANES, called [BaPbO] nanoscale units Finally, we have shown that the amplitude of the spatial fluctuations of the tensile microstrain in the [BaPbO] nanoscale units is about −0.5% and −0.8% in the x = 0.28 and x = 0.19 samples, respectively. In these two samples, the average tensile microstrain was quite a bit larger than predicted by Vegard’s law, i.e., −0.38% and −0.56%. We assign these results to nanoscale phase separation with the first nanoscale units of metallic strained ε < 0.2 and insulating ε > 0.72% units which favors interface superconductivity triggered by the nanoscale phase separation. While the two samples investigated in this work have similar critical temperatures, the x = 0.19 sample is made of larger metallic units and a smaller insulating phase and the x = 0.28 sample is made of larger insulator units and smaller metallic units. While in the literature many authors usually assume that in these systems the lead local structure is not affected by Bi content, we have shown that the local structure near the Pb site is affected by Bi doping. Finally, this work shows the feasibility of spatial mapping intrinsic inhomogeneity by scanning micro XANES in the dispersive mode, which can be implemented by advances on focusing the X-ray beam down to the nanoscale to provide further unique additional information on the micro fluctuations of local complexity at the atomic scale in quantum materials [77,78].

Author Contributions

Conceptualization, P.G.-G., S.M. and A.B.; methodology, A.A.I., A.P.M., A.M., W.X., A.B. and G.C.; software, G.C.; validation, A.P.M., A.B. and A.M.; formal analysis, R.A., S.M., G.C. and A.B.; investigation, B.J., A.P., V.M., S.M. and A.A.I.; sample synthesis, P.G.-G. and I.R.F.; data curation, R.A., S.M., G.C. and A.B.; writing—original draft preparation, R.A., S.M., G.C. and A.B.; writing—review and editing, R.A., S.M., G.C. and A.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research received funding from Superstripes onlus. Supported by the National Natural Science Foundation of China (Grant No. 12075273), and work at Stanford University was supported by the U.S. Department of Energy, Office of Basic Sciences, under Contract no. DE-AC02-76SF0051.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author (G.C.) upon reasonable request.

Acknowledgments

We thank T. H. Geballe, who passed away during the course of this study, for his long-standing contributions to the study of complexity of superconducting materials, and for his specific contributions to this particular project over a span of many years. We are grateful to Sakura Pascarelli, Olivier Mathon, the ID24 beamline staff and to Michael di Gioacchino for their experimental help. A.A.I. and A.P.M. acknowledge the support of the Ministry of Science and Higher Education of the Russian Federation (Agreement no. 075-15-2021-1352).

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Zavaleta, R.C.; Fomichev, S.; Khaliullin, G.; Berciu, M. Effects of reduced dimensionality, crystal field, electron-lattice coupling, and strain on the ground state of a rare-earth nickelate monolayer. Phys. Rev. B 2021, 104, 205111. [Google Scholar] [CrossRef]
  2. Jiang, M.; Berciu, M.; Sawatzky, G.A. Critical nature of the Ni spin state in doped NdNiO2. Phys. Rev. Lett. 2020, 124, 207004. [Google Scholar] [CrossRef] [PubMed]
  3. Melinte, S.; Berciu, M.; Zhou, C.; Tutuc, E.; Papadakis, S.J.; Harrison, C.; De Poortere, E.P.; Wu, M.; Chaikin, P.M.; Shayegan, M.; et al. Laterally modulated 2D electron system in the extreme quantum limit. Phys. Rev. Lett. 2004, 92, 036802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  4. Yan, D.; Tasan, C.C.; Raabe, D. High resolution in situ mapping of microstrain and microstructure evolution reveals damage resistance criteria in dual phase steels. Acta Mater. 2015, 96, 399–409. [Google Scholar] [CrossRef]
  5. Mocherla, P.S.; Karthik, C.; Ubic RN, A.R.; Ramachandra Rao, M.S.; Sudakar, C. Tunable bandgap in BiFeO3 nanoparticles: The role of microstrain and oxygen defects. Appl. Phys. Lett. 2013, 103, 022910. [Google Scholar] [CrossRef]
  6. Fratini, M.; Caivano, R.; Puri, A.; Ricci, A.; Ren, Z.-A.; Dong, X.-L.; Yang, J.; Lu, W.; Zhao, Z.-X.; Barba, L.; et al. The effect of internal pressure on the tetragonal to monoclinic structural phase transition in ReOFeAs: The case of NdOFeAs. Supercond. Sci. Technol. 2008, 21, 092002. [Google Scholar] [CrossRef] [Green Version]
  7. Tarantini, C.; Gurevich, A.; Jaroszynski, J.; Balakirev, F.; Bellingeri, E.; Pallecchi, I.; Ferdeghini, C.; Shen, B.; Wen, H.H.; Larbalestier, D.C. Significant enhancement of upper critical fields by doping and strain in iron-based superconductors. Phys. Rev. B 2011, 84, 184522. [Google Scholar] [CrossRef] [Green Version]
  8. Imai, Y.; Nabeshima, F.; Maeda, A. Comparative review on thin film growth of iron-based superconductors. Condens. Matter 2017, 2, 25. [Google Scholar] [CrossRef] [Green Version]
  9. Ozaki, T.; Wu, L.; Zhang, C.; Jaroszynski, J.; Si, W.; Zhou, J.; Zhu, Y.; Li, Q. A route for a strong increase of critical current in nanostrained iron-based superconductors. Nat. Commun. 2016, 7, 13036. [Google Scholar] [CrossRef] [Green Version]
  10. Wiecki, P.; Frachet, M.; Haghighirad, A.A.; Wolf, T.; Meingast, C.; Heid, R.; Böhmer, A.E. Emerging symmetric strain response and weakening nematic fluctuations in strongly hole-doped iron-based superconductors. Nat. Commun. 2021, 12, 4824. [Google Scholar] [CrossRef]
  11. Kang, J.; Kemper, A.F.; Fernandes, R.M. Manipulation of gap nodes by uniaxial strain in iron-based superconductors. Phys. Rev. Lett. 2014, 113, 217001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  12. Kim, J.S.; Tam, G.N.; Stewart, G.R. Unusual sensitivity of superconductivity to strain in iron-based 122 superconductors. Phys. Rev. B 2015, 91, 144512. [Google Scholar] [CrossRef] [Green Version]
  13. Tan, S.; Zhang, Y.; Xia, M.; Ye, Z.; Chen, F.; Xie, X.; Peng, R.; Xu, D.; Fan, Q.; Xu, H.; et al. Interface-induced superconductivity and strain-dependent spin density waves in FeSe/SrTiO3 thin films. Nat. Mater. 2013, 12, 634–640. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  14. Worasaran, T.; Ikeda, M.S.; Palmstrom, J.C.; Straquadine, J.A.; Kivelson, S.A.; Fisher, I.R. Nematic quantum criticality in an Fe-based superconductor revealed by strain-tuning. Science 2021, 372, 973–977. [Google Scholar] [CrossRef]
  15. Sato, H.; Hiramatsu, H.; Kamiya, T.; Hosono, H. Strain engineering at heterointerfaces: Application to an iron pnictide superconductor, cobalt-doped BaFe2As2. ACS Appl. Mater. Interfaces 2020, 12, 50096–50104. [Google Scholar] [CrossRef] [PubMed]
  16. Phan, G.N.; Nakayama, K.; Sugawara, K.; Sato, T.; Urata, T.; Tanabe, Y.; Tanigaki, K.; Nabeshima, F.; Imai, Y.; Maeda, A.; et al. Effects of strain on the electronic structure, superconductivity, and nematicity in FeSe studied by angle-resolved photoemission spectroscopy. Phys. Rev. B 2017, 95, 224507. [Google Scholar] [CrossRef] [Green Version]
  17. Philippe, J.C.; Lespinas, A.; Faria, J.; Forget, A.; Colson, D.; Houver, S.; Cazayous, M.; Sacuto, A.; Paul, I.; Gallais, Y. Nematic-fluctuation-mediated superconductivity revealed by anisotropic strain in Ba (Fe1−xCox)2As2. Phys. Rev. Lett. 2022, 129, 187002. [Google Scholar] [CrossRef]
  18. Di Castro, D.; Agrestini, S.; Campi, G.; Cassetta, A.; Colapietro, M.; Congeduti, A.; Continenza, A.; Negri, S.D.; Giovannini, M.; Massidda, S.; et al. The amplification of the superconducting Tc by combined effect of tuning of the Fermi level and the tensile microstrain in Al1−xMgxB2. EuroPhysics Lett. 2002, 58, 278. [Google Scholar] [CrossRef]
  19. Agrestini, S.; Saini, N.L.; Bianconi, G.; Bianconi, A. The strain of CuO2 lattice: The second variable for the phase diagram of cuprate perovskites. J. Phys. A Math. Gen. 2003, 36, 9133. [Google Scholar] [CrossRef] [Green Version]
  20. Bianconi, A.; Saini, N.L.; Agrestini, S.; Castro, D.D.; Bianconi, G. The strain quantum critical point for superstripes in the phase diagram of all cuprate perovskites. Int. J. Mod. Phys. B 2000, 14, 3342–3355. [Google Scholar] [CrossRef]
  21. Di Castro, D.; Bianconi, G.; Colapietro, M.; Pifferi, A.; Saini, N.L.; Agrestini, S.; Bianconi, A. Evidence for the strain critical point in high Tc superconductors. Eur. Phys. J. B-Condens. Matter Complex Syst. 2000, 18, 617–624. [Google Scholar] [CrossRef]
  22. Macis, S.; Paolozzi, M.C.; D’Arco, A.; Tomarchio, L.; Di Gaspare, A.; Lupi, S. Terahertz Resonators Based on YBa2Cu3O7 High-Tc Superconductor. Appl. Sci. 2022, 12, 10242. [Google Scholar] [CrossRef]
  23. Poccia, N.; Ricci, A.; Bianconi, A. Misfit strain in superlattices controlling the electron-lattice interaction via microstrain in active layers. Adv. Condens. Matter Phys. 2010, 7, 261849. [Google Scholar] [CrossRef] [Green Version]
  24. Müller, K.A.; Bussmann-Holder, A. (Eds.) Superconductivity in Complex Systems; Springer: Berlin, Germany, 2005; Volume 114. [Google Scholar]
  25. Kagan, M.Y.; Kugel, K.I.; Rakhmanov, A.L. Electronic phase separation: Recent progress in the old problem. Phys. Rep. 2021, 916, 1–105. [Google Scholar] [CrossRef]
  26. Kagan, M.Y.; Kugel, K.I. Inhomogeneous charge distributions and phase separation in manganites. Phys.-Uspekhi 2001, 44, 553. [Google Scholar] [CrossRef]
  27. Campi, G.; Barba, L.; Zhigadlo, N.D.; Ivanov, A.A.; Menushenkov, A.P.; Bianconi, A. Q-Balls in the pseudogap phase of Superconducting HgBa2CuO4+y. Condens. Matter 2023, 8, 15. [Google Scholar] [CrossRef]
  28. Bianconi, A.; Di Castro, D.; Bianconi, G.; Pifferi, A.; Saini, N.L.; Chou, F.C.; Johnston, D.C.; Colapietro, M. Coexistence of stripes and superconductivity: Tc amplification in a superlattice of superconducting stripes. Phys. C Supercond. 2000, 341, 1719–1722. [Google Scholar] [CrossRef]
  29. Mazziotti, M.V.; Bianconi, A.; Raimondi, R.; Campi, G.; Valletta, A. Spin–orbit coupling controlling the superconducting dome of artificial superlattices of quantum wells. J. Appl. Phys. 2022, 132, 193908. [Google Scholar] [CrossRef]
  30. Bianconi, G. Superconductor-insulator transition on annealed complex networks. Phys. Rev. E 2012, 85, 061113. [Google Scholar] [CrossRef] [Green Version]
  31. Bianconi, A.; Saini, N.L.; Lanzara, A.; Missori, M.; Rossetti, T.; Oyanagi, H.; Oka, Y.K.; Ito, T. Determination of the Local Lattice Distortions in the CuO2 plane of La1.85Sr0.15CuO4. Phys. Rev. Lett. 1996, 76, 3412. [Google Scholar] [CrossRef] [Green Version]
  32. Egami, T.; Billinge, S.J.L. Lattice effects in high-Tc superconductors. Phys. Prop. High Temp. Supercond. V 1996, 5, 265. [Google Scholar]
  33. Campi, G.; Proffen, T.; Qiu, X.; Bozin, E.S.; Billinge, S.J.L.; Agrestini, S.; Saini, N.L.; Bianconi, A. Local lattice dynamics in the Mg0.5Al0.5B2 superconductor. J. Supercond. Nov. Magn. 2007, 20, 505–510. [Google Scholar] [CrossRef]
  34. Gavrichkov, V.A.; Shan’ko, Y.; Zamkova, N.G.; Bianconi, A. Is there any hidden symmetry in the stripe structure of perovskite high-temperature superconductors? J. Phys. Chem. Lett. 2019, 10, 1840–1844. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  35. Gavrichkov, V.A.; Polukeev, S.I. Magnetic interaction in doped 2D perovskite cuprates with nanoscale inhomogeneity: Lattice nonlocal effects vs. superexchange. Condens. Matter 2022, 7, 57. [Google Scholar] [CrossRef]
  36. Climent-Pascual, E.; Ni, N.; Jia, S.; Huang, Q.; Cava, R.J. Polymorphism in BaPb1−xBixO3 at the superconducting composition. Phys. Rev. B 2011, 83, 174512. [Google Scholar] [CrossRef]
  37. Giraldo-Gallo, P.; Lee, H.; Zhang, Y.; Kramer, M.J.; Beasley, M.R.; Geballe, T.H.; Fisher, I.R. Field-tuned superconductor-insulator transition in BaPb1−xBixO3. Phys. Rev. B 2012, 85, 174503. [Google Scholar] [CrossRef] [Green Version]
  38. Giraldo-Gallo, P.; Lee, H.; Beasley, M.R.; Geballe, T.H.; ·Fisher, I.R. Inhomogeneous Superconductivity in BaPb1−xBixO3. J. Supercond. Nov. Magn. 2013, 26, 2675–2678. [Google Scholar] [CrossRef]
  39. Luna, K.; Giraldo-Gallo, P.; Geballe, T.; Fisher, I.; Beasley, M. Disorder driven Metal-Insulator transition inBaPb1−xBixO3 and inference of disorder-free critical temperature. Phys. Rev. Lett. 2014, 113, 17004. [Google Scholar] [CrossRef] [Green Version]
  40. Giraldo-Gallo, P.; Zhang, Y.; Parra, C.; Manoharan, H.; Beasley, M.; Geballe, T.; Kramer, M.; Fisher, I. Stripe-like nanoscale structural phase separation in superconducting BaPb1−xBixO3. Nat. Commun. 2015, 6, 8231. [Google Scholar] [CrossRef] [Green Version]
  41. Sleight, A.W.; Gillson, J.L.; Bierstedt, P.E. High-temperature superconductivity in the BaPb1−xBixO3 systems. Solid State Commun. 1975, 17, 27–28. [Google Scholar] [CrossRef]
  42. Balzarotti, A.; Menushenkov, A.P.; Motta, N.; Purans, J. EXAFS of the superconducting oxide BaPb1−xBixO3. Solid State Commun. 1984, 49, 887–890. [Google Scholar] [CrossRef]
  43. Murakami, T. Basic Properties in Superconducting Perovskite-Type oxide BaPb1−xBixO3. Jpn. J. Appl. Phys. 1985, 24 (Suppl. S2), 10. [Google Scholar] [CrossRef]
  44. Oda, M.; Hidaka, Y.; Katsui, A.; Murakami, T. The crystallographic symmetries of single BaPb1−xBixO3 crystals grown from BaCO3-PbO2-Bi2O3 solutions. Solid State Commun. 1986, 60, 897–900. [Google Scholar] [CrossRef]
  45. Uchida, S.; Kitazawa, K.; Tanaka, S. Superconductivity and metal-semiconductor transition in BaPb1−xBixO3. Phase Transit. 1987, 8, 95–128. [Google Scholar] [CrossRef]
  46. Claeson, T.; Boyce, J.B.; Bridges, F.; Geballe, T.H.; Remeika, J.M.; Sleight, A.W. X-ray absorption study of superconducting BaBi1−xPbxO3 and BaBiO3. Phys. C Supercond. Its Appl. 1989, 162, 544–545. [Google Scholar] [CrossRef]
  47. Boyce, J.B.; Bridges, F.G.; Claeson, T.; Geballe, T.H.; Li, G.G.; Sleight, A.W. Local structure of BaBixPb1−x O3 determined by x-ray-absorption spectroscopy. Phys. Rev. B 1991, 44, 6961. [Google Scholar] [CrossRef]
  48. Marx, D.T.; Radaelli, P.G.; Jorgensen, J.D.; Hitterman, R.L.; Hinks, D.G.; Shiyou Pei Dabrowski, B. Metastable behavior of the superconducting phase in the BaBi1−xPbxO3 system. Phys. Rev. B 1992, 46, 1144. [Google Scholar] [CrossRef]
  49. Menushenkov, A.P.; Ignatov, A.Y.; Klementev, K.V.; Benazeth, S.; Purans, J. Debye-Waller factor low temperature anomalies in BaPb1−xBixO3. J. Physique. 1997, 7 Pt 2, 1073–1075. [Google Scholar] [CrossRef]
  50. Menushenkov, A.P.; Klementev, K.V. Extended X-ray absorption fine-structure indication of a double-well potential for oxygen vibration in Ba1−xKxBiO3. J. Phys. Condens. Matter 2000, 12, 3767. [Google Scholar] [CrossRef]
  51. Liu, S.Y.; Meng, Y.; Liu, S.; Li, D.J.; Li, Y.; Liu, Y.; Shen, Y.; Wang, S. Phase stability, electronic structures, and superconductivity properties of the BaPb1−xBixO3 and Ba1−xKxBiO3 perovskites. J. Am. Ceram. Soc. 2017, 100, 1221–1230. [Google Scholar] [CrossRef]
  52. Harris, D.T.; Campbell, N.; Uecker, R.; Brützam, M.; Schlom, D.G.; Levchenko, A.; Rzchowski, M.S.; Eom, C.B. Superconductivity-localization interplay and fluctuation magnetoresistance in epitaxial BaPb1−xBixO3 thin films. Phys. Rev. Mater. 2018, 2, 041801. [Google Scholar] [CrossRef]
  53. Fu, W.T.; Visser, D.; IJdo, D.J.W. High-resolution neutron powder diffraction study on the structure of BaPbO3. Solid State Commun. 2005, 134, 647–652. [Google Scholar] [CrossRef]
  54. Visser, D.; Knight, K.S.; IJdo, D.J. High-resolution neutron powder diffraction study on the phase transitions in BaPbO3. J. Solid State Chem. 2007, 180, 1559–1565. [Google Scholar] [CrossRef]
  55. Seiler, P.; Bartel, R.; Kopp, T.; Hammerl, G. Electronic transport in thin films of BaPbO3: Unraveling two-dimensional quantum effects. Phys. Rev. B 2019, 100, 165402. [Google Scholar] [CrossRef] [Green Version]
  56. Meir, B.; Gorol, S.; Kopp, T.; Hammerl, G. Observation of two-dimensional superconductivity in bilayers of BaBiO3 and BaPbO3. Phys. Rev. B 2017, 96, 100507. [Google Scholar] [CrossRef] [Green Version]
  57. Kim, J.; Mun, J.; Kim, B.; Lee, H.G.; Lee, D.; Kim, T.H.; Lee, S.; Kim, M.; Chang, S.H.; Noh, T.W. Coherent-strained superconducting BaPb1−xBixO3 thin films by interface engineering. Phys. Rev. Mater. 2019, 3, 113606. [Google Scholar] [CrossRef]
  58. Di Napoli, S.; Helman, C.; Llois, A.M.; Vildosola, V. Two-dimensional superconductivity driven by interfacial electron-phonon coupling in a BaPbO3/BaBiO3 bilayer. Phys. Rev. B 2021, 103, 174509. [Google Scholar] [CrossRef]
  59. Parra, C.; Niestemski, F.C.; Contryman, A.W.; Giraldo-Gallo, P.; Geballe, T.H.; Fisher, I.R.; Manoharan, H.C. Signatures of two-dimensional superconductivity emerging within a three-dimensional host superconductor. Proc. Natl. Acad. Sci. USA 2021, 118, e2017810118. [Google Scholar] [CrossRef]
  60. Zheng, X.; Farid, M.A.; Wang, X.; Wang, Y.; Geng, J.; Liao, F.; Sun, J.; Li, J.; Liu, L.; Lin, J. Synthesis, crystal structure, and superconductivity of Ba (Bi0.25Pb0.75)1−xMgxO3−δ. Solid State Commun. 2023, 360, 115051. [Google Scholar] [CrossRef]
  61. Bianconi, A. Surface X-ray absorption spectroscopy: Surface EXAFS and surface XANES. Appl. Surf. Sci. 1980, 6, 392–418. [Google Scholar] [CrossRef]
  62. Bianconi, A.; Bauer, R.S. Evidence of SiO at the Si-oxide interface by surface soft X-ray absorption near edge spectroscopy. Surf. Sci. 1980, 99, 76–86. [Google Scholar] [CrossRef]
  63. Bianconi, A. XANES Spectroscopy in X-ray Absorption: Principles, Applications, Techniques of EXAFS, SEXAFS and XANES; Koningsberger, D.C., Prins, R., Eds.; John Wiley & Sons, Inc.: New York, NY, USA, 1988; ISBN 978-0-471-87547-5. [Google Scholar]
  64. Della Longa, S.; Soldatov, A.; Pompa, M.; Bianconi, A. Atomic and electronic structure probed by X-ray absorption spectroscopy: Full multiple scattering analysis with the G4XANES package. Comput. Mater. Sci. 1995, 4, 199–210. [Google Scholar] [CrossRef]
  65. Della Ventura, G.; Galdenzi, F.; Cibin, G.; Oberti, R.; Xue, W.; Macis, S.; Marcelli, A. Iron oxidation dynamics vs. temperature of synthetic potassic-ferro-richterite: A XANES investigation. Phys. Chem. Chem. Phys. 2018, 20, 21764–21771. [Google Scholar] [CrossRef] [PubMed]
  66. Rezvani, S.J.; D’Elia, A.; Macis, S.; Nannarone, S.; Lupi, S.; Schütt, F.; Rasch, F.; Adelung, R.; Lu, B.; Zhang, Z.; et al. Structural anisotropy in three dimensional macroporous graphene: A polarized XANES investigation. Diam. Relat. Mater. 2021, 111, 108171. [Google Scholar] [CrossRef]
  67. Macis, S.; Rezvani, J.; Davoli, I.; Cibin, G.; Spataro, B.; Scifo, J.; Faillace, L.; Marcelli, A. Structural Evolution of MoO3 Thin Films Deposited on Copper Substrates upon Annealing: An X-ray Absorption Spectroscopy Study. Condens. Matter 2019, 4, 41. [Google Scholar] [CrossRef] [Green Version]
  68. Rehr, J.J.; Kas, J.J.; Vila, F.D.; Prange, M.P.; Jorissen, K. Parameter-free calculations of X-ray spectra with FEFF9. Phys. Chem. Chem. Phys. 2010, 12, 5503–5513. [Google Scholar] [CrossRef]
  69. Menushenkov, A.P.; Ignatov AYu Klementev, K.V.; Kochubey, D.I. X-ray absorption spectroscopy of BaPb1−xBixO3 and Ba1−x Kx BiO3 superconducting oxides. Phys. B Condens. Matter 1995, 208, 295–296. [Google Scholar] [CrossRef]
  70. Ignatov AYu Menushenkov, A.P.; Chernov, V.A. Valency states of Bi BaPb1−x BixO3-d and BaK1−xBixO3-d superconducting oxide. Nucl. Instrum. Methods Phys. Res. A 1995, 359, 244–247. [Google Scholar] [CrossRef]
  71. Ignatov, A.Y.; Menushenkov, A.P.; Chernov, V.A. Influence of oxygen deficiency on the electronic and local structure of BaPb1−xBixO3-d and Ba0.6K0.4BiO3-d superconducting oxides: An X-ray absorption study. Phys. C Supercond. 1996, 271, 1–2. [Google Scholar] [CrossRef]
  72. Glazer, A.M. The classification of tilted octahedra in perovskites. Acta Crystallogr. B 1972, 28, 3384. [Google Scholar] [CrossRef]
  73. Glazer, A.M. Simple ways of determining perovskite structures. Acta Crystallogr. A 1975, 31, 756. [Google Scholar] [CrossRef] [Green Version]
  74. Howard, C.J.; Stokes, H.T. Group-theoretical analysis of octahedral tilting in perovskites. Acta Crystallogr. B 1998, 54, 782. [Google Scholar] [CrossRef] [Green Version]
  75. Sleight Arthur, W. Bismuthates: BaBiO3 and related superconducting phases. Phys. C Supercond. Its Appl. 2015, 514, 152–165. [Google Scholar] [CrossRef]
  76. Pascarelli, S.; Mathon, O. Energy Dispersive XAS. In XAFS Techniques for Catalysts, Nanomaterials, and Surfaces; Iwasawa, Y., Asakura, K., Tada, M., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
  77. Campi, G.; Bianconi, A. Functional nanoscale phase separation and intertwined order in quantum complex materials. Condens. Matter 2021, 6, 40. [Google Scholar] [CrossRef]
  78. Campi, G.; Bianconi, A.; Poccia, N.; Bianconi, G.; Barba, L.; Arrighetti, G.; Innocenti, D.; Karpinski, J.; Zhigadlo, N.D.; Kazakov, S.M.; et al. Inhomogeneity of charge-density-wave order and quenched disorder in a high-T c superconductor. Nature 2015, 525, 359–362. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Condensedmatter 08 00057 g001 550
Figure 1. (a) Phase diagram for the BaPb1−xBixO3 with the different space groups indicated. The CDW region is indicated with shaded colors, while the superconducting range 0.05 < x < 0.35 is outlined by the red bar. (b) Superconducting critical temperature Tc as a function of the bismuth content, x. The white dots from Climent-Pasqual et al. [36] and the full red circles represent the nominal concentrations of the doped BaPb1−xBixO3 samples investigated. The green region indicates the metal insulator transition centered at x = 0.36.
Figure 1. (a) Phase diagram for the BaPb1−xBixO3 with the different space groups indicated. The CDW region is indicated with shaded colors, while the superconducting range 0.05 < x < 0.35 is outlined by the red bar. (b) Superconducting critical temperature Tc as a function of the bismuth content, x. The white dots from Climent-Pasqual et al. [36] and the full red circles represent the nominal concentrations of the doped BaPb1−xBixO3 samples investigated. The green region indicates the metal insulator transition centered at x = 0.36.
Condensedmatter 08 00057 g001
Condensedmatter 08 00057 g002 550
Figure 2. Panel (a) The nanoscale cluster of 29 atoms centered at the Pb-absorbing atom called the BPO unit where the photoelectron is confined at the multiple scattering resonance (MSR) giving the main peak in the Pb L3 XANES shown in panel (b). Panel (b) Full multiple scattering Pb L3 edge XANES spectra for the BPO cluster in panel (a) calculated by increasing the lattice parameter of the 0.5 nm nano cluster, shown in panel (a), relative to the original lattice parameter in the nanocluster in undoped BaPbO3, which called XANES microstrain values for the nano BaPbO units. Panel (c) shows the relative variation of the energy of the highest peak in the XANES spectrum due to the multiple scattering resonance (MSR) ΔE/E relative to the first weak absorption peak in the edge region as a function of the microstrain of the lattice parameter in the nano 0.5 nm cluster shown in panel (a) used in the XANES calculation using the FEFF9.6 code [68], the dashed line is a linear fit.
Figure 2. Panel (a) The nanoscale cluster of 29 atoms centered at the Pb-absorbing atom called the BPO unit where the photoelectron is confined at the multiple scattering resonance (MSR) giving the main peak in the Pb L3 XANES shown in panel (b). Panel (b) Full multiple scattering Pb L3 edge XANES spectra for the BPO cluster in panel (a) calculated by increasing the lattice parameter of the 0.5 nm nano cluster, shown in panel (a), relative to the original lattice parameter in the nanocluster in undoped BaPbO3, which called XANES microstrain values for the nano BaPbO units. Panel (c) shows the relative variation of the energy of the highest peak in the XANES spectrum due to the multiple scattering resonance (MSR) ΔE/E relative to the first weak absorption peak in the edge region as a function of the microstrain of the lattice parameter in the nano 0.5 nm cluster shown in panel (a) used in the XANES calculation using the FEFF9.6 code [68], the dashed line is a linear fit.
Condensedmatter 08 00057 g002
Condensedmatter 08 00057 g003 550
Figure 3. Upper panel (a) The experimental set up to collect X-ray absorption near edge structure (XANES) in the dispersive mode at the ID24 ESRF beamline. The X-ray synchrotron radiation emitted by the undulator is focused on a 5 μm spot on the thin crystal sample. The X-ray absorption is measured in transmission, and we recorded both the spatial variation of the bismuth atomic concentration x in superconducting crystals of BaPb1−xBixO3 and the spatial fluctuations of the lattice strain in selected BaPbO3 nanoclusters. Lower panels (b) X-ray absorption near edge structure (XANES) at the Pb L3 edge of BaPb1−xBixO3 samples with x = 0, 0.19 and 0.28, where the maximum absorption peak is due to the multiple scattering resonance (MSR) of the excited photoelectron in the continuum above the absorption threshold taken as zero energy. The derivatives of the signal from Pb show three peaks. E0 at 13,027 eV has been chosen as reference zero value for the energy scale. The energy of the multiple scattering resonance (EMSR) has been defined as the difference between the zero of the first derivative peak (P1). The energy of the MSR of the photoelectron confined in a nanoscale cluster, is highlighted by full circles in the rectangular inset of the derivative.
Figure 3. Upper panel (a) The experimental set up to collect X-ray absorption near edge structure (XANES) in the dispersive mode at the ID24 ESRF beamline. The X-ray synchrotron radiation emitted by the undulator is focused on a 5 μm spot on the thin crystal sample. The X-ray absorption is measured in transmission, and we recorded both the spatial variation of the bismuth atomic concentration x in superconducting crystals of BaPb1−xBixO3 and the spatial fluctuations of the lattice strain in selected BaPbO3 nanoclusters. Lower panels (b) X-ray absorption near edge structure (XANES) at the Pb L3 edge of BaPb1−xBixO3 samples with x = 0, 0.19 and 0.28, where the maximum absorption peak is due to the multiple scattering resonance (MSR) of the excited photoelectron in the continuum above the absorption threshold taken as zero energy. The derivatives of the signal from Pb show three peaks. E0 at 13,027 eV has been chosen as reference zero value for the energy scale. The energy of the multiple scattering resonance (EMSR) has been defined as the difference between the zero of the first derivative peak (P1). The energy of the MSR of the photoelectron confined in a nanoscale cluster, is highlighted by full circles in the rectangular inset of the derivative.
Condensedmatter 08 00057 g003
Condensedmatter 08 00057 g004 550
Figure 4. Panel (a) show the maps of spatial fluctuations of the microstrain over a square of 200 × 200 microns measured by ΔR/R = −ΔEMSR/2EMSR for the undoped (BaPbO3), x = 0, and the BaPb1−xBixO3 doped samples with x = 0.19 and x = 0.28. The bar corresponds to 25 µm. Panel (b) shows the probability distribution function (PDF) of the microstrain extracted from the three BaPb1−xBixO3 maps shown in panel (a). For the undoped non-superconducting sample, with x = 0, the distribution’s dark PDF peak is centered at zero microstrain, the distribution of the microstrain in the superconducting sample with x = 0.28 (red curve) is centered at around 1% with no overlap with the PDF distribution of the undoped reference sample. The distribution of the microstrain in the x = 0.19 sample (blue dots) shows a broad distribution overlapping the non-superconducting phase, and the spatial map clearly shows microscale phase separation.
Figure 4. Panel (a) show the maps of spatial fluctuations of the microstrain over a square of 200 × 200 microns measured by ΔR/R = −ΔEMSR/2EMSR for the undoped (BaPbO3), x = 0, and the BaPb1−xBixO3 doped samples with x = 0.19 and x = 0.28. The bar corresponds to 25 µm. Panel (b) shows the probability distribution function (PDF) of the microstrain extracted from the three BaPb1−xBixO3 maps shown in panel (a). For the undoped non-superconducting sample, with x = 0, the distribution’s dark PDF peak is centered at zero microstrain, the distribution of the microstrain in the superconducting sample with x = 0.28 (red curve) is centered at around 1% with no overlap with the PDF distribution of the undoped reference sample. The distribution of the microstrain in the x = 0.19 sample (blue dots) shows a broad distribution overlapping the non-superconducting phase, and the spatial map clearly shows microscale phase separation.
Condensedmatter 08 00057 g004
Condensedmatter 08 00057 g005 550
Figure 5. (a) XAS spectrum of the BaPb1−xBixO3 over a large range including either the Pb L3 edge and the Bi L3 edge jumps plotted with spectra of stoichiometric compounds at x = 0 and x = 1. The ratio between the amplitude of the absorption jumps of both Bi and Pb edges allows the direct measurement of the bismuth content, x, at the same spot where the microstrain is measured. Panels (b,c) show the maps of Bi x content measured by the absorption jump ratio of the XANES profile going from Pb L3 to the Bi L3 edge. (d) The local macrostrain plotted vs. the local Bi content x in two BaPb1−xBixO3 samples with nominal x = 0.19 (blue squares) and x = 0.28 (red circles). The full blue and yellow full circles represent the mean values of tensile local XANES microstrain [61,62,63,64] in the x = 0.19 and x = 0.28 samples, respectively. The dashed line indicates the average lattice strain as a function of Bi content, measured by diffraction [36], which agrees with the Vegard’s law. Very large fluctuation of local XANES microstrain are unveiled at microscale by our experimental method.
Figure 5. (a) XAS spectrum of the BaPb1−xBixO3 over a large range including either the Pb L3 edge and the Bi L3 edge jumps plotted with spectra of stoichiometric compounds at x = 0 and x = 1. The ratio between the amplitude of the absorption jumps of both Bi and Pb edges allows the direct measurement of the bismuth content, x, at the same spot where the microstrain is measured. Panels (b,c) show the maps of Bi x content measured by the absorption jump ratio of the XANES profile going from Pb L3 to the Bi L3 edge. (d) The local macrostrain plotted vs. the local Bi content x in two BaPb1−xBixO3 samples with nominal x = 0.19 (blue squares) and x = 0.28 (red circles). The full blue and yellow full circles represent the mean values of tensile local XANES microstrain [61,62,63,64] in the x = 0.19 and x = 0.28 samples, respectively. The dashed line indicates the average lattice strain as a function of Bi content, measured by diffraction [36], which agrees with the Vegard’s law. Very large fluctuation of local XANES microstrain are unveiled at microscale by our experimental method.
Condensedmatter 08 00057 g005
Condensedmatter 08 00057 g006 550
Figure 6. Typical 12 derivatives of Pb L3 XANES spectra collected using the dispersive mode in 12 spots of the 1681 spots measured by scanning mode in BaPbO3 sample where the photon energy scale is measured from the absorption edge E0 at 13,027 eV. The different color of the dots indicates different XANES spectra in different spatial.
Figure 6. Typical 12 derivatives of Pb L3 XANES spectra collected using the dispersive mode in 12 spots of the 1681 spots measured by scanning mode in BaPbO3 sample where the photon energy scale is measured from the absorption edge E0 at 13,027 eV. The different color of the dots indicates different XANES spectra in different spatial.
Condensedmatter 08 00057 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Albertini, R.; Macis, S.; Ivanov, A.A.; Menushenkov, A.P.; Puri, A.; Monteseguro, V.; Joseph, B.; Xu, W.; Marcelli, A.; Giraldo-Gallo, P.; et al. Tensile Microstrain Fluctuations in the BaPbO Units in Superconducting BaPb1−xBixO3 by Scanning Dispersive Micro-XANES. Condens. Matter 2023, 8, 57. https://doi.org/10.3390/condmat8030057

AMA Style

Albertini R, Macis S, Ivanov AA, Menushenkov AP, Puri A, Monteseguro V, Joseph B, Xu W, Marcelli A, Giraldo-Gallo P, et al. Tensile Microstrain Fluctuations in the BaPbO Units in Superconducting BaPb1−xBixO3 by Scanning Dispersive Micro-XANES. Condensed Matter. 2023; 8(3):57. https://doi.org/10.3390/condmat8030057

Chicago/Turabian Style

Albertini, Ruben, Salvatore Macis, Andrei A. Ivanov, Alexey P. Menushenkov, Alessandro Puri, Virginia Monteseguro, Boby Joseph, Wei Xu, Augusto Marcelli, Paula Giraldo-Gallo, and et al. 2023. "Tensile Microstrain Fluctuations in the BaPbO Units in Superconducting BaPb1−xBixO3 by Scanning Dispersive Micro-XANES" Condensed Matter 8, no. 3: 57. https://doi.org/10.3390/condmat8030057

Article Metrics

Back to TopTop