Abstract
Positron annihilation spectroscopy is a powerful probe to investigate the interfaces in materials relevant for energy storage such as Li-ion batteries. The key to the interpretation of the results is the positron implantation profile, which is a spatial function related to the characteristics of the materials forming the battery. We provide models for the positron implantation profile in a cathode of a Li-ion battery coin cell. These models are the basis for a reliable visualization of multilayer geometries and their interfaces in thin cathodes of lithium-ion batteries.
1. Introduction
Positron annihilation spectroscopy (PAS) is a non-invasive probing technique widely used as a quantum-mechanical approach for the characterization of the electronic and structural properties of metals, alloys, semi-conductors, porous materials, and advanced battery materials at the atomic scale [1]. Due to its high defect sensitivity, PAS has been extensively applied in the rapidly developing field of battery technologies to investigate the type, size, and distribution of vacancy-like defects formed in the cathode lattice during the Li+ ion charge and discharge processes [1,2]. Positrons emitted by the commonly used 22Na isotope have an energy spectrum with an end-point energy ( in Equation (2)) of 546 keV and an average energy of 216 keV [3]. When implanted in a solid, a positron typically thermalizes within a few picoseconds, then diffuses approximately a few hundred of nanometers in a defect-free material, while up to tens of nanometers in a defective cathode material until annihilation with an atomic electron in a characteristic lifetime of 100–350 ps [1].
As the demand for high performing Li-ion batteries is emerging at a swift pace, conventional cathode materials having a low Li-ion mobility through the microstructure are facing the challenge to fulfil the desired charging-discharging characteristics. Two effective strategies for improving the battery charging efficiency and rate capability are downsizing the grains of the nanostructured active material and coating the active nanoparticles with a conductive carbon layer [4,5]. Battery cathodes with downsized nanograins allow Li-ion dynamics through the structure in a shorter pathway, and hence improve the rate capability performance. Due to the increased surface-to-volume ratio of the nanostructured cathode materials, the energy density can be increased by downsizing the nanograins of the electrode materials [5]. In this context, the high defect sensitivity makes the positron annihilation techniques useful tools mutually complementary with other techniques in the study of cathode nanomaterials. Coating the cathode nanoparticles with a conductive carbon layer has been proven to boost the Li-ion dynamics through the nanograins. On the other hand, the coating layer also plays a protective role against cycling-induced excessive formation of the solid–electrolyte interphase (SEI) and offers the battery an effective buffering effect against volume expansion, and consequently enhances battery stability, longevity, and safety [5]. Pagot et al. [2] studied defect formation in the LiCoO2 (LCO) cathode in the measurements of positron annihilation lifetime spectroscopy (PALS) using 22Na as a positron source and Doppler Broadening employing a positron beam in the cases of partially charged and discharged cathodes. In their study, the cathodes were prepared with a thickness of approximately 60 and deposited on the 15 Al support foils, and positron lifetimes in the Al samples were measured as a reference. The PALS experiments showed that the source contributions were approximately 12% for Al and 14% for LCO samples, respectively, with a lifetime of 382 ps [2].
Knowledge of the source component (SC) resulting from annihilation events inside the 22NaCl source and the Kapton foils plays an essential role in analyzing a measured positron lifetime spectrum for evaluating the individual lifetime components using computer-based deconvolution algorithms [6,7]. To perform accurate analyses in our extensive study of Li-ion and Na-ion battery materials using PAS techniques, a practical approach was developed for positron implantation profile and source contribution estimation based on theoretical and experimental investigations. The aim of this paper is to demonstrate how the source component of a positron lifetime spectrum can be calculated for semi-infinite single and multilayer configurations using a method based on implantation profile approximation and backscattering correction in comparison with experimental results.
2. The Positron Implantation Profile in Solids
2.1. Effect of the Implantation Profile
Over decades, several models have been developed for exploring the positron implantation profile in conventional PALS experiments, in which positrons emitted by the isotope are implanted into the full solid angle of the homogeneous sample material in a sandwich geometry [8,9]. The effect of the positron implantation profile as a function of penetration depth z in solids was proposed by Brandt and Paulin [10,11,12] in an exponential form:
in which represents the probability that a positron, after thermalizing and diffusing, is localized and annihilated at a depth between z and dz into the sample in contact with the source, and the parameter [] is the positron absorption coefficient of the absorber material, expressed as [12]:
Mourino et al. [13] proposed an alternative expression which states that the absorption coefficient depends on the atomic number Z and mass density of the material, and on the mean energy of the emitted energy continuum by fitting the experimental data, as expressed in Equation (3):
Determination of the fraction of positrons annihilating inside a particular layer of a multilayer configuration is of the primary concern of PALS experimentalists. The fraction of positrons annihilating within a depth z from the entrance surface (z = 0) in a homogeneous material can be obtained by integrating Equation (1) over z [11]:
A two-exponent model describing the positron implantation profile was proposed by Dubov et al. [14] using Monte Carlo simulations as
in which the short-range component is associated with the positrons having low energy and impinging the sample surface at small angles and the long-range component are discriminated into two exponents, respectively. Based on their analyses of a series of materials with atomic numbers ranging from 6 to 82, the contribution of the short-range component is obtained as for all the analyzed materials. The absorption coefficients of the short- and long-range components show a dependence on the density and atomic number Z (or effective atomic number Zeff in the case of compound or mixture) of the implanted material described by:
These empirical formulae enable estimating the implantation profile of positrons as emitted by a 22Na source encapsulated with Kapton thin foils in good agreement with the results obtained using the model proposed by Dryzek and Singleton [14,15].
2.2. Positron Backscattering at Interfaces
Positrons implanted through a layered medium consisting of different materials may undergo backscattering at the interface between adjacent layers, and thus drastically influence the probability of positrons stopping in the source-supporting foil [11]. A simplified geometry of the multilayer sandwich consisting of a pair of Kapton foils and two identical semi-infinite layers of the sample on both sides of the 22Na source is presented in Figure 1 to illustrate the possible positron propagation processes. Due to the mirror symmetry of the setup, analysis on one side of the 22Na source (as illustrated by the inset of Figure 1) is normalized to the total amount of positrons to yield an accurate estimation of the source contribution in terms of the fraction of the total implanted positrons annihilating inside the Kapton foils. The fraction of the implanted positrons scattered back is referred to as the backscattering coefficient R, which mainly depends on the atomic number of the material. Several empirical models have been developed for theoretical calculations of R for elements over a wide range of atomic number [16]. The model reported by Dryzek and Dryzek [10,17] was used to calculate the relative backscattering coefficients in our analysis:
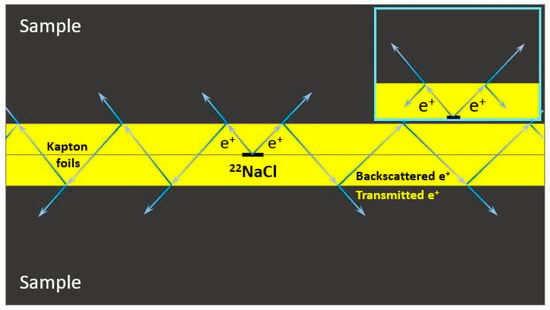
Figure 1.
Simplified schematic of the layered source/sample setup for implantation profile and SC estimation in PALS measurements. The inset illustrates the analyzed positron propagation processes without multiscattering on one side of the source. Arrows are drawn showing transmitted and backscattered positrons at the interface to guide the eye.
Proper correction of the implantation profile with backscattering effects enables obtaining a more accurate estimate of the annihilation intensity associated with each lifetime component identified in deconvolution of the lifetime spectrum.
Aers et al. [18] proposed a generalized method for scaling of the implantation profiles of positron beams in the form of a Makhov function P(E,z), within the low e+ energy range by correction of the backscattering effects of interfaces:
These authors proposed that the positron stopping profiles P(E,z) in elements and elemental multilayers calculated for incident positron energies in the range 1–10 keV, can be scaled to reproduce the stopping profiles in elemental multilayer systems in the incident energy range 1–25 keV. This was performed by multiplication of P(E,z) with the mean implantation depth within a particular ith layer and adopting the correction terms and associated with the backscattering between adjacent layers calculated using the backscattering coefficients R corresponding to each layer. The corrected profile is normalized by the constant to ensure the total fraction of positrons unity.
In our case, the positrons emitted by a 22NaCl source with definite energy characteristics are implanted in the samples. The implantation profiles P(z) in the source/sample configurations are approximated according to the Dubov’s profile (Equation (5)), requiring no scaling term in the calculation. The profile in each layer was normalized throughout the analysis to ensure the total fraction of positrons 100%. Treating the backscattering processes in a similar way, we propose an approach of profile correction for each (ith) layer in a multilayer source/sample configuration based on the tendency of the profile behavior influenced by the backscattering processes, as expressed by Equation (9):
with the layer index increasing along the direction of e+ implantation. are correction terms involving the adjacent layers as functions of depth z into the ith layer in question, dn is the thickness of the nth layer, and represents the positron mean penetration depth in the ith layer rather accurately as a function of the energy of a monoenergetic positron beam E+ [19,20]:
This empirical equation originates from electron stopping in solids. At low energies, the stopping mechanisms and penetration ranges through matter are considerably different for electron and positron. At sufficiently high energy levels (up to 0.546 MeV in our case), the differences tend to vanish in estimations of the positron stopping power and range through matter using analogous approaches [21]. The constant A in Equation (10) was empirically established to be , is the mass density of the absorber, for positrons implanted in most materials [20]. For non-monoenergetic positrons emitted by a radioactive isotope, the average value <E+> of the e+ energy spectrum is used to calculate the mean penetration depth.
Correction for positron backscattering in two adjacent layers will result in the profile in the layer having a lower backscattering coefficient lifted, whereas the profile in the other layer with a higher backscattering coefficient will be reduced. This effect is well described by Equation (9) that, for example, for a triple layers’ system with , the correction term will have a positive value, while will be negative. Addition of these terms to the numerator of Equation (9) will yield an increase and a reduction in the profile , respectively within the ith layer. With the simplified geometry formed by a Kapton foil and a single layer of the sample, as depicted by the inset of Figure 1, profile correction using Equation (9) for the involved layers can be reduced to
where the parameters related to the Kapton and sample layers are subscripted with K and S, respectively.
3. Profile Analysis with Single and Multilayer Configurations
Semi-infinite aluminum (Al) and titanium (Ti) samples are investigated using the approach discussed in Section 2. A multilayer stack of LCO cathodes and Al support foils is analyzed as an example of the multilayer profile estimation. The Kapton® [poly(4,4′-oxydiphenylene-pyromellitimide)] foil developed by Dupont has a chemical formula C22H10N2O5 and mass density of [22,23]. With the fraction by weight and atomic number of each constituent element of the chemical composition available in the NIST Database [24], the effective atomic number of the Kapton foil is calculated to be according to Equation (13) proposed by Murty [25]:
Positrons penetrating through an absorber material lose a certain fraction of their initial energies. This loss depends on the initial energies and the material-dependent stopping power and thickness of the absorber due to interactions with the atomic electrons in the material. When treated as monoenergetic positrons, the energy loss of the positrons having an average energy of 216 keV emitted by the 22Na source after penetrating the 7.5 μm thick Kapton foil was calculated to be based on the stopping power available in the standard reference data [21]. Therefore, the average penetration depth of the positrons having an average energy of in each sample can be calculated using Equation (10). The parameters calculated for the Kapton foil, Al, Ti, and LCO samples involved in this study are tabulated in Table 1 and used in the profile analyses.

Table 1.
Properties of the Kapton foil, Al, and Ti calculated and used in the analysis.
3.1. Single-Layer Estimation with Aluminum and Titanium Samples
The positron implantation profiles in the Kapton/sample configurations with the Al and Ti samples are corrected and analyzed using the approach deployed in Section 2. Identical Kapton foils with a thickness of were used throughout the measurements and analyses. The influence of backscattering at the Kapton/sample interface on the behavior of the profiles obtained with the Al and Ti samples are illustrated in Figure 2a,b, respectively.
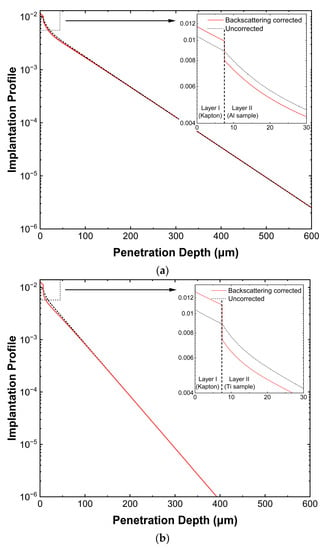
Figure 2.
Positron implantation profiles in the Kapton/sample configurations with single-layer Al and Ti samples estimated with backscattering corrections. (a) Profile of the Kapton ()/Al (1.5 mm) setup. (b) Profile of the Kapton ()/Ti (1 mm) setup.
Positrons impinging the backscattering medium are partially reflected not only due to the elastic and inelastic collisions with the atomic electrons and nuclei in the material, but also due to the Coulomb repulsion of the positive charges in the backscattering medium. After backscattering correction, the profile in the Kapton layer is enhanced while that in the sample layer is reduced accordingly as the Kapton foil has a density and atomic number considerably smaller compared to that of the samples. The corrected profiles of the simplified source/sample configuration given by Equations (11) and (12) can be integrated over the corresponding layer depths, respectively, to obtain the relative annihilation intensity inside each layer. The contribution of the source component for each studied sample is hereby revealed by the ratio between the source intensity and the total intensity . The source component in the Kapton layer was experimentally determined to have a lifetime of 382 ps and an associated intensity corresponding to each sample by fitting the PALS spectra with the LT program. To verify the calculated source contributions, PALS measurements were performed using a fast-fast coincidence lifetime spectrometer with a time resolution of and a time calibration of 25.35 ps/channel for a multichannel analyzer (MCA). In each measurement, the 22Na () source encapsulated by Kapton foils was sandwiched by two identical sample plates with a specific thickness, as indicated in Table 2.

Table 2.
Source contributions without correction (), values estimated with backscattering corrections (Cor. ), and experimental results (Exp. ) for Al, Ti, and LCO samples.
3.2. Profile Analysis in a PALS study of A Multilayer Source/Sample Configuration
In this section, the use of the positron implantation profile and source contribution estimation method in our study [4] of the effect of carbon coating on Li+ ion mobility in LCO cathodes is demonstrated as an example of the profile analysis with multilayer configurations.
Instead of the analysis with the single-layer sample setups, the multilayer estimation was carried out by correction of the estimated implantation profile in all the layers and interfaces involved in the multilayer configuration, as illustrated by Figure 3b. Figure 3a shows that the influence of positron backscattering on the profile behavior at the Kapton/LCO interface is similar as the cases of single-layer Al and Ti samples. It is noteworthy that the profile within the Al (Layer II) in Figure 3b is lifted after the correction since LCO is a denser material having a backscattering coefficient (RLCO = 0.327) larger than that of Al (RAl = 0.23).
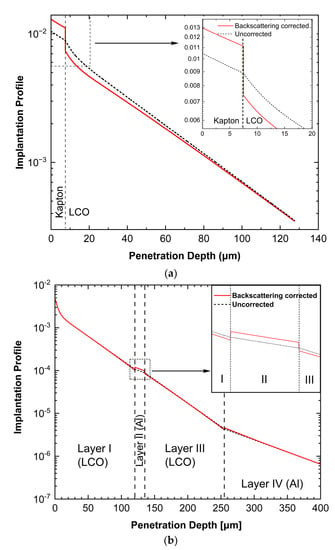
Figure 3.
Positron implantation profiles in the multilayer LCO-Al-LCO-Al configuration estimated with backscattering corrections. (a) Corrected profile of the Kapton ()/LCO (120 ) setup. (b) Profile of the multilayer setup used in the LCO measurement, excluding the Kapton layer by subtraction of the source contribution. The insets of Panel a and b are set for visualizing the profile behavior with and without correction at the Kapton/LCO and LCO/Al interfaces, respectively.
Using the method discussed in Section 2, the source contribution with the LCO multilayer sample was calculated to be 14.1%, which was experimentally verified by fitting the measured spectrum using the LT program. Due to positronium formation at the source/sample interface, a very long lifetime component of approximately 2 ns is commonly observed in the spectra, which is considered “spurious” in the analysis. This spurious component usually has a very low intensity depending on the surface porosity of the material, which is measured to be approximately 0.2–0.4% in our case of the Kapton/LCO interface (see Refs. [2,4] for more details). After subtraction of the source and spurious components, the remaining fraction of the implanted positrons is normalized to unity in the analysis. Considering one half of the symmetric geometry, upon subtraction of the source and spurious components, the fraction of positrons annihilating within the LCO cathodes was estimated to be approximately , with the remaining thermalized in aluminum, as depicted in Figure 4b.
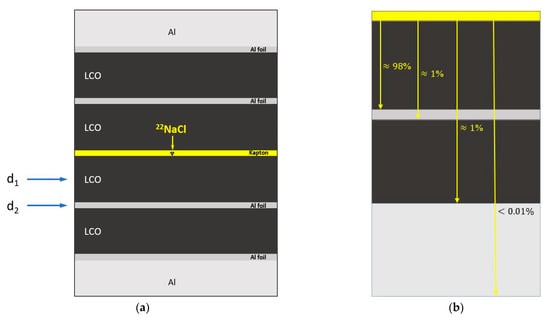
Figure 4.
(a) Schematic of the LCO multilayer measurement setup. The sandwich configuration for PALS measurements consists of two identical pairs of the LCO sample separated by Al foils on both sides of the 22NaCl source, with and . (b) Estimation of the annihilation intensity in each layer of half of the symmetric geometry.
The PALS experiments employed a multilayer source/sample configuration with a sufficiently large lateral dimension to have most of the implanted positrons annihilating inside the sample. The 22Na () source encapsulated by Kapton foils was sandwiched by two pairs of identical LCO samples with a thickness of d1 = 120 μm deposited on supporting aluminum foils with a thickness of d2 = 15 μm, as illustrated in Figure 4a. This setup was secured by two external Al plates (1.5 mm thick). The measurements were carried out using the apparatus identical as discussed in Section 3.1. Considering the relatively low radioactivity of the 22Na source, each lifetime spectrum was recorded on annihilation events in an acquisition time up to 48 h. To avoid systematic errors resulting from possible shift of the centroid position of the spectrum over a long data acquisition time, the spectra statistics were accumulated from separate brief spectra collected in every 6 h and corrected to an eventual shift before the integration over the analyzed spectra.
The source contributions for the single and multilayer configurations calculated with and without backscattering correction and the experimental results are presented in Table 2 for comparison under the assumption that all the measured samples are semi-infinite to keep the total annihilation intensity unity.
It is observed that correction of the implantation profile with backscattering effect results in a certain increase in the estimated source contribution depending on the backscattering property of the sample. It can be seen from Figure 2 and Figure 3 that the backscattering effect at the Kapton/sample interface tends to increase with the density and atomic number of the sample in the order . It is worth noting that the corrected profile (red lines in Figure 2) tends to approach the uncorrected curve (black lines in Figure 2) as the penetration depth increases. This phenomenon is due to the fact that for low-energy positrons, the influence of backscattering on the profile appears dominant around the interface region and tends to vanish at larger distances from the backscattering interface. The probability density function (pdf) of positron spatial distribution decreases by several fold as the depth increases, as shown in Figure 2, thus, the backscattering tends to cause negligible influence on the profile at larger penetration depths. This tendency is governed by the exponential factors in the correction terms in Equation (9), i.e., the values of and tend to increase as the depth z approaches the involved backscattering interface. The estimated and experimental values of source contributions (Cor. and Exp. ) are in good agreement with a discrepancy within 1%. The Cor. value with Al sample is slightly underestimated by approximately 1.5%. Since Ti and LCO have very close densities and atomic numbers, the backscattering characteristics of these samples at the interface with Kapton foil are similar and consequently, the source intensities measured with these samples are very close (), in consistence with the nature of positron backscattering effect. However, with the thickness of the LCO (120 μm) considered in this analysis, the value was slightly over-estimated as a part of the implanted positrons annihilating outside this range of depth was excluded. When an LCO thickness of 1 mm is considered, the source intensity can be estimated to be 13.4%, which is very close to the value estimated with the Ti sample. Therefore, a well-predefined sample thickness and setup geometry will help obtaining an estimation of the source contribution for analyzing the PALS spectra with an improved accuracy in the fittings.
4. The Role of Implantation Profile Estimation in a PALS Characterization of Cathode Materials in Li-Ion Batteries
The analyzing algorithm for positron lifetime spectrum deconvolution is parameter sensitive [6]. For instance, in a trail analysis of the spectrum measured with Al sample, a slight variation of the fixed source contribution resulted in significant discrepancies in the intensities of the deconvoluted lifetime components. Therefore, an accurate PALS analysis originates from precisely obtained parameters used in the spectrum analysis. On the other hand, an accurate source contribution obtained through profile analysis can be used for accuracy check of the experimental data. In our study of the effect of carbon coating on Li-ion mobility in LCO cathodes, positrons as a quantum analogue to the Li+ ions, were used to study the interactions between the C/LCO interface and the positrons by measurements of the annihilation properties around the interface. The estimated source contribution of 14 % is fixed constant throughout the analysis. To characterize the influence of carbon coating on the PALS spectrum, a comparison of the spectral characteristics of the pristine LCO sample (No C) and the LCO cathode coated with carbon nanotubes (NT) is visualized in Figure 4a after subtraction of the source and spurious components. The NT cathode was prepared by mixing LCO: C: PVDF-binder with a weight composition of 93.75:4.00:2.25. Addition of a trace amount of C and PVDF-binder causes negligible change to the effective atomic number Zeff of the cathode. Therefore, the implantation profiles and source contributions in the cases of No C and NT cathodes are assumed to be approximately equal.
A lifetime component of 145–165 ps associated with annihilations inside the LCO nanoparticles is observed with both types of cathodes. The measurements indicate that the value of is slightly increased by approximately 12% in the case of carbon-coated sample as coating by ball milling may introduce more vacancy-like defects in the active particles, resulting in an increased positron lifetime. This effect can be seen from the slopes of in Figure 5a slightly deviating from each other. It is noteworthy that a second lifetime component is identified with the carbon-coated cathode.
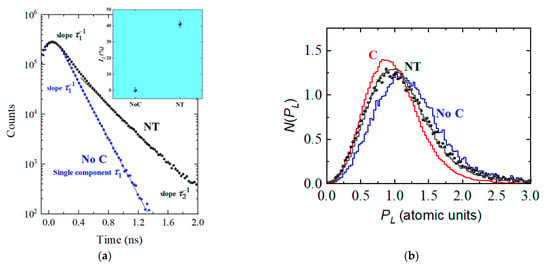
Figure 5.
PALS and CDB spectra reproduced by adopting the data published in [4]. (a) PALS spectra of LCO cathodes measured using a 22Na source, normalized to the same peak height: No C represents the pristine LCO cathode without carbon coating and NT denotes the cathode coated with carbon nanotubes. The inset shows the intensity of the second lifetime component as a function of the sample. Error bars are generated based on the experimental error. (b) Momentum distribution of the e+–e− annihilating pairs in the No C and NT cathodes and in carbon obtained in CDB measurements using a variable energy positron beam (1–17 keV).
In our first postulate, there exists a connection between the emergence of the second lifetime component and the presence of carbon coating. However, since the fitting accuracy in spectrum deconvolution is very sensitive to the parameters and mode used in the fitting, the No C and NT cathodes were further studied to shed light on the origin of the second lifetime component. The momentum distribution N(PL) of the annihilating pair at the annihilation site was measured with the cathodes and with carbon as a reference using the coincidence doppler broadening (CDB) technique. This measurement was performed by implanting positrons at various depths into the samples using a variable energy positron beam ranging between 1 and 17 keV. The momentum distribution which provides information of the atomic orbital electrons as a reflection of the chemical environment at the annihilation sites was measured with the No C and NT cathodes, and with carbon as a reference, as illustrated in Figure 5b. Obviously, when coated with carbon, the momentum distribution in the cathode is shifted towards the carbon side. This effect is well described by the linear combination of the individual contributions of the No C cathode NNo C(PL) and carbon NC(PL), providing a good approximation of the momentum distribution in the carbon-coated NT cathode as
which combines the individual quantum states associated with the LCO crystal and the carbon coating weighted by and , respectively . Therefore, the CDB results provide direct evidence that the second lifetime component originates from a significant fraction of positrons spilled over from the implanted LCO grain into the carbon layer, annihilating therein with a lifetime longer than the first component.
The Li-ion conductivity of the cathode material is characterized by . As illustrated by the inset of Figure 5a, the remarkable intensity of the second lifetime component observed in the PALS experiments shows that the NT cathode has an improved Li-ion diffusivity through the grain boundary than that of the No C cathode. This is in good agreement with the macroscopic characterization of the Li-ion diffusion coefficient using broadband electrical spectroscopy (BES). The expression of is given by Equation (15):
where is the Li+ ion conductivity in the bulk LCO material, R is the gas universal constant, T is the temperature in Kelvin, is the actual concentration of the mobile Li+ ions in the sample, and F is the Faraday constant. BES measurements were carried out with the No C and NT cathodes by applying a constant external electric field of 0.03 V to drive the Li+ ion dynamics through the grain boundary. Studies using both techniques allow us to obtain a qualitative and quantitative characterization that the Li-ion conductivity of the LCO cathode can be improved by approximately 4 fold upon coating the active particles with carbon nanotubes. Detailed results obtained in the PALS and BES measurements are summarized in Table 3.

Table 3.
Positron lifetime components and BES measurements of Li+ diffusion coefficients.
Since the volume of the carbon layer is considerably smaller than that of the LCO grain, positron annihilations inside the carbon layer should tend to be much less probable than in the LCO grain. However, the great intensity of () indicates that there must exists an attractive Coulomb potential at the interface formed by the LCO grain and carbon coating to boost the positrons to migrate through the interface and get localized in the carbon layer. Carbon exhibits excellent electric conductivity while the LCO crystal is a p-type semi-conductor. A Schottky or ohmic junction can be formed at the carbon/LCO interface due to the different work functions of the conductive carbon and the semi-conductive LCO, resulting in the negative charges in the LCO grain migrating into the carbon layer and a depletion region on the LCO side. The negative charges locally populated at the carbon/LCO interface create an intrinsic Coulomb field attractive to boost the diffusions of positively charged positrons and Li-ions from the LCO grains into the carbon layer [4]. The BES results of (in Table 3) indicate that at the same applied external field, Li-ion diffusion in the NT cathode is approximately 4-fold higher than that of the No C cathode attributing to the attractive field created at the carbon/LCO interface. Therefore, coating the LCO active particles with carbon nanotubes could enhance the cathode performance not only in its structural and chemical stability, but also in the Li-ion diffusivity aiming at high-current charging and discharging of LIBs.
5. Conclusions
Conventionally, positron annihilation spectroscopy functions in Materials Sciences as a quantum probe of the structural evolution and defect formation in the bulk and surfaces at the atomic scale. In this work, we demonstrated a distinctive application of PAS in parallel with BES as complementary techniques in interfacial characterizations of the electronic and ionic conductivity of functional energy materials. With sufficiently large statistics collected in each measurement ( events in our case), positrons as a quantum analogue of Li-ions, can be used to probe the Li-ion dynamics at the LCO/carbon interface [4]. Various computer programs have been developed for analyzing the positron lifetime by deconvolution of the spectra. In PALS measurements employing a foil-encapsulated positron source, knowledge of the fraction of the total implanted positrons annihilating in the source envelope is essential in obtaining an accurate spectral analysis and interpretation. Moreover, an accurate estimation of the positron implantation profile throughout the source/sample configuration will not only provide an accuracy check of the measured lifetime components, but also facilitate setting up the configuration with a rational geometry to optimize the acquisition of the annihilation data. The demonstrated methods for positron implantation profile estimation provided us with a fundamental approach in PALS spectrum analysis, which will be used in our future studies of Li-ion and Na-ion battery materials. The profile analysis showed that different types of the sample differ in their backscattering properties. Generally, the higher atomic number Z of the sample as a positron backscatterer, the greater fraction of positrons is reflected at the source/sample interface. Using the simplified approach discussed in this article, a rather accurate approximation of the positron implantation profile was obtained with the multilayer setup of semi-infinite samples, where multiscattering processes at the interfaces between the stacked layers (illustrated in Figure 1) were assumed to have negligible contribution to the profile. Nevertheless, for a more rigorous analysis of the implantation profile through multilayered configurations, particularly with low Z and/or thin layers, where the influence of multiscattering on the fraction of positrons annihilating in each layer tends to strengthen, a generalized approach involving the multiscattering processes needs to be established. For instance, Dryzek and Siemek using theoretical analysis and experimental verification, proposed a multiscattering model (MSM) in [10] for estimation of the spatial distribution of positrons emitted by radioactive isotopes into multilayer sample stacks. The implanted positrons continuously lose their kinetic energies upon interactions with matter and meanwhile, such energy struggling of positrons modifies the energy-dependent stopping power of the medium, and hence affect the positron range penetrated in the medium. Such processes need to be included in our future exploration of the generalized approach for studying the multilayer configurations of thin cathode materials.
Author Contributions
Conceptualization, R.F., B.B. and V.D.N.; methodology, R.F. and X.L.; validation, G.P., V.D.N. and B.B.; sample preparation and BES experiments, G.P. and V.D.N.; PAS experiments and data analysis, R.F., X.L. and M.Z.; writing—original draft preparation, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research is partially supported by the LUT University INERCOM platform. The work at Politecnico di Milano was supported by internal funding. The work at Padova University was funded by the program”Budget Integrato per la Ricerca Interdipartimentale—BIRD 2021” of the University of Padova (project ACHILLES, protocol number BIRD219831).
Data Availability Statement
Data are available upon reasonable request.
Acknowledgments
We acknowledge the Finnish Ministry of Education and Culture for support. We are grateful to Valerio Toso and Alberto Caruso for their help with the PAS measurements and data analysis. We are thankful to Keti Vezzù for her help with sample preparation and the BES measurements.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nokelainen, J.; Barbiellini, B.; Kuriplach, J.; Eijt, S.; Ferragut, R.; Li, X.; Kothalawala, V.; Suzuki, K.; Sakurai, H.; Hafiz, H.; et al. Identifying Redox Orbitals and Defects in Lithium-Ion Cathodes with Compton Scattering and Positron Annihilation Spectroscopies: A Review. Condens. Matter 2022, 7, 47. [Google Scholar] [CrossRef]
- Pagot, G.; Toso, V.; Barbiellini, B.; Ferragut, R.; Di Noto, V. Positron Annihilation Spectroscopy as a Diagnostic Tool for the Study of LiCoO2 Cathode of Lithium-Ion Batteries. Condens. Matter 2021, 6, 28. [Google Scholar] [CrossRef]
- Basunia, M.S. Nuclear Data Sheets for A = 22. Nucl. Data Sheets 2015, 127, 69–190. [Google Scholar] [CrossRef]
- Pagot, G.; Di Noto, V.; Vezzù, K.; Barbiellini, B.; Toso, V.; Caruso, A.; Zheng, M.; Li, X.; Ferragut, R. Quantum View of Li-Ion High Mobility at Carbon-Coated Cathode Interfaces. iScience 2023, 26, 105794. [Google Scholar] [CrossRef] [PubMed]
- Hwang, J.; Yadav, D.; Yang, H.; Jeon, I.; Yang, D.; Seo, J.-W.; Kang, M.; Jeong, S.-Y.; Cho, C.-R. In Situ Electrochemical Impedance Measurements of α-Fe2O3 Nanofibers: Unravelling the Li-Ion Conduction Mechanism in Li-Ion Batteries. Batteries 2022, 8, 44. [Google Scholar] [CrossRef]
- Giebel, D.; Kansy, J. LT10 Program for Solving Basic Problems Connected with Defect Detection. Phys. Procedia 2012, 35, 122–127. [Google Scholar] [CrossRef]
- Dryzek, J. Remarks on a Source Contribution in Positron Lifetime Measurements. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2022, 521, 1–6. [Google Scholar] [CrossRef]
- Dryzek, J. Detection of Positron Implantation Profile in Different Materials. Acta Phys. Pol. A 2005, 107, 598–607. [Google Scholar] [CrossRef]
- Płotkowski, K.; Panek, T.J.; Kansy, J. Positron Implantation Profile in Kapton. Nuovo Cimento D 1988, 10, 933–940. [Google Scholar] [CrossRef]
- Dryzek, J.; Siemek, K. The Multi-Scattering Model for Calculations of Positron Spatial Distribution in the Multilayer Stacks, Useful for Conventional Positron Measurements. J. Appl. Phys. 2013, 114, 074904. [Google Scholar] [CrossRef]
- Tuomisto, F.; Makkonen, I. Defect Identification in Semiconductors with Positron Annihilation: Experiment and Theory. Rev. Mod. Phys. 2013, 85, 1583–1631. [Google Scholar] [CrossRef]
- Brandt, W.; Paulin, R. Positron Implantation-Profile Effects in Solids. Phys. Rev. B 1977, 15, 2511–2518. [Google Scholar] [CrossRef]
- Mourino, M.; Löbl, H.; Paulin, R. Profiles and Absorption Coefficients of Positrons Implanted in Solids from Radioactive Sources. Phys. Lett. A 1979, 71, 106–108. [Google Scholar] [CrossRef]
- Dubov, L.Y.; Akmalova, Y.A.; Stepanov, S.V.; Shtotsky, Y.V. Evaluation of Positron Implantation Profiles in Various Materials for 22Na Source. Acta Phys. Pol. A 2017, 132, 1482–1486. [Google Scholar] [CrossRef]
- Dryzek, J.; Singleton, D. Implantation Profile and Linear Absorption Coefficients for Positrons Injected in Solids from Radioactive Sources 22Na and 68Ge\68Ga. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2006, 252, 197–204. [Google Scholar] [CrossRef]
- McGuire, S.; Keeble, D.J. Positron Lifetime and Implantation in Kapton. J. Phys. Appl. Phys. 2006, 39, 3388–3393. [Google Scholar] [CrossRef]
- Dryzek, J.; Dryzek, E. Measurement of Backscattering Coefficient of Positron Using the Characteristic X-rays. Phys. Lett. A 2003, 320, 238–241. [Google Scholar] [CrossRef]
- Aers, G.C.; Marshall, P.A.; Leung, T.C.; Goldberg, R.D. Defect Profiling in Multilayered Systems Using Mean Depth Scaling. Appl. Surf. Sci. 1995, 85, 196–209. [Google Scholar] [CrossRef]
- Puska, M.J.; Nieminen, R.M. Theory of Positrons in Solids and on Solid Surfaces. Rev. Mod. Phys. 1994, 66, 841–897. [Google Scholar] [CrossRef]
- Schultz, P.J.; Lynn, K.G. Interaction of Positron Beams with Surfaces, Thin Films, and Interfaces. Rev. Mod. Phys. 1988, 60, 701–779. [Google Scholar] [CrossRef]
- Berger, M.J.; Seltzer, S.M. Stopping Powers and Ranges of Electrons and Positrons, 2nd ed.; Report No. NBSIR 82-2550-A; National Bureau of Standards: Gaithersburg, MD, USA, 1983. [Google Scholar] [CrossRef]
- Kwon, K.-S.; Rahman, M.d.K.; Phung, T.H.; Hoath, S.; Jeong, S.; Kim, J.S. Review of Digital Printing Technologies for Electronic Materials. Flex. Print. Electron. 2020, 5, 043003. [Google Scholar] [CrossRef]
- Baxter, L.; Herrman, K.; Panthi, R.; Mishra, K.; Singh, R.; Thibeault, S.; Benton, E.; Vaidyanathan, R. Thermoplastic Micro- and Nanocomposites for Neutron Shielding. In Micro and Nanostructured Composite Materials for Neutron Shielding Applications; Elsevier: Amsterdam, The Netherlands, 2020; pp. 53–82. ISBN 978-0-12-819459-1. [Google Scholar]
- Composition of Kapton Polyimide Film. Available online: https://physics.nist.gov/cgi-bin/Star/compos.pl?matno=179 (accessed on 7 February 2023).
- Murty, R.C. Effective Atomic Numbers of Heterogeneous Materials. Nature 1965, 207, 398–399. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).