Elucidation of Structures, Electronic Properties, and Chemical Bonding of Monophosphorus-Substituted Boron Clusters in Neutral, Negative, and Positively Charged PB_n/${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{–}$/${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{+}$ (n = 4–8)

Abstract

This paper reports the computational study of phosphorus-doped boron clusters PB_n/${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{–}$/${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{+}$ (n = 4–8). First, a global search and optimization of these clusters were performed to determine the stable structures. We used density functional theory (DFT) methods and ab initio calculations to study the stability of the atomic clusters and to explore the arrangement of stable structures. We found that the lowest energy structures of the smaller phosphorus-doped boron clusters tend to form planar or quasi-planar structures. As additional boron atoms are added to the smallest structures, the boron atoms expand in a zigzag arrangement or in a net-like manner, and the phosphorus atom is arranged on the periphery. For larger structures with seven or eight boron atoms, an unusual umbrella-like structure appears. We calculated the binding energy as well as other energies to study cluster stability. We calculated the ionization energy, electron affinity, and the HOMO–LUMO gaps. In addition, we used the adaptive natural density partitioning program to perform bond analysis so that we have a comprehensive understanding of the bonding. In order to have a suitable connection with the experiment, we simulated the infrared and photoelectron spectra.

1. Introduction

The exploration of boron clusters has developed rapidly over the past few decades due to boron being a typical electron-deficient atom. When clusters are formed, many strong multi-center chemical bonds can be formed. Therefore, related research on boron clusters has been widely pursued. The stable structures of gas-phase anion clusters B_n⁻ (n = 3–25, 27–30, 35, 36) [1,2,3,4,5,6,7,8,9,10] of pure boron clusters have been experimentally verified. Due to the superior physicochemical properties of experimentally observed pure boron clusters, the study of doped boron clusters has been a hot topic [11]. Related studies have shown that some boron clusters have unique aromaticity and the ability to store hydrogen [12,13]. For example, one can consider the related physicochemical properties of aluminum-doped boron clusters and what kind of arrangement characteristics are formed when forming stable structures. In the field of aluminum-doped boron clusters, there is a relatively mature understanding. Experimental studies have shown that boron clusters can be used as raw materials for the preparation of metal nanocomposites, and boron clusters play an important role as reducing agents and stabilizers in the preparation process [14]. It has also been reported that non-metal/heavy atom boron clusters can be used to prepare high-performance phosphors [15]. In recent years, there has been outstanding research progress in terms of the electronic stability, bonding properties, and chemical reactivity of closo-[B_nX_n]²⁻ dianions as a function of boron cage scaffold n (n = 12, 11, 10, 6) as well as the ligand X (X = H, F, Cl, Br, I, CN) [16,17,18,19,20]. However, there are few theoretical studies on the doping of boron clusters with phosphorus atoms. There is only a small amount of carbon and phosphorus doping-related research [21].

We recently published a paper on similar P₂B_n systems [22]. Other pertinent work includes doped small boron clusters [23] and aluminum-doped boron clusters [24]. A number of other related interesting results have been recently published [25,26,27,28,29,30,31,32]. In order to have a comprehensive understanding of the global structure and properties of phosphorus-doped boron clusters, we systematically studied the mono-phosphorus-doped boron clusters.

2. Computational Methods

We first performed a global search for the stable structure of PB_n/${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{–}$/${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{+}$ clusters. The traditional method is minima hopping (MH) search [33,34,35]. This is carried out through molecular dynamics and local optimization only on the potential energy surface. This can waste computing resources by repeatedly searching for structures on the same potential energy surface. An alternative method uses basin-hopping [36]. This has certain advantages compared with the previous MH method but is still not perfect. That is, if there is an invalid disturbance in the global search, or the structure obtained after the disturbance does not conform to the normal arrangement, then a repeated search cannot be avoided. These disturbances appear because the change of energy is a single variable. We used the Coalescence Kick (CK) [37] program written by Averkiev, which is superior to the previous two methods. The initial structure of the cluster PB_n/${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{–}$/${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{+}$ was generated by this program, followed by preliminary optimization of the structure. Due to the roughness of the initial structure, it is not advisable to use a higher precision method and basis set. Therefore, we started with HF/STO – 3G [38] to optimize the initial structure. These structures still required further optimization. Next, we used the B3LYP/6 – 31G (d) [39,40] method and basis set for all optimization and frequency calculations. The lowest energy structures were now located. Single point energies at the accurate CCSD (T)/6 − 311 + G (2df) level were calculated. The relative energies using B3LYP/6 − 311 + G (d) were also calculated as a comparison.

To determine the stability of these structures, we calculated the binding energies and different energies. Next, we calculated the ionization energies and electron affinities of the clusters. We then determined the HOMO–LUMO gap [41,42] values. Finally, an adaptive natural density partitioning program (AdNDP) analysis was performed. In order to make a connection between theoretical research and experiment, we carried out the calculation of the infrared spectrum and photoelectron spectroscopy. This paper is part of a series of papers on PB_n clusters. For consistency, we maintained the same computational methods for the entire series.

3. Results and Discussion

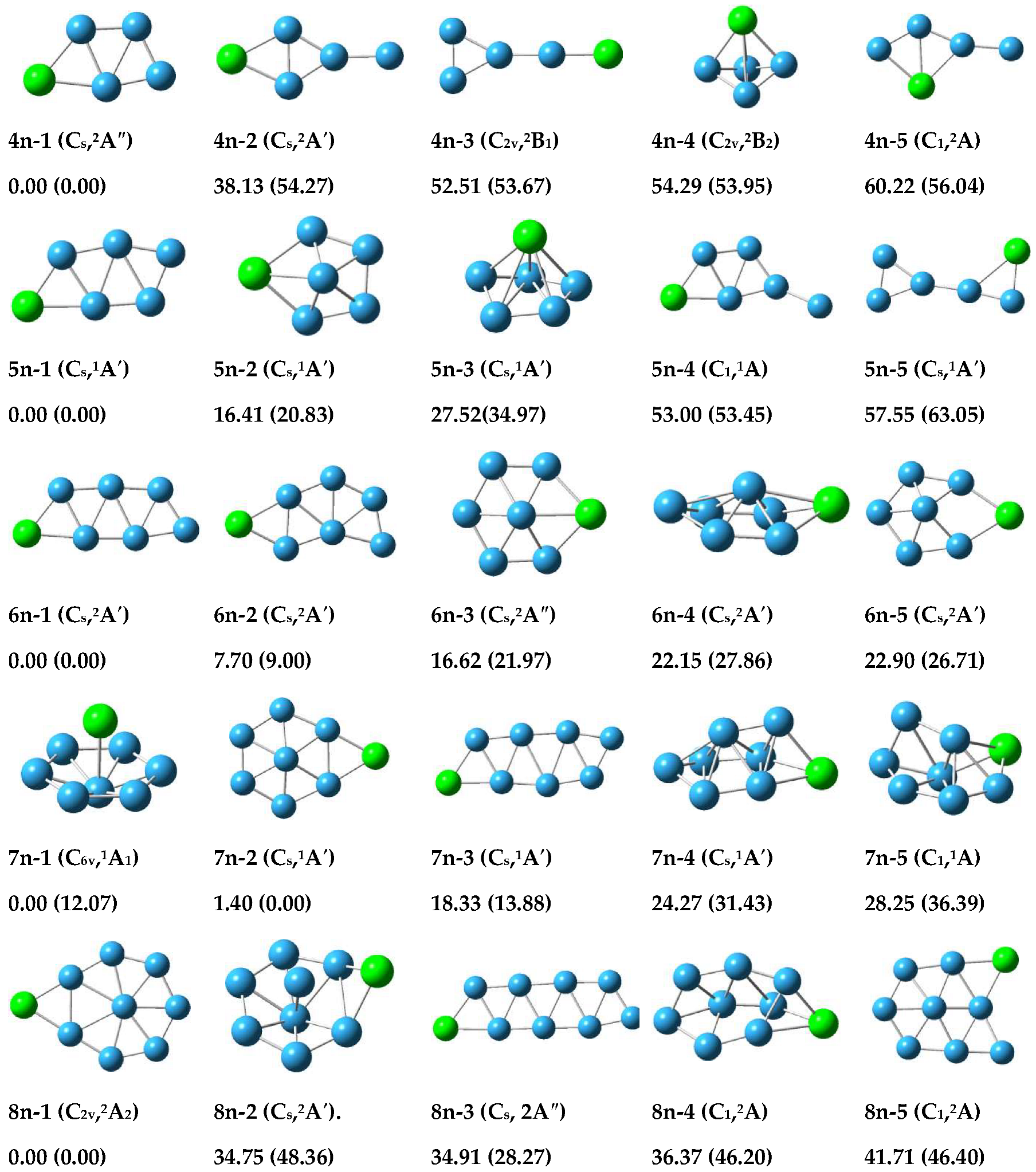
3.1. Growth Behavior of Different Sized Phosphorus-Doped Boron Clusters

3.1.1. Structure of Neutral PB_n (n = 4–8) Clusters

The point groups, electronic states, relative energies, and structures of the neutral clusters PB_n are listed in Figure 1. Considering the isomers of PB₄, we observe that the four boron atoms are arranged in a parallelogram, and the phosphorus atom is arranged around the flat quadrilateral. When the parallelogram formed by the boron atoms is broken, the energy increases. For example, it can be seen by a comparison of the 4n-1 structure with the 4n-2 structure. The relative energy of 4n-2 is 38.13 kcal/mol, which is much larger than 4n-1, indicating that 4n-1 is the global minimum and the most stable structure of cluster PB₄.

For the neutral PB₅ cluster, the five B atoms of the lowest energy structure 5n-1 form a triangular 2D raft. The P atom is located in the outer position. Comparing the structures of 4n-1 and 5n-1, it can be seen that B atoms grow in a zigzag pattern. Therefore, the presence of P atoms does not change the preference of the B atoms to form triangular 2D rafts. The relative energy of 5n-2 is 16.41 kcal/mol, and the 5n-1 structure is the global minimum and the most stable structure of cluster PB₅.

For the neutral PB₆ cluster, the 6n-1 structure is similar to that of 5n-1. The B atoms are arranged in a narrow 2D zigzag pattern based on triangular elements. The P atom is located on the periphery. The 6n-2, 6n-3, and 6n-5 structures can be seen as mesh structures, which are formed by adding a boron atom onto different locations of the 5n-2 structure. 6n-2 and other structures have higher relative energies, indicating that 6n-1 is the global minimum and the most stable structure of cluster PB₆. From the perspective of relative energy, for the six boron structures, the zigzag structure is lower energy than the mesh structure.

In Figure 1, the most stable structure of the neutral cluster PB₇ is significantly different from the first three clusters of PB₆. When the number of boron atoms is increased to seven, the boron atoms and the phosphorus atoms are arranged in an unusual and appealing umbrella shape. This has C_6v symmetry. The seven boron atoms form a concave hexagon, and the single phosphorus atom is located directly above the concave hexagon. It has the highest stability using CCSD (T) but not with B3LYP. The 7n-2 structure forms a mesh structure, like 6n-3 and 6n-5. The relative energy of the 7n-3 structure arranged in a zigzag shape is significantly greater than that of the 7n-2 structure. When the number of boron atoms is increased to seven, the umbrella structure or mesh structure is better than the zigzag structure.

For the neutral PB₈ cluster, the most stable 8n-1 structure is a mesh structure rather than a zigzag structure. The center of the structure is a boron atom, and it is surrounded by a heptagonal structure of seven boron atoms. This could be considered a molecular wheel. The phosphorus atom is arranged on the periphery, and their shape forms a planar structure with C_2v symmetry and ²A₂ electronic state. In contrast, the structure 8n-3 formed in a zigzag arrangement has a higher relative energy. Similar to the PB₇ clusters, the network structure is better than the zigzag structure.

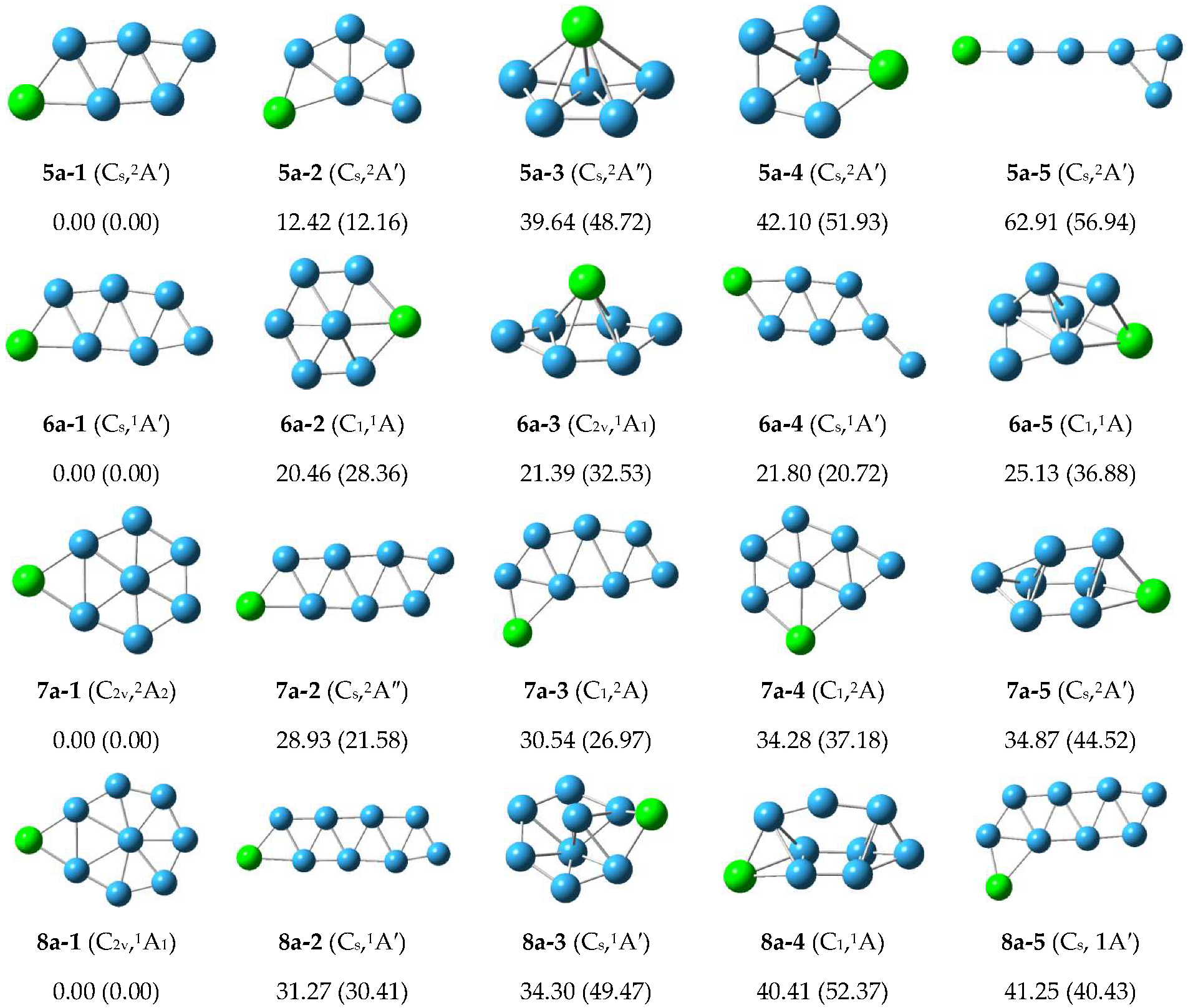
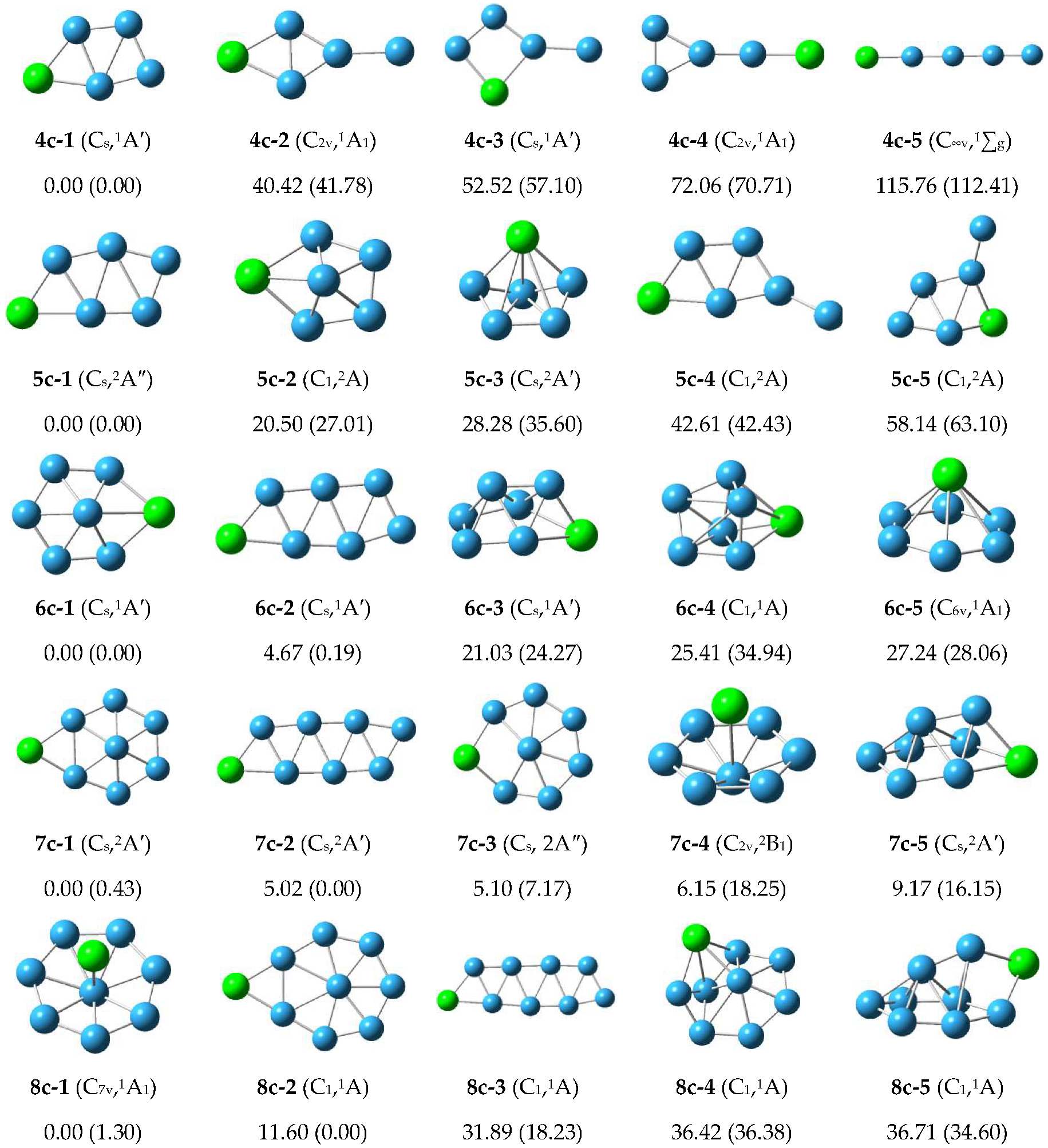
3.1.2. Structure of Anionic ${\mathrm{PB}}_{\mathrm{n}}^{-}$ Clusters

The structures, symmetries, electronic states, and relative energies of anionic ${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{-}$ clusters are shown in Figure 2. For the anionic PB₄⁻ cluster, the 4a-1 structure with the P atom at the periphery of the boron quadrilateral is similar to the 4n-1 structure, which is the global minimum of the cluster. For the PB₅⁻ and PB₆⁻ clusters, the 5a-1 and 6a-1 structures can be seen as growing via an extension of the zigzag on the 4a-1 structure. The structures of 5a-1 and 6a-1 are the global minima and the most stable structures of PB₅⁻ and PB₆⁻ clusters. The structures 5a-2 and 6a-2 are net-like, and the relative energies are 12.42 and 20.46 kcal/mol higher than the global minimum, respectively. Therefore, when n ≤ 6, the zigzag structure is more stable than the mesh structure. This conclusion is the same as that of neutral clusters.

When n = 7, for the PB₇⁻ cluster, the neutral 7n-1 structure is an umbrella structure, while the anionic 7a-1 structure has a planar structure with C_2v symmetry and ²A₂ electronic state. The 7a-1 structure is the global minimum, which is similar to the 7n-2 structure. The net-like structure of 7a-1 is more stable than the zigzag structure of 7a-2. When n = 8, for the PB–8 cluster, the 8a-1 structure is the same as the 8n-1 structure, which is the global minimum and the most stable structure of the cluster. The 8a-2 structure has relative energy of 31.27 kcal/mol and grows in a zigzag shape. The 8a-1 mesh structure is more stable than the 8a-2 zigzag structure.

The structures, symmetries, electronic states, and relative energies of cationic ${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{+}$ clusters are shown in Figure 3. For the cationic PB₄⁺ cluster, the planar structure of 4c-1 with C_s symmetry is similar to the 4n-1 and 4a-1 structure, which is the global minimum of the PB₄⁺ cluster. For the cationic PB₅⁺ cluster, the structure of 5c-1 is similar to the structures of 5a-1 and 5n-1, with their internal boron atoms still growing linearly in a zigzag pattern. Phosphorus atoms are arranged at the outermost periphery of the structure. The structure of 5c-2 is similar to the structure of 5n-2, which is 20.50 kcal/mol higher energy than 5c-1. It is worth noting that one boron atom at the edge of each of the structures 5c–4 and 5c–5 are arranged with a single bond, which causes a significant increase in energy.

For the cationic PB₆⁺ cluster, the 6c-1 structure can be seen as net-like addition to the 4c-1 and 5c-2 structures. The 6c-1 structure is the global minimum and the most stable structure of the PB₆⁺ cluster. The 6c-2 structure is in a zigzag shape, and the relative energy is 4.67 kcal/mol higher than the global minimum 6c-1, indicating that when n ≥ 6, the network structure is more stable than the zigzag structure. This conclusion is somewhat different from the neutral and anionic clusters. When the 6c-1 structure and the 6c-2 structure in Figure 3 are arranged in an anionic structure, and a neutral molecular structure, the stability of the former is lower than that of the latter. With a positive charge, the stability changes. The reason may be that the hexagonal structure of 6c-1 is close to the planar structure. The phosphorus atom is an electron-rich atom with a lone pair of electrons. For this reason, the stability of 6c-1 is slightly higher than that of the 6c-2 structure.

When n = 7, for the cationic PB₇⁺ cluster, the 7c-1 structure is the global minimum, which is similar to the 7n-2 and 7a-1 structure and has higher stability, which may be due to its planar ring structure. When a six-membered ring structure composed of boron atoms carries a unit of positive charge, the lone pair of electrons of the phosphorus atom can delocalize to the hexagonal structure formed by the boron atom, and neutralizing a portion of the positive charge enhances the stability of the entire structure. In addition, it can be seen from the figure that the 7c-1 mesh structure has lower energy than the zigzag structure of 7a-2 and the umbrella structure 7c-4, so the 7c-1 structure is better than 7a-2 and 7c-4.

The structure of 8c-1 in Figure 3 is unusual because the boron atom in the 8c-1 structure forms an umbrella-like structure. The reason why the structure has high stability may be that seven boron atoms form a large planar structure. When a positive charge is applied to this structure, it is beneficially distributed by the unique position of the phosphorus atom. The structures 8c-2 to 8c-5 show different possibilities.

It is interesting to compare the results of this paper on PB_n to our previous work on P₂B_n clusters [22]. For PB_n for larger structures with 7 or 8 boron atoms, an unusual umbrella–like structure appears. This structure is rarely seen. This is not seen in the lowest energy P₂B_n structures. The HUMO–LUMO gaps are much larger for P₂B_n than PB_n.

3.2. Relative Stabilities

In

Table 1. Calculation formula for atomic cluster stability measurement.

PBn	Eb(PBn) = [E(P) + nE(B) − E(PBn)]/(1+n)	(1)
	Δ1E (PBn) = E(PBn−1) + E(B) − E(PBn)	(2)
	Δ2E (PBn) = E(PBn−1) + E(PBn+1) − 2E(PBn)	(3)
${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{–}$	Eb(${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{–}$) = [E(P−) + nE(B) − E(${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{-}$)]/(1+n)	(4)
	Δ1E (${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{–}$) = E(${\mathrm{P}\mathrm{B}}_{\mathrm{n}–1}^{–}$) + E(B) − E(${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{–}$)	(5)
	Δ2E (${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{–}$) = E(${\mathrm{P}\mathrm{B}}_{\mathrm{n}-1}^{-}$) + E(${\mathrm{P}\mathrm{B}}_{\mathrm{n}+1}^{-}$) − 2E(${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{–}$)	(6)
${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{+}$	Eb(${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{+}$) = [E(P) + (n − 1)E(B) + E(B+) − E(${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{+}$)]/(1+n)	(7)
	Δ1E (${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{+}$) = E(${\mathrm{P}\mathrm{B}}_{\mathrm{n}-1}^{+}$) + E(B) − E(${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{+}$)	(8)
	Δ2E (${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{+}$) = E(${\mathrm{P}\mathrm{B}}_{\mathrm{n}-1}^{+}$) + E(${\mathrm{P}\mathrm{B}}_{\mathrm{n}+1}^{+}$) − 2E(${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{+}$)	(9)

, E_b represents the average cohesive energy of the phosphorus–boron clusters, and Δ₁E is the fragmentation energy. This is calculated by comparing the energy of a cluster with one less boron plus the energy of the boron atom alone with the cluster energy. Larger values correspond with more stability. Δ₂E is the energy difference of the two clusters with one additional and one fewer B atom minus twice the energy of the original cluster. Δ₂E is also related to cluster stability under growth or annealing conditions.

In Figure 4a, we see that the average cohesive energies are gradually increasing as the number of atoms increases. Therefore, the clusters with more atoms are more stable. The anions are slightly more stable than the others. The values range from 3.7 to 4.7 eV. Considering the fragmentation energy, in Figure 4b, we see that for anionic clusters, n = 6 has a lower ∆₁E. For neutral and cationic clusters, we see that n = 8 has higher values. In Figure 4c, for the anionic clusters, for n = 5, the ∆₂E value is higher; when n = 6, it is lower. For anion n = 6, this suggests lower stability during growth conditions. For neutral and cationic clusters, n = 7 has lower values.

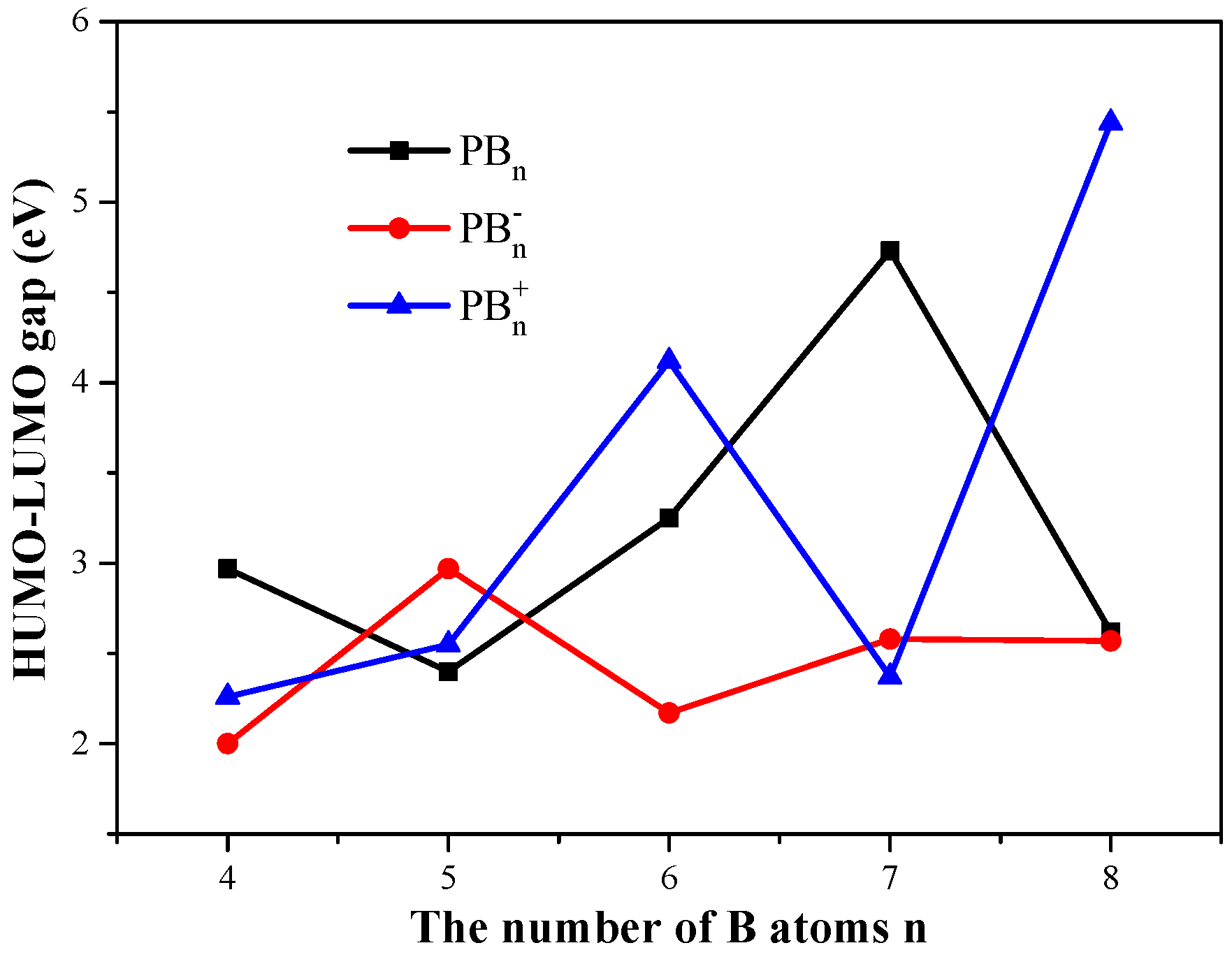
3.3. HOMO–LUMO Gaps

To better understand the properties of the PB_n/${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{-}$/${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{+}$ systems, we calculated the HOMO–LUMO gaps in each system. It can be seen from Figure 5 that the HOMO–LUMO gaps are all large. For n = 4 and n = 5, the gaps range between 2 and 3 eV. For n = 6, The cation gap is substantially larger, while the anion is lower. For n = 7, the neutral gap is substantially larger than the others. For n = 8, the cation gap is twice as large as the other two and the largest in the study.

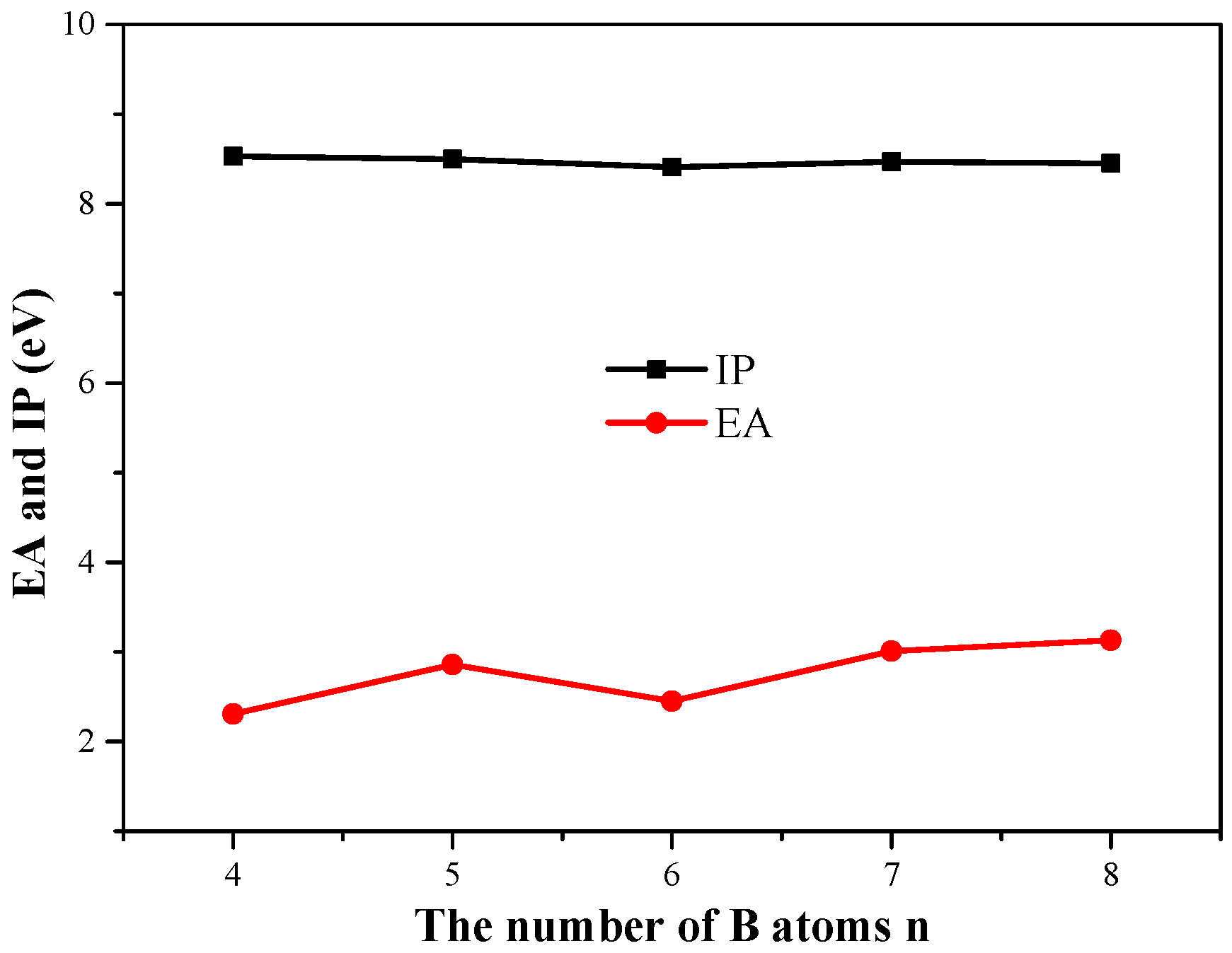
3.4. The Ionization Potential (IP) and Electron Affinity (EA)

Figure 6 shows the ionization energies and electron affinity energies of these systems. We can see that the ionization energy (IP) stays roughly constant, near 8.3 eV. The electron affinity (EA) is increasing slowly for these systems from roughly 2.2 to 3 eV.

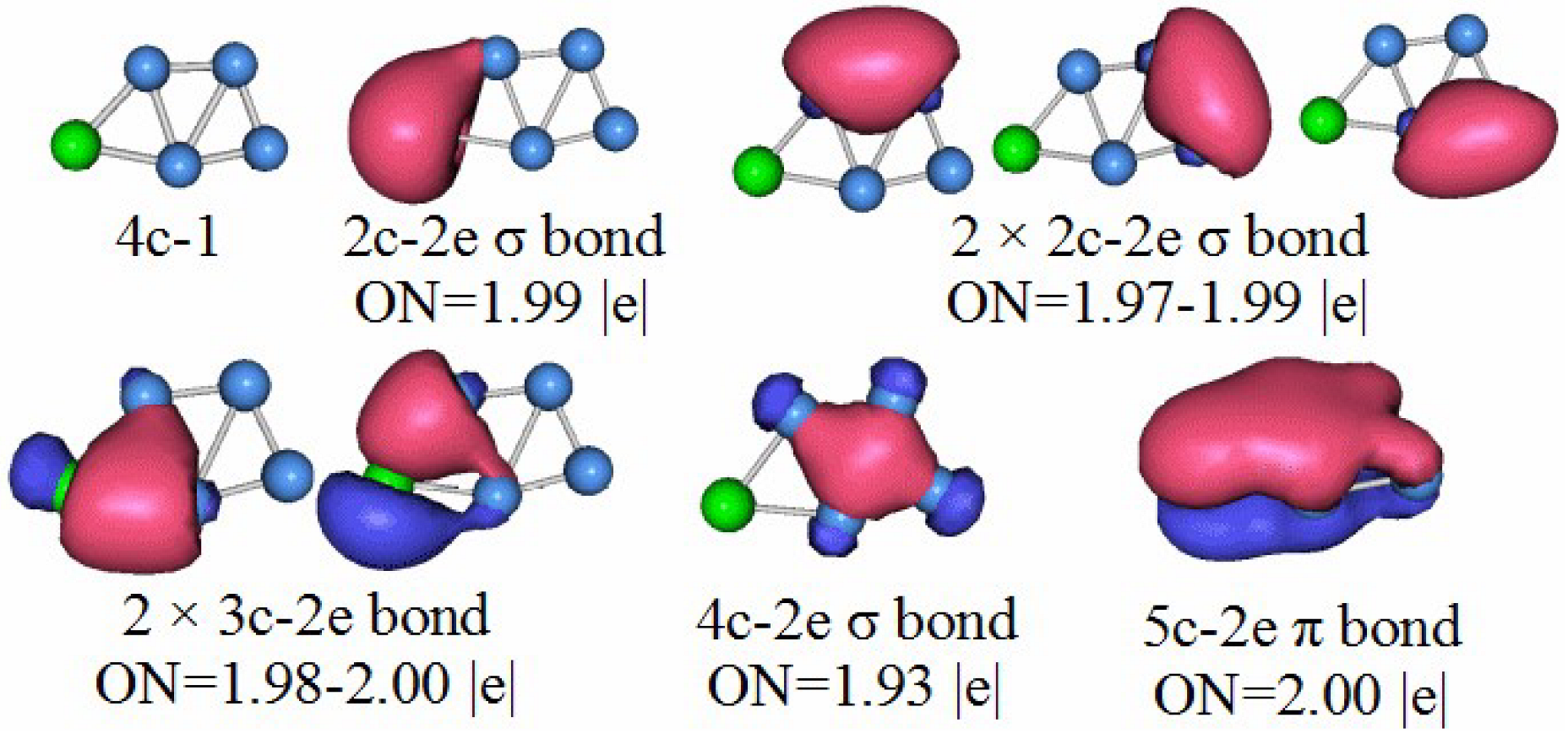
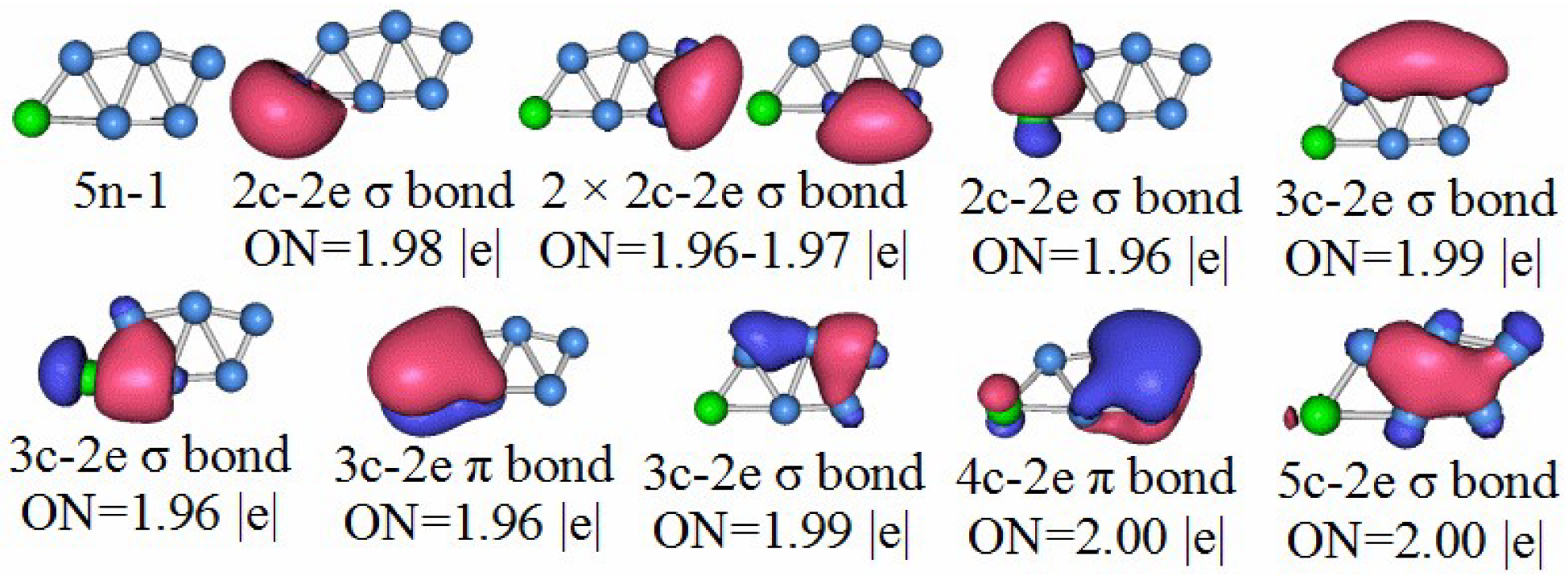
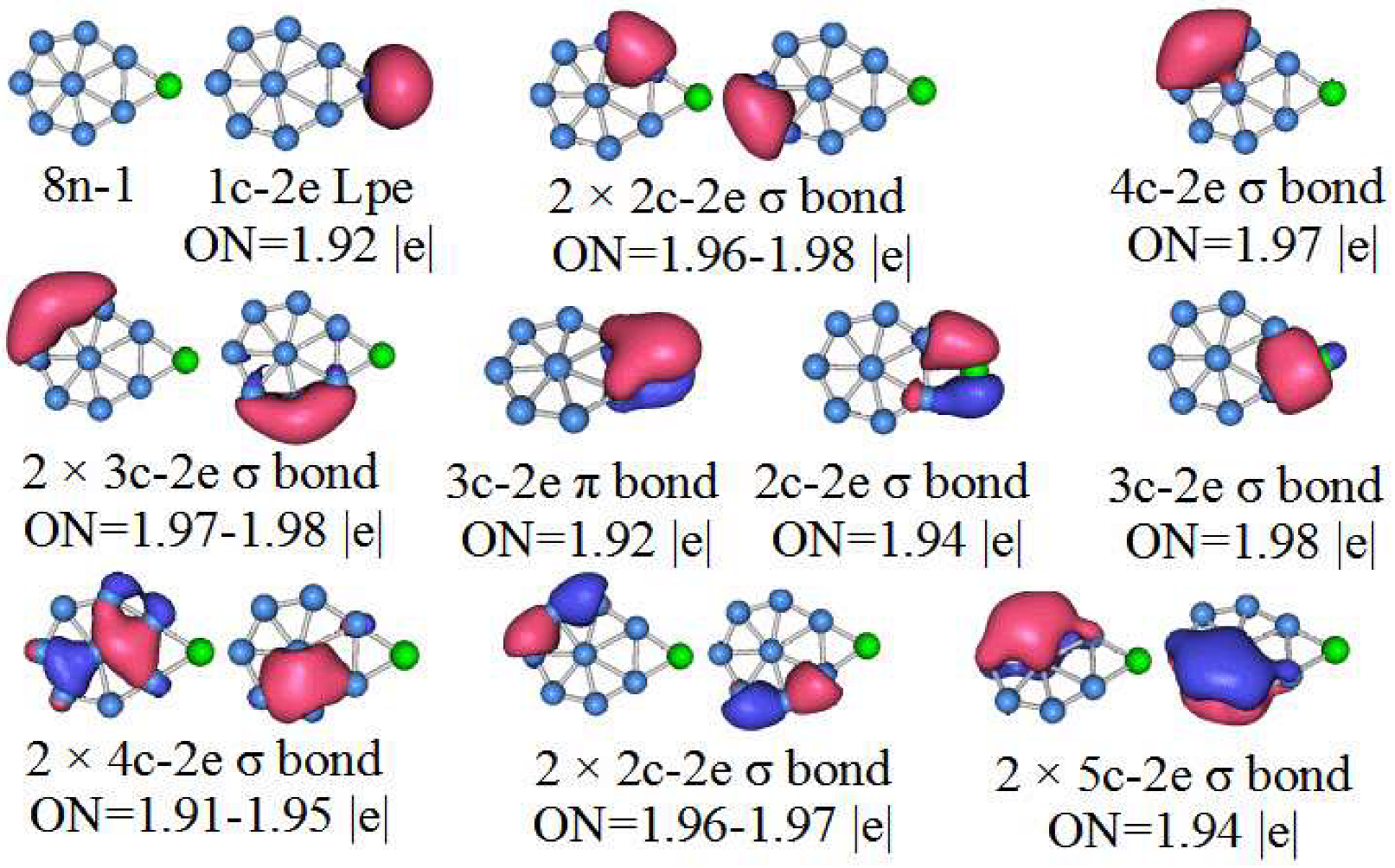
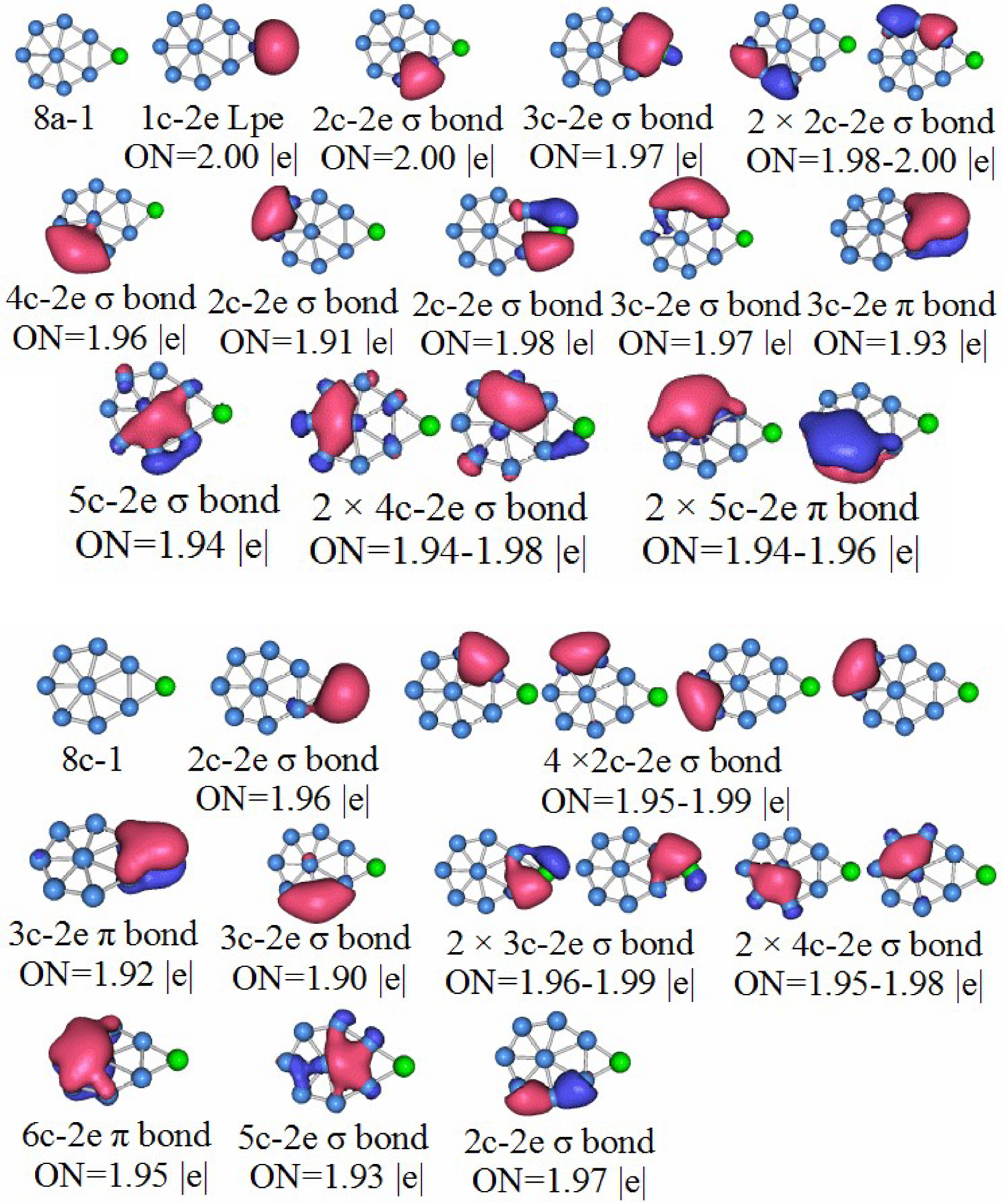
3.5. Chemical Bonding Analysis

Figure 7 shows the chemical bonding analysis for the neutral 4n-1 structure. The structure has nine bonds in total. This consists of four 2c-2e chemical bonds, one P–B σ bond (with ON = 1.99), and three B–B σ bonds (the ON value range from 1.93 to 1.98). Then there are two 3c-2e σ bonds with an ON value between 1.96 and 1.99. The π bonds of the next two 3c-2e have ON = 1.99 and 1.91, respectively. The last bond is a 4c-2e σ bond, with ON = 1.95.

The 4a-1 structure is the most stable structure of the anionic cluster PB₄⁻. This has nine chemical bonds. The analysis results are as follows: one 2c-2e σ bond with an ON = 1.99, three 2c-2e σ bonds with ON = 1.92 and 1.97, two 3c-2e π bonds have an ON value between 1.96 and 1.99. There are also two 3c-2e π bonds with ON values of 1.99 and 1.93, respectively. The last chemical bond is a 4c-2e σ bond and ON = 1.95. The bonding structure for 4a-1 is very similar to that of 4n-1, with some changes seen in the occupation numbers.

The 4c-1 structure is a stable structure of the anionic cluster PB₄⁺. This has eight chemical bonds. The analysis is as follows: one 2c-2e P–B σ bond with an ON = 1.99, three 2c-2e B–B σ bonds with ON = 1.97–1.99, and the two 3c-2e π bonds have ON = 1.98 and 2.00. A 4c-2e σ bond with an ON = 1.93. The last one is a 5c-2e π bond, with ON = 2.00. Compared with the 4n-1 structure, the 4c-1 has two fewer 3c-2e π bonds. However, one 5c-2e π bond was added.

Figure 8 shows the chemical bonding analysis for the neutral 5n-1 structure. 5n-1 is the stable structure of the neutral cluster PB₅. This has 10 chemical bonds. The analysis results are as follows: one 2c-2e P–B σ bond with ON = 1.98, another 2c-2e P–B σ bond with ON = 1.96, and two 2c-2e B–B σ bonds, with ON values ranging from 1.96 to 1.97. A 3c-2e σ bond with ON = 1.99. A 3c-2e P–B σ bond with ON = 1.96. A 3c-2e P–B π bond with ON = 1.96. A 3c-2e B–B σ bond with ON = 1.99. A 4c-2e π bond with ON = 2.00. A 5c-2e σ bond with ON = 2.00.

The 5a-1 structure is the most stable structure of the PB₅⁻ anion cluster. This has 11 chemical bonds. The analysis results are as follows: one 2c-2e P–B σ bond with ON = 1.99; another 2c-2e P–B σ bond with ON = 1.96; the three 2c-2e σ bonds have ON values ranging from 1.94 to 1.98; a 3c-2e P–B σ bond with ON = 1.99; a 3c-2e π bond with ON = 1.97; the two 3c-2e B–B σ bonds have ON values ranging from 1.90 to 1.98; a 4c-2e π bond with ON = 1.96; a 4c-2e σ bond with ON = 1.93. Unlike 5n-1, 5a-1 has a 3c-2e B–B σ bond. In addition, the 5n-1 structure has a 5c-2e σ bond, and the 5a-1 structure has a 4c-2e σ bond.

The 5c-1 structure is the most stable structure of the cationic cluster PB₅⁺. This has 10 chemical bonds. The analysis results are as follows: the two 2c-2e P–B σ bonds have ON values of 1.98 and 1.95, respectively; the four 2c-2e B–B σ bonds have ON values ranging from 1.91 to 1.97, a 3c-2e P–B σ bond, and ON = 1.96; a 3c-2e π bond has ON = 1.95; a 4c-2e B–B π bond with ON = 1.99; the last one is a 5c-2e σ bond, with ON = 1.94. Unlike the 5n-1 structure, a 2c-2e B–B σ bond is added, and a linear 3c-2e B–B σ bond is missing.

Figure 9 shows the chemical bonding analysis for the neutral 6n-1 structure. The 6n-1 structure is the most stable structure of the neutral cluster PB₆. This has 12 chemical bonds. The analysis results are as follows: there are two 2c-2e P–B σ bonds with ON values of 1.99 and 1.95, respectively; a 3c-2e P–B σ bond with an ON = 1.98; a 3c-2e P–B π bond with an ON = 1.92; a 4c-2e B–B π bond with an ON = 1.93; five 2c-2e B–B σ bonds, with ON values ranging from 1.91 to 1.97; finally, there are two 4c-2e B–B σ bonds, and the ON value ranges from 1.91 to 1.95.

The 6a-1 structure is the most stable structure of the anionic cluster PB₆⁻. The analysis results of the 6n-1 structure are similar, and each has 12 chemical bonds. There is a small difference in partial ON values. The chemical bond analysis results are as follows: the two P–B σ bonds have ON values of 1.99 and 1.93, respectively; a 3c-2e P–B σ bond with an ON value of 1.98; a 3c-2e π bond with an ON value of 1.92; a 4c-2e B–B σ bond with an ON value of 1.93; the five 2c-2e B–B σ bonds have ON values ranging from 1.93 to 1.97; the remaining two bonds are 4c-2e σ bonds, with ON value ranging from 1.91 to 1.96.

The 6c-1 structure is the most stable structure of the cationic cluster PB₆⁺, which has 11 chemical bonds. The chemical bond analysis results are as follows: the two 2c-2e P–B σ bonds have an ON value of 1.98; the four 2c-2e B–B σ bonds have an ON value of 1.93; a 3c-2e P–B σ bond with an ON value of 1.90; the 4c-2e B–B σ bond has an ON = 1.97; a 4c-2e P–B σ bond with an ON value of 1.96; the last one is the 6c-2e B–B σ bond, whose ON value is 1.96.

Figure 10 shows the chemical bonding analysis for the neutral 7n-1 structure. The 7n-1 structure is the most stable structure of the neutral cluster PB₇, and has a total of 13 chemical bonds. The analysis of the chemical bond results is as follows: there is a lone pair of 1c-2e bonds with an ON = 1.95; a 2c-2e B–B σ bond, with ON = 1.96; the three 2c-2e B–B σ bonds have ON values ranging from 1.94 to 1.98; the three 4c-2e B–B σ keys have ON values ranging from 1.92 to 1.96; a 3c-2e P–B π bond with an ON value of 1.98; two 3c-2e B–B σ bonds, one with an ON value of 1.98 and the other with an ON value of 1.94; the last two are the 5c-2e P–B σ bonds, and the ON values range from 1.95 to 1.96.

The 7a-1 structure is the most stable structure of the anionic cluster PB₇⁻, which has 14 chemical bonds. The chemical bond analysis results are as follows: a 1c-2e lone pair has an ON value of 1.97; five 2c-2e B–B σ bonds, with ON values ranging from 1.94 to 1.98; two 2c-2e P–B σ bonds with ON values ranging from 1.96 to 1.97; a 3c-2e P–B π bond with an ON value of 1.93; two 5c-2e B–B π bonds have an ON value of 1.96; a 4c-2e B–B σ bond with an ON value of 1.98; two 5c-2e σ bonds, the ON value ranges from 1.93 to 1.94.

The 7c-1 structure is the most stable structure of the cationic cluster PB₇⁺, which has 13 chemical bonds. The chemical bond analysis results are as follows: five 2c-2e B–B σ bonds, and the ON value ranges from 1.94 to 1.97. A 1c-2e lone pair, the ON value is 1.97, the two 2c-2e P–B σ bonds, and the ON value ranges from 1.95 to 1.96. A 3c-2e P–B π bond with an ON value of 1.93. A 4c-2e B–B σ bond with an ON value of 1.97. A 5c-2e π bond with an ON value of 1.95. The two 5c-2e σ bonds, where the ON value of the P–B σ bond is 1.92, and the ON value of the P–B σ bond is 1.96.

Figure 11 shows the chemical bonding analysis for the neutral 8n-1 structure. The 8n-1 structure is the most stable structure of the neutral cluster PB₈, which has 15 chemical bonds. The results of the chemical bond analysis are as follows: a 1c-2e lone pair with an ON value of 1.92; two 2c-2e B–B σ bonds, with ON values ranging from 1.96 to 1.98; two 2c-2e B–B σ bonds, with ON values ranging from 1.96 to 1.97; a 4c-2e B–B σ bond with an ON value of 1.97; two linear 3c-2e B–B σ bonds with ON values ranging from 1.97 to 1.98; a 3c-2e B–B π bond with an ON value of 1.92; a 2c-2e P–B σ bond with an ON value of 1.94; a 3c-2e P–B σ bond with an ON value of 1.98; the B–B σ bond of the two 4c-2e has an ON value ranging from 1.91 to 1.95; two 5c-2e B–B π bonds with an ON value equal to 1.94.

The 8a-1 structure is the most stable structure of the anionic cluster PB₈⁻, which has 15 chemical bonds. The chemical bond analysis results are as follows: one 1c-2e lone electron pair, and the ON value is equal to 2.00; two 2c-2e B–B σ bonds have an ON value of 1.91 and 2.00, respectively; two special B–B σ bonds, the ON value ranges from 1.98 to 2.00; a 3c-2e P–B σ bond with an ON value of 1.97; three 4c-2e B–B σ bonds, with ON ranging from 1.94 to 1.98; a 1c-2e P–B σ bond with an ON value of 1.98: a linear σ bond of 3c-2e with an ON = 1.97: a 3c-2e P–B π bond with an ON value equal to 1.93; a 5c-2e B–B σ bond with an ON value of 1.94. The B–B π bonds of the two 5c-2e have an ON value ranging from 1.94 to 1.96.

The 8c-1 structure is the most stable structure of the cationic cluster PB₈⁺, which has 14 chemical bonds. The chemical bond analysis results are as follows: a 2c-2e P–B σ bond has an ON value of 1.96; five 2c-2e B–B σ bonds, with ON value ranging from 1.95 to 1.99; a 3c-2e P–B π bond with an ON value of 1.92; a 3c-2e B–B σ bond with an ON value equal to 1.90; the two 3c-2e P–B π bonds have ON values range from 1.96 to 1.99; two 4c-2e B–B σ bonds, the ON value ranges from 1.95 to 1.98; a 6c-2e B–B π bond with an ON value of 1.95. There is also a 5c-2e σ bond with an ON = 1.93.

Other recent work on MB₇ and MB₈ clusters (M = Bi, La …) concludes that these structures are stabilized by the double aromaticity within the B₇ and B₈ unit, which should be three delocalized sigma bonds and three delocalized pi bonds [43]. We expect that double aromaticity is also stabilizing our structures.

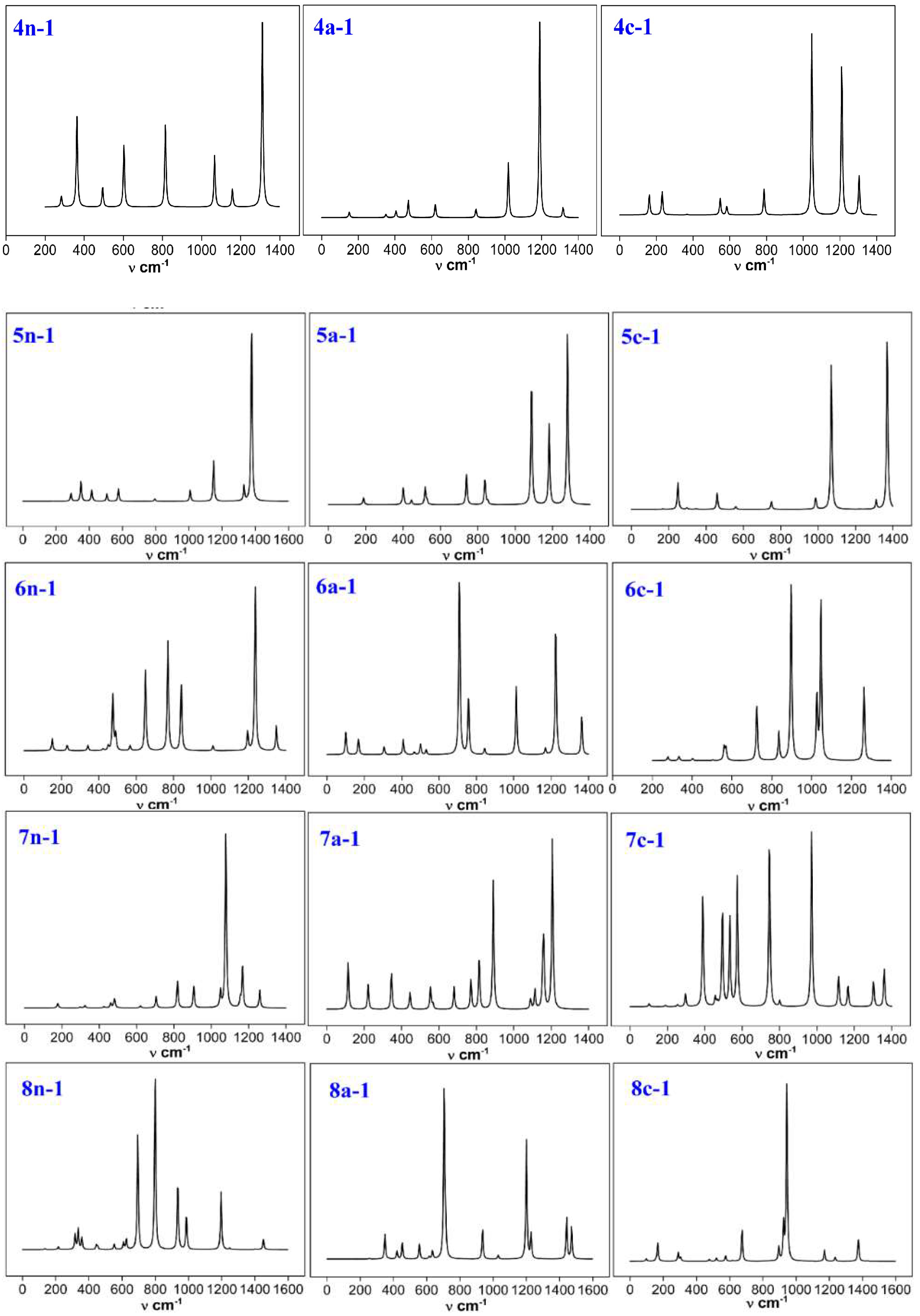
3.6. Infrared Spectroscopy

In order to confirm the structures of these PB_n/${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{–}$/${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{+}$ clusters with the experimental results, one popular method is to use infrared spectroscopy. We, therefore, calculated the infrared spectra. The simulation results are shown below and Figure 12.

3.7. Simulated Photoelectron Spectrum

Photoelectron spectroscopy uses the photoelectric effect to measure the kinetic energy of photoelectrons emitted from a sample by monochromatic radiation to determine the binding energy, the photoelectron intensity, and the angular distribution of these electrons. One can use this information to study atoms, molecules, condensed phases, and especially the electronic structure of solid surfaces. In order to predict the related properties of these materials properly, we used the TD-DFT method at the TD-B3LYP/6 – 311 + G (d) level to calculate the VDEs. The first VDE value is the energy difference between the lowest energy structure of the anionic cluster and their neutral species at the optimized anionic geometry. Other higher VDE values are obtained by adding vertical excitation energy to the first VDE value. The results for the anion clusters ${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{–}$ are shown in Figure 13.

A PES simulation of each anion cluster is shown in Figure 13, and the energy of the ground and excited states of each structure are listed. The ground-state energies from the 4a-1 structure to the 8a-1 structure are 2.38 eV, 3.18 eV, 2.57 eV, 3.31 eV, and 3.20 eV, respectively. There are certain differences in the ground-state energy of the different structures, and there is not a linear relationship where the excited state energy gets larger as the number of atoms increases. When the difference between the first excited state energy difference and the ground-state energy is large, this indicates that the structure has strong binding to electrons. It can be seen from Figure 13 that the energy difference between the first excited state energy and the ground state of the structures 4a-1, 6a-1, and 8a-1 is greater than 1 eV, and the energy difference between the structures 5a-1 and 7a-1 is less than 1 eV. This shows that the former has a greater ability to bind electrons.

4. Conclusions

We have completed a theoretical study of the atomic clusters PB_n/${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{–}$/${\mathrm{P}\mathrm{B}}_{\mathrm{n}}^{+}$ (n = 4–8). We used density functional theory and ab initio methods to study the stability of the atomic clusters and to explore the arrangement of stable structures. Structures were searched using the Coalescence Kick method. We found that the lowest energy structures of the smaller phosphorus-doped boron clusters tend to form planar or quasi-planar structures. As additional boron atoms are added to the smallest structures, the boron atoms expand in a zigzag arrangement or in a net-like manner, and the phosphorus atom is arranged on the periphery. For larger structures with seven or eight boron atoms, an unusual umbrella-like structure appears. We calculated the binding energy as well as different energies to study cluster stability. We calculated the ionization energy, electron affinity, and the HOMO–LUMO gaps. In addition, we used the adaptive natural density partitioning program to perform bond analysis so that we have a comprehensive understanding of the bonding. In order to have a suitable connection with the experiment, we simulated the infrared and photoelectron spectra.