Abstract
This article begins with an interdisciplinary review of a hydrodynamic approach to understanding the origins and nature of macroscopic quantum phenomena in high-temperature superconductivity, superfluidity, turbulence and biological systems. Building on this review, we consider new theoretical insights into the origin and nature of pointer states and their role in the emergence of quantum systems. The approach includes a theory of quantum coherence underpinned by turbulence, generated by a field of pointer states, which take the form of recirculating, spin-1/2 vortices (toroids), interconnected via a cascade of spin-1 vortices. Decoherence occurs when the bosonic network connecting pointer states is disrupted, leading to their localisation. Building further on this work, we explore how quantum particles (in the form of different vortex structures) could emerge as the product of a causal dynamic process, within a turbulent (fractal) spacetime. The resulting particle structures offer new insights into intrinsic spin, the probabilistic nature of the wave function and how we might consider pointer states within the standard “point source” representation of a quantum particle, which intuitively requires a more complexed description.
1. Introduction
1.1. Overview
A well-established mathematical framework exists to describe the outcome of an experiment in quantum mechanics (QM) with high levels of precision. However, a number of questions remain relating to the fundamental physical processes that define a quantum system, which we begin to explore in the current paper
As indicated by Delphenich [1], we are beginning to see the emergence of a number of “common elements” in different fields of condensed matter such as superconductivity, superfluidity and turbulence in viscous fluids. The authors of the present paper have collaborated over several years on a body of work focused on identifying and understanding common threads that link quantum coherence in condensed matter and biological systems [2,3,4,5,6]. In a continuation of this research, we consider a number of unresolved questions and new insights into the processes that underpin macroscopic quantum coherence and how this impacts on our understanding of a number of inter-related postulates (the complex state function, Born’s postulate, spin–statistics theorem, Pauli exclusion principle) that underlie the present axiomatic foundation of standard QM [7].
1.1.1. The General Principles Underpinning Decoherence in Quantum Systems
As described in [5], a diffusive system of environmental fluctuations that leads to the collapse of a wave function can be written in the form of a Euler equation (Equation (1)), in which D represents a standard diffusion coefficient, with the force expressed in terms of probability density P
Comparing this with the quantum equivalent in the free case [8]
we see an equivalence between a standard fluid subjected to a force field and a diffusion process with the force expressed in terms of the probability density at each point and instant.
The “diffusion force” derives from an external potential
whilst the quantum force is the exact opposite, derived from an internally generated “quantum potential”,
This interpretation offers an insight into quantum decoherence in both standard QM and macroscopic quantum systems such as high-temperature superconductivity (HTSC) [2]. At both scales, the two forms of potential energy exist and compete in quantum systems, summarised by the total System–Environment Hamiltonians (-), and their interaction ()
When the diffusive potential (Equation (3)) exceeds the internal quantum potential (Equation (4)), it leads to wave function collapse. This fits with decoherence theory in “quantum Brownian motion”, where during the decoherence process, the time evolution of position space and momentum space is reflected in the superpositions of two Gaussian wave packets [9]. Interaction with the environment damps oscillations between the direct peaks, leading to the emergence of “pointer states”, described as minimum-uncertainty Gaussians (coherent states), well-localized in both position and momentum, thus approximating to classical points in phase space [9,10,11,12,13,14,15]. Whilst the process has been discussed extensively, a detailed description of the origin and nature of “pointer states” and how they fit within the description of a wave function remains an open question.
1.1.2. The Origin of Pointer States and Their Role in Decoherence
Within the theoretical framework of scale relativity, a coherent wave packet is underpinned by a fractal velocity field [2,4,16]. Whilst the concept of pointer states was highlighted in this earlier work, it has not yet been described in detail. However, what does emerge is a sense that “pointer states” equate with a fundamental “root structure”, which represents a ubiquitous characteristic of fractal networks. This implies that the emergence of pointer states during wave function collapse somehow equates with the collapse of the fractal velocity field (which underpins the wave packet) to a more robust root structure, which accounts for the transition from a quantum to a classical description.
To better understand what this means in practice, we begin with a brief review of work on macroscopic quantum phenomena observed in high-temperature superconductivity (HTSC), biological systems, superfluid helium and fully developed turbulence. From these case studies, a number of insights are distilled, which lend support to a new description of pointer states and their role in quantum systems.
Note that each of the papers under review contains its own literature review. For the sake of brevity, we refer the reader to the original source material for references and more detailed background information.
2. A Review of Progress in Understanding Macroscopic Quantum Phenomena
2.1. High-Temperature Superconductivity: The Role of Fractal Networks in the Emergence of a Coherent State
As discussed in detail in [2,3] and references therein, when we consider a lattice of the p-type cuprates, collective excitations of the electron spin structure lead to spin waves (magnons), which appear to play a key role in forming a superconducting fluid. However, the coupling mechanism that underpins the formation of an electron pair (e-pair) has not yet been fully described. In what follows, we build on the foundations of this earlier work to construct a theoretical description of the e-pair coupling process.
We begin with a summary of factors reported in [2], which contribute to the emergence of macroscopic quantum coherence. Key to this is the incorporation of charged dopants within the structure. To summarise their role, we denote the wave function of all doping charges, whilst represents the fraction of mobile e-pairs (≈20%), which form a superconducting fluid, and represents the fraction of charges which do not participate in superconductivity, i.e.,
During the annealing stage in the manufacture of the cuprates, charged dopants diffuse in a thermodynamically driven process to create a disordered network across the cuprate lattice [2].
At low levels of doping, repulsive forces (coulomb interactions) between dopants are minimal. However, as dopant density (which equates with charge density ) increases, random fluctuations lead to increasing interactions between dopants. Beyond a critical charge density, dopants will begin to cluster, creating attractive -scale potential wells, with the capability to harbour one or more electron pairs. Simple models described in [2] show that this can occur in the case of four or more dopants with a range of possible “well configurations”. An example involving eight dopants is given in Figure 1a, along with its computed quantum potential (Figure 1b).
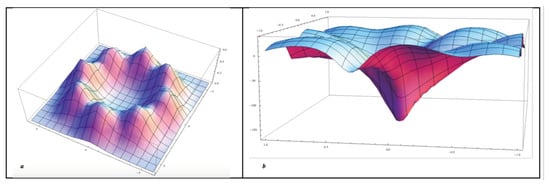
Figure 1.
Reproduced from [2]. (a) A model of dopant density distribution, with 8 dopant sites surrounding a void zone. (b) A quantum potential well computed from the dopant density distribution, which can trap (localise) one or more electron pairs.
At this scale, a small cluster of charges can be seen as a quantum fluid
which is expected to be the solution of a Schrödinger equation
where represents an external potential.
Introducing and phase, defined as a dimensioned action A of the wave function along with the velocity field of the quantum fluid (d), given by , we can rewrite the Schrödinger equation in equivalent form as Euler (Equation (9)) and continuity equations (Equation (10)), which reflect the real and imaginary parts of the Schrödinger equation,
where represents a localized quantum potential,
which is implicit in the Schrödinger equation (Equation (8)), but now explicit in the Euler equation (Equation (9)).
Whilst a superconductive fluid is expected to lie preferentially in such a well, connectivity between adjacent wells is required to support macroscopic quantum coherence and superconductivity (SC) [2]. A hint at a potential mechanism is illustrated in a second, more random assembly of eight dopants in Figure 2A. The geometry of its corresponding potential well (Figure 2B) reveals three open channels radiating from a central point. The probability of forming such a structure increases with increasing .
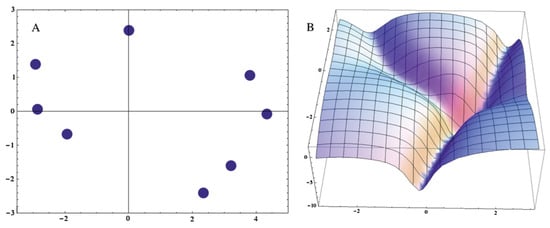
Figure 2.
Reproduced from [2]. (A) A more random assembly of 8 dopant sites. (B) A quantum potential well, calculated from the distribution of the eight dopants, in which three open channels emerge to support an interconnected network at a larger scale.
At a larger scale, the interaction of a randomised distribution of individual dopants (at a critical point), leads to a charge-induced fractal network of interconnected channels of the kind illustrated in Figure 3.
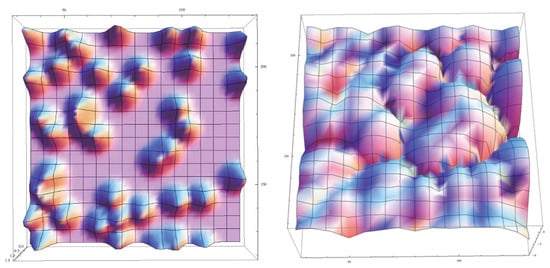
Figure 3.
Reproduced from [3]. A disordered distribution of individual charges (left). The interactions of quantum potentials associated with each charge collectively create a fractal network of hills and valleys (right).
When the fractal network reaches a “percolation threshold” (), previously localised quantum potentials such as in Figure 1b begin to merge with the network. The change reflects a transition from a collection of localised charges (where is a microscopic action) into a charge-induced fractal network, which takes the form of a macroscopic wave function ,
where is a macroscopic action, (Equation (13)) is ’s associated macroscopic quantum potential (QPR) and ℏ is substituted with a macroscopic parameter , which characterizes the amplitude and correlation length of fractal fluctuations across the MQP. The net effect is a system-specific, macroscopic de Broglie scale . In standard QM, [2,3].
At the onset of the SC phase at , transforms from a microscopic scale (where is a microscopic action) to a macroscopic scale, i.e.,
where is a macroscopic action, framed by the charge-induced scaffold and its associated fractal network .
During the formation of this fractal network, bosonic quasiparticles (e.g., magnons and phonons) may initially be present at a range of frequencies. However, at , destructive interference effects cancel out most frequencies, leaving a coherent resonant frequency, analogous with coherent random lasing [2], which is discussed in more detail in Section 6. Earlier studies [2,3] and references therein, suggest that magnons (mg), rather than phonons, play the dominant role in e-pair coupling. In what follows, we consider a coupling mechanism in more detail.
As doping increases beyond , equilibrium between dopant repulsion and the thermodynamic drive to fractal organisation of the charges is reached, which correlates with a peak in (optimal doping). Up to this point, wells, which constitute the PG phase , remain localised. However, at optimum doping, merges with , creating a single macroscopic condensate
To clarify the different contributions to , we first separate the different components.
which when written in terms of a Euler and continuity equation, reveals the four quantum potentials (, , and )
Whilst remains static, in analogy with Equations (9) and (10), it plays a key, but indirect role as a fractal electromagnetic scaffold, generating an exterior potential (), within which spin waves merge to form a macroscopic bosonic condensate ,
As initially proposed in [2], on re-integration under the form of a macroscopic Schrödinger equation, the exterior macroscopic quantum potentials and become explicit, whilst , present as an exterior potential in the microscopic equation (Equation (8)), disappears as it becomes internalized as part of at the macroscopic scale. This allows a simplification of Equation (16) to
However, in [2], a second scenario was proposed in which and its associated quantum potential might play a more dynamic, integral part of the conducting fluid . In this scenario, and would become absorbed into and Equation (20) becomes
To clarify which of these two interpretations is correct, we need to determine the precise role of magnons in the e-pairing mechanism. In addition, we revisit two unresolved questions, including:
- Why is significantly higher in HTSC materials, compared with conventional SC materials?
- Why are critical temperatures in the pseudo gap significantly higher than in the superconducting fluid ?
We consider these questions alongside a proposed new mechanism to account for the role of as an internal potential (implicit in Equation (21)), which is fundamental to the coupling of e-pairs and . Before addressing these issues (in Section 6), we consider a number of additional factors, which contribute to the construction of a more detailed picture of the underlying mechanisms at play.
2.2. Macroscopic Quantum Behaviour in Biological Structures
On first sight, HTSC and biological systems appear to have little in common. However, recent studies [3,4,5,6] have identified a number of shared macroscopic quantum processes, which have the potential to explain the emergence of a range of structures and processes typically associated with living organisms.
The concept is illustrated in work on biomimetic structures grown from BaCO3-SiO2 solutions [4,5], where sources of “charge”, as conceived in Section 2.1, included protons (from atmospheric ) and charged biomolecules, in the form of gibberellic acid (GA) and cytokinin (CK).
An example of a biological structure being underpinned by macroscopic quantum forces is illustrated in Figure 4. Figure 4a illustrates the morphogenesis of a flower-like structure, which is the solution of a time-dependent Schrödinger equation describing a growth process from a centre (l = 5, m = 0). The “petals”, “sepals” and “stamen” are traced along angles of maximal probability density. A constant force of tension has been added, involving an additional curvature of “petals” and a quantization of the angle that gives an integer number of “petals” (here k = 5).
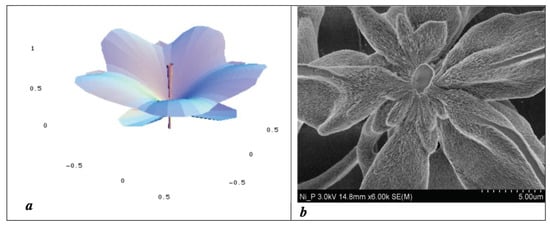
Figure 4.
(a) A Schrödinger flower reproduced from [16]. (b) An inorganic flower grown from a BaCO3-SiO2 solution reproduced from [4].
One of the objectives of experimental studies in [4] was to establish conditions that could lead to the growth of plant-like structures comparable to results from the modelling of a Schrödinger equation. Figure 4b represents just one example of many inorganic plant-like structures grown from BaCO3-SiO2 solutions.
Considering the emergence of biological structures and systems in more detail, molecular scale assembly is strongly influenced by quantum vacuum and thermal fluctuations (collectively “environmental fluctuations”) which act as a sea of harmonic oscillators. A combination of “environmental fluctuations” and levels of ionisation (which dictate charge density ) have a fundamental impact on the trajectory and dynamics of particles as they interact to form larger structures. The principle is illustrated in Figure 5a, where in an inert gas environment. In this scenario, BaCO3-SiO2 assembly, unhindered by repulsive charges (normally generated by protons from atmospheric ), led to the growth of a crystal lattice.

Figure 5.
(a) A BaCO3-SiO2 crystalline lattice structure, reproduced from [4]. (b) A model of bifurcation, described by successive solutions of the time-dependent 2D Schrödinger equation in a harmonic oscillator potential plotted as isodensities, reproduced from [8].
By contrast, as increases, repulsive forces between adjacent charged particles create a barrier to bonding, facilitating greater particle interaction with environmental fluctuations. The implications of this are illustrated in Figure 5b, where we see successive solutions during the evolution of a time-dependent Schrödinger equation in a 2D harmonic oscillator potential, which leads to a model of bifurcation at a molecular scale. The jump from a one-body to a two-body branched structure occurs as the energy level increases from a fundamental level () to the first excited level (). An iterative bifurcation process leads to a branched molecular assembly, high levels of disorder and a fractal charge density distribution.
As with the discussions on HTSC in Section 2.1, as a charge-induced fractal network increases beyond a percolation threshold , the interaction of quantum potentials associated with individual charges creates a fractal network of interconnected channels. This can be seen as analogous with that illustrated in Figure 3, but now in 3D, that can support the emergence of a bosonic condensate, which underpins the emergence of a range of different plant-like structures [4,5].
To illustrate this principle, we consider a series of images reproduced from [4], which reflect structures grown from BaCO3-SiO2 solutions, with being dictated by protons, released through dissolution of atmospheric CO2. As described in [4], Figure 6a illustrates a fern-like (fractal leaf) structure, which reflects partial decoherence of a macroscopic wave function. Despite its relatively low fractal dimension (), it still exhibits a component of long-range order, with its being determined by the strength of a residual field and associated fractal fluctuations , relative to external diffusive forces. As increases further, we see a change in packing of dendritic -scale fibrils, with an increase in leading to a more classic leaf-like form illustrated in Figure 6b.
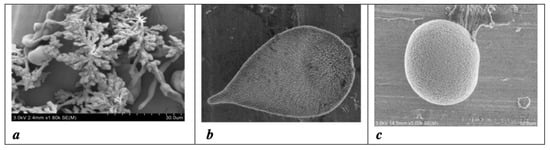
Figure 6.
(a) A fractal leaf-like structure. (b) A standard leaf structure. (c) A cell-like structure. Images reproduced from [4].
As illustrated in Figure 6c, a further increase in , through the incorporation of GA as an additional source of charge in the BaCO3-SiO2 system, led to a spherical, non-differentiated stem cell-like structure of ≈15 m diameter. The structure is composed of densely packed (≈5 nm diameter) dendrites, grown symmetrically from a centre to fill the space via an iterative process of bifurcation. The structure closely resembles a real cell (without a cell wall) with BaCO3-SiO2/GA composite dendrites replicating the dendritic structures formed by microtubules and actin filaments, which dominate the cytoplasm where most cellular activities, including cell division, occur [5].
The hypothesis that this cell-like structure is underpinned by a macroscopic quantum wave function is illustrated in Figure 7a, which reveals a collection of structures comparable to the single cell in Figure 6c. Some structures are captured in a process of division. The process is better illustrated in a magnified example in Figure 7b, which captures the transition from a one-body to a two-body structure.
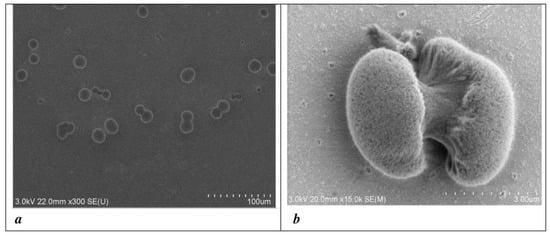
Figure 7.
(a) A monoculture of spherical structures with evidence of a division process. (b) The process of cell division. In order to grow beyond a critical point, a symmetric one-body structure, composed of a fractal fluid of molecular trajectories, becomes unstable and is forced to divide. Here, frozen in time, we see an unstable intermediate step in the dynamic transition from a one-body to a two-body structure. Images reproduced from [5].
We identify the process which underpins the cell division process captured in Figure 7b with that in Figure 8a, which reveals stationary solutions of a time-dependent Schrödinger equation in a 3D harmonic oscillator potential, whilst Figure 8b reveals successive figures, giving the isovalues of the density of probability for 16 time steps. The first and last steps ( and ) are solutions of the stationary (time-independent) Schrödinger equation, whilst intermediate steps are exact solutions of the time-dependent Schrödinger equation reflecting transient structures. Figure 8b shares a number of common features with the bifurcation process in Figure 5b, the key difference being that in the case of bifurcation, the previous structures remain and add to themselves instead of disappearing as in cell division. The only other difference lies in the quantum of action, with Figure 5b being based on ℏ rather than a macroscopic constant in Figure 8b, although the bifurcation process (Figure 5b) is also valid for a macroscopic quantum system at both sub-cellular and multicellular scales.
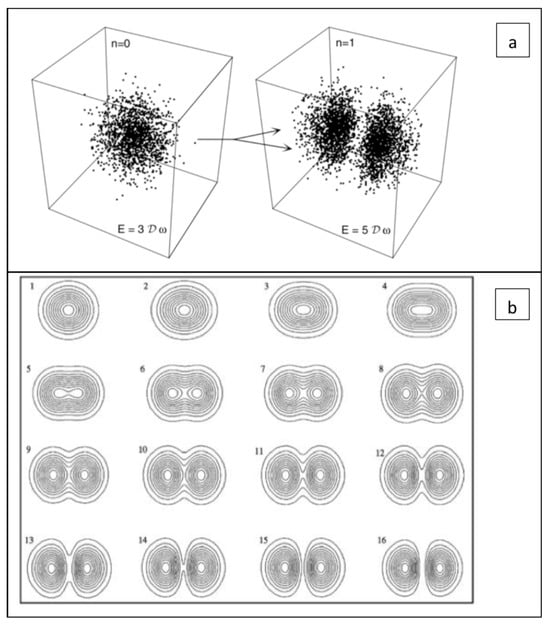
Figure 8.
Reproduced from [5]. (a) A model of division based upon stationary solutions of a time-dependent Schrödinger equation in a 3D harmonic oscillator potential. (b) Model of cell division based upon a series of solutions of a Schrödinger equation.
Like Figure 8a, Figure 7b reflects a point-like probability density. However, it also reveals that division is supported by a single, interconnected system of coherent fluctuations, in which at each point in the initial one-body system, trajectories exist that connect the two-body structures. This observation lends credibility to a proposal in [5] that the cell division process is underpinned by a macroscopic quantum system, with an increase in energy, associated with higher levels of quantisation, being linked to increasing charge density .
Alongside charge density, bifurcation processes, driven by environmental fluctuations, are fundamental to the emergence of the fractal architecture required to support the emergence of a macroscopic quantum system. Depending on conditions, the process of bifurcation can repeat itself over a broad range of scales, to create a range of structures, from proteins to cell organelles and cell walls, which constitute a living cell. The cell as the “quanta of life” then has the potential to repeat the process, creating new networks and levels of organisation, through spontaneous duplication and bifurcation.
The fractal dimension of a multicellular structure is dictated by charge density and its spatial distribution. Depending on the average charge on each cell and the level of interaction with the environment (external to the system under consideration), we see the emergence of a diverse range of cellular and multicellular structures [4,5].
One of the experimental phenomena reported in [5], of particular interest when considering intrinsic spin in quantum systems, relates to the emergence of spiral structures (e.g., Figure 9a) at higher levels of charge density generated using CK. These structures share features analogous with structures in single-celled spiral diatoms such as Chaetoceros debilis and multicellular organisms such as Arapidopsis thaliana, where spiral thickening occurs in tracheary elements [5].
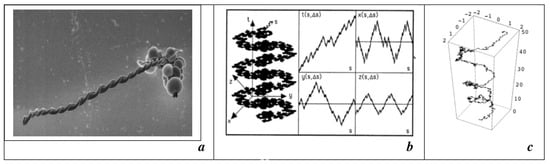
Figure 9.
(a) Reproduced from [5]. Growth of continuous spiral, underpinned by a coherent bosonic field. Each stage of assembly adds to previous growth, creating an aggregated time series. (b) Schematic representation of a fractal curve in spacetime from [17]. The evolution of its coordinates is described by four fractal functions of the normalized curvilinear coordinate s intrinsic to the fractal curve. (c) Numerical simulation of a typical spinorial geodesic in a fractal space, reproduced from [18]. The coordinates of the spiral path are quantized in units of ℏ.
A step towards understanding these spiral features emerges in earlier work, which modelled the emergence of a spin-like internal angular momentum in a fractal spacetime [17,18,19]. The principle, illustrated in Figure 9b, shows a schematic representation of the fractal path of a particle in an inertial frame of reference. The spiral path emerges as a dynamic causal structure, with causal order being determined by the specific spacetime coordinates in a series of sequential events within a 4D spacetime, in which all four dimensions, including the invariant proper time s, are fractal.
Both Figure 9a,b feature a vortex-like structure, which reflects the physical integration of consecutive slices of a fractal space. As the cell in Figure 9a grows in length, rotational forces lead to the emergence of a spiral structure, supported by a macroscopic wave front, as it evolves over time, to produce a continuous 4D fractal spacetime construct [5].
The helical (solenoidal) structure in Figure 9a emerges as an aggregated time series, with not just one but a range of probable outcomes (paths) being revealed, with an average wavelength ≈ 6 m in the mid-infrared range of 3–8 m (37–100 THz). It suggests that the force dictating the structure is underpinned by coherent thermal phonons in the mid-IR range.
The phenomenon offers an important insight into some recent developments in quantum biology [5]. For example, it is a small step to visualise how such a system could play a role in photosynthetic systems, offering a mechanism for translating photons into a coherent energy flux, which is transferred via coherent thermal phonons within the macroscopic vortex (via a very large number of potential paths) to different sites within a plant. In the case of the single-celled spiral diatoms where this kind of spiral structure dominates the cell’s anatomy, it could play a particularly effective role in facilitating photosynthetic processes.
This concept of spin in macroscopic quantum systems is of interest, not just for biological systems but also for insights it might offer with respect to spin in standard quantum systems. We explore this further in Section 3, once we have completed the preliminary background work required to support new proposals.
2.3. Turbulent Fluids and the Link to Quantum Coherence
The emergence of quantum-like forces in fractal media represents one of the founding principles of the theory of scale relativity. However, an important question remains relating to the origin of a fractal spacetime.
In developing the theory of scale relativity, it was suggested as early as 1993 ([17] Chap. 7) that a fractal medium could simulate, at some level, a fractal space, and that particles moving in such a medium may therefore acquire macroscopic quantum-type properties.
A key objective of earlier work [2,3,4,5] was to test the hypothesis that quantum forces could emerge in fractal media, at macroscopic scales. Work on HTSC and biological systems, summarised in Section 2.1 and Section 2.2, demonstrated a striking level of support for this hypothesis.
Pursuing this idea a step further, recent work [20] reveals fresh insights into the properties of turbulent systems, including the identification of a quantum signature at high levels of turbulence in “classical fluids”.
The analysis in [20] involved data generated from von Karman experiments, with turbulence generated by two contra-rotative disks. During this work, pathways through the fluid were monitored with the aid of tracer particles (⪅100 m). Results suggest that in fully developed turbulence (a Reynolds number ), a cascade of eddies/vortices, collectively generate a saturated, interconnected, vortex field and the emergence of macroscopic fluctuations, which underpin what appears to be a first stage in the emergence of a macroscopic wave function, within which both classical and coherent signatures were identified. An analogy with such a system can be found in the early onset of a coherent state, described at (Equation (14)) in HTSC [2], where we see the emergence of a critical percolation threshold within the fractal network. Within this context, we identify the emergence of a macroscopic wave function as the sum of interconnected individual (classical) vortices (), leading to a vortex-induced macroscopic field (VO).
where is a macroscopic action and (Equation (23)) is its associated MQP.
The above discussions are based upon a 2D analogy between HTSC and turbulent systems. Figure 14 in [21] illustrates simulations of a high-intensity 3D vortex network in homogeneous and isotropic turbulence reported for . The simulation suggests that the strongest vorticity is organised in elongated thin tubes.
As a general point, vortices, in close proximity and circulating in the same direction, attract and interconnect at points along their length. This can ultimately lead to the merger of vortices to form larger vortex structures whose circulation will equal the sum of the circulations of the constituent vortices. In the simulation work reported in [21], there is no mention of interconnection between vortices. However, the high vortex density image in Figure 14 (in [21]) suggests that this could be reasonably anticipated within a network of vortices at . When considering vortex densities at , reported in [20], the probability of an interconnected vortex field .
In a turbulent fluid, the largest, most energetic vortices dominate the space. As they interact, they generate a cascade of smaller eddies/vortices, which act as carriers of force between them. In trying to explain the quantum signature observed in turbulent fluids in [20], it appears intuitive that larger vortices (with the potential to facilitate transport of tracer particles) may be regarded as analogous with quantum tunnelling, whilst the less energetic component of the turbulent field reflects the classical component of the system.
The analysis raises an interesting question around the relationship between turbulent spacetime and the origins of quantum particles (bosons and fermions). It suggests that the origins of fractal spacetime, chaos and irreversibility that sit at the heart of a coherent quantum system in scale relativity theory emerge from pure turbulence. The concept is developed further in relation to superfluid helium in Section 2.4 and HTSC materials in Section 6.
2.4. Superfluid Helium
The report of a quantum signature in fully developed turbulence () [20] suggests that a macroscopic quantum system such as superfluid helium may be underpinned by turbulence at microscopic scales. To explore this idea further, we consider the different processes that define a coherent state.
In the turbulent fluid scenario in Section 2.3, two contra-rotating discs generate a turbulent fluid, which can lead to partial coherence. If we attempt to draw an analogy between this and superfluid helium, then the mechanism that underpins a turbulent fluid (leading to coherence) is generated by a collection of spinning nuclei, whose magnetic flux interacts to create a Bose–Einstein Condensate (BEC). Within this system, the nuclei remain localised, surrounded by a now delocalised (shared) magnetic flux. From this description, and within the context of decoherence, as discussed in Section 1.1.2, it seems intuitive to identify the spinning nuclei with a set of “pointer states” within the BEC.
In Section 2.2, we discuss how a rotating, vortex-like structure naturally emerges from a fractal network as a causal dynamic structure in both classical and quantum systems, but with important differences between the two. In a classical turbulent fluid (Section 2.3) where the fractal network is not completely interconnected, a vortex generated as a causal dynamic structure will dissipate within the fluid when interconnectivity of the fractal network drops off. We see this clearly in a recent study of quantized vortex cores in liquid helium under different conditions, which are highlighted by small, frozen tracer particles of hydrogen [22]. Just above the critical transition temperature (), Figure 1a, within the paper reveals a chaotic distribution of localised vortices. The image is typical of what one might expect in a classical turbulent fluid. It provides confirmation that not all turbulent systems result in a coherent fluid.
Contrasting Figure 1a with the superfluid phase of helium, illustrated in Figure 1b,c in [22], viscosity , so vortices propagate without resistance as “string-like” vortex filaments [23]. Under such conditions, fluid in the form of a vortex (and matter trapped by it) can transport mass, energy and momentum over considerable distances without dissipation. According to Helmholtz’s second theorem, a vortex filament cannot end in a fluid; it must extend to the boundaries of the fluid or form a closed path. In practice, this could mean a vortex connection with itself (to form an ouroboros) or a neighbouring vortex [23]. During each of these potential interactions, energy is removed from the system via phonon emission [24]. In addition to the potential for new connections, vortex filaments may also bifurcate, as shown in Figure 1b,c in [22], leading to the emergence of an interconnected fractal vortex network. As suggested in Section 2.3, this has the potential to facilitate tunnelling in quantum systems.
The example illustrates how the emergence of quantised vortices represents a key feature of a quantum fluid such as a BEC. By implication, it is interesting to consider the occurrence of an analogous mechanism within a quanta of superfluid that takes the form of a particle in standard QM. We explore this idea further in Section 4.
A further insight from the results reported in [22] is highlighted in the forth image within the paper (Figure 1d). The figure reveals that when a force (rotational in this case) is applied to superfluid helium, vortices align in the direction of the force applied. In an analogous way (see Section 6), one would expect vortices in a magnon condensate in HTSC media to align within an electric field and facilitate superconductivity.
3. A Geometric Interpretation of Spin
Having summarised some key findings relating to macroscopic quantum coherence in earlier studies, we build on this work with a more detailed consideration of the properties of quantum systems. We begin with a review of the current status of spin as generally portrayed within the context of and the Lorentz group .
3.1.
In the special unitary group , the representation (Equation (24)) represents quantum mechanical spin in spin-1/2 particles, as rotations in complex space,
where are the Pauli matrices. Choosing the Cartan generator as the diagonal, its eigenvectors
are the basis vectors upon which acts, with eigenvalues
In contrast to the j=1/2 representation, particles with spin-1 are portrayed by the adjoint, representation of the rotation group (Equation (27)), in which only is diagonal, with eigenvalues ,.
The tau matrices represent the analog of the Pauli matrices.
Within this “framework”, intrinsic spin of a “point particle” such as an electron is seen as a purely quantum mechanical phenomenon, generally visualised within the context of a Bloch sphere interpretation [25], in which the two spin states () reflect the two sides of a complex projective plane .
This interpretation falls short of an intuitive description of the internal structure of a spin-1/2 particle and the concept of spin as a rotation through spacetime, analogous with in classical physics. The gap necessitates a fresh look at the underlying meaning of and additional information required to describe the structures and processes that are implicit (but not explicit) within the group.
As part of the process of painting a picture of intrinsic spin as an emergent property of a 4D fractal spacetime, we start with Figure 9c, which represents a model of a spiral fractal path of an electron, underpinned by a Pauli spinor. The figure represents just one of an infinite number of possible realisations of an electron, which collectively represent a coherent rotating “fluid” of geodesics. However, this does not reveal the full picture.
To develop a more comprehensive description, we begin with the vortex-like rotating matter wave illustrated in Figure 9a, which is underpinned by a macroscopic wave function. Whilst the structure is quantised along x and y coordinates, the axis of rotation (the z coordinate) remains open. If we compare this with an electron’s vortex-like path in Figure 9c, there are some important differences.
- As previously stated in [5], with respect to Figure 9a, only the macroscopic bosonic field (which underpins the structure as it grows along its z-axis) is coherent.
- The nature of a coherent packet of matter such as an electron, quantised along all three (x,y,z) coordinates, suggests some form of closed, recirculating “fluid of geodesics” in the form of a torus, such as that illustrated in (Figure 10).
 Figure 10. A torus.
Figure 10. A torus.
Within this context, the idea of a toroidal particle, which actually predates the establishment of quantum physics [26], seems intuitive.
A theory of atoms in the form of vortex rings was first proposed in 1867 by W.Thomson [27,28], who made a connection between smoke rings and Helmholtz’s theory of vortex hydrodynamics [29,30]. One particularly appealing property of vortices was the definite modes of vibration, which offered both an interesting mathematical challenge and a possible explanation of the spectra produced by chemical elements [26].
By 1880, the vortex atom championed by Thomson (with the support of Maxwell) had attracted the interest of a number of British physicists [26]. In one notable example, the concept played an indispensable role in the process that led J.J. Thomson to his discovery of the electron [31].
In 1885, M. Hill published a study on cylindrical vortices [32], followed by one on spherical vortices [33]. In this latter work, it was noted that a spherical mass of fluid in vortical motion would move through the surrounding fluid as if it was a rigid sphere. More recent work [34] illustrates how spherical vortices may be regarded as limiting cases of highly distorted ring vortices.
In what turned out to be a final development of Thomson’s historical work on the vortex atom, Hicks produced a considerable body of work on the motion and vibrations of vortex rings and spiral vortex filaments [35,36,37]. Beyond this point, further development of the theory appears to have stalled, partly due to a number of overwhelming challenges, including:
- A lack of progress in addressing the mathematical complexity of the theory.
- An unresolved question of how electrical charge related to a vortex atom. See Section 3.3 for a proposed solution.
- The vortex ring was considered potentially unstable.
- The theory was unable to account for gravitation, which was perhaps more a problem of an unrealistic expectation.
Although the work was essentially abandoned by the end of the 1890s, it was never effectively refuted or falsified. It was argued (at the time) that the vortex atom theory was so rich and flexible, and so undetermined, that it was practically beyond falsification and, for the same reason, also unverifiable [26].
What emerged from this period of activity was a hope that the insurmountable difficulties may one day be resolved in future development of the theory and progress in mathematics. As the field of quantum physics had not yet been conceived, the lack of progress at the time was perhaps unsurprising.
With the benefit of decades of development in QM and condensed matter research, we have seen the re-emergence of some of the concepts developed by Thompson and his colleagues, which we now explore in more depth.
Digging deeper into questions specifically related to the vortices illustrated in Figure 9, consider a tracer trapped within a rotating vortex analogous to that illustrated in Figure 9c. We begin with a tracer sitting in the North East (NE) quadrant of the vortex, pointing NE, then map the tracer’s position and orientation as it rotates around the z-axis. After a rotation, it will have changed position along the z-axis but will point once again in the same direction (NE). In other words, an open vortex clearly reflects the statistical description of a representation of (Equation (27)), in which a spin-1 particle (a boson) requires a rotation to resume its original state.
At a simplistic level, it seems intuitive that a vortex plays the role of a boson with the capability to transfer energy, via the fabric from which it is constructed.
If we consider the emergence of vortex-like structures at a larger scale, an analogous scenario can be found in a highly ionised atmosphere (or plasma), associated with an intense fire or thunderstorm, where charge density reaches extremely high levels. At a critical point, the build up of a potential difference between different points in space creates a force and an associated “action”, in the form of a rotating vortex (a tornado) as an emergent property of a charge-induced fractal network. Once the difference in charge between points in space reaches equilibrium (via the action of the vortex), the vortex dissipates. This description represents a striking example of boson-like behaviour, with the vortex transferring energy from one point to another. As seen in superfluid helium it can also transport matter. This principle has important implications with respect to HTSC, which we elucidate in Section 6.
Reflecting on these insights, we see the validation of an earlier prediction of the emergence of a macroscopic quantum potential and quantum force from an ionised fractal media such as plasma [38]. Figure 1 from this earlier work maps the numerical integration of a Euler plus continuity one-dimensional system, with generalised quantum potential. The figure modelled the expected motion of a quantum oscillating wave packet in an harmonic oscillator field. In practice, the emergence of a 3D wave packet as revealed in Figure 9a offers an insight into how the simplified, one-dimensional model in [38] translates into a 3D scenario.
To shed further light on the difference between a spin-1 and a spin-1/2 structure, we contrast the spin-1 vortex scenario with a continuously recirculating fluid in the form of a torus such as that in Figure 10. Once again, we visualise a tracer starting in the NE quadrant (of the torus) pointing NE and map its orientation relative to its position, as it travels through the structure.
After a rotation through the torus, there is an equal probability that the tracer will sit in either the NE or North West (NW) quadrant. If by chance it returns to the same (NE) quadrant, it will (in all scenarios) have reoriented to face the opposite direction to which it started.
As the tracer continues its path on a second rotation through the torus, there is once again an equal probability that it will sit in the NE or NW quadrant. In the event that it returns to the original NE quadrant, it will have reoriented once again, to point in the original direction (NE).
The scenario clearly describes the representation of (Equation (24)) in which a spin-1/2 particle requires a rotation to resume its original state. This observation, which has also been reported independently [34,39], offers an intuitive insight into the mechanism that defines a spin-1/2 particle.
In considering a toroidal ansatz for a spin-1/2 particle, we now have an intuitive visualization of Madelung’s hydrodynamic interpretation of wave mechanics and how it relates to a statistical interpretation. This includes an intuitive link with the quantum potential function,
or
in a relativistic scenario. Within the context of a vortex or toroidal vortex scenario, the quantum potential relates directly to the deformation of the fluid associated with a spinning core. As proposed by Delphenich [1], such an approach seems consistent with Sakharov’s conception of “metrical elasticity” [40]. It means that spin is fundamental to the emergence of a quantum particle and its associated quantum potential. The idea is supported by Salesi [41], with the proposal that the quantum potential associated with a probabilistic fluid (that constitutes the fabric of a quantum particle) relates in a natural way to the non-classical energy term associated with particle spin (s). When , we have a vanishing quantum potential and a transition to a classical system [41].
As stated earlier within the context of Thomson’s research on the vortex atom, these proposals do not sit in isolation. During the 20th century, a number of related ideas have emerged within both experimental and theoretical studies in quantum physics.
It is important to note that whilst there are common threads running through these studies, they generally reflect different approaches and interpretations with respect to the implications of the work. In what follows, comments on individual papers do not therefore necessarily represent a general endorsement of all ideas contained within a paper but rather aim to distil specific ideas which converge with proposals developed in the present article.
Moving to more recent developments which could be considered as an extension of Thomson’s work, the concept of vortices linked to quantum particles was considered by Faddeev in the 1970s [42]. Since then, research in the field has proliferated and we have seen the re-emergence of the principle of a vortex particle.
An example to illustrate the point at a general level was reported by Fedi [39]. Whilst the scope of this work extends beyond that of the present paper, it supports the hypothesis of a quantum hydrodynamic approach to particle physics. In a similar vein, Huang [43] proposed that quantum turbulence in the early universe was able to create all the matter in the universe.
In work more closely associated with the current paper, Sbitnev [34] speculated on the emergence of quantum particles in the form of toroidal vortices from a superfluid quantum space. Note that the study does not consider the specifics of how a toroidal structure might emerge. In addition, the primary goal of the study involved a reconsideration of the de Broglie interpretation of QM, which falls outside the remit of the present paper. However, the work on vortex transformations is of particular interest, as it goes beyond the simplistic approach in Figure 10, to explore a range of potential variations on the vortex toroidal theme. This has relevance when considering relations between different toroidal geometries and particle properties.
Studies by Kyriakos [44] and Johnson [45] reached a similar conclusion regarding the toroidal nature of an electron. This contrasts with the toroidal description of a spin-1/2 particle proposed by Haramein and Rauscher [46], which took the form of “a double torus stacked in such a way as to have contiguous surfaces in the equitorial plane”. Whilst this approach solved the “Dirac string trick”, it reflects an overcomplicated approach when compared with the simpler concept of a double pass through a single torus.
At another level, more recent developments in condensed matter have emerged out of work inspired by Thomson’s vortex atom. In the 1960s, T. Skyrme developed a theory exploring the potential of skyrmions as particle-like solutions with attributes of baryons [47,48]. Since this initial theoretical work, experimental verification of skyrmions and a range of alternate vortex-like quasiparticles has proliferated in research on condensed matter. A review by Göbel [49] highlights a range of skyrmion structures with different properties, including 3D skyrmion tubes (spin-1 vortices) and a spin-1/2 scenario (a hopfion) when a vortex tube connects with itself to form a torus.
A Summary of New Insights Relating to
A number of useful insights emerge from the proposals we have considered, which support our understanding of the main postulates of QM discussed in detail in [7].
- Vortex structures emerge as causal dynamic structures from a turbulent fractal fluid.
- When considering flow within a recirculating torus, it is impossible to predict the precise position and orientation of a tracer at any specific point in time. It can only be described in terms of a probability (the Born postulate) after two full rotations of the torus, explaining the statistical origins of a spin-1/2 particle in standard QM. Quantum indetermination is therefore fundamentally linked with the existence of particle spin [41].
- A particle’s quantum potential is also fundamentally linked with its spin.
- The double rotation through a torus gives physical meaning to the relationship between and [25].
- A toroidal interpretation of a spin-1/2 particle resolves the problem of infinities associated with a point particle, in which the angular momentum of a point mass following a classical spiral path should vanish as . Instead, we can intuitively link ℏ (or multiples of ℏ) as a minimum measure of action with the rotation of a torus (or a vortex in the case of a spin-1 boson).The proposed connection between the concept of a spin-1/2 particle as a torus and its relation to ℏ is consistent with work by Mathisson [50], who noted that electron frequency is identical with the frequency of Schrödinger’s of a Dirac electron if and is equal to the mass of an electron (in the non-relativistic case). As proposed by Salesi [41], if we turn this around so , we can make an intuitive connection between ℏ and a double pass through a torus, which we can relate to both the action of the particle and its probabilistic nature.
- If we consider a particle as a dynamic recirculating torus and represents an upper limit on rotational velocity (), its rotational energy equates with the mass of a stationary particle, i.e., . It means that as a measure of action, ℏ defines a lower limit on a scale at which velocity, scale and mass are unified.
The results indicate a potential solution to the historical conflict between causality and effect (defended by Einstein) and the fundamental concept of probability (defended by Bohr). Whilst the statistical interpretation of wave mechanics became established as the reigning dogma of quantum physics, the fundamental conflict has never been fully resolved. We now see an intuitive description of a particle as a causal dynamic structure, as well as offering an explanation of the statistical origins of a spin-1 and spin-1/2 particle.
3.2. The Lorentz Group
As the double cover of , the Lorentz group represents transformations in flat, 4D Minkowski space, but how do we explain this in terms of relations between the Euclidean, Kronecker delta matrix () and the Minkowski metric () and how relates to an intuitive understanding of a quantum particle?
Having established a fermion as a recirculating torus represented by the representation of , we consider the transition to a relativistic scenario represented by as . If we exclude the influence of other possible factors, we can expect that in such a scenario, rotation of a particle with mass will lead to extreme dilation of its toroidal structure along x and y coordinates with a corresponding contraction in the z coordinate. The action reflects symmetry breaking associated with a transition from a 3D torus, represented by , into an approximation of a 2D torus, represented by and the dot product
Although an event measured in different inertial reference frames may give different values (observer A sees t, x, y and z, and observer B sees , , and ), they are still physically equivalent, i.e.,
being related through Lorentz transformations (a combination of Euler transformations and Lorentz boosts) that preserve the dot product (Equation (30)), whilst Euler transformations take the form of rotations (R) of vectors around the origin, where represents an angle mixing spatial dimensions,
Lorentz boosts (B) mix space and time dimensions. For a rotation mixing time and the x spatial dimension, the dot product is the equation for a hyperbola [25],
From the general hyperbolic trig relationship
Angle represents three boosts, which mix space and time.
To clarify the meaning of .
and
so . We can therefore write the transformation
as
and rewrite Equation (34) as
where
Thus, Equation (38) becomes
To visualise this in an intuitive way, it is helpful to consider three separate stages:
- Transform Euclidean geodesics on a complex plane under Lorentz boosts to generate the equivalent of a “Poincare disk” (Figure 11), whose hyperbolic geodesics can be represented at varying levels of complexity.
 Figure 11. A Poincare hyperbolic disk.
Figure 11. A Poincare hyperbolic disk. - Substitute the Poincare disk with an approximation of a static, 2D torus, constructed from a set of hyperbolic geodesics to create what might be termed a “Poincare hyperbolic torus”.
- A final step in the visualisation would be to represent an infinite set of geodesics associated with the dynamic, fluid nature of the recirculating torus under rotation at relativistic velocities. However, even the most detailed set of visualisable geodesics would represent only a fraction of the geodesics associated with such a complexed fluid structure.
Thus, the Lorentz transformations (Equations (32) and (35)), summarised as
reflect the emergence of a causal dynamic structure from a 4D fractal, fluid spacetime, which approximates a 2D, hyperbolic spin-1/2 torus, induced by rotational forces as .
In addition to a transformation of geodesics under rotation, we also need to accommodate a doubling of the wave function associated with the Lorentz group. Whilst a representation of is specified by j (either integer or half-integer), is specified by two copies of [25], which reflect a particle and its antiparticle partner in the Dirac equation. This reverts to a single copy of at its non-relativistic limit in the Pauli equation.
3.3. The Interaction of a Torus with the Quantum Vacuum
As a toroidal particle rotates, the background media (the quantum vacuum) in which it sits will be continually drawn through its core and recirculated, creating a secondary, polarised flux. Such a scenario should generate a two-component nested torus, analogous with that illustrated in Figure 12.
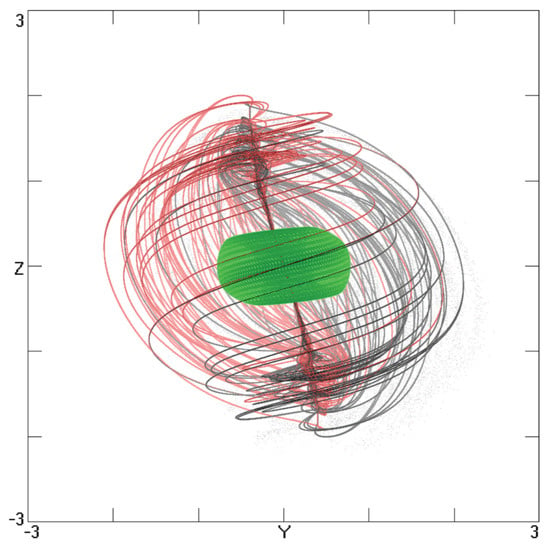
Figure 12.
A model of a proton and a secondary, polarised flux (not to scale), creating a charged particle, reproduced from [51].
With a quantum vacuum defined as a field of virtual electrons and photons, it is a small step to identify the outer torus with the permanent magnetic moment (charge) along the axis of a fermion. Such a model offers a clear insight into the mechanism which underpins the Pauli exclusion principle.
Whilst not to scale, or necessarily of a geometry that reflects a real scenario, we can identify Figure 12 with a simplistic model of a proton with an orbit, which binds an electron, to produce hydrogen. The model implies a composite, spin-1/2 particle in which an electron is free to pass through its core, traversing parallel hyperbolic flux lines, as it absorbs or emits a quanta of energy (a photon) and changes wavelength. It is a simple step to see how a group of such structures could interact to form a turbulent (shared) fluid that falls within the description of a coherent superfluid.
3.4. A Reinterpretation of the Macroscopic Helix in Figure 9a
In earlier comments relating to the double helix structure in Figure 9a [5], it was proposed that the representation (Equation (24)) of formed the basis of the macroscopic Pauli equation
which could be used as a basis to describe the structure. Within Equation (44), charge (q) may include an “average charge” on a macroscopic quantum object, such as a protein complex or a stem cell. In this context, helicity is generally defined as the projection of spin along the direction of motion:
with eigenvalues equal to +1 (right-handed) where the spin vector is aligned in the same direction as the momentum vector or −1 (left-handed), where the spin vector is aligned in the opposite direction. Helicity, as defined in terms of Equation (45) for a spin particle, represents the product of a two-component spinor,
However, we now consider an alternative perspective, motivated by a study of vortices in polariton condensates [52]. Images from this work illustrate how coherent quantum vortices can “co-wind”, to create a vortex doublet with a structure very similar to that in Figure 9b. Within this context, and that of the more detailed analysis relating to different spin representations in Section 3.1, we conclude that the vortex-like double helix in Figure 9a more accurately reflects the co-winding of two macroscopic spin-1 vortices propagating as a wave doublet. The concept is aligned with the proposal by Thompson [53] that the helical deformation of a line vortex propagates as a wave.
This reinterpretation also offers a natural fit with the hypothesis that the vortex structure in Figure 9a is underpinned by a coherent macroscopic phonon wave function in the mid-infrared range [4]. The wave function emerges through a process analogous with coherent random lasing (CRL), within the fractal mesoscale substructure of the vortex. The mechanism which underpins the process is discussed in Section 6.
Building on earlier proposals [54,55], a solution to this change in perspective can be found in , by substituting the scenario, represented by the Pauli matrices in Equation (24), with the spin-1 scenario represented by the tau matrices in Equation (27). The result is a three-component wave function
which we substitute for the two-component wave function (Equation (46)) within the macroscopic Pauli equation (Equation (44)). Within this new context, helicity in Equation (45) is now redefined
4. The Origin of Pointer States and Their Role in the Emergence of Quantum Particles as Causal Dynamic Structures
Moving beyond the intrinsic spin of a particle, we examine the concept of “pointer states”, whose existence implies some form of hidden, “root-like” substructure, yet to be described as part of the internal geometric description of a particle.
To describe these pointer states, we need to understand their origin, nature and role within a wave packet, including its transition from a probabilistic to a deterministic classical description and how the new description impacts on a broader understanding of quantum and classical systems.
We begin with a conceptual model in which superfluid helium represents a macroscopic analog of the basic “fabric” of a quantum particle. Within this context, the individual magnetic flux generated by each nucleus (as proposed in Figure 12) is shared, with the spinning nuclei generating a cascade of eddies/vortices, to create a composite (spin-1/2, spin-1) turbulent field, which defines a BEC. In a decoherence scenario, individual nuclei remain coherent, but localised, thus meeting the definition of pointer states described in Section 1.1.1.
As a next step, consider the behaviour of a classical fluid in zero gravity space, where a free floating droplet of fluid forms an approximation of a spherical “spin-0” structure, which rotates under the collective angular momentum of individual nuclei. Contrast this with a hypothetical experiment, in which a drop of superfluid helium (below ) is allowed to float freely, suspended in zero gravity. In such a scenario, we would again, initially, expect the emergence of a spin-0 structure. However, in the absence of friction (associated with a superfluid), rotational velocity () should increase with time. At a critical point in the process of acceleration, one can envisage a process in which centrifugal forces drive a transition from a spin-0 structure to a spin-1 (open) vortex, which falls within the definition of a representation of (Equation (27)).
From here, consider a hypothetical process in which a continued increase in drives an increase in x and y coordinates and a contraction along the z-axis of the vortex. At a critical point in vortex dilation, an increasingly large potential energy, in the form of the basin of attraction (i.e., a macroscopic quantum potential) created by the vortex core, will attract fluid expelled from the vortex to create a 3D, recirculating torus.
In a final step, as , the torus would, as described in Section 3.2, transform into an approximation of a 2D “Poincare torus”, which falls within our definition of a j = 1/2 representation of (Equation (24)).
The concept offers an insight into a fractal landscape of bifurcating, hyperbolic geodesics within a quantum particle. In this scenario, pointer states (helium nuclei,) as roots of a finer fractal network, play a key role, generating and maintaining the coherent field that would underpin a macroscopic quantum particle.
Whilst individual nuclei represent pointer states in this scenario, we have yet to describe their equivalence and general applicability of the principle in standard QM.
Within the context of He nuclei representing the roots of a macroscopic quantum particle, it seems a small step to consider a set of nucleons in a larger nuclei in the periodic table, as pointer states, which generate a turbulent field that underpins a coherent nucleus. A cascade of eddies filling the space between nucleons explains the breaking of the internal symmetry of the particle under reflection described in Scale Relativity Theory [4,16].
The description of the macroscopic spin-0 structure described above shares some features with the nuclear “liquid-drop model”, but with nucleons substituting for nuclei. The proposal shares another limitation with the liquid-drop model in that it fails to accommodate the nuclear force and the existence of lines of greater binding energy at certain numbers of protons and neutrons, which forms the basis of the “nuclear shell model”.
As in the case for individual nucleons proposed in Section 3.3, we can anticipate a breaking of 3D Euclidean symmetry of a large nucleus under rotation. However, it is not clear if this always translates into a spin-1/2 torus, as spin in large nuclear structures is normally quoted as an aggregated value of the spin of individual nucleons. Whilst large nuclear structures take on different shapes depending on n, they are generally reported as broken 3D spherical (e.g., prolate) structures, rather than two dimensional. The work of Sbitnev [34] shows how such a structure could be formed by a toroidal vortex. Although the structures observed experimentally neither confirm or preclude a toroidal structure, a toroidal scenario is supported by NMR measurements on Plutonium 239 (239Pu) [56], which reveal a spin-1/2 nucleus, rotating at ≈ times per second.
5. Future Work on Pointer States in Standard QM
If the concept of nucleons as pointer states within an atom is correct, it still leaves a question relating to a description of equivalent generators of turbulence (pointer states) which underpin a subatomic particle such as a proton or electron.
Any future model to accommodate the concept of pointer states within a new representation must, at a more simplistic level of interpretation, be naturally reducible to and . At the same time, one must ultimately be able to describe the smallest level (e.g., quark or sub-quark structure) at which such an interpretation is valid.
If a subatomic particle such as a proton or quark is represented by a fractal fluid, it suggests some form, of as yet to be defined, toroidal field at a smaller scale. As summarised in Equation (5), below a critical energy level associated with the quantum force/s within the system (HS), environmental perturbation of the system (HE) is insufficient to induce decoherence at a specific scale of quantisation. This theoretically applies until the minimal scale of quantisation at the Planck scale, where forces dictated by the limits of C reach a maximum. Since no external potential could exceed this force, it forms the bedrock of quantum systems. Wave function collapse at this scale would lead to pure chaos in which quantum forces would cease to exist.
One final point of interest from the description above relates to the implication that different structures (spin-0, spin-1 and spin-1/2) may emerge as “dynamic causal structures” from the same 4D turbulent spacetime geometry. Whilst this interpretation does not necessarily imply the existence of supersymmetry, it does offer a possible insight into how an underlying principle of shared symmetry might work in practice.
6. Outstanding Questions Relating to the Emergence of E-Pairs and Macroscopic Quantum Coherence in HTSC Materials
Section 2.1 summarises the progress in describing the emergence of superconductivity in the p-type cuprates, when charged dopants are incorporated in a thermodynamically driven fractal arrangement. As charge density () increases, it reaches a point where individual charges () begin to interact to generate a charge-induced network of channels (Equation (12)), as illustrated in Figure 3. Above a critical charge density, a critical percolation threshold is crossed. At this point (if ), magnetic flux associated with individual charges begin to interact. Based upon earlier discussions, it seems intuitive that spinning charges (Equation (6)) act as pointer states, which generate a turbulent (coherent) magnon condensate (Equation (14)).
sits in both localised wells (e.g., Figure 1b) and the interconnected network of wells and channels (Figure 3). Within this scenario, vortices analogous with that in superfluid helium spontaneously emerge within the magnon condensate in both the SC phase and pseudo gap .
If we consider mechanically induced turbulence in a classical fluid (Section 2.3), we see the transfer of rotational energy throughout the fluid via a cascade of “short-lived”, short-range, interacting vortices. By contrast, in a zero viscosity superfluid, there is no dissipation of energy within a vortex. It has the potential to persist indefinitely. However, as seen in Figure’s 1b and 1c in [22] and more extensively discussed in [57], vortices can bifurcate, with a series of iterations, facilitated by the fractal network of channels generated in HTSC media (see Figure 3), leading to the emergence of a fractal vortex network.
From the discussion so far we can see the emergence of a theory in which the interactions of a collective field of recirculating spin-1/2 toroidal structures act as generators of a turbulent field. Vortices, which emerge as causal dynamic structures from this turbulence, act as bosons, transferring energy between the generators.
As a next step, we describe how these interactions lead to the emergence of a coherent superfluid which underpins superconductivity:
- When it comes to a description of the mechanism which underpins e-pair formation, we consider a parallel with an e-pair traversing the recirculating (spin-1/2) magnetic flux of a proton nucleus, idealised in Figure 12. In an analogous way, an e-pair can be trapped within spin-1 vortices, which emerge within the magnon condensate.To clarify the processes which lead to the emergence of a magnon condensate, we begin by considering two adjacent photon vortices rotating at different frequencies. At some point they will collide, with energy associated with the lower energy vortex being absorbed in part (or completely) into the dominant vortex, leading to a change in its wavelength. Following an iterative series of such interactions in a constrained cavity (which plays the role of a Fabry–Perot resonator), lower energy frequencies will eventually be cancelled out, leaving a dominant wavelength, which we associate with the emergence of a coherent light source, i.e., “lasing”. When we consider this process within the context of an HTSC scenario, two separate, analogous mechanisms co-exist. A direct analogy with photon lasing can be found in the PG phase. Here, we see a parallel between photon interactions in a Fabry–Perot resonator and magnon interactions in a localised potential well (e.g., Figure 1b) associated with the PG.In the SC phase, a process of magnon interactions in the charge-induced fractal network will once again lead to the emergence of a single coherent wavelength (magnon condensate). In this instance, the process is constrained by the geometry of the network (rather than a localised potential well), which we identify with the process of coherent random lasing (CRL) [2,3], discussed in Section 2.1.In both the PG and SC phase, vortices in the magnon condensate, comparable with vortices in superfluid helium can act as both a binding and transport mechanism for e-pairs.As seen in superfluid He (Section 2.4), when applying a rotational force to the network of vortices in a superfluid, vortices align with that force. An analogous action is anticipated in HTSC. If an electric current is passed through the material, e-pair carrying vortices will align with the electric field, leading to the resistance-free transport of electrons through the vortex network, creating a superconducting medium.
As a potential well in the PG is in effect isolated from the main body of the superconducting fluid, it explains the potential for an energy differential between vortex-bound e-pairs in and . In practice, the difference in between the two phases may be linked to several factors.
- The greater potential of a vortex network to fractionate in a fractal network should lead to the emergence of lower frequency (lower energy) vortices, which should contribute to a lower critical temperature when compared with the PG.
- In the environment described above, IR vortex frequencies normally associated with e-pair decoherence will be effectively cancelled out, as the fractal network acts as an insulator against frequencies outside a specific range. This should contribute to a higher , compared to conventional SC materials. At the same time, the localised nature of a potential well in the PG (which itself sits within the fractal network) provides an additional level of insulation against spectral perturbation and resistance to decoherence of vortices trapped within it.
A final point to emerge from this analysis relates to decoherence when an HTSC material is exposed to a high-energy magnetic field, which takes the form of magnetic flux vortices [57,58,59]. When energy associated with magnetic vortices exceeds that of e-pair carrying vortices it leads to decoherence. Interestingly, discussions by Kwok et al. in [58] indicate that fractal systems generated by dopants in HTSC materials offer an effective insulation against both spectral and magnetic flux vortices. The phenomenon offers an additional insight into why HTSC materials exhibit a higher compared with conventional superconducting materials.
7. Conclusions
7.1. The Origins of Macroscopic Quantum Coherence
The identification of a quantum signature in turbulent fluids [20] lends support to the hypothesis that a superfluid is underpinned by turbulence generated by a set of interacting pointer states which take the form of a toroidal field. If we reconsider the language of decoherence summarised in Section 1.1.1, the space between Gaussians, associated with peaks of high-energy rotation (in the form of toroidal vortices), is filled with an interconnected cascade of eddies/vortices. Higher energy vortices cancel out lower energy vortices, leaving the surviving (high-energy) vortices to define the energy of the coherent quantum state. Decoherence occurs when an external potential (e.g., spectral or magnetic flux vortices) exceeds the cohesive force of the eddy/vortex cascade, leading to a breakdown of interconnectivity and the localisation of pointer states.
In Section 3.4, we discussed the origin of the magnetic flux (Figure 12) which forms the orbit of an atom. Taking collective insights from this, superfluid helium (Section 2.4) and the p-type cuprates (Section 2.1), a new mechanism for e-pair coupling via magnon vortices in HTSC media is proposed in which a densely packed assembly of charges, acting as pointer states, generate a turbulent magnon superfluid. Vortices which spontaneously emerge as causal dynamic structures within the magnon superfluid bind electron pairs, offering a resistance-free highway across the material, to create a superconducting medium.
The concept of macroscopic quantum coherence in HTSC materials has an analog in biological systems (Section 2.2), where a bosonic condensate remains coherent in fractal mesoscale networks at room temperatures.
Whilst helium nuclei act as generators of coherence in superfluid helium, dopant charges play an analogous role in generating a superfluid magnon condensate in HTSC materials. By contrast, the generators of macroscopic coherence which we associate with biological systems appear far more complex. Pointer states could range from simple protons to a vast array of charged biomolecules, which are the product of the unique DNA within each organism. Within such an organism, one can anticipate the emergence of a complex array of interacting regions of coherence defined at different scales. To give an example to illustrate the principle, it is possible to visualise a process in which solar energy (photons) could be transported throughout a plant via a phonon condensate in photosynthetic processes. When we add to this new insights relating to the emergence of macroscopic vortices emerging within a BEC, then bosonic condensates associated with fractal media such as cell cytoplasm offer the potential to facilitate superfluid transport of a range of different “charges” (e.g., electrons, protons, ions and charged biomolecules) across cellular structures, to support processes fundamental to life.
7.2. The Limits of and the Requirement for a More Complexed Representation
Whilst is effective in representing a particle such as a proton, it is limited to the extent that it fails to accommodate any form of internal structure at macroscopic scales, which might relate to a description of pointer states and their role in quantum decoherence in standard QM. It also fails to offer an intuitive insight into intrinsic spin.
In the development of a more detailed description, a number of useful insights have emerged which build upon the basic level of interpretation of :
- A spin-1/2 fermion is represented by a closed recirculating torus, with its own localised energy and mass, quantised along all three (x,y,z) coordinates. A secondary flux drawn through a rotating torus generates the particles magnetic moment (charge).
- A spin-1 boson is represented by an “open vortex”, quantised on its x,y coordinates, which facilitates the role of energy transfer. A coherent quantum fluid emerges when higher energy vortices cancel out lower energy vortices to produce a dominant vortex frequency, which defines the properties and scale of the coherent fluid.
- A spin-1 boson could also be represented by a closed vortex if the vortex forms a closed loop (or ouroboros). In this scenario, rotation remains along the axis of the vortex, with the winding number (n) impacting on the properties of the system.
- The problem of infinities associated with a point particle is eliminated within the context of a torus or vortex.
- A vortex/torus hypothesis accounts for the probabilistic nature of QM, including spin-1 and spin-1/2 statistics.
Through this process, we identify the complex plane generated by 2D toroidal structures, with the origin of spinors and the complex projective plane (), which leads to a doubling of the wave function () and a description in terms of quaternions and the Pauli equation. A further doubling of the wave function leads to particles and antiparticles, and a description in terms of bi-quaternions and the Dirac equation.
implies no internal structure, which might reflect pointer states within a standard quantum particle. This is at odds with decoherence theory as discussed in Section 1.1.2. Further work is required to define a more complexed representation of pointer states, which translates to an intuitive sense that some form of internal structure emerges from a turbulent fluid, which underpins a wave function.
Author Contributions
Conceptualization, P.T. and L.N.; Software, L.N.; Validation, P.T. and L.N.; Formal analysis, P.T. and L.N.; Investigation, P.T. and L.N.; Resources, P.T. and L.N.; Writing—original draft, P.T.; Writing—review & editing, P.T. and L.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article. Further inquiries can be directed to the corresponding author/s.
Acknowledgments
The authors would like to thank J. C Sprott for use of the image incorporated in Figure 12, reprinted from [51], with permission from Elsevier.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Delphenich, D. Possibilities for a Causal Interpretation for Quantum Mechanics. arXiv 2004, arXiv:quant-ph/0401105v1. [Google Scholar]
- Turner, P.; Nottale, L. A New Ab Initio Approach to the Development of High Temperature Superconducting Materials. Physica C 2015, 515, 15–30. [Google Scholar] [CrossRef]
- Turner, P.; Nottale, L. The origins of macroscopic quantum coherence in high temperature super conductivity. J. Supercond. Nov. Magetism 2016, 29, 3113–3118. [Google Scholar] [CrossRef]
- Turner, P.; Nottale, L. The physical principles underpinning self-organization in plants. Prog. Biophys. Mol. Biol. 2017, 123, 48–73. [Google Scholar] [CrossRef] [PubMed]
- Turner, P.; Nottale, L.; Zhao, J.; Pesquet, E. New insights into the physical processes that underpin cell division and the emergence of different cellular and multicellular structures. Prog. Biophys. Mol. Biol. 2020, 150, 13–42. [Google Scholar] [CrossRef] [PubMed]
- Auffray, C.; Noble, D.; Nottale, L.; Turner, P. Progress in integrative systems biology, physiology and medicine: Towards a scale-relative biology. Eur. Phys. J. A 2020, 56, 88. [Google Scholar] [CrossRef]
- Nottale, L.; Célérier, M.N. Derivation of the postulates of quantum mechanics from the first principles of scale relativity. J. Phys. A Math. Theor. 2007, 40, 14471–14498. [Google Scholar] [CrossRef]
- Nottale, L.; Auffray, C. Scale relativity theory and integrative systems biology: 2. Marcroscopic quantum-type mechanics. Prog. Biophys. Mol. Biol. 2008, 97, 115–157. [Google Scholar] [CrossRef] [PubMed]
- Schlosshauer, M. The quantum-to-classical transition and decoherence. arXiv 2014, arXiv:1404.2635v1. [Google Scholar]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715. [Google Scholar] [CrossRef]
- Joos, E.; Zeh, H.D.; Kiefer, C.; Giulini, D.; Kupsch, J.; Stamatescu, I.O. Decoherence and the Appearance of a Classical World in Quantum Theory, 2nd ed.; Springer: New York, NY, USA, 2003. [Google Scholar]
- Kubler, O.; Zeh, H.D. Dynamics of quantum correlations. Ann. Phys. 1973, 76, 405–418. [Google Scholar] [CrossRef]
- Paz, J.P.; Habib, S.; Zurek, W.H. Reduction of the wave packet: Preferred observable and decoherence time scale. Phys. Rev. D 1993, 47, 488. [Google Scholar] [CrossRef] [PubMed]
- Zurek, W.H. Preferred states, predictability, classicality and the environment-induced decoherence. Prog. Theor. Phys. 1993, 89, 281–312. [Google Scholar] [CrossRef]
- Diosi, L.; Kiefer, C. Robustness and diffusion of pointer states. Phys. Rev. Lett. 2000, 85, 3552. [Google Scholar] [CrossRef] [PubMed]
- Nottale, L. Scale Relativity and Fractal Space-time. In A New Approach to Unifying Relativity and Quantum Mechanics; Imperial College Press: London, UK, 2011; ISBN 978-1-84816-650-9. [Google Scholar]
- Nottale, L. Fractal Space-Time and Microphysics: Towards a Theory of Scale Relativity; World Scientific: Singapore, 1993; ISBN 9810208782. [Google Scholar]
- Célérier, M.N.; Nottale, L. The Pauli Equation in scale relativity. J. Phys. A 2006, 39, 12565. [Google Scholar] [CrossRef]
- Célérier, M.N.; Nottale, L. Dirac Equation in scale relativity. J. Phys. A 2004, 37, 931–955. [Google Scholar] [CrossRef]
- Nottale, L.; Lehner, T. Turbulence and scale relativity. Phys. Fluids 2019, 31, 105109. [Google Scholar] [CrossRef]
- Vincent, A.; Meneguzzi, M. The spatial structure and statistical properties of homogeneous turbulence. J. Fluid Mech. 1991, 225, 1–20. [Google Scholar] [CrossRef]
- Bewely, G.P.; Lathrop, D.P.; Sreenivasan, K.R. Superfluid helium. Visualization of quantized vortices. Nature 2006, 44, 588. [Google Scholar] [CrossRef]
- Fonda, E.; Meichle, D.P.; Ouellette, N.T.; Hormoz, S.; Lathrop, D.P. Direct observation of Kelvin waves excited by quantized vortex reconnection. Proc. Natl. Acad. Sci. USA 2014, 111, 4707–4710. [Google Scholar] [CrossRef]
- Leadbeater, M.; Winiecki, T.; Samuels, D.C.; Barenghi, C.F.; Adams, C.S. Sound emission due to superfluid vortex reconnections. Phys. Rev. Lett. 2001, 86, 1410–1413. [Google Scholar] [CrossRef]
- Robinson, R. Symmetry and the Standard Model Mathematics and Particle Physics; Springer: Berlin/Heidelberg, Germany, 2011; ISBN 978-1-4419-8266-7. [Google Scholar]
- Kragh, H. The Vortex Atom: A Victorian Theory of Everything. Blackwell Munksgaard Centaur. 2002, 44, 32–114. [Google Scholar] [CrossRef]
- Thomson, W. On Vortex Atoms. Philos. Mag. 1867, 34, 15–24. [Google Scholar] [CrossRef]
- Thomson, W. On Vortex Motion; Transactions of the Royal Society of Edinburgh 25; 1869; pp. 217–260. [Google Scholar]
- von Helmholtz, H. Ueber Integrale der hydrodynamischen Gleichungen, welche den Wirbelbewegung-en entsprechen. J. Reine Angew. Math. 1858, 55, 25–55. [Google Scholar]
- von Helmholtz, H. On the Integrals of the Hydrodynamical Equations, which Express Vortex Motions. Philos. Mag. 1867, 33, 485–512. [Google Scholar] [CrossRef]
- Kragh, H. The Electron, the Protyle, and the Unity of Matter. In Histories of the Electron: The Birth of Microphysics; Buchwald, J., Warwick, A., Eds.; MIT Press: Cambridge, MA, USA, 2001; pp. 195–226. [Google Scholar]
- Hill, M On the Motion of Fluid, Part of Which is Moving Rotationally and Part Irrotationally. Philos. Trans. 1885, 175, 363–409.
- Hill, M On a Spherical Vortex. Philos. Trans. A 1895, 185, 213–245.
- Sbitnev, V.I. Hydrodynamics of Superfluid Quantum Space: De Broglie interpretation of the quantum mechanics. arXiv 2017, arXiv:1707.08508. [Google Scholar] [CrossRef]
- Hicks, W.M. On the Steady Motion of a Hollow Vortex. Proc. R. Soc. 1883, 35, 304–308. [Google Scholar]
- Hicks, W.M. On the Steady Motion and Small Vibrations of a Hollow Vortex. Philos. Trans. 1885, 175, 161–195. [Google Scholar]
- Hicks, W.M. Researches in Vortex Motion. Part III. On Spiral or Gyrostatic Vortex Aggre- gates. Proc. R. Soc. 1898, 62, 332–338. [Google Scholar]
- Nottale, L.; Lehner, T. Numerical simulation of a macro-quantum experiment: Oscillating wave packet. Int. J. Mod. Phys. 2012, C23, 1250035. [Google Scholar] [CrossRef]
- Fedi, M. Hydrodynamics of the Dark Superfluid: I. Genesis of Fundamental Particles. Available online: https://hal.archives-ouvertes.fr/hal-01549082v2/document (accessed on 15 June 2024).
- Sakharov, A.D. Vacuum quantum fluctuations in curved space and the theory of gravitation. Dokl. Akad. Nauk SSSR 1967, 177, 70–71. [Google Scholar]
- Salesi, G. Spin and Madelung fluid. Mod. Phys. Lett. 1996, A11, 1815. [Google Scholar] [CrossRef]
- Faddeev, L.D. Quantization of Solitons. In Proceedings of the 8th International Conference on High-Energy Physics (ICHEP 76), Tbilisi, Russia, 15–21 July 1976. [Google Scholar]
- Huang, K. A Superfluid Universe; World Scientific: Singapore, 2016; ISBN 978-981-3148-45-1. [Google Scholar]
- Kyriakos, A.G. Non-linear field theory III. Geometrical illustration of the electromagnetic representation of Dirac’s electron theory. arXiv 2004, arXiv:quant-ph/0407071. [Google Scholar]
- Johnson, D. The Spin Torus Energy Model and Electricity. Open J. Appl. Sci. 2019, 9, 451–479. [Google Scholar] [CrossRef]
- Haramein, N.; Rauscher, E.A. Spinors, Twistors, Quaternions and the Spacetime Torus Topology; Dubois, D., Ed.; Institute of Mathematics, Liege University: Liege, Belgium, 2007. [Google Scholar]
- Skyrme, T.H.R. A non-linear field theory. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1961, 260, 127–138. [Google Scholar]
- Skyrme, T.H.R. A unified field theory of mesons and baryons. Nucl. Phys. 1962, 31, 556–569. [Google Scholar] [CrossRef]
- Göbel, B.; Mertig, I.; Treiakov, O.A. Beyond skyrmions: Review and perspectives of alternative magnetic quasiparticles. Phys. Rep. 2021, 895, 1–28. [Google Scholar] [CrossRef]
- Mathisson, M. New mechanics of material systems. Acta Phys. Pol. 1937, VI, 163. [Google Scholar]
- Sprott, J.C. A dynamical system with a strange attractor and invariant tori. Phys. Lett. A 2014, 378, 1361–1363. [Google Scholar] [CrossRef]
- Dominici, L.; Carretero-Gonzlez, R.; Gianfrate, A.; Cuevas-Maraver, J.; Rodrigues, A.S.; Frantzeskakis, D.J.; Lerario, G.; Ballarini, D.; De Giorgi, M.; Gigli, G.; et al. Interactions and scattering of quantum vortices in a polariton condensate. Nat. Commun. 2018, 9, 1467. [Google Scholar] [CrossRef] [PubMed]
- Thomson, W. Vibrations of a columnar vortex. Philos. Mag. 1880, 10, 155–168. [Google Scholar] [CrossRef]
- Oppenheimer, J.R. Note on light quanta and the electromagnetic field. Phys. Rev. 1931, 38, 725–746. [Google Scholar] [CrossRef]
- Mohr, P.J. Solutions of the Maxwell equations and photon wave functions. Ann. Phys. 2010, 325, 607–663. [Google Scholar] [CrossRef]
- Yasuoka, H.; Koutroulakis, G.; Chudo, H.; Richmond, S.; Veirs, D.K.; Smith, A.I.; Bauer, E.D.; Thompson, J.D.; Jarvinen, G.D.; Clark, D.L. Observation of 239Pu Nuclear Magnetic Resonance. Science 2012, 336, 901–904. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Peterka, T.; Glatz, A. In Situ Magnetic Flux Vortex Visualization in Time-Dependent Ginzburg-Landau Superconductor Simulations. In Proceedings of the IEEE Pacific Visualization Symposium, Seoul, Republic of Korea, 18–21 April 2017. [Google Scholar] [CrossRef]
- Kwok, W.-K.; Welp, U.; Glatz, A.; Koshelev, A.E.; Kihlstrom, J.K.; Crabtree, G.W. Vortices in high-performance high-temperature superconductors. Rep. Prog. Phys. 2016, 79, 116501. [Google Scholar] [CrossRef]
- Abrikosov, A.A. On the magnetic properties of superconductors of the second group. Sov. Phys. JETP 1957, 5, 1174. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).