Study of Interacting Heisenberg Antiferromagnet Spin-1/2 and 1 Chains

Abstract

Haldane conjectures the fundamental difference in the energy spectrum of the Heisenberg antiferromagnetic (HAF) of the spin S chain is that the half-integer and the integer S chain have gapless and gapped energy spectrums, respectively. The ground state (gs) of the HAF spin-1/2 and spin-1 chains have a quasi-long-range and short-range correlation, respectively. We study the effect of the exchange interaction between an HAF spin-1/2 and an HAF spin-1 chain forming a normal ladder system and its gs properties. The inter-chain exchange interaction $J_{\perp }$ can be either ferromagnetic (FM) or antiferromagnetic (AFM). Using the density matrix renormalization group method, we show that in the weak AFM/FM coupling limit of $J_{\perp }$, the system behaves like two decoupled chains. However, in the large AFM $J_{\perp }$ limit, the whole system can be visualized as weakly coupled spin-1/2 and spin-1 pairs which behave like an effective spin-1/2 HAF chain. In the large FM $J_{\perp }$ limit, coupled spin-1/2 and spin-1 pairs can form pseudo spin-3/2 and the whole system behaves like an effective spin-3/2 HAF chain. We also derive the effective model Hamiltonian in both strong FM and AFM rung exchange coupling limits.

1. Introduction

A one-dimensional interacting Heisenberg antiferromagnetic (HAF) spin system has been a playground for condensed matter physicists [1,2,3,4,5,6,7,8,9,10,11,12,13,14], and one of the most striking features of this one-dimensional system is the nature of the energy spectrum. These systems can be either a gapped or gapless spectrum for an integer or a half-integer spin as conjectured by Haldane [15,16]. The ground state (gs) of the HAF half-integer spin chains have a quasi-long-range order and this was shown explicitly for spin-1/2, spin-3/2 and spin-5/2 [17,18]. On the other hand, the HAF integer spin systems exhibit short-range correlations due to the formation of a valance bond solid (VBS) [19]. In fact, two edge modes at the end of the spin-1 HAF chain show an interesting topological order and the gs has a four-fold degeneracy [19,20].

The HAF integer and half-integer spin ladder systems are some other interesting low-dimensional systems. These ladders were extensively studied and show an interesting behavior of the spin-dimer formation along the rung for a spin-1/2 ladder [21] and topological states for a spin-1 ladder [22,23]. Many ladder materials were extensively synthesized for a spin-1/2 ladder, such as CuCl${}_2$·2N(C${}_5$D${}_5$) [24], KCuF${}_3$ [25], KCuGaF${}_6$ [26], etc., and a spin-1 ladder, such as CsNiCl${}_3$ [27], Ni(C${}_2$H${}_8$N${}_2$)${}_2$NO${}_2$(ClO${}_4$) [28], Ni(C${}_5$H${}_{14}$N${}_2$)${}_2$N${}_3$(PF${}_6$) [29], etc. Some of these systems can be modeled by a simple Heisenberg model with the nearest neighbor (NN) antiferromagnetic (AFM) exchange interaction. However, the Ni, Co and other heavy elements have a tendency to have large single-ion anisotropy and the effect of anisotropy is explored theoretically [30,31].

The studies of mixed spin chains, where two dissimilar spins are placed next to each other, have attracted much attention due to recently synthesized chain materials such as NiCu(pba)(H${}_2$O)${}_3$2H${}_2$O with $(S_1,S_2)=(1,1/2)$, ACu(pbaOH)(H${}_2$O)${}_{3}n$H${}_2$O, where A = Ni, Co, Fe, Mn with $(S_1,S_2)=(1,1/2),(3/2,1/2),(2,1/2),(5/2,1/2)$, respectively [32]. According to the Lieb–Mattis theorem [33], the mixed spin chains exhibit the ferrimagnetic gs with a total spin $S=(N/2)(S_1-S_2)$, where $N/2$ is the total number of unit cells. The Heisenberg mixed spin chain models are studied extensively using the linear spin wave theory (LSWT) and the density matrix renormalization group (DMRG) which shows that the correlation length in the spin correlation reduces to $\xi \approx 1.44$ for a mixed spin chain with $S_1=1$ and $S_2=1/2$ [13,14]. Similar spin ladders could also be experimentally realized through artificial quantum matter, such as magnetic adatoms [34], nanographenes [35] or cold atoms [36].

The behavior of the HAF spin-1/2 and spin-1 chains is drastically different; therefore, it is an important question to ask about the effect of the exchange interaction between an HAF spin-1/2 and an HAF spin-1 chain. In this work, we consider a spin ladder system as shown in Figure 1, where spins on each leg are interacting through an AFM exchange interaction, but the rung interaction between two legs can be either ferro- or antiferromagnetic. In this manuscript, we focus on the limiting cases: weak and strong rung couplings. In a strong ferromagnetic rung coupling, the nearest $S=1$ and $s=1/2$ from different legs form a pair which has an effective $S=3/2$ spin and these interacting effective spins form an effective antiferromagnetic spin-3/2 chain, whereas the equivalence of this system with AFM rung coupling is not clear yet [37]. In this work, we also show that in a strong AFM rung exchange interaction limit, this system behaves like a spin-1/2 chain. We have extensively studied the effect of FM and AFM rung couplings on the energy gap, spin density and spin correlation on individual legs in both strong and weak rung exchange coupling limits.

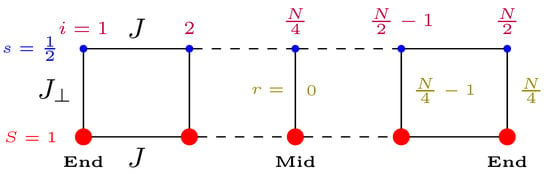
Figure 1. Mixed spin ladder with spin-1/2 and spin-1 legs. The exchange interaction strength on both spin-1/2 and 1 legs is J. The inter-leg exchange interaction is $J_{\perp }$. i represents the site index on each leg and r is the distance between a spin and the reference spin considered at the middle of the same leg.

The paper is organized into five sections. In Section 2, we present the Hamiltonian and numerical method. The numerical results are explained in Section 3. The effective Hamiltonians from perturbative calculations are represented in Section 4. The conclusion is given in Section 5.

2. Model Hamiltonian and Numerical Method

We consider a mixed spin ladder made of spin $s=1/2$ and $S=1$ legs which are interacting with each other through either FM or AFM $J_{\perp }$ exchange interaction. The interaction between the spins on both spin-1/2 and spin-1 legs is AFM J. The system is represented schematically in Figure 1. A general model Hamiltonian for this system can be written as

$$\begin{array}{ccc}\hfill \mathrm{H}& =& J\sum _i{\mathbf{s}}_i·{\mathbf{s}}_{i+1}+J\sum _i{\mathbf{S}}_i·{\mathbf{S}}_{i+1}\hfill \\ & & +J_{\perp }\sum _i{\mathbf{s}}_i·\mathbf{S}i.\hfill \end{array}$$

(1)

Here, we have studied the influence of both FM and AFM rung coupling $J_{\perp }$ on the energy gap of the system, spin density and spin–spin correlations on each individual legs as a function of $\alpha =|J_{\perp }|/J$.

We have considered the systems of size $4n$, where n is an integer. Each leg contains an even ($2n$) number of spins. The physics will be different for the system with an odd number of spins on each leg, especially at the edges.

We use density matrix renormalization group (DMRG) method to deal with the large degrees of freedom in our system. This method is a state-of-the-art numerical technique suitable for 1D or quasi-1D systems, and it is based on the systematic truncation of irrelevant degrees of freedom [38,39,40]. We use the recently developed DMRG method where we add four new sites at every DMRG step [10]. This method avoids the old-old operator multiplication while constructing a superblock and reduces the number of non-essential non-zero small matrix elements in the superblock Hamiltonian. Up to $m=400$ eigenvectors corresponding to the largest eigenvalues of the density matrix are kept for the renormalization of operators and the Hamiltonian of the system block. This restricts the truncation error below ${10}^{-10}$. We have used system sizes up to $N=160$ to minimize the finite size effect.

3. Results

As pointed out earlier, the HAF spin-1 and spin-1/2 chains have distinct behavior, such as spin-1 forms a VBS in the bulk of the chain and has topological edge modes at the ends of the chain [19,20,41,42]. The spectrum of the spin-1 chain is gapped and has a four-fold degeneracy in a thermodynamic limit [20], whereas in the case of the HAF spin-1/2 chain, the gs is a singlet and has a gapless spectrum [15,16]. In this paper, we show the effect of exchange coupling $J_{\perp }$ on the behavior of the spin correlation $C\left(r\right)=⟨S_i^z{S}_{i+r}^z⟩$, spin density $\rho \left(i\right)=⟨S_i^z⟩$ and low-lying excitations ${\mathrm{\Gamma }}_n$. The distance r from the reference site at the middle of a leg and site i is shown in Figure 1. The energy gap ${\mathrm{\Gamma }}_n$ is defined as

$$\begin{array}{c}\hfill {\mathrm{\Gamma }}_n(\alpha ,N)=E_0(\alpha ,N,S^z=n)-E_0(\alpha ,N,S^z=0).\end{array}$$

(2)

$E_0(\alpha ,N,S^z=n)$ and $E_0(\alpha ,N,S^z=0)$ are the lowest energy states in the given $S^z=n$ and 0 sectors, respectively. In this paper, the following questions will be addressed: what happens to the quasi-long-range order and gapless excitation of the spin-1/2 chain and the short-range correlation, edge states and Haldane gaps of the spin-1 chain in the presence of an inter-chain interaction $J_{\perp }$.

To answer the above questions, we first study energy gaps ${\mathrm{\Gamma }}_n$ and then analyze the spin density $\rho \left(i\right)$ and spin correlation $C\left(r\right)$ in the gs.

3.1. Energy Gaps ${\mathrm{\Gamma }}_n$

In the decoupled limit, we expect that the spectrum of each individual chain should be intact. For the spin-1/2 chain, the first and second lowest excitation gaps are in triplet and singlet manifolds, respectively, and have algebraic decay with the system size. On the other hand, the first lowest excitation gap ${\mathrm{\Gamma }}_1$ in the spin-1 chain decays exponentially, whereas the second excited state gap ${\mathrm{\Gamma }}_2$ is the Haldane gap and has a very weak finite size effect in a chain with an open boundary condition (OBC) [15,16,20].

In the small $\alpha$ limit, the ${\mathrm{\Gamma }}_1$ of the ladder with the OBC is very close to ${\mathrm{\Gamma }}_1$ of the spin-1 chain (OBC) as the lowest excitation cost is corresponding to the flipping of the weakly coupled spin-1/2 edge modes of the spin-1 leg and this gap vanishes exponentially with the system size. On the other hand, the lowest spin-1/2 excitation on the spin-1/2 leg is much larger in the small system and decays algebraically with N. However, for the moderate value of $\alpha$, the gap shows a flattening behavior for a large N as shown in Figure 2a, and this should vanish for accurate larger system size calculations. In fact, in the thermodynamic limit, ${\mathrm{\Gamma }}_1$ goes to zero for the AFM $J_{\perp }$. The lower dashed and upper solid black curves are the lowest excitation energy ${\mathrm{\Gamma }}_1$ for isolated spin-1 (with $J=1$) and spin-1/2 (with $J=17/9$) chains, respectively. In the weak rung coupling limit, ${\mathrm{\Gamma }}_1$ is similar to that of a spin-1 chain. However, in a large $\alpha$ limit, ${\mathrm{\Gamma }}_1$ is zero in the thermodynamic limit, and in this limit, the one unit of the spin-1 and spin-1/2 along the rung form an effective spin-1/2, and their low-lying spectrum behaves as an isolated spin-1/2 chain (with an effective $J=17/9$) spectrum. In a large AFM $\alpha$ limit, the effective spin-1/2 Hamiltonian can be derived from the perturbation theory discussed later in Section 4.

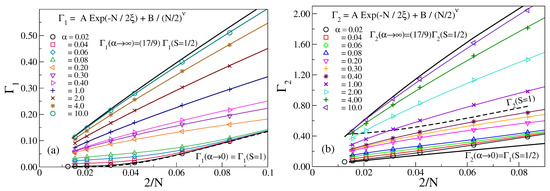
Figure 2. The energy gap (a) ${\mathrm{\Gamma }}_1(\alpha ,N)$ and (b) ${\mathrm{\Gamma }}_2(\alpha ,N)$ for different $\alpha$ for AFM $J_{\perp }$. For small value $\alpha (<0.1)$, the exponential part is dominant, while for $\alpha >0.1$, the gaps follow only power-law decay. The solid thick line represents the spin-1/2 HAF with effective $J=17/9$.

In Figure 2b, the second excitation for various values of AFM $\alpha$ is shown. The solid black curves represent the first and second excitation gaps of spin-1/2 and the dashed black curve represents the second excitation gap of the spin-1 chain with the OBC. The spin-1/2 chain has a continuous spectrum, and the lowest excitation is a gapless triplet and the second excitation is the 1st excited singlet which is zero in the thermodynamic limit. In the case of the ladder, ${\mathrm{\Gamma }}_2$, in the small AFM $\alpha$ limit, has similar behavior as ${\mathrm{\Gamma }}_1$ in the large $\alpha$ limit. The second or higher excitations are much higher in energy for the spin-1 leg compared to the spin-1/2 leg spectrum. In the large AFM $\alpha$ limit, ${\mathrm{\Gamma }}_1$ and ${\mathrm{\Gamma }}_2$ are consistent with the effective spin-1/2 Hamiltonian given in Equation (15) of Section 4.

In the FM $\alpha$ limit, we notice that ${\mathrm{\Gamma }}_1$ has exponential decay with the system size in the small $\alpha$ limit and goes to zero in the thermodynamic limit, whereas ${\mathrm{\Gamma }}_1$ shows algebraic decay for the large $\alpha$ as shown in Figure 3a. The solid black curve shows $5/9$ times the scaled lowest excitation ${\mathrm{\Gamma }}_1$ of the spin-3/2 chain. ${\mathrm{\Gamma }}_1$ is fitted with Equation (3) as shown in Figure 3a. The second excitation ${\mathrm{\Gamma }}_2$ for the FM $\alpha$ shows algebraic decay behavior with the system size N as shown in Figure 3b. The gap has very similar behavior as the scaled ${\mathrm{\Gamma }}_2(S=3/2)$ ($5/9$ times) in the large FM $\alpha$ limit. In fact, the spin-(1/2,1) ladder behaves as the spin-3/2 chain in the large FM $\alpha$ limit. The effective Hamiltonian in this limit is derived as in Equation (20) and both ${\mathrm{\Gamma }}_1$ and ${\mathrm{\Gamma }}_2$, in the large $\alpha$ limit, are consistent with the effective Hamiltonian.

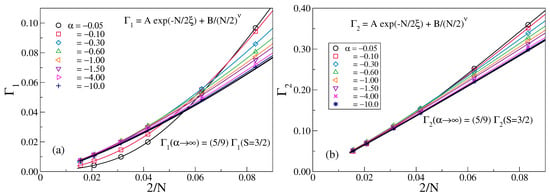
Figure 3. The energy gap (a) ${\mathrm{\Gamma }}_1(\alpha ,N)$ and (b) ${\mathrm{\Gamma }}_2(\alpha ,N)$ for different $\alpha$ for FM $J_{\perp }$. The solid thick lines represent the corresponding energy gaps for an HAF $S=3/2$ chain with effective $J=5/9$.

The ${\mathrm{\Gamma }}_1$ vs. the inverse of the system size curve can be fitted with the sum of algebraic and exponential functions. The exponential decay of the energy gap is a signature of the presence of the edge mode or signifies that spin-1 behavior is dominant. On the other hand, the decaying of the energy gap following a power law with the system size originates from the spin-1/2 leg. However, the finite energy gap shows the dimer formation along the rung and has a contribution from both the spin-1/2 and spin-1 legs. Therefore, the fitting expression for the energy gap can be written as

$$\begin{array}{c}\hfill {\mathrm{\Gamma }}_n(0,N)=Aexp(-N/2\xi )+B/{(N/2)}^{\nu }.\end{array}$$

(3)

For different $\alpha$, the values of coefficients $A,B,\xi ,\nu$ are shown in Table 1 and Table 2 for antiferromagnetic and ferromagnetic rung interactions, respectively. In Table 1, we note that ${\mathrm{\Gamma }}_1(\alpha ,N)$ for small $\alpha$ exhibits dominant exponential behavior as the value of A is much larger compared to B. However, for a large value of $\alpha$, the value of B is much larger than A (almost zero). This indicates the decaying behavior of the gap with N changes from exponential to power law. In Table 2, the value of B is always larger than A for all values of $\alpha$. This behavior indicates the spin-3/2 spin chain behavior of the system.

Table 1. Values of various exponents and constants are evaluated from the fitting of the ${\mathrm{\Gamma }}_1(\alpha ,N)$ shown in Figure 2a using Equation (3).

$\mathit{\alpha }$	A	$\mathit{\xi }$	B	$\mathit{\nu }$
$0.02$	$0.719$	$5.638$	$0.141$	$0.992$
$0.04$	$0.765$	$5.163$	$0.068$	$0.410$
$0.06$	$0.821$	$4.457$	$0.136$	$0.422$
$0.08$	$0.981$	$3.633$	$0.245$	$0.485$
$0.20$	0	−	$0.800$	$0.642$
$0.30$	0	−	$1.13$	$0.704$
$0.40$	0	−	$1.39$	$0.744$

Table 2. Values of various exponents and constants are evaluated from the fitting of the ${\mathrm{\Gamma }}_1(\alpha ,N)$ shown in Figure 3a using Equation (3).

$\mathit{\alpha }$	A	$\mathit{\xi }$	B	$\mathit{\nu }$
$0.05$	$0.405$	$5.641$	$3.975$	$1.770$
$0.1$	$0.164$	$5.444$	$5.411$	$1.715$
$0.3$	$0.089$	$6.453$	$4.855$	$1.088$
$0.6$	$0.041$	$7.149$	$4.580$	$1.071$
$0.8$	$0.031$	$7.711$	$4.460$	$1.065$
$1.00$	$0.026$	$8.202$	$4.370$	$1.061$
$1.50$	$0.022$	$8.971$	$4.223$	$1.055$

3.2. Spin Densities $\rho \left(r\right)$

To understand the low-lying excitation in the system, we also study the spin densities in the lowest excited state in the $S^z=1$ spin manifold. The spin density at each site i is defined as

$$\begin{array}{c}\hfill \rho \left(i\right)=⟨S_i^z⟩.\end{array}$$

(4)

The site numbering is shown in Figure 1 and represented as i on each leg. The site numbering starts from the end and has a value $N/4$ in the mid of a leg. The ladder is made up of both spin-1/2 and spin-1 legs; therefore, the excited states of the system have different contributions from different legs. In the weak AFM rung coupling limit, the lowest excitation is dominated by the spin-1 leg contribution; therefore, the spin densities on the spin-1 leg resemble that of an isolated spin-1 chain, shown as a solid black circle in Figure 4a. On the other hand, the wave-like behavior of the spin density on this leg is similar to an isolated spin-1/2 chain (shown as a solid square) in the strong AFM rung coupling limit [37,43]. The scaling factor $1.61$ in Figure 4a comes from just fitting the spin density in the spin-1 leg with that for an isolated spin-1/2 chain. It decays exponentially toward the middle of the leg with the distance from the end. ${\rho }_i$ on the spin-1/2 leg is small for a given N, and odd and even effects are visible, as shown in Figure 4b. Because we are calculating the density in the $S_z=1$ sector, all the odd sites have a positive density and even sites have a negative density so that the sum of the spin densities of the system becomes 1. The spin density on the spin-1/2 leg increases as we increase $\alpha$, but it again starts to decrease after a certain value of $\alpha$. ${\rho }_i$ on both legs has the largest value at the boundary but decays as one moves toward the bulk.

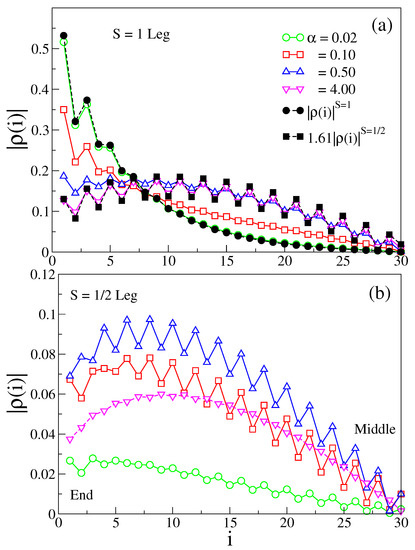
Figure 4. (a) The magnitudes of spin densities on the spin-1 leg are shown in the upper panel; (b) for the spin-1/2 leg, spin densities are shown in lower panel for AFM $J_{\perp }$ with $N=120$ in $S^z=1$ sector.

In the FM rung coupling limit, the lowest excitation is in the triplet sector. In this coupling limit, ${\rho }_i$ in the spin-1 and 1/2 legs is plotted in Figure 5a,b, respectively. In the weak rung exchange coupling limit, the ${\rho }_i$ in the spin-1 leg has similar behavior to ${\rho }_i$ of an isolated spin-1 chain, shown as a solid black circle in Figure 5a, whereas it behaves like an isolated spin-3/2 chain in a strong $\alpha$ limit as shown by a solid triangle in Figure 5a. The value $1/1.61$ is the scaling factor. The magnitude of the spin density is much smaller in the spin-1/2 leg and decays on going toward the bulk as shown in Figure 5b. In the large $\alpha$ limit, this ladder behaves as a spin-3/2 chain; therefore, the lowest excitation is in the triplet sector and ${\rho }_i$ on both legs behaves similarly to that in a spin-3/2 chain, as shown in Figure 5a,b. It is noticeable that a spin=3/2 HAF chain has a sufficiently large edge state as the spin density waves are not localized as opposed to a spin-1/2 chain [42].

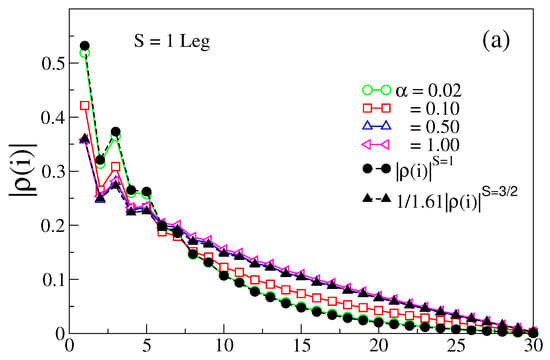
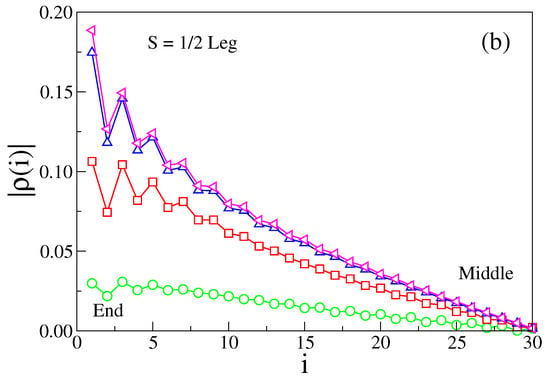
Figure 5. (a) The magnitudes of spin densities on the spin-1 leg are shown in the upper panel; (b) for the spin-1/2 leg, spin densities are shown in lower panel for FM $J_{\perp }$ with $N=120$ in $S^z=1$ sector.

The exponential decay of the edge spin density is an important quantity to study the edge modes. We notice the effect of $\alpha$ on the edge modes in Figure 4a. The exponential nature of the spin density in the spin-1 leg is visible for finite $\alpha =0.1$ but has spin-1/2-like behavior for $\alpha \ge 0.5$. In the ferromagnetic $\alpha$ side, the edge mode in the spin-1 leg exists always. However, the spin density decays exponentially for smaller $\alpha$ but has an algebraic decay in the large $\alpha$ limit as shown in ref. [42], where the system behaves like spin-3/2 chains.

3.3. Spin–Spin Correlations

The longitudinal correlation functions $C\left(r\right)$ defined in Equation (5) are an excellent measure of an effective interaction among the spins of a system. For an isolated spin-1/2 chain, the $C\left(r\right)$ goes as $\sqrt{ln\left(r\right)}/r$, where r is the distance from the reference spin [18,44,45]. For our system, the reference spin is set at the middle of each leg and it is numbered as $r=0$, as shown in Figure 1. In an isolated spin-1 chain, $C\left(r\right)$ decays exponentially due to the valance bond-state formation. The longitudinal spin–spin correlation at a distance r with respect to a reference spin at $r=0$ is defined as

$$\begin{array}{c}\hfill C\left(r\right)=⟨S_0^z·S_r^z⟩,\end{array}$$

(5)

where r is the distance from the reference spin. The gs of the system is always in the singlet state; therefore, the total correlation is thrice of the longitudinal correlation $C\left(r\right)$. $C\left(r\right)$ in both the spin-1/2 and spin-1 legs is plotted in Figure 6 for the AFM rung coupling and in Figure 7 for the FM rung coupling. Figure 6a shows the correlation on the spin-1 leg in the log-normal scale to identify the exponential behavior. In the AFM rung system, $C\left(r\right)$ in the spin-1 leg of the ladder has the exponential behavior for $\alpha =0.02$ and matches well with the scaled $C\left(r\right)$ of an isolated spin-1 chain, shown as a solid black circle with a dotted line, whereas in the strong limit $\alpha \ge 0.1$, there is a clear deviation from the exponential behavior as shown in Figure 6a. At a very strong $\alpha$, the $C\left(r\right)$ of the spin-1 leg matches with the scaled $C\left(r\right)$ of an isolated spin-1/2 chain as shown by the solid black square in Figure 6a. Figure 6b illustrates $C\left(r\right)$ in the log-log scale for the spin-1/2 leg, where $C\left(r\right)$ exhibits algebraic behavior. Here, the $C\left(r\right)$ value increases with an increasing $\alpha$ but decreases after a certain value of $\alpha$. In both the small and large $\alpha$ limit, the $C\left(r\right)$ in the spin-1/2 leg matches well with the scaled $C\left(r\right)$ of an isolated spin-1/2, shown as a solid square with a dotted line in Figure 6b. In the large rung coupling limit, the effective spin of the per-unit cell can behave as the spin-1/2 as one spin-1/2 of spin-1 gets involved in forming a rung singlet, whereas other effective spin-1/2 couples with neighboring effective spin-1/2 with an effective coupling are shown in Section 4 of the analytical calculations using the perturbation theory.

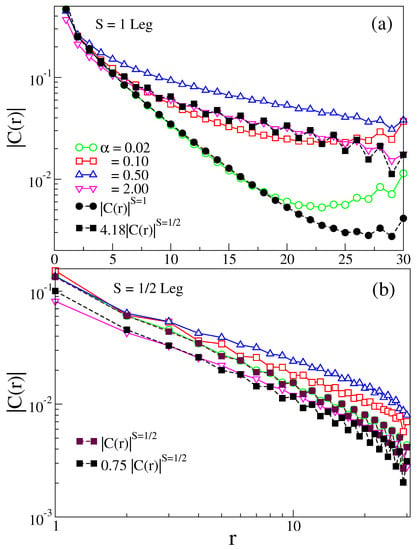
Figure 6. (a) The spin–spin correlations on the spin-1 leg are shown in log-normal scale in the upper panel; (b) for the spin-1/2 leg, spin–spin correlations are shown in the log-log scale in the lower panel for AFM $J_{\perp }$ for $N=120$.

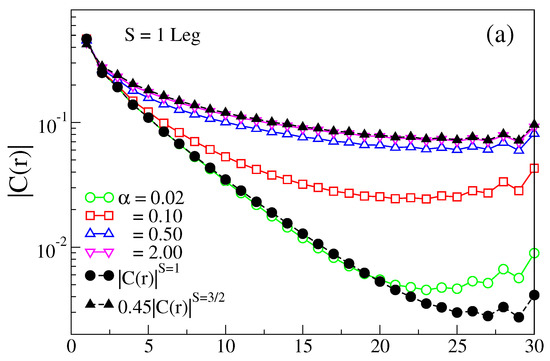
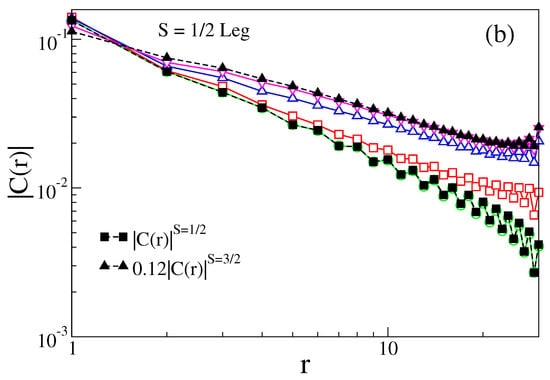
Figure 7. (a) The spin–spin correlations on the spin-1 leg are shown in log-normal scale in the upper panel; (b) for the spin-1/2 leg, spin–spin correlations are shown in the log-log scale in the lower panel for FM $J_{\perp }$ for $N=120$.

In the small FM rung exchange coupling limit, the systems can behave as decoupled chains of spin-1/2 and spin-1, whereas in the strong coupling limit, the behavior of $C\left(r\right)$ on both the legs is similar to the scaled $C\left(r\right)$ of spin-3/2, shown by the triangle with dotted lines as shown in Figure 7a,b. We note that, for small $\alpha$, the spin-1 leg $C\left(r\right)$ has exponential behavior as usual, but for $\alpha >0.1$, the behavior changes toward the power law and is similar to that of an isolated spin-3/2 chain, as shown in Figure 7a. In the spin-1/2 leg, $C\left(r\right)$ is always algebraic and it behaves like $C\left(r\right)$ of an isolated spin-1/2 chain in a small $\alpha$ limit, whereas it behaves like an isolated spin-3/2 chain in a strong $\alpha$ limit, as shown in Figure 7b.

4. Effective Hamiltonian in Strong Coupling Limit

In this section, the strong rung coupling limit $|J_{\perp }|>>J$ of the Hamiltonian in Equation (1) is considered. For both strong the ferromagnetic and antiferromagnetic $|J_{\perp }|>>J$, it can be rewritten as

$$\begin{array}{ccc}\hfill H& =& H_0+H^{\prime }\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill H_0& =& \sum _{i=1}^N{H}_i=J_{\perp }\sum _{i=1}^N{\widehat{s}}_i·{\widehat{S}}_i\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill H^{\prime }& =& \sum _{i=1}^N{H}_{i,i+1}=J\sum _{i=1}^N{\widehat{s}}_i·{\widehat{s}}_{i+1}+J\sum _{i=1}^N{\widehat{S}}_i·{\widehat{S}}_{i+1}.\hfill \end{array}$$

(8)

where $H_0$ is the strong coupling part of the Hamiltonian or exchange interaction between spin-1/2 and 1 along the rung, whereas $H^{\prime }$ is the perturbation term along the legs. In the limit of $J=0$, the system is a collection of interacting spin (1/2, 1) pairs with an exchange interaction $J_{\perp }$ between them. The pair have a total spin of either 1/2 or 3/2 with energies $E_{1/2}=-J_{\perp }$ and $E_{3/2}=J_{\perp }/2$. The states are either a doublet or quartet. The doublet states D can be written as

$$\begin{array}{ccc}\hfill {\left|D_{\frac{1}{2}}\right.⟩}_i& =& \frac{1}{\sqrt{3}}\left[-{\left|\frac{1}{2},0\right.⟩}_i+\sqrt{2}{\left|-\frac{1}{2},1\right.⟩}_i\right]\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill {\left|D_{-\frac{1}{2}}\right.⟩}_i& =& \frac{1}{\sqrt{3}}\left[{\left|-\frac{1}{2},0\right.⟩}_i-\sqrt{2}{\left|\frac{1}{2},-1\right.⟩}_i\right]\hfill \end{array}$$

(10)

whereas the quartet Q can be written as

$$\begin{array}{ccc}\hfill {\left|Q_{\frac{3}{2}}\right.⟩}_i& =& {\left|\frac{1}{2},1\right.⟩}_i\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill {\left|Q_{\frac{1}{2}}\right.⟩}_i& =& \frac{1}{\sqrt{3}}\left[\sqrt{2}{\left|\frac{1}{2},0\right.⟩}_i+{\left|-\frac{1}{2},1\right.⟩}_i\right]\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill {\left|Q_{-\frac{1}{2}}\right.⟩}_i& =& \frac{1}{\sqrt{3}}\left[\sqrt{2}{\left|-\frac{1}{2},0\right.⟩}_i+{\left|\frac{1}{2},-1\right.⟩}_i\right]\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill {\left|Q_{-\frac{3}{2}}\right.⟩}_i& =& {\left|-\frac{1}{2},-1\right.⟩}_i.\hfill \end{array}$$

(14)

The gs of the rung is a doublet when the rung interaction is antiferromagnetic, and it is a quartet when the rung interaction is ferromagnetic. For the AFM $J_{\perp }$, the effective Hamiltonian can be written in terms of pseudo spin-1/2 operators $\sigma$ which can have three components, x, y and z, and form an equivalent spin-1/2 antiferromagnetic Heisenberg chain. The effective Hamiltonian up to the first-order correction for the AFM $J_{\perp }$ can be written as

$$H=-N{J}_{\perp }+\frac{17J}{9}\sum _{i=1}^N{\widehat{\sigma }}_i·{\widehat{\sigma }}_{i+1},$$

(15)

where ${\widehat{\sigma }}_i$ are the pseudo spin-1/2 operators.

Similarly, for the ferromagnetic rung interaction, the gs of the spin pairs on a rung is in $S_{tot}^z=3/2$ and the energy is $J_{\perp }/2$. The effective Hamiltonian in this case can be written as

$$\begin{array}{c}\hfill H=N{J}_{\perp }/2+\sum _{i=1}^N⟨{\mu }_{i,i+1}|H_{i,i+1}|{\nu }_{i,i+1}⟩|{\mu }_{i,i+1}⟩⟨{\nu }_{i,i+1}|,\end{array}$$

(16)

where $\left\{\right|{\mu }_{i,i+1}⟩,|{\nu }_{i,i+1}⟩={\left|Q_{\beta }\right.⟩}_i\otimes {|Q_{{\beta }^{\prime }}⟩}_{i+1}\}$ are sixteen-fold degenerate. Let us first define the pseudo spin-3/2 operators:

$$\begin{array}{ccc}\hfill {\tau }_i^z{\left|Q_{\pm \beta }\right.⟩}_i& =& \pm \beta {\left|Q_{\pm \beta }\right.⟩}_i,\hfill \end{array}$$

(17)

where $\beta =-3/2,-1/2,1/2,3/2$.

$$\begin{array}{ccc}\hfill {\tau }_i^{+}{\left|Q_{\beta }\right.⟩}_i& =& C_{\beta +}{\left|Q_{\beta +1}\right.⟩}_i\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill {\tau }_i^{-}{\left|Q_{\alpha }\right.⟩}_i& =& C_{\alpha -}{\left|Q_{\alpha -1}\right.⟩}_i\hfill \end{array}$$

(19)

where $C_{\beta +}=\sqrt{3}$ for $\beta =-3/2,1/2$ and $C_{\beta +}=2$ for $\beta =-1/2$. Moreover, $C_{\alpha -}=\sqrt{3}$ for $\alpha =3/2,-1/2$ and $C_{\alpha -}=2$ for $\alpha =1/2$.

We can find the coefficients $⟨{\mu }_{i,i+1}\left|H_{i,i+1}\right|{\nu }_{i,i+1}⟩$ and express the Hamiltonian in terms of the pseudo spin-3/2 operators. After some algebras, the effective Hamiltonian up to first order becomes

$$\begin{array}{ccc}\hfill H& =& N{J}_{\perp }/2+\frac{5J}{9}\sum _{i=1}^N{\widehat{\tau }}_i·{\widehat{\tau }}_{i,i+1}\hfill \end{array}$$

(20)

The spectrum and correlations of these are similar to that of the spin-1/2 and spin-3/2 chains. The factor $\frac{17}{9}$ in Equation (15) and $\frac{5}{9}$ in Equation (20) are close to our numerical findings.

5. Discussion

It is well known that isolated HAF spin-1/2 and spin-1 chains are fundamentally different both in spectrum as well as in the nature of the gs [15,16,19,41]. In this work, we have studied the effect of magnetic exchange coupling $J_{\perp }$ between isolated HAF spin-1/2 and spin-1 chains. In fact, coupled spin-1/2 and spin-1 chains can be visualized as a normal ladder-like structure, as shown in Figure 1. The exchange interaction $J_{\perp }$ between the legs can be either ferromagnetic or antiferromagnetic. In the weak AFM coupling limit of $J_{\perp }$, the system behaves like two decoupled chains. However, in the large $J_{\perp }$ limit, the whole system behaves as an effective HAF spin-1/2 chain due to the formation of a singlet pair along the rung, leaving an effective spin-1/2 per rung which can interact via an effective antiferromagnetic exchange interaction, as shown in Section 4. For the FM $J_{\perp }$, the system behaves similarly to decoupled chains in a small $\alpha$ limit. However, for a large FM $J_{\perp }$ limit, coupled spin-1/2 and spin-1 pairs can form a pseudo spin-3/2 and the whole system behaves like a spin-3/2 HAF chain.

To understand the low-lying spectrum, we have also analyzed two of the lowest-lying energy gaps ${\mathrm{\Gamma }}_1$ and ${\mathrm{\Gamma }}_2$ as well as the spin densities ${\rho }_i$ in the lowest excited state on each leg and the spin correlations along each leg in the gs of the system. The decay behavior of ${\mathrm{\Gamma }}_1$ changes from exponential to power law upon increasing $J_{\perp }$. We notice that there is a large spin density at the edge of the spin-1 leg, and it decays exponentially in the small AFM $\alpha$ limit, but it vanishes and behaves like an HAF spin-1/2 chain for $\alpha \ge 0.5$. In the ferromagnetic $\alpha$ limit, the spin density is very high at the end of the leg (especially for the spin-1 leg), but the decay behavior is similar to that of a spin-3/2 HAF chain in a strong coupling limit. The correlations on both legs behave like that of isolated spin-1/2 and spin-3/2 HAF chains for strong AFM and FM rung couplings, respectively.

In the last section, the perturbative calculations in strong rung coupling limits are discussed, and the effective model Hamiltonians for large ferromagnetic and antiferromagnetic exchange rung interactions were formulated in terms of the pseudo spin-3/2 and 1/2, respectively.