Influence of f Electrons on the Electronic Band Structure of Rare-Earth Nickelates
Abstract
:1. Introduction
2. Calculation Details
3. Results and Discussion
3.1. Crystal Structure
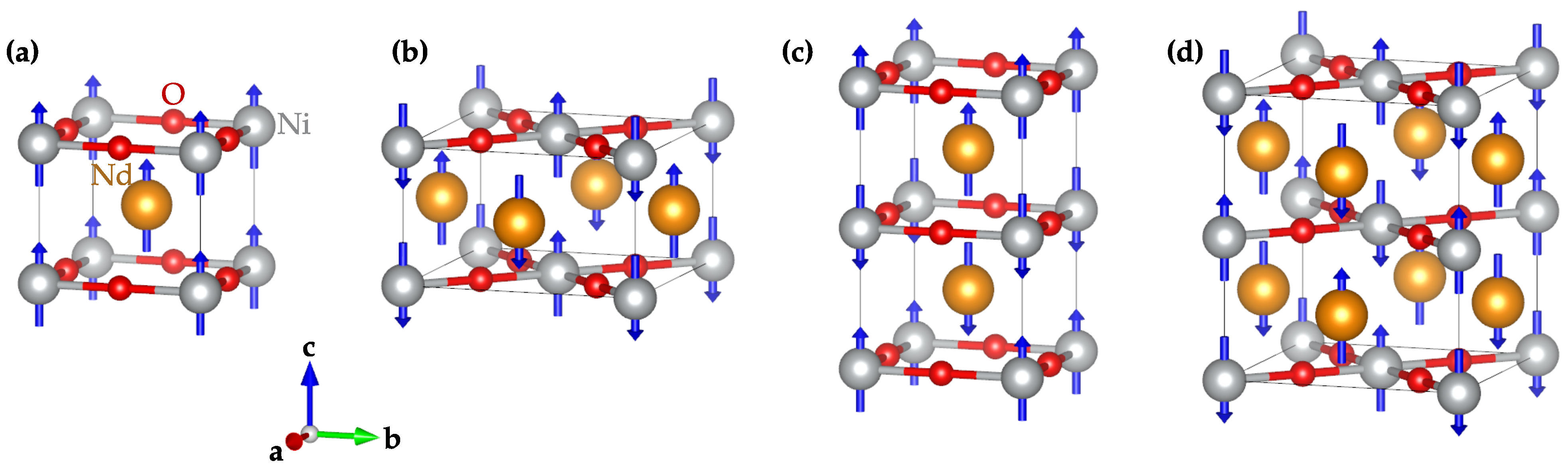
3.2. Magnetic Ground State
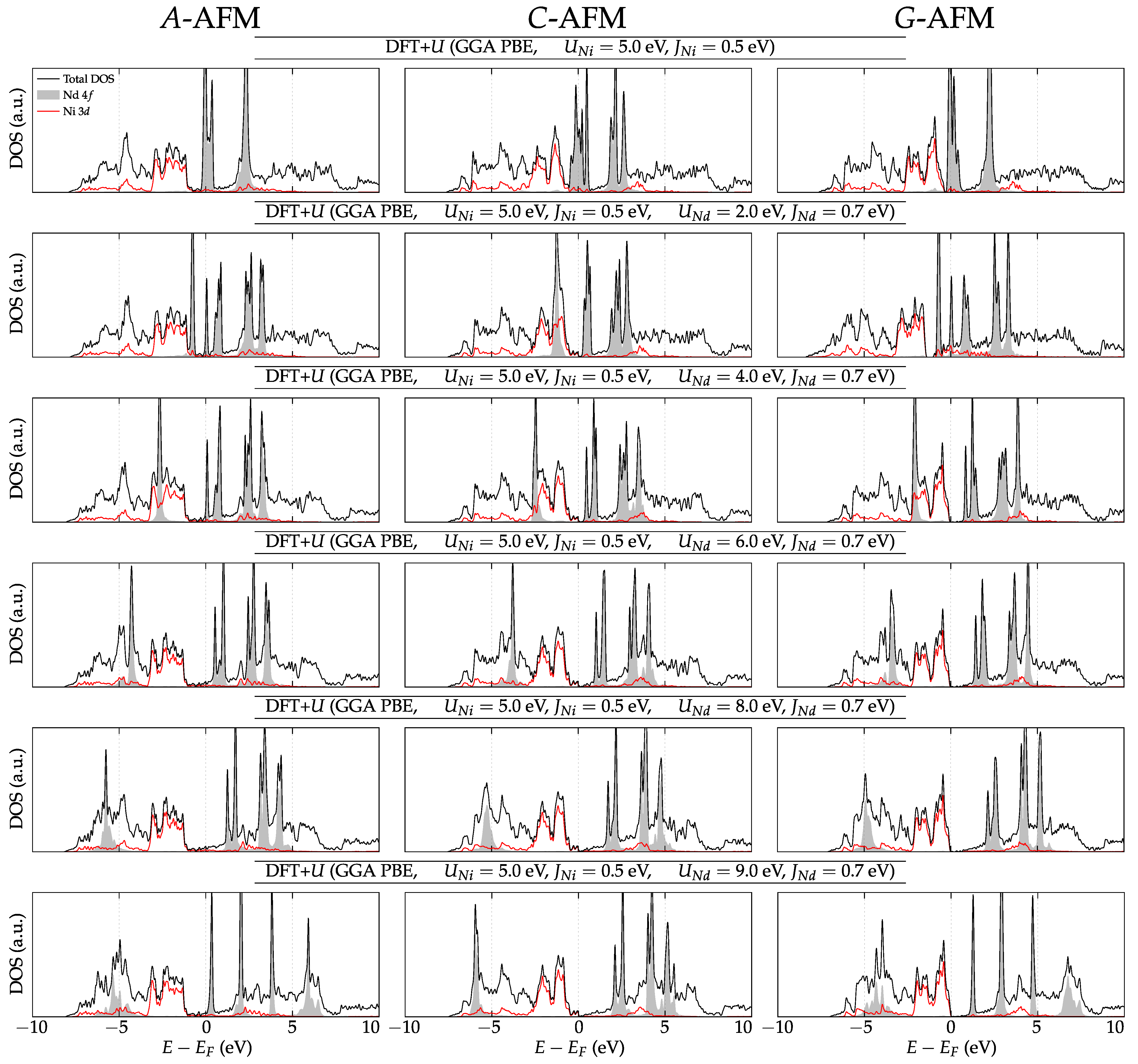
3.3. Electronic Density of States
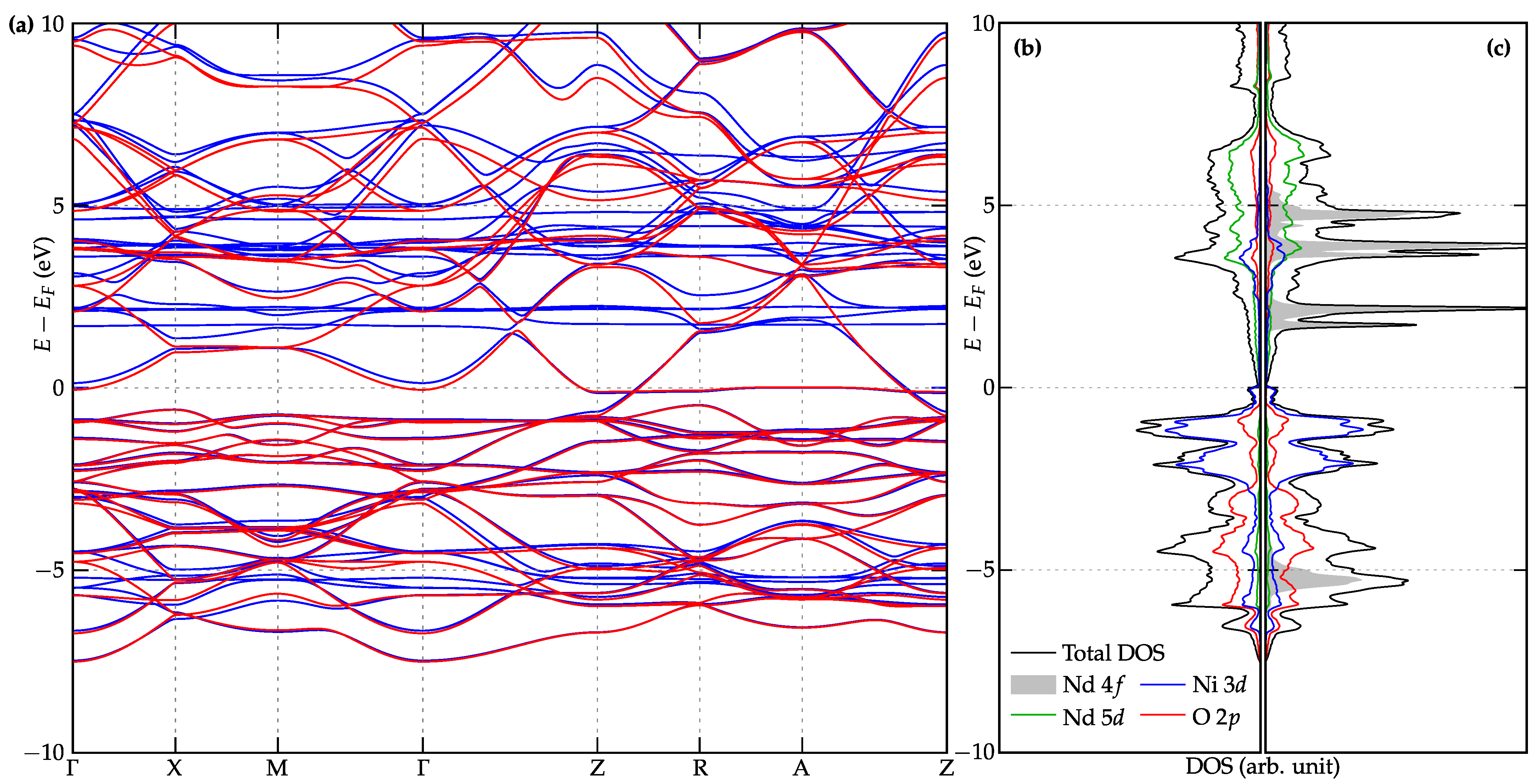
3.4. The Changes in the Electronic Bands due to f Electron States
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, D.; Lee, K.; Wang, B.Y.; Osada, M.; Crossley, S.; Lee, H.R.; Cui, Y.; Hikita, Y.; Hwang, H.Y. Superconductivity in an infinite-layer nickelate. Nature 2019, 572, 624. [Google Scholar] [CrossRef] [PubMed]
- Zeng, S.; Tang, C.S.; Yin, X.; Li, C.; Li, M.; Huang, Z.; Hu, J.; Liu, W.; Omar, G.J.; Jani, H.; et al. Phase Diagram and Superconducting Dome of Infinite-Layer Nd1−xSrxNiO2 Thin Films. Phys. Rev. Lett. 2020, 125, 147003. [Google Scholar] [CrossRef] [PubMed]
- Gu, Q.; Li, Y.; Wan, S.; Li, H.; Guo, W.; Yang, H.; Li, Q.; Zhu, X.; Pan, X.; Nie, Y.; et al. Single particle tunneling spectrum of superconducting Nd1−xSrxNiO2 thin films. Nat. Commun. 2020, 11, 6027. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.X.; Zheng, H.; Krivyakina, E.; Chmaissem, O.; Lopes, P.P.; Lynn, J.W.; Gallington, L.C.; Ren, Y.; Rosenkranz, S.; Mitchell, J.F.; et al. Synthesis and characterization of bulk Nd1−xSrxNiO2 and Nd1−xSrxNiO3. Phys. Rev. Mater. 2020, 4, 084409. [Google Scholar] [CrossRef] [PubMed]
- Osada, M.; Wang, B.Y.; Goodge, B.H.; Lee, K.; Yoon, H.; Sakuma, K.; Li, D.; Miura, M.; Kourkoutis, L.F.; Hwang, H.Y. A Superconducting Praseodymium Nickelate with Infinite Layer Structure. Nano Lett. 2020, 20, 5735–5740. [Google Scholar] [CrossRef]
- Osada, M.; Wang, B.Y.; Lee, K.; Li, D.; Hwang, H.Y. Phase diagram of infinite layer praseodymium nickelate Pr1−xSrxNiO2 thin films. Phys. Rev. Mater. 2020, 4, 121801. [Google Scholar] [CrossRef]
- Osada, M.; Wang, B.Y.; Goodge, B.H.; Harvey, S.P.; Lee, K.; Li, D.; Kourkoutis, L.F.; Hwang, H.Y. Nickelate Superconductivity without Rare-Earth Magnetism: (La,Sr)NiO2. Adv. Mater. 2021, 33, 2104083. [Google Scholar] [CrossRef]
- Nomura, Y.; Arita, R. Superconductivity in infinite-layer nickelates. Rep. Prog. Phys. 2022, 85, 052501. [Google Scholar] [CrossRef]
- Adhikary, P.; Bandyopadhyay, S.; Das, T.; Dasgupta, I.; Saha-Dasgupta, T. Orbital-selective superconductivity in a two-band model of infinite-layer nickelates. Phys. Rev. B 2020, 102, 100501. [Google Scholar] [CrossRef]
- Plienbumrung, T.; Daghofer, M.; Schmid, M.; Oleś, A.M. Screening in a two-band model for superconducting infinite-layer nickelate. Phys. Rev. B 2022, 106, 134504. [Google Scholar] [CrossRef]
- Nomura, Y.; Hirayama, M.; Tadano, T.; Yoshimoto, Y.; Nakamura, K.; Arita, R. Formation of a two-dimensional single-component correlated electron system and band engineering in the nickelate superconductor NdNiO2. Phys. Rev. B 2019, 100, 205138. [Google Scholar] [CrossRef]
- Jiang, P.; Si, L.; Liao, Z.; Zhong, Z. Electronic structure of rare-earth infinite-layer RNiO2 (R = La, Nd). Phys. Rev. B 2019, 100, 201106. [Google Scholar] [CrossRef]
- Choi, M.Y.; Lee, K.W.; Pickett, W.E. Role of 4f states in infinite-layer NdNiO2. Phys. Rev. B 2020, 101, 020503. [Google Scholar] [CrossRef]
- Zhang, H.; Jin, L.; Wang, S.; Xi, B.; Shi, X.; Ye, F.; Mei, J.W. Effective Hamiltonian for nickelate oxides Nd1−xSrxNiO2. Phys. Rev. Res. 2020, 2, 013214. [Google Scholar] [CrossRef]
- Wu, X.; Di Sante, D.; Schwemmer, T.; Hanke, W.; Hwang, H.Y.; Raghu, S.; Thomale, R. Robust dx2−y2-wave superconductivity of infinite-layer nickelates. Phys. Rev. B 2020, 101, 060504. [Google Scholar] [CrossRef]
- Zhang, R.; Lane, C.; Singh, B.; Nokelainen, J.; Barbiellini, B.; Markiewicz, R.S.; Bansil, A.; Sun, J. Magnetic and f-electron effects in LaNiO2 and NdNiO2 nickelates with cuprate-like 3dx2−y2 band. Commun. Phys. 2021, 4, 118. [Google Scholar] [CrossRef]
- Sakakibara, H.; Usui, H.; Suzuki, K.; Kotani, T.; Aoki, H.; Kuroki, K. Model Construction and a Possibility of Cupratelike Pairing in a New d9 Nickelate Superconductor (Nd,Sr)NiO2. Phys. Rev. Lett. 2020, 125, 077003. [Google Scholar] [CrossRef]
- Wang, Y.; Kang, C.J.; Miao, H.; Kotliar, G. Hund’s metal physics: From SrNiO2 to LaNiO2. Phys. Rev. B 2020, 102, 161118. [Google Scholar] [CrossRef]
- Botana, A.S.; Norman, M.R. Similarities and Differences between LaNiO2 and CaCuO2 and Implications for Superconductivity. Phys. Rev. X 2020, 10, 011024. [Google Scholar] [CrossRef]
- Liu, Z.; Ren, Z.; Zhu, W.; Wang, Z.; Yang, J. Electronic and magnetic structure of infinite-layer NdNiO2: Trace of antiferromagnetic metal. npj Quant. Mater. 2020, 5, 31. [Google Scholar] [CrossRef]
- Wan, X.; Ivanov, V.; Resta, G.; Leonov, I.; Savrasov, S.Y. Exchange interactions and sensitivity of the Ni two-hole spin state to Hund’s coupling in doped NdNiO2. Phys. Rev. B 2021, 103, 075123. [Google Scholar] [CrossRef]
- Deng, F.; Jiang, P.; Lu, Y.; Zhong, Z. First-principle study of Sr-doping effect in Nd1−xSrxNiO2. EPL 2021, 135, 67001. [Google Scholar] [CrossRef]
- Gu, Y.; Zhu, S.; Wang, X.; Hu, J.; Chen, H. A substantial hybridization between correlated Ni-d orbital and itinerant electrons in infinite-layer nickelates. Commun. Phys. 2020, 3, 84. [Google Scholar] [CrossRef]
- Lechermann, F. Late transition metal oxides with infinite-layer structure: Nickelates versus cuprates. Phys. Rev. B 2020, 101, 081110. [Google Scholar] [CrossRef]
- Ryee, S.; Yoon, H.; Kim, T.J.; Jeong, M.Y.; Han, M.J. Induced magnetic two-dimensionality by hole doping in the superconducting infinite-layer nickelate Nd1−xSrxNiO2. Phys. Rev. B 2020, 101, 064513. [Google Scholar] [CrossRef]
- Leonov, I.; Skornyakov, S.L.; Savrasov, S.Y. Lifshitz transition and frustration of magnetic moments in infinite-layer NdNiO2 upon hole doping. Phys. Rev. B 2020, 101, 241108. [Google Scholar] [CrossRef]
- Lechermann, F. Multiorbital Processes Rule the Nd1−xSrxNiO2 Normal State. Phys. Rev. X 2020, 10, 041002. [Google Scholar] [CrossRef]
- Karp, J.; Botana, A.S.; Norman, M.R.; Park, H.; Zingl, M.; Millis, A. Many-Body Electronic Structure of NdNiO2 and CaCuO2. Phys. Rev. X 2020, 10, 021061. [Google Scholar] [CrossRef]
- Kitatani, M.; Si, L.; Janson, O.; Arita, R.; Zhong, Z.; Held, K. Nickelate superconductors—A renaissance of the one-band Hubbard model. npj Quant. Mater. 2020, 5, 59. [Google Scholar] [CrossRef]
- Karp, J.; Hampel, A.; Millis, A.J. Superconductivity and antiferromagnetism in NdNiO2 and CaCuO2: A cluster DMFT study. Phys. Rev. B 2022, 105, 205131. [Google Scholar] [CrossRef]
- Chen, D.; Jiang, P.; Si, L.; Lu, Y.; Zhong, Z. Magnetism in doped infinite-layer NdNiO2 studied by combined density functional theory and dynamical mean-field theory. Phys. Rev. B 2022, 106, 045105. [Google Scholar] [CrossRef]
- Ortiz, R.A.; Puphal, P.; Klett, M.; Hotz, F.; Kremer, R.K.; Trepka, H.; Hemmida, M.; von Nidda, H.A.K.; Isobe, M.; Khasanov, R.; et al. Magnetic correlations in infinite-layer nickelates: An experimental and theoretical multimethod study. Phys. Rev. Res. 2022, 4, 023093. [Google Scholar] [CrossRef]
- Lu, H.; Rossi, M.; Nag, A.; Osada, M.; Li, D.F.; Lee, K.; Wang, B.Y.; Garcia-Fernandez, M.; Agrestini, S.; Shen, Z.X.; et al. Magnetic excitations in infinite-layer nickelates. Science 2021, 373, 213. [Google Scholar] [CrossRef] [PubMed]
- Tam, C.C.; Choi, J.; Ding, X.; Agrestini, S.; Nag, A.; Wu, M.; Huang, B.; Luo, H.; Gao, P.; García-Fernández, M.; et al. Charge density waves in infinite-layer NdNiO2 nickelates. Nat. Mater. 2022, 21, 1116. [Google Scholar] [CrossRef]
- Krieger, G.; Martinelli, L.; Zeng, S.; Chow, L.E.; Kummer, K.; Arpaia, R.; Moretti Sala, M.; Brookes, N.B.; Ariando, A.; Viart, N.; et al. Charge and Spin Order Dichotomy in NdNiO2 Driven by the Capping Layer. Phys. Rev. Lett. 2022, 129, 027002. [Google Scholar] [CrossRef]
- Rossi, M.; Osada, M.; Choi, J.; Agrestini, S.; Jost, D.; Lee, Y.; Lu, H.; Wang, B.Y.; Lee, K.; Nag, A.; et al. A broken translational symmetry state in an infinite-layer nickelate. Nat. Phys. 2022, 18, 869. [Google Scholar] [CrossRef]
- Delin, A.; Fast, L.; Johansson, B.; Eriksson, O.; Wills, J.M. Cohesive properties of the lanthanides: Effect of generalized gradient corrections and crystal structure. Phys. Rev. B 1998, 58, 4345. [Google Scholar] [CrossRef]
- Delin, A.; Fast, L.; Eriksson, O.; Johansson, B. Effect of generalized gradient corrections on lanthanide cohesive properties. J. Alloys Compd. 1998, 275–277, 472. [Google Scholar] [CrossRef]
- Strange, P.; Svane, A.; Temmerman, W.M.; Szotek, Z.; Winter, H. Understanding the valency of rare earths from first-principles theory. Nature 1999, 399, 756. [Google Scholar] [CrossRef]
- Söderlind, P.; Turchi, P.E.A.; Landa, A.; Lordi, V. Ground-state properties of rare-earth metals: An evaluation of density-functional theory. J. Phys. Condens. Matter 2014, 26, 416001. [Google Scholar] [CrossRef]
- Waller, O.; Piekarz, P.; Bosak, A.; Jochym, P.T.; Ibrahimkutty, S.; Seiler, A.; Krisch, M.; Baumbach, T.; Parlinski, K.; Stankov, S. Lattice dynamics of neodymium: Influence of 4f electron correlations. Phys. Rev. B 2016, 94, 014303. [Google Scholar] [CrossRef]
- Moore, G.C.; Horton, M.K.; Ganose, A.M.; Siron, M.; Linscott, E.; O’Regan, D.D.; Persson, K.A. High-throughput determination of Hubbard U and Hund J values for transition metal oxides via linear response formalism. arXiv 2022. [Google Scholar] [CrossRef]
- Nilsson, F.; Sakuma, R.; Aryasetiawan, F. Ab initio calculations of the Hubbard U for the early lanthanides using the constrained random-phase approximation. Phys. Rev. B 2013, 88, 125123. [Google Scholar] [CrossRef]
- Kozub, A.L.; Shick, A.B.; Máca, F.; Kolorenč, J.; Lichtenstein, A.I. Electronic structure and magnetism of samarium and neodymium adatoms on free-standing graphene. Phys. Rev. B 2016, 94, 125113. [Google Scholar] [CrossRef]
- Ma, F.; Zhang, Z.; Jiang, D.; Zhang, Z.; Kou, H.; Strzep, A.; Tang, Q.; Zhou, H.; Zhang, M.; Zhang, P.; et al. Neodymium Cluster Evolution in Fluorite Laser Crystal: A Combined DFT and Synchrotron X-ray Absorption Fine Structure Study. Cryst. Growth Des. 2022, 22, 4480. [Google Scholar] [CrossRef]
- Reshak, A.H.; Piasecki, M.; Auluck, S.; Kityk, I.V.; Khenata, R.; Andriyevsky, B.; Cobet, C.; Esser, N.; Majchrowski, A.; Świrkowicz, M.; et al. Effect of U on the Electronic Properties of Neodymium Gallate (NdGaO3): Theoretical and Experimental Studies. J. Phys. Chem. B 2009, 113, 15237–15242. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505. [Google Scholar] [CrossRef]
- Been, E.; Lee, W.S.; Hwang, H.Y.; Cui, Y.; Zaanen, J.; Devereaux, T.; Moritz, B.; Jia, C. Electronic Structure Trends Across the Rare-Earth Series in Superconducting Infinite-Layer Nickelates. Phys. Rev. X 2021, 11, 011050. [Google Scholar] [CrossRef]
- Gao, J.; Peng, S.; Wang, Z.; Fang, C.; Weng, H. Electronic structures and topological properties in nickelates Lnn+1NinO2n+2. Natl. Sci. Rev. 2020, 8, nwaa218. [Google Scholar] [CrossRef]
- Hampel, A.; Liu, P.; Franchini, C.; Ederer, C. Energetics of the coupled electronic–structural transition in the rare-earth nickelates. npj Quant. Mater. 2019, 4, 5. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Hayward, M.; Rosseinsky, M. Synthesis of the infinite layer Ni(I) phase NdNiO2+x by low temperature reduction of NdNiO3 with sodium hydride. Solid State Sci. 2003, 5, 839. [Google Scholar] [CrossRef]
- Li, Q.; He, C.; Si, J.; Zhu, X.; Zhang, Y.; Wen, H.H. Absence of superconductivity in bulk Nd1−xSrxNiO2. Commun. Mater. 2020, 1, 16. [Google Scholar] [CrossRef]
- Lin, H.; Gawryluk, D.J.; Klein, Y.M.; Huangfu, S.; Pomjakushina, E.; von Rohr, F.; Schilling, A. Universal spin-glass behaviour in bulk LaNiO2, PrNiO2 and NdNiO2. New J. Phys. 2022, 24, 013022. [Google Scholar] [CrossRef]
- Kapeghian, J.; Botana, A.S. Electronic structure and magnetism in infinite-layer nickelates RNiO2 (R = La − Lu). Phys. Rev. B 2020, 102, 205130. [Google Scholar] [CrossRef]
- Lee, K.W.; Pickett, W.E. Infinite-layer LaNiO2: Ni1+ is not Cu2+. Phys. Rev. B 2004, 70, 165109. [Google Scholar] [CrossRef]
- Karp, J.; Hampel, A.; Millis, A.J. Dependence of DFT+DMFT results on the construction of the correlated orbitals. Phys. Rev. B 2021, 103, 195101. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. Vesta3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272. [Google Scholar] [CrossRef]
| Phase | Lattice Constant (Å) | E (eV/f.u.) | () | () | |
|---|---|---|---|---|---|
| a | c | ||||
| Experimental values | |||||
| Ref. [57] | 3.919 | 3.307 | - | - | - |
| Ref. [58] | 3.914 | 3.239 | - | - | - |
| Ref. [59] | 3.928 | 3.279 | - | - | - |
| DFT (GGA PBE) | |||||
| NM | 3.909 | 3.314 | −28.464 | - | - |
| FM | 3.896 | 3.277 | −31.462 | 3.155 | 0.184 |
| A-AFM | 3.894 | 3.312 | −31.397 | 3.123 | 0.081 |
| C-AFM | 3.900 | 3.267 | −31.448 | 3.123 | 0.404 |
| G-AFM | 3.903 | 3.283 | −31.424 | 3.083 | 0.406 |
| DFT+U (GGA PBE, eV, eV) | |||||
| NM | 3.891 | 3.306 | −26.203 | - | - |
| FM | 3.925 | 3.249 | −29.618 | 3.129 | 0.854 |
| A-AFM | 3.926 | 3.273 | −29.568 | 3.089 | 0.892 |
| C-AFM | 3.952 | 3.216 | −29.594 | 3.076 | 1.007 |
| G-AFM | 3.871 | 3.303 | −29.170 | 3.112 | 0.000 |
| DFT+U (GGA PBE, eV, eV, eV, eV) | |||||
| NM | 3.891 | 3.306 | −26.203 | - | - |
| FM | 3.937 | 3.292 | −29.287 | 3.125 | 0.924 |
| A-AFM | 3.929 | 3.307 | −28.948 | 3.138 | 0.867 |
| C-AFM | 3.941 | 3.263 | −29.303 | 3.046 | 0.962 |
| G-AFM | 3.879 | 3.333 | −28.629 | 3.162 | 0.000 |
| DFT+U (GGA PBE, eV, eV, eV, eV) | |||||
| NM | 3.891 | 3.306 | −26.203 | - | - |
| FM | 3.940 | 3.284 | −28.712 | 3.061 | 0.893 |
| A-AFM | 3.940 | 3.290 | −28.714 | 3.056 | 0.938 |
| C-AFM | 3.950 | 3.263 | −28.742 | 3.031 | 0.940 |
| G-AFM | 3.949 | 3.264 | −28.740 | 3.004 | 0.945 |
| DFT+U (GGA PBE, eV, eV, eV, eV) | |||||
| NM | 3.891 | 3.306 | −26.203 | - | - |
| FM | 3.943 | 3.286 | −28.483 | 3.016 | 0.905 |
| A-AFM | 3.944 | 3.287 | −28.483 | 3.006 | 0.936 |
| C-AFM | 3.955 | 3.274 | −28.517 | 3.017 | 0.941 |
| G-AFM | 3.954 | 3.275 | −28.515 | 2.997 | 0.948 |
| DFT+U (GGA PBE, eV, eV, eV, eV) | |||||
| NM | 3.891 | 3.306 | −26.203 | - | - |
| FM | 3.950 | 3.294 | −28.321 | 3.014 | 0.910 |
| A-AFM | 3.948 | 3.297 | −28.319 | 3.004 | 0.933 |
| C-AFM | 3.958 | 3.285 | −28.351 | 3.013 | 0.944 |
| G-AFM | 3.960 | 3.286 | −28.349 | 2.996 | 0.951 |
| DFT+U (GGA PBE, eV, eV, eV, eV) | |||||
| NM | 3.891 | 3.306 | −26.203 | - | - |
| FM | 3.951 | 3.299 | −28.256 | 3.016 | 0.911 |
| A-AFM | 3.951 | 3.301 | −28.255 | 3.006 | 0.933 |
| C-AFM | 3.959 | 3.288 | −28.285 | 3.014 | 0.946 |
| G-AFM | 3.962 | 3.289 | −28.283 | 2.998 | 0.953 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ptok, A.; Basak, S.; Piekarz, P.; Oleś, A.M. Influence of f Electrons on the Electronic Band Structure of Rare-Earth Nickelates. Condens. Matter 2023, 8, 19. https://doi.org/10.3390/condmat8010019
Ptok A, Basak S, Piekarz P, Oleś AM. Influence of f Electrons on the Electronic Band Structure of Rare-Earth Nickelates. Condensed Matter. 2023; 8(1):19. https://doi.org/10.3390/condmat8010019
Chicago/Turabian StylePtok, Andrzej, Surajit Basak, Przemysław Piekarz, and Andrzej M. Oleś. 2023. "Influence of f Electrons on the Electronic Band Structure of Rare-Earth Nickelates" Condensed Matter 8, no. 1: 19. https://doi.org/10.3390/condmat8010019
APA StylePtok, A., Basak, S., Piekarz, P., & Oleś, A. M. (2023). Influence of f Electrons on the Electronic Band Structure of Rare-Earth Nickelates. Condensed Matter, 8(1), 19. https://doi.org/10.3390/condmat8010019










