Influence of Anharmonic and Frustration Effects on Josephson Phase Qubit Characteristics
Abstract
1. Introduction
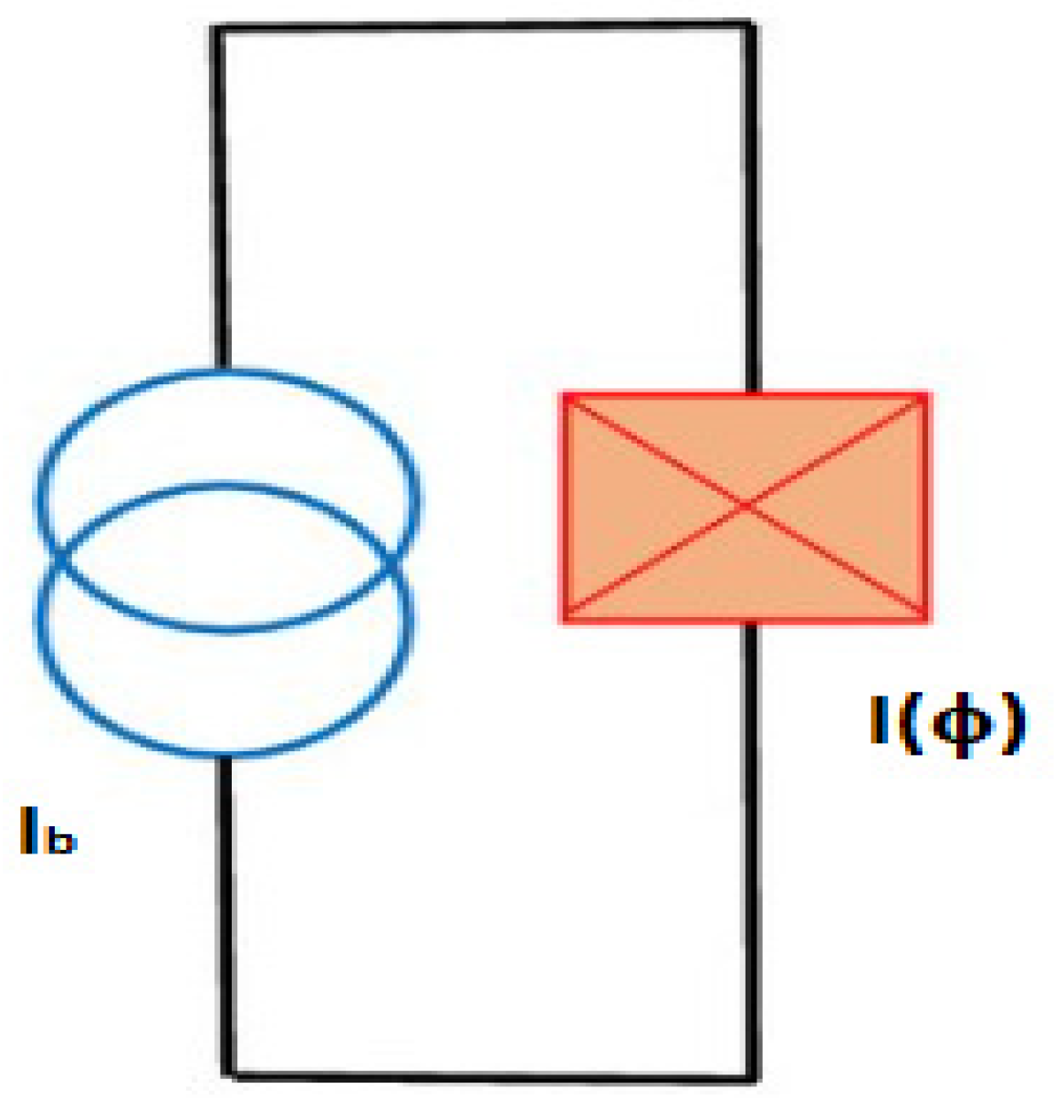
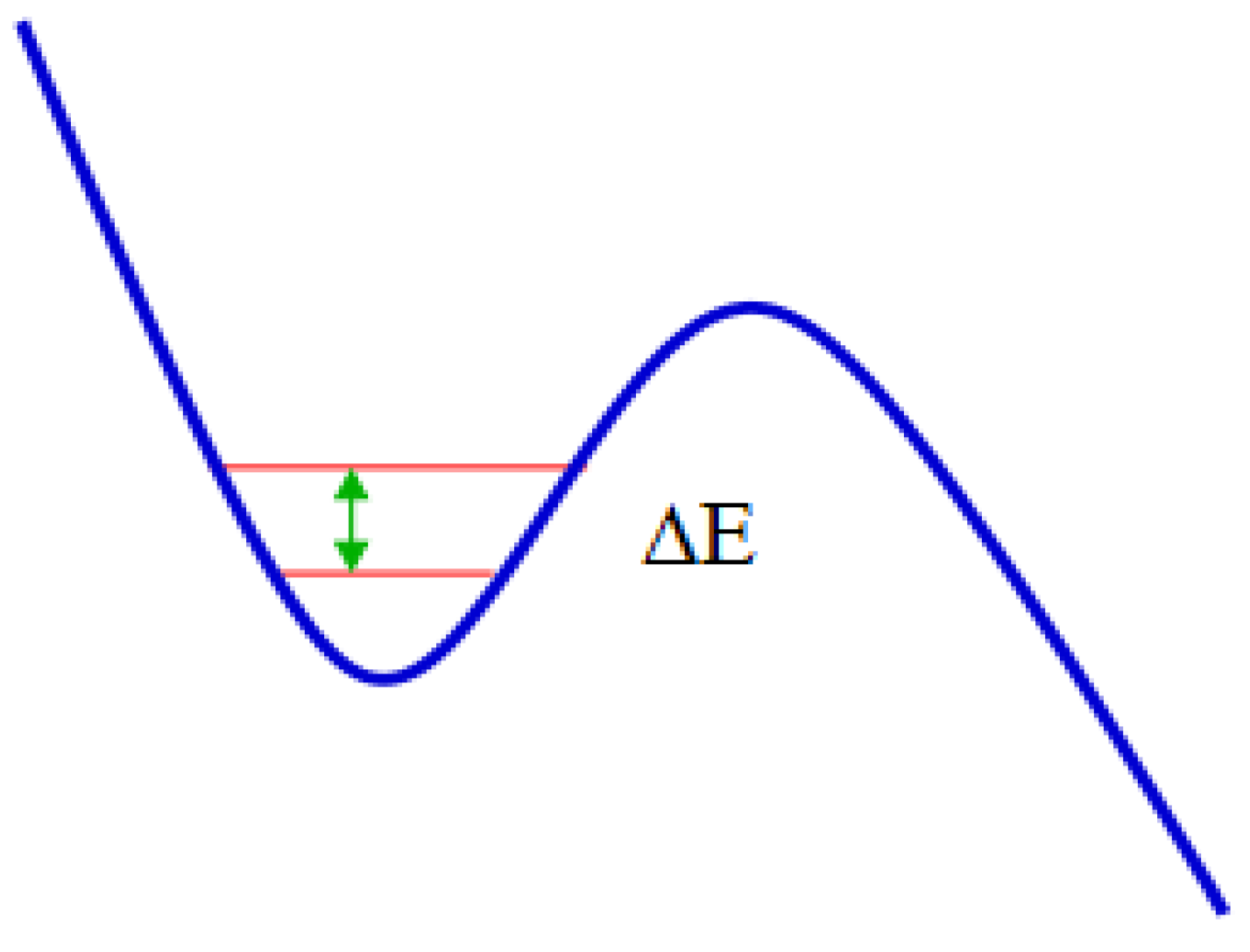
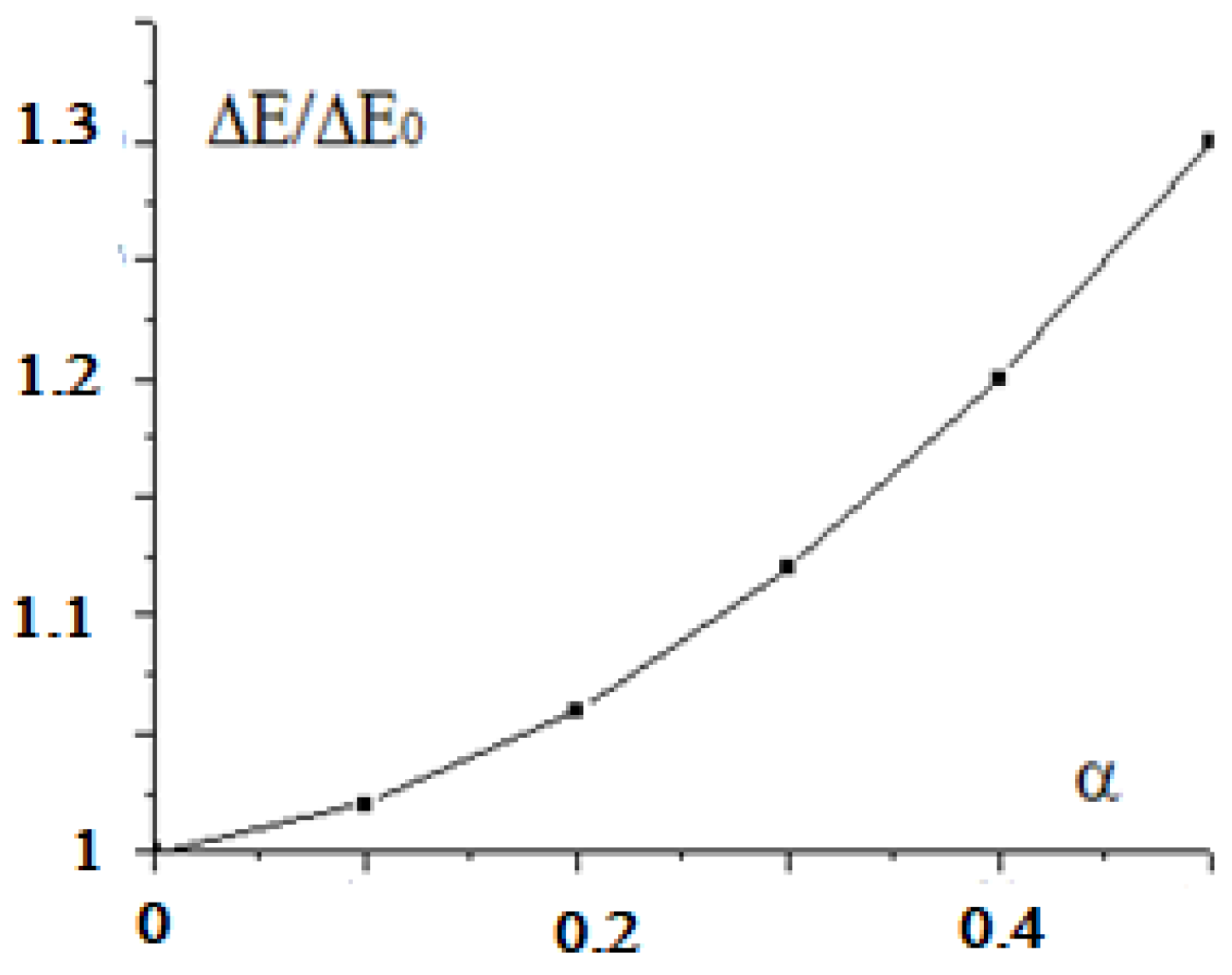
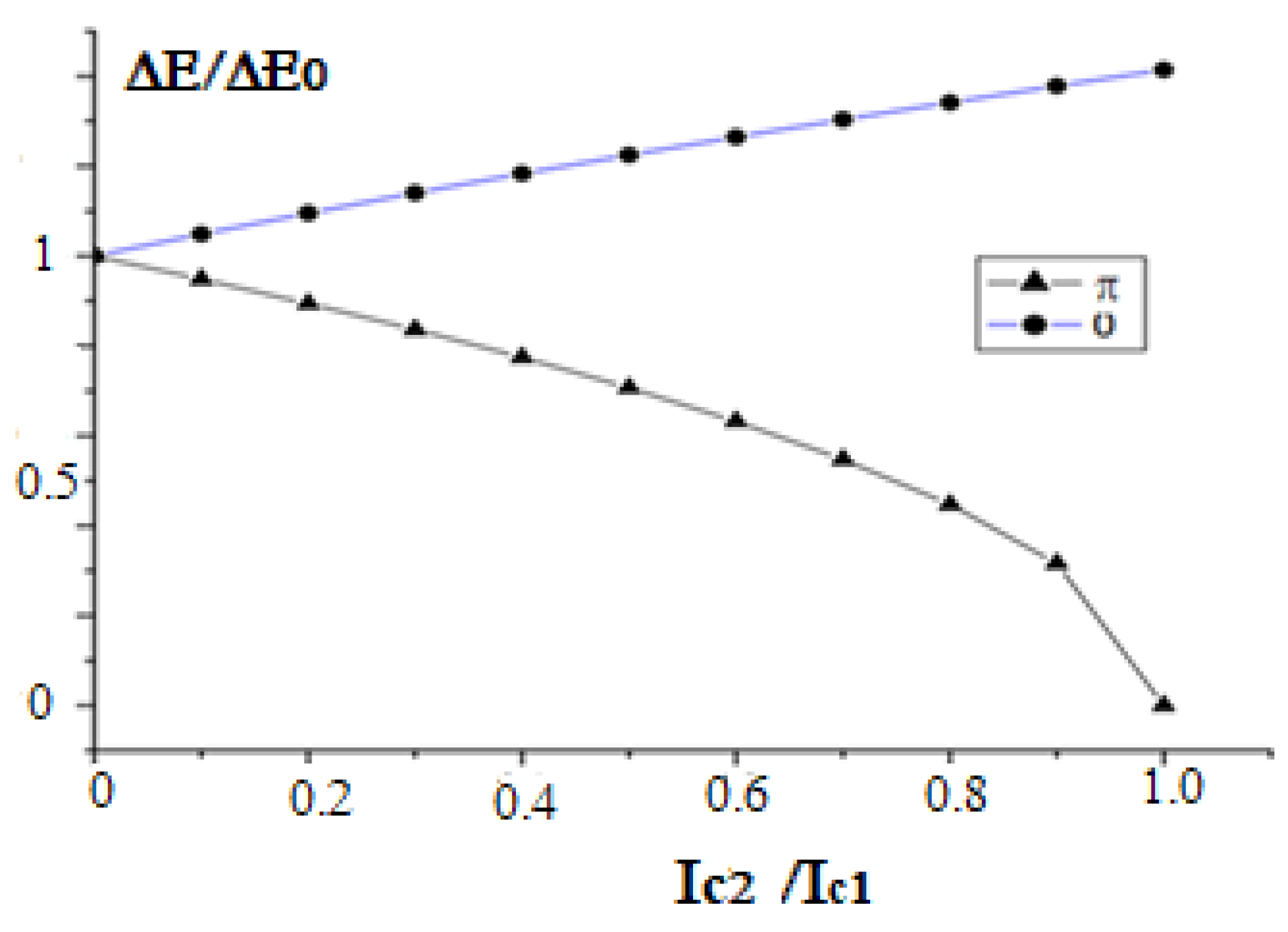
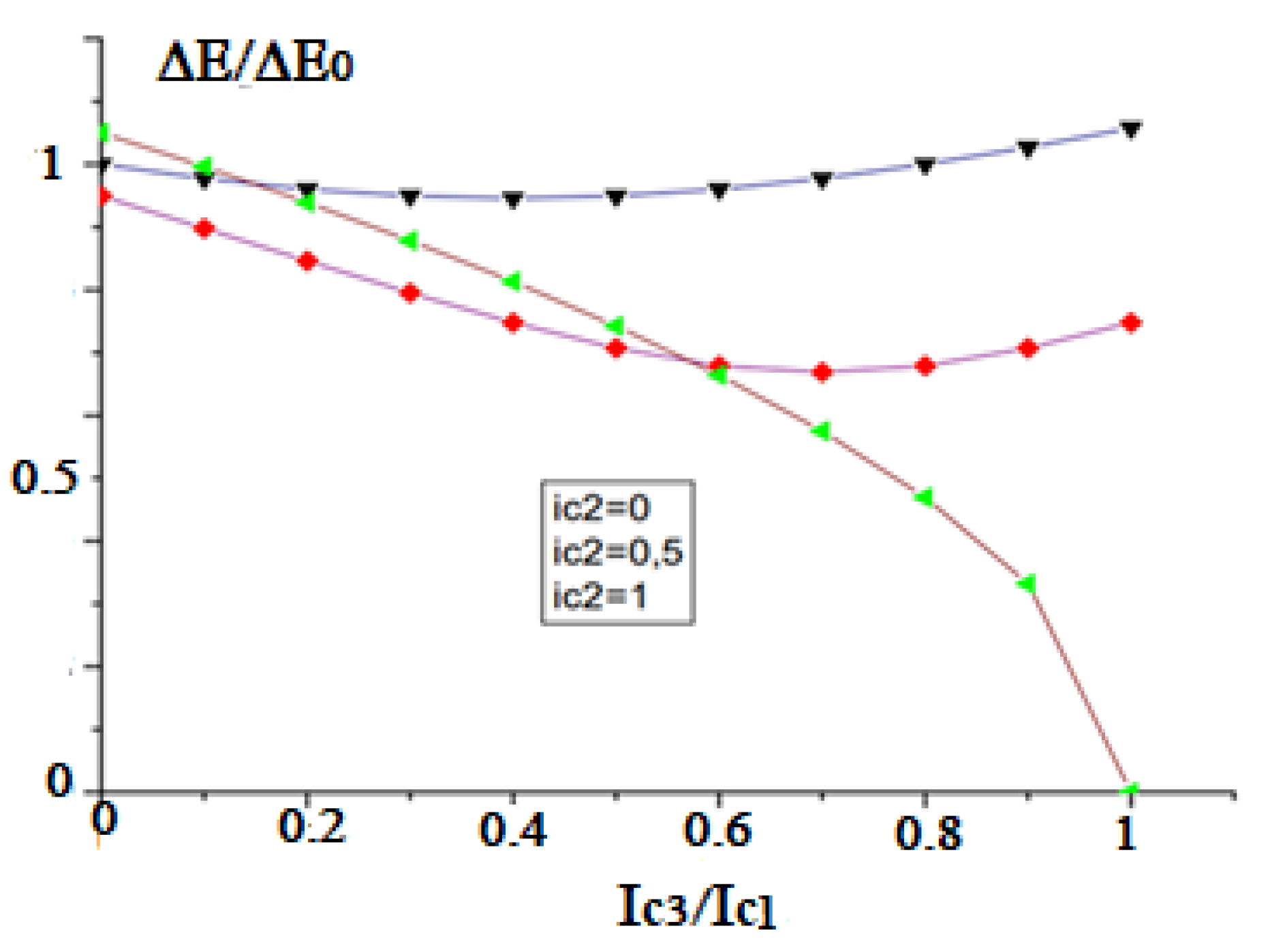
2. Results
3. Discussion
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nielsen, M.; Chiang, I. Quantum Computation, Quantum Information; Cambridge University Press: Cambridge, UK, 2000; 676p. [Google Scholar]
- Likharev, K. Introduction into Dynamics of Josephson Junctions and Circuits; Gordon Breach: New York, NY, USA, 1986; 586p. [Google Scholar]
- Askerzade, I.; Bozbey, A.; Canturk, M. Modern Aspects of Josephson Dynamics and Superconductivity Electronics; Springer: Berlin, Germany, 2017; 211p. [Google Scholar] [CrossRef]
- Wendin, G.; Shumeiko, V. Quantum bits with Josephson junctions. Low Temp. Phys. 2007, 33, 724–757. [Google Scholar] [CrossRef]
- Il’ichev, V.; Zakosarenko, I.; Fritzsch, L.; Stolz, R.; Hoenig, H.E.; Meyer, H.-G. Radio-frequency based monitoring of small supercurrents. Rev. Sci. Instrum. 2001, 72, 1882–1922. [Google Scholar] [CrossRef]
- Yerin, Y.; Omelyanchouk, A.N. Frustration phenomena in Josephson point contacts between single-band and three-band superconductors. Low Temp. Phys. 2014, 40, 943–949. [Google Scholar] [CrossRef]
- Askerzade, I. Unconventional Superconductors: Anisotropy and Multiband Effects; Springer: Berlin, Germany, 2012; 177p. [Google Scholar]
- Yerin, Y.; Omelyanchouk, A.N.; Il’Ichev, E. DC SQUID based on a three-band superconductor with broken time-reversal symmetry. Supercond. Sci. Technol. 2015, 28, 095006. [Google Scholar] [CrossRef]
- Ng, T.; Nagaosa, N. Broken time-reversal symmetry in Josephson junction involving two-band superconductors. EPL 2009, 87, 17003. [Google Scholar] [CrossRef]
- Stanev, V.; Tešanović, Z. Three-band superconductivity and the order parameter that breaks time-reversal symmetry. Phys. Rev. B 2010, 81, 134522. [Google Scholar] [CrossRef]
- Dias, R.; Marques, A. Frustrated multiband superconductivity. Supercond. Sci. Technol. 2011, 24, 085009. [Google Scholar] [CrossRef]
- Lin, S.-Z. Josephson effect between a two-band superconductor with s++ or s± pairing symmetry and a conventional s-wave superconductor. Phys. Rev. B 2012, 86, 014510. [Google Scholar] [CrossRef]
- Bojesen, T.; Babaev, E.; Sudbø, A. Time reversal symmetry breakdown in normal and superconducting states in frustrated three-band systems. Phys. Rev. B 2013, 88, 220511. [Google Scholar] [CrossRef]
- Askerzade, I.N. Escape rate in Josephson junctions between single -band and two -band superconductors. Physical C 2020, 374, 1353647. [Google Scholar] [CrossRef]
- Askerzade, I.N.; Aydın, A. Frustration effect on escape rate in Josephson junctions between single-band and three-band superconductors in the macroscopic quantum tunneling regime. Low Temp. Phys. 2021, 47, 282–286. [Google Scholar] [CrossRef]
- Askerzade, I.N.; Askerbeyli, R.; Ulku, I. Effect of unconventional current-phase relation of Josephson junction on escape rate in ac SQUID. Physical C 2022, 598, 1354068. [Google Scholar] [CrossRef]
- Goldobin, E.; Koelle, D.; Kleiner, R.; Buzdin, A. Josephson junctions with second harmonic in the current-phase relation: Properties of φ- junctions. Phys. Rev. B 2007, 76, 224523. [Google Scholar] [CrossRef]
- Bauch, T.; Lombardi, F.; Tafuri, F.; Barone, A.; Rotoli, G.; Delsing, P.; Claeson, T. Macroscopic quantum tunneling in d-wave YBCO Josephson junctions. Phys. Rev. Lett. 2005, 94, 087003. [Google Scholar] [CrossRef]
- Askerzade, I.; Gencer, A.; Guclu, N. On the Ginsburg-Landau analysis of the upper critical field H-c2 in MgB2, Supercond. Sci. Technol. 2002, 15, L13–L16. [Google Scholar] [CrossRef]
- Askerzade, I.; Gencer, A.; Guclu, N.; Kılıc, A. Two-band Ginzburg-Landau theory for the lower critical field H-c1 in MgB2, Supercond. Sci. Technol. 2002, 15, L17–L20. [Google Scholar] [CrossRef]
- Askerzade, I. Study of layered superconductors in the theory of an electron-phonon coupling mechanism. Phys. Uspekhi 2006, 49, 977–988. [Google Scholar] [CrossRef]
- Döring, S.; Schmidt, S.; Schmidl, F.; Tympel, V.; Haindl, S.; Kurth, F.; Iida, K.; Mönch, I.; Holzapfel, B.; Seidel, P. Edge-type Josephson junctions with Co-doped Ba-122 thin filmsSuper. Sci. Technol. 2012, 25, 084020. [Google Scholar] [CrossRef]
- Zhang, X.H.; Oh, Y.S.; Liu, Y.; Yan, L.; Kim, K.H.; Greene, R.L.; Takeuchi, I. Observation of the Josephson Effect in Pb/BaKaFeAs Single Crystal Junctions. Phys. Rev. Lett. 2009, 102, 147002. [Google Scholar] [CrossRef]
- Burmistrova, A.V.; Devyatov, I.A.; Golubov, A.A.; Yada, K.; Tanaka, Y.; Tortello, M.; Gonnelli, R.S.; Stepanov, V.A.; Ding, X.; Wen, H.-H.; et al. Josephson current in Fe-based superconducting junctions: Theory and experiment. Phys. Rev. B 2015, 91, 214501. [Google Scholar] [CrossRef]
- Kalenyuk, A.A.; Pagliero, A.; Borodianskyi, E.A.; Kordyuk, A.A.; Krasnov, V.M. Phase-Sensitive Evidence for the Sign-Reversal s± Symmetry of the Order Parameter in an Iron-Pnictide Superconductor Using Nb/Ba1−xNaxFe2As2 Josephson Junctions. Phys. Rev. Lett. 2018, 120, 067001. [Google Scholar] [CrossRef] [PubMed]
- Kalenyuk, A.A.; Borodianskı, A.; Kordyuk, A.A.; Krasnov, V.M. Influence of the Fermi surface geometry on the Josephson effect between iron-pnictide and conventional superconductors. Phys. Rev. B 2021, 103, 214507. [Google Scholar] [CrossRef]
- Ota, Y.; Machida, M.; Koyama, T.; Aoki, H. Collective modes in multiband superfluids and superconductors: Multiple dynamical classes. Phys. Rev. B 2011, 83, 060507. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Askerzade, I.N. Influence of Anharmonic and Frustration Effects on Josephson Phase Qubit Characteristics. Condens. Matter 2023, 8, 20. https://doi.org/10.3390/condmat8010020
Askerzade IN. Influence of Anharmonic and Frustration Effects on Josephson Phase Qubit Characteristics. Condensed Matter. 2023; 8(1):20. https://doi.org/10.3390/condmat8010020
Chicago/Turabian StyleAskerzade, Iman N. 2023. "Influence of Anharmonic and Frustration Effects on Josephson Phase Qubit Characteristics" Condensed Matter 8, no. 1: 20. https://doi.org/10.3390/condmat8010020
APA StyleAskerzade, I. N. (2023). Influence of Anharmonic and Frustration Effects on Josephson Phase Qubit Characteristics. Condensed Matter, 8(1), 20. https://doi.org/10.3390/condmat8010020








