Ground States of Heisenberg Spin Clusters from a Cluster-Based Projected Hartree–Fock Approach
Abstract
1. Introduction
2. Theory and Computations
3. Results and Discussion
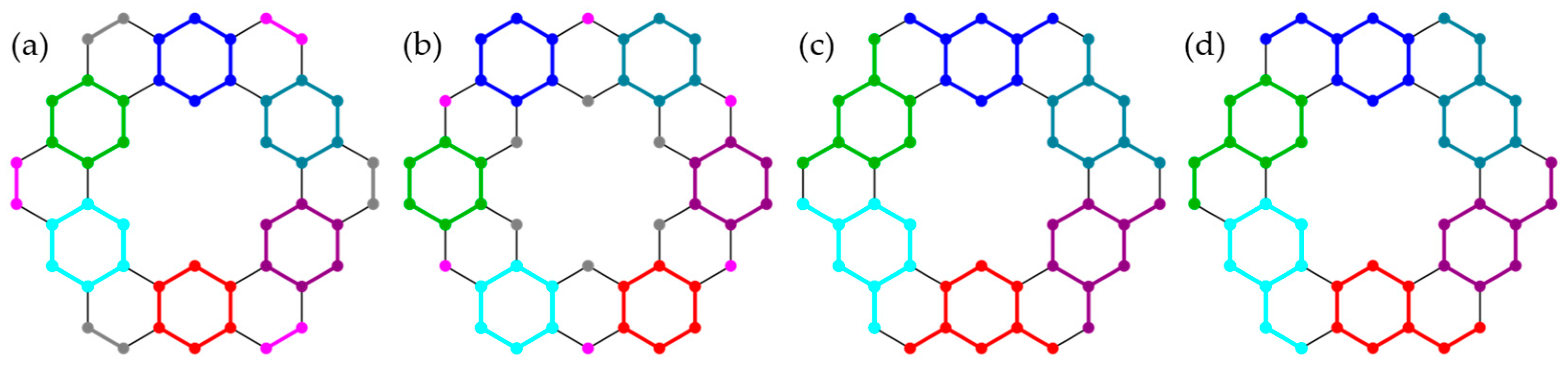
3.1. Symmetric Rings
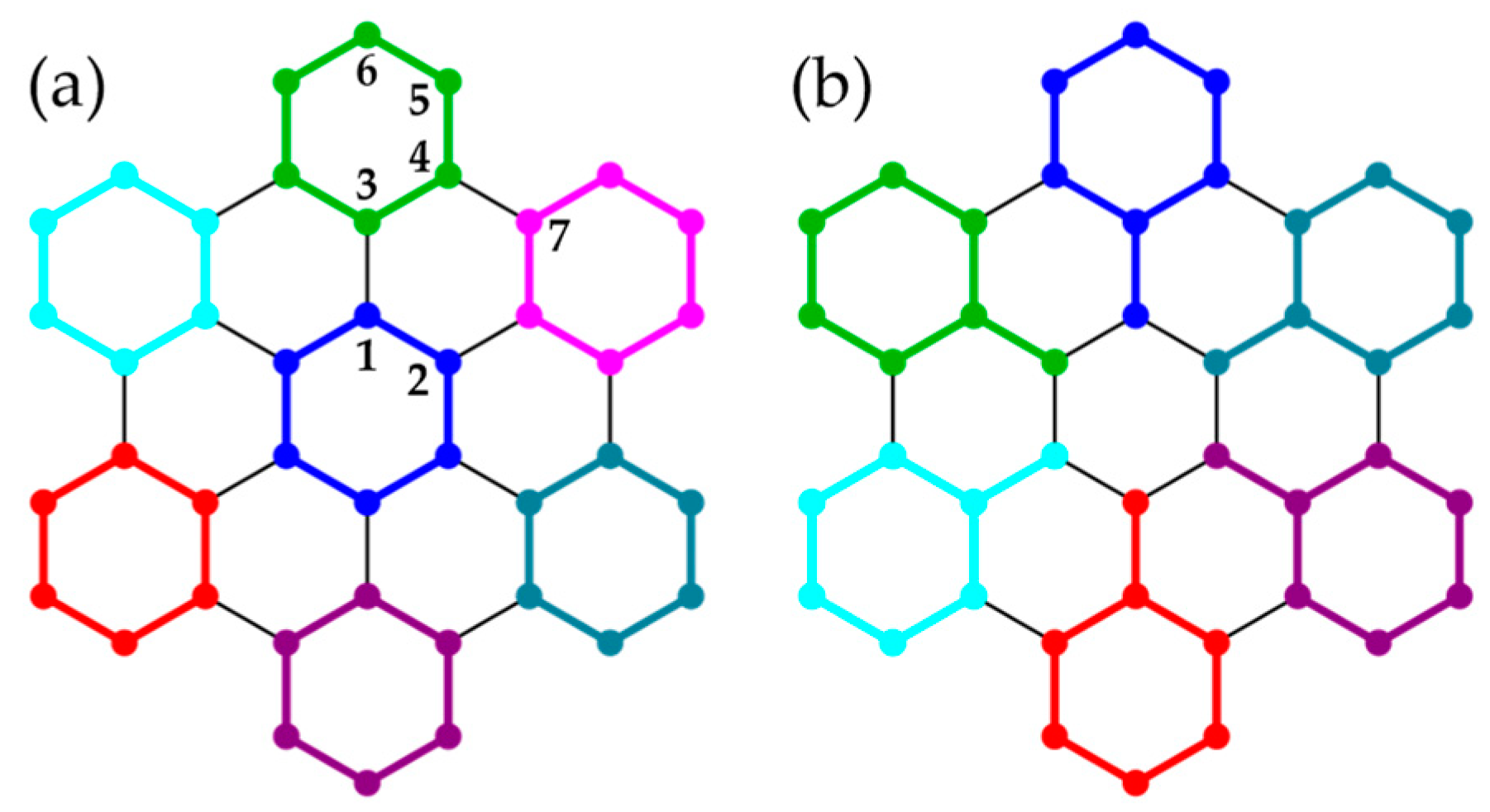
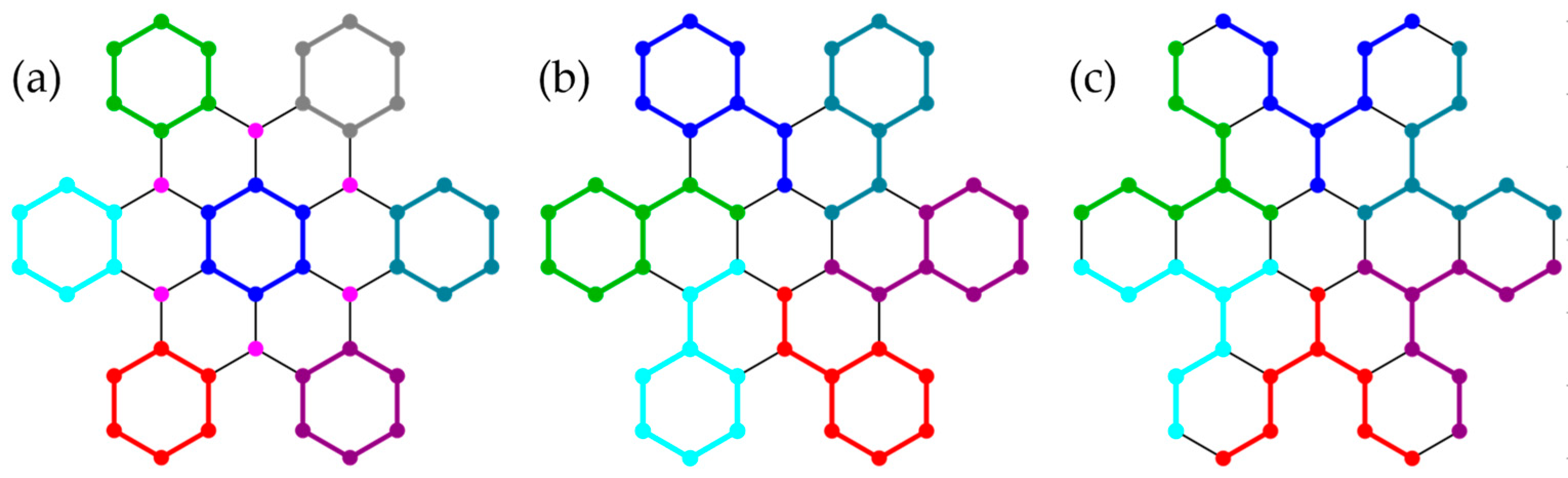
3.2. Honeycomb Lattice Fragments
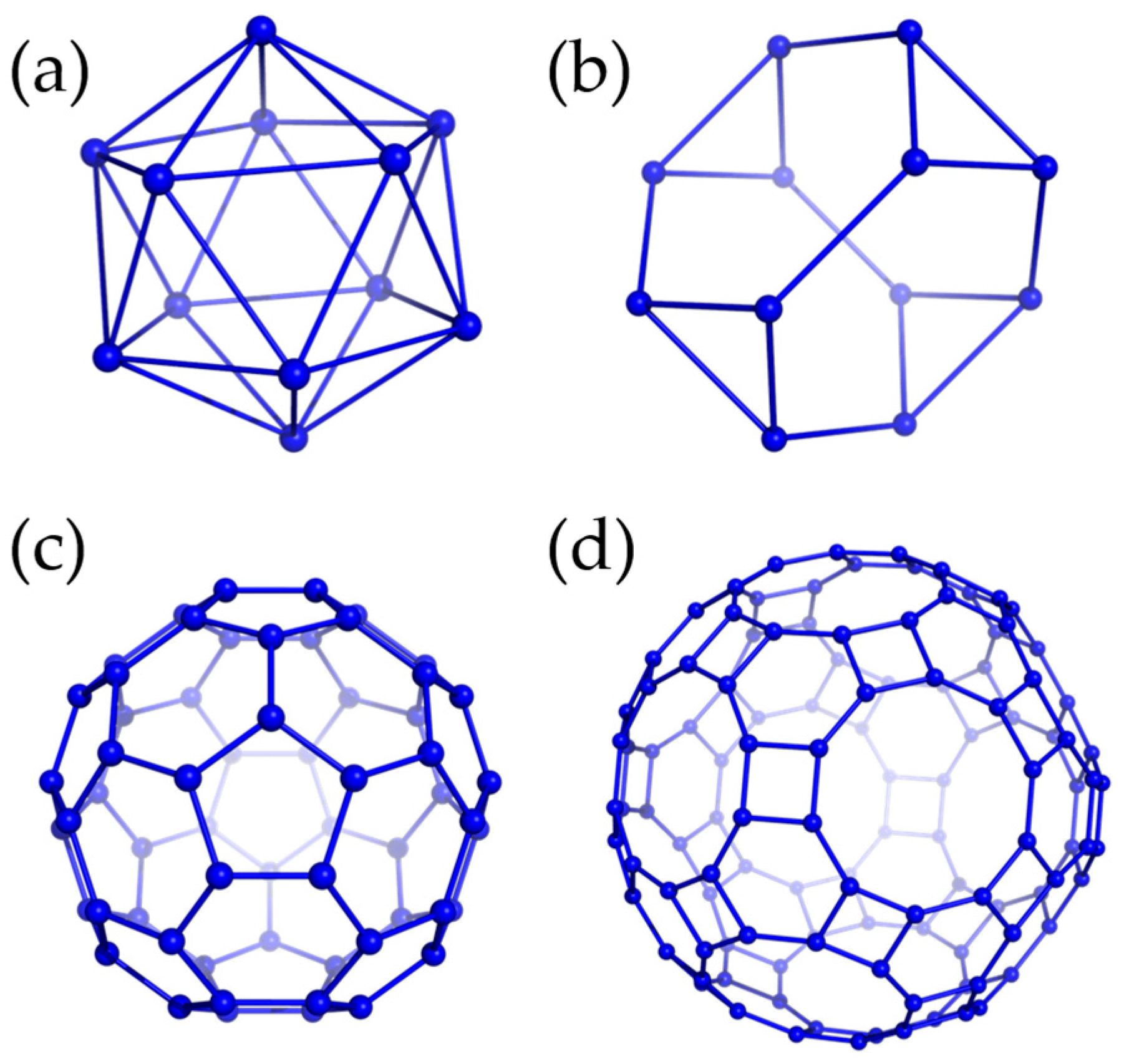
3.3. Polyhedra
- (a)
- Icosahedron
- (b)
- Truncated Tetrahedron
- (c)
- Truncated Icosahedron
- (d)
- Truncated icosidodecahedron
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Optimization of the Broken-Symmetry Reference


Appendix B. Spin-Pair Correlation Functions (SPCFs)
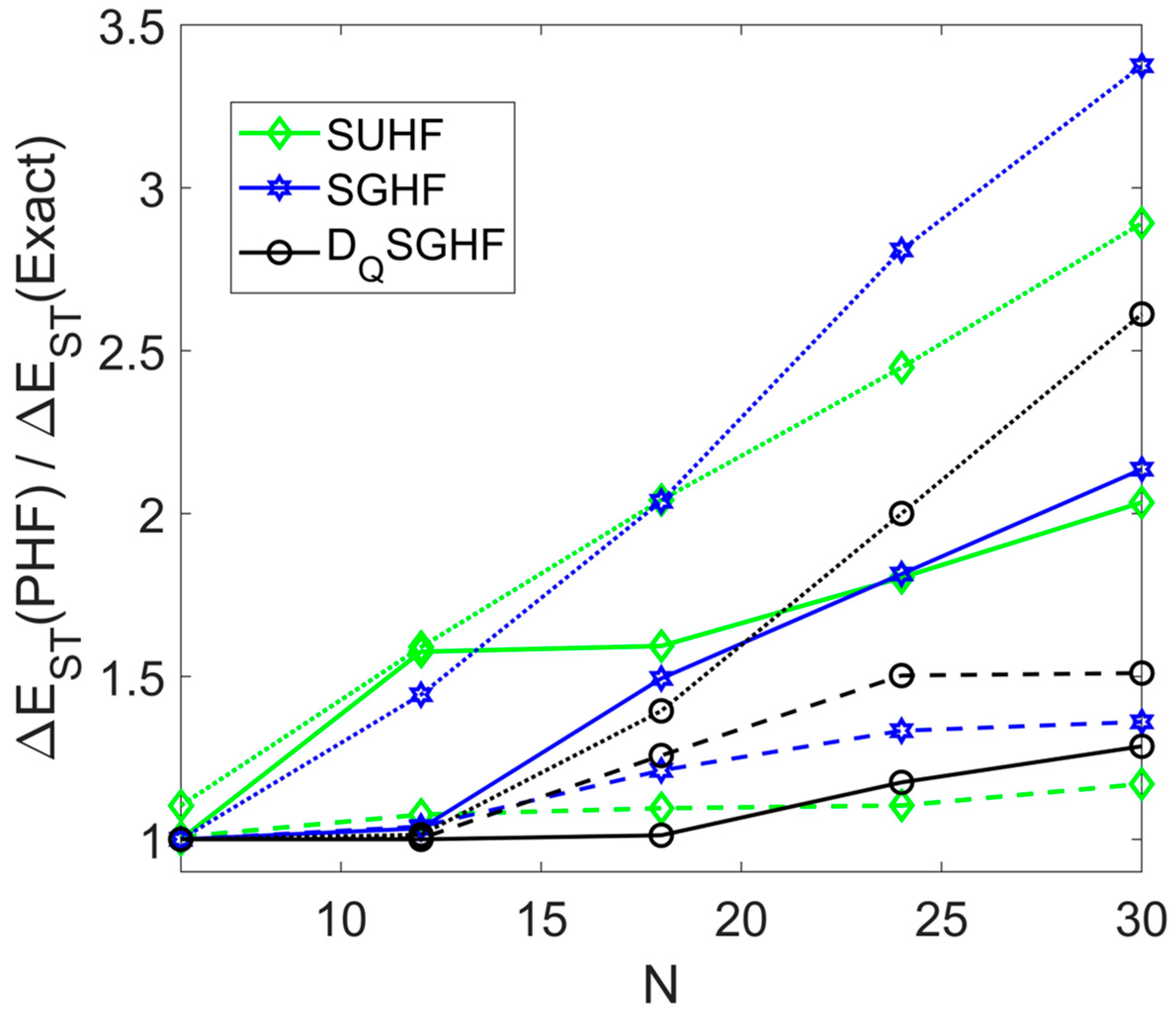
Appendix C. Reference Energies for Spin Rings
| N | ||||||
|---|---|---|---|---|---|---|
| q | 6 | 12 | 18 | 24 | 30 | |
| 2 | −2.6514 | −4.8770 | −7.1335 | −9.3914 | −11.6485 | |
| −1.8956 | −4.3114 | −6.6414 | −8.9434 | −11.2237 | ||
| 0.756 | 0.566 | 0.492 | 0.448 | 0.425 | ||
| 6 | −2.8028 | −5.3482 | −7.7332 | −10.2071 | −12.6941 | |
| −2.1180 | −4.7874 | −7.3492 | −9.8772 | −12.3954 | ||
| 0.685 | 0.561 | 0.384 | 0.330 | 0.299 | ||
| Exact | −2.803 | −5.387 | −8.023 | −10.670 | −13.322 | |
| Exact | 0.685 | 0.356 | 0.241 | 0.183 | 0.147 | |
| N | ||||||
|---|---|---|---|---|---|---|
| q | 6 | 12 | 18 | 24 | 30 | |
| 2 | −2.8028 | −5.0625 | −7.3603 | −9.6589 | −11.9416 | |
| −2.1180 | −4.5485 | −6.8696 | −9.1446 | −11.4453 | ||
| 0.685 | 0.514 | 0.491 | 0.514 | 0.496 | ||
| 6 | −2.8028 | −5.3768 | −7.9641 | −10.4728 | −12.9231 | |
| −2.1180 | −5.0090 | −7.6042 | −10.1411 | −12.6090 | ||
| 0.685 | 0.368 | 0.360 | 0.332 | 0.314 | ||
| Exact | −2.803 | −5.387 | −8.023 | −10.670 | −13.322 | |
| Exact | 0.685 | 0.356 | 0.241 | 0.183 | 0.147 | |
| N | ||||||
|---|---|---|---|---|---|---|
| q | 6 | 12 | 18 | 24 | 30 | |
| 2 | −2.8028 | −5.3710 | −7.8905 | −10.3945 | −12.8677 | |
| −2.1180 | −5.0104 | −7.5544 | −10.0287 | −12.4834 | ||
| 0.685 | 0.361 | 0.336 | 0.366 | 0.384 | ||
| 6 | −2.8028 | −5.3874 | −8.0224 | −10.6501 | −13.2762 | |
| −2.1180 | −5.0315 | −7.7782 | −10.4356 | −13.0870 | ||
| 0.685 | 0.356 | 0.244 | 0.215 | 0.189 | ||
| Exact | −2.803 | −5.387 | −8.023 | −10.670 | −13.322 | |
| Exact | 0.685 | 0.356 | 0.241 | 0.183 | 0.147 | |
References
- Bencini, A.; Gatteschi, D. Electron Paramagnetic Resonance of Exchange Coupled Systems; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Schnack, J. Large Magnetic Molecules and What We Learn from Them. Contemp. Phys. 2019, 60, 127. [Google Scholar] [CrossRef]
- Ghassemi Tabrizi, S.; Arbuznikov, A.; Kaupp, M. Understanding Thermodynamic and Spectroscopic Properties of Tetragonal Mn12 Single-Molecule Magnets from Combined Density Functional Theory/Spin-Hamiltonian Calculations. J. Phys. Chem. A 2016, 120, 6864. [Google Scholar] [CrossRef] [PubMed]
- White, S.R. Density Matrix Formulation for Quantum Renormalization Groups. Phys. Rev. Lett. 1992, 69, 2863. [Google Scholar] [CrossRef]
- Jiménez-Hoyos, C.A.; Henderson, T.M.; Tsuchimochi, T.; Scuseria, G.E. Projected Hartree–Fock Theory. J. Chem. Phys. 2012, 136, 164109. [Google Scholar] [CrossRef]
- Ghassemi Tabrizi, S.; Jiménez-Hoyos, C.A. Ground States of Heisenberg Spin Clusters from Projected Hartree–Fock Theory. Phys. Rev. B 2022, 105, 35147. [Google Scholar] [CrossRef]
- Mayer, I. The Spin-Projected Extended Hartree–Fock Method. Adv. Quant. Chem. 1980, 12, 189. [Google Scholar]
- Jiménez-Hoyos, C.A.; Rodríguez-Guzmán, R.; Scuseria, G.E. Multi-Component Symmetry-Projected Approach for Molecular Ground State Correlations. J. Chem. Phys. 2013, 139, 204102. [Google Scholar] [CrossRef]
- Papastathopoulos-Katsaros, A.; Jiménez-Hoyos, C.A.; Henderson, T.M.; Scuseria, G.E. Coupled Cluster and Perturbation Theories Based on a Cluster Mean-Field Reference Applied to Strongly Correlated Spin Systems. J. Chem. Theory Comput. 2022, 18, 4293. [Google Scholar] [CrossRef]
- Potthoff, M. Cluster Extensions of Dynamical Mean-Field Theory. In DMFT: From Infinite Dimensions to Real Materials; Pavarini, E., Kock, E., Lichtenstein, A., Vollhardt, D., Eds.; Forschungszentrum Jülich GmbH: Jülich, Germany, 2018. [Google Scholar]
- Waldmann, O. Symmetry and Energy Spectrum of High-Nuclearity Spin Clusters. Phys. Rev. B 2000, 61, 6138. [Google Scholar] [CrossRef]
- Schmid, K.W.; Dahm, T.; Margueron, J.; Müther, H. Symmetry-Projected Variational Approach to the One-Dimensional Hubbard Model. Phys. Rev. B 2005, 72, 85116. [Google Scholar] [CrossRef]
- Tinkham, M. Group Theory and Quantum Mechanics; McGraw-Hill: New York, NY, USA, 1964. [Google Scholar]
- Percus, J.K.; Rotenberg, A. Exact Eigenfunctions of Angular Momentum by Rotational Projection. J. Math. Phys. 1962, 3, 928. [Google Scholar] [CrossRef]
- Ren, Y.-Z.; Tong, N.-H.; Xie, X.-C. Cluster Mean-Field Theory Study of J1 − J2 Heisenberg Model on a Square Lattice. J. Phys. Condens. Matter 2014, 26, 115601. [Google Scholar] [CrossRef] [PubMed]
- Jiménez-Hoyos, C.A.; Henderson, T.M.; Scuseria, G.E. Generalized Hartree–Fock Description of Molecular Dissociation. J. Chem. Theory Comput. 2011, 7, 2667. [Google Scholar] [CrossRef] [PubMed]
- Hendeković, J. Method of Complex Molecular Orbitals. Int. J. Quantum Chem. 1974, 8, 799. [Google Scholar] [CrossRef]
- Jiménez-Hoyos, C.A.; Rodríguez-Guzmán, R.; Scuseria, G.E. N-Electron Slater Determinants from Nonunitary Canonical Transformations of Fermion Operators. Phys. Rev. A 2012, 86, 52102. [Google Scholar] [CrossRef]
- Ghassemi Tabrizi, S.; Arbuznikov, A.; Jiménez-Hoyos, C.A.; Kaupp, M. Hyperfine-Coupling Tensors from Projected Hartree–Fock Theory. J. Chem. Theory Comput. 2020, 16, 6222. [Google Scholar] [CrossRef] [PubMed]
- Lestrange, P.J.; Williams-Young, D.B.; Petrone, A.; Jiménez-Hoyos, C.A.; Li, X. Efficient Implementation of Variation after Projection Generalized Hartree–Fock. J. Chem. Theory Comput. 2018, 14, 588. [Google Scholar] [CrossRef] [PubMed]
- Jiménez-Hoyos, C.A. Variational Approaches to the Molecular Electronic Structure Problem Based on Symmetry-Projected Hartree–Fock Configurations. Ph.D. Thesis, Rice University, Houston, TX, USA, 2013. [Google Scholar]
- Jiménez-Hoyos, C.A.; Rodríguez-Guzmán, R.R.; Henderson, T.M.; Scuseria, G.E. On a Dual Representation of the Goldstone Manifold. arXiv 2020, arXiv:2004.05047. [Google Scholar]
- Schurkus, H.F.; Chen, D.; O’Rourke, M.J.; Cheng, H.-P.; Chan, G.K.-L. Exploring the Magnetic Properties of the Largest Single-Molecule Magnets. J. Phys. Chem. Lett. 2020, 11, 3789. [Google Scholar] [CrossRef]
- Lebedev, V.I.; Laikov, D.N. A Quadrature Formula for the Sphere of the 131st Algebraic Order of Accuracy. Dokl. Math. 1999, 59, 477. [Google Scholar]
- Rivero, P.; Jiménez-Hoyos, C.A.; Scuseria, G.E. Entanglement and Polyradical Character of Polycyclic Aromatic Hydrocarbons Predicted by Projected Hartree–Fock Theory. J. Phys. Chem. B 2013, 117, 12750. [Google Scholar] [CrossRef] [PubMed]
- Heitmann, T.; Schnack, J. Combined Use of Translational and Spin-Rotational Invariance for Spin Systems. Phys. Rev. B 2019, 99, 134405. [Google Scholar] [CrossRef]
- Ummethum, J.; Nehrkorn, J.; Mukherjee, S.; Ivanov, N.B.; Stuiber, S.; Strässle, T.; Tregenna-Piggott, P.L.W.; Mutka, H.; Christou, G.; Waldmann, O.; et al. Discrete Antiferromagnetic Spin-Wave Excitations in the Giant Ferric Wheel Fe18. Phys. Rev. B 2012, 86, 104403. [Google Scholar] [CrossRef]
- Szabo, A.; Ostlund, N.S. Modern Quantum Chemistry; Dover Publications, Courier Corporation: Chelmsford, MA, USA, 1996. [Google Scholar]
- Coffey, D.; Trugman, S.A. Magnetic Properties of Undoped. C60 Phys. Rev. Lett. 1992, 69, 176. [Google Scholar] [CrossRef]
- Jiménez-Hoyos, C.A.; Scuseria, G.E. Cluster-Based Mean-Field and Perturbative Description of Strongly Correlated Fermion Systems: Application to the One-and Two-Dimensional Hubbard Model. Phys. Rev. B 2015, 92, 85101. [Google Scholar] [CrossRef]
- Schnack, J. Properties of the First Excited State of Nonbipartite Heisenberg Spin Rings. Phys. Rev. B 2000, 62, 14855. [Google Scholar] [CrossRef]
- Ummethum, J. Calculation of Static and Dynamical Properties of Giant Magnetic Molecules Using DMRG. Ph.D. Thesis, Bielefeld University, Bielefeld, Germany, 2012. [Google Scholar]
- Schnack, J. Effects of Frustration on Magnetic Molecules: A Survey from Olivier Kahn until Today. Dalt. Trans. 2010, 39, 4677. [Google Scholar] [CrossRef]
- Clar, E. The Aromatic Sextet and its Significance in Relation to the Stability of Aromatic Systems. In Polycyclic Hydrocarbons; Springer: Berlin/Heidelberg, Germany, 1964; pp. 32–39. [Google Scholar]
- Schmidt, H.-J.; Luban, M. Classical Ground States of Symmetric Heisenberg Spin Systems. J. Phys. A. Math. Gen. 2003, 36, 6351. [Google Scholar] [CrossRef]
- Coffey, D.; Trugman, S.A. Correlations for the S = 1/2 Antiferromagnet on a Truncated Tetrahedron. Phys. Rev. B 1992, 46, 12717. [Google Scholar] [CrossRef]
- Müller, A.; Todea, A.M.; van Slageren, J.; Dressel, M.; Bögge, H.; Schmidtmann, M.; Luban, M.; Engelhardt, L.; Rusu, M. Triangular Geometrical and Magnetic Motifs Uniquely Linked on a Spherical Capsule Surface. Angew. Chem. 2005, 117, 3925. [Google Scholar] [CrossRef]
- Botar, B.; Kögerler, P.; Hill, C.L. [{(Mo)Mo5O21(H2O)3(SO4)}12(VO)30(H2O)20]36−: A Molecular Quantum Spin Icosidodecahedron. Chem. Commun. 2005, 3138–3140. [Google Scholar] [CrossRef] [PubMed]
- Todea, A.M.; Merca, A.; Bögge, H.; Glaser, T.; Engelhardt, L.; Prozorov, R.; Luban, M.; Müller, A. Polyoxotungstates Now Also with Pentagonal Units: Supramolecular Chemistry and Tuning of Magnetic Exchange in {(M)M5}12V30 Keplerates (M = Mo, W). Chem. Commun. 2009, 3351–3353. [Google Scholar] [CrossRef]
- Todea, A.M.; Merca, A.; Boegge, H.; van Slageren, J.; Dressel, M.; Engelhardt, L.; Luban, M.; Glaser, T.; Henry, M.; Mueller, A. Extending the {(Mo)Mo5}12M30 Capsule Keplerate Sequence: A {Cr30} Cluster of S = 3/2 Metal Centers with a {Na(H2O)12} Encapsulate. Angew. Chemie Int. Ed. 2007, 46, 6106. [Google Scholar] [CrossRef] [PubMed]
- Müller, A.; Sarkar, S.; Shah, S.Q.N.; Bögge, H.; Schmidtmann, M.; Sarkar, S.; Kögerler, P.; Hauptfleisch, B.; Trautwein, A.X.; Schünemann, V. Archimedean Synthesis and Magic Numbers: “Sizing” Giant Molybdenum-Oxide-Based Molecular Spheres of the Keplerate Type. Angew. Chemie Int. Ed. 1999, 38, 3238. [Google Scholar] [CrossRef]
- Müller, A.; Luban, M.; Schröder, C.; Modler, R.; Kögerler, P.; Axenovich, M.; Schnack, J.; Canfield, P.; Bud’ko, S.; Harrison, N. Classical and Quantum Magnetism in Giant Keplerate Magnetic Molecules. ChemPhysChem 2001, 2, 517. [Google Scholar] [CrossRef]
- Krivnov, V.Y.; Shamovsky, I.L.; Tornau, E.E.; Rosengren, A. Electronic Correlation Effects in a Fullerene Molecule Studied by the Variational Monte Carlo Method. Phys. Rev. B 1994, 50, 12144. [Google Scholar] [CrossRef]
- Sheng, D.N.; Weng, Z.Y.; Ting, C.S.; Dong, J.M. Magnetism and Pairing in a C60 Molecule: A Variational Monte Carlo Study. Phys. Rev. B 1994, 49, 4279. [Google Scholar] [CrossRef]
- Flocke, N.; Schmalz, T.G.; Klein, D.J. Variational Resonance Valence Bond Study on the Ground State of C60 Using the Heisenberg Model. J. Chem. Phys. 1998, 109, 873. [Google Scholar] [CrossRef]
- Konstantinidis, N.P. Unconventional Magnetic Properties of the Icosahedral Symmetry Antiferromagnetic Heisenberg Model. Phys. Rev. B 2007, 76, 104434. [Google Scholar] [CrossRef]
- Rausch, R.; Plorin, C.; Peschke, M. The Antiferromagnetic S = 1/2 Heisenberg Model on the C60 Fullerene Geometry. SciPost Phys. 2021, 10, 87. [Google Scholar] [CrossRef]
- Ghassemi Tabrizi, S. Point-Group Selection Rules and Universal Momentum-Transfer Dependencies for Inelastic Neutron Scattering on Molecular Spin Clusters. Phys. Rev. B 2021, 103, 214422. [Google Scholar] [CrossRef]
- Ghassemi Tabrizi, S. Symmetry-Induced Universal Momentum-Transfer Dependencies for Inelastic Neutron Scattering on Anisotropic Spin Clusters. Phys. Rev. B 2021, 104, 14416. [Google Scholar] [CrossRef]
- Jiménez-Hoyos, C.A.; Rodríguez-Guzmán, R.; Scuseria, G.E. Polyradical Character and Spin Frustration in Fullerene Molecules: An Ab Initio Non-Collinear Hartree–Fock Study. J. Phys. Chem. A 2014, 118, 9925. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Head-Gordon, M. Distinguishing Artificial and Essential Symmetry Breaking in a Single Determinant: Approach and Application to the C60, C36, and C20 Fullerenes. Phys. Chem. Chem. Phys. 2019, 21, 4763. [Google Scholar] [CrossRef] [PubMed]
- Altmann, S.L.; Herzig, P. Point-Group Theory Tables; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Sakurai, J.J. Modern Quantum Mechanics, 2nd ed.; Tuan, S.F., Ed.; Addison Wesley: Reading, MA, USA, 1993. [Google Scholar]
- Brown, H.A. A Simple Derivation of the Spin-Exchange Operator. Am. J. Phys. 1972, 40, 1696. [Google Scholar] [CrossRef]
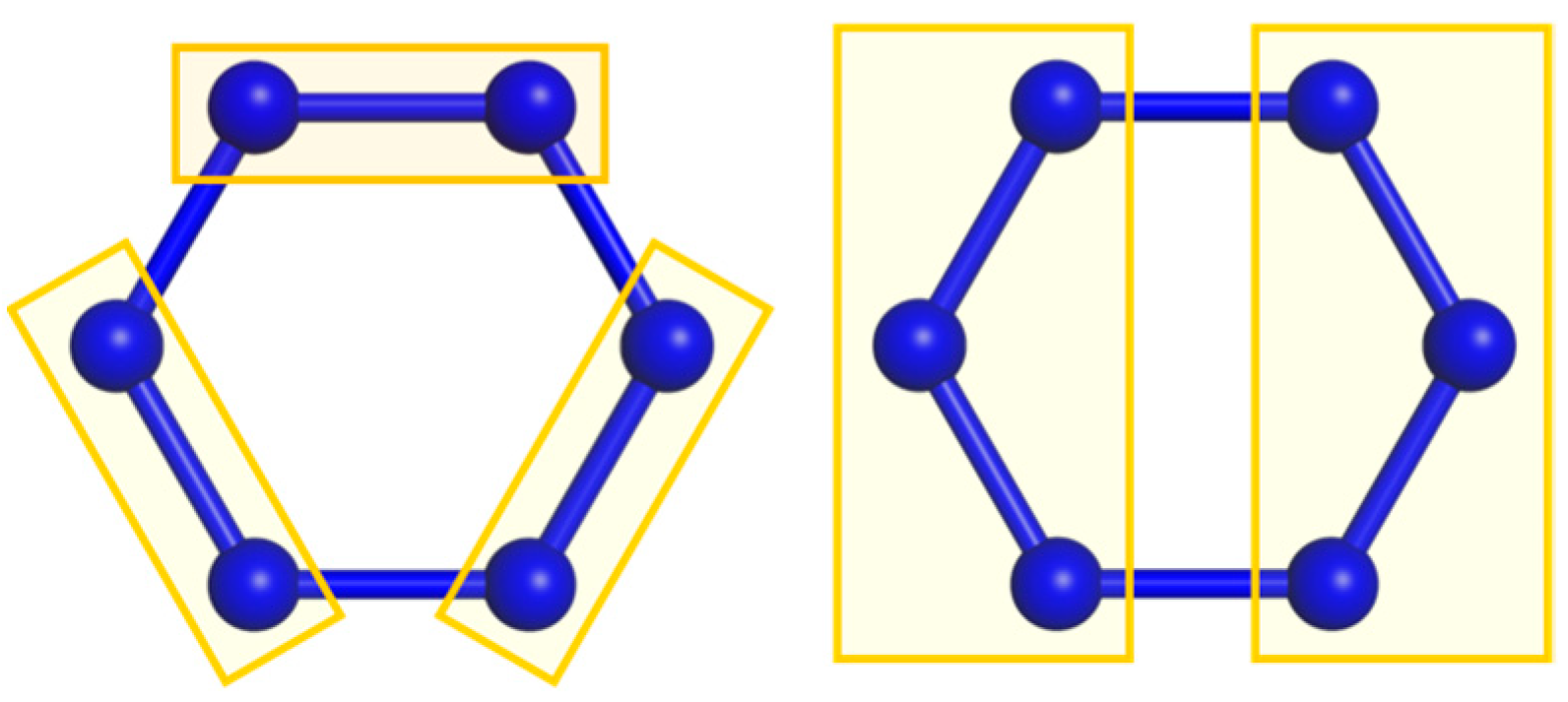
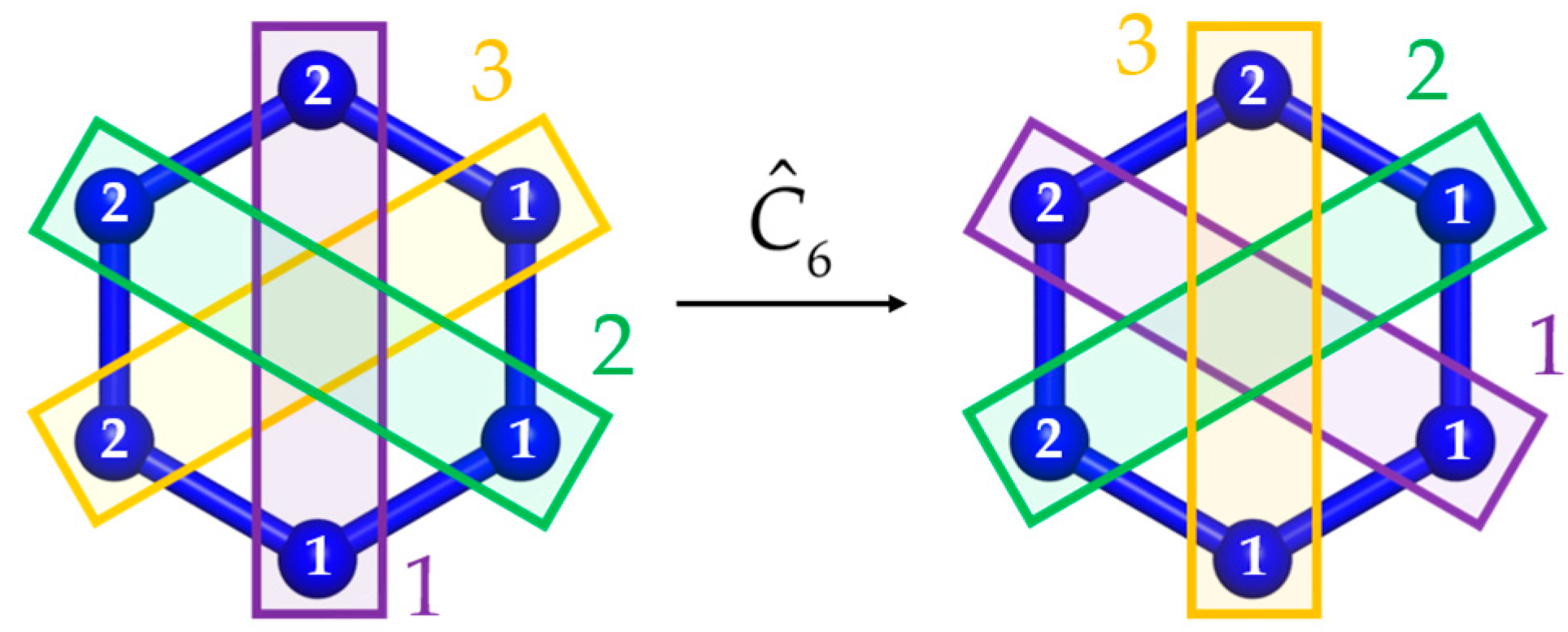
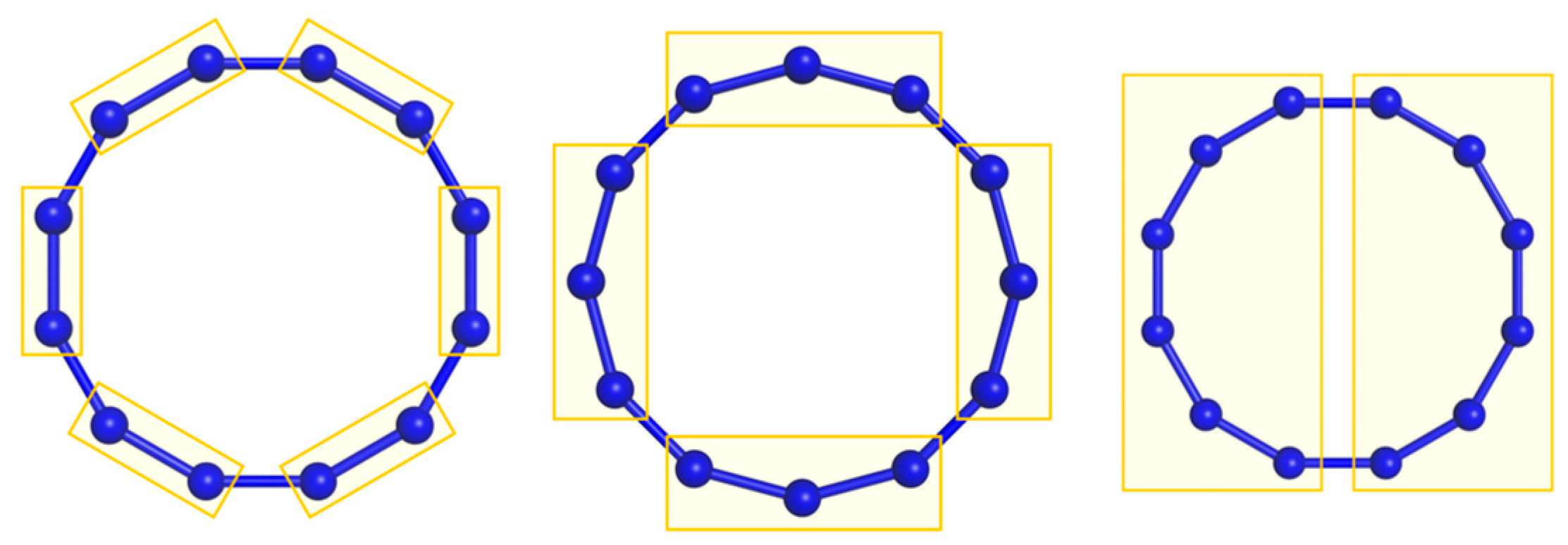



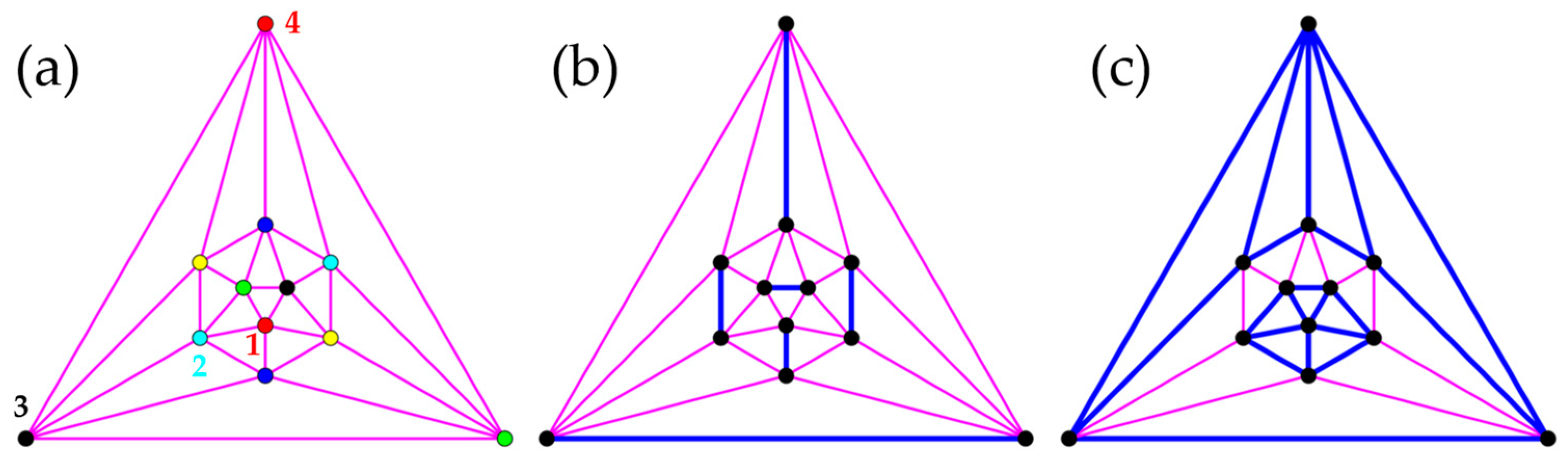
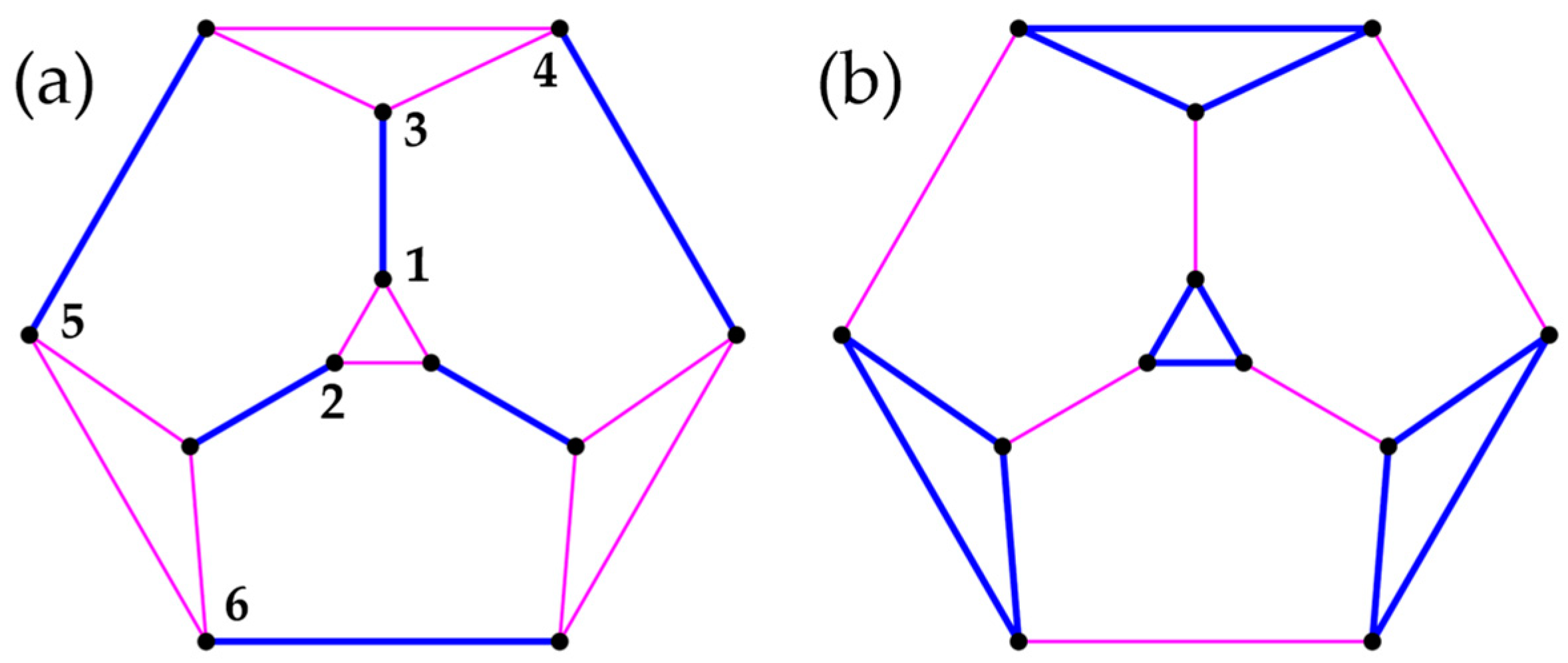
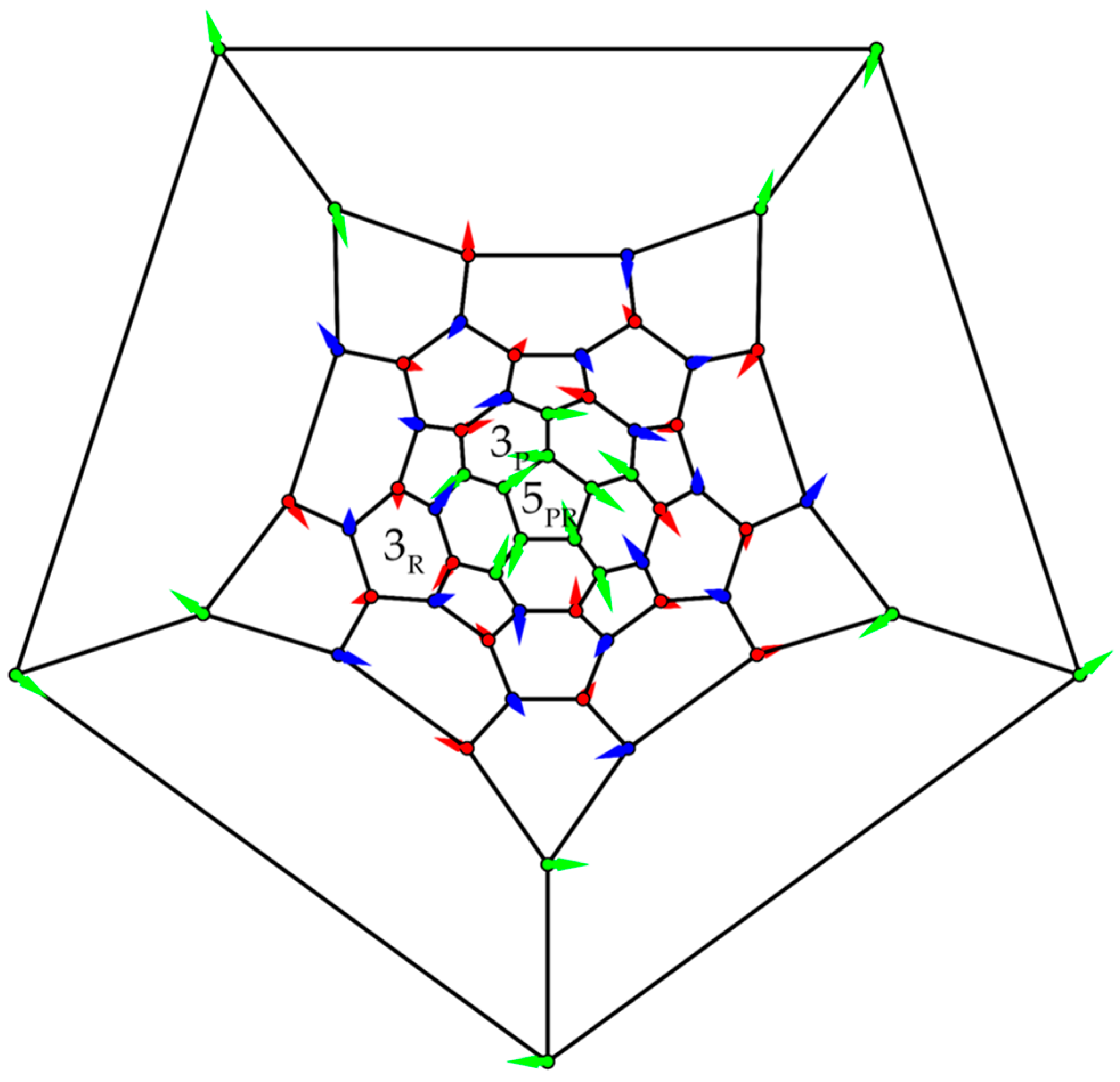
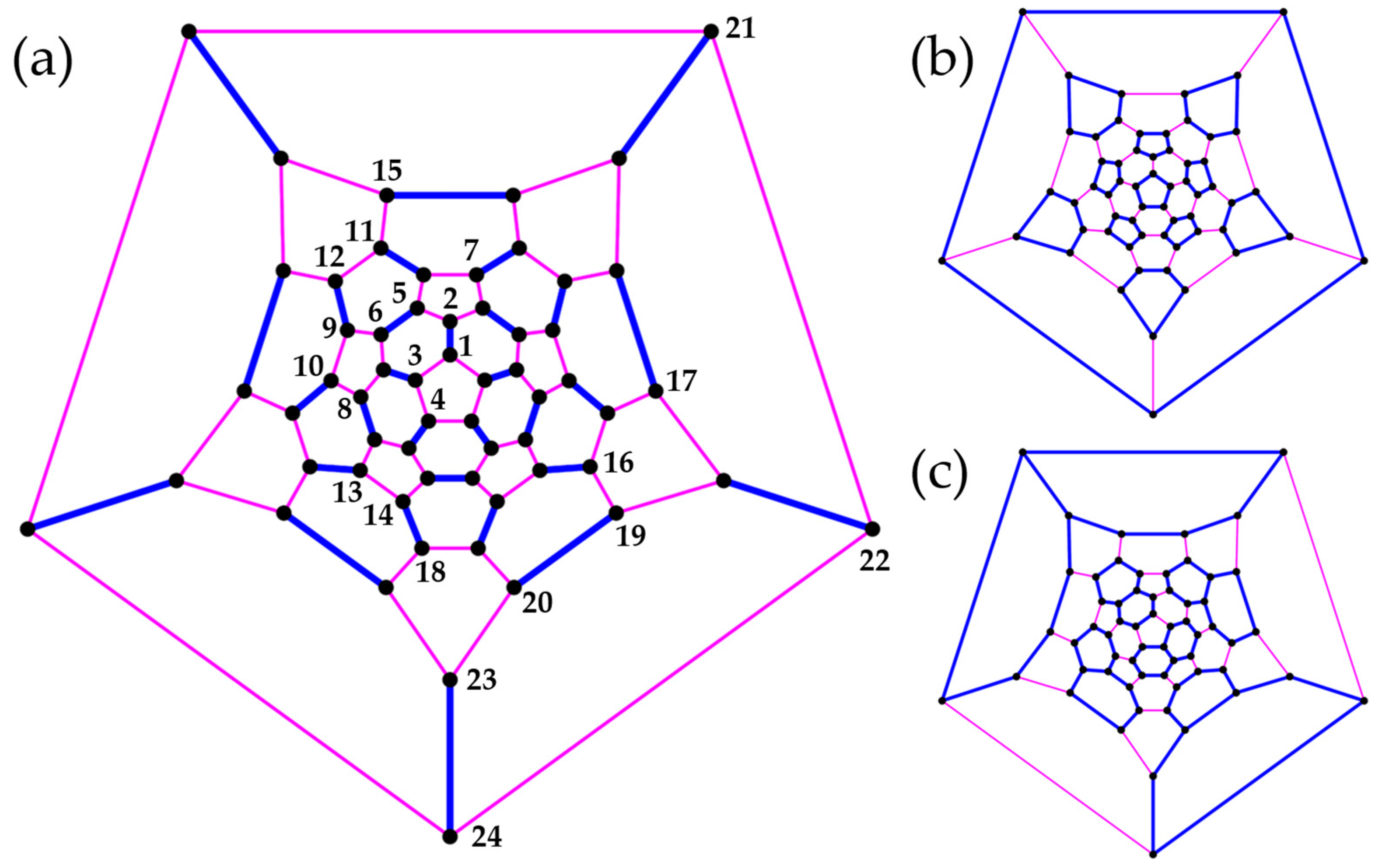
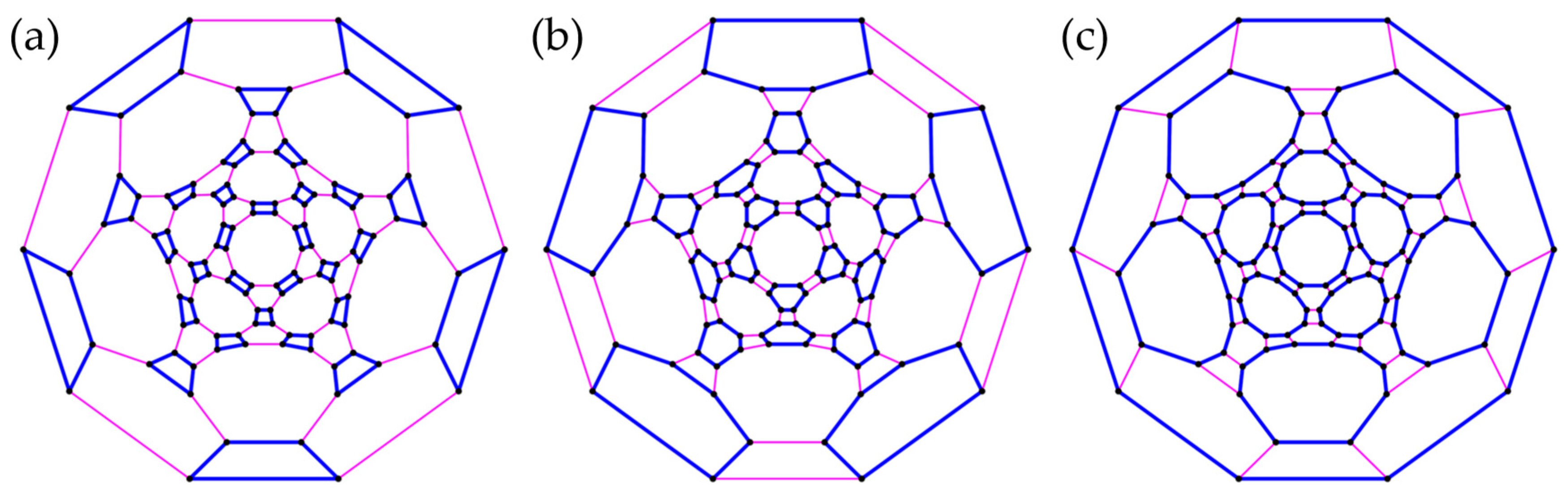
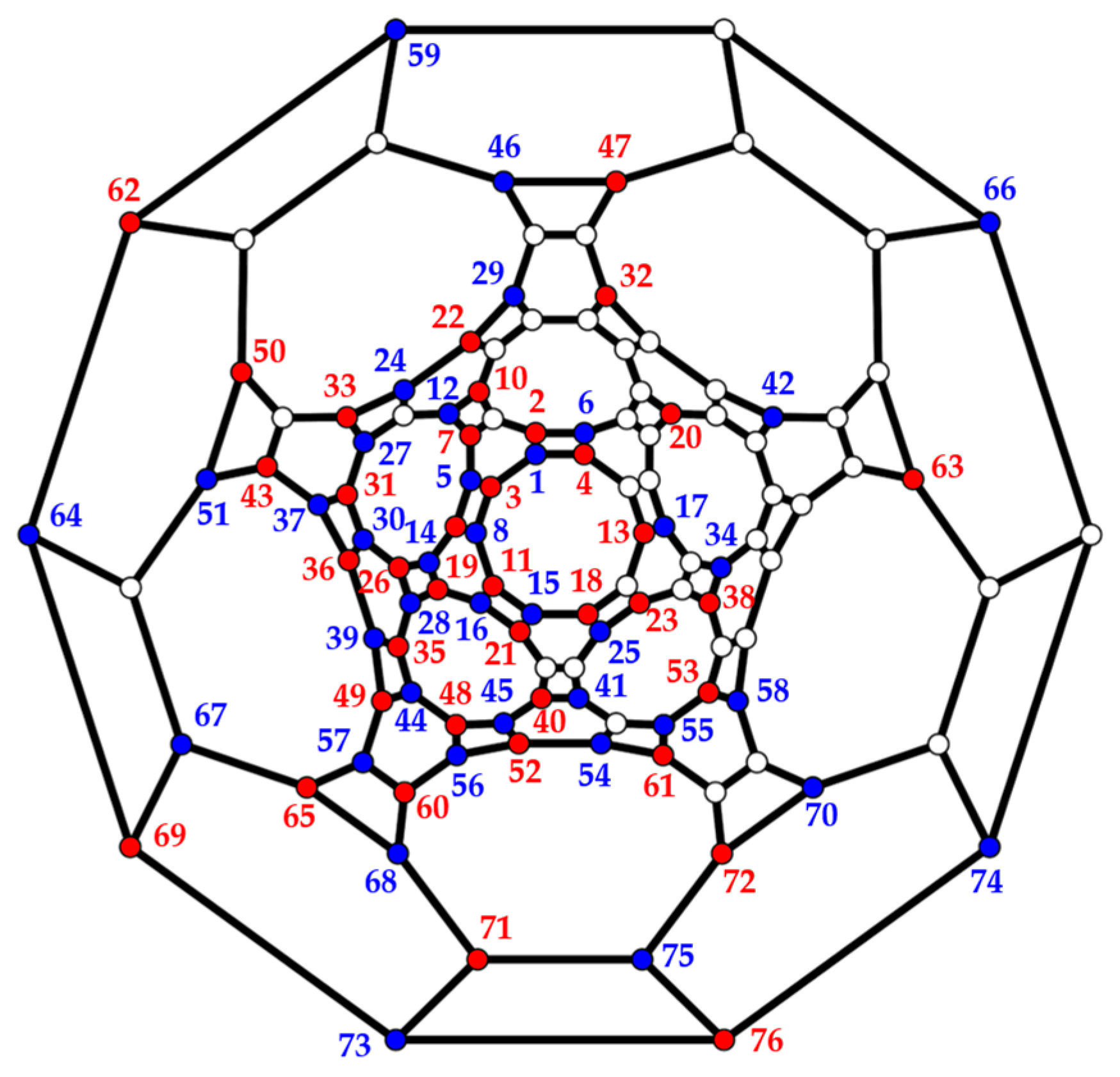

| q even | q odd | q even | q odd | q even | q odd | q even | q odd |
| A2 | B1 | A1 | A1 | A1 | A1 | A2 | B1 |
| System | Grouping (q, Bonds) a | UHF | SGHF | PT2 | Exact | |
|---|---|---|---|---|---|---|
| Triphenylene | a (3, 12) | −7.2753 | −8.2062 | −8.6556 (A2) | −8.6445 | −8.7697 |
| b (6, 15) | −7.5804 | −8.4865 | −8.7342 (A2) | −7.8205 | ||
| c (6, 18) | −8.4083 | −8.7556 | −8.7696 (A2) | −8.6640 | ||
| d (2, 9) | −7.0229 | −8.0255 | −8.5364 (A2) | −8.2068 | ||
| e (2, 9) | −6.9584 | −7.8672 | −8.4093 (A2) | −8.1914 | ||
| Coronene | a (4, 24) | −10.2764 | −11.2733 | −11.7966 (A) | −11.4628 | −11.9755 |
| b (4, 18) | −9.7660 | −10.7447 | −11.6399 (A1) | −11.3781 | ||
| c (6, 21) | −10.5736 | −11.3457 | −11.8103 (A1) | −11.3740 | ||
| d (8, 24) | −10.8304 | −11.6961 | −11.9459 (A1) | −11.4992 | ||
| e (2, 12) | −9.5702 | −10.6676 | −11.2997 (A1) | −11.3109 | ||
| f (2, 12) | −9.6055 | −10.7084 | −11.6190 (A1) | −11.3968 | ||
| g (6, 18) | −9.9867 | −10.9182 | −11.6693 (A1) | −11.1837 | ||
| h (6, 12) | −9.4117 | −11.1230 | −11.8635 (A1) | −11.1287 | ||
| Hexabenzo- coronene | a (6, 42) | −19.8044 | −20.4297 | −21.0044 (B1) | −20.7082 | – b |
| b (7, 42) | −19.6337 | −20.4824 | −21.0786 (B1) | −20.7724 | ||
| Hexa-cata-hexabenzo-coronene | a (6, 42) | −21.5999 | −23.0983 | −23.8296 (A1) | −23.1753 | – b |
| b (8, 48) | −22.4271 | −23.3169 | −23.7980 (A) | −23.4848 | ||
| c (8, 42) | −21.1057 | −21.9885 | −23.0109 (A1) | −23.0836 | ||
| Kekulene | a (6, 48) | −21.4983 | −22.2249 | −22.7387 (A1) | −22.9403 | – b |
| b (6, 36) | −19.8349 | −20.9791 | −22.4499 (A1) | −22.2943 | ||
| c (8, 48) | −21.4735 | −22.2083 | −23.0747 (A1) | −22.9187 | ||
| d (8, 48) | −22.1306 | −22.7459 | −23.3603 (A) | −23.2404 |
| i–j | Exact | ||||
|---|---|---|---|---|---|
| 1–2 | −0.33729 | −0.35059 | −0.39063 | −0.36850 | −0.35875 |
| 2–3 | −0.33729 | −0.35059 | −0.38706 | −0.33627 | −0.35875 |
| 1–4 | −0.40404 | −0.35322 | −0.30621 | −0.37926 | −0.37507 |
| 4–5 | −0.37034 | −0.40476 | −0.37196 | −0.37095 | −0.36665 |
| 5–6 | −0.54911 | −0.42665 | −0.52422 | −0.52685 | −0.52881 |
| 6–7 | −0.30533 | −0.40476 | −0.37196 | −0.37095 | −0.36665 |
| 7–8 | −0.37034 | −0.40476 | −0.41287 | −0.36483 | −0.36665 |
| 8–9 | −0.54911 | −0.42665 | −0.45278 | −0.52027 | −0.52881 |
| (1–3) | 0.17744 | 0.19472 | 0.19503 | 0.16792 | 0.16641 |
| (1–5) | 0.18265 | 0.20098 | 0.16410 | 0.17971 | 0.17661 |
| (2–6) | 0.18009 | 0.20098 | 0.16410 | 0.17971 | 0.17661 |
| (4–6) | 0.20777 | 0.18967 | 0.19643 | 0.19440 | 0.19291 |
| (5–7) | 0.17515 | 0.18967 | 0.19643 | 0.19440 | 0.19291 |
| s | ||||
|---|---|---|---|---|
| 1/2 | Exact | −0.2063 | 0.0841 | −0.1397 |
| PHF | −0.2063 | 0.0841 | −0.1397 | |
| 1 | Exact | −0.6187 | 0.3680 | −0.7463 |
| PHF | −0.6187 | 0.3680 | −0.7464 | |
| 3/2 | Exact | −1.2580 | 0.9060 | −1.9899 |
| PHF | −1.2580 | 0.9062 | −1.9910 | |
| 2 | Exact | −2.1237 | 1.6616 | −3.6897 |
| PHF | −2.1236 | 1.6621 | −3.6926 |
| s | Grouping | GHF | SGHF | PGSGHF | |
|---|---|---|---|---|---|
| 1/2 | −4.5000 | −5.3224 | −6.1717 | −6.1879 (Au) | |
| −3.3541 | −5.7644 | −6.1879 a | |||
| 1 | −14.3025 | −17.4565 | −18.1678 | −18.5611 (Ag) | |
| −13.4164 | −18.2225 | −18.5609 | |||
| 3/2 | −31.4256 | −36.2633 | −37.3073 | −37.7412 (Au) | |
| −30.1869 | −37.3842 | −37.7396 | |||
| 2 | −55.2658 | −61.7751 | −63.1481 | −63.7104 (Ag) | |
| −53.6656 | −63.2529 | −63.7075 |
| s | q | GHF | SGHF | TdSGHF | |
|---|---|---|---|---|---|
| 1/2 | 2 | −4.5000 | −5.2700 | −5.7009 a | −5.7009 (A2) |
| 3 | −3.8881 | −4.8147 | −5.7009 a | ||
| 1 | 2 | −14.0173 | −16.0342 | −17.1649 | −17.1955 (A1) |
| 3 | −13.8696 | −15.7195 | −17.1775 | ||
| 3/2 | 2 | −29.7756 | −32.8938 | −34.4456 | −34.6402 (A2) |
| 3 | −29.6977 | −32.5614 | −34.4796 | ||
| 2 | 2 | −51.5616 | −55.7815 | −57.7827 | −58.1140 (A1) |
| 3 | −51.5327 | −55.3924 | −57.8181 |
| q | GHF | SGHF | PGSGHF a |
|---|---|---|---|
| 2 | −24.2705 | −25.5486 | −27.8429 |
| 5 | −25.8525 | −26.6072 | −28.5653 |
| 10 | −28.6199 b | −29.2195 | −29.9842 |
| q = 2 | q = 5 | ||||
|---|---|---|---|---|---|
| E | −25.5486 | −27.8429 | −26.6072 | −28.5653 | −30.69 |
| j | SGHF | SGHF | VMC | ||
| 2 | −0.562 | −0.610 | −0.186 | −0.277 | −0.529 |
| 3 | −0.145 | −0.159 | −0.351 | −0.337 | −0.247 |
| 4 | 0.051 | 0.051 | 0.076 | 0.073 | 0.030 |
| 5 | 0.136 | 0.137 | 0.142 | 0.154 | 0.141 |
| 6 | −0.145 | −0.154 | −0.151 | −0.154 | −0.142 |
| 7 | −0.056 | −0.054 | −0.059 | −0.061 | −0.023 |
| 8 | −0.090 | −0.080 | −0.094 | −0.093 | −0.038 |
| 9 | 0.084 | 0.070 | 0.087 | 0.083 | 0.031 |
| 10 | −0.002 | 0.001 | −0.003 | −0.001 | 0.001 |
| 11 | 0.051 | 0.049 | 0.052 | 0.051 | 0.027 |
| 12 | −0.090 | −0.072 | −0.094 | −0.088 | −0.026 |
| 13 | −0.090 | −0.042 | −0.094 | −0.084 | −0.002 |
| 14 | 0.051 | 0.017 | 0.052 | 0.046 | −0.001 |
| 15 | −0.002 | −0.002 | −0.003 | −0.003 | −0.004 |
| 16 | 0.084 | 0.037 | 0.087 | 0.078 | 0.001 |
| 17 | −0.090 | −0.036 | −0.094 | −0.081 | 0.002 |
| 18 | −0.056 | −0.018 | −0.059 | −0.051 | 0.013 |
| 19 | −0.145 | −0.042 | −0.151 | −0.129 | 0.000 |
| 20 | 0.136 | 0.039 | 0.142 | 0.124 | −0.002 |
| 21 | 0.051 | 0.016 | 0.053 | 0.046 | −0.030 |
| 22 | −0.145 | −0.040 | −0.150 | −0.128 | 0.007 |
| 23 | −0.179 | −0.046 | −0.186 | −0.158 | 0.016 |
| 24 | 0.168 | 0.044 | 0.176 | 0.152 | −0.008 |
| s | GHF (2) | SGHF (2) | IhSGHF (2) | PT2 (1) | PT2 (2) | |
|---|---|---|---|---|---|---|
| 1/2 | −24.2705 | −25.5486 | −27.8429 | −28.6199 | −31.0543 | −29.1216 |
| 1 | −85.6371 | −87.7764 | −90.1147 | −89.8943 | −96.7113 | −96.9910 |
| 3/2 | −186.6961 | −189.5706 | −192.4293 | −183.7630 | −202.2428 | −203.7112 |
| 2 | −327.0802 | −330.4438 | −343.1173 | −310.5941 | −347.1526 | −349.5852 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghassemi Tabrizi, S.; Jiménez-Hoyos, C.A. Ground States of Heisenberg Spin Clusters from a Cluster-Based Projected Hartree–Fock Approach. Condens. Matter 2023, 8, 18. https://doi.org/10.3390/condmat8010018
Ghassemi Tabrizi S, Jiménez-Hoyos CA. Ground States of Heisenberg Spin Clusters from a Cluster-Based Projected Hartree–Fock Approach. Condensed Matter. 2023; 8(1):18. https://doi.org/10.3390/condmat8010018
Chicago/Turabian StyleGhassemi Tabrizi, Shadan, and Carlos A. Jiménez-Hoyos. 2023. "Ground States of Heisenberg Spin Clusters from a Cluster-Based Projected Hartree–Fock Approach" Condensed Matter 8, no. 1: 18. https://doi.org/10.3390/condmat8010018
APA StyleGhassemi Tabrizi, S., & Jiménez-Hoyos, C. A. (2023). Ground States of Heisenberg Spin Clusters from a Cluster-Based Projected Hartree–Fock Approach. Condensed Matter, 8(1), 18. https://doi.org/10.3390/condmat8010018





