Abstract
The experimental discovery that compressed sulfur hydride exhibits superconducting transition temperature of by Drozdov et al. (Nature 2015, 525, 73–76) sparked studies of compressed hydrides. This discovery was not a straightforward experimental examination of a theoretically predicted phase, but instead it was a nearly five-decade-long experimental quest for superconductivity in highly compressed matters, varying from pure elements (hydrogen, oxygen, sulfur), hydrides (SiH4, AlH3) to semiconductors and ionic salts. One of these salts was cesium iodide, CsI, which exhibits the transition temperature of at (Eremets et al., Science 1998, 281, 1333–1335). Detailed first principles calculations (Xu et al., Phys Rev B 2009, 79, 144110) showed that CsI should exhibit (). In an attempt to understand the nature of this discrepancy between the theory and the experiment, we analyzed the temperature-dependent resistance in compressed CsI and found that this compound is a perfect Fermi liquid metal which exhibits an extremely high ratio of Debye energy to Fermi energy, . This implies that direct use of the Migdal–Eliashberg theory of superconductivity to calculate the transition temperature in CsI is incorrect, because the theory is valid for . We also showed that CsI falls into the unconventional superconductors band in the Uemura plot.
1. Introduction
Since superconducting transition at 203 K was observed in highly compressed sulfur hydride by Drozdov et al. [1], dozens of superconducting hydrogen-based phases have been discovered [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] (extended reviews on the current status of the topic can be found elsewhere [18,19,20]). The report by Drozdov et al. [1] was the triumphant culmination of a nearly five-decade-long journey in the terra incognita of hydrogen-rich compounds [21] and highly compressed matter [22]. On this journey, the superconductors family was significantly extended and the superconducting transition was experimentally observed in many non-superconducting (at ambient conditions) elements/compounds. At the same time, the transition was not observed in materials for which the first principles calculations (FPC) and the Eliashberg theory [23] of the electron–phonon mediated superconductivity predicted a high critical temperature, . We may mention AlH3 [24,25] as an outstanding case of this class of materials.
However, more often, the superconducting transition was observed, but predicted significantly exceeds the experimental value. The most notable case of this class of materials is compressed SiH4 for which Feng et al. [26] calculated a Debye temperature of and , while the experiment performed by Eremets et al. [27] showed that .
More intriguingly, there are several highly compressed compounds in which experimentally observed significantly exceeds the calculated value. The most famous case of these highly pressurized compounds is sulfur hydride, for which Li et al. [28] initially predicted . However, Drozdov et al. [1] reported that the experimentally observed transition temperature is significantly higher, , and the observed value is in excellent agreement with theoretical calculations reported by Duan et al. [29].
Another material from this category is highly compressed CsI, for which detailed first principles calculations performed by Xu et al. [30] predicted at a pressure of , while the experimental value reported by Eremets et al. [31] is (at ).
In this work, we answer the question, why highly compressed CsI exhibits nearly two orders of magnitude higher in comparison with the predicted value by FPC and the Eliashberg theory of electron–phonon mediated superconductivity. Our answer is that highly compressed CsI exhibits an enormous ratio of the Debye temperature, , to the Fermi temperature, , , while the Eliashberg theory [23] of the electron–phonon mediated superconductivity is valid for .
2. Results
2.1. The Electron–Phonon Coupling Constant and the Debye Temperature in CsI at p = 206 GPa
Cesium iodide is isoelectronic with the noble gas solid xenon (i.e., Cs+ and I− ions in ionic salt have closed xenon-like electronic shells, and the short-range interaction between Cs+ and I− ions in uncompressed salt and two Xe atoms in solid xenon is identical). The main difference between Xe and CsI is the very strong Coulomb interaction in cesium iodide in comparison with xenon [32,33]. The strength of the Coulomb interaction decreases on compression, and at CsI is metallized [31,33].
In the theory of the electron–phonon mediated superconductivity [23,34], the phonon spectrum is one of the primary properties that determine the superconducting transition temperature, , and, thus, this is of great interest to determining the main characteristic parameter of this spectrum, i.e., the Debye temperature, . This value can be deduced from the fit of temperature-dependent resistance, , to the Bloch–Grüneisen (BG) equation [35,36,37,38,39,40]:
where is the residual resistance at , and the second term describes the electron–phonon scattering, where and are free-fitting parameters. Equation (1) was applied to deduce the Debye temperature in many highly compressed superconductors, for instance, in black phosphorus [41], boron [41], sulphur [42,43], lithium [42], -phase of O2 [42], SnS [37], GeAs [41], SiH4 [41], H3S [41,43], D3S [41,43], LaH10 [41,43], C2/m-SnH12 [44], Th4H15 [45], ThH9 [45], ThH10 [45], YD6 [45], metallic hydrogen phase-III [45], and [46].
The fit of the curve of compressed CsI () reported by Eremets et al. [31] in their Figure 3B of [31] to Equation (1) is shown in Figure 1a. The derived Debye temperature is . From this value and the measured [31] (see Figure 5 of [31]), one can calculate the electron-–phonon coupling constant, , as the root of an advanced McMillan equation [41]:
where is the Coulomb pseudopotential; it can be assumed that [4,18,19,20]. In the result, was calculated as a root of Equations (2)–(4). It can be noted that the deduced is close to for aluminum [47]. It should also be mentioned that deduced for CsI is not very different from –428 K [48,49] for aluminum.
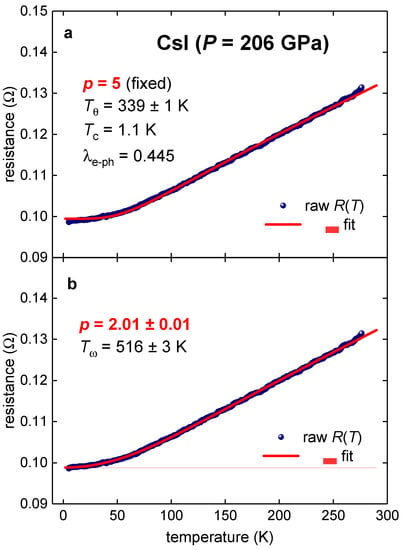
Figure 1.
Temperature-dependent resistance data, , in highly compressed cesium iodide () and data fits to Equation (1) (panel a) and Equation (5) (panel b). Raw data are from [31]. (a) p = 5, deduced , , fit quality R-Squared (COD) = 0.9993; (b) deduced , , , fit quality R-Squared (COD) = 0.9998. 95% confidence bands (in pink) are narrower than the fitting curves width.
One can make a comparison of the and values derived from experiment () with the values computed by first principles calculations [30]. Xu et al. [30] reported () and (), and both these values are significantly lower than the one deduced from the experiment here. Xu et al. [30] also calculated the logarithmic phonon frequency (), and (). By its definition, is close, but does not exactly equal, to the Debye frequency, , and this is what one can see for these values in highly compressed CsI.
By utilizing the Allen–Dynes equation [47,48] and , Xu et al. [30] calculated () and (). Both calculated that the values (and this was acknowledged by the authors of [30]) are by about two orders of magnitude lower than the experimental value. To explain this discrepancy, Xu et al. [30] hypothesized that because first principles calculations show that the CsI exhibits an anisotropic crystalline structure (under pressure), then the Allen–Dynes equation [48,50] (developed for the single-band isotropic superconductors) cannot accurately average an anisotropic case.
Our explanation for the discrepancy is based on a different idea which arose from a more advanced analysis of the temperature-dependent resistance curve described below.
2.2. Perfect Fermi Liquid Conductor CsI at p = 206 GPa
Despite the fit of the curve for the compressed CsI to the BG equation (Equation (1)) having a high quality (Figure 1a), more advanced analysis is based on the approach when the power–law exponent in Equation (1) is a free-fitting parameter [51,52,53,54,55]:
In this approach, the (Equation (5)) is not any longer the Debye temperature; however, this temperature represents a characteristic energy scalar for the charge carrier interaction in the conductor. There are several integer -values which associate with a particular charge-carrier interaction mechanism [56,57,58] and, in particular, implies that charge carriers in the conductor obey a perfect Landau’s Fermi liquid phenomenology [56,57,58].
It should be mentioned that for some materials, such as ReBe22 [53,59] and (ScZrNb)0.65[RhPd]0.35 [54,60], the power–law exponent is indistinguishable from 5, which implies that these materials are pure electron–phonon-mediated superconductors. However, for the majority of highly compressed superconductors, including the ε-Fe phase, the power–law exponent, p, varies between [53,54,55].
The fit of the curve in the CsI (P = 206 GPa) to Equation (5) is shown in Figure 1b, where it can be seen that the deduced is indistinguishable from . This means that the highly compressed CsI at () is a perfect Fermi liquid metal.
2.3. Compressed CsI (p = 206 GPa) in the Uemura Plot
One of the widely accepted ways to classify the superconducting state in the material is to position the material in the Uemura plot, i.e., in the plot where the X-axis is the Fermi temperature, , and the Y-axis is the transition temperature, [61,62]. The Fermi temperature in the superconductor can be calculated by the equation [42,63,64]:
where is the Fermi energy, is the Boltzmann constant, , and is the amplitude of the ground state energy gap, is the reduced Planck constant, and is the ground state coherence length. Based on a very large database on electron–phonon-mediated superconductors [47], one can expect that the CsI () which exhibits should have not very different from 3.53, and we used this value in our calculations. Thus, to calculate in the compressed CsI, one needs to estimate the ground state coherence length (Equation (6)).
We deduce for the compressed CsI () from the fit of the temperature-dependent upper critical field, , to the simplest equation of the Werthamer–Helfand–Hohenberg theory [65,66]:
The upper critical field represents the applied magnetic field in which the superconducting state collapses in the experiment. We extracted the Bc2(T) dataset in highly compressed CsI from the magnetoresistance data reported by Eremets et al. [31] in their Figure 5. To define Bc2(T) we utilized a 50% normal state resistance criterion. The fit of the Bc2(T) data is shown in Figure 2, from which was estimated.
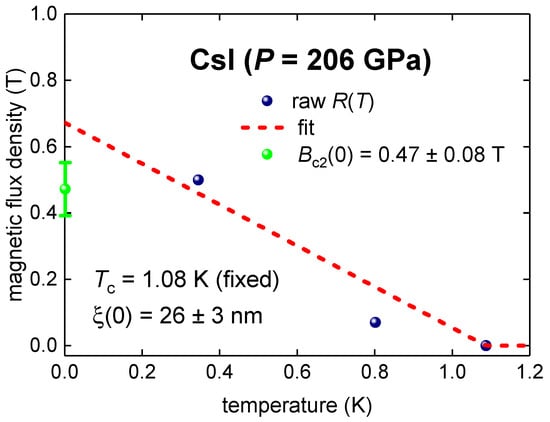
Figure 2.
Superconducting upper critical field, B(T), data (blue) for compressed CsI at pressure p = 206 GPa (data is from [31]) and fit to WHH model [65,66] (Equation (7)) for which was fixed it is experimental value of 1.087 K; fit quality R-Squared (COD) = 0.90.
From all determined/estimated values, one can calculate and the ratio of , which varies within a range:
In the result, the CsI () falls into the unconventional superconductors band in the Uemura plot (Figure 3).
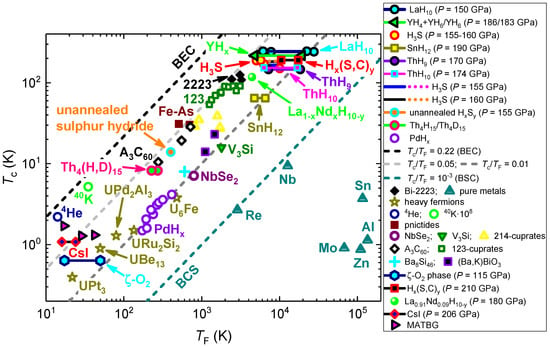
Figure 3.
Uemura plot (Tc vs. TF), where the CsI (p = 206 GPa) is shown together with other superconducting families. References on original data (Tc vs. TF) can be found in [42,44,68,69].
It should be noted that the A-15 superconductor V3Si (which exhibits the electron–phonon-mediated superconductivity with and [47,67]) is also located in the unconventional superconductors band in the Uemura plot (Figure 3).
Another material which can be mentioned is the magic-angle twisted bilayer graphene (MATBG) which exhibits very close and values [68,69] (Figure 3) to the compressed CsI.
Thus, our result that the highly compressed CsI (exhibited ) falls into the unconventional superconducting band manifests itself as an interesting, but not unique, case. The explanation of this result is based on, roughly speaking, the degree of Cooper pairs overlapping [70]. In CsI and V3Si, the average size of the Cooper pairs at the low temperature, , is comparable with the average distance between pairs and, thus, the pairs overlapping is not significant and is close to the Bose–Einstein condensate [70]. However, in superconductors located on the BCS side of the Uemura plot (Figure 3), the distance between the Cooper pairs centers is significantly smaller than the and the pairs’ overlapping is high. Details for the position of the superfluid 4He in Figure 3 can be found elsewhere [62].
2.4. Nonadiabalic Superconductivity in CsI (P = 206 GPa)
It is important to note that one of our central findings is that our analysis shows that the compressed CsI is a remarkably prominent nonadiabatic superconductor. This finding directly follows from the ratio of the Debye temperature, (for which we used the value deduced from the R(T) data fit to Equation (1), to the Fermi temperature, :
Roughly speaking, the Eliashberg theory of electron–phonon-mediated superconductivity [23] is based on Migdal’s theorem [71], which is the many-body version of the principle of Born–Oppenheimer [72]. Namely, it is an argument over adiabaticity, since charge-carrier particles are expected to move faster than ions. Thus, instead of taking the interaction with an electron in a certain position, it is easier to consider the interaction with the full electronic cloud. This consideration is applicable if the electrons are much faster than ions, but in some materials (such as in the C60 compound), the Fermi energy and the average phonon energy are just the same, and for these materials the Migdal theorem [71] and the Eliashberg theory [23] are no longer valid.
These kinds of superconductors, designated as nonadiabatic superconductors [73], were first theoretically considered by Pietronero and co-workers nearly three decades ago [73,74,75,76,77]. Pietronero and co-workers [73,74,75,76,77] considered the generalization of the many-body theory of superconductivity in the cases in which the Migdal theorem does not work, typically the systems with very low Fermi energy (or Fermi velocity, or Fermi temperature).
3. Discussion
Equation (9) shows that the compressed CsI () exhibits relatively “very fast” phonons and relatively “very slow” charge-carriers. For instance, one can make a comparison of the ratio for the CsI (Equation (9)) with the ratio for elemental electron–phonon superconductors (data for the ratios are taken from [49]):
Equation (9) shows that the standard Migdal–Eliashberg theory [23,71] of the electron–phonon-mediated superconductivity is inapplicable for highly compressed CsI and, therefore, this is our explanation for the discrepancy between the superconducting transition temperature, , predicted by first-principles calculations [30] (following standard Allen–Dynes methodology [48,50]) and the observed in experiment [31].
To the best of our knowledge, such a large ratio has not been reported for any superconductor to date.
4. Conclusions
In ambient conditions, CsI represents typical ionic salt, which transforms into a metallic state at high pressure. Xu et al. [30] performed first principle calculations for compressed CsI and established that within the Migdal–Eliashberg theory [23,69] this compound should exhibit the superconducting transition temperature Tc(p = 180 K)~0.03 K. Experiments performed by Eremets et al. [31] showed that highly compressed CsI exhibited a nearly two orders of magnitude higher transition temperature Tc(p = 206 K)~1.5 K.
In attempts to find the primary origin for the discrepancy between the theory and the experiment, here we analysed available experimental data measured in highly compressed CsI (p = 206 GPa) and found that:
- CsI is a perfect Fermi liquid metal.
- CsI exhibits an extremely high ratio of Debye energy to Fermi energy, . Based on this, one can conclude that the superconducting state in this compound cannot be described by the Migdal–Eliashberg theory [23,69] because the theory is valid when .
- CsI exhibits the ratio of and, thus, it falls to the unconventional superconductors band in the Uemura plot. This level of the ratio is typical for many superconductors, including the electron–phonon-mediated A-15 compound V3Si. It should be mentioned that the magic-angle twisted bilayer graphene exhibits close and values [68,69].
Funding
This research was funded by the Ministry of Science and Higher Education of the Russian Federation, grant number No. AAAA-A18-118020190104-3 (theme “Pressure”).
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Drozdov, A.P.; Eremets, M.I.; Troyan, I.A.; Ksenofontov, V.; Shylin, S.I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 2015, 525, 73–76. [Google Scholar] [CrossRef] [PubMed]
- Drozdov, A.P.; Kong, P.P.; Minkov, V.S.; Besedin, S.P.; Kuzovnikov, M.A.; Mozaffari, S.; Balicas, L.; Balakirev, F.F.; Graf, D.E.; Prakapenka, V.B.; et al. Superconductivity at 250 K in lanthanum hydride under high pressures. Nature 2019, 569, 528–531. [Google Scholar] [CrossRef] [PubMed]
- Somayazulu, M.; Ahart, M.; Mishra, A.K.; Geballe, Z.M.; Baldini, M.; Meng, Y.; Struzhkin, V.V.; Hemley, R.J. Evidence for superconductivity above 260 K in lanthanum superhydride at megabar pressures. Phys. Rev. Lett. 2019, 122, 027001. [Google Scholar] [CrossRef] [PubMed]
- Semenok, D.V.; Kvashnin, A.G.; Ivanova, A.G.; Svitlyk, V.; Fominski, V.Y.; Sadakov, A.V.; Sobolevskiy, O.A.; Pudalov, V.M.; Troyan, I.A.; Oganov, A.R. Superconductivity at 161 K in thorium hydride ThH10: Synthesis and properties. Mater. Today 2020, 33, 36–44. [Google Scholar] [CrossRef]
- Chen, W.; Semenok, D.V.; Kvashnin, A.G.; Huang, X.; Kruglov, I.A.; Galasso, M.; Song, H.; Duan, D.; Goncharov, A.F.; Prakapenka, V.B.; et al. Synthesis of molecular metallic barium superhydride: Pseudocubic BaH12. Nat. Commun. 2021, 12, 273. [Google Scholar] [CrossRef]
- Wang, N.; Shan, P.F.; Chen, K.Y.; Sun, J.P.; Yang, P.T.; Ma, X.L.; Wang, B.S.; Yu, X.H.; Zhang, S.; Chen, G.F.; et al. A low-Tc superconducting modification of Th4H15 synthesized under high pressure. Supercond. Sci. Technol. 2021, 34, 034006. [Google Scholar] [CrossRef]
- Troyan, I.A.; Semenok, D.V.; Kvashnin, A.G.; Sadakov, A.V.; Sobolevskiy, O.A.; Pudalov, V.M.; Ivanova, A.G.; Prakapenka, V.B.; Greenberg, E.; Gavriliuk, A.G.; et al. Anomalous high-temperature superconductivity in YH6. Adv. Mater. 2021, 33, 2006832. [Google Scholar] [CrossRef]
- Kong, P.; Minkov, V.S.; Kuzovnikov, M.A.; Drozdov, A.P.; Besedin, S.P.; Mozaffari, S.; Balicas, L.; Balakirev, F.F.; Prakapenka, V.B.; Chariton, S.; et al. Superconductivity up to 243 K in yttrium hydrides under high pressure. Nat. Commun. 2021, 12, 5075. [Google Scholar] [CrossRef]
- Ma, L.; Wang, K.; Xie, Y.; Yang, X.; Wang, Y.; Zhou, M.; Liu, H.; Yu, X.; Zhao, Y.; Wang, H.; et al. High-temperature superconducting phase in clathrate calcium hydride CaH6 up to 215 K at a pressure of 172 GPa. Phys. Rev. Lett. 2022, 128, 167001. [Google Scholar] [CrossRef]
- Semenok, D.V.; Troyan, I.A.; Ivanova, A.G.; Kvashnin, A.G.; Kruglov, I.A.; Hanfland, M.; Sadakov, A.V.; Sobolevskiy, O.A.; Pervakov, K.S.; Lyubutin, I.S.; et al. Superconductivity at 253 K in lanthanum–yttrium ternary hydrides. Mater. Today 2021, 48, 18–28. [Google Scholar] [CrossRef]
- Zhou, D.; Semenok, D.V.; Duan, D.; Xie, H.; Chen, W.; Huang, X.; Li, X.; Liu, B.; Oganov, A.R.; Cui, T. Superconducting praseodymium superhydrides. Sci. Adv. 2020, 6, eaax6849. [Google Scholar] [CrossRef] [PubMed]
- Hong, F.; Shan, P.F.; Yang, L.X.; Yue, B.B.; Yang, P.T.; Liua, Z.Y.; Sun, J.P.; Dai, J.H.; Yu, H.; Yin, Y.Y.; et al. Possible superconductivity at ∼70 K in tin hydride SnHx under high pressure. Mater. Today Phys. 2022, 22, 100596. [Google Scholar] [CrossRef]
- Chen, W.; Semenok, D.V.; Huang, X.; Shu, H.; Li, X.; Duan, D.; Cui, T.; Oganov, A.R. High-temperature superconducting phases in cerium superhydride with a Tc up to 115 K below a pressure of 1 Megabar. Phys. Rev. Lett. 2021, 127, 117001. [Google Scholar] [CrossRef] [PubMed]
- Osmond, I.; Moulding, O.; Cross, S.; Muramatsu, T.; Brooks, A.; Lord, O.; Fedotenko, T.; Buhot, J.; Friedemann, S. Clean-limit superconductivity in Im3m H3S synthesized from sulfur and hydrogen donor ammonia borane. Phys. Rev. B 2022, 105, L220502. [Google Scholar] [CrossRef]
- Semenok, D.V.; Troyan, I.A.; Sadakov, A.V.; Zhou, D.; Galasso, M.; Kvashnin, A.G.; Ivanova, A.G.; Kruglov, I.A.; Bykov, A.A.; Terent’ev, K.Y.; et al. Effect of magnetic impurities on superconductivity in LaH10. Adv. Mater. 2022, 34, 2204038. [Google Scholar] [CrossRef]
- Bi, J.; Nakamoto, Y.; Zhang, P.; Shimizu, K.; Zou, B.; Liu, H.; Zhou, M.; Liu, G.; Wang, H.; Ma, Y. Giant enhancement of superconducting critical temperature in substitutional alloy (La,Ce)H9. Nat. Commun. 2022, 13, 5952. [Google Scholar] [CrossRef]
- Li, Z.; He, X.; Zhang, C.; Wang, X.; Zhang, S.; Jia, Y.; Feng, S.; Lu, K.; Zhao, J.; Zhang, J.; et al. Superconductivity above 200 K discovered in superhydrides of calcium. Nat. Commun. 2022, 13, 2863. [Google Scholar] [CrossRef]
- Flores-Livas, J.A.; Boeri, L.; Sanna, A.; Profeta, G.; Arita, R.; Eremets, M. A perspective on conventional high-temperature superconductors at high pressure: Methods and materials. Phys. Rep. 2020, 856, 1–78. [Google Scholar] [CrossRef]
- Boeri, L.; Hennig, R.; Hirschfeld, P.; Profeta, G.; Sanna, A.; Zurek, E.; Pickett, W.E.; Amsler, M.; Dias, R.; Eremets, M.I.; et al. The 2021 room-temperature superconductivity roadmap. J. Phys. Condens. Matter 2022, 34, 183002. [Google Scholar] [CrossRef]
- Troyan, I.A.; Semenok, D.V.; Ivanova, A.G.; Kvashnin, A.G.; Zhou, D.; Sadakov, A.V.; Sobolevskiy, O.A.; Pudalov, V.M.; Lyubutin, I.S.; Oganov, A.R. High-temperature superconductivity in hydrides. Phys. Uspekhi 2022, 65, 748–761. [Google Scholar] [CrossRef]
- Satterthwaite, C.B.; Toepke, I.L. Superconductivity of hydrides and deuterides of thorium. Phys. Rev. Lett. 1970, 25, 741–743. [Google Scholar] [CrossRef]
- Wittig, J.; Matthias, B.T. Superconducting phosphorus. Science 1968, 160, 994–995. [Google Scholar] [CrossRef] [PubMed]
- Eliashberg, G.M. Interactions between electrons and lattice vibrations in a superconductor. Sov. Phys. JETP 1960, 11, 696–702. [Google Scholar]
- Hou, P.; Belli, F.; Bianco, R.; Errea, I. Strong anharmonic and quantum effects in -AlH3 under high pressure: A first-principles study. Phys. Rev. B 2021, 103, 134305. [Google Scholar] [CrossRef]
- Goncharenko, I.; Eremets, M.I.; Hanfland, M.; Tse, J.S.; Amboage, M.; Yao, Y.; Trojan, I.A. Pressure-induced hydrogen-dominant metallic state in aluminum hydride. Phys. Rev. Lett. 2008, 100, 045504. [Google Scholar] [CrossRef]
- Feng, J.; Grochala, W.; Jaroń, T.; Hoffmann, R.; Bergara, A.; Ashcroft, N.W. Structures and potential superconductivity in SiH4 at high pressure: En route to “metallic hydrogen”. Phys. Rev. Lett. 2006, 96, 017006. [Google Scholar] [CrossRef]
- Eremets, M.I.; Trojan, I.A.; Medvedev, S.A.; Tse, J.S.; Yao, Y. Superconductivity in hydrogen dominant materials: Silane. Science 2008, 319, 1506–1509. [Google Scholar] [CrossRef]
- Li, Y.; Hao, J.; Liu, H.; Li, Y.; Ma, Y. The metallization and superconductivity of dense hydrogen sulfide. J. Chem. Phys. 2014, 140, 174712. [Google Scholar] [CrossRef]
- Duan, D.; Liu, Y.; Tian, F.; Li, D.; Huang, X.; Zhao, Z.; Yu, H.; Liu, B.; Tian, W.; Cui, T. Pressure-induced metallization of dense (H2S)2H2 with high-Tc superconductivity. Sci. Rep. 2014, 4, 6968. [Google Scholar] [CrossRef]
- Xu, Y.; Tse, J.S.; Oganov, A.R.; Cui, T.; Wang, H.; Ma, Y.; Zou, G. Superconducting high-pressure phase of cesium iodide. Phys. Rev. B 2009, 79, 144110. [Google Scholar] [CrossRef]
- Eremets, M.I.; Shimizu, K.; Kobayashi, T.C.; Amaya, K. Metallic CsI at pressures of up to 220 gigapascals. Science 1998, 281, 1333–1335. [Google Scholar] [CrossRef] [PubMed]
- Knittle, E.; Jeanloz, R. Structural and bonding changes in cesium iodide at high pressures. Science 1984, 223, 53–56. [Google Scholar] [CrossRef] [PubMed]
- Makarenko, I.N.; Goncharov, A.F.; Stishov, S.M. Optical absorption of cesium iodide (CsI) at pressure up to 60 GPa. Phys. Rev. B 1984, 29, 6018–6019. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef]
- Bloch, F. Zum elektrischen Widerstandsgesetz bei tiefen Temperaturen. Z. Phys. 1930, 59, 208–214. [Google Scholar] [CrossRef]
- Grüneisen, E. Die abhängigkeit des elektrischen widerstandes reiner metalle von der temperatur. Ann. Phys. 1933, 408, 530–540. [Google Scholar] [CrossRef]
- Matsumoto, R.; Song, P.; Adachi, S.; Saito, Y.; Hara, H.; Yamashita, A.; Nakamura, K.; Yamamoto, S.; Tanaka, H.; Irifune, T. Pressure-induced superconductivity in tin sulfide. Phys. Rev. B 2019, 99, 184502. [Google Scholar] [CrossRef]
- Kudo, K.; Hiiragi, H.; Honda, T.; Fujimura, K.; Idei, H.; Nohara, M. Superconductivity in Mg2Ir3Si: A fully ordered Laves phase. J. Phys. Soc. Jpn. 2020, 89, 013701. [Google Scholar] [CrossRef]
- Susner, M.A.; Bhatia, M.; Sumption, M.D.; Collings, E.W. Electrical resistivity, Debye temperature, and connectivity in heavily doped bulk MgB2 superconductors. J. Appl. Phys. 2009, 105, 195901. [Google Scholar] [CrossRef]
- Pyon, S.; Kudo, K.; Matsumura, J.-I.; Ishii, H.; Matsuo, G.; Nohara, M.; Hojo, H.; Oka, K.; Azuma, M.; Garlea, V.O.; et al. Superconductivity in noncentrosymmetric iridium silicide Li2IrSi3. J. Phys. Soc. Jpn. 2014, 83, 093706. [Google Scholar] [CrossRef]
- Talantsev, E.F. Advanced McMillan’s equation and its application for the analysis of highly-compressed superconductors. Supercond. Sci. Technol. 2020, 33, 094009. [Google Scholar] [CrossRef]
- Talantsev, E.F. An approach to identifying unconventional superconductivity in highly compressed superconductors. Supercond. Sci. Technol. 2020, 33, 124001. [Google Scholar] [CrossRef]
- Talantsev, E.F.; Stolze, K. Resistive transition of hydrogen-rich superconductors. Supercond. Sci. Technol. 2021, 34, 064001. [Google Scholar] [CrossRef]
- Talantsev, E.F. Comparison of highly-compressed C2/m-SnH12 superhydride with conventional superconductors. J. Phys. Condens. Matter 2021, 33, 285601. [Google Scholar] [CrossRef]
- Talantsev, E.F. The electron–phonon coupling constant and the Debye temperature in polyhydrides of thorium, hexadeuteride of yttrium, and metallic hydrogen phase III. J. Appl. Phys. 2021, 130, 195901. [Google Scholar] [CrossRef]
- Talantsev, E.F. Electron–phonon coupling constant and BCS ratios in LaH10−y doped with magnetic rare-earth element. Supercond. Sci. Technol. 2022, 35, 095008. [Google Scholar] [CrossRef]
- Carbotte, J.P. Properties of boson-exchange superconductors. Rev. Mod. Phys. 1990, 62, 1027–1157. [Google Scholar] [CrossRef]
- McMillan, W.L. Transition temperature of strong-coupled superconductors. Phys. Rev. 1968, 167, 331–344. [Google Scholar] [CrossRef]
- Poole, C.P., Jr. Properties of the normal metallic state. In Handbook of Superconductivity, 1st ed.; Poole, C.P., Jr., Ed.; Academic Press: New York, NY, USA, 1999; Volume 1, pp. 31–32. [Google Scholar]
- Allen, P.B.; Dynes, R.C. Transition temperature of strong-coupled superconductors reanalyzed. Phys. Rev. B 1975, 12, 905–922. [Google Scholar] [CrossRef]
- Jiang, H.; Bao, J.-K.; Zhai, H.-F.; Tang, Z.-T.; Sun, Y.-L.; Liu, Y.; Wang, Z.-C.; Bai, H.; Xu, Z.-A.; Cao, G.-H. Physical properties and electronic structure of Sr2Cr3As2O2 containing CrO2 and Cr2As2 square-planar lattices. Phys. Rev. B 2015, 92, 205107. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Wang, D.; Zhang, Y.; Liu, Z.-H.; Feng, Q.-R.; Gan, Z.-Z. Suppression of superconductivity in epitaxial MgB2 ultrathin films. J. Appl. Phys. 2013, 114, 023903. [Google Scholar] [CrossRef]
- Talantsev, E.F. Quantifying the charge carrier interaction in metallic twisted graphene superlattices. Nanomaterials 2021, 11, 1306. [Google Scholar] [CrossRef] [PubMed]
- Talantsev, E.F. The dominance of non-electron–phonon charge carrier interaction in highly-compressed superhydrides. Supercond. Sci. Technol. 2021, 34, 115001. [Google Scholar] [CrossRef]
- Talantsev, E.F. Classifying charge carrier interaction in highly compressed elements and silane. Materials 2021, 14, 4322. [Google Scholar] [CrossRef]
- White, G.K.; Woods, S.B. Electrical and thermal resistivity of the transition elements at low temperatures. Phil. Trans. R. Soc. Lond. A 1959, 251, 273–302. [Google Scholar] [CrossRef]
- Poker, D.B.; Klabunde, C.E. Temperature dependence of electrical resistivity of vanadium, platinum, and copper. Phys. Rev. B 1982, 26, 7012–7014. [Google Scholar] [CrossRef]
- Matula, R.A. Electrical resistivity of copper, gold, palladium, and silver. J. Phys. Chem. Ref. Data 1979, 8, 1147–1298. [Google Scholar] [CrossRef]
- Shang, T.; Amon, A.; Kasinathan, D.; Xie, W.; Bobnar, M.; Chen, Y.; Wang, A.; Shi, M.; Medarde, M.; Yuan, H.Q.; et al. Enhanced Tc and multiband superconductivity in the fully-gapped ReBe22 superconductor. New J. Phys. 2019, 21, 073034. [Google Scholar] [CrossRef]
- Stolze, K.; Tao, J.; von Rohr, F.O.; Kong, T.; Cava, R.J. Sc–Zr–Nb–Rh–Pd and Sc–Zr–Nb–Ta–Rh–Pd high-entropy alloy superconductors on a CsCl-type lattice. Chem. Mater. 2018, 30, 906–914. [Google Scholar] [CrossRef]
- Uemura, Y.J.; Luke, G.M.; Sternlieb, B.J.; Brewer, J.H.; Carolan, J.F.; Hardy, W.N.; Kadono, R.; Kempton, J.R.; Kiefl, R.F.; Kreitzman, S.R. Universal correlations between Tc and (carrier density over effective mass) in high-Tc cuprate. Phys. Rev. Lett. 1989, 62, 2317–2320. [Google Scholar] [CrossRef] [PubMed]
- Uemura, Y.J. Condensation, excitation, pairing, and superfluid density in high-Tc superconductors: The magnetic resonance mode as a roton analogue and a possible spin-mediated pairing. J. Phys. Condens. Matter 2004, 16, S4515–S4540. [Google Scholar] [CrossRef]
- Talantsev, E.F. Classifying superconductivity in compressed H3S. Mod. Phys. Lett. B 2019, 33, 1950195. [Google Scholar] [CrossRef]
- Talantsev, E.F.; Mataira, R.C. Classifying superconductivity in ThH-ThD superhydrides/superdeuterides. Mater. Res. Express 2020, 7, 016003. [Google Scholar] [CrossRef]
- Helfand, E.; Werthamer, N.R. Temperature and purity dependence of the superconducting critical field, Hc2. II. Phys. Rev. 1966, 147, 288–294. [Google Scholar] [CrossRef]
- Werthamer, N.R.; Helfand, E.; Hohenberg, P.C. Temperature and purity dependence of the superconducting critical field, Hc2. III. Electron spin and spin-orbit effects. Phys. Rev. 1966, 147, 295–302. [Google Scholar] [CrossRef]
- Orlando, T.P.; McNiff, E.J., Jr.; Foner, S.; Beasley, M.R. Critical fields, Pauli paramagnetic limiting, and material parameters of Nb3Sn and V3Si. Phys. Rev. B 1979, 19, 4545–4561. [Google Scholar] [CrossRef]
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magic-angle graphene superlattices. Nat. Cell Biol. 2018, 556, 43–50. [Google Scholar] [CrossRef]
- Talantsev, E.F.; Mataira, R.C.; Crump, W.P. Classifying superconductivity in Moiré graphene superlattices. Sci. Rep. 2020, 10, 212. [Google Scholar] [CrossRef]
- Suzuki, Y.; Wakamatsu, K.; Ibuka, J.; Oike, H.; Fujii, T.; Miyagawa, K.; Taniguchi, H.; Kanoda, K. Mott-driven BEC-BCS crossover in a doped spin liquid candidate κ-(BEDT-TTF)4Hg2.89Br8. Phys. Rev. X 2022, 12, 011016. [Google Scholar] [CrossRef]
- Migdal, A.B. Interaction between electrons and lattice vibrations in a normal metal. Sov. Phys. JETP 1958, 7, 996–1001. [Google Scholar]
- Born, M.; Oppenheimer, J.R. Zur Quantentheorie der Molekeln [On the Quantum Theory of Molecules]. Ann. Der Phys. 1927, 389, 457–484. [Google Scholar] [CrossRef]
- Pietronero, L.; Strässler, S.; Grimaldi, C. Nonadiabatic superconductivity. I. Vertex corrections for the electron-phonon interactions. Phys. Rev. B 1995, 52, 10516–10529. [Google Scholar] [CrossRef] [PubMed]
- Grimaldi, C.; Pietronero, L.; Strässler, S. Nonadiabatic superconductivity. II. Generalized Eliashberg equations beyond Migdal’s theorem. Phys. Rev. B 1995, 52, 10530–10546. [Google Scholar] [CrossRef]
- Grimaldi, C.; Cappelluti, E.; Pietronero, L. Isotope effect on m* in high Tc materials due to the breakdown of Migdal’s theorem. Europhys. Lett. 1998, 42, 667–672. [Google Scholar] [CrossRef]
- Cappelluti, E.; Ciuchi, S.; Grimaldi, C.; Pietronero, L.; Strässler, S. High Tc superconductivity in MgB2 by nonadiabatic pairing. Phys. Rev. Lett. 2002, 88, 117003. [Google Scholar] [CrossRef] [PubMed]
- Pietronero, L.; Boeri, L.; Cappelluti, E.; Ortenzi, L. Conventional/unconventional superconductivity in high-pressure hydrides and beyond: Insights from theory and perspectives. Quantum Stud. Math. Found. 2018, 5, 5–21. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).