The Evolution of Geometric Structures, Electronic Properties, and Chemical Bonding of Small Phosphorus-Boron Clusters

Abstract

We report a comprehensive theoretical investigation on phosphorus–boron mixed neutral, anionic, and cationic clusters P₂B_n/P₂B_n⁻/P₂B_n⁺ (n = 3–7) with two phosphorus atoms and three to seven boron atoms. We reveal the common character of all the structures (i.e., the phosphorus atoms choose to occupy the peripheral position), whereas the boron atoms tend to be in the central and inside position of the ground state phosphorus—boron mixed clusters at each stoichiometry. Any three atoms preferentially form a stable triangle and grow with zigzag shape in a planar network. Interestingly, a series of planar motifs (including tetra-, penta-, and hexa-coordination) have been discovered in the phosphorus–boron clusters. The large binding energies (3.6 to 4.6 eV/atom) and quite large HOMO–LUMO gaps (5 to 10 eV) indicate the high stability of the clusters. The energy differences Δ₁E, Δ₂E, and energy gaps display oscillating behavior with increasing numbers of boron atoms. The electron affinity (EA) and ionization potential (IP) generally have small variations, with the EA values ranging from 2 to 3 eV, and the IP values ranging from 7 to 9 eV. Chemical bond analysis shows that the existence of multi-center delocalized bonds stabilize the clusters.

1. Introduction

The planar hypercoordinate motif is a fascinating structure with ever growing interest in the chemical community [1,2]. Boron is a very special element with a fantastic ability to form hypercoordinate motifs since small and medium-sized boron clusters almost all exhibit (quasi-) planar hypercoordinate configurations. Experimental studies have shown that boron clusters can be used as important reducing agents and stabilizers [3]. It has been shown that the planar boron clusters consist of a peripheral ring featuring strongly localized two-center-two-electron (2c–2e) B-B σ bonds, and one or more central atoms bonded to the outer ring almost exclusively via delocalized multi-center-two-electron (nc–2e) σ and π bonds [4]. Small boron clusters have become an important platform for the creation of hypercoordinate motifs via doping with the formation of binary alloys. Boron and phosphorus are typical III and V group elements with intriguing properties and their 2D forms (borophene [5] and 2D phosphorus [6]) have attracted great attention worldwide recently. More coincidentally, experiments have shown that non-metal atom-doped boron clusters can be used to prepare high-performance phosphors [7]. Thus, doping phosphorus into boron clusters might lead to novel hypercoordinate species with interesting properties since the aluminum–doped boron clusters [8,9,10] and 2D nanosheets [11], and carbon–doped boron clusters [12,13] have already shown appealing phenomena. Furthermore, due to potential applications of binary clusters in meteorological catalysis [14], exploration of phosphorus–doped boron clusters is desirable.

In this work, we performed comprehensive theoretical studies on the structure, stability, electronic properties, chemical bonding, and spectroscopy of di-phosphorus–doped boron clusters P₂B_n/P₂B_n⁻/P₂B_n⁺ (n = 3–7) with a focus on the formation of planar tetracoordinate motifs requiring a minimum of five atoms (one central and four peripheral atoms). Thus, the number of boron atoms starts from three in this series. First, we used the evolutionary algorithm together with density functional theory (DFT) calculations to search the global minimum and low-lying structures, followed by single-point CCSD(T) calculations based on the B3LYP geometries to determine the relative energies. The ionization potentials, electron affinities, and HOMO–LUMO gaps of the global minimum structures were obtained using B3LYP calculations. Furthermore, AdNDP analysis was performed to have an in–depth understanding of the interactions between the constituent atoms, and of the formation of the stable structures. The predicted infrared spectrum and photoelectron spectroscopy of the global minimum structures should contribute to eventual experimental identification.

2. Computational Details

This paper mainly searches for the most stable and low-lying structures of P₂B_n/P₂B_n⁻/P₂B_n⁺ (n = 3–7) clusters. Regarding the choice of global search method, previous research was done by adding or replacing pure boron clusters into target clusters. However, in this paper, to more accurately determine the stable structures of these phosphorus–doped boron clusters, we used a superior method. The computational search for the global minima was performed using the Coalescence Kick (CK) [15] program written by Averkiev. This evolutionary algorithm randomly generates a large number of structures, which then pass through a coalescing process during which all atoms are gradually pushed to the molecular center of mass to avoid fragmentation and then optimized to the nearest local minimum. To improve the initial proposed CK structures, we used the HF/STO–3G method. In order to obtain reliable and stable structures, we then used density functional theory (DFT) with the B3LYP [16,17] functional and the 6–31G(d) [18] basis set to re–optimize the structures. We then calculated the frequencies to confirm that the structures had no virtual frequencies. Before the calculations of the single point energies of the stable structures, the B3LYP/6–311+G(d) [19] method was used to obtain further structural optimization and frequency calculations. Then, the lowest energy stable structures with relative energies less than 50 kcal/mol were calculated using the very reliable CCSD(T) [20,21,22]/6–311+G(2df) method. In addition, the calculations of ionization potential, electron affinity, HOMO–LUMO gap, photoelectron spectroscopy simulation, and infrared spectroscopy were done using B3LYP/6–311+G(d). The AdNDP [23] method was used to elucidate the chemical bonding of the ground state structures. Because AdNDP analysis is insensitive to the basis set, B3LYP/6–31+G(d) was used for the AdNDP analysis. The results of the AdNDP analysis were visualized using Molekel 5.4.0.8 [24]. The relevant calculations for all the above stable structures were performed with Gaussian 09 [25].

This paper is organized as follows. First, we discuss the stable structures of P₂B_n/P₂B_n⁻/P₂B_n⁺ (n = 3–7), then we discuss the evolution of properties. The HOMO–LUMO gaps are discussed, then, the ionization potential and electron affinity are discussed. Finally, the AdNDP analysis is presented, and the infrared spectrum and photoelectron spectroscopy are shown. Detailed formulas for the calculation of energies for cluster stabilities are shown in

Table 1. Calculation formula for atomic cluster stability.

P2Bn	Eb(P2Bn) = [2E(P) + nE(B) − E(P2Bn)]/(2 + n)	(1)
	Δ1E(P2Bn) = E(P2Bn−1) + E(B) − E(P2Bn)	(2)
	Δ2E(P2Bn) = E(P2Bn−1) + E(P2Bn+1) − 2E(P2Bn)	(3)
P2Bn−	Eb(P2Bn−) = [E(P) + E(P−) + nE(B) − E(P2Bn−)]/(2 + n)	(4)
	Δ1E(P2Bn−) = E(P2Bn−1−) + E(B) − E(P2Bn−)	(5)
	Δ2E(P2Bn−) = E(P2Bn−1−) + E(P2Bn+1−) − 2E(P2Bn−)	(6)
P2Bn+	Eb(P2Bn+) = [2E(P) + (n − 1)E(B) + E(B+) − E(P2Bn+)]/(2 + n)	(7)
	Δ1E(P2Bn+) = E(P2Bn−1+) + E(B) − E(P2Bn+)	(8)
	Δ2E(P2Bn+) = E(P2Bn−1+) + E(P2Bn+1+) − 2E(P2Bn+)	(9)

.

3. Results and Discussion

3.1. Growth Behavior of Small Phosphorus–Doped Boron Clusters

The low-lying isomers of phosphorus-doped boron P₂B_n^0/−/+clusters are shown in Figure 1, Figure 2 and Figure 3. All have real vibrational frequencies. Based on the high-precision CCSD(T) energies, five low-lying isomers for each P₂B_n^0/−/+ cluster are enumerated and shown in the main text. In the following discussion and analysis, unless otherwise stated, we will mainly use the CCSD(T) energies.

3.1.1. Low-Lying Isomers of Neutral P₂B_n (n = 3–7) Clusters

In Figure 1, five low-lying isomers for each neutral P₂B_n cluster are ordered starting with the lowest energy configurations. For the neutral P₂B₃ cluster, the lowest isomer structure 3n–1 is flat, and has a stable equilateral boron triangle. The two P atoms are located on the periphery. The relative energies of the 3n–2 to 3n–5 structures are more than 20 kcal/mol, demonstrating a sufficient gap away from the lowest energy state.

Figure 1. The optimized structures and relative energies (kcal/mol) of neutral P₂B_n clusters. The relative order of different isomers is determined using the CCSD(T)/6–311+G(2df) energies. The energies in parentheses are the B3LYP/6–311+G(d) results.

Figure 1. The optimized structures and relative energies (kcal/mol) of neutral P₂B_n clusters. The relative order of different isomers is determined using the CCSD(T)/6–311+G(2df) energies. The energies in parentheses are the B3LYP/6–311+G(d) results.

For the neutral P₂B₄ cluster, the lowest energy structure 4n–1 has C_2h symmetry. Its four boron atoms form a stable rhombus. The structure is flat, and the four boron atoms form two stable equilateral triangles. The two P atoms are located in the corners of the raft–like structure. The structure 4n–2 has relative energy 14.7 kcal/mol and C_2v symmetry. Four boron atoms also form a stable rhombus, and two phosphorus atoms are added on the periphery. The relative energies of 4n–3 and other higher energy structures exceed 20 kcal/mol. 4n–3 starts to show 3D structure. In general, the 4n–1 structure is the most stable structure of the neutral P₂B₄ cluster.

For the neutral P₂B₅ cluster, the lowest energy structure 5n–1 has the symmetry of C_2v with five boron atoms forming a W-shape pentagon, or the five boron atoms forming three stable equilateral triangles. Lower lying energy isomers 5n–2 and 5n–3 have 6.43 and 15.47 kcal/mol with five boron atoms preferentially forming a pentagon, and the remaining two phosphorus atoms are located at different positions on the periphery. The energy of the other structures is higher than 20 kcal/mol. The 5n–1 structure is the most stable structure of the P₂B₅ cluster.

For the neutral P₂B₆ cluster, the structure 6n–1 at the CCSD(T)/6–311+G(2df) level has the lowest energy. The two-dimensional planar structure 6n–2 at the B3LYP/6–311+G(d) level has the lowest energy. The structure of 6n–2 is arranged in a zigzag pattern. Other higher energy structures are shown in the Figure. Structures 6n–1 and 6n–2 may compete with each other to become the most stable structure of P₂B₆ cluster.

For the neutral P₂B₇ cluster, the lowest energy structure 7n–1 with C_2v symmetry has a zigzag arrangement in which two phosphorus atoms are located at both ends. The higher energy 7n–2, 7n–3, and 7n–4 structures are planar or planar-like configurations. The 7n–1 structure is the most stable structure of the neutral P₂B₇ cluster.

In general, for the neutral P₂B_n (n = 3–7) structures, the most stable structures present planar or planar-like configurations, and are arranged in a zigzag pattern with two phosphorus atoms located at the two ends.

3.1.2. Low-Lying Isomers of Anionic P₂B_n⁻ (n = 3–7) Clusters

The low-lying isomers for anionic P₂B_n⁻ clusters are shown in Figure 2. For P₂B₃, the lowest energy structure 3a–1 with planar C_2v symmetry is similar to the structure 3n–1 of the neutral P₂B₃ cluster. The energy of the other structures are more than 20 kcal/mol. We can conclude that the structure 3a–1 is the most stable anionic P₂B₃⁻ cluster.

Figure 2. Optimized global minimum and low-lying isomers for anionic P₂B_n⁻ clusters. The relative energies at the CCSD(T)/6–311+G(2df) level are shown below each structure. The B3LYP/6–311+G(d) energies are shown in parentheses.

Figure 2. Optimized global minimum and low-lying isomers for anionic P₂B_n⁻ clusters. The relative energies at the CCSD(T)/6–311+G(2df) level are shown below each structure. The B3LYP/6–311+G(d) energies are shown in parentheses.

For the anionic P₂B₄⁻ cluster, the structure 4a–1 with C_2v symmetry has the lowest energy and is similar to the structure 4n–2 of the neutral P₂B₄ cluster. The structure 4a–2 is 0.53 kcal/mol higher than the energy of structure 4a–1, and is similar to the structure 4n–1 of the neutral P₂B₄ cluster. The relative energies of the other structures are more than 20 kcal/mol. We can conclude that the structure 4a–1 and 4a–2 may compete with each other to become the most stable anionic P₂B₄⁻ cluster.

For the anionic P₂B₅⁻ cluster, the structures 5a–1 and 5a–2 with C_2v symmetry have lower energy, and are similar to the structures 5n–3 and 5n–1 of the neutral P₂B₅ cluster, respectively. The structure 5a–3 is similar to the structure 5n–2, and the other structures have higher energy. The structures 5a–1 and 5a–2 may compete with each other to become the most stable anionic P₂B₅⁻ cluster.

The structure 6a–1 with the lowest energy and C_2h symmetry grows in zigzag shape, and is similar to the structure 6n–2. The structures 6a–2 and 6a–3 with higher energy are similar to structures 6n–4 and 6n–1, respectively. The other structures are higher energy and the structure 6a–1 is the most stable anionic P₂B₆⁻ cluster.

The structure 7a–1 has the lowest energy and is similar to the structure 7n–2. The structure 7a–2 growing in a zigzag shape is similar to the structure 7n–1. The other structures are higher energy, and the structures 7a–1 and 7a–2 may compete with each other to become the most stable anionic P₂B₇⁻ cluster.

In general, it can be seen from Figure 2 that any three atoms can preferentially form stable triangles and grow in a planar network.

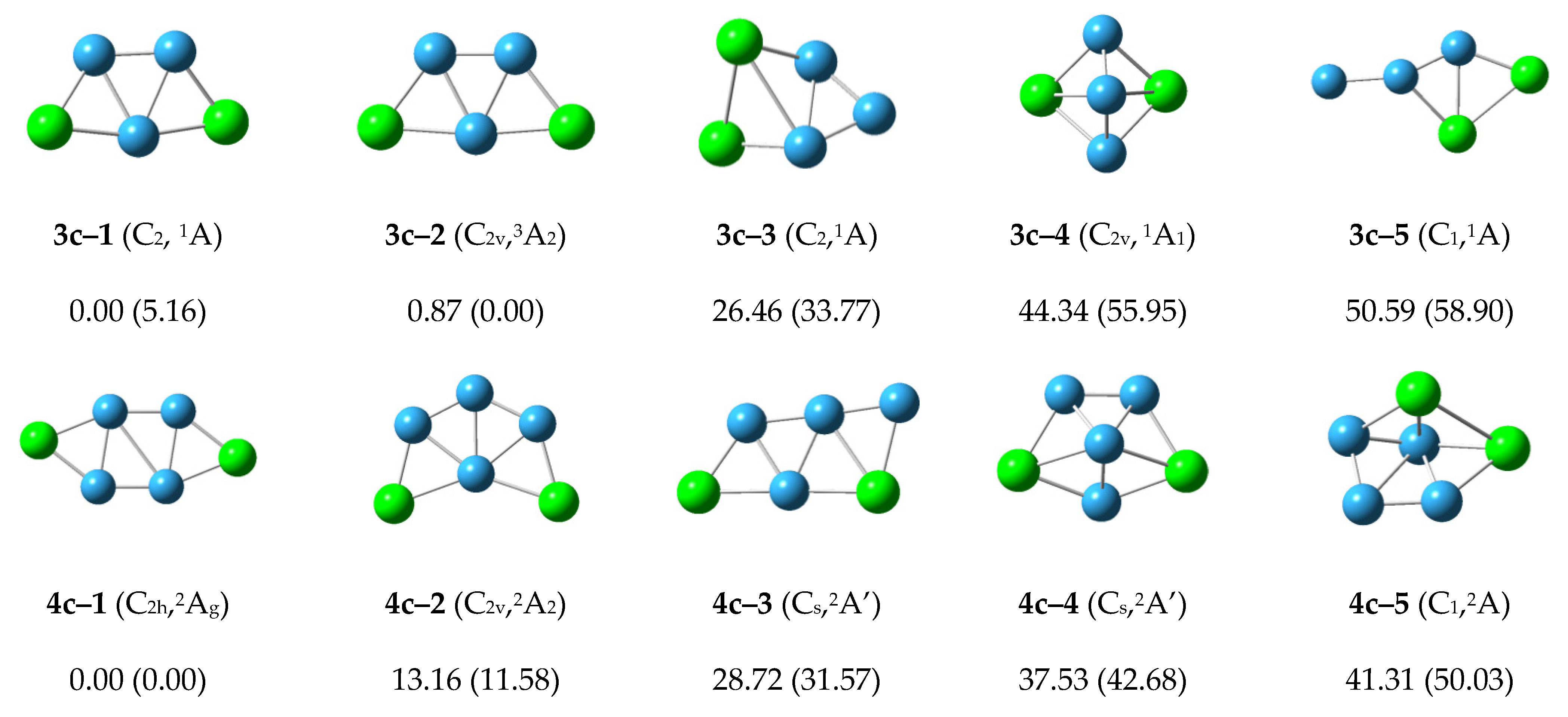
3.1.3. Low-Lying Isomers of Cationic P₂B_n⁺ (n = 3–7) Clusters

The low-lying isomers for each cationic P₂B_n⁺ cluster are shown in Figure 3. For the cationic P₂B₃⁺ cluster, the lowest energy structure 3c–1 with C₂ symmetry is similar to the structure 3n–1 and 3a–1. The second structure 3c–2 is 0.87 kcal/mol higher than structure 3c–1 with C_2v symmetry and ³A₂ electronic state. The relative energy of other structures is more than 20 kcal/mol. We can conclude that the structures 3c–1 and 3c–2 may compete with each other to become the most stable structure in the cationic P₂B₃⁺ cluster.

Figure 3. Optimized global minimum and low-lying isomers for cationic P₂B_n⁺ clusters. The relative energies at CCSD(T)/6–311+G(2df) level are shown below each structure. The B3LYP/6–311+G(d) energies are shown in parentheses.

Figure 3. Optimized global minimum and low-lying isomers for cationic P₂B_n⁺ clusters. The relative energies at CCSD(T)/6–311+G(2df) level are shown below each structure. The B3LYP/6–311+G(d) energies are shown in parentheses.

For the cationic P₂B₄⁺ cluster, the structure 4c–1 with C_2h symmetry has the lowest energy and is similar to the structures 4n–2 and 4a–2. The structure 4c–2 is 13.16 kcal/mol more than the energy of structure 4c–1, and is similar to the structure 4n–1 and 4a–2. The energy of the other structures is more than 20 kcal/mol, so we can conclude that the structure 4c–1 is the most stable structure in cationic P₂B₄⁺ cluster.

For the cationic P₂B₅⁺ cluster, the structure 5c–1 with C_2v symmetry has the lowest energy and is similar to the structures 5n–1 and 5a–2. The second lower energy structure 5c–2 and the other structures have higher energy. The structure 5c–1 is the most stable structure in the cationic P₂B₅⁺ cluster.

The structure 6c–1 with the lowest energy and C_2h symmetry. It grows in a zigzag shape, and is similar to the structures 6n–2 and 6a–1. The structures 6c–2, 6c–3 and 6c–4 with higher energy similar to structures 6n–3, 6n–4 and 6n–1, respectively. The other structures are higher energy, and the structure 6c–1 is the most stable structure in the cationic P₂B₆⁺ cluster.

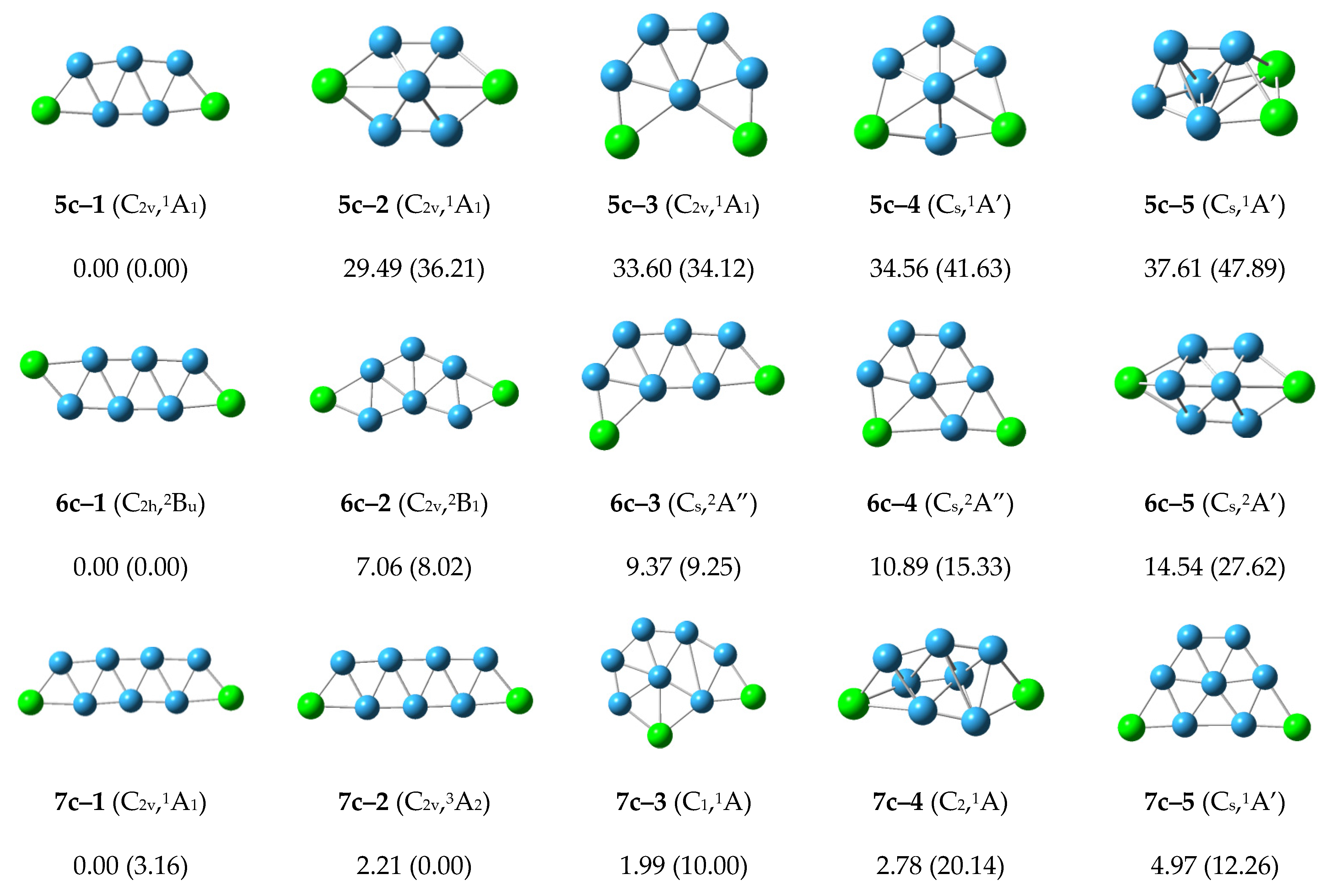
The structures 7c–1 and 7c–3 grow in a zigzag shape, and have lower energy. These are similar to the structures 7n–1 and 7a–2. The structures 7c–2 and 7c–5 grow in a net-like fashion with relative energies of 1.99 and 4.97 kcal/mol. The other structures are higher energy and the structure 7c–1 is the most stable structure in the cationic P₂B₇⁺ cluster.

According to Figure 3, the structures of the cationic P₂B_n⁺ clusters tend to preferentially show zigzag shapes and grow in a flat network. This may reduce the energy of the structures and make the structures more stable.

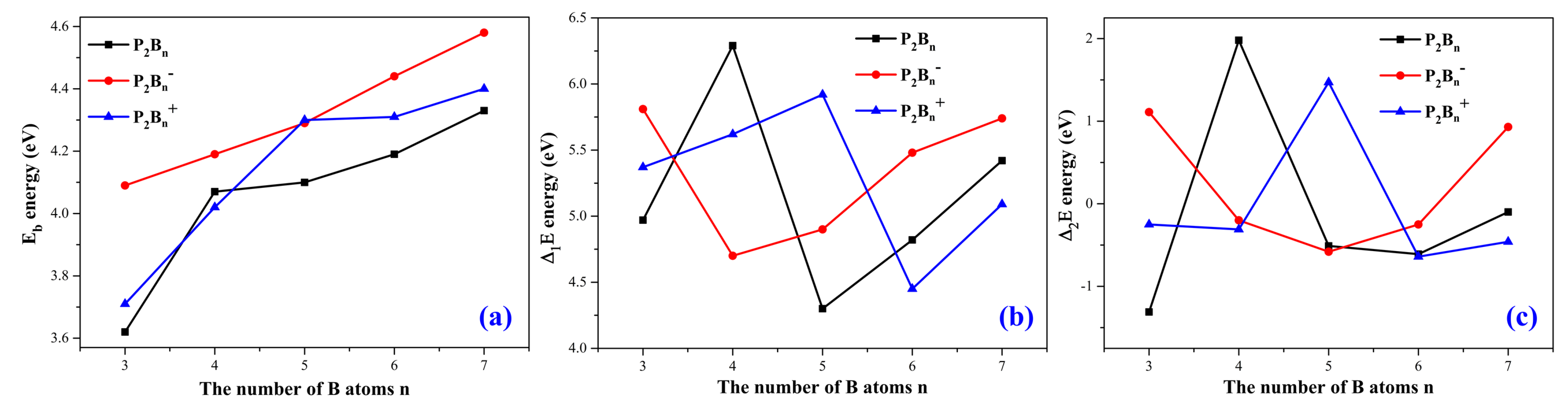
3.2. Relative Stabilities

In order to understand the stability of the structures of the phosphorus–doped boron clusters, we can calculate the average bonding energies, the fragmentation energies, and the difference energies for the clusters. They are represented by E_b, ∆E₁ and ∆E₂, respectively. These energies are calculated using the formulas above in Table 1.

The average bonding energy (E_b) of the atomic clusters P₂B_n/P₂B_n⁻/P₂B_n⁺ are shown in Figure 4a. All three curves show steady increase as the number of boron atoms increases. Therefore, an increase in the number of boron atoms can lead to higher stability of the structures.

The fragmentation energies (∆₁E) of the atomic clusters P₂B_n/P₂B_n⁻/P₂B_n⁺ are shown in Figure 4b. For the neutral P₂B_n clusters, P₂B₄ is the maximum, and P₂B₅ is the minimum. For the anionic P₂B_n⁻ clusters, as n increases, the value of ∆₁E first decreases, and then gradually increases. For the cationic P₂B_n⁺ clusters, as n increases, the value of ∆₁E first rises, then gradually decreases, and finally rises.

The second–order energy differences (∆₂E) for these clusters P₂B_n/P₂B_n⁻/P₂B_n⁺ are shown in Figure 4c. We see that this has a small range of ±2 eV.

3.3. HOMO–LUMO Gap

HOMO and LUMO are collectively referred to as frontier orbital theory, the energy difference between HOMO and LUMO is called the energy band gap. This energy difference is called the HOMO–LUMO energy level, and used to measure whether a molecule is easily excited. The smaller the gap, the easier for the molecule to be excited.

As shown in Figure 5, for the anionic P₂B_n⁻ clusters, as the number of boron atoms increases, the HUMO–LUMO gaps show a downward trend, but when the number of boron atoms is seven, the value increases rapidly. The P₂B₃⁻ and P₂B₇⁻ clusters have higher stability than the other clusters. For the neutral P₂B_n clusters, we observe an odd–even oscillation rule. Therefore, we conjecture that when the number of boron atoms is even, more energy needs to be provided when electron transition occurs. For the HOMO–LUMO gap curve of cationic P₂B_n⁺ clusters in Figure 5, the curve first rises and then continues to fall. The cationic P₂B₄⁺ cluster has the maximum, and the P₂B₇⁺ cluster has the minimum value and stability. In general, the gap values are large, ranging between 5.5 and 9.5 eV.

3.4. The Ionization Potential (IP) and Electron Affinity (EA)

Next, we consider the ionization potential and electron affinity. The definition of ionization potential and electron affinity are given below:

IP(P₂B_n) = E (optimized cation P₂B_n⁺) − E (optimized neutral P₂B_n)

EA(P₂B_n) = E (optimized neutral P₂B_n) − E (optimized anion P₂B_n⁻)

All of the IP values in Figure 6 are large and in the range of 8 eV. The P₂B₄ ionization energy in the P₂B_n system is the largest. The IP and EA values indicate that when the P₂B₄ cluster molecule gains or loses electrons, the stability of P₂B₄⁻ formed by obtaining one electron is much greater than that of P₂B₄⁺. The IP of P₂B₅ is the lowest. For the EA curve of the P₂B_n system, the lowest point is at P₂B₅. The EA values range from 2 to 3 eV with a minimum at n = 4 and 5.

3.5. Chemical Bonding Analysis

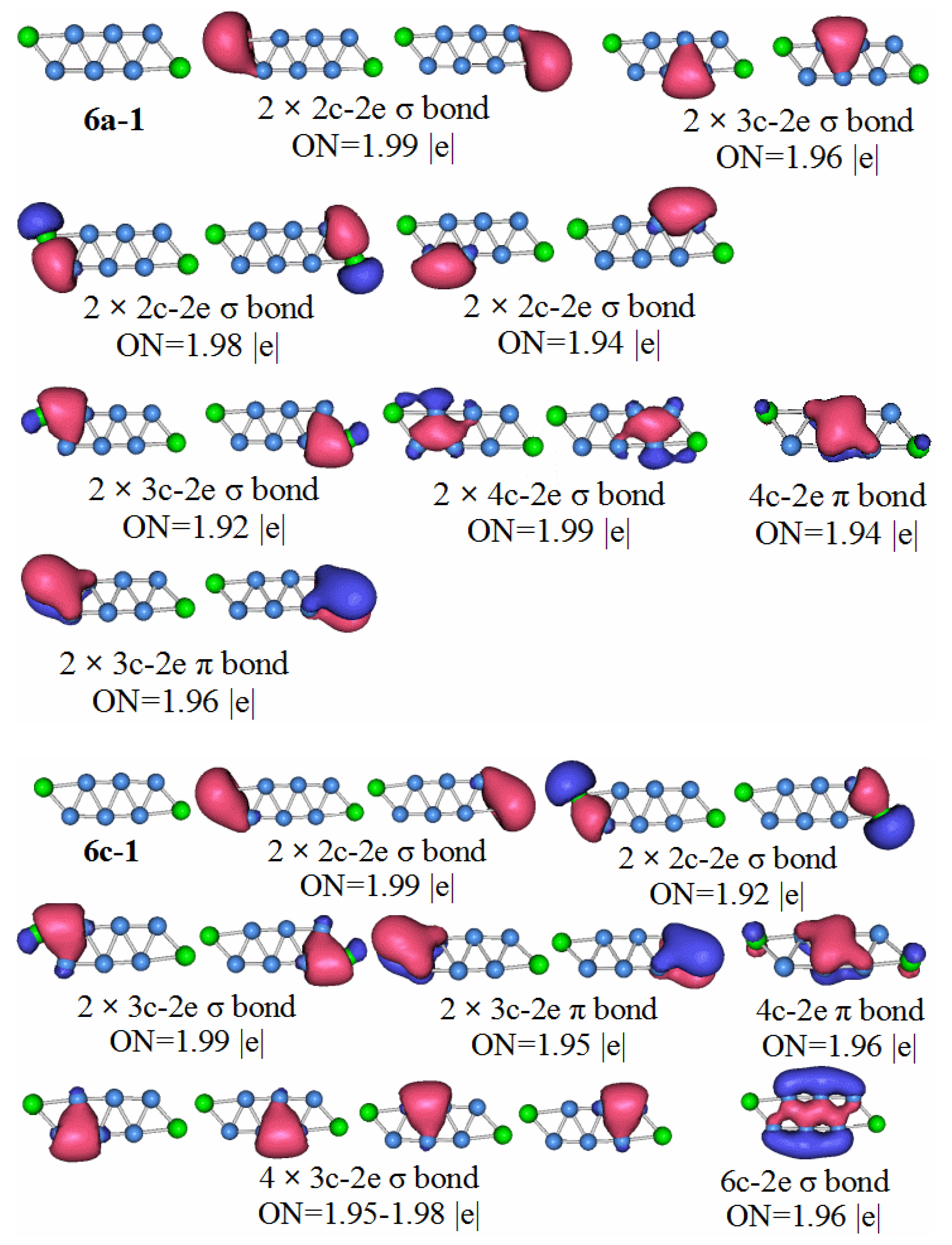
In order to have a deeper understanding of the stable structure of these clusters, chemical bond analysis is important. Below is a chemical bond analysis of the stable structure of these clusters using AdNDP code. Although the figure shows the bond formation of neutral molecules, anions, and cations, we only analyze the bond formation of neutral molecules here.

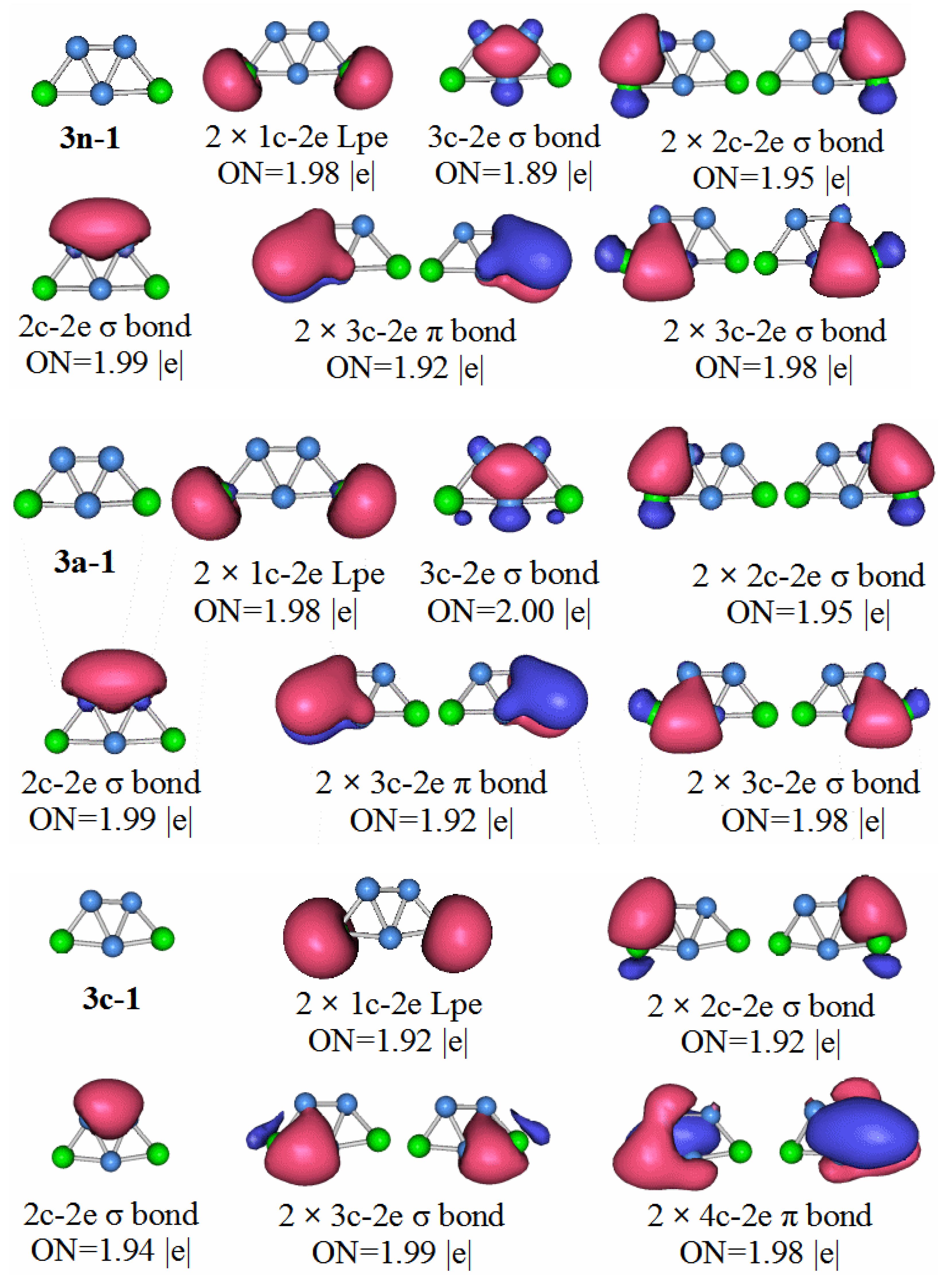
For an anion with a unit of negative charge, if its HOMO–LUMO gap is larger, it will have higher stability when it loses an electron and becomes a neutral molecule. Our previous analysis of the HOMO–LUMO gaps of cluster anion molecules shows that the HOMO–LUMO gap value of P₂B₃⁻ is larger than that of the other phosphorus-boron cluster molecules. Therefore, P₂B₃ neutral molecules should have high stability, and thus stronger chemical bonds.

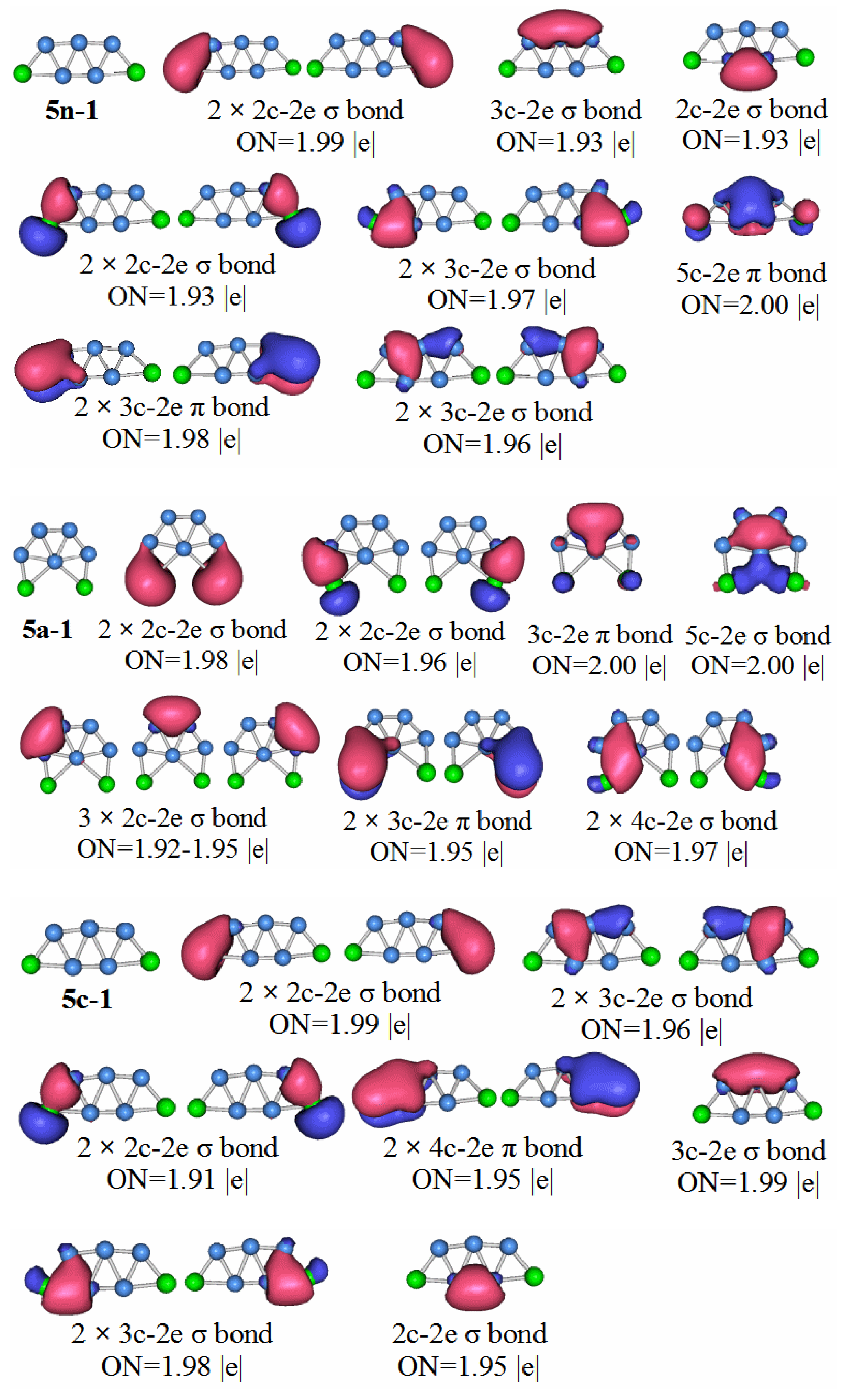
P₂B₃: According to the AdNDP analysis of the 3n–1 structure in Figure 7, it can be seen that the structure has three 2c–2e chemical bonds, one of which is the B–B bond. The other two are P–B bonds. The structure also has two 3c–2e B–P–B σ bonds, and one 3c–2e B–B–B σ bond, as well as two 3c–2e B–P–B π bonds. Finally, there are two lone pairs. It can be seen that the chemical bond formed by the P₂B₃ molecule has six delocalized sigma electrons, which can be regarded as having sigma electron aromaticity, and two pairs of delocalized π electrons can be regarded as having π electron aromaticity, making the P₂B₃ molecule more stable.

Compared with the P₂B₃ anion, the HOMO–LUMO gap value of P₂B₄⁻ is smaller. For neutral molecules, P₂B₄ molecules are slightly less stable than P₂B₃ molecules. The results of the chemical bond analysis of P₂B₄ molecules also support this view.

P₂B₄: Looking at the structure of 4n–1 in Figure 8, it is found that the P–B chemical bonds of the two 2c–2e bonds has ON = 1.93, and the other P–B bond of the two 2c–2e bonds has ON = 1.99. Two 2c–2e B–B bonds have ON = 1.94. Two 3c–2e P–B bonds have ON = 1.99, 3c–2e P–B π bonds with two ON = 1.89, and 4c–2e B–B bonds with ON = 1.94. The P₂B₄ molecule has two pairs of sigma electrons connected. This can be regarded as having sigma electron antiaromaticity, which is not conducive to the stability of P₂B₄. The two pairs of π delocalized π electrons can be regarded as having π electron aromaticity, so the P₂B₄ molecule is stable. This stability is slightly weaker than the P₂B₃ molecule.

Compared with the previous HOMO–LUMO gap of P₂B₃⁻ and P₂B₄⁻, the value of P₂B₅⁻ is smaller. It shows that in terms of stability, the P₂B₅ molecule is weaker than the previous two types of molecules. Through the chemical bond analysis of the P₂B₅ molecule, we have also found the corresponding basis.

P₂B₅: Figure 9 shows the AdNDP analysis of the stable structure of the P₂B₅ neutral cluster. The results of the analysis are as follows, the structure contains five 2c–2e chemical bonds containing a B–B bond, two P–B bonds with ON = 1.99, and two P–B bonds of ON = 1.93. There are also seven 3c–2e chemical bonds, and two 3c–2e π bonds. In addition, a 5c–2e chemical bond with ON = 2.00. We can regard the 3c–2e sigma bonds with ON values equal to 1.97 and 1.96 as two pairs of 4c–4e sigma bonds. This means that the P₂B₅ molecules have two pairs of anti-aromatic delocalized sigma bonds, which is not conducive to the stability of the molecule. Although the P₂B₅ molecule has a large aromatic delocalized π bond, it still makes the stability of the molecule lower than that of P₂B₃ and P₂B₄.

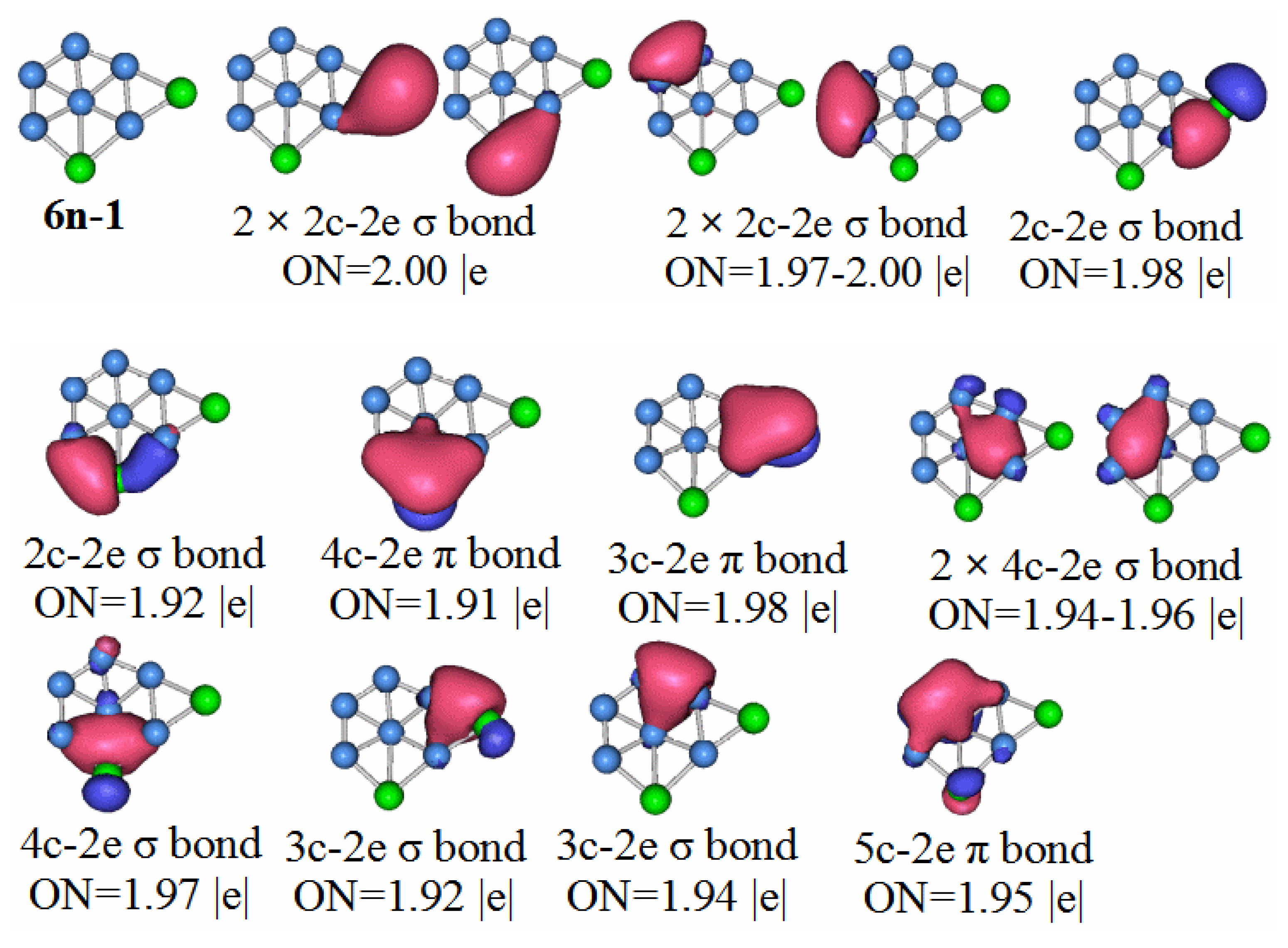
Compared with the other clusters, the HOMO–LUMO gap value of the P₂B₆ anion is the smallest. It is not difficult to conclude that the stability of neutral molecules of P₂B₆ is the worst. The symmetry of the neutral molecules of P₂B₆ is the C₁ point group. Let us look at the chemical bond analysis of the P₂B₆ molecule.

P₂B₆: According to the AdNDP analysis of 6n–1 in Figure 10, the bonding of the most stable structure of the P₂B₆ neutral cluster is as follows. The structure has six 2c–2e chemical bonds, five 3c–2e chemical bonds, two 4c–2e chemical bonds, and one 5c–2e chemical bond. Only two of the 2c–2e bonds are B–B. The rest are P–B. Three of the 3c–2e chemical bonds are σ bonds, two are π bonds, and there is a single π bond of 5c–2e. We can regard the delocalized 4c–2e and 5c–2e π bonds as antiaromatic delocalized π bonds. For the delocalized sigma bonds formed by P₂B₆ molecules, the ON values are 1.97 for the 4c–2e sigma bond, 1.92 for the 3c–2e sigma, and 1.94–1.96 for the sigma bonds. We can regard these as two sets of antiaromatic delocalized sigma bonds. This is the main reason that makes the P₂B₆ molecules weaker than other the other molecules under study.

The HOMO–LUMO gap value of the P₂B₇ anion is the largest of the molecules in this paper. Therefore, the P₂B₇ neutral molecule should be the most stable. Of course, the results of the chemical bond analysis of the neutral P₂B₇ molecule also confirmed this.

P₂B₇: For the 7n–1 structure in Figure 11, we see six 2c–2e chemical bonds, and nine 3c–2e chemical bonds. Two 2c–2e chemical bonds are B–B bonds, and the other four are P–B bonds. Five of the chemical bonds are 3c–2e σ bonds of B–B, two P–B σ bonds, and two P–B π bonds. We can divide the delocalized sigma electrons into two categories. The first category contains the 3c–2e sigma bond with ON = 1.98, the 4c–2e sigma bond with ON = 2.00, and the 3c–2e sigma bonds with ON range of 1.96 to 1.99 (we can consider these to be like a large 9c-10e aromatic delocalized sigma bond). The second type, the 3c–2e delocalized sigma bond with ON value between 1.96 and 1.99 is regarded as a pair of small aromatic sigma bonds. The π bonds in the P₂B₇ molecule can all be regarded as aromatic delocalized π bonds, which is also in line with the HOMO–LUMO gap value and high molecular stability.

3.6. Infrared Spectroscopy

In order to contribute to potential future synthesis of these systems experimentally, we simulated the infrared spectrum of the stable structure of these boron–doped boron clusters. This will allow the experimenters to compare and identify these materials using the experimental infrared spectrum. The infrared spectrum of each stable structure is shown in Figure 12.

We briefly introduce a few major peaks for each structure. The 3n–1 structure has three main absorption peaks at 576.29 cm⁻¹, 907.44 cm⁻¹, and 972.41 cm⁻¹. 576.29 cm⁻¹ is the asymmetric stretching vibration absorption peak of the central boron atom and the two peripheral boron atoms. 907.44 cm⁻¹ is the symmetric stretching vibration absorption peak of the central boron atom and the two peripheral boron atoms. 972.41 cm⁻¹ is an asymmetric stretching vibration absorption peak formed by the central boron atom and two phosphorus atoms. For the 3a-1 structure, 335.77 cm⁻¹ is the in-plane bending vibration absorption peak of the peripheral phosphorus-boron bond, and 749.73 cm⁻¹ is the asymmetric stretching vibration absorption peak of the two phosphorus-boron bonds formed by the phosphorus atom. 1001.16 cm⁻¹ is an asymmetric stretching vibration absorption peak formed by a central boron atom and two phosphorus atoms. The 3c–1 structure has a peak at 550.96 cm⁻¹, which is the out-of-plane bending vibration absorption peak of the boron-boron bond formed by the central boron atom.

The 4n-1 structure has four main absorption peaks at 387.79 cm⁻¹, 700.08 cm⁻¹, 962.17 cm⁻¹, and 1193.82 cm⁻¹, respectively. 387.79 cm⁻¹ is the in-plane bending vibration absorption peak of the phosphorus-boron bond. 700.08 cm⁻¹ is the asymmetric stretching vibration absorption peak of the boron-boron bond. 962.17 cm⁻¹ is a symmetric stretching vibration absorption peak formed by a phosphorus atom and a boron atom. 1193.82 cm⁻¹ is an asymmetric stretching vibration absorption peak formed by a phosphorus atom and a boron atom. The 4a–1 structure has 1140.42 cm⁻¹ which is a symmetric stretching vibration absorption peak formed by three peripheral boron atoms. 1270.17 cm⁻¹ is an asymmetric stretching vibration absorption peak formed by three peripheral boron atoms. The infrared spectral absorption peaks of the 4c–1 structure have been described in the absorption peaks of the above two structures.

The 5n-1 structure has 1268.67 cm⁻¹ which is a main absorption peak. It is an asymmetric stretching vibration absorption peak of three boron atoms arranged in a straight line in the structure. The 5a–1 structure has three main absorption peaks. 682.49 cm⁻¹ is an asymmetric stretching vibration absorption peak of the boron-boron bond. 1092.44 cm⁻¹ is the symmetric stretching vibration absorption peak of the peripheral boron atoms in the structure. 1221.02 cm⁻¹ is the asymmetric stretching vibration absorption peak of the peripheral boron atoms in the structure. The 5c–1 structure has 764.29 cm⁻¹ which is a symmetric stretching vibration absorption peak of a boron-boron bond.

The 6n-1 structure has four main absorption peaks. 673.90 cm⁻¹ is an asymmetric stretching vibration absorption peak of the boron-boron bond. 803.61 cm⁻¹ is the symmetric stretching vibration absorption peak of the boron-boron bond at the center of the structure. 1005.92 cm⁻¹ is an asymmetric stretching vibration absorption peak of the phosphorus-boron bond. 1175.87 cm⁻¹ is the symmetric stretching vibration absorption peak of the phosphorus-boron bond. 1222.82 cm⁻¹ in the 6a-1 structure is a symmetric stretching vibration absorption peak of the phosphorus-boron bond. 1241.85 cm⁻¹ of the 6c-1 structure is also a symmetric stretching vibration absorption peak of the phosphorus-boron bond.

The 7n–1 structure has 1115.80 cm⁻¹, which is an asymmetric stretching vibration absorption peak of phosphorus-boron bond and boron-boron bond. 1212.60 cm⁻¹ is the asymmetric stretching vibration absorption peak of the linear boron-boron bond. The structure of 7a–1 has 938.49 cm⁻¹, which is the symmetry stretching vibration absorption peak of the boron-boron bond of the central boron atom. At 1141.40 cm⁻¹, is an asymmetric stretching vibration absorption peak of a boron-boron bond formed by a central boron atom. At 1265.38 cm⁻¹, there is an asymmetric stretching vibration absorption peak of the peripheral boron-boron bond. The 7c–1 structure has only one main absorption peak, at 1307.65 cm⁻¹, which is an asymmetric stretching vibration absorption peak of a boron-boron bond arranged linearly in the structure.

3.7. The Simulated Photoelectron Spectrum

In order to facilitate future research work, we calculated the vertical detachment energies (VDE) of the ground state P₂B_n⁻ anion clusters at the B3LYP level. The vertical ionization energy of the excited state transition was calculated using TD-B3LYP. The first VDE value for each cluster is the energy difference between the lowest energy structure of the anionic cluster and their neutral species at the optimized anionic geometry. Other higher VDE values are obtained by adding the vertical excitation energy to the first VDE value. We also simulated the photoelectron spectroscopy of each stable anion structure of P₂B_n⁻.

The ground state energy of each anion cluster stabilizing structure and the excited state energies can be seen in Figure 13. The ground state energies of the 3a–1 structure to the 7a–1 structure are 3.09 eV, 2.29 eV, 2.41 eV, 2.68 eV, and 3.29 eV, respectively. Their corresponding first excited state energies are 3.32 eV, 3.50 eV, 2.78 eV, 3.44 eV, and 3.71 eV, respectively. Only the difference between the first excited state energy and the ground state energy of the 4a–1 structure and the 7a–1 structure is greater than 1 eV. The remaining differences are less than 1 eV. This shows that the 4a–1 and 7a–1 structures have stronger binding to electrons than the other three structures.

4. Conclusions

In this paper, we used high precision theoretical calculations to explore the P₂B_n/P₂B_n⁻/P₂B_n⁺ cluster systems. First, we started with the most stable structures in a global search to find the point group and electronic states of the most stable structure. In order to better understand the chemical properties, we calculated the ionization energy, electron affinity energy, and HOMO–LUMO gaps. Finally, we used the adaptive natural density partitioning method to uncover the exotic bonding details. To provide direction for experimental research, we also performed infrared spectrum and photoelectron spectroscopy simulations.

We found that the phosphorus atoms preferentially choose to occupy the peripheral positions, whereas the boron atoms tend to be in the central and inside positions of the ground state phosphorus–boron mixed clusters at each stoichiometry. The clusters have interesting shapes. Any three atoms preferentially form a stable triangle and grow with zigzag shape in a planar network. Interestingly, a series of planar hypercoordinate motifs (including tetra-, penta-, and hexa-coordination) have been discovered in the phosphorus–boron clusters. Large binding energies (3.6 to 4.6 eV/atom) and large HOMO–LUMO gaps (5 to 10 eV) indicate the high stability of the clusters. The electron affinity (EA) and ionization potential (IP) generally stay in a narrow range with the EA values between 2 and 3 eV, and the IP values ranging from 7 to 9 eV. Chemical bond analysis shows that multi-center delocalized bonds stabilize the clusters. We hope that our work inspires future experimental or theoretical work in this area.