Abstract
We have studied the superexchange interaction in doped cuprates. The AFM interaction strongly depends on the state of the lattice of a CuO layer surrounded by two LaO rock salt layers. In a static U and D stripe nanostructure, the homogeneous AFM interaction is impossible due to the periodic stripe sequence and . In a dynamic stripe nanostructure, the ideal CuO layer with nonlocal effects and the homogeneous AFM interaction are restored. However, the interaction decreases by the exponential factor due to partial dynamic quenching. The meaning of the transition from the dynamic to the static cases lies in the spontaneous -symmetry breaking with respect to the rotation of all the tilted CuO octahedra by an orientation angle (where ) in the U and D stripe nanostructure of the CuO layer. Moreover, the structural features help to study various experimental data on the charge inhomogeneity, Fermi level pinning in the p type cuprates only and time reversal symmetry breaking from a unified point of view.
1. Introduction
The unique functionality of several materials with a perovskite structure, such as cuprates Refs. [1,2,3,4], can be tuned by atomic substitutions, tolerance factor, misfit strain and pressure, which control structural tilts and nanoscale phase separation. The scanning tunneling microscopy and spectroscopy (STM and STS) [5,6,7,8,9] and advanced experimental X-ray methods [10,11,12,13,14] in a wide range of temperature and doping unambiguously indicate that there is a clear connection between the multiscale stripe texture and the quantum coherence of quasiparticles in perovskite high-Tc superconductors. The stripe charge nanostructure is also accompanied by spin inhomogeneity [15,16,17,18,19,20,21,22,23], and it is believed that high-temperature superconductivity (HTSC) originates from magnetic spin excitations that bind Cooper pairs [24,25,26,27]. The magnetic interaction in parent AFM cuprates is the well-known superexchange interaction [28]. The AFM interaction between the nearest spins of Cu ions in the CuO layer is strong (∼0.146 eV) [29], and it is much stronger than the interplanar exchange, which is mainly responsible for long-range magnetic ordering observed in undoped cuprates. For La2CuO4 (LCO), the Neel temperature is K. In the traditional picture of BCS superconductivity, magnetism destroys Cooper pairs. However, superconductivity in these HTSCs develops from a “bad metal”, whose resistivity is higher than that of BCS superconductors, and the AFM magnetism itself is related to the initial “bad metal” state, where superconductivity occurs when long-range magnetic ordering is suppressed at a relatively weak hole doping . Indeed, in the resonating-valence bond (RVB) approach and model [24,30,31,32,33], HTSC emerges due to the condensation of hole pairs, induced by the exchange interaction . Pairing of holes in this mechanism is caused by the interband transfer of quasiparticles in the CuO layer with short-range AFM ordering. Retardation effects for this mechanism are insignificant. Another view on the HTSC state in the cuprates (see for example [34,35]) is that AFM spin fluctuations become particularly longer-ranged and soft at low hole doping. In fact, there is a resonant magnetic mode [36,37,38] within the HTSC phase, where the scenario of spin fluctuations represents the lowest bosonic mode relevant for the d-wave HTSC pairing in the energy range ∼.
If the magnetic interaction is a reliable candidate that can be used as a glue for holes [39], then how will it change in the inhomogeneous nanostructure of doped 2D cuprates? Actual research on the properties of a quantum spin liquid in the double perovskite oxides with the general formula of A2Me2O6 [40,41,42] does not provide a direct answer to this question, since there is no anion substitution in the CuO2 layer of HTSC cuprates. However, the dynamical charge and spin nanoinhomogeneities are identified and discussed in current neutron and STM experiments [43,44,45,46]. Based on the large isotope effect in high-Tc superconductors with the stripe nanostructure [47,48,49], here we study superexhange interaction taking into account the phonon nature of the stripe structure in high-Tc cuprates. It will be shown that the charge and spin nanoscale phase separation can be derived at least qualitatively in the lattice approach, and the homogeneous interaction is restored at a certain hole concentration corresponding to an equal-dimensional periodic stripe structure of a linear or chess type. Furthermore, this is a good reason to test your feelings in accordance with the opinion: “…there remains the nagging feeling that even if the basic pairing mechanism ultimately arises from the short-range antiferromagnetic correlations in the layer, some important ingredient may be missing from the theory we have described” (see the review [25]). In conclusion, we discuss the observable consequences from the lattice concept of the stripe nature.
2. Color Approach to Nanoscale Inhomogeneity and D and U Stripe Structure
We focus on the tilting effects as a required attribute of the observed stripes [50]. The idea of the color approach [51] is the identification of stripes due to the tilting effects (tilting of the CuO octahedron as a whole). The fact is that different stripes differ not only in the hole concentration and spin, but in the type of nuclear configuration (see Figure 1).
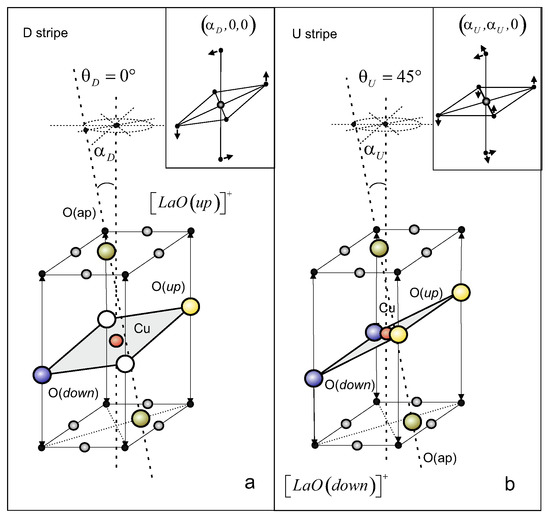
Figure 1.
View of the tilted CuO octahedra of the D (a) and U (b) stripes with different tilting effects in LSCO. The insets show the tilting effects in accordance with the Glazer’s notations [52].
We have classified the observed stripe configurations into a ninth-order symmetric Abelian group consisting of two types of stripes and rotated at the right angle relative to each other [51]. The sought stripe group represents all possible reaction products between different initial nuclear configurations in the form of group multiplication, where an ideal non-tilted prototype of the perovskite CuO octahedron is used as a group unit. In all the “structural reactions” of nuclear configurations of the stripes, the tilting angle of the perovskite octahedron with respect to the rock salt LaO layers is retained, rather than their initial symmetry, as is the case, for example, of chemical reactions, in accordance with the Woodworth–Hoffman rules [53]. The number of nuclear configurations of the observed stripes in LSCO is reduced to one of the two (where ) or (where ) stripes, and their spatial distribution in the CuO layer is represented by possible plane graphs with the chromatic number in the four-color theorem. Using four colors: —red (R), —blue (B) and also —green (G); —yellow (Y), we can always color an arbitrary plane map, and the four colors R, G, B, Y are just four subgroups in . The group can also be represented as a direct product of the subgroups of any different colors, e.g., , etc. The stripes occur as overlapping different and stripes in an sequence, for example, upon stripes disordering with doping, and vice versa, stripes can occur as overlapping and stripes in the sequence.
These two stripe sequences can be combined into one, for example into , from which, by rotating all the tilted CuO octahedra around the c axis by the angle , we can obtain other three , and . The rotation also leads to a shift over the group and transverse shift of the linear stripe and diagonal shift of the checkerboard structures in Figure 2. This means that the ground state of the CuO layer in Figure 2 is fourfold degenerate with respect to the rotation. Indeed, we can also form a novel JT cell (see Figure 2), and during its translation the number of hole carriers and spins in the JT cell is retained. The state of the JT cell is fourfold degenerate by the initial phase , which splits upon tunneling the CuO octahedra over the states of the and stripes. With the spontaneous -symmetry breaking, a static picture which is formed with the help of the JT cell is shown in Figure 2.
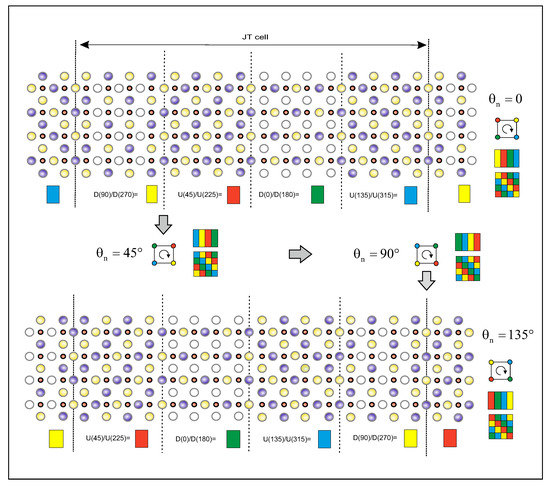
Figure 2.
Structural motive for the four-fold degenerate state of the novel JT cell. The initial phase , —color code and coloring of the graph with are also shown.
Let us consider the JT cell to understand the nature of the inhomogeneous distribution of the hole and spin density in the CuO layer. The cell has the Jahn–Teller (JT) nature, as shown in Figure 3, where the (pseudo) JT effect is non-local and associated with the presence of positively charged LaO rock salt layers. The tilting angle at the orientation angle corresponds to the relaxation modes, and the tilting angle at the orientation angle corresponds to the JT active modes.
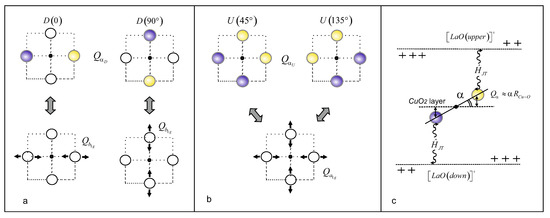
Figure 3.
Graphic scheme: (a) tilting modes active in the non-local CuO octahedron JT effect, as well as (b) relaxation modes in the D and U stripes. The arrows in (a,b) show the relationship between the tilting and conventional local modes. (c) Non-local JT effect in the CuO layer surrounded by the symmetrical LaO rock salt layers.
The absence of superconductivity in the AFM CuO layers on graphene [54,55] indicates the key role of rock salt layers in doped cuprates [4]. The direct similarity of the structures of the undoped LCO and non-JT La2NiO4 materials [56], where Ni2+ ions are in the high spin state , which also indicates the missing JT effect in the sector of the configuration space of the CuO layer. However, in the sector of the doped LSCO, the hole carriers are in the Zhang–Rice singlet state [57], and this is a JT state [58]. Moreover, the JT pseudo-effect depends on the doping concentration in a threshold way. Indeed, the hole carriers in the stripes can induce a non-local JT pseudo-effect in the i-th CuO octahedron with a Hamiltonian (see Figure 3).
in the hole sector of the configuration space of the CuO layer. Here, and are two hole parts of the quasiparticle operator
generating two-hole and states in the sector. If , then the operator takes the well-known form for the Hubbard model [59]. It is assumed that the potential is created by the LaO rock salt layers, and the equilibrium ion positions in the CuO layer can be obtained from the equation . Here, we use the set and , which are observed at K for the D stripes [50]. The concentration dependence of the magnitude in the JT effect can be obtained using the transformation in the Hamiltonian (1) with the coefficients
where and , . Then, the Hamiltonian (1) may be written as
where are the energies of the hole quasiparticles in the two-hole singlets and taking into account the JT interaction . The equilibrium tilting angle at takes the form where . Thus, in the doped LSCO cuprates, there is a hole doping level , and above which, the JT pseudo effect with can be observed. At [60] we obtain the quadratic hole doping dependence for the JT contribution:
where . Any homogeneous hole density at will be unstable to the creation of local D areas with a higher hole density and . The boundaries contribution to the lattice energy is absent, because the boundaries between the stripes are in fact atomically sharp. At the small hole doping, the total JT contribution due to the increasing width of the D stripes with the constant hole concentration . This is a —constant scenario, where .
3. Electron-Hole Pairs in the Superexchange Interaction
Let us consider the superexchange interaction in the static stripe structure in Figure 2. In the case of spontaneous -symmetry breaking (the JT cell state is non-degenerate), the doped LSCO cuprate has a static nanostructure, where the exchange interaction is missing in the D stripes (where ), and in the U stripes the superexchange interaction is equal to the one in undoped LCO materials:
Here, the interaction can be calculated in the adiabatic approximation. Superexchange interaction (6) arises as a result of the superposition of contributions from all possible virtual electron-hole pairs on the interacting i-th and j-th ions (see Figure 4). The sign of the contribution to the interaction is determined by a simple rule. If the spins of an electron and a hole in a virtual pair are equal, , this is the AFM contribution. If , it is the FM contribution. Other terms are missing, and all the electron-hole wave functions and in the hopping integral [61,62,63] in the superexchange
are calculated in the adiabatic approximation, where
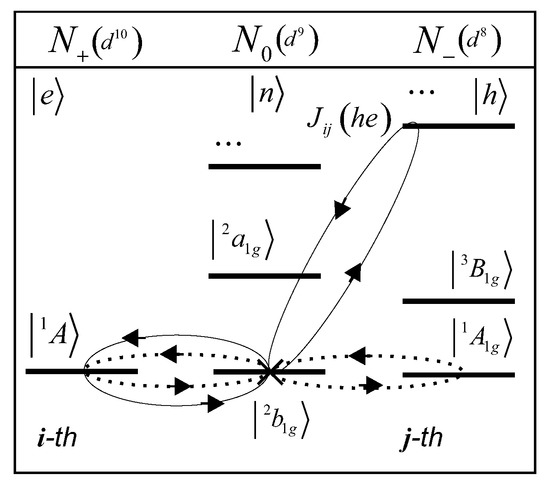
Figure 4.
Graphic representation of the electron-hole pairs for the interacting i-th and j-th Cu ions. Each pair corresponds to a double exchange loop (solid or dotted lines).
The pairs of indices and run over all possible quasiparticle excitations and between many-electron states and with the energies and in the sectors and of the configuration space in Figure 4.
These quasiparticle excitations are described by non-diagonal elements . In the Hubbard’s model there is only one such element corresponding to the excitations between lower and upper Hubbard bands. In cuprates, the main contribution from the electron-hole pair with , and has the AFM character (see Figure 4) [64], where
where and . However, the transverse percolation of the exchange interaction , where and in the octahedra CuO are in different red(R) and blue(B) stripes in the static regular stripe structure, is unlikely.
If there is no spontaneous -symmetry breaking and the JT cell state is four-fold degenerate, then the exchange interaction in the JT cell presented above is incomplete, due to the the novel configuration space. Here, the i-th CuO octahedron (the black point in Figure 5) can simultaneously be in the U and D stripe states of any color of the four possible and . In addition to the initial quasiparticles in the static stripe structure, specific hole quasiparticles appear in the CuO layer, but they are accompanied by changes and shown in Figure 5.
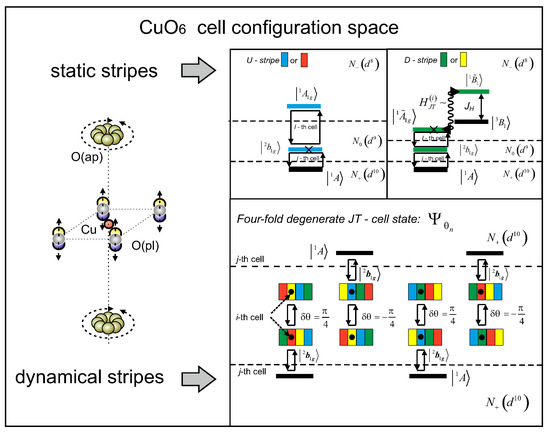
Figure 5.
Left graphical representation shows the anisotropic non-local effects in the CuO octahedron located in the JT cell with the fourfold degeneracy. The right diagram presents the electron-hole pairs contributing to the exchange interaction when both the i-th and j-th magnetic ions are in the JT cell. Here, the U and D stripe widths are the same to demonstrate the appearance of an ideal CuO layer with mobile hole carriers only with the equal stripe widths.
To obtain contributions into from the electron-hole pairs with a change in the angles and in the JT cell, we need the i-th CuO octahedron and states, where the indices U and D denote the stripe affiliation for the i-th octahedron
where and . Each of the colors in Figure 2 corresponds to a harmonic oscillator wave function with a displaced oscillator. These states differ by , and , , and the matrix elements in Equation (8) for the i-th CuO octahedron cell will be calculated with the functions and located at the four equivalent nuclear configurations of the JT cell corresponding to the phase (see black dot in Figure 5). The matrix elements contain vibronic reduction factors or partial dynamic quenching [65]:
where (—Debye frequency) and
where , , and
with . With the absence of spontaneous -symmetry breaking, the homogeneous superexchange interaction in the hole-doped LSCO cuprates is equal to
This result (14) is independent of the choice of the i and j pair of the interacting CuO octahedra and the exchange is homogeneous in the ideal CuO layer with nonlocal effects. Indeed, the neutron experiments in LCO cuprates demonstrate the thermal anisotropic motion [66] similar to the oxygen ion motion shown in Figure 5. Similar reduction factors in n doped LNCO cuprates are impossible, since there is no JT effect in the electron sector.
4. Discussion and Conclusions
The JT pseudo effect in the hole sector with the hole concentration x in the range is accompanied by the charge and spin inhomogeneities due to the nonzero tilting angle [50] of the CuO octahedra at the orientation angle in the stripes (see Figure 1). The stripes with the CuO octahedra tilted at an angle [67] and oriented at an angle form dielectric regions. The observed regular line and checkerboard stripe structures [68,69] with the chromatic number generate a novel element of symmetry in the CuO layer: simultaneously rotating all the tilted CuO6 octahedra by the angle (where ) around the c axis. We can choose a novel JT cell, the initial structure and number of hole carriers and spins in the JT cell will be retained during its translation. The state of the JT cell is fourfold degenerate by the initial phase (see Figure 2). In particular, any CuO octahedron can be located simultaneously, both in the and stripes without any well-specified orientation and tilting angles. The exchange interaction will be different, depending on whether the spontaneous phase -symmetry breaking occurs or not:
- (i)
- The spontaneous -symmetry breaking leads to a static spatial distribution of the and stripes in the doped LSCO. The static distribution origins from the different stripe width and shape, when there is no phase degeneracy. The signature of the static structure depend on the experimental timescale ranging from s to s, but is sensitive to the temperature and hole concentration [47]. In the static structure of the CuO layer, the superexchange interaction has the Anderson’s form for the interacting ions Cu2+ with spin 1/2, but is limited in space by the stripes with the zero hole concentration.
- (ii)
- Without spontaneous -symmetry breaking a novel JT cell can be constructed in the periodic stripe nanostructure with the fourfold degenerate state. The ideal CuO2 structure with nonlocal anisotropic effects and the homogeneous superexchange are restored. The stripe boundaries, spin and charge inhomogeneities disappear, and the superexchange is suppressed from its magnitude (in the undoped cuprate) by the exponential factor due to dynamic quenching for the CuO octahedra. We can evaluate the magnitude as , where , because the stripe fluctuations are observed at the temperature ∼100 K. Thus , where and eV. The strip signatures noticeably weaken with the decreasing temperature, but they are still detected as density waves of the hole pairs [43,44,45,46].
There is no direct analogy with a free rotator, since there is no continuous series of the tilted CuO octahedra for which the potential energy is minimal. Only tunneling and hopping effects are possible at the low and high temperatures, respectively. This conclusion does not contradict the results, where the low-temperature optical pump, soft X-ray probe measurements [13] detected the unexpected gapless nature of the charge ordering. Indeed, the characteristic tunneling JT splitting ≤ 10 sm (1 meV) [70] has the energy scale of the transverse fluctuations observed in [13], and the magneto-optical measurements identify the effects of time reversal symmetry breaking [71,72,73,74].
Note that a period of the charge stripes sequence is two times less than the period of the lattice stripe structure , since the hole concentration does not depend on the orientation angle . In (nonpseudo) Jahn–Teller materials, where such as 3D AMeO perovskites with regular MeO6 octahedra, the hole segregation into strip structures is impossible. The hole concentration in the D stripes does not depend on the total hole concentration x in the CuO layer, but the total D stripe area rises with increasing hole doping. This constant scenario has clear experimental features such as Fermi level pinning, where a shift of chemical potential is suppressed in the underdoped region of p type LSCO cuprates [75]. In the n type LNCO cuprates, the JT effect in configuration sector is missing. In contrast to LSCO, the superexchange interaction should not be subject to dynamic quenching, and the monotonous increase of the chemical potential is consistent with the absence of stripe fluctuations [75]. The dynamic quenching magnitude in Equation (14) decreases exponentially with the increasing Debye temperature . A similar trend for the critical temperature in the La, Y, Tl and Hg based cuprates with Debye temperatures from 200 K to 600 K was found in Refs. [76,77]. Note also that our arguments in favor of the JT nature of the charge inhomogeneity is an alternative to the fact that the competition between the kinetic energy and Coulomb repulsion could cause holes to segregate into strip structures [78].
Author Contributions
Conceptualization, V.A.G.; investigation, V.A.G. and S.I.P.; writing—review and editing, V.A.G. and S.I.P.; supervision, V.A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Russian Science Foundation, research grant RSF No.22-22-00298.
Data Availability Statement
We are grateful to the colleagues who made useful comments after the draft paper in arXiv:2205.11959 [cond-mat.str-el].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bussmann-Holder, A.; Keller, H.; Bianconi, A. (Eds.) High-Tc Copper Oxide Superconductors and Related Novel Materials; Springer Series in Materials Science; Springer International Publishing AG: Berlin/Heidelberg, Germany, 2017; Volume 255. [Google Scholar]
- Egami, T. Alex and the Origin of High-Temperature Superconductivity. In High-Tc Copper Oxide Superconductors and Related Novel Materials; Springer Series in Materials Science; Springer International Publishing AG: Berlin/Heidelberg, Germany, 2017; pp. 35–46. [Google Scholar]
- Benedek, G.; Muller, K. Phase Separation in Cuprate Superconductors; World Scientific: Singapore, 1993. [Google Scholar]
- Bianconi, A.; Agrestini, S.; Bianconi, G.; Di Castro, D.; Saini, N. A Quantum Phase Transition Driven by the Electron Lattice Interaction Gives High TC Superconductivity. J. Alloys Compd. 2001, 317, 537–541. [Google Scholar] [CrossRef]
- Zhao, H.; Ren, Z.; Rachmilowitz, B.; Schneeloch, J.; Zhong, R.; Gu, G.; Wang, Z.; Zeljkovic, I. Charge stripe crystal phase in an insulating cuprate. Nat. Mater. 2019, 18, 103–107. [Google Scholar] [CrossRef] [PubMed]
- Maggio-Aprile, I.; Berthod, C.; Jenkins, N.; Fasano, Y.; Piriou, A.; Fischer, O. Nanoscience and Engineering in Superconductivity. NanoScience and Technolog; Chapter Scanning Tunneling Spectroscopy of High Tc Cuprates; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Fischer, O.; Kugler, M.; Maggio-Aprile, I.; Berthod, C.; Renner, C. Scanning tunneling spectroscopy of high-temperature superconductors. Rev. Mod. Phys. 2007, 79, 353–419. [Google Scholar] [CrossRef]
- da Silva Neto, E.; Aynajian, P.; Frano, A.; Comin, R.; Schierle, E.; Weschke, E.; Gyenis, A.; Wen, J.; Schneeloch, J.; Xu, Z.; et al. Ubiquitous Interplay Between Charge Ordering and High-TemperatureSuperconductivity in Cuprates. Science 2014, 343, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Ma, J. Scanning Tunneling Microscopy Studies of Single Layer High-Tc Cuprate Bi2Sr2−xLaxCuO6+δ. Ph.D. Thesis, Boston College, Chestnut Hill, MA, USA, 2009. [Google Scholar]
- Lanzara, A.; Saini, N.; Brunelli, M.; Valletta, A.; Bianconi, A. Evidence for onset of charge density wave in the La-based Perovskite superconductors. J. Supercond. 1997, 10, 319–321. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A.; Poccia, N.; Bianconi, G.; Barba, L.; Gand, A.; Innocenti, D.; Karpinski, J.; Zhigadlo, N.; Kazakov, S.; et al. Inhomogeneity of charge-density-wave order and quenched disorder in a high-Tc superconductor. Nature 2015, 525, 359–362. [Google Scholar] [CrossRef]
- Comin, R.; Damascelli, A. Resonant X-ray Scattering Studies of Charge Order in Cuprates. Annu. Rev. Condens. Matter Phys. 2016, 7, 369–405. [Google Scholar] [CrossRef]
- Mitrano, M.; Lee, S.; Husain, A.; Delacretaz, L.; Zhu, M.; de la Pena Munoz, G.; Sun, S.X.-L.; Joe, Y.I.L.; Reid, A.; Wandel, S.; et al. Ultrafast time-resolved X-ray scattering reveals diffusive charge order dynamics in La2−xBaxCuO4. Sci. Adv. 2019, 5, eaax3346. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A. Functional Nanoscale Phase Separation and Intertwined Order in Quantum Complex Materials. Condens. Matter 2021, 6, 40. [Google Scholar] [CrossRef]
- Zaanen, J.; Gunnarsson, O. Charged magnetic domain lines and the magnetism of high-Tc oxides. Phys. Rev. B 1989, 40, 7391–7394. [Google Scholar] [CrossRef]
- Machida, K. Magnetism in La2CuO4 based compounds. Phys. C 1989, 158, 192–196. [Google Scholar] [CrossRef]
- Tranquada, J.M.; Sternlieb, B.J.; Axe, J.D.; Nakamura, Y.; Uchida, S. Evidence for stripe correlations of spins and holes in copper oxide superconductors. Nature 1995, 375, 561–563. [Google Scholar] [CrossRef]
- Fujita, M.; Goka, H.; Yamada, K.; Tranquada, J.M.; Regnault, L.P. Stripe order, depinning, and fluctuations in La1.875Ba0.125CuO4 and La1.875Ba0.075Sr0.050CuO4. Phys. Rev. B 2004, 70, 104517. [Google Scholar] [CrossRef]
- Hucker, M.; van Zimmermann, M.; Gu, G.D.; Xu, Z.J.; Wen, J.S.; Xu, G.; Kang, H.J.; Zheludev, A.; Tranquada, J.M. Stripe order in superconducting La2−xBaxCuO4 (0.095 < x < 0.155). Phys. Rev. B 2011, 83, 104506. [Google Scholar]
- Fujita, M.; Hiraka, H.; Matsuda, M.; Matsuura, M.; Tranquada, J.; Wakimoto, S.; Xu, G.; Yamada, K. Progress in Neutron Scattering Studies of Spin Excitations in High-Tc Cuprates. J. Phys. Soc. Jpn. 2012, 81, 011007–011025. [Google Scholar] [CrossRef]
- Wen, J.J.; Huang, H.; Lee, S.J.; Jang, H.; Knight, J.; Lee, Y.S.; Fujita, M.; Suzuki, K.M.; Asano, S.; Kivelson, S.A.; et al. Observation of two types of charge-density-wave orders in superconducting La2−xSrxCuO4. Nat. Commun. 2019, 10, 3269. [Google Scholar] [CrossRef]
- Miao, H.; Fabbris, G.; Koch, R.J.; Mazzone, D.G.; Nelson, C.S.; Acevedo-Esteves, R.; Gu, G.D.; Li, Y.; Yilimaz, T.; Kaznatcheev, K.; et al. Charge density waves in cuprate superconductors beyond the critical doping. NPJ Quantum Mater. 2021, 6, 31. [Google Scholar] [CrossRef]
- Ma, Q.; Rule, K.C.; Cronkwright, Z.W.; Dragomir, M.; Mitchell, G.; Smith, E.M.; Chi, S.; Kolesnikov, A.I.; Stone, M.B.; Gaulin, B.D. Parallel spin stripes and their coexistence with superconducting ground states at optimal and high doping in La1.6−xNd0.4SrxCuO4. Phys. Rev. Res. 2021, 3, 023151. [Google Scholar] [CrossRef]
- Anderson, P.W. The Resonating Valence Bond State in La2CuO4 and Superconductivity. Science 1987, 235, 1196–1198. [Google Scholar] [CrossRef]
- Scalapino, D. The Case for dx2-y2 Pairing in the Cuprate Superconductors. Phys. Rep. 1995, 250, 329–365. [Google Scholar] [CrossRef]
- Dagotto, E. Correlated Electrons in High-Temperature Superconductors. Rev. Mod. Phys. 1994, 66, 763–841. [Google Scholar] [CrossRef]
- Izyumov, Y.A. Spin-fluctuation mechanism of high-Tc superconductivity and order-parameter symmetry. Physics-Uspekhi 1999, 42, 215–243. [Google Scholar] [CrossRef]
- Anderson, P.W. New Approach to the Theory of Superexchange Interactions. Phys. Rev. 1959, 115, 2–13. [Google Scholar] [CrossRef]
- Coldea, R.; Hayden, S.M.; Aeppli, G.; Perring, T.; Frost, C.D.; Mason, T.E.; Cheong, S.W.; Fisk, Z. Spin Waves and Electronic Interactions in La2CuO4. Phys. Rev. Lett. 2001, 86, 5377–5380. [Google Scholar] [CrossRef] [PubMed]
- Bascaran, G.; Zou, Z.; Anderson, P.W. The resonating valence bond state and high-Tc superconductivity—A mean field theory. Solid State Commun. 1987, 63, 973–976. [Google Scholar] [CrossRef]
- Gros, C.; Joynt, R.; Rice, T.M. Antiferromagnetic correlations in almost-localized Fermi liquids. Phys. Rev. B 1987, 36, 381–393. [Google Scholar] [CrossRef] [PubMed]
- Kotliar, G.; Liu, J. Superexchange mechanism and d-wave superconductivity. Phys. Rev. B 1988, 38, 5142–5145. [Google Scholar] [CrossRef]
- Suzumura, Y.; Hasegawa, Y.; Fukuyama, H. Mean Field Theory of RVB and Superconductivity. J. Phys. Soc. Jpn. 1988, 57, 2768–2778. [Google Scholar] [CrossRef]
- Prelovsek, P.; Ramsak, A. Spin-fluctuation mechanism of superconductivity in cuprates. Phys. Rev. B 2005, 72, 012510. [Google Scholar] [CrossRef]
- Plakida, N.M.; Anton, L.; Adam, S.; Adam, G. Exchange and Spin-Fluctuation Mechanisms of Superconductivity in Cuprates. J. Exp. Theor. Phys. 2003, 97, 331–342. [Google Scholar] [CrossRef][Green Version]
- Rossat-Mignod, J.; Regnault, L.P.; Vettier, C.; Bourges, P.; Burlet, P.; Bossy, J.; Henry, J.Y.; Lapertot, G. Neutron scattering study of the YBa2Cu3O6+x system. Phys. C Supercond. 1991, 185–189, 86–92. [Google Scholar] [CrossRef]
- Fong, H.F.; Bourges, P.; Sidis, Y.; Regnault, L.P.; Bossy, J.; Ivanov, A.; Milius, D.L.; Aksay, I.A.; Keimer, B. Spin susceptibility in underdoped YBa2Cu3O6+x. Phys. Rev. B 2000, 61, 14773–14776. [Google Scholar] [CrossRef]
- Dai, P.; Mook, H.A.; Hunt, R.D.; Dogan, F. Evolution of the resonance and incommensurate spin fluctuations in superconducting YBa2Cu3O6+x. Phys. Rev. B 2001, 63, 054525. [Google Scholar] [CrossRef]
- Scalapino, D.J. A common thread: The pairing interaction for unconventional superconductors. Rev. Mod. Phys. 2012, 84, 1383. [Google Scholar] [CrossRef]
- Vasala, S.; Cheng, J.G.; Yamauchi, H.; Goodenough, J.B.; Karppinen, M. Synthesis and Characterization of Sr2Cu(W1−xMox)O6: A Quasi-Two-Dimensional Magnetic System. Chem. Mater. 2012, 24, 2764–2774. [Google Scholar] [CrossRef]
- Katukuri, V.M.; Babkevich, P.; Mustonen, O.; Walker, H.C.; Fak, B.; Vasala, S.; Karppinen, M.; Ronnow, H.M.; Yazyev, V.O. Exchange Interactions Mediated by Nonmagnetic Cations in Double Perovskites. Phys. Rev. Lett. 2020, 124, 077202. [Google Scholar] [CrossRef]
- Thakur, G.S.; Feng, H.L.; Schnelle, W.; Felser, C.; Jansen, M. Structure and magnetism of new A- and B-site ordered double perovskites ALaCuOsO6 (A = Ba and Sr). J. Solid State Chem. 2021, 293, 121784. [Google Scholar] [CrossRef]
- Li, Y.; Terzic, J.; Baity, P.G.; Popovic, D.; Gu, G.D.; Li, Q.; Tsvelik, A.M.; Tranquada, J.M. Tuning from failed superconductor to failed insulator with magnetic field. Sci. Adv. 2019, 5, eaav7686. [Google Scholar] [CrossRef]
- Du, Z.; Li, H.; Joo, S.H.; Donoway, E.P.; Lee, J.; Seamus Davis, J.C.; Gu, G.; Johnson, P.D.; Fujita, K. Imaging the energy gap modulations of the cuprate pair-density-wave state. Nature 2020, 580, 65–70. [Google Scholar] [CrossRef]
- Tsvelik, A.M. Superconductor-metal transition in odd-frequency-paired superconductor in a magnetic field. Proc. Natl. Acad. Sci. USA 2019, 116, 12729–12732. [Google Scholar] [CrossRef]
- Chen, W.; Ren, W.; Kennedy, N.; Hamidian, M.H.; Uchida, S.; Eisaki, H.; Johnson, P.D.; O’Mahony, S.M.; Seamus Davis, J.C. Identification of a nematic pair density wave state in Bi2Sr2CaCu2O8+x. Proc. Natl. Acad. Sci. USA 2022, 119, e2206481119. [Google Scholar] [CrossRef] [PubMed]
- Lanzara, A.; Zhao, G.M.; Saini, N.L.; Bianconi, A.; Conder, K.; Keller, H.; Muller, K.A. Oxygen-isotope shift of the charge-stripe ordering temperature in La2−xSrxCuO4 from X-ray absorption spectroscopy. J. Phys. Condens. Matter 1999, 11, L541–L546. [Google Scholar] [CrossRef]
- Rubio, D.; Mesot, J.; Conder, K.; Janssen, S.; Mutka, H.; Furrer, A.J. Doping and isotope dependence of the pseudogap in high-Tc cuprates observed by neutron crystal-field spectroscopy: A fast local probe. J. Supercond. 2000, 13, 727–730. [Google Scholar] [CrossRef]
- Suryadijaya, T.; Sasagawa, T.; Takagi, H. Oxygen isotope effect on charge/spin stripes in La1.8−xEu0.2SrxCuO4. Phys. C Supercond. 2005, 426–431, 402–406. [Google Scholar] [CrossRef]
- Bianconi, A.; Saini, N.L.; Lanzara, A.; Missori, M.; Rossetti, T.; Oyanagi, H.; Yamaguchi, H.; Oka, K.; Ito, T. Determination of the Local Lattice Distortions in the CuO2 Plane of La1.85Sr0.15CuO4. Phys. Rev. Lett. 1996, 76, 3412–3415. [Google Scholar] [CrossRef] [PubMed]
- Gavrichkov, V.A.; Shan’ko, Y.; Zamkova, N.G.; Bianconi, A. Is There Any Hidden Symmetry in the Stripe Structure of Perovskite High-Temperature Superconductors? J. Phys. Chem. Lett. 2019, 10, 1840–1844. [Google Scholar] [CrossRef]
- Glazer, A.M. A Brief History of Tilts. Phase Transit. 2011, 84, 405–420. [Google Scholar] [CrossRef]
- Woodward, R.B.; Hoffmann, R. The Conservation of Orbital Symmetry; Verlag Chemie GmbH; Academic Press Inc.: Cambridge, MA, USA, 1971. [Google Scholar]
- Kano, E.; Kvashnin, D.G.; Sakai, S.; Chernozatonskii, L.A.; Sorokin, P.B.; Hashimoto, A.; Takeguchi, M. One-atom-thick 2D copper oxide clusters on graphene. Nanoscale 2017, 9, 3980–3985. [Google Scholar] [CrossRef]
- Kvashnin, D.G.; Kvashnin, A.G.; Kano, E.; Hashimoto, A.; Takeguchi, M.; Naramoto, H.; Sakai, S.; Sorokin, P.B. Two-Dimensional CuO Inside the Supportive Bilayer Graphene Matrix. J. Phys. Chem. C 2019, 123, 17459–17465. [Google Scholar] [CrossRef]
- Rodriguez-Carvajal, J.; Fernandez-Diaz, M.T.; Martinez, J.L. Neutron diffraction study on structural and magnetic properties of La2NiO4. J. Phys. Condens. Matter 1991, 3, 3215–3234. [Google Scholar] [CrossRef]
- Zhang, F.C.; Rice, T.M. Effective Hamiltonian for the superconducting Cu oxides. Phys. Rev. B 1988, 37, 3759–3761. [Google Scholar] [CrossRef] [PubMed]
- Bersuker, G.I.; Gorinchoy, N.N.; Polinger, V.Z.; Solonenko, A.O. Jahn-Teller Mechanism of Coupling in the HTSC. Supercond. Phys. Chem. Eng. 1992, 5, 1003–1013. [Google Scholar]
- Hubbard, J. Electron correlations in narrow bands. Proc. Roy. Soc. 1964, 84, 455–560. [Google Scholar] [CrossRef]
- Gavrichkov, V.A.; Gavrichkov, S.A. The Jahn-Teller instability criterion for resonance impurity states. Phys. Lett. A 1990, 145, 353–357. [Google Scholar] [CrossRef]
- Gavrichkov, V.A.; Polukeev, S.I.; Ovchinnikov, S.G. Cation spin and superexchange interaction in oxide materials below and above spin crossover under high pressure. Phys. Rev. B 2020, 101, 094409. [Google Scholar] [CrossRef]
- Gavrichkov, V.A.; Polukeev, S.I.; Ovchinnikov, S.G. Contribution from optically excited many-electron states to the superexchange interaction in Mott-Hubbard insulators. Phys. Rev. B 2017, 95, 144424. [Google Scholar] [CrossRef]
- Mikhaylovskiy, R.; Huisman, T.; Gavrichkov, V.; Polukeev, S.I.; Ovchinnikov, S.; Afanasiev, D.; Pisarev, R.; Rasing, T.; Kimel, A. Resonant Pumping of d-d Crystal Field Electronic Transitions as a Mechanism of Ultrafast Optical Control of the Exchange Interactions in Iron Oxides. Phys. Rev. Lett. 2020, 125, 157201. [Google Scholar] [CrossRef]
- Gavrichkov, V.A.; Pchelkina, Z.V.; Nekrasov, I.A.; Ovchinnikov, S.G. Pressure effect on the energy structure and superexchange interaction in undoped orthorhombic La2CuO4. Int. J. Mod. Phys. B 2016, 30, 1650180. [Google Scholar] [CrossRef]
- Ham, F.S. Dynamical Jahn-Teller Effect in Paramagnetic Resonance Spectra: Orbital Reduction Factors and Partial Quenching of Spin-Orbit Interaction. Phys. Rev. 1965, 138, A1727–A1740. [Google Scholar] [CrossRef]
- Hafliger, P.S.; Gerber, S.; Pramod, R.; Schnells, V.I.; dalla Piazza, B.; Chati, R.; Pomjakushin, V.; Conder, K. Quantum and thermal ionic motion, oxygen isotope effect, and superexchange distribution in La2CuO4. Phys. Rev. B 2014, 89, 085113. [Google Scholar] [CrossRef]
- Pickett, W.E. Electronic Structure of the High-temperature Oxide Superconductors. Rev. Mod. Phys. 1989, 61, 433–512. [Google Scholar] [CrossRef]
- Seibold, G.; Lorenzana, J.; Grilli, M. Checkerboard and Stripe Inhomogeneities in Cuprates. Phys. Rev. B 2007, 75, 100505. [Google Scholar] [CrossRef]
- Okamoto, S.; Furukawa, N. Spontaneous Fourfold-symmetry Breaking Driven by Electron-lattice Coupling and Strong Correlations in High-TC Cuprates. Phys. Rev. B 2012, 86, 094522. [Google Scholar] [CrossRef]
- Bersuker, I.B. Electronic Structure and Properties of Transition Metal Compounds: Introduction to the Theory; John Wiley & Sons: New York, NY, USA, 2010. [Google Scholar]
- Xia, J.; Beyersdorf, P.T.; Fejer, M.M.; Kapitulnik, A. Modified Sagnac interferometer for high-sensitivity magneto-optic measurements atcryogenic temperatures. Appl. Phys. Lett. 2006, 89, 062508. [Google Scholar] [CrossRef]
- Xia, J.; Schemm, E.R.; Deutscher, G.; Kivelson, S.A.; Bonn, D.A.; Hardy, N.W.; Liang, R.; Siemons, W.; Koster, G.; Fejer, M.M.; et al. Polar Kerr-Effect Measurements of the High-Temperature YBa2Cu3O6+x Superconductor: Evidence for Broken Symmetry near the Pseudogap Temperature. Phys. Rev. Lett. 2008, 100, 127002. [Google Scholar] [CrossRef]
- Li, L.; Alidoust, N.; Tranquada, J.M.; Gu, G.D.; Ong, N.P. Unusual Nernst Effect Suggesting Time-Reversal Violation in the Striped Cuprate Superconductor La2−xBaxCuO4. Phys. Rev. Lett. 2011, 107, 277001. [Google Scholar] [CrossRef]
- He, R.H.; Hashimoto, M.; Karapetyan, H.; Koralek, J.D.; Hinton, J.P.; Testaud, J.P.; Nathan, V.; Yoshida, Y.; Yao, H.; Tanaka, K.; et al. From a Single-Band Metal to a High-Temperature Superconductor via Two Thermal Phase Transitions. Science 2011, 331, 1579. [Google Scholar] [CrossRef]
- Harima, N.; Matsuno, J.; Fujimori, A.; Onose, Y.; Taguchi, Y.; Tokura, Y. Chemical potential shift in Nd2−xCexCuO4: Contrasting behavior between the electron- and hole-doped cuprates. Phys. Rev. B 2001, 64, 220507. [Google Scholar] [CrossRef]
- Ledbetter, H.; Kim, S.; Roshko, A. Critical-temperature/Debye-temperature correlation in (La-M)2CuO4 superconductors. Phys. C 1991, 190, 129–130. [Google Scholar] [CrossRef]
- Ledbetter, H. Dependence of on Debye temperature OD for various cuprates. Phys. C 1994, 235–240, 1325–1326. [Google Scholar] [CrossRef]
- Imada, M. Charge Order and Superconductivity as Competing Brothers in Cuprate High-Tc Superconductors. J. Phys. Soc. Jpn. 2021, 90, 111009. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).