Abstract
Low-temperature dielectric properties of charge/orbital-ordered manganite, Pr1−xCaxMnO3 for 0.40 ≤ x ≤ 0.50, was investigated systematically as a function of Ca content, x. The Ca content dependence of dielectric permittivity and dissipation factor exhibited distinct maxima near x~0.45. The overall dielectric response of charge-ordered Pr1−xCaxMnO3 was dominated by dielectric polarization induced by polaron hopping and exhibited thermally activated relaxation behaviour. The thermally activated dielectric relaxation behaviour over the investigated temperature range was further analysed with the help of two models: the small polaron hopping model and the Mott three-dimensional variable range hopping model. The estimated polaron transport parameters also displayed non-monotonic variation with x and exhibited a broad minima between x = 0.425 and 0.45. Considering the previous work reported so far, the charge order pattern of Pr1−xCaxMnO3 below x = 0.425 was most likely to be of Zener-polaron type, while near x = 0.50 was checker-board type and for in-between compositions; neither pure checker-board type nor pure Zener-polaron type can be considered a ground state. The observed results suggest that a modulation of the checkerboard-type charge/orbital ordering pattern in Pr1−xCaxMnO3 possibly takes place in the Ca content range of investigation, 0.40 ≤ x ≤ 0.50.
1. Introduction
Mixed valence perovskite manganite has renewed considerable interest after the discovery of colossal magnetoresistance [1,2]. The physical property of manganite involves a complex interplay among the charge, spin, and orbital degree of freedoms of an electron [1]. It leads to the appearance of a wide variety of competitive electronic phases with comparable energy scale across a phase diagram, principally, the antiferromagnetic insulating (AFMI) phase, ferromagnetic metallic (FMM) phase, ferromagnetic insulating (FMI) phase, paramagnetic insulating (PMI) phase, etc. The delicate balance among these diverse phases can be easily tuned through minute external or internal perturbations, and accordingly, physical properties can be manipulated [1,2,3,4]. Of particular importance to the present investigation is the charge/orbital ordered insulating (COI) phase in Pr1−xCaxMnO3 (PCMO), which appears along with the CE-type of antiferromagnetic (AF) order in almost all perovskite-type manganite near the half doping (x = 0.5), where the presence of an equal amount of Mn3+ and Mn4+ is expected [5,6]. In general, for large bandwidth perovskite manganite, the COI phase appears only in a narrower doping range near x = 0.5 [6]. However, for a narrow bandwidth manganite, such as PCMO, it is quite striking that the COI phase exists over a wider range of doping, i.e., [7,8,9]. The high-temperature phase of PCMO is PMI, where all the Mn sites appear to be equivalent. Below a critical temperature (e.g., TCO~250 K for x = 0.5), the charge/orbital ordering transition occurs, being concomitant with a structural transition and two distinct charge sites, Mn3+ and Mn4+, which are stabilised by strong Coulomb interaction along with the co-operative Jahn–Teller distortion of MnO6 octahedra [9,10,11,12]. Further lowering of the temperature of the PCMO also leads to exhibition of a paramagnetic to antiferromagnetic transition (e.g., TN~175 K for x = 0.5), which is also associated with an incommensurate to commensurate charge ordering transition [12].
The ground state of PCMO near half filling is still an unresolved question, despite the existence of extensive studies. Goodenough [5] proposed checkerboard-type (CB-type) charge/orbital ordering, which seems to realise exactly at half filling, x = 0.5. This phase assumes a Mn-site-centred charge/orbital order. Another state, namely, bond-centred charge order, was proposed by Daoud-Aladine et al. from the analysis of neutron diffraction data close to x = 0.40 [13]. In between, neither pure CB-type nor pure Zener polaron can be considered as a ground state; instead, the coexistence of the CB-type of charge/orbital and Zener-polaron-type (ZP-type) orderings can be present [14,15,16]. Interestingly, the coexistence of CB-type (site-centred) and ZP-type (bond-centred) ordering in intermediate compositions 0.40 < x < 0.50 can break the inversion symmetry and can give rise to ferroelectric instability [16]. Several experimental efforts have been devoted in order to investigate the role of charge/orbital ordering in intrinsic dielectric response of PCMO, but ferroelectric instability due to charge/orbital ordering in PCMO has never been found experimentally [17,18,19,20,21]. The anomalous increase in dielectric constant at the vicinity of TCO in PCMO affirms the significant role of charge/orbital ordering in intrinsic dielectric response [19,20]. Lopes et al., by measuring the electric field gradient (EFG) in PCMO, revealed a typical signature of phase transition involving long range ordering of local dipoles, confirming ferroelectric instability at least in the local scale due to charge/orbital ordering [22]. Therefore, it is expected that the nature charge/orbital ordered phase in PCMO is not essentially the same across the doping range ; instead, there is a possibility of evolution/modulation of the charge ordering pattern. In spite of such expectations, there is no one reported clear piece of evidence for such modulation of the charge ordering pattern. However, in our earlier report, we showed abrupt changes in thermoelectric power and saturation magnetisation in PCMO at x~0.425, which is interpreted as a phase boundary between two different charge/orbital ordered phases [23].
In the present study, we considered Ca content dependence of the crystal structure and dielectric properties in the charge-ordered manganite PCMO near half filling () with a close variation of Ca content, x. Abrupt change in the dielectric properties near x~0.45 was demonstrated. The distinct maxima in dielectric permittivity and in dissipation factor were observed near x~0.45. The observed dielectric relaxation in PCMO originated from thermally activated polaron hopping, and transport parameters associated with polaron hopping also exhibited an abrupt change below x~0.45. The observed results were interpreted as a signature of phase transition between two different charge/orbital ordered phases, possibly between CB-type charge/orbital ordered phase and ZP-type ordered phase.
2. Results
The systematic investigation of the crystal structure of PCMO for 0.4 ≤ x ≤ 0.5 was conducted by employing high-resolution X-ray diffraction (HRXRD). All the compositions were found to be single phased, and at room temperature, they exhibited an orthorhombic unit cell with a Pnma space group. Estimated unit cell parameters, a, b, and c and cell volume V from the refinement of HRXRD data were found to be decreased monotonically as Ca content, x, gradually increased (Figure 1), which was in accordance with the smaller ionic radius of Ca+ than that of Pr+.
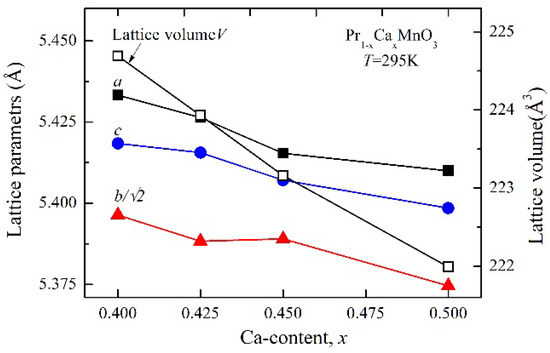
Figure 1.
Room temperature variation of unit cell parameters (a, b, c) and unit cell volume, V, of Pr1−xCaxMnO3 with orthorhombic (Pnma) setting as a function of Ca content, x. Connecting lines exist to guide the eye.
The real part of dielectric permittivity, ϵ’(ω, T), versus temperature (T) patterns measured for several frequencies across the temperature range 4−150 K are shown in the upper panels of Figure 2 for representative samples of PCMO with Ca contents: x = 0.40, 0.45, and 0.5. The dissipation factor D(ω, T) versus the T plot for those compositions are also shown in the lower panels of Figure 2. A typical feature of dielectric relaxation behaviour for all the samples was observed clearly. At temperatures above 100 K, ϵ’(ω, T) reached a value as high as ε’~104 with almost no variation with temperature and frequency, and with decreasing temperature, ϵ’(ω, T) showed step-like decrease and attained a temperature- and frequency-independent value of about ϵ’~30−50. The characteristic temperature (T) at which the inflection in ϵ’(ω, T) occurred was also associated with a peak in the corresponding D(ω, T) versus the T plot, which gradually shifted towards the higher temperature with increasing frequency. This confirmed the thermally activated dielectric relaxation process [17,18].
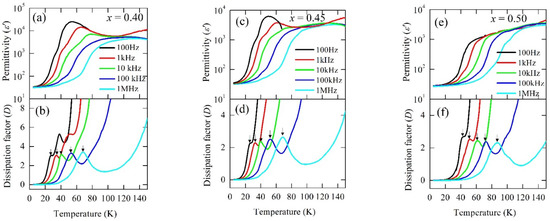
Figure 2.
Dielectric properties of Pr1−xCaxMnO3 samples measured as a function of temperature for test frequencies 100 Hz, 1 kHz, 10 kHz, 100 kHz, and 1 MHz. The temperature variation of the real part of the dielectric permittivity (ε’) for Ca content (a) x = 0.40, (c) x = 0.45, and (e) x = 0.50 (upper panels) and dissipation factor (D) for (b) x = 0.40, (d) x = 0.45, and (f) x = 0.50 (lower panels). Arrows indicate the peak positions.
The isothermal measurements of the real part of the dielectric permittivity ϵ’(ω) and dissipation factor D(ω) as a function of frequency were performed at T = 4.5 K and are shown in the upper and lower panels of Figure 3a, respectively. The dielectric response in PCMO at a higher temperature is usually dominated by the dielectric polarisation induced by polaron hopping and exhibits thermally activated relaxation behaviour [18].
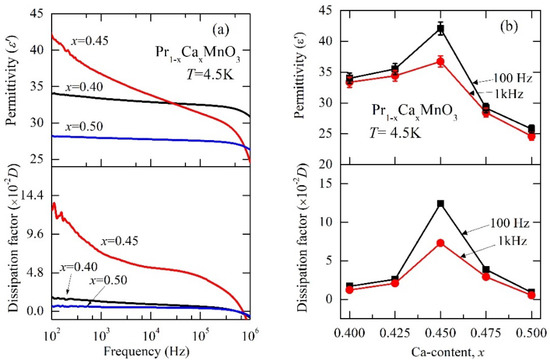
Figure 3.
Dielectric properties of Pr1−xCaxMnO3 samples measured at 4.5 K. (a) Typical frequency dispersion pattern of the real part of dielectric permittivity (upper panel) and the dissipation factor (lower panel) for Pr1−xCaxMnO3 samples with different Ca content, x. (b) The Ca content, x, variations of the real part of the dielectric permittivity (upper panel) and dissipation factor (lower panel) for 100 Hz and 1 KHz as a function of x. Connecting lines exist to guide the eye.
However, at a sufficiently low temperature, the thermally activated charge carriers were frozen out, the dielectric response was free from the relaxation behaviour due to polaron hopping, and the dielectric response was dominated by the ionic lattice contributions [24,25]. As shown in Figure 3a, the frequency window (100 Hz to 1 MHz) over which the ϵ’(ω) and D(ω) were measured was free from the typical dielectric relaxation due to polaron hopping and whatever frequency dispersion was observed at T = 4.5 K arose from the ionic-lattice contributions. In Figure 3b, we plotted the variation of ϵ’(x) and D(x) as functions of Ca content, x, for 100 Hz and 1 kHz frequencies. For both the frequencies, the ϵ’(ω) and D(ω) exhibited similar x-dependence, and one can observe a conspicuous peak in ϵ’(x) and D(x) at x = 0.45.
The dielectric relaxation of PCMO originated from the polarisation induced by thermally activated polaron hopping and as a signature; the shifting of peak position, T, towards the higher temperature with increasing relaxation frequency was clearly observed. Due to the presence of strong electron-phonon interactions in the charge/orbital ordered manganite, the polaron formation was inevitable and polaron hopping conduction was expected. Generally, the variable range hopping model proposed by Mott [26] has been applied to the semiconductor-like conductivity of low-bandwidth manganates, such as PCMO at low temperature [17,18]. However, impurity hopping conductivity is expected at temperatures well below half of the Debye temperature, which is of the order of θDebye~320 K [27]. In charge/orbital-ordered PCMO, below the TCO, the charge careers became localised three-dimensionally due to by strong Coulomb interaction and also by the co-operative Jahn–Teller distortion of MnO6 octahedra [10,11,12]. Therefore, hopping conduction in three dimensions is expected [17]. However, sometimes, the charge career localisation in the form of a two-dimensional stripe can also be observed for PCMO near x~0.7, i.e., above half filling [5]. Therefore, in order to understand the mechanism of dielectric relaxation due hopping conduction of a polaron, we analysed the temperature-dependent relaxation data for the temperature range of 25−90 K, using a small polaron hopping model (SPH) and also a three-dimensional Mott-variable-range hopping (VRH) model [17]. The relaxation frequency, f (or relaxation time, τ), of dielectric relaxation due to SPH is given by
where Ea is the activation energy of the polaron hopping conduction, f01 is the pre-exponential factor, and kB is the Boltzmann constant. As shown in Figure 4a, the variation of Tτ−1 was plotted as a function of 1000/T in the temperature range 25−90 K. In the low-temperature side, certain deviations of the experimental data from the linearity were observed while the plotted data were fitted with SPH using Equation (1). From the linear fit, values of Ea and f01 were estimated and plotted as functions of x in the upper and lower panels of Figure 5a, respectively.
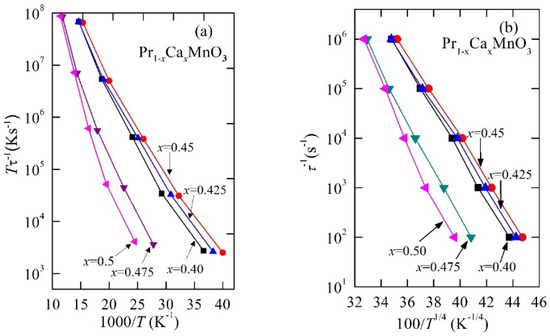
Figure 4.
(a) The small polaron hopping (SPH) and (b) the variable range hopping (VRH) plots of dielectric relaxations of Pr1−xCaxMnO3 samples with different Ca content, x = 0.40, 0.425, 0.45, 0.475, and 0.50. Connecting lines exist to guide the eye.
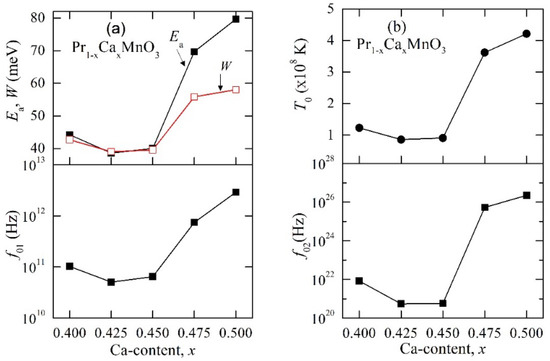
Figure 5.
(a) Variation of activation energy, Ea (upper panel), and pre-exponential factor, f01 (lower panel), with x of Pr1-xCaxMnO3 samples, obtained from the fitting of Tτ−1 vs. 1000/T by the small polaron hopping model. (b) Ca content, x, dependence of T0 and pre-exponential factor, f02, estimated from the variable range hopping model. The Ca content x-dependence of the polaron hopping energy, W (open symbol), estimated from T0, is also plotted in the upper panel of (a) along with the Ea. Connecting lines exist to guide the eye.
It can be seen that both the parameters, Ea and f01, exhibited similar x dependence. For x = 0.40 and 0.425, the Ea-value slightly decreased from 44.7 meV to 38.6 meV with an increase in x, while from x = 0.45 to 0.50, the Ea-value steadily increased from 40.3 meV to 79.6 meV with an increase in x. In an earlier publication, we reported similar x-dependence of the activation-energy-extracted temperature-dependent resistivity data of Pr1−xCaxMnO3 for , wherein the minimum Ea-value was also found near x = 0.425 [23]. Therefore, this particular Ca concentration, x = 0.425, roughly corresponded to a phase boundary between two different charge/orbital ordered phases. It is worth mentioning that the Ea-values estimated from the dielectric relaxation were fairly similar to the activation energy for polaron hopping estimated from the resistivity data, which strongly indicates the polaronic nature of charge-ordered PCMO samples [17,18].
The Mott VRH model [17,26], based on the thermally assisted hopping of charge carriers between the localised states near the Fermi level, is given by Equation (2), where f02 is the pre-exponential factor; T0 is a characteristic Mott temperature that is given by , where N(EF) is the density of localised states at the Fermi level and ξ is the decay length of the localised wave function; and for d-dimensional conduction.
In Figure 4b, we plotted the variation of τ−1 as a function of 100/T1/4 in the temperature range 25–90 K, i.e., according to the three-dimensional VRH model. The linearity of the plot indicates that the conduction mechanism in PCMO was governed by thermally assisted hopping of charge carriers in three dimensions. It is important to note that the SPH plots showed certain deviations from the linearity, which indicates that VRH was the dominant mechanism for charge conduction of PCMO in the measured temperature range. Mott activation energy, T0, and pre-exponential factor, f02, were estimated from the linear fitting τ−1 vs. 100/T1/4 plot and plotted as a function of x in the upper and lower panels of Figure 5b, respectively. Similar to the SPH model, both the parameters exhibited a broad minima near x = 0.425. In the Mott VRH mechanism, the hopping energy, W, of a polaron can be estimated using the relation . Taking T = 50 K, an average temperature around which the dielectric relaxation was analysed, we obtained the value of polaron hopping energy, W, for PCMO samples and plotted them as a function of x in the upper panel of Figure 5a alongside of Ea(x) for comparison. The W(x) also showed a similar Ca content dependence to that of the activation energy, Ea(x), estimated from the SPH model.
3. Discussion
Let us turn our discussion towards the possible origin of observed anomalous x-dependence of dielectric properties. Presently, the origin observed peak in the x-dependence of the dielectric permittivity of PCMO near x~0.45 is not clearly understood. However, two possible explanations can be drawn on the basis of earlier literature: One possibility is related to the inhomogeneous CB-type charge-ordered phase. The CB-type charge/orbital ordered phase in PCMO for was susceptible to phase separation due to the presence of an unequal amount of Mn3+ and Mn4+ ions. The evolution from homogeneous to inhomogeneous CB-type charge-ordered phase with decreasing x was found at a critical doping near x = 0.425 [22,23]. Therefore, the observed enhancement of a dielectric constant near x = 0.45 may roughly correspond to the phase boundary between inhomogeneous and homogeneous phases.
Another possibility is based on the formation of a ZP-type ordered phase. In this context, using the tight binding model calculation based on the degenerate double exchange framework, Efremov et al. showed that the character of the charge/orbital-ordered phase in PCMO was not essentially the same over the doping range ; instead, the character of the ordered phase changed in a systematic manner from x = 0.50 down to x = 0.40 [16]. The charge/orbital ordering pattern was found to have evolved from a pure CB-type charge-ordered phase at x = 0.50 to an admixture phase of CB-type- and ZP-type-ordered phases with decreasing x and finally to a pure ZP-type ordered phase at x = 0.40. The admixture phase can break the inversion symmetry and leads to the development of a local ferroelectric moment. In fact, the direct experimental evidence of subtle macroscopic ferroelectric polarisation has recently been found in remnant electrical polarisation measurements in PCMO samples [28,29], while indirect evidence of a local ferroelectric moment was confirmed earlier in EFG measurement [22]. Therefore, the observed peak in ϵ’(x) near x~0.45 may have a trace of the local ferroelectric moment due to the presence of the admixture phase composed of CB-type- and ZP-type-ordered phases. However, direct measurement of the macroscopic electric polarisation is difficult because of relatively high conductivity of PCMO samples (dissipation factor ≈0.03), which can obscure the finite macroscopic polarisation if it exists, at least at the local scale. In addition, the charge-ordered state in PCMO can be collapsed by a sufficient electric field and it provides a huge electroresistance effect that further complicates the experimental situation in terms of directly probing the macroscopic polarisation [30]. Furthermore, the PCMO sample with x = 0.45 exhibited a stronger frequency dispersion in ϵ’(ω) and D(ω) than the two end compositions x = 0.40 and 0.50. Typically, the amount of frequency dispersion in ϵ’(ω) and D(ω) depends on the degree of phase separation (electronic inhomogeneity) present in a system. Therefore, the larger amount of frequency dispersion observed in ϵ’(ω) and D(ω) for the sample with x = 0.45 indicated that this intermediate composition possesses a stronger tendency towards phase separation than the two end compositions due to coexistence of ZP-ordered and CB-type-charge/orbital-ordered phases [31]. Therefore, the observed result strongly suggests the presence of an admixture phase in the intermediate composition range.
4. Materials and Methods
For this study, polycrystalline samples with nominal compositions of Pr1−xCaxMnO3 (x = 0.40, 0.425, 0.450, 0.475, and 0.50) were synthesised by a conventional solid state reaction method. The stoichiometric mixtures of the starting materials, Pr2O3 (3N), CaCO3 (3N), and MnO2 (3N), were calcined at 1373 K in air for 24 h. The calcined powders were pressed into circular pallet form and sintered at 1673 K in air for 48 h. The detailed structural characterisations and physical property measurements were carried out on the as-synthesised samples that were reported in our earlier publication [28]. The temperature-dependent dielectric property was measured in the frequency range of 100 Hz to 1 MHz by using an LCR meter (Kesight) from 4 to 150 K in closed cycle cryostat. The circular disc-shaped samples with a typical diameter of ≈8 mm and thickness of ≈0.5 mm were used for the measurement. For the electrode, air-drying silver pasted was coated on pallet surfaces and cured at 623 K.
5. Conclusions
In summary, the low-temperature dielectric properties of charge-ordered manganite Pr1−xCaxMnO3 for were investigated systematically as a function of Ca content, x. The x dependence of dielectric permittivity exhibited distinct maxima near x = 0.45. The overall dielectric response exhibited thermally activated relaxation behaviour due to polaron hopping conduction and the estimated polaron transport parameters, i.e., the activation energy of polaron hopping and polaron hopping frequency also showed broad minima between x = 0.425 and 0.45. The enhancement of dielectric constant near x = 0.45 may roughly correspond to the phase boundary between inhomogeneous and homogeneous phases. On the other hand, if we assume the ZP-type order phase below the boundary, x = 0.425, of course, another possibility will be the phase boundary between CB-type charge/orbital phase and ZP-type-ordered phases, and the observed peak in ϵ’(x) near x~0.45 may provide a trace of the local ferroelectric moment due to the presence of admixture phase composed of CB-type-charge/orbital-ordered and ZP-type-ordered phases.
Author Contributions
Supervision, conceptualisation, reviewing and editing: P.S.M.; methodology, validation: P.S.M. and A.K.S.; formal analysis, original draft preparation, visualisation: A.K.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by DST-SERB, Government of India (grant no. CRG/2019/00006618).
Data Availability Statement
Not applicable.
Acknowledgments
The authors also gratefully acknowledge Ichiro Terasaki and Ryuji Okazaki for valuable discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tokura, T. Colossal Magnetoresistive Oxides; Gordon and Breach Science: Amsterdam, The Netherlands, 2000. [Google Scholar]
- van den Brink, J.; Khaliullin, G.; Khomskii, D.I. Colossal Magnetoresistive Manganitesed; Chatterji, T., Ed.; Kluwer: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Dagotto, E. Nanoscale Phase Separation and Colossal Magnetoresistance; Springer Series in Solid-State Sciences; Springer: New York, NY, USA, 2003. [Google Scholar]
- Uehara, M.; Mori, S.; Chen, C.H.; Cheong, S.W. Percolative phase separation underlies colossal magnetoresistance in mixed-valent manganites. Nature 1999, 399, 560. [Google Scholar] [CrossRef]
- Goodenough, J.B. Theory of the role of covalence in the perovskite-type manganites [La, M (II)] Mn O3. Phys. Rev. 1955, 100, 564. [Google Scholar] [CrossRef]
- Rao, C.N.R.; Arulraj, A.; Santosh, P.N.; Cheetham, A.K. Charge-ordering in manganates. Chem. Mater. 1998, 10, 2714. [Google Scholar] [CrossRef]
- Pollert, E.; Krupicka, S.; Kuzmicova, E. Structural study of Pr1−xCaxMnO3 and Y1−xCaxMnO3 perovskites. J. Phys. Chem. Solids 1982, 43, 1137. [Google Scholar] [CrossRef]
- Jirak, Z.; Krupicka, S.; Simsa, Z.; Dloua, M.; Vratislav, S. Neutron diffraction study of Pr1−xCaxMnO3 perovskites. J. Magn. Magn. Mater. 1985, 53, 153. [Google Scholar] [CrossRef]
- Radaelli, P.G.; Cox, D.E.; Marezio, M.; Cheong, S.W. Charge, orbital, and magnetic ordering in La0.5Ca0.5MnO3 s. Phys. Rev. B 1997, 55, 3015. [Google Scholar] [CrossRef]
- Khomski, D.I. Spin Electronics; Ziese, M., Thornton, M.J., Eds.; Springer: Berlin, Germany, 2001. [Google Scholar]
- Tomioka, Y.; Asamitsu, A.; Kuwahara, H.; Moritomo, Y.; Tokura, Y. Magnetic-field-induced metal-insulator phenomena in Pr1−xCaxMnO3 with controlled charge-ordering instability. Phys. Rev. B 1996, 53, R1689. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.H.; Mori, S.; Cheong, S.W. Anomalous melting transition of the charge-ordered state in manganites. Phys. Rev. Lett. 1999, 83, 4792. [Google Scholar] [CrossRef]
- Daoud-Aladine, A.; Rodriguez-Carvajal, J.; Pinsard-Gaudart, L.; Fernandez-Diaz, M.T.; Revcolevschi, A. Zener polaron ordering in half-doped manganites. Phys. Rev. Lett. 2002, 89, 097205. [Google Scholar] [CrossRef]
- Thomas, K.J.; Hill, J.P.; Grenier, S.; Kim, Y.; Abbamonte, P.; Venema, L.; Rusydi, A.; Tomioka, Y.; Tokura, Y.; McMorrow, D.F.; et al. Soft X-ray resonant diffraction study of magnetic and orbital correlations in a manganite near half doping. Phys. Rev. Lett. 2004, 92, 237204. [Google Scholar] [CrossRef] [PubMed]
- Grenier, S.; Hill, J.P.; Gibbs, D.; Thomas, K.J.; Zimmermann, M.V.; Nelson, C.S.; Kiryukhin, V.; Tokura, Y.; Tomioka, Y.; Casa, D.; et al. Resonant X-ray diffraction of the magnetoresistant perovskite Pr0.6Ca0.4MnO3. Phys. Rev. B 2004, 69, 134419. [Google Scholar] [CrossRef]
- Efremov, D.V.; van den Brink, J.; Khomskii, D.I. Bond-versus site-centred ordering and possible ferroelectricity in manganites. Nat. Mater. 2004, 3, 853. [Google Scholar] [CrossRef]
- Yamada, Y.; Arima, T.; Takita, K.J. Dielectric Spectra in Charge Ordering State of Pr1−xCaxMnO3. Phys. Soc. Jpn. 1999, 68, 3701. [Google Scholar] [CrossRef]
- Wang, C.C.; Zhang, L.W. Polaron relaxation related to localized charge carriers in Pr1−xCaxMnO3. New J. Phys. 2007, 9, 210. [Google Scholar] [CrossRef]
- Mercone, S.; Wahl, A.; Pautrat, A.; Pollet, M.; Simon, C. Anomaly in the dielectric response at the charge-orbital-ordering transition of Pr0.67Ca0.33MnO3. Phys. Rev. B 2004, 69, 174433. [Google Scholar] [CrossRef]
- Freitas, R.S.; Mitchel, J.F.; Schiffer, P. Magnetodielectric consequences of phase separation in the colossal magnetoresistance manganite Pr0.7Ca0.3MnO3. Phys. Rev. B 2005, 72, 144429. [Google Scholar] [CrossRef]
- Biskup, N.; de Andres, A.; Matinez, J.L. Origin of the colossal dielectric response of Pr0.6Ca0.4MnO3. Phys. Rev. B 2005, 72, 024115. [Google Scholar] [CrossRef]
- Lopes, A.M.L.; Araujo, J.P.; Amaral, V.S.; Correia, J.G.; Tomioka, Y.; Tokura, Y. New phase transition in the Pr1−xCaxMnO3 system: Evidence for electrical polarization in charge ordered manganites. Phys. Rev. Lett. 2008, 100, 155702. [Google Scholar] [CrossRef]
- Mondal, P.S.; Asai, S.; Igarashi, T.; Suzuki, T.; Okazaki, R.; Terasaki, I.; Yasui, Y.; Kobayashi, K.; Kumai, R.; Nakao, H.; et al. Possible Existence of Two Charge-Ordered Phases in Pr1−xCaxMnO3 for 0.40 ≤ x ≤ 0.50. J. Phys. Soc. Jpn. 2014, 83, 064709. [Google Scholar] [CrossRef]
- Cohn, J.L.; Peterca, M.; Neumeier, J.J. Low-temperature permittivity of insulating perovskite manganites. Phys. Rev. B 2004, 70, 214433. [Google Scholar] [CrossRef]
- Neupane, K.P.; Cohn, J.L.; Terashita, H.; Neumeier, J.J. Doping dependence of polaron hopping energies in La1−xCaxMnO3 (0 ≤ x ≤ 0.15). Phys. Rev. B 2006, 74, 144428. [Google Scholar] [CrossRef]
- Mott, N.F.; Davis, E.A. Electronic Processes in Non-Crystalline Materials, 2nd ed.; International Series of Monographs on Physics; Clarendon Press: Oxford, UK, 2012. [Google Scholar]
- Lees, M.R.; Petrenko, O.A.; Balakrishnan, G.; Paul, D.M. Specific heat of Pr0.6(Ca1−xSrx)0.4 MnO3 (0<∼ x<∼ 1). Phys. Rev. B 1999, 59, 1298. [Google Scholar] [CrossRef]
- Shukla, V.K.; Mukhopadhyaya, S.; Das, K.; Sharma, A.; Das, I. Direct experimental evidence of multiferroicity in a nanocrystalline Zener polaron ordered manganite. Phys. Rev. B 2014, 90, 245126. [Google Scholar] [CrossRef]
- Shukla, V.K.; Mukhopadhyaya, S. Emergence of low dimensional ferroelectricity in Pr0.67Ca0.33MnO3 nanocrystal arrays. RSC Adv. 2016, 6, 93130. [Google Scholar] [CrossRef]
- Asamitsu, A.; Tomioka, Y.; Kuwahara, H.; Tokura, Y. Current switching of resistive states in magnetoresistive manganites. Nature 1997, 388, 50. [Google Scholar] [CrossRef]
- Sheng, Z.; Nakamura, M.; Kagawa, F.; Kawasaki, M.; Tokura, Y. Dynamics of multiple phases in a colossal-magnetoresistive manganite as revealed by dielectric spectroscopy. Nat. Commun. 2012, 3, 944. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).