Abstract
The existence of thermally-activated quasiparticles in amphiboles is an important issue, as amphiboles are among the main hydrous complex silicate minerals in the Earth’s lithosphere. The amphibole structure consists of stripes of 6-membered TO4-rings sandwiching MO6 octahedral slabs. To elucidate the atomistic origin of the anomalous rock conductivity in subduction-wedge regions, we studied several Fe-containing amphiboles with diverse chemistry by using in situ, temperature-dependent, polarised Raman spectroscopy. The occurrence of resonance Raman scattering at high temperatures unambiguously reveal temperature-activated small polarons arising from the coupling between polar optical phonons and electron transitions within Fe2+O6 octahedra, independently of the amphibole chemical composition. The FeO6-related polarons coexist with delocalised H+; that is, at elevated temperatures Fe-bearing amphiboles are conductive and exhibit two types of charge carriers: electronic polarons with highly anisotropic mobility and H+ cations. The results from density-functional-theory calculations on the electron band structure for a selected amphibole compound with a relatively simple composition are in full agreement with experimental data. The polaron activation temperature, mobility, and polaron-dipole magnitude and alignment can be controlled by varying the mineral composition, which makes amphiboles attractive “geo-stripes” that can serve as mineral-inspired technology to design thermally-stable smart materials with anisotropic properties.
1. Introduction
Mineral-inspired technology is a key approach in materials science because by studying the relationship composition-structure-properties of naturally-occurring solids as well as their pressure-temperature (p-T) stability field, we can learn how to synthesise better-quality crystals and, in the future, how to design novel smart materials. The now famous perovskite-type oxides (ABO3) are probably the best example of a mineral group that, depending on the type of the A-site and B-site cations, exhibits a vast variety of functional properties [1] and whose performance can be tailored via compositionally-directed nanoscale structural heterogeneities [2]. Moreover, perovskite layers intercalated with metal-oxide layers build up the structure of high-temperature superconductors, the classical superstripes, exhibiting ordered defects to form lower-dimensional systems [3,4]. In fact, quasi one-dimensional (1D) and two-dimensional (2D) systems also exist in nature and they are relatively abundant. Among the rock-forming complex silicate minerals (general formula: M’kM’’lM’’’m…[SinOp]), which are essential constituents of the rocks in the Earth’s lithosphere (the rigid, outermost shell of our planet, approximately 140 km thick), there are three such types (see Figure 1): pyroxenes, whose structure consists of a quasi-1D system of SiO4-tetrahedra linked to MO6 octahedra; amphiboles, whose structure consists of a quasi-1D system of six-membered SiO4-rings linked to MO6 octahedra; and phyllosilicates, having a quasi-2D system of six-membered SiO4-rings linked to MO6 octahedra.
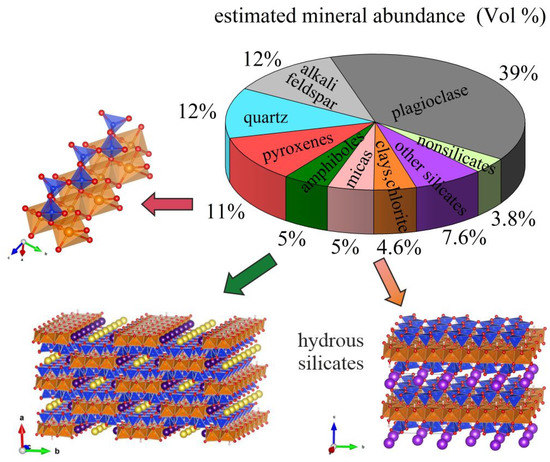
Figure 1.
Mineral abundance in the Earth’s crust (after [5]) along with sketches of the three major groups of rock-forming minerals with quasi one-dimensional (pyroxenes and amphiboles) and quasi two-dimensional (micas, clays, chlorite) structures. The TO4 tetrahedra (in blue) chiefly contain Si at the centre, while Mg, Fe2+, Al, Fe3+ commonly occupy the octahedrally coordinated sites (in orange). The plots with atomic structures in all figures were prepared using VESTA [6].
Amphiboles and phyllosilicates can also be intercalated to form biopyriboles [7] and more importantly, they contain hydroxyl groups in their structure, which makes them important hydrogen reservoirs [8]. Moreover, if divalent iron is present in the octahedrally coordinated M sites, a co-exchange Fe2+ + (OH)− → Fe3+ + O2− can take place at high temperatures without any structural breakdown. During such a reaction H+ and e− can be released and this process has been assumed to be the origin of polaron and/or hydrogen conductivity as a plausible mechanism to explain the existence of anomalously high and anisotropic lithospheric conductivity near the subduction wedges [9,10,11,12].
It should also be mentioned that most phyllosilicates are fragile and easily decompose into other minerals upon variations of T and p, whereas amphiboles are stable over a wide range of T-p conditions (up to ~1400 K and up to several GPa) [13] and can accommodate diversity of chemical elements in their structure [14,15], which makes them extremely attractive for potential technological applications such as “smart stripes”. Thus, motivated to gain further insights into the atomistic mechanism of lithospheric conductivity as well as to explore the potential of natural and/or synthetic amphiboles to be used as thermally stable materials with highly anisotropic properties, we have applied in situ high-temperature Raman spectroscopy, a method sensitive to both phonon and electron states, and complementary density-functional-theory (DFT) modelling to grunerite [16], nominally A☐BFe2+2CFe2+5Si8O22(OH)2: a ferrous amphibole mineral with a relatively simple chemistry, which can be found in nature with a near-end-member composition. The latter facilitated the direct comparison between computational and experimental results [16]. Encouraged by the results on grunerite, which unambiguously revealed the formation of thermally-activated small polarons due to the coupling between FeO6 longitudinal optical phonon and electron excitation, we extended our Raman study to include riebeckite (nominal formula given in Table 1), which was initially studied only in one scattering geometry [17]. Moreover, we thoroughly analysed by polarised Raman spectroscopy two other amphibole compounds (potassic-ferro-richterite and actinolite, see Table 1). Here we summarise the results on these four representative amphiboles (published [16] and augmented by new data) which clearly show that the occurrence of thermally-activated small polarons is a universal feature of all Fe-bearing amphiboles. Moreover, we critically analyse the relationship between the amphibole chemical composition and polaron characteristics.

Table 1.
Chemical composition of the studied amphiboles (general formula: AB2C5T8O22W2); the symbol ☐ denotes a vacant site.
2. Results
All studied samples have monoclinic C2/m structure [14]. The mineral names as well as the nominal and actual chemical formulae of the studied crystals are given in Table 1.
The general formula of amphiboles is AB2C5T8O22W2, with the octahedrally coordinated C-type cations distributed over three distinct crystallographic sites, C5 = M12M22M3, and the hydroxyl groups occupying the anionic W site, as two W(OH)− are shared between three octahedra M1M1M3 (see Figure 2a,b). The main building unit of amphiboles is called I-beam: a quasi-1D sandwich-like structure of TO4-rings linked to stripes of M(1,2,3)O6 octahedra, running along the crystallographic c axis (Figure 2b) and which to a certain extent is similar to a nanorod with a cross-section ~2.0 × 1.0 nm2.
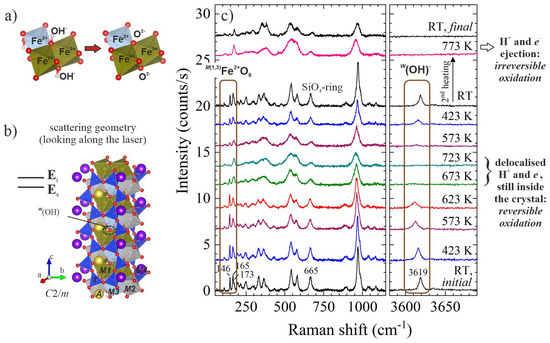
Figure 2.
Structural fragments of amphibole (AB2C5T8O22W2, B = M4, C5 = M12M22M3) and in situ high-temperature Raman spectra of riebeckite, ideally A☐BNa2C(Fe2+3Fe3+2)Si8O22(OH)2: (a) sketch of co-exchange MFe2+ + W(OH)− → MFe3+ + WO2− that can take place in amphibole upon heating; (b) view of the atomic structure of monoclinic amphibole (C2/m) as measured in backscattering geometry, with the crystallographic c axis perpendicular to the incident light polarisation Ei and Ei parallel to the scattered-light polarisation Es; (c) parallel polarised (Ei||Es) spectra of riebeckite measured in air in the scattering geometry shown in (b); data taken from [17].
2.1. First Evidence for Delocalised H+ and e− in Amphiboles at High Temperatures
While studying oxidation processes in riebeckite (nominally, A☐BNa2C(Fe2+3Fe3+2)Si8O22(OH)2) via in situ Raman spectroscopy [17], we observed a rather intriguing phenomenon. In the parallel polarised spectra collected in air with the c axis perpendicular to the incident light polarisation Ei (scattering geometry shown in Figure 2b), the OH-stretching peak near 3619 cm−1 completely disappears in the temperature range 673–723 K. This peak fully recovers upon cooling down the sample (see Figure 2c). The same behaviour is observed for the Raman peaks in the range 146–165 cm−1, which arise from MFe2+O6 vibrations [17]. These results clearly demonstrate that in the temperature range 673–723 K there are delocalised H+ and e− in the structure resulting from a reversible reduction-oxidation (redox) process: MFe2+ + W(OH)− ↔ MFe3+ + e− + WO2− + H+. Only upon further heating do the Raman spectral changes not recover upon subsequent cooling, indicating the occurrence of irreversible oxidation due to the loss of H+ and e− from the crystal bulk (see Figure 2c) at higher temperatures.
2.2. Grunerite as Model Pure MFe2+-Amphibole
To check whether this temperature-induced state of delocalised charge carriers also occurs in amphiboles that do not contain trivalent iron in the primary chemical formula, we studied in detail grunerite (nominally, A☐BFe2+2CFe2+5Si8O22(OH)2) [16]. Raman scattering experiments were performed in air as well as in N2 to better understand the role of external O2 on the process. In addition, parallel polarised spectra were collected in two different scattering geometries: with the c axis either perpendicular or parallel to Ei (see the sketches in Figure 3), to follow the effect of the I-beam orientation on the temperature-dependent inelastic light scattering by atomic vibrations.
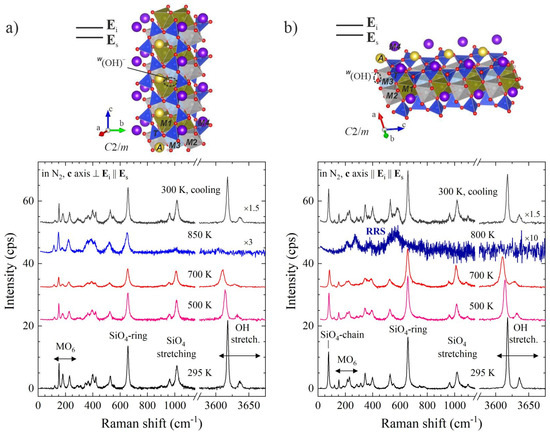
Figure 3.
Parallel polarised Raman spectra of grunerite, A☐BFe2+2CFe2+5Si8O22(OH)2, measured at different temperatures in N2 along with sketches of the amphibole structure in the corresponding scattering geometry: (a) c axis perpendicular to Ei, demonstrating the formation of mobile H+ via the disappearance of the OH-stretching peaks; (b) c axis parallel to Ei, demonstrating the formation of mobile polarons via the appearance of resonance Raman scattering (RRS). Data taken from [16].
Quite surprisingly at first glance, in the spectra collected with c||Ei not only the OH-stretching but also all silicate peaks disappeared upon heating, while new peaks, e.g., a broad signal near 570 cm−1, appeared (see Figure 3b). This behaviour is not compatible with a structural collapse of the sample because at the same temperatures the spectra collected with c ⊥ Ei exhibited all features characteristic of the amphibole framework (see Figure 3a, the spectral range below 1200 cm−1). The same drastic, orientation-dependent spectral changes are observed in air, but they occur at slightly lower temperatures, ~700 K [16]. The spectral changes fully recover when the in situ high-temperature experiments are conducted in N2 (Figure 3), whereas they are quenched upon cooling when the heating experiment is performed in air after a certain threshold temperature [16].
These observations can be easily understood if we recall the basics of the resonance Raman scattering (RRS) effect in terms of quasiparticles. Under non-resonance conditions a photon interacts solely with a phonon, whereas under resonance conditions, when an electron excitation also occurs, there is a multiple interaction among a photon, a phonon and an electron. Therefore, the RRS selection rules depend on both phonon- and electron-orbital symmetries [18,19,20]. In addition, only those polar longitudinal optical modes that are related to the electronic configuration involved in the transition are enhanced [19,20,21]. For centrosymmetrical crystals such as amphiboles, this leads to drastic changes in the spectrum because the ‘normally’ Raman-active phonon modes are non-polar and will become forbidden under resonance conditions, while the phonon modes which are ‘normally’ IR-active will be enhanced. In addition, when the electron transition occurs between Fe and O electronic levels, only polar phonons related to iron-oxygen octahedra will be enhanced, but not those from silicon-oxygen vibrations. Thus, the appearance of new peaks characteristic of FeO6 modes, e.g., near 570 cm−1 [22] (Figure 3b), along with the suppression of all silicate peaks, indicate the occurrence of thermally-activated FeO6-related small polarons due to Fröhlich-type electron-phonon interactions [16]. Moreover, when the polaron dipoles dp are parallel to the c axis, one can detect polarons in inelastic light scattering experiments only if the polarisation of the laser is parallel to the c axis (if c ⊥ Ei, the scalar product dp·Ei is zero). Hence, the strong orientational dependence of the occurrence of RRS at elevated temperatures reveals a good mutual alignment of polaron dipoles parallel to the c axis.
The experimental results are fully supported by DFT calculations of electron density of states (DOSs) for three model compounds with the structure of grunerite, but having different occupancy of the “intra-strip” octahedrally coordinated M(1,2,3) sites and the “inter-strip” M4 site [16]: M1Fe2+M2Fe2+M3Fe2+M4Fe2+, M1Fe2+M2Fe2+M3Fe2+M4Mg and M1MgM2MgM3MgM4Fe2+. The DFT modelling reveals that the energy gap Eg of grunerite (M1Fe2+M2Fe2+M3Fe2+M4Fe2+) results from a direct electron transition [16] and is approximately 0.05 eV (Figure 4a), close to the experimental value of 0.06 eV estimated from the temperature of polaron activation in air (~700 K). The projected DOS for the two imaginary compounds, M1Fe2+M2Fe2+M3Fe2+M4Mg (Figure 4b) and M1MgM2MgM3MgM4Fe2+ [16], clearly show that the energy gap is exclusively related to electron states of “intra-strip” octahedrally coordinated Fe2+. Furthermore, projected orbital DOSs of Fe and O from the M(1,2,3)O6-stripes show that the top of the valence band is formed predominantly from hybridised Fe dxy and O px levels, while the bottom of the conduction band is formed predominantly from hybridised Fe and O px levels; in other words, the electron transition across Eg is realised along the c axis, in full accordance with the strong orientational dependence of the experimentally observed RRS at high temperatures.
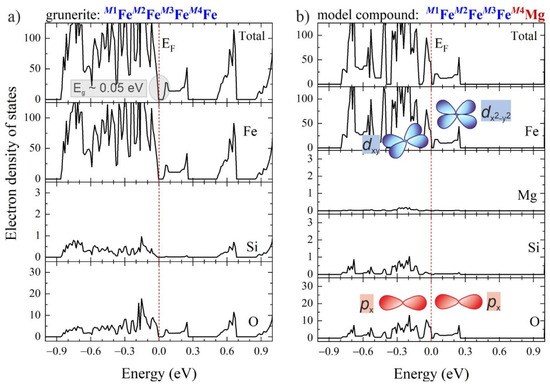
Figure 4.
Calculated total and projected electron density-of-states (DOSs): (a) for grunerite with an end-member composition A☐BFe2+2CFe2+5Si8O22(OH)2; (b) for a model compound with the structure of grunerite, but the M4 site entirely occupied by Mg, along with artistic impression of the electron orbitals dominating the top of the valence band and the bottom of conduction band, according to DOSs projected on Fe d and O p orbitals [16]. The vertical dashed lines mark the Fermi level fixed at 0 eV. Data taken from [16].
The exchange Fe2+ → Fe3+ is realised when the vibrational energy is sufficient to adjust the silicate ring geometry to the smaller size of neighboring octahedra when a polaron is formed (see Figure 5a,b). The temperature at which such a local structural modification occurs can be deduced from the minimum of the temperature dependence of the wavenumber of the ring-breathing mode near 660 cm−1, ωring(T) [17,23]. Another intriguing observation is that ωring(T) has a minimum at different temperatures when measured in different scattering geometries (Figure 5c), indicating an anisotropy in the crystal potential due to the development of a vector term δU || c, related to the polaron formation and the subsequently evolving local intrinsic electric fields. As a result, the flatting of the energy potential with temperature is faster along the I-beams than in the perpendicular direction. Hence, the anisotropy in the energy potential at elevated temperatures is additional robust evidence for the formation of polarons with aligned dipole moments. The temperature of ωring(T) minimum derived from spectra measured in the c || Ei || Es scattering geometry, T’, marks the beginning of e- delocalisation, while the temperature of ωring(T) minimum derived from spectra measured in c ⊥ Ei || Es scattering geometry, T”, marks the end of e- delocalisation and the onset of the ejection of the already-delocalised electrons from the crystal bulk. Furthermore, the width of this temperature range should be proportional to δU and hence, points out the average polaron-dipole magnitude, which allows us to compare the polaron dipole <dp> in chemically distinct amphiboles.
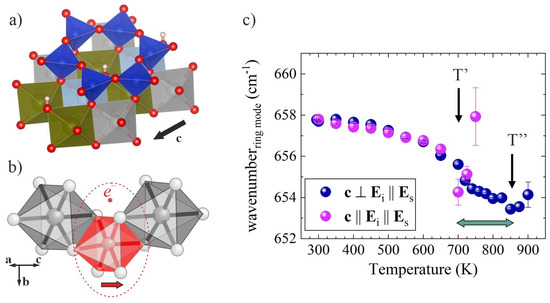
Figure 5.
Local arrangements of the amphibole structure and a selected-phonon wavenumber against temperature for grunerite, A☐BFe2+2CFe2+5Si8O22(OH)2: (a) TO4-ring linked to M(1,2,3)O6 octahedra; (b) sketch of M(1,2,3)FeO6-related polaron in amphibole; (c) temperature dependence of the ring-mode wavenumber measured in air with the c axis parallel (purple symbols) and perpendicular (blue symbols) to Ei; the horizontal double arrow indicates the temperature range between the beginning (at T’) and the end (at T”) of electron delocalisation from M(1,2,3)Fe2+.
2.3. Compositional Effects on the Polaron Characteristics
2.3.1. Mix-Valence Iron in the Octahedral Stripes
To study the effect of coexisting Fe3+ and Fe2+ in the octahedral stripes, we re-investigated riebeckite (A☐BNa2C(Fe2+3Fe3+2)Si8O22(OH)2) in both scattering geometries in N2 as well as in air [24], similar to those used for grunerite (see sketches in Figure 3). Inspection of Figure 6 shows that temperature-activated anisotropic RRS, i.e., the development of polarons with well-aligned dipoles, occurs in riebeckite and likewise in grunerite; the process is fully reversible upon heating in N2. The copresence of Fe3+ reduces both T’ and T” by ~200 K, however it does not influence |T”−T’| nor |δU|, which is ~150 K ⇔ 0.013 eV, as for grunerite.
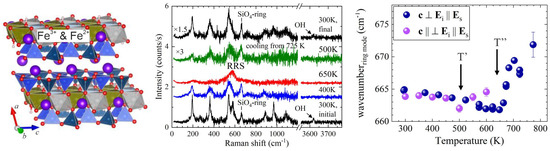
Figure 6.
Fragment of the riebeckite (A☐BNa2C(Fe2+3Fe3+2)Si8O22(OH)2) structure, along with parallel polarised spectra measured in N2 with the c axis parallel to Ei and the temperature dependence of the ring-mode wavenumber derived from spectra measured in air with the c axis parallel (purple symbols) and perpendicular (blue symbols) to Ei.
2.3.2. Filled A-Sites in the Voids Formed by the I-Beams
The effect of intercalated A-site cations was analysed by comparing the results obtained on synthetic potassic-ferro-richterite, nominally AKB(CaNa)CFe2+5Si8O22(OH)2, with those of grunerite (A☐BFe2+2CFe2+5Si8O22(OH)2). Polarons with well-aligned dipoles along the octahedral stripes also occur in this amphibole species, as revealed by the strong RRS in c || Ei || Es scattering geometry (see Figure 7). However, A-site cations slow down the re-localisation of electrons upon cooling, which is indicated by the fact that the Raman spectrum recovers 2 h after reaching room temperature. The presence of A-site cations in the voids between the I-beams decreases both T’ and T”, but, in contrast to the case of riebeckite, it also reduces |T” − T’| ⇔ |δU| to ~55 K ⇔ 0.005 eV.
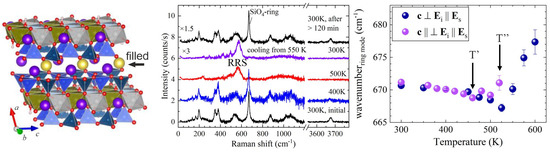
Figure 7.
Fragment of the potassic-ferro-richterite (AKB(CaNa)CFe2+5Si8O22(OH)2) structure, along with parallel polarised spectra measured in N2 with the c axis parallel to Ei and the temperature dependence of the ring-mode wavenumber derived from spectra measured in air with the c axis parallel (purple symbols) and perpendicular (blue symbols) to Ei.
2.3.3. Effect of the Fe2+ Content: Fe-Poor Magnesian Amphiboles
To check whether thermally-activated polarons are also formed in amphiboles in which iron is not the dominant element in the octahedral stripes, we analysed actinolite, nominally A☐BCa2C(Mg1−xFe2+x)5Si8O22(OH)2, with x~0.11 [25].
A complete change in the Raman-scattering selection rules is not observed for actinolite, since in actinolite Fe2+ is a substitutional defect rather than a host-matrix element. Nevertheless, RRS still appears in the spectra measured with c || Ei, but at much higher temperatures of ~1150 K (see Figure 8). In addition, after heating in air and then cooling down to room temperature, RRS is observed in both scattering geometries. This result indicates that the polaron dipoles are not mutually aligned as in the case of iron-rich amphiboles. Incidentally, after a prolonged time at room temperature in air, the intensity ratio between the strongest RRS signal (near 600 cm−1) and the strongest non-RRS peak (the SiO4-ring mode near 670 cm−1) changes. Given that Raman spectroscopy probes a surface layer of approximately 2 μm in thickness, this effect is compatible with a polaron diffusion at room temperature from the bulk to the periphery of the crystal due to ejection of e- and H+ from the surface and, consequently, the development of chemical potential [25]. The comparison of the IRRS/Iring-mode intensity ratio in the spectra measured with c || Ei and c ⊥ Ei, three days after the heating-cooling run (Figure 8), indicates that the room-temperature polaron diffusion occurs preferably along the octahedral stripes. It is also worth noting that all OH-stretching peaks (in the range of 3640–3675 cm−1) disappear at high temperature and then the peak related to hydroxyl groups attached to MgMgMg octahedral triads fully recovers at room temperature [25]. Its presence shows that even a small concentration of FeO6 polarons triggers the delocalisation of all H+ cations, i.e., even those not directly bonded to Fe-containing octahedral triads.
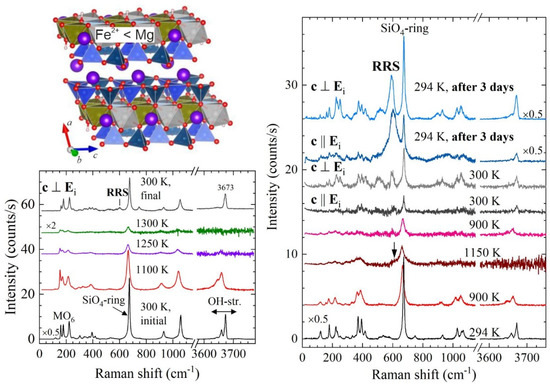
Figure 8.
Fragment of actinolite (A☐BCa2C(Mg1-xFe2+x)5Si8O22(OH)2, 0.1 < x < 0.5) structure, along with parallel polarised spectra measured in air in different scattering geometries, as labelled in the plots.
3. Discussion
The results of our in situ, high-temperature, polarised, Raman spectroscopic experiments on Fe-containing amphiboles clearly demonstrate the formation of highly anisotropic FeO6 polarons: anisotropically hopping electrons (see Figure 9a), coupled with phonons carrying the local structural distortion associated with a smaller-sized octahedron with effectively trivalent iron. The polaron activation temperature, dipole magnitude, mutual alignment and mobility can be tuned by varying the amphibole crystal chemistry. In particular, filled A-sites or substitutions of larger atomic species in the inter-stripe voids might stabilise polarons upon cooling to temperatures lower than the activation temperature.
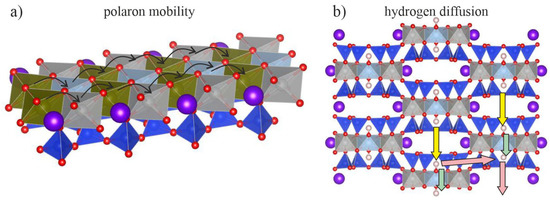
Figure 9.
Sketch of temperature-activated mobile charge carriers in amphiboles: (a) polaron mobility along the stripes of linked SiO4-rings and MO6 octahedra; (b) hydrogen diffusion in a direction perpendicular to the stripes.
At elevated temperatures mobile polarons exist along with delocalised H+ cations in both oxidising and reducing atmospheres. However, previous infrared-absorption mapping [26] has demonstrated that the diffusion of delocalised hydrogen cations is stronger across the octahedral stripes than parallel to them (see Figure 9b); this suggests that H+ cations and polarons move independently along two mutually perpendicular directions.
These results also show that even small amounts of polarons can trigger the complete delocalisation of H+ cations at high temperatures, including those not connected to Fe-containing octahedral triads; in other words, the development of FeO6 polarons facilitates the H+ diffusion. When heating in air, the maximum amount of H+ that can eject from the crystal should be equal to the initial content of divalent iron (as required by local charge balance). Therefore, due to the low concentration of Fe in Mg-dominant amphiboles, only a small amount of H+ can be ejected by the crystal. Hence, at elevated temperatures and in air conditions, even Fe-poor magnesian amphiboles are full of mobile H+, whose diffusion can potentially be controlled by chemical, temperature or electric-field gradients.
It should be mentioned that amphiboles possess a high thermal resistivity, which could be related to an intrinsic structural feature of theirs: presence of SiO4-rings linked via their apical oxygen atoms to edge-sharing MO6 octahedra. Due to the flexibility of the silicate rings to connect with neighbouring octahedra of variable size via slight tetrahedral tilting, amphiboles can incorporate a large diversity of chemical elements at the octahedrally-coordinated sites [14]; this same structural feature should also be critical for the development of hopping polarons across the crystal bulk. This hypothesis implies that, if the SiO4 tetrahedra are isolated or arranged in isolated dimers or rings, the diffusion of polarons should be much more difficult than in the case of one-dimensional systems of silicate rings, such as amphiboles. In this regard, anisotropic electrical conductivity due to the hopping of electronic polarons should be an intrinsic property of Fe-rich complex silicates with amphibole-type structure, whereas electrical conductivity due to the diffusion of H+ can be an intrinsic property of any hydrous Fe2+-bearing silicate. However, these results suggest that existing mobile polarons in quasi low-dimensional structures along with structural voids such as those in amphiboles should enhance the mobility of H+ cations.
To sum up, the implications of our study are two-fold:
- (i)
- in geophysics: we provide direct evidence for the existence of polarons with anisotropic mobility in various amphiboles to explain the anisotropic rock conductivity near subduction wedges. Thus, our results fully support the suggested mechanism of polaronic conductivity, based on in situ electrical measurements on amphiboles and amphibole-containing rocks [9,10,11].
- (ii)
- in materials science: amphiboles have the potential to be used as functional materials having two types of charge carriers with an anisotropic mobility in two mutually perpendicular directions. Synthetic amphibole counterparts with controlled chemistry can be relatively easily produced at 600–900 K and 2–3 kbar [15,27], which could be the basis for mineral-inspired technologies for designing functional materials with highly anisotropic polaron conductivity and hydrogen diffusion.
4. Materials and Methods
Natural single crystals of grunerite, riebeckite and actinolite [16,24,25] as well as synthetic single crystals of potassic ferro-richterite [28] were investigated. The exact chemical composition was determined via wavelength-dispersive electron microprobe analysis combined with Mössbauer spectroscopy [16,17,28,29,30]. The crystal structure of the initial material as well as of the heated samples was verified by X-ray diffraction.
High-temperature Raman spectra were collected in situ with a Horiba Jobin-Yvon T64000 triple-monochromator spectrometer equipped with an Olympus BX41 microscope, using the 514.532-nm line of a Coherent Innova 90C FreD Ar+ laser, either in a LINKAM THMS-E600 or in a LINKAM TS1200 EV-1015 heating stage. The spectral resolution was ~2 cm−1, while the instrumental precision in determining the peak positions was ~0.35 cm−1. Parallel polarised spectra (incident-light polarisation Ei parallel to scattered-light polarisation Es) were collected in backscattering geometry with the crystallographic c axis either parallel or perpendicular to Ei. Additional Raman-scattering experiments were performed with the 488-nm laser line to verify the phonon origin of the observed peaks. The measured spectra were baseline-corrected, temperature-reduced and fitted with pseudo-Voigt functions [30].
Density functional theory based on the generalised gradient approximation (GGA) of Perdew-Burke-Ernzerhof (PBE) as implemented in the Vienna Ab-initio Simulation Package (VASP) was used to calculate the electron band structure and density of states of grunerite. The electron and core interactions were included using the frozen-core projector augmented wave (PAW) method, with the plane-wave cut-off energy chosen as 360 eV for model structures. The structures were fully relaxed with a mesh of 4 × 2 × 6. For the doping model the M4Fe was replaced by Mg for structural relaxation with energy convergence to 10−7 eV. During the structural relaxation, the forces were calculated with the variation of atomic positions while keeping the cell shape and cell volume fixed.
5. Conclusions
- At high temperatures Fe-bearing amphiboles develop both mobile FeO6 polarons and H+ cations and therefore can be considered as hydrous “geo-stripes”;
- The temperature-activated polarons exist independently of the presence or absence of external O2 as well as independently of the amphibole composition;
- The cationic site occupancy can tune the polaron activation temperature (i.e., via A-site population as well as Fe3+/Fetot and Mg/(Mg++Fe2+) concentrations in the octahedral stripes), the polaron-dipole magnitude (via A-site population) and mutual polaron-dipole alignment (highly aligned along the stripes of linked SiO4-rings and MO6 octahedra, if the occupancy of octahedrally coordinated sites by Fe2+ exceeds 50%);
- The room-temperature lifetime of polarons, pre-activated at elevated temperatures, can be lengthened by the presence of A-site cations;
- Even a low concentration of polarons triggers the delocalisation of all H+ cations at high temperatures.
- The existence of thermally-activated compositionally-controlled quasiparticles in amphiboles explains the anomalous rock conductivity in subduction wedge regions, but also opens a new route to designing novel smart materials with highly anisotropic properties working up to high temperatures.
Author Contributions
Conceptualisation, B.M. and G.D.V.; Raman spectroscopic analyses, N.W. and S.B.; DFT calculations, W.X. and A.M.; writing—original draft preparation, B.M.; writing—review and editing, G.D.V. and A.M.; funding acquisition, B.M., G.D.V. and W.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deutsche Forschungsgemeinschaft, grant number MI 1127/7-2, the National Natural Science Foundation of China, grant number 12075273 and the MIUR-Italy Dipartimenti di Eccellenza, grant number ARTICOLO 1, COMMI 314-337 LEGGE 232/2016.
Data Availability Statement
The datasets generated and/or analysed during the current study are available from the corresponding author on reasonable request.
Acknowledgments
The authors wish to thank Jochen Schlüter (Universität Hamburg) and Roberta Oberti (CNR Pavia) for their fruitful discussions as well as Constanze Rösche (Universität Hamburg), Günther J. Redhammer (University of Salzburg) and Massimo Boiocchi (Università di Pavia) for their help with data collection.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study, in the collection, analyses or interpretation of data, in the writing of the manuscript nor in the decision to publish the results.
References
- Bhalla, A.S.; Guo, R.; Roy, R. The perovskite structure—A review of its role in ceramic science and technology. Mat. Res. Innov. 2000, 4, 3–26. [Google Scholar] [CrossRef]
- Uchino, K. Glory of piezoelectric perovskites. Sci. Technol. Adv. Mater. 2015, 16, 046001. [Google Scholar] [CrossRef] [PubMed]
- Fratini, M.; Poccia, N.; Ricci, A.; Campi, G.; Burghammer, M.; Aeppli, G.; Bianconi, A. Scale-free structural organization of oxygen interstitials in La2CuO4+y. Nature 2010, 466, 841–844. [Google Scholar] [CrossRef]
- Poccia, N.; Ricci, A.; Campi, G.; Fratini, M.; Puri, A.; Di Gioacchino, D.; Marcelli, A.; Reynolds, M.; Burghammer, M.; Lal Saini, N.; et al. Optimum inhomogeneity of local lattice distortions in La2CuO4+y. Proc. Natl. Acad. Sci. USA 2012, 109, 15685–15690. [Google Scholar] [CrossRef]
- Ronov, A.B.; Yaroshevsky, A.A. Chemical Composition of the Earth’s Crust; Washington DC American Geophysical Union Geophysical Monograph Series; AGU: Washington, DC, USA, 1969; Volume 13, pp. 37–57. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. Vesta: A three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]
- Thompson, J.B. Biopyriboles and polysomatic series. Am. Mineral. 1978, 63, 239–249. [Google Scholar]
- Schmidt, M.W.; Poli, S. Experimentally based water budgets for dehydrating slabs and consequences for arc magma generation. Earth Plan. Sci. Lett. 1998, 163, 361–379. [Google Scholar] [CrossRef]
- Schmidbauer, E.; Kunzmann, T.; Fehr, T.; Hochleitner, R. Electrical conductivity, thermopower and 57Fe Mössbauer spectroscopy on an Fe-rich amphibole, arfvedsonite. Phys. Chem. Miner. 1996, 23, 99–106. [Google Scholar] [CrossRef]
- Schmidbauer, E.; Kunzmann, T.; Fehr, T.; Hochleitner, R. Electrical resistivity and 57Fe Mössbauer spectra of Fe-bearing calcic amphiboles. Phys. Chem. Miner. 2000, 27, 347–356. [Google Scholar] [CrossRef]
- Hu, H.; Dai, L.; Li, H.; Sun, W.; Li, B. Effect of dehydrogenation on the electrical conductivity of Fe-bearing amphibole: Implications for high conductivity anomalies in subduction zones and continental crust. Earth Planet Sci Lett. 2018, 498, 27–37. [Google Scholar] [CrossRef]
- Wang, D.; Karato, S.-I. Electrical conductivity of talc aggregates at 0.5 GPa: Influence of dehydration. Phys. Chem. Miner. 2013, 40, 11–17. [Google Scholar] [CrossRef]
- Deer, W.A.; Howie, R.A.; Zussman, J. Introduction to the Rock-Forming Minerals; Mineralogical Society of Great Britain & Ireland: London, UK, 2013; pp. 137–171. [Google Scholar]
- Hawthorne, F.C.; Oberti, R. Amphiboles: Crystal chemistry. In Amphiboles: Crystal Chemistry, Occurrence, and Health Issues, Reviews in Mineralogy and Geochemistry; Hawthorne, F.C., Oberti, R., Della Ventura, G., Mottana, A., Eds.; Mineralogical Society of Amer: Chantilly, VA, USA, 2007; Volume 67, pp. 1–54. [Google Scholar] [CrossRef]
- Oberti, R.; Della Ventura, G.; Camara, F. New amphibole compositions: Natural and synthetic. In Amphiboles: Crystal Chemistry, Occurrence, and Health Issues, Reviews in Mineralogy and Geochemistry; Hawthorne, F.C., Oberti, R., Della Ventura, G., Mottana, A., Eds.; Mineralogical Society of Amer: Chantilly, VA, USA, 2007; Volume 67, pp. 89–124. [Google Scholar] [CrossRef]
- Mihailova, B.; Della Ventura, G.; Waeselmann, N.; Xu, W.; Schlüter, J.; Galdenzi, F.; Marcelli, A.; Redhammer, G.J.; Boiocchi, M.; Oberti, R. Atomistic insight into lithospheric conductivity revealed by phonon-electron excitations in hydrous iron-bearing silicates. Commun. Mater. 2021, 2, 57. [Google Scholar] [CrossRef]
- Della Ventura, G.; Mihailova, B.; Susta, U.; Cestelli Guidi, M.; Marcelli, A.; Schlüter, J.; Oberti, R. The dynamics of Fe oxidation in riebeckite: A model for amphiboles. Am. Mineral. 2018, 103, 1103–1111. [Google Scholar] [CrossRef]
- Friedman, J.M.; Hochstrasser, R.M. Approximate selection sules for resonance raman spectroscopy. J. Am. Chem. Soc. 1976, 98, 4043–4048. [Google Scholar] [CrossRef]
- Yu, P.Y.; Cardona, M. Fundamentals of Semiconductors, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 107–158. Available online: https://link.springer.com/book/10.1007/978-3-642-00710-1 (accessed on 13 October 2022).
- de la Flor, G.; Wehber, M.; Rohrbeck, A.; Aroyo, M.I.; Bismayer, U.; Mihailova, B. Resonance Raman scattering of perovskite-type relaxor ferroelectrics under non-ambient conditions. Phys. Rev. B 2014, 90, 064107. [Google Scholar] [CrossRef]
- Thomsen, C. Light scattering in high-Tc superconductors. In Light Scattering in Solids VI, Topics in Applied Physics; Cardona, M., Güntherodt, G., Eds.; Spinger: Berlin/Heidelberg, Germany, 1991; Volume 68, pp. 285–360. [Google Scholar] [CrossRef]
- Ivanov, V.G.; Dyulgerov, M.; Oberti, R. Polarized Raman spectroscopy and lattice dynamics of potassicmagnesio-arfvedsonite. Phys. Chem. Miner. 2019, 46, 181–191. [Google Scholar] [CrossRef]
- Watenphul, A.; Macherek, T.; Wilke, F.; Schlüter, J.; Mihailova, B. Composition–thermal expandability relations and oxidation processes in tourmaline studied by in situ Raman spectroscopy. Phys. Chem. Miner. 2017, 44, 735–749. [Google Scholar] [CrossRef]
- Bernardini, S.; Della Ventura, G.; Schluter, J.; Mihailova, B. Thermally activated electron hopping in Fe-rich amphiboles: Implications for the high-conductivity anomalies in subduction zones. Geochemistry, 2022; submitted. [Google Scholar]
- Rösche, C.; Waeselmann, N.; Petrova, N.; Malcherek, T.; Schlüter, J.; Mihailova, B. Oxidation processes and thermal stability of actinolite. Phys. Chem. Mineral. 2022; accepted for publication. [Google Scholar]
- Della Ventura, G.; Radica, F.; Galdenzi, F.; Susta, U.; Cinque, G.; Mihailova, B.; Marcelli, A. Kinetics of hydrogen diffusion in riebeckite, Na2Fe3+2Fe2+3Si8O22(OH)2: An HT-FTIR study. Am. Mineral. 2022, 107, 754–764. [Google Scholar] [CrossRef]
- Evans, B.W. The synthesis and stability of some end-member amphiboles. In Amphiboles: Crystal Chemistry, Occurrence, and Health Issues, Reviews in Mineralogy and Geochemistry; Hawthorne, F.C., Oberti, R., Della Ventura, G., Mottana, A., Eds.; Mineralogical Society of Amer: Chantilly, VA, USA, 2007; Volume 67, pp. 261–286. [Google Scholar] [CrossRef]
- Della Ventura, G.; Galdenzi, F.; Cibin, G.; Oberti, R.; Xu, W.; Macis, S.; Marcelli, A. Iron oxidation dynamics vs. temperature of synthetic potassic-ferro-richterite: A XANES investigation. Phys. Chem. Chem. Phys. 2018, 20, 21764–21771. [Google Scholar] [CrossRef] [PubMed]
- Leissner, L.; Schlüter, J.; Horn, I.; Mihailova, B. Exploring the potential of Raman spectroscopy for crystallochemical analysis of complex hydrous silicates: I. Amphiboles. Am. Mineral. 2015, 100, 2682–2694. [Google Scholar] [CrossRef]
- Waeselmann, N.; Schlüter, J.; Malcherek, T.; Della Ventura, G.; Oberti, R.; Mihailova, B. Non-destructive determination of the amphibole crystal-chemical formulae by Raman spectroscopy: One step closer. J. Raman Spectrosc. 2020, 51, 1530–1548. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).