Structural, Magnetic, and Electrical Properties and Magnetoresistance of Monovalent K-Substituted La0.7Ba0.3−xKxMnO3 (x = 0 and 0.04) Manganite
Abstract
1. Introduction
2. Results and Discussion
2.1. Structural Properties
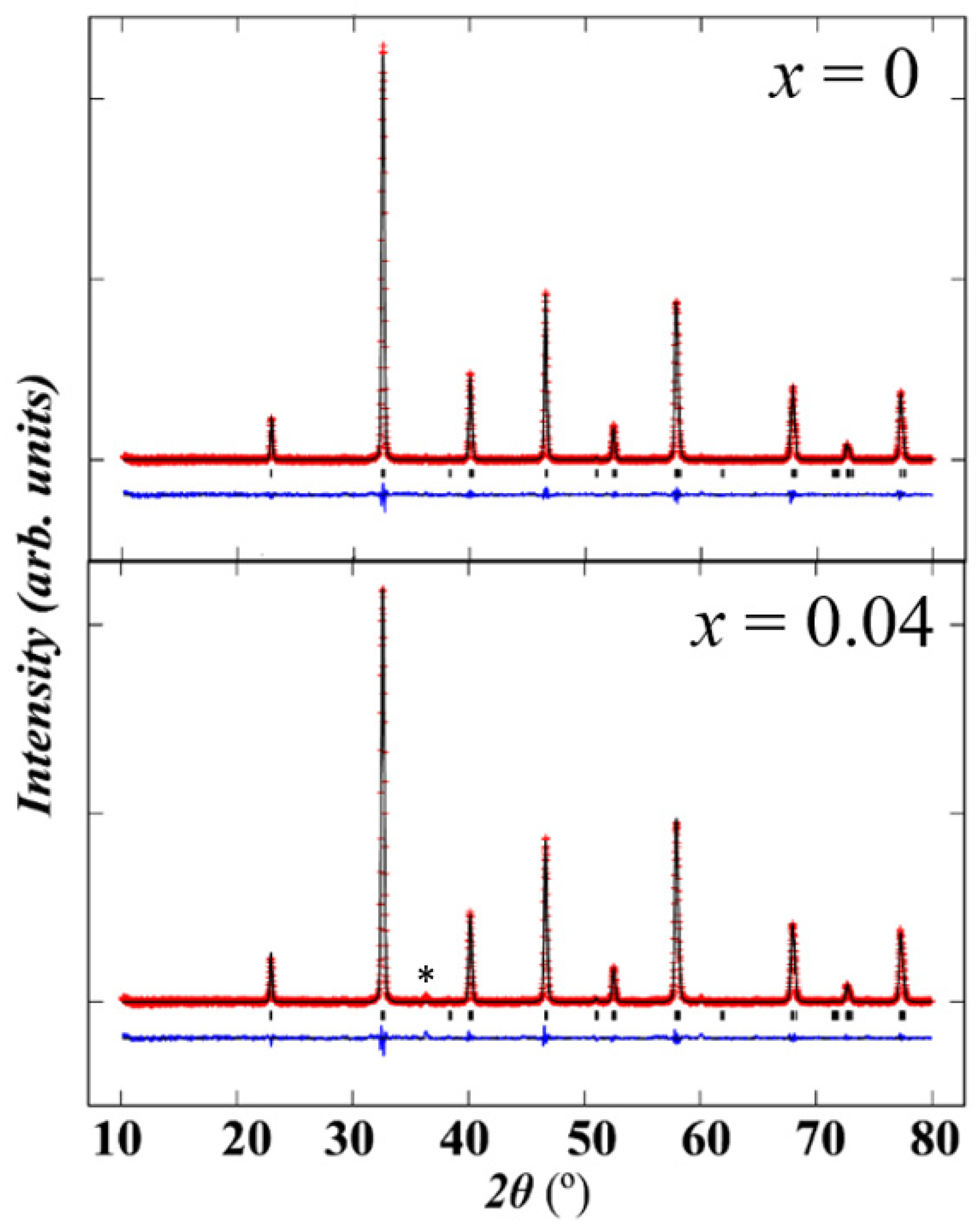
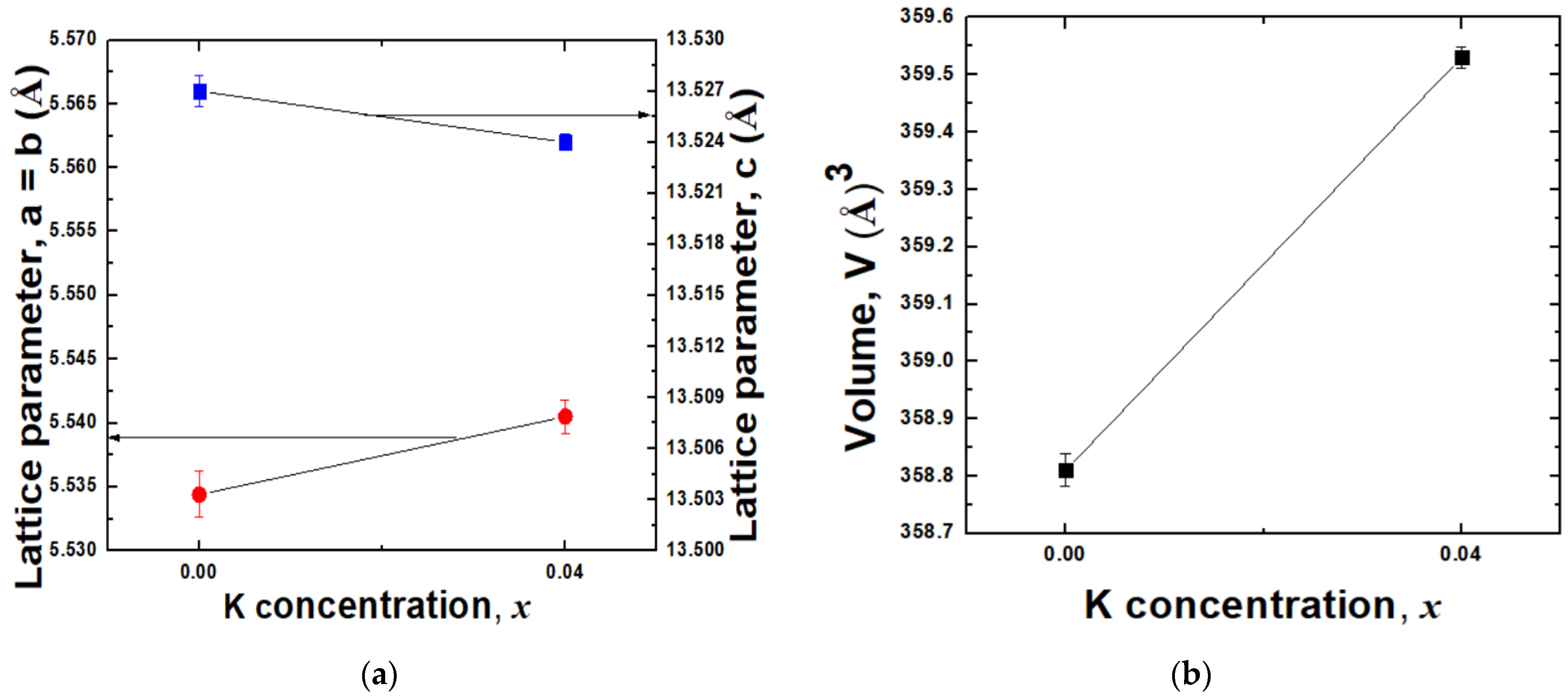
2.1.1. X-ray Diffraction (XRD) Analysis
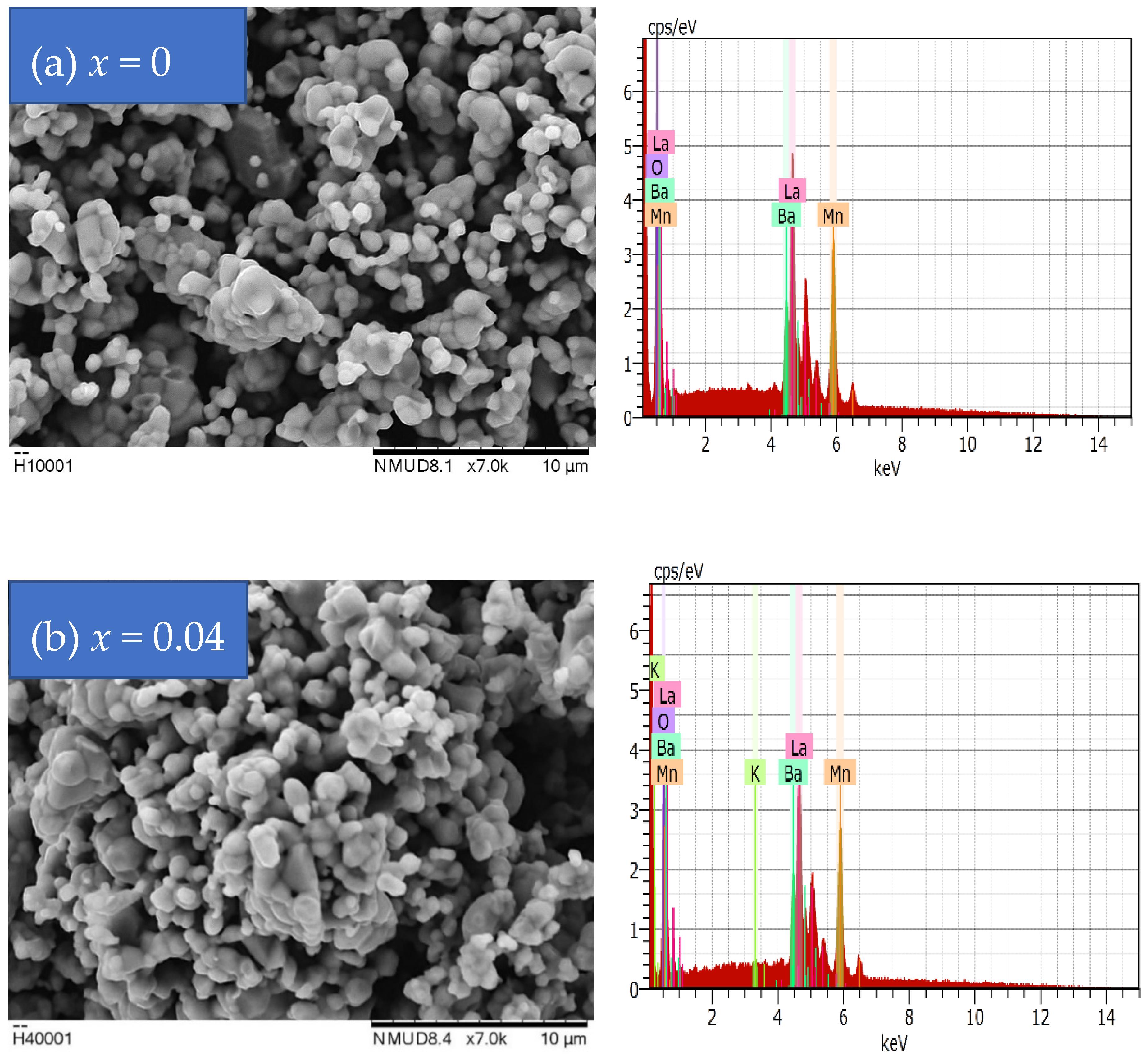
2.1.2. Scanning Electron Microscope
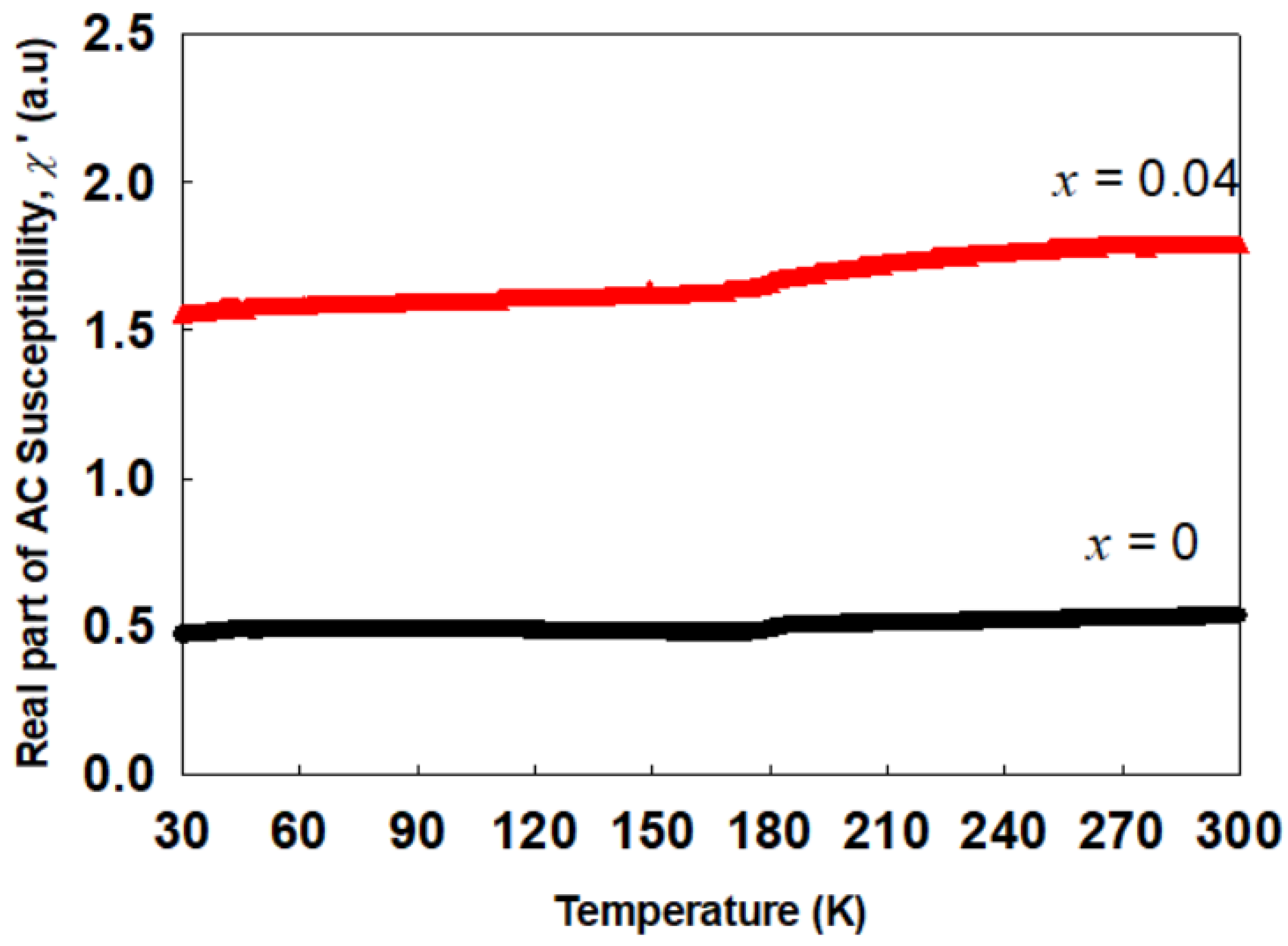
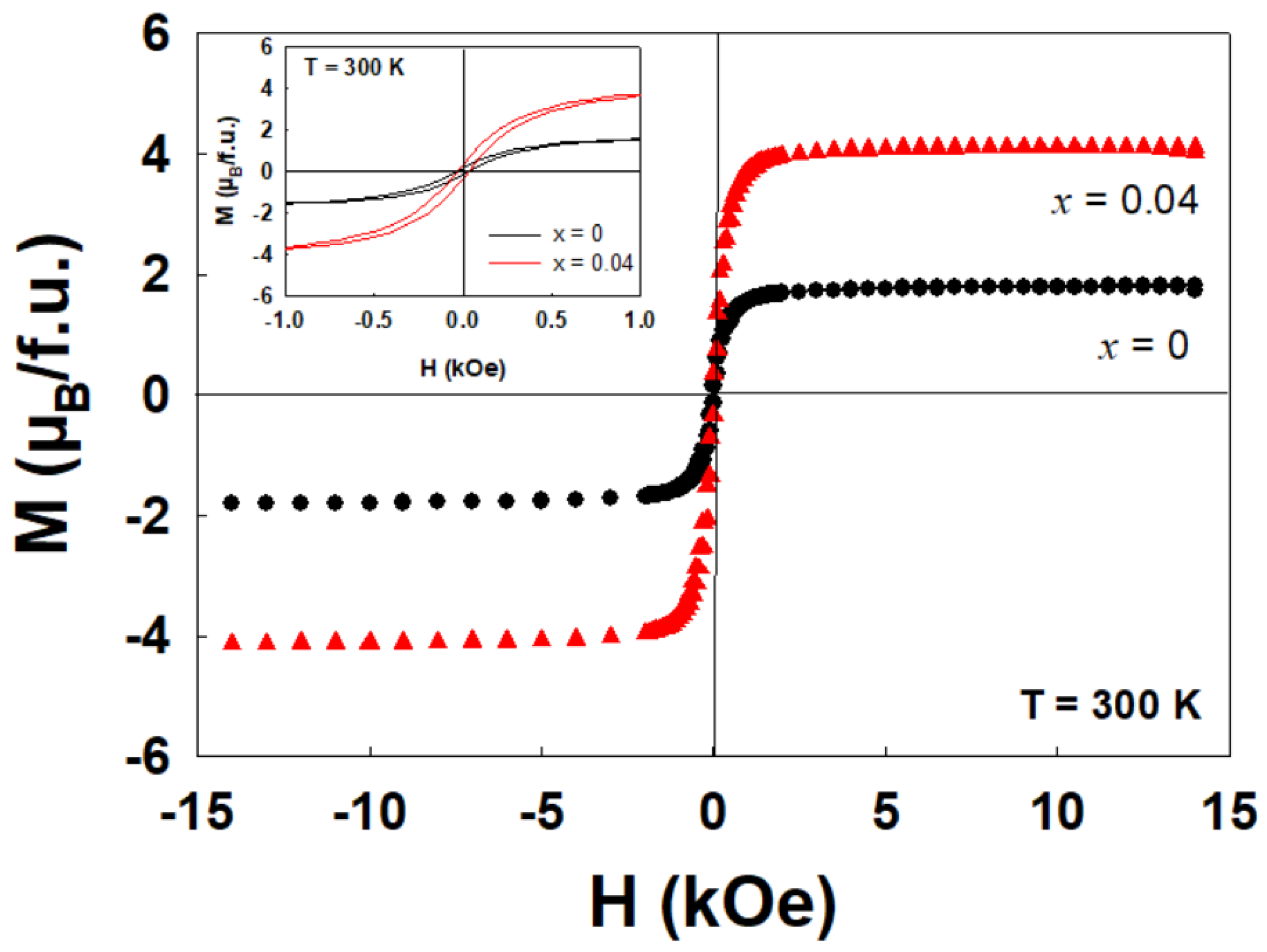
2.2. Magnetic Properties
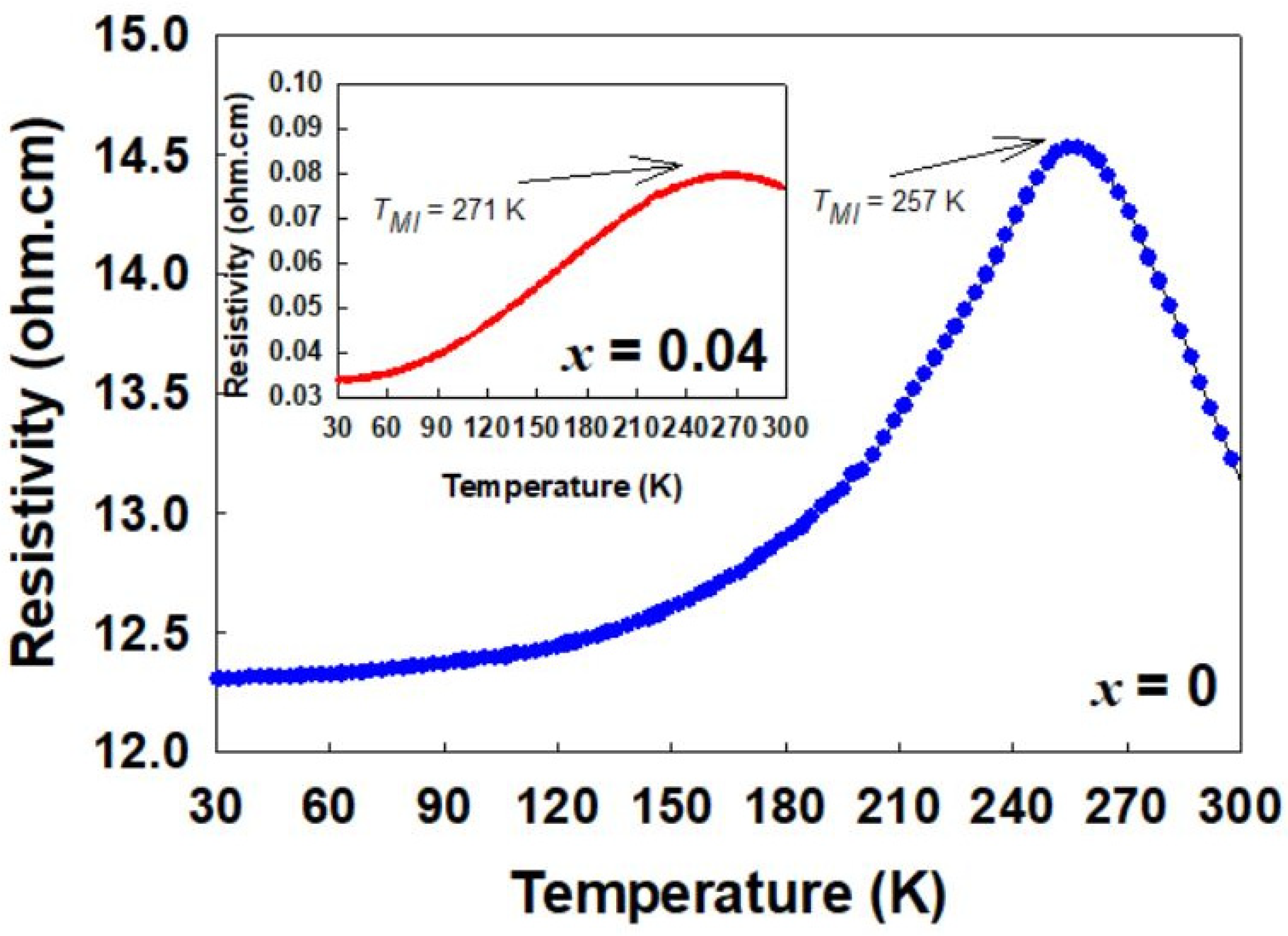
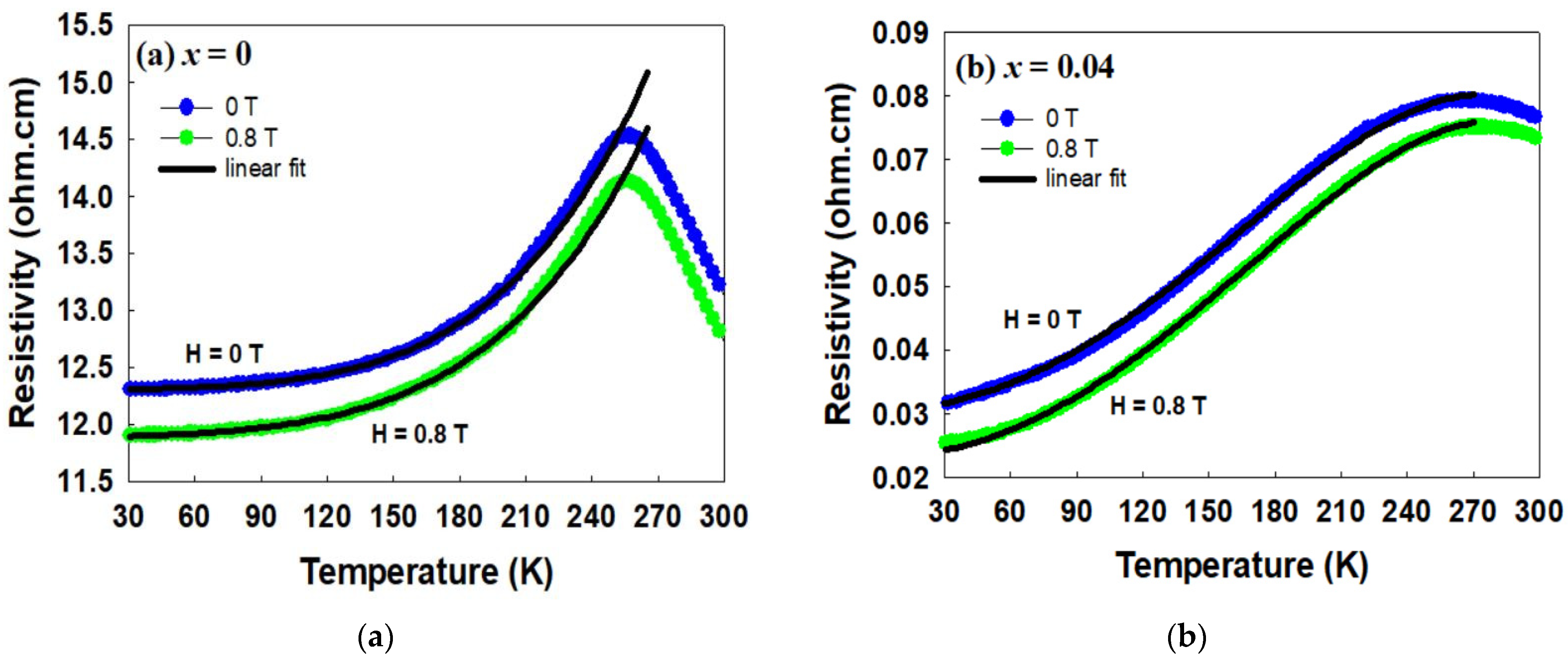
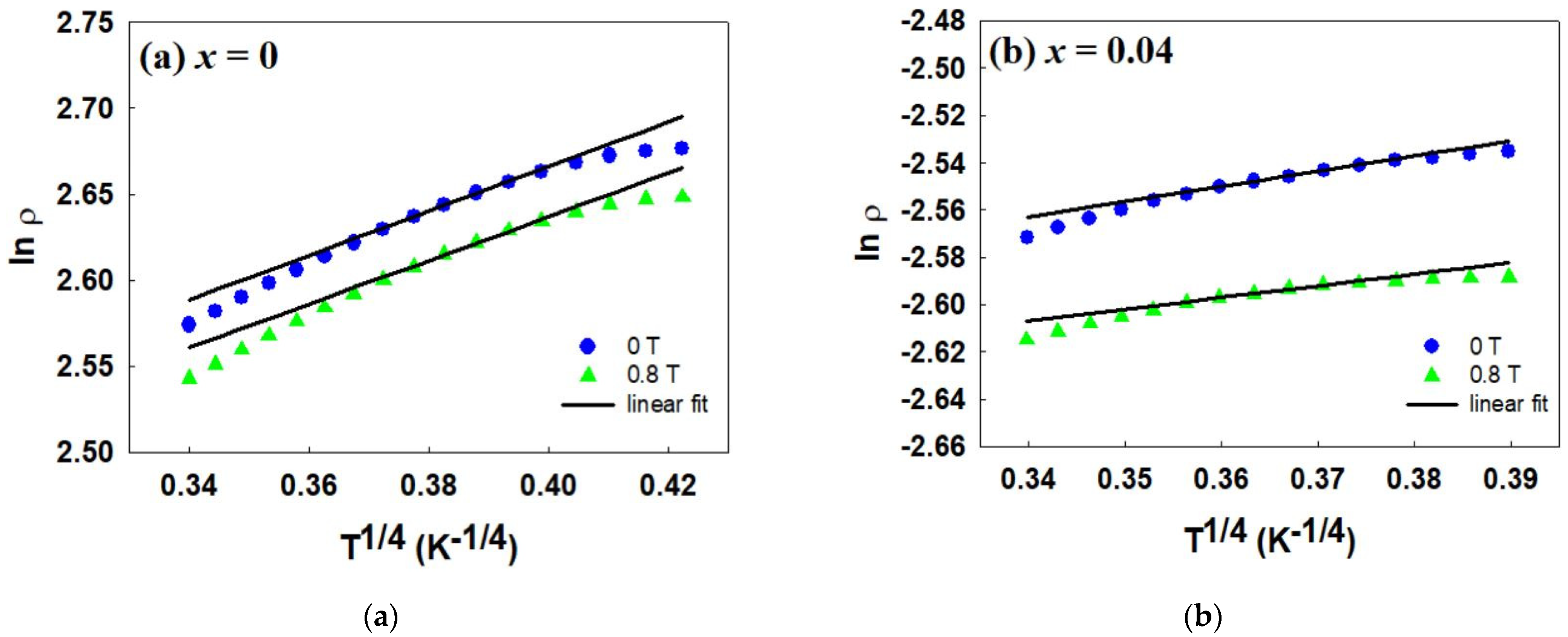
2.3. Electrical Properties
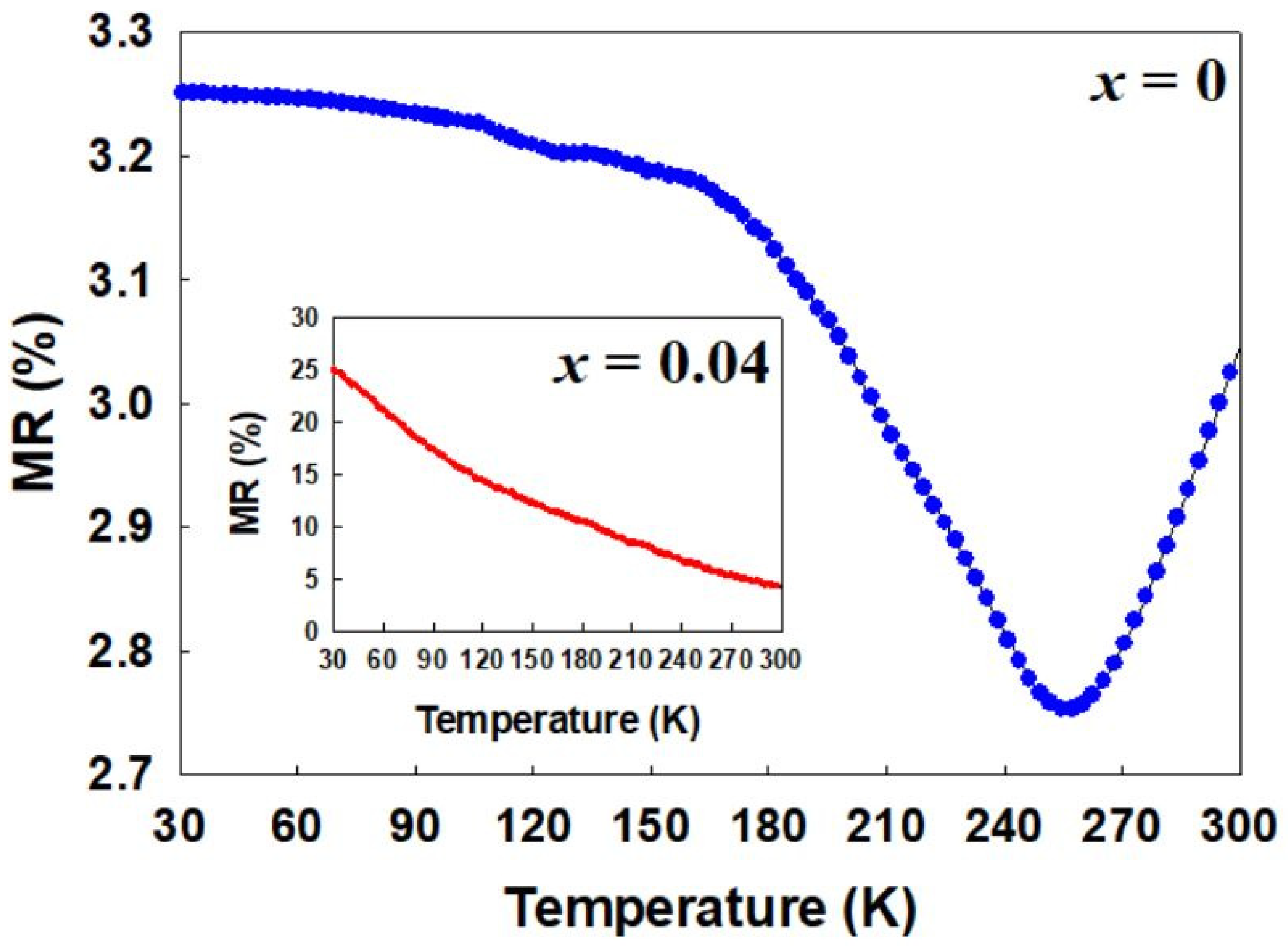
2.4. Magnetoresistance (MR)
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumar, D.; Singh, A.K. Quenching of spin-orbit coupling and signature of Griffiths Phase in nanocrystalline La0.6Ba0.4MnO3 perovskite manganite. J. Solid State Chem. 2022, 309, 122986. [Google Scholar] [CrossRef]
- Dhahri, A.; Dhahri, J.; Dhahri, E. Effect of potassium doping on physical properties of perovskites La0.8Cd0.2−xKxMnO3. J. Alloys Compd. 2010, 489, 9–12. [Google Scholar] [CrossRef]
- Das, S.; Dey, T.K. Magnetic entropy change in polycrystalline La1−xKxMnO3 perovskites. J. Alloys Compd. 2007, 440, 30–35. [Google Scholar] [CrossRef]
- Zaidi, A.; Alharbi, T.; Dhahri, J.; Alzobaidi, S.; Zaidi, M.A.; Hlil, E.K. La0.67Pb0.33−xKxMnO3 perovskites synthesized by sol–gel method: The effect of potassium substitution on the magnetic and electrical properties. Appl. Phys. A Mater. Sci. Process. 2017, 123, 94. [Google Scholar] [CrossRef]
- Daivajna, M.D.; Rao, A.; Okram, G.S. Electrical, thermal and magnetic studies on Bi-substituted LSMO manganites. J. Magn. Magn. Mater. 2015, 388, 90–95. [Google Scholar] [CrossRef]
- Koubaa, M.; Cheikhrouhou-Koubaa, W.; Cheikhrouhou, A. Effect of K doping on the physical properties of La0.65Ca0.35−xKxMnO3 (0 ≤ x ≤ 0.2) perovskite manganites. J. Phys. Chem. Solids 2009, 70, 326–333. [Google Scholar] [CrossRef]
- Ma, F.; Jiao, Y.; Jiang, Z.; Du, A. Rhombohedral Lanthanum Manganite: A New Class of Dirac Half-Metal with Promising Potential in Spintronics. ACS Appl. Mater. Interfaces 2018, 10, 36088–36093. [Google Scholar] [CrossRef] [PubMed]
- Zener, C. Interaction between the d-shells in the transition metals. II. Ferromagnetic compounds of manganese with Perovskite structure. Phys. Rev. 1951, 82, 403–405. [Google Scholar] [CrossRef]
- Jeddi, M.; Massoudi, J.; Gharsallah, H.; Ahmed, S.I.; Dhahri, E.; Hlil, E.K. Impact of potassium substitution on structural, magnetic, magnetocaloric and magneto-transport properties of Nd0.6Sr0.4−xKxMnO3 (0.0 ≤ x ≤ 0.2) manganite. J. Mater. Sci. Mater. Electron. 2021, 32, 18751–18764. [Google Scholar] [CrossRef]
- Thaljaoui, R.; Boujelben, W.; Pȩkała, M.; Pȩkała, K.; Fagnard, J.F.; Vanderbemden, P.; Donten, M.; Cheikhrouhou, A. Magnetocaloric effect of monovalent K doped manganites Pr0.6Sr0.4−xKxMnO3 (x = 0 to 0.2). J. Magn. Magn. Mater. 2014, 352, 6–12. [Google Scholar] [CrossRef]
- Vadnala, S.; Pal, P.; Asthana, S. Influence of A-site cation disorder on structural and magnetocaloric properties of Nd0.7−xLaxSr0.3MnO3 (x = 0.0, 0.1, 0.2 & 0.3). J. Rare Earths 2015, 33, 1072–1080. [Google Scholar]
- Kalyana Lakshmi, Y.; Reddy, P.V. Influence of silver doping on the electrical and magnetic behavior of La0.7Ca0.3MnO3 manganites. Solid State Sci. 2010, 12, 1731–1740. [Google Scholar] [CrossRef]
- Zaidi, A.; Cherif, K.; Dhahri, J.; Hlil, E.K.; Zaidi, M.; Alharbi, T. Influence of Na-doping in La0.67Pb0.33−xNaxMnO3 (0 ≤ x ≤ 0.15) on its structural, magnetic and magneto-electrical properties. J. Alloys Compd. 2015, 650, 210–216. [Google Scholar] [CrossRef]
- Cheikh-Rouhou Koubaa, W.; Koubaa, M.; Cheikhrouhou, A. Structural, magnetotransport, and magnetocaloric properties of La0.7Sr0.3−xAgxMnO3 perovskite manganites. J. Alloys Compd. 2008, 453, 42–48. [Google Scholar] [CrossRef]
- Regaieg, Y.; Koubaa, M.; Cheikhrouhou Koubaa, W.; Cheikhrouhou, A.; Sicard, L.; Ammar-Merah, S.; Herbst, F. Structure and magnetocaloric properties of La0.8Ag0.2−xKxMnO3 perovskite manganites. Mater. Chem. Phys. 2012, 132, 839–845. [Google Scholar] [CrossRef]
- Razaq, D.S.; Kurniawan, B.; Munazat, D.R.; Watanabe, K.; Tanaka, H. Role of potassium substitution in the magnetic properties and magnetocaloric effect in La0.8−xKxBa0.05Sr0.15MnO3 (0 ≤ x ≤ 0.20). Crystals 2020, 10, 407. [Google Scholar] [CrossRef]
- Shaikh, M.W.; Varshney, D. Structural properties and electrical resistivity behaviour of La1−xKxMnO3 (x = 0.1, 0.125 and 0.15) manganites. Mater. Chem. Phys. 2012, 134, 886–898. [Google Scholar] [CrossRef]
- Ben Rejeb, M.; Cheikhrouhou-Koubaa, W.; Koubaa, M.; Cheikhrouhou, A. Effect of Elaborating Method on Magnetic and Magnetocaloric Properties of La0.65Ca0.35−xKxMn03(0 ≤ x ≤ 0.2) Manganites. J. Supercond. Nov. Magn. 2015, 28, 839–846. [Google Scholar] [CrossRef]
- Sdiri, N.; Jemai, R.; Bejar, M.; Hussein, M.; Khirouni, K.; Dhahri, E.; Mazen, S. Electrical conductivity and dielectric analysis of the perovskite La0.7Ca0.3−xKxMnO3 (x = 0.00, 0.05 and 0.10). Solid State Commun. 2008, 148, 577–581. [Google Scholar] [CrossRef]
- Ben Khlifa, H.; Regaieg, Y.; Cheikhrouhou-Koubaa, W.; Koubaa, M.; Cheikhrouhou, A. Structural, magnetic and magnetocaloric properties of K-doped Pr0.8Na0.2−xKxMnO3 manganites. J. Alloys Compd. 2015, 650, 676–683. [Google Scholar] [CrossRef]
- Rozilah, R.; Ibrahim, N.; Mohamed, Z.; Yahya, A.K.; Khan, N.A.; Khan, M.N. Inducement of ferromagnetic-metallic phase in intermediate-doped charge-ordered Pr0.75Na0.25MnO3 manganite by K+ substitution. Phys. B Condens. Matter. 2017, 521, 281–294. [Google Scholar] [CrossRef]
- Kumari, K.; Thakur, A.D.; Ray, S.J. The effect of graphene and reduced graphene oxide on the resistive switching behavior of La0.7Ba0.3MnO3. Mater. Today Commun. 2021, 26, 102040. [Google Scholar] [CrossRef]
- Esmaeili, S.; Ehsani, M.H.; Fazli, M. Structural, optical and photocatalytic properties of La0.7Ba0.3MnO3 nanoparticles prepared by microwave method. Chem. Phys. 2020, 529, 110576. [Google Scholar] [CrossRef]
- Mohamed, H.F.; Ahmed, A.M.; Diab, A.K.; Omar, E.Y. Impact of aluminum on the Seebeck coefficient and magnetic properties of La0.7Ba0.3MnO3 manganites. Chem. Phys. Lett. 2019, 726, 22–28. [Google Scholar] [CrossRef]
- Mohamed, A.E.M.A.; Mohamed, A.M.; ElShafaie, A.; Mohamed, H.F.; Diab, A.K.; Ahmed, A.M. Effect of NiO impurity on the magneto-transport properties of the La0.7Ba0.3MnO3 granular manganite. Chem. Phys. Lett. 2018, 713, 272–276. [Google Scholar] [CrossRef]
- Arbuzova, T.I.; Naumov, S.V. Magnetic polarons in doped La0.7Ca0.3MnO3, La0.7Ba0.3MnO3, and La0.7Sr0.3MnO3 manganites. JETP Lett. 2015, 101, 760–764. [Google Scholar] [CrossRef]
- Nguyen, L.H.; Dang, N.T.; Dang, N.V.; Bau, L.V.; Nam, P.H.; Phong, L.T.H.; Manh, D.H.; Phong, P.T. Structural, magnetic, and electrical properties of Ti-doped La0.7Ba0.3Mn1−xTixO3 (0 ≤ x ≤ 0.3) ceramics. J. Alloys Compd. 2021, 859, 157831. [Google Scholar] [CrossRef]
- Mohamed, A.E.M.A.; Hernando, B.; Díaz-García, M.E. Room temperature magneto-transport properties of La0.7Ba0.3MnO3 manganite. J. Alloys Compd. 2017, 695, 2645–2651. [Google Scholar] [CrossRef]
- Bally, M.A.A.; Ahsan, M.Z.; Islam, M.A.; Khan, F.A. Magnetic properties of La0.55CaxSr0.45−xMnO3 perovskite manganite. Results Phys. 2021, 21, 103800. [Google Scholar] [CrossRef]
- Lau, L.N.; Lim, K.P.; Ishak, A.N.; Kechik, M.M.A.; Chen, S.K.; Ibrahim, N.B.; Miryala, M.; Murakami, M.; Shaari, A.H. The physical properties of submicron and nano-grained La0.7Sr0.3MnO3 and Nd0.7Sr0.3MnO3 synthesised by sol–gel and solid-state reaction methods. Coatings 2021, 11, 361. [Google Scholar] [CrossRef]
- Ahmed, S.A. Structural and electrical properties in La1−xLixMnO3. J. Magn. Magn. Mater. 2013, 340, 131–139. [Google Scholar] [CrossRef]
- Messaoui, I.; Riahi, K.; Kumaresavanji, M.; Cheikhrouhou Koubaa, W.; Cheikhrouhou, A. Potassium doping induced changes of magnetic and magnetocaloric properties of La0.78Cd0.22−xKxMnO3 (x = 0.00, 0.10, 0.15 and 0.20) manganites. J. Magn. Magn. Mater. 2018, 446, 108–117. [Google Scholar] [CrossRef]
- Mtiraoui, N.; Dhahri, A.; Oumezine, M.; Dhahri, J.; Dhahri, E. Effects of nonmagnetic silver Ag doping on the structural, magnetic and electric properties in La0.67Pb0.33MnO3 manganese oxides. J. Magn. Magn. Mater. 2011, 323, 2831–2836. [Google Scholar] [CrossRef]
- Varshney, D.; Dodiya, N. Electrical resistivity of alkali metal doped manganites LaxAyMnwO3 (A = Na, K, Rb): Role of electron-phonon, electron-electron and electron-magnon interactions. Curr. Appl. Phys. 2013, 13, 1188–1198. [Google Scholar] [CrossRef]
- Mohamed, Z.; Sharon, I.S.; Ibrahim, N.; Maulud, M.F. Influence of Ruthenium Doping on the Crystal Structure and Magnetic Properties of Pr0.67Ba0.33Mn1−xRuxO3 Manganites. Crystals 2020, 10, 295. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Mohamed, H.F.; Diab, A.K.; Omar, E.Y. Crossover effect of magnetotransport and magnetocaloric effect in (La0.7Ba0.3MnO3) 1−x/(Al2O3)x composites. J. Magn. Magn. Mater. 2019, 489, 165388. [Google Scholar] [CrossRef]
- Rozilah, R.; Ibrahim, N.; Yahya, A.K. Inducement of ferromagnetic–metallic phase and magnetoresistance behavior in charged ordered monovalent-doped Pr0.75Na0.25MnO3 manganite by Ni substitution. Solid State Sci. 2019, 87, 64–80. [Google Scholar]
- Kansara, S.B.; Dhruv, D.; Kataria, B.; Thaker, C.M.; Rayaprol, S.; Prajapat, C.L.; Singh, M.R.; Solanki, P.S.; Kuberkar, D.G.; Shah, N.A. Structural, transport and magnetic properties of monovalent doped La1−xNaxMnO3 manganites. Ceram. Int. 2015, 41, 7162–7173. [Google Scholar] [CrossRef]
- Ibrahim, N.; Rusop, N.A.M.; Rozilah, R.; Asmira, N.; Yahya, A.K. Effect of grain modification on electrical transport properties and electroresistance behavior of Sm0.55Sr0.45MnO3. Int. J. Eng. Technol. 2018, 7, 113–117. [Google Scholar]
- Soylu Koc, N.; Altintas, S.P.; Mahamdioua, N.; Terzioglu, C. Cation size mismatch effect in (La1−yREy)1.4Ca1.6Mn2O7 perovskite manganites. J. Alloys Compd. 2019, 797, 471–476. [Google Scholar] [CrossRef]
- Huang, Y.H.; Huang, K.F.; Luo, F.; He, L.L.; Wang, Z.M.; Liao, C.S.; Yan, C.H. Enhanced ferromagnetic transition and magnetoresistance in granular Ag-added La0.7Ca0.3MnO3. J. Solid State Chem. 2003, 174, 257–263. [Google Scholar] [CrossRef]
- Mohamed, H.F. Influence of sodium doping on the electrical and magnetic properties of La0.90Li0.10MnO3 manganites. J. Magn. Magn. Mater. 2017, 424, 44–52. [Google Scholar] [CrossRef]
- Siwach, P.K.; Prasad, R.; Gaur, A.; Singh, H.K.; Varma, G.D.; Srivastava, O.N. Microstructure-magnetotransport correlation in La0.7Ca0.3MnO3. J. Alloys Compd. 2007, 443, 26–31. [Google Scholar] [CrossRef]
- Verma, M.K.; Sharma, N.D.; Sharma, S.; Choudhary, N.; Singh, D. Structural and magneto-transport properties of Li-substituted La0.65Ca0.35−xLixMnO3 (0 ≤ x ≤ 0.15) CMR manganites. J. Alloys Compd. 2020, 814, 152279. [Google Scholar] [CrossRef]
- Tripathi, R.; Awana, V.P.S.; Kishan, H.; Balamurugan, S.; Bhalla, G.L. Impact of silver addition on room temperature magneto-resistance in La0.7Ba0.3MnO3 (LBMO): Agx (x = 0.0, 0.1, 0.2, 0.3, 0.4). J. Supercond. Nov. Magn. 2008, 21, 151–159. [Google Scholar] [CrossRef][Green Version]
- Mansuri, I.; Varshney, D. Structure and electrical resistivity of La1−xBa xMnO3 (0.25 ≤ x ≤ 0.35) perovskites. J. Alloys Compd. 2012, 513, 256–265. [Google Scholar] [CrossRef]
- Pal, A.; Rao, A.; Kekuda, D.; Nagaraja, B.S.; Mondal, R.; Biswas, D. Investigation of cationic disorder effects on the transport and magnetic properties of perovskite Pr0.7−xRExSr0.3MnO3 (x = 0.0, 0.2; RE = Nd, Sm & Gd). J. Magn. Magn. Mater. 2020, 512, 167011. [Google Scholar]
- Manjunatha, S.O.; Rao, A.; Poornesh, P.; Lin, W.J.; Kuo, Y.K. Magnetic inhomogeneity and Griffiths phase in Bi substituted La0.65−xBixCa0.35MnO3 manganites. Phys. B Condens. Matter. 2016, 498, 82–91. [Google Scholar] [CrossRef]
- Ibrahim, N.; Rozilah, R.; Mohamed, Z.; Yahya, A.K. Magnetic and electronic transport properties of electron-doped La0.9−xBixTe0.1MnO3 (0.00 ≤ x ≤ 0.2) Manganites. Mater. Chem. Phys. 2020, 248, 122940. [Google Scholar] [CrossRef]
- Yadav, A.; Shah, J.; Gupta, R.; Shukla, A.; Singh, S.; Kotnala, R.K. Role of spin-glass phase for magnetoresistance enhancement in nickel substituted lanthanum calcium manganite. Ceram. Int. 2016, 42, 12630–12638. [Google Scholar] [CrossRef]
- Sangeetha, M.; Babu, V.H. Effect of yttrium substitution on the electrical and magnetic properties of La0.7Ba0.3MnO3 compound. J. Magn. Magn. Mater. 2015, 389, 5–9. [Google Scholar] [CrossRef]
- Daivajna, M.D.; Rao, A.; Okram, G.S. Electrical, thermal and magnetic properties of Bi doped La 0.7−xBixSr0.3MnO3 manganites. J. Alloys Compd. 2014, 617, 345–351. [Google Scholar] [CrossRef]
- Ben Abdelkhalek, S.; Kallel, N.; Kallel, S.; Guizouarn, T.; Peña, O.; Oumezzine, M. Transport behavior and mechanism of conduction of simultaneously substituted y and Fe in La0.7Ba0.3MnO3 perovskite. Phys. B Condens. Matter 2011, 406, 4060–4067. [Google Scholar] [CrossRef]
- Khan, M.H.; Roychowdhury, A.; Das, D.; Pal, S. Adiabatic polaron hopping conduction and Griffiths phase in electron-doped Ca0.85Dy0.15MnO3. J. Alloys Compd. 2015, 650, 328–335. [Google Scholar] [CrossRef]
- Saleh, J.A.; Sarsari, I.A.; Kameli, P.; Salamati, H. Influence of Al-doping on the structural, magnetic, and electrical properties of La0.8Ba0.2Mn1−xAlxO3 (0 ≤ x ≤ 0.25) manganites. J. Magn. Magn. Mater. 2018, 465, 339–347. [Google Scholar] [CrossRef]
- Venkataiah, G.; Krishna, D.C.; Vithal, M.; Rao, S.S.; Bhat, S.V.; Prasad, V.; Subramanyam, S.V.; Reddy, P.V. Effect of sintering temperature on electrical transport properties of La0.67Ca0.33MnO3. Phys. B Condens. Matter 2005, 357, 370–379. [Google Scholar] [CrossRef]
- Manjunatha, S.O.; Rao, A.; Awana, V.P.S.; Okram, G.S. Investigation on magnetic, electrical and thermoelectric power of Bi-substituted La0.8Ca0.2MnO3 manganites. J. Magn. Magn. Mater. 2015, 394, 130–137. [Google Scholar] [CrossRef]
- Asmira, N.; Ibrahim, N.; Mohamed, Z.; Yahya, A.K. Effect of Cr3+ substitution at Mn-site on electrical and magnetic properties of charge ordered Bi0.3Pr0.3Ca0.4MnO3 manganites. Phys. B Condens. Matter 2018, 544, 34–46. [Google Scholar] [CrossRef]
- Ghani, M.A.; Supardan, S.N.; Yahya, A.K. Effect of Bi Substitution on Transport and Magnetoresistance Properties of Electron-Doped La0.7−xBixCe0.3MnO3 Ceramics. J. Supercond. Nov. Magn. 2015, 28, 1835–1841. [Google Scholar] [CrossRef]
- Kumar Verma, M.; Dutt Sharma, N.; Sharma, S.; Choudhary, N.; Singh, D. High magnetoresistance in La0.5Nd0.15Ca0.25A0.1MnO3 (A = Ca, Li, Na, K) CMR manganites: Correlation between their magnetic and electrical properties. Mater. Res. Bull. 2020, 125, 110813. [Google Scholar] [CrossRef]
- Mendonca, L.D.; D’Souza, A.; Murari, M.S.; Daivajna, M.D. Magneto Transport Anomaly of Bismuth Substituted (La, Na) MnO3. J. Supercond. Nov. Magn. 2020, 33, 1809–1819. [Google Scholar] [CrossRef]
- Trukhanov, S.V.; Kasper, N.V.; Troyanchuk, I.O.; Tovar, M.; Szymczak, H.; Bärner, K. Evolution of magnetic state in the La1−xCaxMnO3−γ (x = 0.30, 0.50) manganites depending on the oxygen content. J. Solid State Chem. 2002, 169, 85–95. [Google Scholar] [CrossRef]

| Sample | x = 0 | x = 0.04 |
|---|---|---|
| Crystal structure | Rhombohedral | |
| Space group | R3 | |
| a = b (Å) | 5.5344 (18) | 5.5405 (13) |
| c (Å) | 13.527 (9) | 13.524 (5) |
| V (Å)3 | 358.81 (28) | 359.53 (18) |
| Average ionic radius, <rA> | 1.295 | 1.299 |
| Bond length, <Mn–O> Å | 1.969 (6) | 1.966 (7) |
| Bond angle, <Mn–O–Mn> (°) | 166.6 (0) | 168.7 (4) |
| χ2 | 1.70 | 2.14 |
| Rwp (%) | 6.87 | 7.59 |
| Rp (%) | 4.90 | 5.25 |
| (×10−2) () | 1.3548 | 1.4932 |
| 0.9523 | 0.9534 | |
| W | 0.0927 | 0.0934 |
| TMI (K) | 257 | 271 |
| Sample | Atomic Composition (%) | |
|---|---|---|
| x = 0 | x = 0.04 | |
| La | 13.75 | 13.78 |
| Ba | 6.25 | 5.45 |
| K | 0 | 0.77 |
| Mn | 20.44 | 20.73 |
| O | 59.56 | 59.27 |
| Total | 100 | 100 |
| Sample | x = 0 | x = 0.04 |
|---|---|---|
| Ms (/f.u.) | 1.81 | 4.11 |
| Hc (G) | 29.7 | 32.4 |
| Sample, x | ||||||
|---|---|---|---|---|---|---|
| H = 0 T | H = 0.8 T | H = 0 T | H = 0.8 T | H = 0 T | H = 0.8 T | |
| 0 | 12.30 | 11.89 | 4.92 × 10−6 | 3.06 × 10−6 | 3.01 × 10−11 | 2.65 × 10−11 |
| 0.04 | 0.03 | 0.02 | 1.19 × 10−6 | 1.08 × 10−6 | −4.26 × 10−13 | −4.13 × 10−13 |
| Sample | x = 0 | x = 0.04 | ||
|---|---|---|---|---|
| H = 0 T | H = 0.8 T | H = 0 T | H = 0.8 T | |
| SPH model | ||||
| Ea (meV) | 48.39 | 47.70 | 40.07 | 38.86 |
| VRH model | ||||
| TOM × 106 (K) | 1.291 | 1.267 | 0.646 | 0.496 |
| Rh (Å) | 13.93 | 13.86 | 11.71 | 10.97 |
| Eh (meV) | 49.46 | 49.22 | 41.59 | 38.94 |
| N(EF) (×1020) (eV−1 cm−3) | 1.774 | 1.810 | 3.550 | 4.620 |
| Sample | MR (%) | ||
|---|---|---|---|
| 30 K | TMI | 300 K | |
| x = 0 | 3.25 | 2.75 | 3.01 |
| x = 0.04 | 25.0 | 5.31 | 4.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zahrin, A.; Azhar, N.A.; Ibrahim, N.; Mohamed, Z. Structural, Magnetic, and Electrical Properties and Magnetoresistance of Monovalent K-Substituted La0.7Ba0.3−xKxMnO3 (x = 0 and 0.04) Manganite. Condens. Matter 2022, 7, 51. https://doi.org/10.3390/condmat7030051
Zahrin A, Azhar NA, Ibrahim N, Mohamed Z. Structural, Magnetic, and Electrical Properties and Magnetoresistance of Monovalent K-Substituted La0.7Ba0.3−xKxMnO3 (x = 0 and 0.04) Manganite. Condensed Matter. 2022; 7(3):51. https://doi.org/10.3390/condmat7030051
Chicago/Turabian StyleZahrin, Amirah, Nurul Atiqah Azhar, Norazila Ibrahim, and Zakiah Mohamed. 2022. "Structural, Magnetic, and Electrical Properties and Magnetoresistance of Monovalent K-Substituted La0.7Ba0.3−xKxMnO3 (x = 0 and 0.04) Manganite" Condensed Matter 7, no. 3: 51. https://doi.org/10.3390/condmat7030051
APA StyleZahrin, A., Azhar, N. A., Ibrahim, N., & Mohamed, Z. (2022). Structural, Magnetic, and Electrical Properties and Magnetoresistance of Monovalent K-Substituted La0.7Ba0.3−xKxMnO3 (x = 0 and 0.04) Manganite. Condensed Matter, 7(3), 51. https://doi.org/10.3390/condmat7030051







