Rabi Coupled Fermions in the BCS–BEC Crossover
Abstract
1. Introduction
2. The Model
3. Mean Field Approach
3.1. Gap and Number Equations
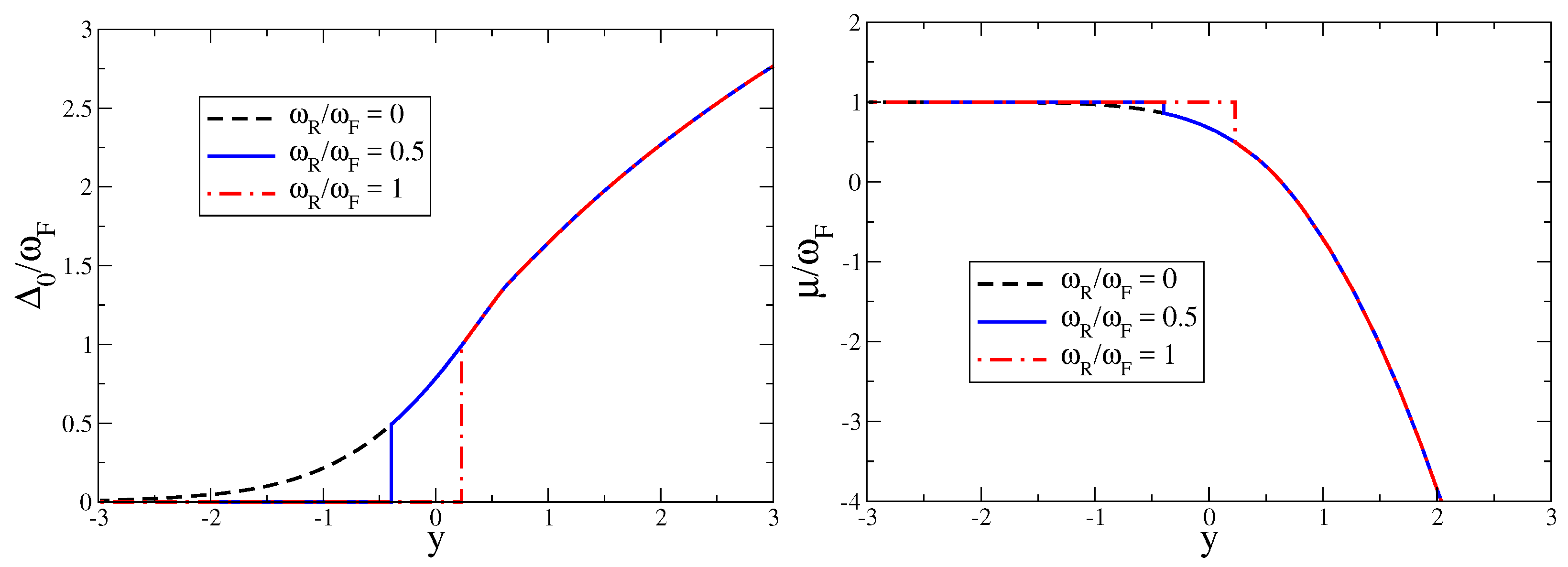
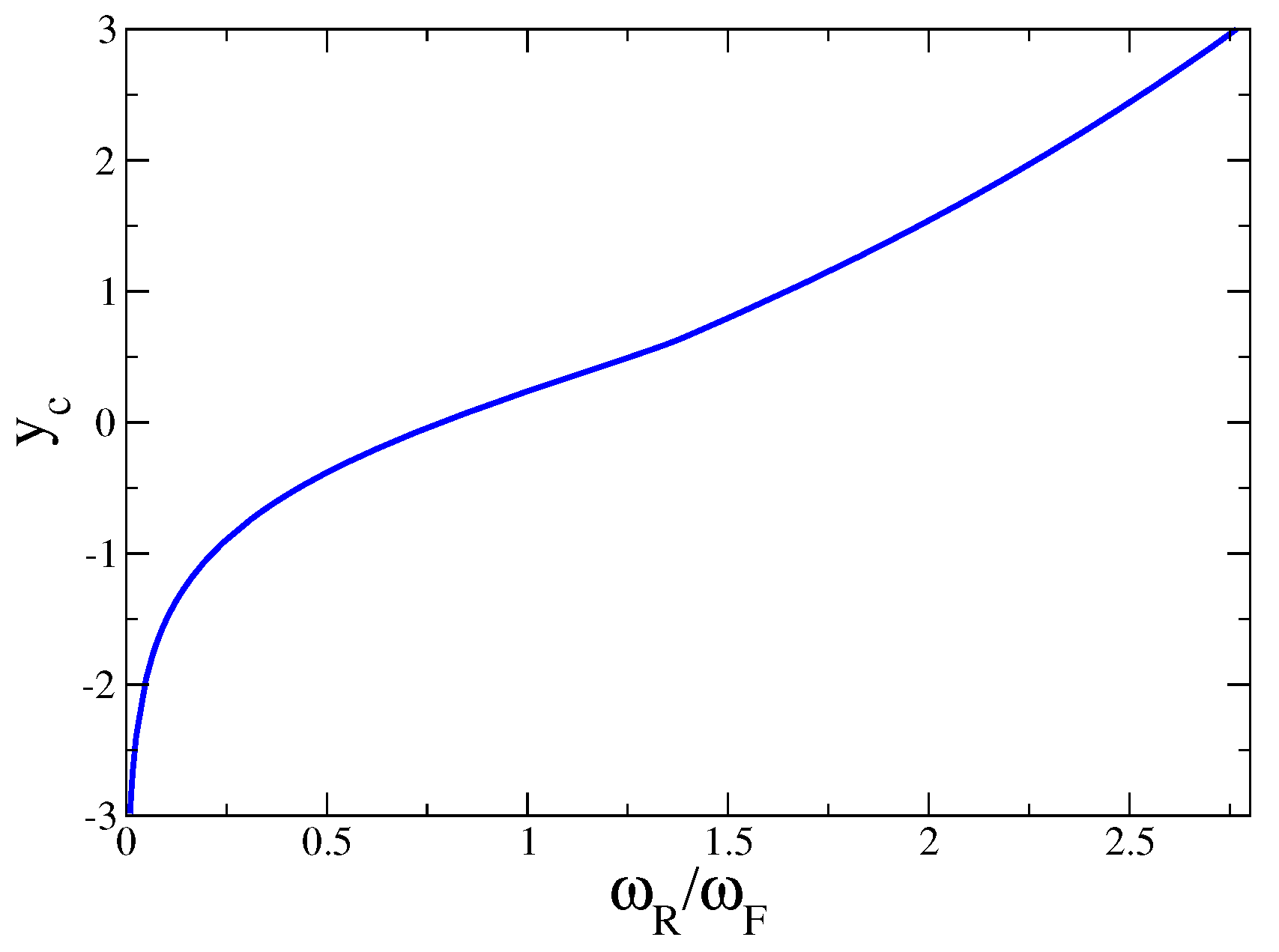
3.2. Zero Temperature
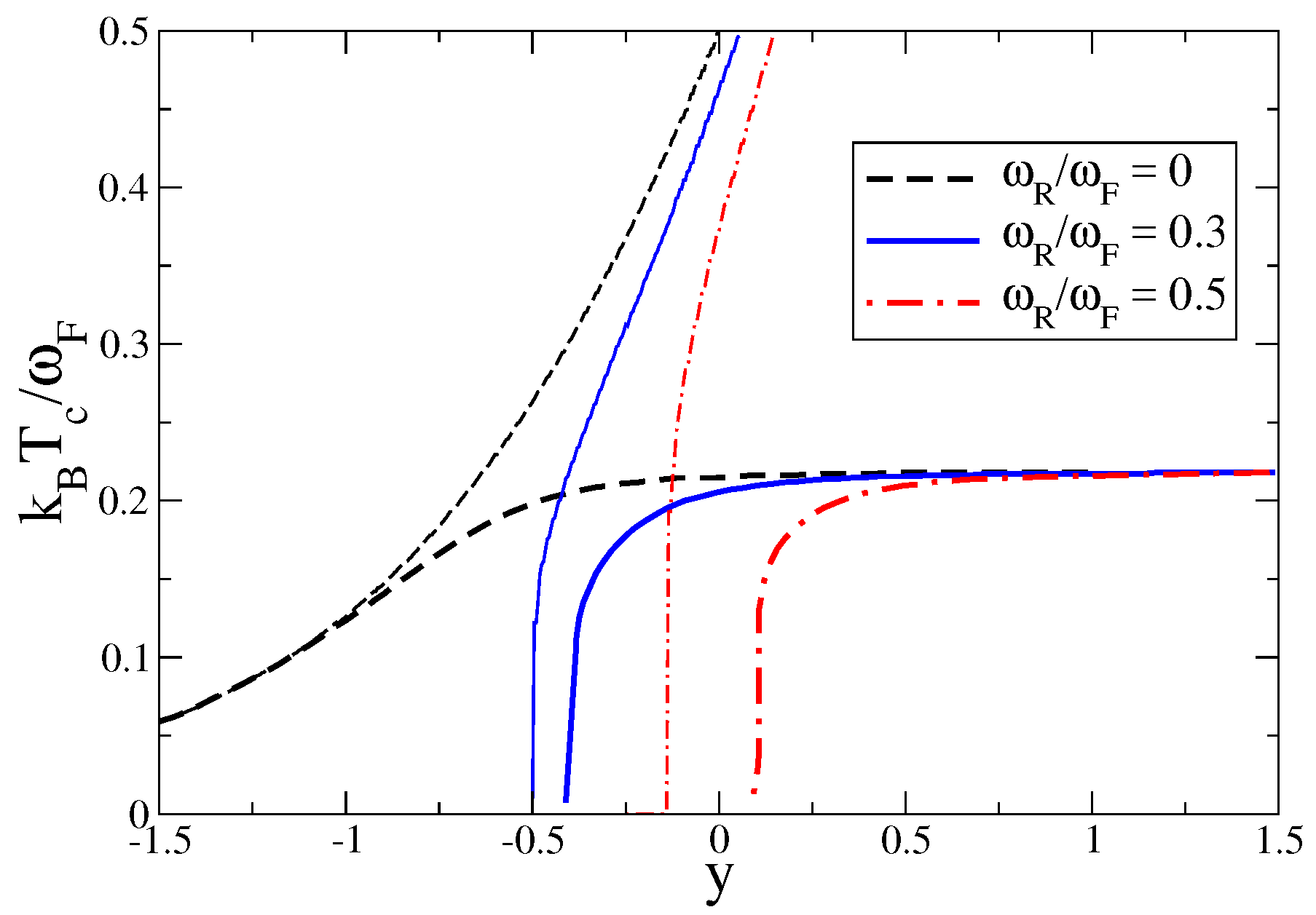
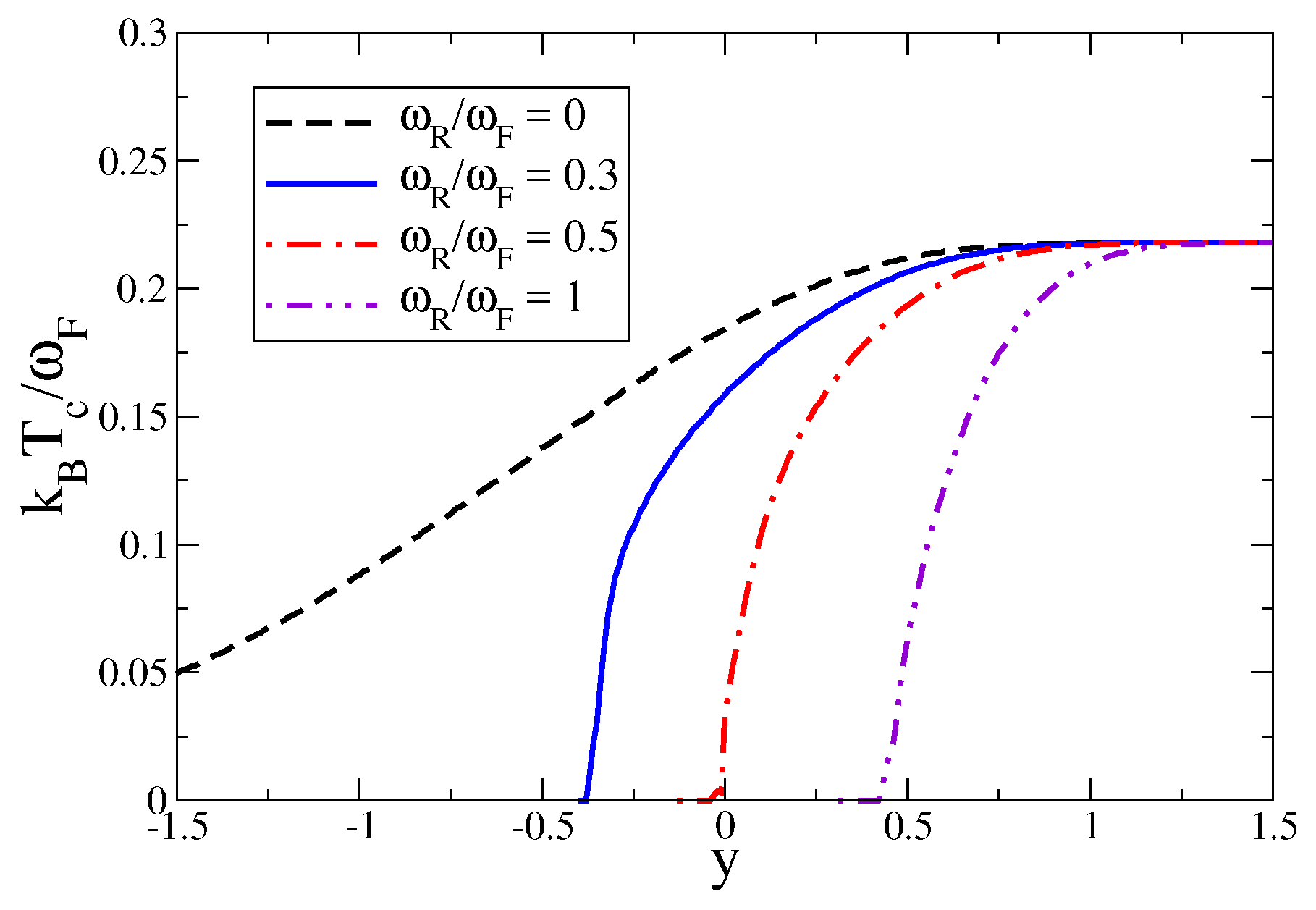
3.3. Critical Temperature
4. Beyond Mean Field
4.1. By Superfluid Density
4.2. Gaussian Fluctuations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Zwerger, W. The BCS–BEC Crossover and the Unitary Fermi Gas; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Lin, Y.J.; Jimenez-Garcia, K.; Spielman, I.B. Spin–orbit-coupled Bose–Einstein Condensates. Nature 2011, 471, 83. [Google Scholar] [CrossRef]
- Zhang, J.-Y.; Ji, S.-C.; Chen, Z.; Zhang, L.; Du, Z.-D.; Yan, B.; Pan, G.-S.; Zhao, B.; Deng, Y.-J.; Zhai, H.; et al. Collective Dipole Oscillations of a Spin-Orbit Coupled Bose-Einstein Condensate. Phys. Rev. Lett. 2012, 109, 115301. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Yu, Z.-Q.; Fu, Z.; Miao, J.; Huang, L.; Ghai, S.; Zhai, H.; Zhang, J. Spin-Orbit Coupled Degenerate Fermi Gases. Phys. Rev. Lett. 2012, 109, 095301. [Google Scholar] [CrossRef] [PubMed]
- Bychkov, Y.A.; Rashba, E.I. Oscillatory Effects and the Magnetic Susceptibility of Carriers in Inversion Layers. J. Phys. C 1984, 17, 6039. [Google Scholar] [CrossRef]
- Dresselhaus, G. Spin-Orbit Coupling Effects in Zinc Blende Structures. Phys. Rev. 1955, 100, 580. [Google Scholar] [CrossRef]
- Li, Y.; Pitaevskii, L.P.; Stringari, S. Quantum Tricriticality and Phase Transitions in Spin-Orbit Coupled Bose-Einstein Condensates. Phys. Rev. Lett. 2012, 108, 225301. [Google Scholar] [CrossRef] [PubMed]
- Martone, G.I.; Li, Y.; Pitaevskii, L.P.; Stringari, S. Anisotropic Dynamics of a Spin-Orbit-Coupled Bose-Einstein Condensate. Phys. Rev. A 2012, 86, 063621. [Google Scholar] [CrossRef]
- Merkl, M.; Jacob, A.; Zimmer, F.E.; Ohberg, P.; Santos, L. Chiral Confinement in Quasirelativistic Bose-Einstein Condensates. Phys. Rev. Lett. 2010, 104, 073603. [Google Scholar] [CrossRef] [PubMed]
- Achilleos, V.; Frantzeskakis, D.J.; Kevrekidis, P.G.; Pelinovsky, D.E. Matter-Wave Bright Solitons in Spin-Orbit Coupled Bose-Einstein Condensates. Phys. Rev. Lett. 2013, 110, 264101. [Google Scholar] [CrossRef] [PubMed]
- Sinha, S.; Nath, R.; Santos, L. Trapped Two-Dimensional Condensates with Synthetic Spin-Orbit Coupling. Phys. Rev. Lett. 2011, 107, 270401. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.; Cheng, J.; Jing, H.; Sun, C.P.; Yi, S. Spin-Orbit-Coupled Dipolar Bose-Einstein Condensates. Phys. Rev. Lett. 2012, 108, 125301. [Google Scholar] [CrossRef] [PubMed]
- Vyasanakere, J.P.; Shenoy, V.B. Bound States of Two Spin-12 Fermions in a Synthetic Non-Abelian Gauge Field. Phys. Rev. B 2011, 83, 094515. [Google Scholar] [CrossRef]
- Vyasanakere, J.P.; Zhang, S.; Shenoy, V.B. BCS-BEC Crossover Induced by a Synthetic Non-Abelian Gauge Field. Phys. Rev. B 2011, 84, 014512. [Google Scholar] [CrossRef]
- Gong, M.; Tewari, S.; Zhang, C. BCS-BEC Crossover and Topological Phase Transition in 3D Spin-Orbit Coupled Degenerate Fermi Gases. Phys. Rev. Lett. 2011, 107, 195303. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Jiang, L.; Liu, X.-J.; Pu, H. Probing Anisotropic Superfluidity in Atomic Fermi Gases with Rashba Spin-Orbit Coupling. Phys. Rev. Lett. 2011, 107, 195304. [Google Scholar] [CrossRef]
- Yu, Z.-Q.; Zhai, H. Spin-Orbit Coupled Fermi Gases Across a Feshbach Resonance. Phys. Rev. Lett. 2011, 107, 195305. [Google Scholar] [CrossRef] [PubMed]
- Iskin, M.; Subasi, A.L. Stability of Spin-Orbit Coupled Fermi Gases with Population Imbalance. Phys. Rev. Lett. 2011, 107, 050402. [Google Scholar] [CrossRef] [PubMed]
- Iskin, M.; Subasi, A.L. Quantum Phases of Atomic Fermi Gases with Anisotropic Spin-Orbit Coupling. Phys. Rev. A 2011, 84, 043621. [Google Scholar] [CrossRef]
- Jiang, L.; Liu, X.-J.; Hu, H.; Pu, H. Rashba Spin-Orbit-Coupled Atomic Fermi Gases. Phys. Rev. A 2011, 84, 063618. [Google Scholar] [CrossRef]
- Han, L.; de Melo, C.A.R.S. Evolution from BCS to BEC Superfluidity in the Presence of Spin-Orbit Coupling. Phys. Rev. A 2012, 85, 011606(R). [Google Scholar] [CrossRef]
- Zhou, K.; Zhang, Z. Opposite Effect of Spin-Orbit Coupling on Condensation and Superfluidity. Phys. Rev. Lett. 2012, 108, 025301. [Google Scholar] [CrossRef] [PubMed]
- Iskin, M. Vortex Line in Spin-Orbit Coupled Atomic Fermi Gases. Phys. Rev. A 2012, 85, 013622. [Google Scholar] [CrossRef]
- He, L.; Huang, X.-G. BCS-BEC Crossover in 2D Fermi Gases with Rashba Spin-Orbit Coupling. Phys. Rev. Lett. 2012, 108, 145302. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.J.; Borunda, M.F.; Liu, X.; Sinova, J. Effect of Induced Spin-Orbit Coupling for Atoms via Laser Fields. Phys. Rev. Lett. 2009, 102, 046402. [Google Scholar] [CrossRef]
- Dell’Anna, L.; Mazzarella, G.; Salasnich, L. Condensate Fraction of a Resonant Fermi Gas with Spin-Orbit Coupling in Three and Two Dimensions. Phys. Rev. A 2011, 84, 033633. [Google Scholar] [CrossRef]
- Dell’Anna, L.; Mazzarella, G.; Salasnich, L. Tuning Rashba and Dresselhaus Spin-Orbit Couplings: Effects on Singlet and Triplet Condensation with Fermi Atoms. Phys. Rev. A 2012, 86, 053632. [Google Scholar] [CrossRef]
- Dell’Anna, L.; Grava, S. Critical Temperature in the BCS-BEC Crossover with Spin-Orbit Coupling. Condens. Matter 2021, 6, 16. [Google Scholar] [CrossRef]
- Powell, P.D.; Baym, G.; de Melo, C.A.R. Superfluid Transition Temperature and Fluctuation Theory of Spin-Orbit- and Rabi-Coupled Fermions with Tunable Interactions. Phys. Rev. A 2022, 105, 063304. [Google Scholar] [CrossRef]
- Salasnich, L.; Penna, V. Itinerant Ferromagnetism of Two-Dimensional Repulsive Fermions with Rabi Coupling. New J. Phys. 2017, 19, 043018. [Google Scholar]
- Penna, V.; Salasnich, L. Polarization in a Three-Dimensional Fermi Gas with Rabi Coupling. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 035301. [Google Scholar] [CrossRef]
- Lepori, L.; Maraga, A.; Celi, A.; Dell’Anna, L.; Trombettoni, A. Effective Control of Chemical Potentials by Rabi Coupling with RF-Fields in Ultracold Mixtures. Condens. Matter 2018, 3, 14. [Google Scholar] [CrossRef]
- Liu, X.-J.; Hu, H. BCS-BEC Crossover in an Asymmetric Two-Component Fermi Gas. Europhys. Lett. 2006, 75, 364. [Google Scholar] [CrossRef]
- Parish, M.M.; Marchetti, F.M.; Lamacraft, A.; Simons, B.D. Finite-Temperature Phase Diagram of a Polarized Fermi Condensate. Nat. Phys. 2007, 3, 124. [Google Scholar] [CrossRef]
- Babaev, E.; Kleinert, H. Nonperturbative XY-model Approach to Strong Coupling Superconductivity in Two and Three Dimensions. Phys. Rev. B 1999, 59, 12083. [Google Scholar] [CrossRef]
- Nozieres, P.; Schmitt-Rink, S. Bose Condensation in an Attractive Fermion Gas: From Weak to Strong Coupling Superconductivity. J. Low Temp. Phys. 1985, 59, 195. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics—Part 2: Theory of the Condensed State, Course of Theoretical Physics; Pergamon Press: Oxford, UK, 1980; Volume 9. [Google Scholar]
- Pini, M.; Pieri, P.; Strinati, G.C. Fermi Gas Throughout the BCS-BEC Crossover: Comparative Study of t-matrix Approaches with Various Degrees of Self-Consistency. Phys. Rev. B 2019, 99, 094502. [Google Scholar] [CrossRef]
- Available online: https://thesis.unipd.it/bitstream/20.500.12608/22969/1/TesiFedericoDeBettin_TESI.pdf (accessed on 13 September 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dell’Anna, L.; De Bettin, F.; Salasnich, L. Rabi Coupled Fermions in the BCS–BEC Crossover. Condens. Matter 2022, 7, 59. https://doi.org/10.3390/condmat7040059
Dell’Anna L, De Bettin F, Salasnich L. Rabi Coupled Fermions in the BCS–BEC Crossover. Condensed Matter. 2022; 7(4):59. https://doi.org/10.3390/condmat7040059
Chicago/Turabian StyleDell’Anna, Luca, Federico De Bettin, and Luca Salasnich. 2022. "Rabi Coupled Fermions in the BCS–BEC Crossover" Condensed Matter 7, no. 4: 59. https://doi.org/10.3390/condmat7040059
APA StyleDell’Anna, L., De Bettin, F., & Salasnich, L. (2022). Rabi Coupled Fermions in the BCS–BEC Crossover. Condensed Matter, 7(4), 59. https://doi.org/10.3390/condmat7040059






