Abstract
Practical mesoscopic devices based on quantum point contacts (QPCs) must function at operating point involving large internal driving fields. Experimental evidence has accumulated to display anomalous nonlinear features of QPC response beyond the capacities of accepted tunnelling-based models of nonlinear quantum transport. Here, we recall the physical setting of three anomalous QPC experiments and review how, for two of them, a microscopically based nonequilibrium quantum kinetic description—the correct physical boundary conditions being crucial—has already overcome the predictive limitations of standard nonequilibrium mesoscopic models. The third experiment remains a significant challenge to all theorists.
1. Introduction
Phenomena in quantum transport unique to two-dimensionally constrained electronic systems, formerly considered exotic, have since become bread-and-butter items for condensed-matter physics. Already, for some time, in the form of quantum-well-confined structures, they have been deeply embedded in the design even of prosaic consumer electronics.
Slightly later than the basic two-dimensional breakthroughs of the 1970s came those at the next level, for structures virtually, if not literally, at one dimension (1D). Their fundamental exploration is very much a current research focus for the physics of electronic transport. While one might argue that their truly large-scale applications have some way to go to outdo the widespread success of their two-dimensional predecessors, it is taken for granted that this is a basic matter of concerted technical development.
It is the physical underpinning of the 1D device realm that forms the topic in the following, somewhat condensed, review. Readers who may want more detailed information on all the accepted methodologies based on the reservoir analogy, as well as background on our own application of established quantum kinetics, are invited to consult the extended references in the long survey paper [1] as well as in the more specialized [2,3,4].
We concentrate on aspects of observed 1D transport behaviour that appear to go against accepted theoretical models. Both experimentalists and theorists tend to refer to these laboratory results as “anomalous”, but any consistent departure from experimental expectations will always be perceived as abnormal—until a tenable explanation emerges. The question is: “anomalous” relative to what? The answer is: relative to the received theoretical understanding. Nature entertains no anomalies. It is we as investigators who are subject to a momentary cognitive dissonance. Anomalous results, by their very presence, tell us that more is demanded of a quantitative theory than anything in common currency.
Anomalies in nonlinear 1D transport emerged around the turn of this century. The actual surprise, there, is not their discovery but that they seemed to remain in the “too-hard basket”, practically unattended to in the literature. Here, we review two cases that have now been addressed, and cite a third intriguing instance still defying analysis.
Our first example is excess 1D conductance in a working region where the conductance quantum is supposed to never be exceeded [5,6]; the second is anomalous hot-electron noise in a 1D wire, or quantum point contact (QPC) [7]. The third striking example, which we can discuss only in passing, is the nonlinear Aharanov–Bohm effect [8]. These measurements, largely bypassed by theorists, supply appreciable evidence for reconsidering the limits of accepted mesoscopic transport models [9].
2. Background
We begin by recapitulating the distinctive transport behaviour of quasi-1D ballistic channels. Some thirty-five years ago, two measurements [10,11] first demonstrated the quantization of 1D conductance as a function of device carrier density, in sequential steps close to the universal quantum , termed the Landauer conductance in this field (the same as the quantum-Hall unit, up to a factor of two). A weighty literature explaining the quantization [12,13,14,15] and its extension to noise [16] was soon established to offer a readily appealing, seemingly adaptable description.
2.1. Standard Account
Consider two macroscopic metallic electron reservoirs, left and right, at chemical potentials and linked by a long, uniform narrow wire supporting a series of discrete quantum levels, or channels, produced by the lateral confinement defining the quasi-1D conductor. The channels are assumed independent, each with its own set of conductive 1D states able to transmit charge carriers.
In the Landauer current formula [14,15], the reservoirs have equilibrium electron distributions and where wave vector k indexes the conductive states in the 1D band, with and the band energy and group velocity, respectively. Phenomenologically, one may argue that the net current should be a difference of right- and left-moving electron fluxes:
where the right-side momentum is defined via and a unitary transmission factor when the wire presents a barrier to coherent transmission. The equation assumes total statistical decoupling of initial and final state occupancies. As such, it is a revisiting of older tunnelling prescriptions [17] such as the early one of Bardeen and of Esaki’s extension to the tunnelling diode.
We remark that tunnelling formulae are appropriate between autonomous reservoirs communicating solely by overlap of the exponential tails inside the barrier region. The fundamentally stochastic coupling of the left- and right-localized carrier distributions, in two disjoint bands, does not apply to metallic transport. In that case, by contrast, the physics is dominated by the flux-bearing eigenstates. These states are delocalized across the entire participating system and support a single distribution (not two) in a unified conduction band, with a quantum barrier or with none.
At equilibrium, with equal chemical potentials , the current given by Equation (1) is zero. A small driving voltage V applied right to left will raise above by . Noting that , in the low-temperature limit, the current becomes
in which the conductance quantum now appears. One can repeat the argument for a number of occupied discrete channels assuming that that they are independent of one another, excluding any cross-talk in the active region as well as any interaction mediated by their common lead reservoirs. Under those terms, the total conductance becomes
with the discrete energy thresholds for the quantum-confined 1D conduction bands, or channels. This accounts for the characteristic constancy of conductance as a function of channel density when this is modulated by altering chemical potential , usually by gate control of the device. Since , it follows from Equation (3) that no individual step can exceed , the ideal maximum.
Efforts to generalize the basic formula, Equation (1), to the nonlinear regime have been made, and keep being made. Few, if any, of the best advertised attempts see fit even to re-evaluate, let alone leave behind, the idea of tunnelling within an environment that is clearly metallically conductive. We have discussed elsewhere [1], in more formal detail, the most popular of these recent approaches: the nonequilibrium Green function (NEGF) formalism.
In any of a variety of guises [18,19], NEGF computes the self-energy for the putative interacting Green function (the purely single-particle version that is) within some correlated electron model in localized form. The result is a locally determined effective transmission amplitude richer than the Landauer version but which nevertheless—based as it is on a one-body object—is a quasiparticle spectral weight that never exceeds the unitarity bound in the way already observed experimentally [5,6] and described in the following. NEGF still does nothing about the imaginative but unfortunately inappropriate boundary conditions insisting on localized tunnelling inside a fully delocalized, if non-uniform, integrally metallic medium.
2.2. Difficulties and Remedies
We need not dwell any more on the use of a tunnelling scenario in cases where the physics of conduction is undoubtedly metallic, for there are two other difficulties with Equation (3) describing conductance quantization. The more obvious issue is that conductance implies ohmic resistance, which implies Joule heating. It is immaterial whether the resistive device is macro-, meso- or nano-scopic. In distilling Equation (1) to get to (3), there is no appeal to the process of dissipation; coherent quantum transmission is dissipationless as well as reversible (unlike Joule heating).
The second, less obvious problem, is the assumption of independent conducting channels. All their carriers are injected from, then received by, bulk metallic leads. It is inevitable that there must be an interplay between band populations in their transition to and from the common leads. This is likely to affect the details of the carriers’ distribution as some level, even if they did not interact in their discrete channels while crossing the active region. In the next section, we return to this aspect in the context of measurements by de Picciotto et al. [5,6]. First, we deal with the problem of dissipation.
Loss of electrical energy absorbed from driving fields is a nonequilibrium effect that impacts directly on the detailed physics of transport. Dissipation always has an immediate role in any quantitative account of what is, in the end, a case of ohmic conduction. As the experiments surveyed below show, the problem becomes pressing well away from linear response where, as is now acknowledged, coherent transmission theory has less to offer in a systematic way.
A solution already exists within quantum kinetics taken in its its long-wavelength limit, the quantum-Boltzmann equation, and in the succinct form of the canonical Kubo–Greenwood relation to which the kinetic equation conforms [20]. We will not reproduce the full derivation of the quantum kinetic formula that corresponds to Equation (3) [1], but give some sense of a different philosophy that leads to an equivalent result while fully including the physics of dissipation. We start with a single metallic channel. If one takes the familiar Drude–Sommerfeld conductance formula in the low-temperature limit, expressing its customary relaxation rates in terms of mean free paths, one has
Parameters are: the operative channel length L; effective mass and Fermi velocity for a quadratically dispersive conduction band; 1D carrier density in terms of , the Fermi wave vector; and are the elastic and inelastic scattering mean free paths respectively, the latter responsible for resistive loss and, crucially, for stability of the steady state [1].
Thus far, the quantitative content is perfectly conventional. The physical reasoning specific to a quasi-ballistic structure now follows.
Transport within the channel is ballistic and not necessarily coherent. There do exist finite mean free paths, but these are not set by the usual considerations in the bulk, rather by the carriers’ interactions with the leads through stochastic injection and extraction. By the same token, the operational length of the channel is also set by the dynamics of its interfaces with the leads—for, at mesoscopic scales, the geographic boundary between channel and leads becomes ill-defined. Conceptually the limiting device boundary L itself becomes identifiable with the maximum mean free path, the scale beyond which any notion of ballisticity is lost. (In transmission parlance, this scale is the “coherence length”).
On these assumptions, in Equation (4), we make the replacement . Rationalizing the factor , we arrive at
There is no functional difference between this expression and the lossless Equation (3). Both have the same ideal maximum ; Equation (5) attains it when the mean free paths are matched. The latter formula gives dissipation its proper role and avoids the conceptual confusion of Equation (3), which pits the complete coherence of a fully delocalized transmitted flux against the complete stochasticity of the localized static boundary conditions, with no rational handle on energy loss. The kinetic basis for Equation (5) also allows a systematic approach to current noise [21]; more on this below.
We come to the task of resolving the second and more challenging issue presented by the hypothesis of total independence for discrete channel populations. When discrete channels are able to interact, the possibility opens up for interband carrier transfer. This immediately turns the transport calculation into a correlated many-body one, a case in which unitarity in each channel fails, and a collective description is required.
3. Interacting One-Dimensional Bands
In an investigation of the so-called 0.7 conductance anomaly in a multi-channel QPC, de Picciotto and co-workers [5,6] went further to present additional measurements of quantized conductance in a close-to-ideal 1D device, covering the density regime where the lowest channel’s band was well occupied right up to the threshold of the next-higher band. When driven beyond weak bias voltages, the surprise was that the size of the step in G, still essentially flat, increased systematically and substantially with V. Figure 1 shows their results.
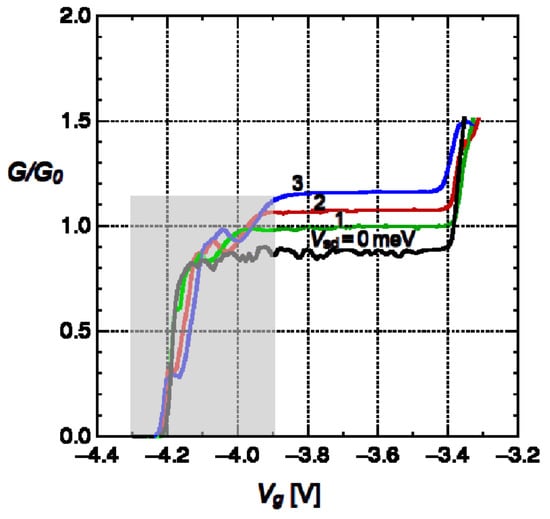
Figure 1.
Quantized differential conductance G measured in a quasi-one-dimensional multi-sub-band ballistic channel, after de Picciotto et al. [6]. G is plotted in units of the quantum = 77.48 S, as a function of control-gate voltage modulating the carrier density within the channel. Beyond the labile structures (grey box) at the threshold of the ground-state band lies a series of very flat extended plateaux for different values of bias voltage driving the current. That the system is beyond linear response is seen in the bias dependence of the conductance. The steps of G above the presumed upper limit is noteworthy. This shows that effects beyond simple quantum-coherent transmission dominate the transport physics, adapted from [6]. © IOP Publishing Ltd.
Other than the structures greyed out in Figure 1, the absolutely flat voltage-dependent plateaux demonstrate that more than single-particle physics is at work. We followed up the experimenters’ own hypothesis [5,6] that exchanges of carriers between the lower and upper band could enhance the conductance of the well populated lower band by depleting it (with no effect on its conductance step size), thereby adding excess carriers to the upper band in its threshold region where G is quite sensitive to small changes in its band density.
We reasoned that, at higher values of V, the coupling between channels leads to greater transfer of carriers to the higher level and that, at the same time, these excited carriers have an increased likelihood of falling back into the lower band, resulting in a steady state regulated by negative feedback and stabilizing the enhancement of G around the threshold of the upper band.
One can compare the results of our calculation in Figure 2 [22] with the experimental data in Figure 1. While the calculated conductances overestimate the measured step values in our simplified simulation, the robust character of the plateaux and their voltage dependence are strikingly similar to experiments.
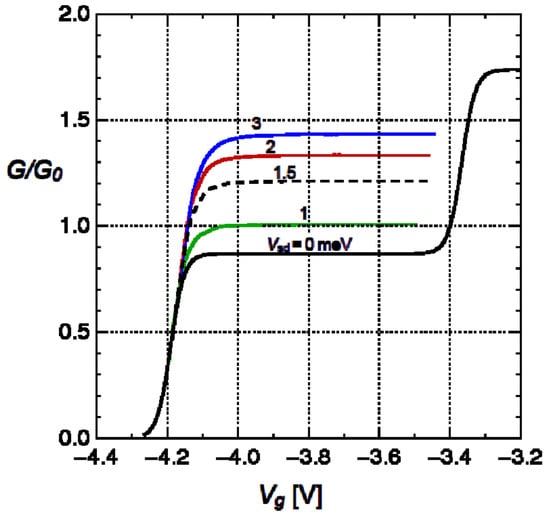
Figure 2.
Anomalous enhancement of conductance for a ballistic device model, equivalent to that of our Figure 1 (after Figure 3a of [6]) at nominal temperature 4K. Axis scales are as for that figure; G is plotted in units of versus gate voltage sweeping the electron density through the band-gap regime from the start of the ground-state band to the threshold of the first excited-state band. Bottom curve: in weak-field response, the quantized conductance matches that for the standard linear response. Higher curves: as the driving voltage increases, the conductance acquires a nonlinear enhancement. The action of interband transitions dynamically redistributes carrier density between bands. This is responsible for the strong enhancement of the step in G, beyond the upper bound posited by quantum-transmission models of conductance, adapted from [22]. © IOP Publishing Ltd.
The calculation involves solving a coupled quantum Boltzmann equation including a generation–recombination mechanism induced by the interband transition rate. Here, we set out the schematics of the procedure; for details, see [22]. We restrict the problem to two channels separated by a given band gap . Since the total density over both bands is constant at global chemical potential , conservation enforces
with the density in the lower band and in the upper. The populations out of equilibrium are no longer determined by but depend on the bias voltage. Therefore, we refer the separate carrier distributions to a pair of nominal equilibrium states at the effective chemical potentials and . We expect the former potential to decrease as the lower channel depletes, and the latter to rise as the upper channel gains extra carriers. At equilibrium, both match , but, in the driven system, they may not and are nevertheless coupled by the need to conform to conservation.
To fix and uniquely, thus closing the now self-consistent problem, a second and physically motivated constitutive relation is necessary. In the parameter space of and , we compute the free energy, plotting its difference with the free energy for totally independent bands, where . When there is no maximum, the solution reverts to the latter case. If there is a nontrivial maximum in the difference, its locus will intersect the contours of constant n generated by Equation (6). In either eventuality, one can find the operating point at a given total density, where the net conductance is calculated. Figure 2 is the result of our strategy.
The physical motivation for using the free energy is that it carries the overhead of available electrical energy absorbed from the driving field and momentarily retained as kinetic energy of the excited carriers—a sort of reservoir in momentum space. It is reasonable to think that this dynamic overhead builds up to a maximum, depending on the capacity of inelastic collisions to dissipate it and sustain a steady state. The operating point will thus arrange itself at the free-energy maximum because the first port of call for the transferred electrical energy is always the carrier motion, not the heat bath, which is accessed only via the lossy collisions forming a bottleneck.
4. QPC Noise at High Fields
Kinetic theories, such as the Boltzmann equation, are explicitly structured to respect microscopic conservation. Subjected to perturbation analysis, the derived equations guarantee that the same conservation properties of particle number, momentum, and energy (the latter in thermodynamic conformity with the dissipation rate) are inherited by the corresponding fluctuations.
We have extended the kinetic approach to studying thermal current fluctuations departing from equilibrium and manifesting as dynamical noise in actual devices. Shot noise, thermodynamically distinct from thermal noise, is also kinetically tractable (other species such as noise require techniques that involve explicit input about the specific environment). For a general introduction, we direct readers to Kittel [23].
Unlike fluctuations in the power output of a conducting structure, routinely probed in device characterization, current–current fluctuations are not easy to measure and need specialized methods. A thorough experimental study of high-field current noise in QPC samples was made by Reznikov et al. [7]. To highlight the anomaly in their experiment over against commonly anticipated expectations for the density dependence of noise, we refer to Figure 3 adapted from [7].
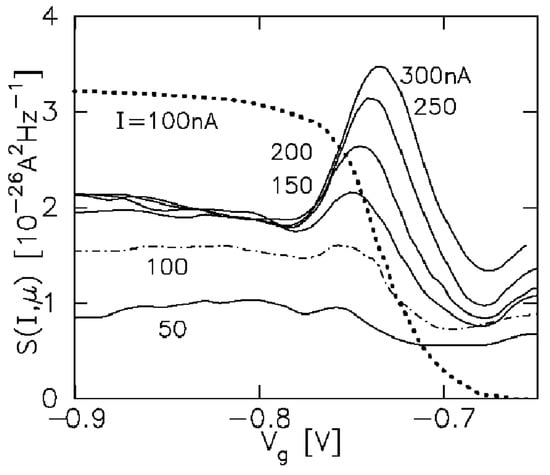
Figure 3.
Measured high-field excess current noise in a quantum point contact at 1.5 K (adapted from [21] after Reznikov et al. [7]) as a function of gate bias at fixed levels of the current. Dotted line: the most widely adopted theoretical noise model [16] predicts a strictly monotonic noise signal at the first band threshold. The very strong noise peaks actually recorded at threshold are not anticipated. © 2004 The American Physical Society.
Figure 3 shows the low-frequency spectral density of excess QPC current noise after subtraction of the normal Johnson–Nyquist thermal noise floor at temperature T. The Reznikov group performed their measurements at fixed levels of current through the structure, while most other investigators choose to fix the driving voltage only.
According to standard descriptions, at very low gate voltage (thus carrier density) up to the threshold, the signal should be dominated by classical shot noise, determined by the Poissonian statistics of electron injection and extraction rather than the fluctuation–dissipation dynamics underlying . As the carrier density rises within the channel, Pauli degeneracy starts to suppress the noise, which dies monotonically above the conduction threshold. This is predicted for any level of the QPC current.
The anticipated uniformly monotonic fall-off of the noise is not seen, however. Against theoretical expectation, a very strong peak structure develops at the threshold where the lowest conduction band of the 1D structure begins to populate. In contrast, a kinetically grounded analysis of the fluctuations in the highly nonequilibrium carrier distribution provides a straightforward and reasonably quantitative account. Figure 4 displays our calculation [21].
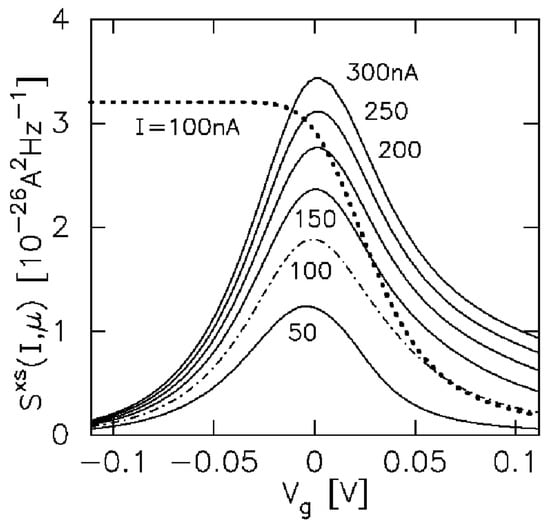
Figure 4.
Computed high-field excess current noise at 1.5 K in a QPC at fixed levels of source-drain current around its lowest band threshold, matching the conditions for Figure 3, after the experiment of Reznikov et al. [7]. Our calculation follows a strictly conserving quantum-Boltzmann analysis of current fluctuations far from equilibrium [21]. Note the quantitative affinity of the calculated peaks with the experimentally observed first-threshold maxima in Figure 3. Dotted line: corresponding prediction at a current of 100 nA, according to a quantum-transmission model of QPC current noise [16], using our associated evaluation of conductance as that model’s phenomenologically required input. This can be compared with the peak at 100 nA (dot-dashed line) resulting from the kinetic theoretical calculation. © 2004 The American Physical Society.
Lacking scope here for a detailed account, we offer sources [21,24] as resources for a quantum Boltzmann approach to nonequilibrium current noise. The origin of the peak structures shown in Figure 4 lies in the interplay of the electrons’ compressibility, which falls off rapidly on entering the degenerate density regime, and the conductance of the QPC which decays in the depletion region but rises at the threshold to a constant fraction of at large occupancy.
At high current, the conductance is degraded by additional inelastic scattering. Roughly speaking, we can write the excess thermal current noise as
where the compressibility is scaled to its classical value , and b is an exponent of order 0.5. While decreases rapidly from unity in the threshold range, the conductance, scaling with exponentially small density below that, rises to its plateau in just that region. The competition between the two generates the peaks at threshold.
We have accounted for the unexplained peak structures in the experimental curves of Reznikov et al. [8] of Figure 3. Thus far, we have not advanced a similar description of the shot-noise-like plateaux seen there at gate voltages below −0.8 V, corresponding to extremely low carrier numbers and high driving fields. In the predicted versus measured 100 nA curves in that figure, standard models [16] overestimate measured levels but contain no further mechanism to correct the predicted excess. The issue is open to a future explicit account of the shot-noise aspect, though from a kinetic standpoint.
Finally, it is noteworthy that the compressibility central to our noise theory does not depend in any way on the size of the current through the QPC; its value is determined by the global chemical potential alone. This is due to strong metallic screening (and rapid thermal dissipation) from the large, degenerate population of free electrons in the macroscopic device leads with the overall device neutrality that follows from it [2].
In physical terms, the total number N of carriers in the working region (metallic channel plus interfaces), and its mean thermal fluctuation , are environmentally fixed; the electrostatic boundary conditions constrain N and to their equilibrium values set globally by irrespective of driving voltage. Any internal redistribution of the driven carriers cannot manifest in the bulk compressibility of the active structure [2]. This is the direct outcome of the physics of charged Fermi liquids [25]; a fundamental collective effect insufficiently considered by treatments of 1D fluctuations and violated by some [3], even to a loss of gauge invariance (charge conservation) [16].
5. Nonlinear Aharonov–Bohm Effect: A Challenge
Our last example presents a fascinating theoretical challenge whose resolution in terms of standard quantum kinetics remains wide open. The Aharonov–Bohm effect has long been understood as a demonstration of the physical reality of the vector potential [26]. The way by which the vector potential enters directly into the wave function of a carrier results in a relative phase shift when the carrier has the option of passing to one or the other side of a tubular region, enclosing a magnetic flux.
Even if the magnetic field was screened to vanish outside its confining tube, the generating vector potential would not be zero, acting differently on the phase of each branch of the carrier’s wave. This provides a variation on the two-slit interference scenario: modulating the magnetic flux induces a phase mismatch between branches, causing a periodic pattern of oscillations in the magnitude of the current.
In the configuration of Neder et al. [8], the difference of maximum (constructive interference) and minimum (destructive interference) current magnitudes, as a ratio with their sum, defines the visibility: this measure lies between one and zero as the magnetic flux is varied. The investigated structure consisted of two QPCs linked in parallel to make up a Mach–Zehnder electron interferometer enclosing an area threaded by a magnetic field. Its flux was modulated by electrostatically modifying one of the QPC branches, altering both its path length and the enclosed area.
For low driving voltage, the visibility should be constant at fixed magnetic field, since all currents scale linearly with voltage. Away from the linear region, based on previous experience with a simpler device, the investigators anticipated a progressive monotonic decay in visibility owing to loss of quantum coherence through increased random scattering [8].
The Neder collaboration found, instead, that the visibility as a function of greater driving voltage first fell rapidly to zero but then recovered and rose substantially, repeating this behavior with a periodicity strictly correlated with an abrupt change by in the stepwise form of the overall phase difference across the interferometer, inferred from the data. As carefully discussed in their paper [8], the effect contradicts conventional explanations.
At this time of writing, we have no light to shed on this remarkable finding. We are, however, intrigued by the robust periodicity of the visibility and consider that it well merits further thought, given that nonequilibrium transport in most cases really should wipe out such delicate effects. One potential consideration may be relevant: a model of the twin-path electron interferometer should perhaps not assume ideal, cost-free 50-50 transmission at its junctions as for, say, half-silvered mirrors in its optical predecessor. Rather, the hole in the conductive geometry presents a different sort of quantum barrier to an incoming carrier, not just dividing but severely distorting its wave function. The barrier is not fully 1D but “one-plus-one-dimensional”, calling for detailed simulation to compute how the wave function negotiates being split, to heal itself after passage.
Calculations show that normal quantum transport through multiply connected structures results in transmission factors with a complex energy dependence, more so as these geometries cause states in discrete bands to hybridize, complicating the eigenstate solutions. Such transmission behaviour, inherent in this topology, would likewise strongly condition the carrier flux. How this might play out for any of the finer details of the Aharonov–Bohm phase shift [8], with carriers in different bands possibly coupled self-consistently and reacting differently to the barrier, is certainly not clear.
6. Conclusions
We have offered a brief recapitulation of several past measurements of anomalous one-dimensional conductance, and of its closely associated current noise. In their quite different ways, they have all provided a strong incentive to look for theoretical understandings of nonequilibrium 1D transport. In order of appearance, we have covered: enhancement of nonlinear conductance beyond the Landauer bound, in the energy gap of a multi-channel device; the unexpected noise peak in a strongly driven quantum point contact; and, still not satisfactorily explained, the remarkable periodic quenching and resurgence of Aharonov–Bohm current oscillations out of equilibrium.
From all these cases, the message is that, beyond phenomenology, a microscopically based many-body methodology is needed for nonequilibrium 1D transport; a toolbox equipped to move, in a controlled way, past single-particle descriptions essentially predicated on tunnelling at linear response. Such approaches have always been possible thanks to the massive extant literature on quantum kinetic theory [20,25,27,28,29,30,31]. In our own studies, we have made honest attempts to adapt this solidly founded body of work to the one-dimensional realm, frequently in simplified models but always respecting conservation.
This brings us to a message gleaned from our own efforts. It is indeed the microscopic conservation laws, including gauge invariance that shapes the solution to problems of 1D charge transport both near and far from equilibrium, often to a surprising extent (a notable example is the previously unsuspected role of bulk electronic compressibility in high-field thermal current noise). While not sufficient on their own to solve these problems, they are absolutely indispensable.
References and Note
Author Contributions
Both authors have contributed equally. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors have no conflict of interest.
References and Notes
- Das, M.P.; Green, F. Nonequilibrium mesoscopic transport: A genealogy. J. Phys. Condens. Matter 2012, 24, 183201. [Google Scholar] [CrossRef] [PubMed]
- Green, F.; Das, M.P. Coulomb screening in mesoscopic noise: A kinetic approach. J. Phys. Condens. Matter 2000, 12, 5251–5273. [Google Scholar] [CrossRef][Green Version]
- Thakur, J.S.; Green, F.; Das, M.P. Sum-rule Constraints for Open Mesoscopic Conductors. Int. J. Mod. Phys. B 2004, 18, 1479–1488. [Google Scholar] [CrossRef]
- Das, M.P.; Green, F. Mesoscopic transport revisited. J. Phys. Condens. Matter 2009, 21, 101001. [Google Scholar] [CrossRef] [PubMed]
- De Picciotto, R.; Pfeiffer, L.N.; Baldwin, K.W.; West, K.W. Nonlinear Response of a Clean One-Dimensional Wire. Phys. Rev. Lett. 2004, 92, 036805. [Google Scholar] [CrossRef] [PubMed]
- De Picciotto, R.; Baldwin, K.W.; Pfeiffer, L.N.; West, K.W. The 0.7 structure in cleaved edge overgrowth wires. J. Phys. Condens. Matter 2008, 20, 164204. [Google Scholar] [CrossRef]
- Reznikov, M.; Heiblum, M.; Shtrikman, H.; Mahalu, D. Temporal Correlation of Electrons: Suppression of Shot Noise in a Ballistic Quantum Point Contact. Phys. Rev. Lett. 1995, 75, 3340–3343. [Google Scholar] [CrossRef] [PubMed]
- Neder, I.; Heiblum, M.; Levinson, Y.; Mahalu, D.; Umansky, V. Unexpected Behavior in a Two-Path Electron Interferometer. Phys. Rev. Lett. 2006, 96, 016804. [Google Scholar] [CrossRef] [PubMed]
- For the reader who may wonder at our omission of the “0.7 anomaly”, or blip, in the QPC threshold conductance (as a ratio with the ideal Landauer value), we have analysed this elsewhere; see Das, M.P.; Green, F. Conductance anomalies in quantum point contacts and 1D wires. Adv. Nat. Sci. Nanosci. Nanotechnol. 2017, 8, 023001. [Google Scholar] Such wide departures in shape, size and location have been recorded for this notorious effect, and with such broad material dependence, that to ascribe any systematics to these results does violence to the concept of measuring an “effect”, anomalous or otherwise.
- Van Wees, B.J.; van Houten, H.; Beenakker, C.W.J.; Williamson, J.G.; Kouwenhoven, L.P.; van der Marel, D.; Foxon, C.T. Quantized conductance of point contacts in a two-dimensional electron gas. Phys. Rev. Lett. 1988, 60, 848–850. [Google Scholar] [CrossRef] [PubMed]
- Wharam, D.A.; Thornton, T.J.; Newbury, R.; Pepper, M.; Ahmed, H.; Frost, J.E.F.; Hasko, D.G.; Peacock, D.C.; Ritchie, D.A.; Jones, G.A.C. One-dimensional transport and the quantization of the ballistic resistance. J. Phys. C Solid State Phys. 1988, 21, L209–L214. [Google Scholar] [CrossRef]
- Büttiker, M. Symmetry of electrical conduction. IBM J. Res. Dev. 1988, 32, 317–334. [Google Scholar] [CrossRef]
- Stone, A.D.; Szafer, A. What is measured when you measure a resistance? The Landauer formula revisited. IBM J. Res. Dev. 1988, 32, 384–413. [Google Scholar] [CrossRef]
- Imry, Y.; Lauer, R. Conductance viewed as transmission. Rev. Mod. Phys. 1999, 71, S306–S312. [Google Scholar] [CrossRef]
- Imry, Y. Introduction to Mesoscopic Physics, 2nd ed.; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Blanter, Y.M.; Büttiker, M. Shot noise in mesoscopic conductors. Phys. Rep. 2000, 336, 1–166. [Google Scholar] [CrossRef]
- Frensley, W.R.; Einspruch, N.G. (Eds.) Heterostructures and Quantum Devices, a Volume of VLSI Electronics: Microstructure Science; Academic Press: San Diego, CA, USA, 1994; Chapter 9. [Google Scholar]
- Paulsson, M. Non Equilibrium Green’s Functions for Dummies: Introduction to the One Particle NEGF Equations. 2006. Available online: https://arxiv.org/abs/cond-mat/0210519 (accessed on 5 August 2022).
- Cornean, H.D.; Moldoveanu, V.; Pillet, C.A. A Mathematical Account of the NEGF Formalism. Ann. Henri Poincaré 2018, 19, 411–442. [Google Scholar] [CrossRef]
- Mahan, G.D. Many-particle Physics, 2nd ed.; Plenum: New York, NY, USA, 1993; pp. 218–221. [Google Scholar]
- Green, F.; Thakur, J.; Das, M.P. Where is the Shot Noise of a Quantum Point Contact? Phys. Rev. Lett. 2004, 92, 156804. [Google Scholar] [CrossRef] [PubMed]
- Green, F.; Das, M.P. Anomalous conductance quantization in the inter-band gap of a one-dimensional channel. J. Phys. Condens. Matter 2018, 30, 385304. [Google Scholar] [CrossRef] [PubMed]
- Kittel, C. Elementary Statistical Physics; John Wiley & Sons: New York, USA, 1958; pp. 117–168. [Google Scholar]
- Green, F.; Das, M.P. Classical to Quantum Crossover in High-current Noise of One-dimensional Ballistic Wires. Fluct. Noise Lett. 2001, 1, C21–C33. [Google Scholar] [CrossRef]
- Pines, D.; Nozières, P. The Theory of Quantum Liquids I; W. A. Benjamin: New York, NY, USA, 1966; pp. 147–268. [Google Scholar]
- Baym, G. Lectures on Quantum Mechanics; Westview Press: New York, NY, USA, 1990; pp. 74–79. [Google Scholar]
- Martin, P.C. Measurements and Correlation Functions; Gordon and Breach: New York, NY, USA, 1968. [Google Scholar]
- Frensley, W.R. Boundary conditions for open quantum systems driven far from equilibrium. Rev. Mod. Phys. 1990, 62, 745–791. [Google Scholar] [CrossRef]
- Rammer, J. Quantum Field Theory of Non-Equilibrium States; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Röpke, G.; Winkel, M. Green’s Functions Technique for Statistical Ensembles; Rostock University: Rostock, Germany, 2009. [Google Scholar]
- Bonitz, M. Quantum Kinetic Theory; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).