On the Kinetic Energy Driven Superconductivity in the Two-Dimensional Hubbard Model
Abstract
1. Introduction
2. Hubbard Hamiltonian
3. Optimized Wave Function
4. Correlated Superconducting State
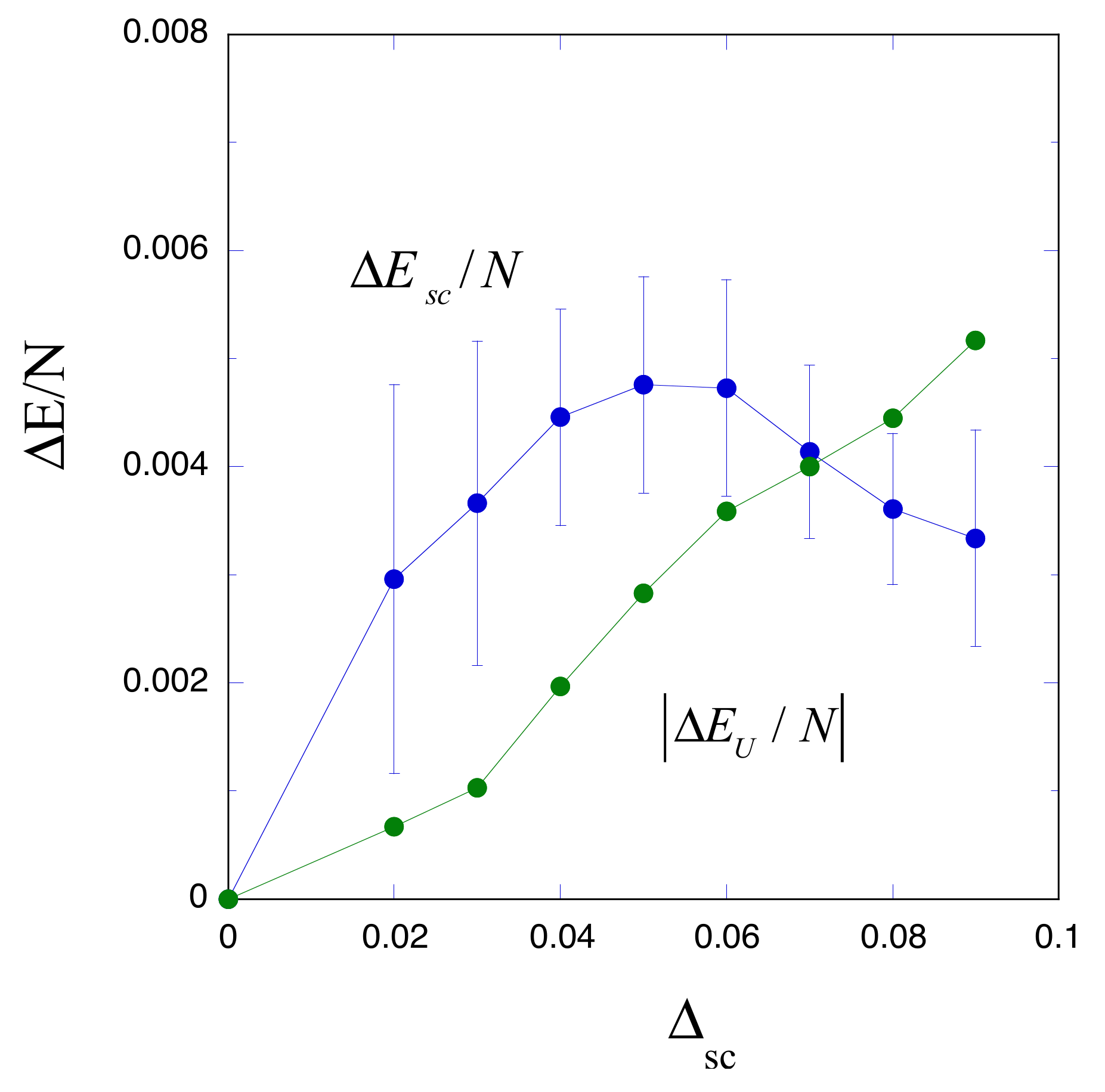
5. Kinetic Energy in the Superconducting State
6. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| VMC | variational Monte Carlo method |
| AF | antiferromagnetic |
| SC | superconductivity or superconducting |
| 2D | two-dimensional |
| AFI | antiferromagnetic insulator |
| PI | paramagnetic insulator |
References
- Bednorz, J.B.; Müller, K.A. Possible high Tc superconductivity in the Ba-La-Cu-O system. Z. Phys. 1986, B64, 189. [Google Scholar] [CrossRef]
- McElroy, K.; Simmonds, R.W.; Hoffman, J.E.; Lee, D.H.; Orenstein, J.; Eisaki, H.; Uchida, S.; Davis, J.C. Relating atomic-scale electronic phenomena to wave-like quasiparticle states in superconducting Bi2Sr2CaCu2O8+δ. Nature 2003, 422, 592. [Google Scholar] [CrossRef] [PubMed]
- Hussey, N.E.; Abdel-Jawad, M.; Carrington, A.; Mackenzie, A.P.; Balicas, L. A coherent three-dimensional Fermi surface in a high-transition-temperature superconductor. Nature 2003, 425, 814. [Google Scholar] [CrossRef]
- Weber, C.; Haule, K.; Kotliar, G. Critical weights and waterfalls in doped charge-transfer insulators. Phys. Rev. 2008, B78, 134519. [Google Scholar] [CrossRef]
- Hybertsen, M.S.; Schlüter, M.; Christensen, N.E. Calculation of Coulomb-interaction parameter for La2CuO4 using a constrained-density-functional approach. Phys. Rev. 1989, B39, 9028. [Google Scholar] [CrossRef] [PubMed]
- Eskes, H.; Sawatzky, G.A.; Feiner, L.F. Effective transfer for singlets formed by hole doping in the high-Tc superconductors. Physica 1989, C160, 424. [Google Scholar] [CrossRef]
- McMahan, A.K.; Annett, J.F.; Martin, R.M. Cuprate parameters from numerical Wannier functions. Phys. Rev. 1990, B42, 6268. [Google Scholar] [CrossRef] [PubMed]
- Eskes, H.; Sawatzky, G. Single-, triple-, or multiple-band Hubbard models. Phys. Rev. 1991, B43, 119. [Google Scholar] [CrossRef] [PubMed]
- Emery, V.J. Theory of high-Tc superconductivity in oxides. Phys. Rev. Lett. 1987, 58, 2794. [Google Scholar] [CrossRef]
- Hirsch, J.E.; Loh, E.Y.; Scalapinom, D.J.; Tang, S. Pairing interaction in CuO clusters. Phys. Rev. 1989, B39, 243. [Google Scholar] [CrossRef]
- Scalettar, R.T.; Scalapino, D.J.; Sugar, R.L.; White, S.R. Antiferromagnetic, charge-transfer, and pairing correlations in the three-band Hubbard model. Phys. Rev. 1991, B44, 770. [Google Scholar] [CrossRef]
- Oguri, A.; Asahatam, T.; Maekawa, S. Gutzwiller wave function in the three-band Hubarf model: A variational Monte Carlo study. Phys. Rev. 1994, B49, 6880. [Google Scholar] [CrossRef] [PubMed]
- Koikegami, S.; Yamada, K. Antiferromagnetic and superconducting correlations on the d-p model. J. Phys. Soc. Jpn. 2000, 69, 768. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Koike, S.; Yamaji, K. Ground state of the three-band Hubbard model. Phys. Rev. 2001, B64, 184509. [Google Scholar] [CrossRef]
- Koikegami, S.; Yanagisawa, T. Superconducting gap of the two-dimensional d-p model with small Ud. J. Phys. Soc. Jpn. 2001, 70, 3499. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Koike, S.; Yamaji, K. Lattice distortions, incommensurability, and stripes in the electronic model for high-Tc cuprates. Phys. Rev. 2003, B67, 132408. [Google Scholar] [CrossRef]
- Koikegami, S.; Yanagisawa, T. Superconductivity in Sr2RuO4 mediated by Coulomb scattering. Phys. Rev. 2003, B67, 134517. [Google Scholar] [CrossRef]
- Koikegami, S.; Yanagisawa, T. Superconductivity in multilayer perovskite. J. Phys. Soc. Jpn. 2006, 75, 034715. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Miyazaki, M.; Yamaji, K. Incommensurate antiferromagnetism coexisting with superconductivity in two-dimensional d-p model. J. Phys. Soc. 2009, 78, 031706. [Google Scholar] [CrossRef]
- Weber, C.; Lauchi, A.; Mila, F.; Giamarchi, T. Orbital currents in extended Hubbard model of High-Tc cuprate superconductors. Phys. Rev. Lett. 2009, 102, 017005. [Google Scholar] [CrossRef]
- Lau, B.; Berciu, M.; Sawatzky, G.A. High spin polaron in lightly doped CuO2 planes. Phys. Rev. Lett. 2011, 106, 036401. [Google Scholar] [CrossRef] [PubMed]
- Weber, C.; Giamarchi, T.; Varma, C.M. Phase diagram of a three-orbital model for high-Tc cuprate superconductors. Phys. Rev. Lett. 2014, 112, 117001. [Google Scholar] [CrossRef]
- Avella, A.; Mancini, F.; Paolo, F.; Plekhanov, E. Emery vs Hubbard model for cuprate superconductors: A composite operator method study. Eur. Phys. J. 2013, B86, 265. [Google Scholar] [CrossRef]
- Ebrahimnejad, H.; Sawatzky, G.A.; Berciu, M. Differences between the insulating limit quasiparticles of one-band and three-band cuprate models. J. Phys. Cond. Matter 2016, 28, 105603. [Google Scholar] [CrossRef]
- Tamura, S.; Yokoyama, H. Variational study of magnetic ordered state in d-p model. Phys. Procedia 2016, 81, 5. [Google Scholar] [CrossRef]
- Hubbard, J. Electron correlations in narrow energy bands. Proc. R. Soc. Lond. 1963, 276, 238. [Google Scholar]
- Hubbard, J. Electron correlations in narrow energy bands III. Proc. R. Soc. Lond. 1964, 281, 401. [Google Scholar]
- Gutzwiller, M.C. Effect of correlation on the ferromagnetism of transition metals. Phys. Rev. Lett. 1963, 10, 159. [Google Scholar] [CrossRef]
- Zhang, S.; Carlson, J.; Gubernatis, J.E. Constrained path Monte Carlo method for fermion ground states. Phys. Rev. 1997, B55, 7464. [Google Scholar] [CrossRef]
- Zhang, S.; Carlson, J.; Gubernatis, J.E. Pairing correlation in the two-dimensional Hubbard model. Phys. Rev. Lett. 1997, 78, 4486. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Shimoi, Y. Exact results in strongly correlated electrons. Int. J. Mod. Phys. 1996, B10, 3383. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Shimoi, Y.; Yamaji, K. Superconducting phase of a two-chain Hubbard model. Phys. Rev. 1995, B52, R3860. [Google Scholar] [CrossRef] [PubMed]
- Nakanishi, T.; Yamaji, K.; Yanagisawa, T. Variational Monte Carlo indications of d-wave superconductivity in the two-dimensional Hubbard model. J. Phys. Soc. Jpn. 1997, 66, 294. [Google Scholar] [CrossRef]
- Yamaji, K.; Yanagisawa, T.; Nakanishi, T.; Koike, S. Variational Monte Carlo study on the superconductivity in the two-dimensional Hubbard model. Physica 1998, C304, 225. [Google Scholar] [CrossRef]
- Koike, S.; Yamaji, K.; Yanagisawa, T. Effect of the medium-range transfer energies to the superconductivity in the two-chain Hubbard model. J. Phys. Soc. Jpn. 1999, 68, 1657. [Google Scholar] [CrossRef]
- Yamaji, K.; Yanagisawa, T.; Koike, S. Bulk limit of superconducting condensation energy in 2D Hubbard model. Physica 2000, B284, 415–416. [Google Scholar] [CrossRef]
- Yamaji, K.; Yanagisawa, T.; Miyazaki, M.; Kadono, R. Superconducting condensation energy of the two-dimensional Hubbard model in the large-negative-t’ region. J. Phys. Soc. Jpn. 2011, 80, 083702. [Google Scholar] [CrossRef]
- Hardy, T.M.; Hague, P.; Samson, J.H.; Alexandrov, A.S. Superconductivity in a Hubbard-Fröhlich model in cuprates. Phys. Rev. 2009, B79, 212501. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Miyazaki, M.; Yamaji, K. Correlated-electron systems and high-temperature superconductivity. J. Mod. Phys. 2013, 4, 33. [Google Scholar] [CrossRef]
- Bulut, N. dx2−y2 superconductivity and the Hubbard model. Adv. Phys. 2002, 51, 1587. [Google Scholar] [CrossRef]
- Yokoyama, H.; Tanaka, Y.; Ogata, M.; Tsuchiura, H. Crossover of superconducting properties and kinetic-energy gain in two-dimensional Hubbard model. J. Phys. Soc. Jpn. 2004, 73, 1119. [Google Scholar] [CrossRef]
- Yokoyama, H.; Ogata, M.; Tanaka, Y. Mott transitions and d-wave superconductivity in half-filled Hubbard model on square lattice with geometric frustration. J. Phys. Soc. Jpn. 2006, 75, 114706. [Google Scholar] [CrossRef]
- Aimi, T.; Imada, M. Does simple two-dimensional Hubbard model account for high-Tc superconductivity in copper oxides? J. Phys. Soc. Jpn. 2007, 76, 113708. [Google Scholar] [CrossRef]
- Miyazaki, M.; Yanagisawa, T.; Yamaji, K. Diagonal stripe states in the light-doping region in the two-dimensional Hubbard model. J. Phys. Soc. Jpn. 2004, 73, 1643. [Google Scholar] [CrossRef]
- Yanagisawa, T. Phase diagram of the t-U2 Hamiltonian of the weak coupling Hubbard model. New J. Phys. 2008, 10, 023014. [Google Scholar] [CrossRef]
- Yanagisawa, T. Enhanced pair correlation functions in the two-dimensional Hubbard model. New J. Phys. 2013, 15, 033012. [Google Scholar] [CrossRef]
- Yanagisawa, T. Crossover from wealy to strongly correlated regions in the two-dimensional Hubbard model-Off-diagonal Monte Carlo studies of Hubbard model II. J. Phys. Soc. Jpn. 2016, 85, 114707. [Google Scholar] [CrossRef]
- Yanagisawa, T. Antiferromagnetic, Superconductivity and phase diagram in the two-dimensional Hubbard model-Off-diagonal wave function Monte Carlo studies of Hubbard model. J. Phys. Soc. Jpn. 2019, 88, 054702. [Google Scholar] [CrossRef]
- Yanagisawa, T. Mechanism of high-temperature superconductivity in correlated-electron systems. Condens. Matter 2019, 4, 57. [Google Scholar] [CrossRef]
- Mott, N.F. Metal-Insulator Transitions; Taylor and Francis Ltd.: London, UK, 1974. [Google Scholar]
- Tranquada, J.M.; Axe, J.D.; Ichikawa, N.; Nakamura, Y.; Uchida, S.; Nachumi, B. Neutron-scattering study of stripe-phase order of holes and spins in La1.48Nd0.4Sr0.12CuO4. Phys. Rev. 1996, B54, 7489. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, T.; Goto, T.; Chiba, K.; Shinoda, T.; Fukase, T.; Kimura, H.; Yamada, K.; Ohashi, M.; Yamaguchi, Y. Observation of modulated magnetic long-range order in La1.88Sr0.12CuO4. Phys. Rev. 1998, B57, R3229. [Google Scholar] [CrossRef]
- Yamada, K.; Lee, C.H.; Kurahashi, K.; Wada, J.; Wakimoto, S.; Ueki, S.; Kimura, H.; Endoh, Y.; Hosoya, S.; Shirane, G.; et al. Doping dependence of the spatially modulated dynamical spin correlations and the superconducting-transition temperature in La2−xSrxCuO4. Phys. Rev. 1998, B57, 6165. [Google Scholar] [CrossRef]
- Arai, M.; Nishijima, T.; Endoh, Y.; Egami, T.; Tajima, S.; Tomimoto, K.; Shiohara, Y.; Takahashi, M.; Garrett, A.; Bennington, S.M. Incommensurate spin dynamics of underdoped superconductor YBa2Cu3Y6.7. Phys. Rev. Lett. 1999, 83, 608. [Google Scholar] [CrossRef]
- Mook, H.A.; Dai, P.; Dogan, F.; Hunt, R.D. One-dimensional nature of the magnetic fluctuations in YBa2Cu3O6.6. Nature 2000, 404, 729. [Google Scholar] [CrossRef]
- Wakimoto, S.; Birgeneau, R.J.; Kastner, M.A.; Lee, Y.S.; Erwin, R.; Gehring, P.M.; Lee, S.H.; Fujita, M.; Yamada, K.; Endoh, Y.; et al. Direct observation of a one-dimensional static spin modulation in insulating La1.95Sr0.05CuO4. Phys. Rev. 2000, B61, 3699. [Google Scholar] [CrossRef]
- Bianconi, A.; Saini, N.L.; Lanzara, A.; Missori, M.; Rossetti, T.; Oyanagi, H.; Yamaguchi, H.; Oka, K.; Ito, T. Determination of the local lattice distortions in the CuO2 plane of La1.85Sr0.15CuO4. Phys. Rev. Lett. 1996, 76, 3412. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, A. Quantum materials: Shape resonances in superstripes. Nat. Phys. 2013, 9, 536. [Google Scholar] [CrossRef]
- Hoffman, J.E.; McElroy, K.; Lee, D.-H.; Lang, K.M.; Eisaki, H.; Uchida, S.; Davis, J.C. Imaging quasiparticle interference in Bi2Sr2CaCu2O8+δ. Science 2002, 295, 466. [Google Scholar] [CrossRef]
- Wise, W.D.; Boyer, M.C.; Chatterjee, K.; Kondo, T.; Takeuchi, T.; Ikuta, H.; Wang, Y.; Hudson, E.W. Charge-density-wave origin of cuprate checkerboard visualized by scanning tunnelling microscopy. Nat. Phys. 2008, 4, 696. [Google Scholar] [CrossRef]
- Hanaguri, T.; Lupien, C.; Kohsaka, Y.; Lee, D.H.; Azuma, M.; Takano, M.; Takagi, H.; Davis, J.C. A checkerboard electronic crystal state in lightly hole-doped Ca2−xNaxCuO2Cl2. Nature 2004, 430, 1001. [Google Scholar] [CrossRef]
- Miyazaki, M.; Yanagisawa, T.; Yamaji, K. Checkerboard states in the two-dimensional Hubbard model with the Bi2212-type band. J. Phys. Soc. Jpn. 2009, 78, 043706. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Koike, S.; Yamaji, K. Off-diagonal wave function Monte Carlo Studies of Hubbard model I. J. Phys. Soc. Jpn. 1998, 67, 3867. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Miyazaki, M. Mott transition in cuprate high-temperature superconductors. EPL 2014, 107, 27004. [Google Scholar] [CrossRef]
- Maier, T.A.; Jarrell, M.; Macridin, A.; Slezak, C. Kinetic energy driven pairing in cuprate superconductors. Phys. Rev. Lett. 2004, 92, 027005. [Google Scholar] [CrossRef]
- Gull, E.; Millis, A.J. Energetics of superconductivity in the two-dimensional Hubbard model. Phys. Rev. B 2012, 86, 241106. [Google Scholar] [CrossRef]
- Tocchio, L.F.; Becca, F.; Sorella, S. Hidden Mott transition and large-U superconductivity in the two-dimensional Hubbard model. Phys. Rev. B 2016, 94, 195126. [Google Scholar] [CrossRef]
- Feng, S. Kinetic energy driven superconductivity in doped cuprates. Phys. Rev. B 2003, 68, 184501. [Google Scholar] [CrossRef]
- Wrobel, P.; Eder, R.; Micnas, R. Kinetic energy driven superconductivity and the pseudogap phase in weakly doped antiferromagnets. J. Phys. Condens. Matter 2003, 15, 2755. [Google Scholar] [CrossRef]
- Guo, H.; Feng, S. Electronic structure of kinetic energy driven superconductors. Phys. Lett. A 2007, 361, 382. [Google Scholar] [CrossRef]
- Otsuka, H. Variational Monte Carlo studies of the Hubbard model in one- and two-dimensions. J. Phys. Soc. Jpn. 1992, 61, 1645. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Koike, S.; Yamaji, K. d-wave state with multiplicative correlation factors for the Hubbard model. J. Phys. Soc. Jpn. 1999, 68, 3608. [Google Scholar] [CrossRef]
- Eichenberger, D.; Baeriswyl, D. Superconductivity and antiferromagnetism in the-dimensional Hubbard model: A variational study. Phys. Rev. 2007, B76, 180504. [Google Scholar] [CrossRef]
- Baeriswyl, D.; Eichenberger, D.; Menteshashvii, M. Variational ground states of the two-dimensional Hubbard model. New J. Phys. 2009, 11, 075010. [Google Scholar] [CrossRef]
- Baeriswyl, D. Superconductivity in the repulsive Hubbards model. J. Supercond. Novel Magn. 2011, 24, 1157. [Google Scholar] [CrossRef]
- Capello, M.; Becca, F.; Fabrizio, M.; Sorella, S.; Tosatti, E. Variational description of Mott insulators. Phys. Rev. Lett. 2005, 94, 026406. [Google Scholar] [CrossRef] [PubMed]
- Misawa, T.; Imada, M. Origin of high-Tc superconductivity in doped Hubbard models and their extensions: Roles of uniform charge fluctuations. Phys. Rev. 2014, B90, 115137. [Google Scholar] [CrossRef]
- Yanagisawa, T. Quantum Monte Carlo diagonalization for many-fermion systems. Phys. Rev. 2007, B75, 224503. [Google Scholar] [CrossRef]
- Deutscher, G.; Santander-Syro, A.F.; Bontemps, N. Kinetic energy change with doping upon superfluid condensation in high-temperature superconductors. Phys. Rev. 2005, B72, 092504. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yanagisawa, T.; Yamaji, K.; Miyazaki, M. On the Kinetic Energy Driven Superconductivity in the Two-Dimensional Hubbard Model. Condens. Matter 2021, 6, 12. https://doi.org/10.3390/condmat6010012
Yanagisawa T, Yamaji K, Miyazaki M. On the Kinetic Energy Driven Superconductivity in the Two-Dimensional Hubbard Model. Condensed Matter. 2021; 6(1):12. https://doi.org/10.3390/condmat6010012
Chicago/Turabian StyleYanagisawa, Takashi, Kunihiko Yamaji, and Mitake Miyazaki. 2021. "On the Kinetic Energy Driven Superconductivity in the Two-Dimensional Hubbard Model" Condensed Matter 6, no. 1: 12. https://doi.org/10.3390/condmat6010012
APA StyleYanagisawa, T., Yamaji, K., & Miyazaki, M. (2021). On the Kinetic Energy Driven Superconductivity in the Two-Dimensional Hubbard Model. Condensed Matter, 6(1), 12. https://doi.org/10.3390/condmat6010012



