1. Introduction
It is remarkable that reduced SrTiO
3−x was the first oxide in which superconductivity was found in 1964 [
1]. Only nine months after the SrTiO
3 discovery, superconductivity was also reported for another perovskite oxide, sodium-doped WO
3 [
2]. Both SrTiO
3−x and Na
xWO
3 have a low
Tc below 1 K. However, superconducting regions with unusually high critical temperature (
Tc = 90 K) were observed on the surface of Na-doped WO
3 crystals [
3,
4]. Unfortunately, the composition of the superconducting regions could not be determined due to their small size. Another possible method to dope charge carriers in a tungsten oxide is to reduce the oxygen content. Filamentary superconductivity below
Tc = 3 K was observed in twin walls of reduced WO
3−x single crystals [
5]. Despite the filamentary characteristics of superconductivity and low
Tc, an unusually large upper critical field
above 15 T was found in WO
3−x. This large
violates the Pauli paramagnetic limit by a factor of three. In our opinion, this interesting finding deserves further study.
The parent compound WO
3 has a perovskite-like structure with a vacant A site and consists of a three-dimensional array of corner-sharing tungsten-oxygen octahedra. Pure WO
3 is insulating since the W
6+ (5
d0) has an empty d-shell. Creating oxygen deficiency in WO
3 leads to a strong increase in conductivity as W
5+ (5
d1) ions are induced, which are a source of the charge carriers. In the octahedral oxygen coordination, W
5+ hosts one 5
d electron in a triply degenerate orbital and therefore is a Jahn-Teller (JT) ion. A number of experimental studies demonstrated that these charge carriers have a polaronic character and form bipolarons in WO
3−x [
6]. The discovery of high-
Tc superconductivity in copper-oxide materials resulted from the concept of JT polarons [
7]. Subsequent experimental and theoretical studies proved the validity of this concept by providing ample evidence of polaron/bipolaron formation and their clustering in cuprates [
8,
9,
10,
11]. Therefore, high-
Tc superconductivity may also exist in oxygen-reduced tungsten oxide. Recently, two authors of this paper, Alexander Shengelaya and Kazimierz Conder, together with Alex Müller, reported that in reduced tungsten oxide with the composition WO
2.9, the signatures of filamentary superconductivity with
Tc = 80 K can be registered by means of magnetization measurements [
12]. By lithium intercalation, the
Tc was further increased to 94 K. These results indicate that there is a potential for high-
Tc superconductivity in oxygen-reduced tungsten oxide, which has not been sufficiently explored.
Until now, not much was known about the low-temperature transport properties of the WO
2.9 phase. A few reports were published where the temperature dependence of resistivity was measured [
13,
14,
15]. However, all these measurements were performed above liquid nitrogen temperature. Here, we report results of combined magnetic, transport, and magnetotransport measurements of oxygen reduced tungsten oxide WO
2.9 in a broad temperature range, including the previously unexplored low temperature (
T < 80 K) region.
3. Results and Discussion
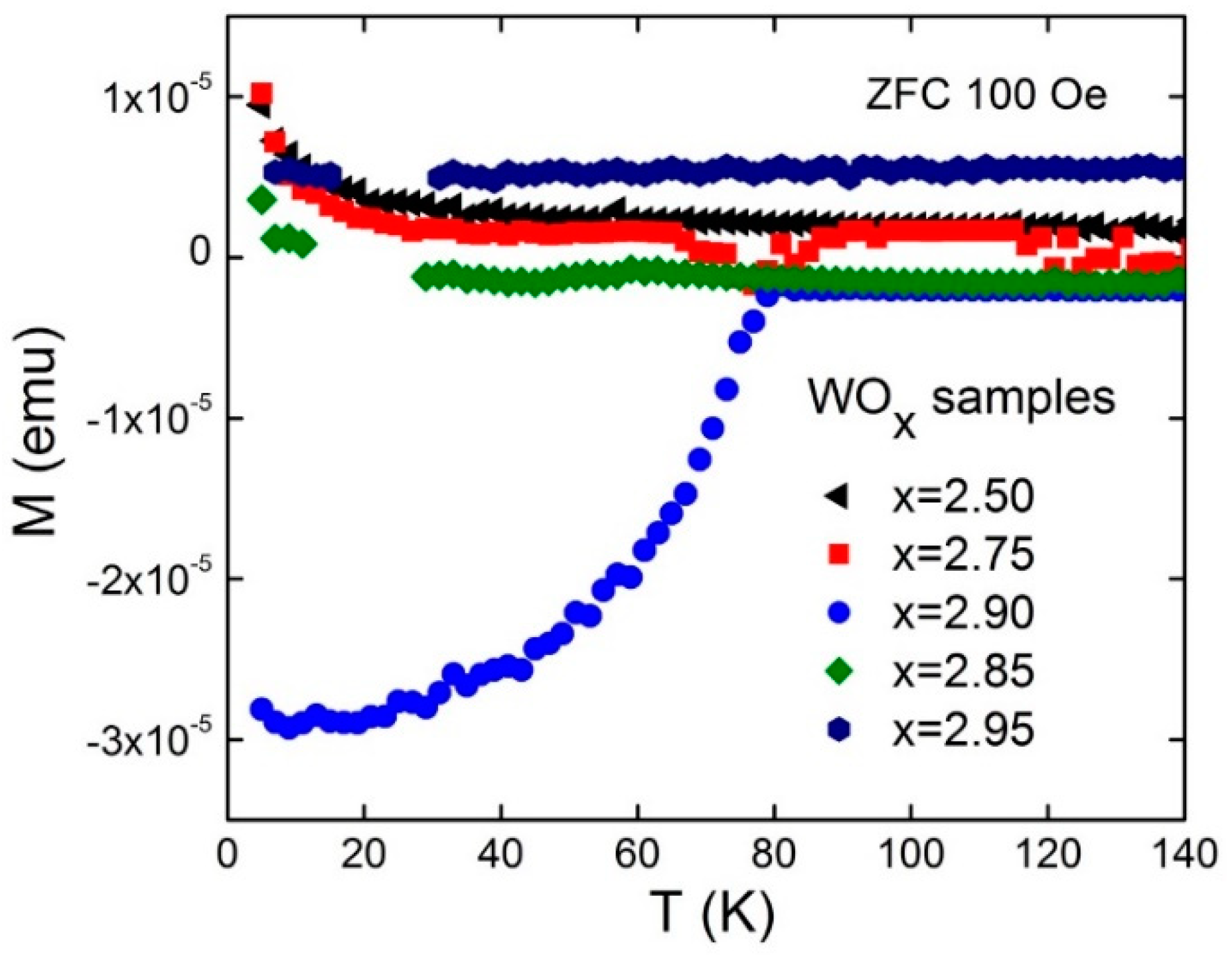
Figure 1 shows the temperature dependence of the ZFC magnetizations in WO
3−x samples measured in a magnetic field of 100 Oe. Among WO
3−x samples with different oxygen contents, only one sample with the composition WO
2.9 exhibited a clear decrease in magnetization below 80 K. This diamagnetic transition is characteristic of the superconducting state. As was demonstrated in a previous publication, various results obtained from magnetization measurements strongly support the superconducting nature of the diamagnetic transitions below
Tc = 80 K in reduced tungsten oxide WO
2.9 [
12].
The magnetization data presented in
Figure 1 demonstrate that the reduced tungsten oxide (WO
2.9) is a special case as it has a high-temperature superconducting phase. To understand why this composition is special, recall that the removal of oxygen from WO
3 induces polaronic charge carriers and also leads to structural changes. The lattice tends to eliminate single oxygen vacancies by the crystallographic shear (CS) process. As the x value in WO
3−x increases, the usual corner-sharing arrangement of octahedra is partially replaced by groups of edge-sharing WO
6 octahedra, which form pockets of shear planes [
16]. If these shear planes become parallel and equidistant, a crystalline phase with a defined structure arises, as shown by Magnéli [
17]. This is the case for the dark blue modification of the tungsten oxide WO
2.9, which was the subject of the present study. It crystallizes in a large unit cell containing 20 tungsten and 58 oxygens atoms. Therefore, its stoichiometry can be represented as W
20O
58. It belongs to the family of the Magnéli-type oxides with the general formula W
nO
3n−2 [
18]. The W
20O
58 phase is one of the most stable and ordered members of the W
nO
3n−2 homologous series, where blocks of 2D corner-sharing WO
6 octahedra are mutually connected along CS planes formed by groups of six edge-sharing octahedra [
17]. This phase also has a very narrow stability range close to the theoretical stoichiometry value WO
2.9 with composition limits of WO
2.89–WO
2.92 [
19]. This well-defined composition of the W
20O
58 phase explains why we observed signatures of superconductivity only within very limited oxygen contents in the series of studied WO
3−x samples.
According to Salje and Güttler, WO
2.9 is also a special compound among reduced tungsten oxides since it is on the verge of the insulator to metal transition [
15]. However, they only measured resistivity in this compound down to 80 K. To better understand transport properties of WO
2.9, we performed resistivity and magnetoresistance measurements in a broad temperature range, including the previously unexplored low temperature region.
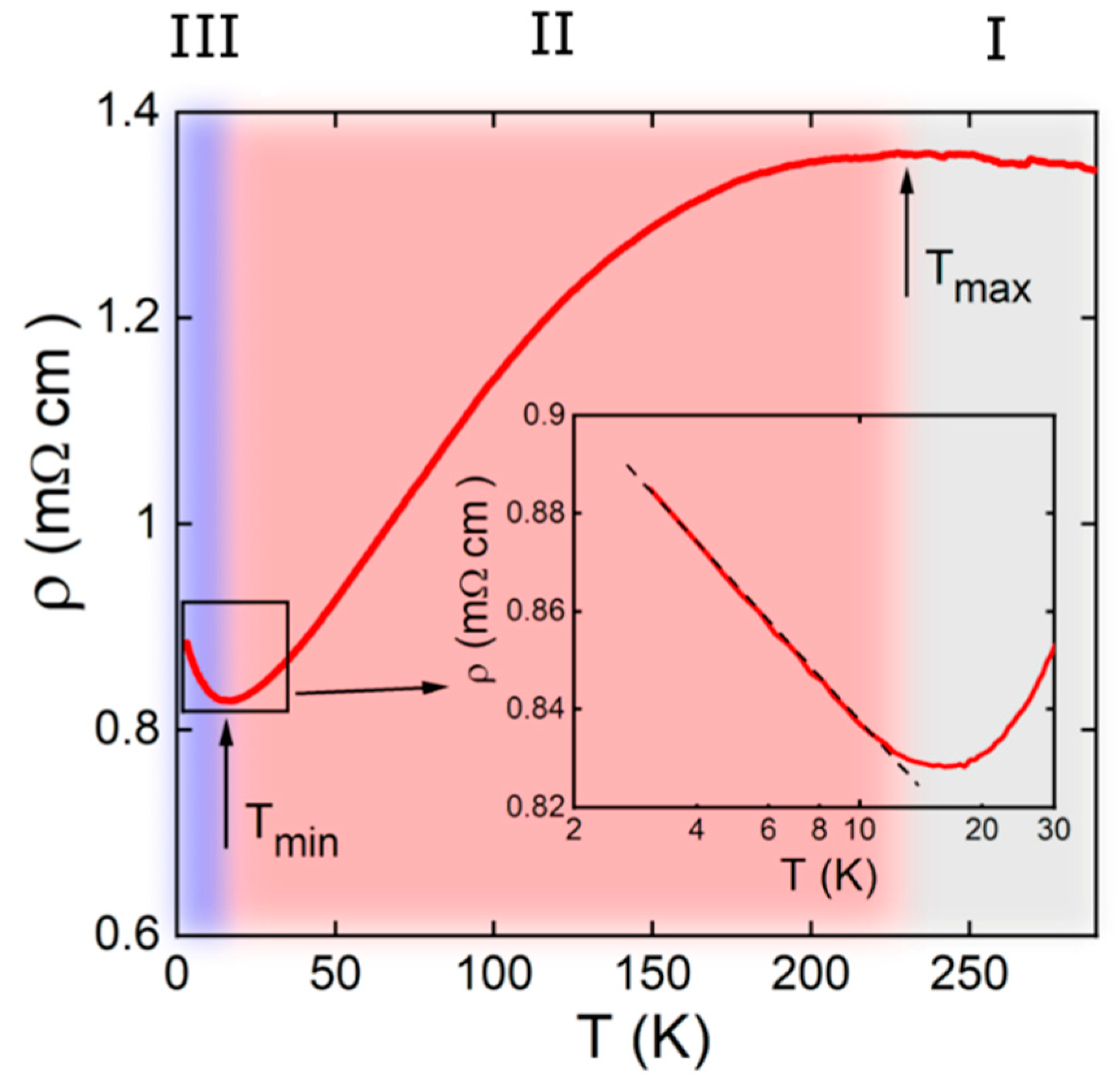
Figure 2 shows the resistivity as a function of temperature for the WO
2.9 sample. Metallic behavior (
dρ/
dT > 0) was observed in the temperature range 16–230 K. In contrast to magnetization measurements, the resistivity had no anomaly at
Tc = 80 K, indicating that the sample had a low superconducting volume fraction. The estimation of the superconducting volume fraction based upon the magnetization measurement shown in
Figure 1 is ~0.01%. Notably, this value is a lower limit valid under the assumption that the size of superconducting regions
d is larger than the London penetration depth
λ. If
d << λ, the volume fraction will be larger. Still, the superconducting volume fraction in WO
2.9 is small and is apparently below the percolation limit. Therefore, the temperature dependences of magnetization and resistivity could be explained by the formation of filamentary, non-percolative superconducting regions below
Tc = 80 K in Magnéli-phase tungsten oxide WO
2.9 (W
20O
58).
It was proposed that WO
2.9 bipolarons can form and cluster in the edge-sharing WO
6 octahedra within CS planes of the Magnéli phase [
12]. According to this model, CS planes represent charge-carrier-rich quasi-1D stripes. With decreasing temperature, the superconducting state can be established locally in regions similar to cuprates [
20]. However, CS planes are very narrow with a thickness of only six edge-sharing WO
6 octahedra in the W
20O
58 phase. The nanoscale bipolaron-rich metallic regions in CS planes can be locally superconducting, but because of the small size and limited coupling between them, global phase coherence and superconductivity are difficult to establish. Therefore, in the absence of percolation between the CS planes, the superconductivity has a filamentary character as indicated by magnetization and resistivity measurements.
Now, we discuss the temperature dependence of resistivity in more detail, as shown in
Figure 2. There are three distinct transport regimes in the
ρ(
T) dependence: (I) a semiconducting-like behavior above ~230 K with a negative temperature coefficient, (II) metallic-like behavior in the temperature range of 16–230 K with a positive temperature coefficient, and (III) resistivity upturn below ~16 K.
A broad maximum in the
ρ(
T) dependence, similar to that shown in
Figure 2, was reported previously for WO
2.9, but its origin was not discussed [
13,
14,
15]. Notably, a similar crossover from semiconducting-like conductivity at high temperature to metallic-like behavior at a lower temperature was observed in the normal state of quasi-2D organic superconductors (BEDT-TTF)
2X (ET
2X) with X = Cu[N(CN)
2]Cl, Cu[N(CN)
2]Br, Cu(NCS)
2 [
21]. Various explanations have been proposed for the different transport regimes and an anomalous resistance maximum [
22]. Some models consider the strongly correlated nature of the electrons in organic superconductors. A smooth crossover from an incoherent ‘‘bad-metal’’ state at high temperatures to a coherent Fermi liquid below the resistivity maximum was obtained within the framework of dynamical mean-field theory [
17]. Other explanations involve polaron physics to describe anomalous transport behavior. Optical spectroscopy revealed polaron formation in (ET)
2Cu(NCS)
2 [
23]. In particular, the spectra reveal a crossover from a small-polaron-dominated regime at high
T to a large-polaron-dominated regime at low
T. At high temperatures, small polarons do not participate in a coherent motion and the conductivity emerges as an activated hopping of self-trapped carriers. At low temperatures, the average size of polarons increases, and a coherent motion of polarons with resulting metallic behavior appears [
24]. Other authors also considered an activated hopping of small polarons at high
T, but low-temperature metallic behavior was ascribed to tunneling conduction by small polarons according to the prediction of small polaron transport theory [
25]. In reduced tungsten oxides, strong electron correlations are not expected, but polaron/bipolaron formation is well documented. Therefore, the observed broad peak in the
T-dependent resistivity for WO
2.9 can be explained as a result of a crossover from high
T activated hopping of small (bi)polarons to low
T metallic transport due to their tunneling conduction or transition to large (bi)polaron state.
Another notable feature in the
ρ(
T) dependence of WO
2.9 is a resistivity minimum and an upturn toward semiconductor-like behavior, as shown in
Figure 2. Interestingly, resistivity increases logarithmically with decreasing temperature, as shown in the inset of
Figure 2. Weak localization and the Kondo effect could both lead to this dependence. A logarithmic divergence in the resistivity can be found in Kondo systems, such as dilute magnetic alloys and dense Kondo compounds, where the conduction electrons are scattered by magnetic impurities [
26]. However, WO
2.9 is clearly not a Kondo system as the presence of magnetic impurities is not supported by our low-temperature magnetization measurements. The logarithmic temperature dependence of the resistivity can also be observed due to the quantum corrections to the resistivity, such as weak localization (WL). WL is a quantum effect caused by constructive interference between the closed-loop trajectories of a diffusive electron. In 2D systems, the WL effect results in a logarithmic rise in resistivity at low temperatures [
27]. The WL effect is sensitive to an applied magnetic field, which disturbs the wave coherence and the self-interference effects [
28]. Therefore, a magnetic field can destroy WL, which is revealed in experiments as a negative magnetoresistance (MR) and the shift of the resistivity minimum
Tmin to lower temperatures.
To obtain more information about the unusual transport properties of WO
2.9, we performed MR measurements.
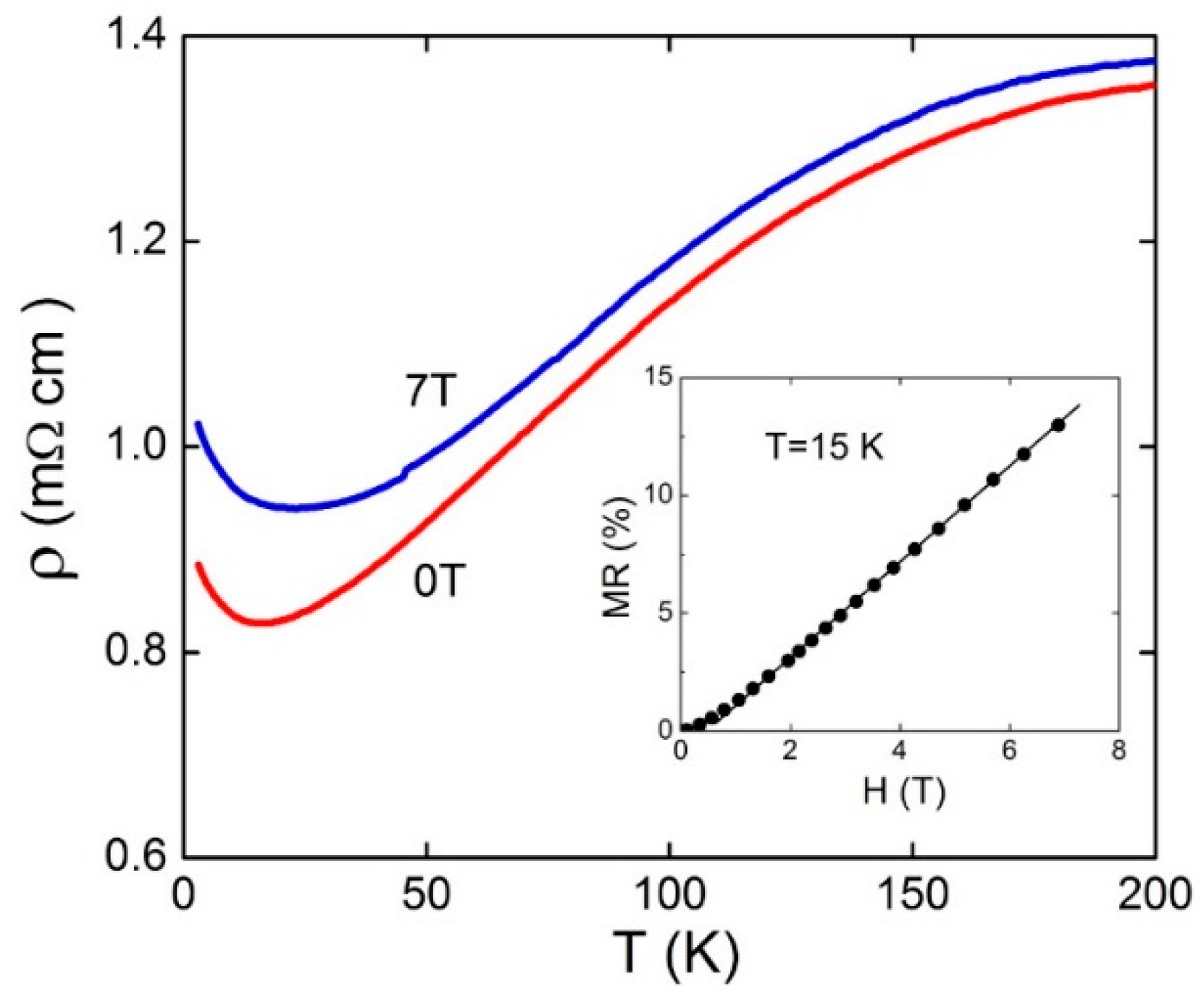
Figure 3 shows the temperature dependence of resistivity measured in 0 and in 7 T applied field. WO
2.9 exhibits a significant increase in resistivity in a magnetic field in the whole temperature range including the low-temperature upturn. In addition, the resistivity minimum
Tmin shifts toward higher temperatures from 16 to 23 K by applying a magnetic field of 7 T. These observations are opposite to what is expected for the WL. Therefore, based on the MR measurements, the WL effect can be excluded in our WO
2.9 sample.
Notably, a logarithmic low-temperature upturn in the resistivity, similar to that observed here for WO
2.9 is a well-known feature of underdoped cuprates [
29,
30,
31]. It was shown that such behavior can be described remarkably well by resonance Wigner scattering of bipolarons by the random potential in underdoped cuprates [
32]. Due to the presence of bipolarons in reduced tungsten oxides, this mechanism provides a very plausible explanation of the observed unusual low-temperature transport properties of WO
2.9.
As MR measurements in reduced tungsten oxides have not been reported before, the large positive MR presented in
Figure 3 is a new observation. The inset in
Figure 3 shows MR as a function of magnetic field at
T = 15 K, with the conventional definition MR = [[
ρ(H) −
ρ(0)]/
ρ(0)] × 100%, where
ρ(H) and
ρ(0) are the values of resistivity at field
H and zero, respectively. Above 1 T, MR increases linearly with the field without any sign of saturation. Such behavior is incompatible with that expected in conventional metals, where a positive MR arises due to the Lorentz force when the electric and magnetic fields are applied transverse to each other. This mechanism leads to the usual quadratic field dependence of the transverse MR [
33]. Even more surprisingly, we found that a positive MR with a similar magnitude also exists in a configuration where a magnetic field was applied parallel to the current direction (longitudinal MR). This isotropic MR excludes the possibility of resulting from the orbital motion of charge carriers. Isotropic MR is usually related to spin scattering mechanisms, but in this case, MR is expected to be negative rather than positive [
34]. Therefore, we conclude that the unusual, isotropic, and positive MR observed in WO
2.9 at low temperatures cannot be explained by known spin and orbital mechanisms related to charge carriers in a normal state of metals.
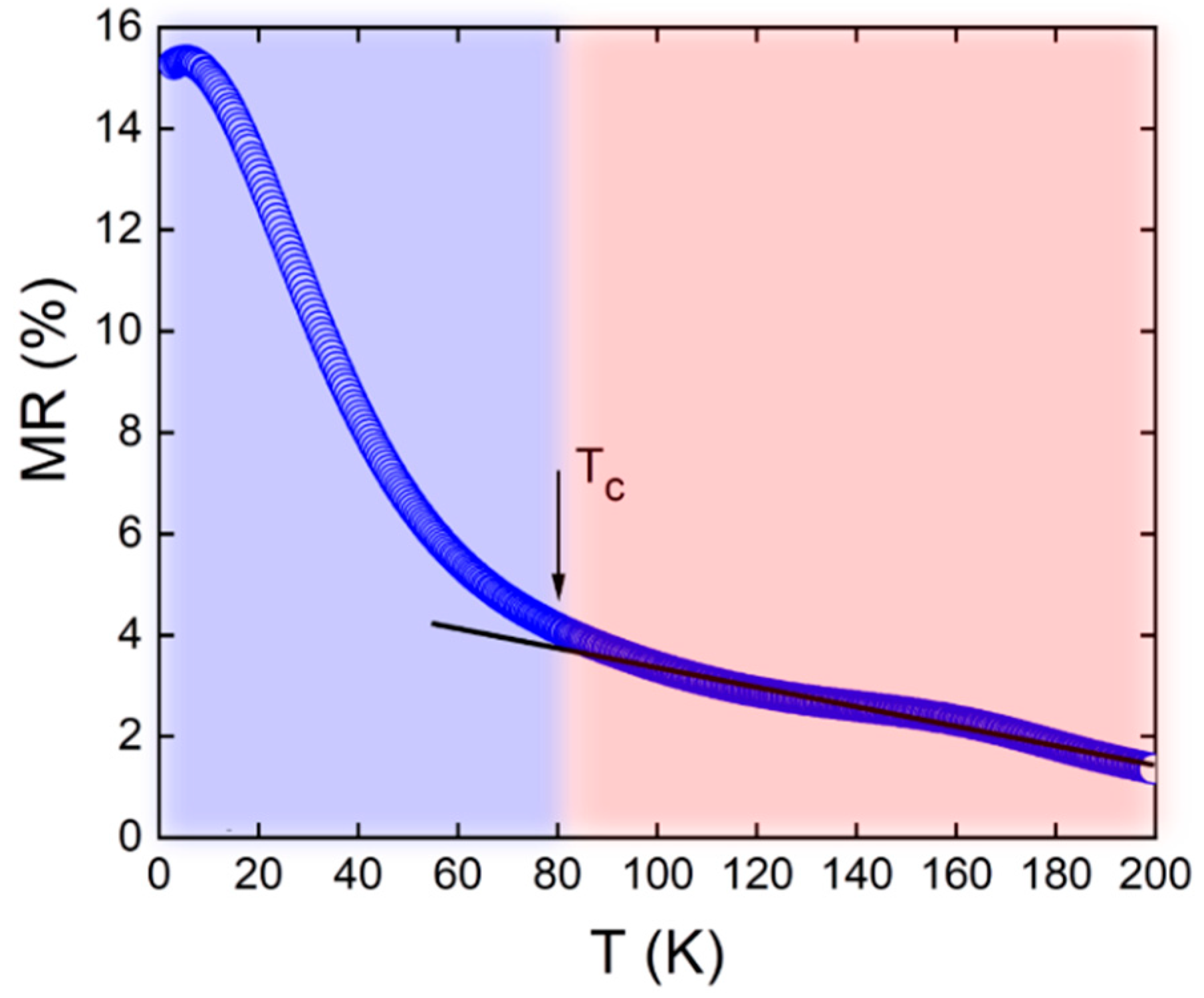
Possibly the most interesting aspect of the MR is its strong temperature dependence, which is presented in
Figure 4. It shows that at high temperatures, the MR is small and increases very gradually with decreasing temperature. However, it increases strongly upon cooling below ~80 K and reaches a value of ~15% at low temperatures in a field of 7 T. This temperature coincides with the superconducting transition observed by magnetization measurements (
Figure 1). This suggests that the substantial increase in positive MR below 80 K could be related to the onset of superconductivity in WO
2.9. We note that a considerable positive MR with unusual temperature dependence was reported recently in strongly underdoped La
2−xSr
xCuO
4 thin films [
35]. For example, in a sample where x = 0.05, a magnetic field of 45 T caused an excess resistivity of 10% at a temperature of 10 K. With increasing temperature, the MR decreased to a constant value of ~2% around 40 K. This temperature corresponds to the maximum
Tc observed in optimally doped La
2−xSr
xCuO
4. Notably, the sample with x = 0.05 did not show signatures of superconductivity in resistivity measurements down to 1.5 K. The considerable excess positive MR observed at low temperatures, which depends non-quadratically on the magnetic field, was attributed to superconducting fluctuations in underdoped La
2−xSr
xCuO
4 [
35]. Magnetic field suppresses superconducting fluctuations, leading to an enhanced resistivity. In our opinion, this scenario also applies to the present case and explains the resistivity and MR data obtained in WO
2.9. It also accounts for the isotropic character of the observed positive MR in this compound at low temperatures.
As discussed above, there are locally-superconducting bipolaron-rich regions in CS planes of WO2.9, but because of the small size and limited coupling between them, global phase coherence and bulk superconductivity are not established. Still, superconducting fluctuations might be present, which are difficult to detect from resistivity measurements. A strong magnetic field would suppress superconducting fluctuations; as a result, resistivity increases. The resulting positive MR will have a strong temperature dependence and should disappear above the Tc of superconducting regions. The positive MR detected in this work for WO2.9 and previously in strongly underdoped cuprates seems to be a very sensitive indicator for the presence of small, isolated superconducting clusters embedded in a nonsuperconducting matrix.
4. Summary and Conclusions
To summarize, we performed magnetic, transport, and magnetotransport measurements in Magnéli-phase oxygen-reduced tungsten oxide WO2.9 (W20O58) in a broad temperature range. We found that the temperature dependence of the resistivity is unusual and three different transport regimes exist in WO2.9: a semiconducting-like behavior above ~230 K with a negative temperature coefficient, metallic-like behavior in the temperature range of 16–230 K with a positive temperature coefficient, and resistivity upturn below ~16 K. The broad maximum can be explained as a result of a crossover from high T-activated hopping of small (bi)polarons to low-T metallic transport due to either tunneling conduction of small (bi)polarons or transition to large (bi)polaron state.
We observed for the first time that the resistivity of WO2.9 has a minimum with an upturn toward insulator-like behavior below 16 K. We found that the resistivity increases logarithmically with decreasing temperature. MR measurements showed that the observed low-temperature resistivity upturn cannot be explained by known mechanisms, such as weak localization or Kondo effects. One possible explanation of this effect is the resonance Wigner scattering of bipolarons by the random potential in WO2.9. This mechanism was suggested previously for the low-temperature upturn of resistivity in underdoped cuprates.
The superconducting transition at
Tc = 80 K observed in the magnetization measurements was not detected in the temperature dependence of resistivity. This indicates that the superconductivity is localized in small regions that do not percolate. Interestingly, we found a strong increase in positive MR below 80 K. This effect is very similar to that observed in strongly underdoped cuprates, where the considerable excess positive MR was attributed to superconducting fluctuations in small regions. Therefore, we conclude that MR measurements in agreement with magnetization data revealed the presence of superconducting clusters in WO
2.9 below 80 K. As suggested in a previous publication, such superconducting clusters form within CS planes that exist in the Magnéli phase of WO
2.9 (W
20O
58) and represent charge-carrier-rich quasi-1D stripes [
12]. These nanoscale clusters can host superconducting pairs, but because of the small size and limited coupling between them, global phase coherence and superconductivity cannot be achieved. Generally, the MR effect is a very sensitive tool for detecting the presence of small, isolated superconducting clusters embedded in a nonsuperconducting matrix.
The obtained results demonstrate that the Magnéli phase of the oxygen-reduced tungsten oxide WO
2.9 (W
20O
58) has interesting normal and superconducting properties that warrant further studies, especially using single crystal samples. We note that, at present, little is known about the electronic band structure of this material. Recent theoretical studies have suggested that there are several flat bands near the Fermi level [
36] and that the electronic properties may be governed by the small number of
d-bands from the tungsten atoms located in CS planes [
37]. So far, experimental studies of the band structure in WO
2.9 are lacking.
Especially promising, in our opinion, would be to study pressure effects on the normal and superconducting properties of this compound. By applying hydrostatic or uniaxial pressure, the band structure and coupling between CS planes can be tuned. A well-known example is the ladder compound (La, Sr, Ca)
14Cu
24O
41, which becomes superconducting under high pressure when the interactions between the ladders are enhanced [
38]. Another interesting and novel approach to achieve bulk high-
Tc superconductivity in doped tungstates was proposed recently by Müller [
39]. Therefore, by improving the coupling and percolation between CS planes, bulk superconductivity and zero resistance state might be achieved in WO
2.9.