Abstract
In this tribute to K Alex Müller, I describe how his early insights have influenced future decades of research on perovskite ferroelectrics and more broadly transition metal oxides (TMOs) and related quantum materials. I use his influence on my own research journey to discuss impacts in three areas: structural phase transitions, precursor structure, and quantum paraelectricity. I emphasize materials functionality in ground, metastable, and excited states arising from competitions among lattice, charge, and spin degrees of freedom, which results in highly tunable landscapes and complex networks of multiscale configurations controlling macroscopic functions. I discuss competitions between short- and long-range forces as particularly important in TMOs (and related materials classes) because of their localized and directional metal orbitals and the polarizable oxygen ions. I emphasize crucial consequences of elasticity and metal–oxygen charge transfer.
1. Introduction
This article is a personal perspective on aspects of perovskites, particularly transition metal oxides (TMOs). It is written through the (limited) lens of my own research journey, as a tribute to K. Alex Müller and the lessons I have accumulated from his prescient insights into this remarkably tunable class of materials. I first met Alex during a several-month visit to IBM Ruschlikon in 1977 to collaborate on nonlinear excitations and structural phase transitions, on which I had begun research in 1974 with Jim Krumhansl at Cornell. I have been privileged by numerous interactions with Alex since then. Science advances relentlessly, but some pioneers are able to perceive the truth beyond the limits of current techniques. Alex is such an individual. I similarly recall many conversations with Heinrich Rohrer during the 1977 visit concerning prospects for Scanning Tunneling Micsoscopy (STM). In particular, discommensurations were only indirectly suggested by k-space scattering techniques at that time and were a topic of strong disagreements regarding data interpretation. STM directly imaged these structures, resolved many of the disagreements, and contributed to important future research on commensurate–incommensurate phase transitions.
In this spirit of important insights, I will highlight just three (among many in his illustrious career) from Alex in the context of his decades of research on TMOs, including ferroelectrics (SrTiO3, BaTiO3, etc.) and of course cuprate superconductors. These insights have resonated though research history as experimental, theoretical, and simulation capabilities have improved.
- (i)
- Structural phase transitionsNeutron and X-ray scattering in the 1970s were beginning to have sufficient resolution to suggest two low-frequency scattering components as the structural phase transition was approached: “central peaks” and ”soft modes.” Alex recognized the need for judicious experiments to probe different timescales [1] and was thereby able to separate phonon oscillations from slow cluster dynamics. This was powerful input to theory and simulation attempting to distinguish mean-field self-consistent phonon approximations from true critical behavior in double-well Landau–Ginzburg phase-transition theories. Advanced time-resolved experiments have now become essential tools in all classes of coupled charge–lattice–spin–orbital materials, including TMOs.
- (ii)
- Precursor StructureLocal structure measurements and inferences of the 1970/80s had relatively poor resolution (spectroscopy, NMR, diffuse scattering, etc.). However, Alex used them [1] to suggest that local distortions appear as precursor structure as Tc is approached in ferroelectric TMOs. Importantly, he showed that these precursors onset at temperatures significantly beyond critical regimes above and below Tc, and are tunable with strain, electric fields, etc. Fifty years later, I can suggest that many of these properties in TMOs and related materials are elastic microstructures. Indeed, as I discuss below, tuning phases and functions through elasticity is now emerging as an important focus in quantum materials [2].
- (ii)
- Quantum ParaelectricityUnlike, e.g., BaTiO3, SrTiO3 does not undergo a ferroelectric phase transition, but one can be induced with appropriate doping or pressure (strain). Alex understood the importance of this and advocated the concept of quantum tunneling between orientations (e.g., octahedral orientations), which had to be frozen out to stabilize a permanent ferroelectric state. He and others created the term “quantum paraelectric” to describe this situation and designed elegant experiments to probe the dynamics [2,3]. This concept now has many diverse analogs, including the internal dynamics of small polarons (below) and excitons, Kondo spin singlets, dynamic magnetism in Pu, and concepts for computational qubits such as Josephson junctions.
In the next sections, I will describe connections of these lessons from Alex to some of my own research on TMOs and related materials.
2. TMOs and Their Lattice
It has long been appreciated (see, e.g., [4]) that TMOs exhibit a striking variety of broken-symmetry ground states, including magnetic, Peierls, Mott, spin-Peierls (SP), charge density wave, (CDW) bond order wave (BOW), superconductivity, etc. We can ascribe this variety to sensitive coupling among degrees of freedom—spin, charge, orbital, and lattice. Much research over recent decades has emphasized the metal d-orbitals, arguing that since these are substantially localized, competitions occur between localized states or flat electronic k-space bands, and, through hybridization, wider (e.g., Op) bands. Many fascinating electronic/magnetic many-body states emerge from modeling these competitions, some of which surely occur in actual current, future, or engineered materials. However, here I will deliberately play the devil’s advocate and emphasize the explicit importance of the lattice degrees of freedom, the oxygen ion polarizability, and functional multiscales beyond asymptotic scaling limits.
It is a fascinating feature of science sociology that “solid-state and correlated electron physics” and “materials” research separated so much in the last several decades. In part, this was the result of experimental, theoretical, and simulation limitations. For example, quantum mechanics could only be implemented for periodic (and small supercell) structures. This led to the creation of a comprehensive conceptual framework in which lattice variations were a linear perturbation used to describe extended phonons, and similarly magnons, etc. In contrast, materials science recognized the functional role of microstructure (dislocations, grains, twinning, etc.) but often omitted important entropic contributions and built interpretative frameworks around the observed microstructure. This situation has begun to change because of decisive advances in experimental probes and their resolution capabilities (real-space, k-space, time, frequency) and concomitant advances in computing power (for all-atom system sizes, ab initio electronic methods, non-adiabatic effects, etc.), as well as data analytics and visualization at scale. Equally importantly, the technologies now based on nanoscales and on active surfaces, internal surfaces, and multilayer interfaces require the unification of the disciplines and the explicit roles of all the degrees of freedom and their coupling.
Under-representing the functional role of the lattice is an oversight for several reasons:
- Although the d-orbital (and even more so, the f-orbital) is indeed electronically localized, resulting in localization–delocalization electronic competition, it is also highly directional. This results in symmetry constrained unit cell structural distortions and a “network” competition for ground and metastable structural patterns (multiscale “landscapes”). This is not the case for extended and symmetrical (e.g., s) orbital materials, where dynamic screening dominates. The constraints are the origin of measured strongly anisotropic elastic constants in these materials, with intrinsically coupled configuration scales from unit cell to long-range, optic to acoustic—and hence high tunability by both local and global perturbations (doping, pressure, external fields).
- Neglecting or “integrating out” the oxygen degrees of freedom in TMOs and related materials is a significant over-simplification for many properties. The O polarizability and metal–O charge transfer (and associated bond length/buckling/rotation changes) must be treated explicitly [5]. Pioneers such as Heinz Bilz (Alex’s professional peer and colleague) appreciated this by augmenting “shell models” of the TMO electronic structure to capture effects of M–O charge transfer and polarizability [6]. We return to such “nonlinear shell models” below, including a successful prediction of the observed quantum paraelectric to ferroelectric transition in O18-doped SrTiO3.
- The electron–lattice coupling strength is typically not weak in TMOs. It may appear so if measured by conventional spatial averaging techniques. However, because of the delicate energy balances affecting electronic/magnetic orders, even rather weak average electron–lattice coupling can dominate globally and locally. We illustrate this with examples below. In addition, exotic (e.g., topological) singularities are usually energetically costly, and nature avoids or smooths them by engaging additional weaker degrees of freedom—as in dislocations, vortices, superconducting flux line cores, etc. Even when the globally averaged el-lattice strength is weak, it can be locally strong around dopants and defects. The formation of small (coupled spin–charge–lattice) polarons is an important example that we return to below. A finite densities of such polarons can order into secondary mesoscopic patterns (clumps, stripes, filaments, checkerboard phases, etc.) because of the long-range, directional elasticity noted above. Small polaron center-of-mass dynamics is very slow (because of Peierls–Nabarro lattice pinning), but unless dissipation is strong, their internal dynamics is a fundamental quantum tunneling property, and the internal charge oscillation is necessarily accompanied by non-adiabatic lattice (e.g., bond–length), and sometimes spin, oscillation. This coupled charge–lattice dynamics is familiar elsewhere, including quantum chemistry (e.g., [7]), “macroscopic quantum tunneling” [8], and perhaps also in the context of quantum paraelectric tunneling [9].
- Lattice anharmonicity is typically important in TMOs and assuming linear lattice dynamics is incomplete. Anharmonicity is the result of slaving among lattice, electronic, and magnetic degrees of freedom, proximity to a structural phase transition, impurities, interfaces, surfaces, etc. The M–O charge transfer is a particularly important source of nonlinear lattice dynamics. Among many interesting emergence and complexity consequences are multi-phonon bound states (“intrinsic local modes,” ILMs). Modern neutron scattering has indeed resolved modes outside linear phonon bands and attributed them to ILMs (e.g., [10]). Below, we will introduce ILMs embedded self-consistently in a sea of extended modes as a description of, e.g., relaxor ferroelectrics.
3. Small Polarons, Filamentary Landscapes, and Local Modes
As noted, TMOs as a materials class exhibit a remarkable variety of often competing broken symmetry ground states, which have been the subject of intensive research using a huge range of experimental, numerical, and analytical techniques [11,12]. For example, ab initio (e.g., density functional theory) and even fully non-adiabatic quantum electronic calculations have advanced significantly in recent years because of great strides in algorithms and computational power, e.g., [13,14]. However, they remain limited for many properties by technique-imposed assumptions such as system or supercell size, periodicity, treatment of polarizability, adiabaticity, etc. This means that accurate TMO description remains a challenge for the inclusion of O polarizability and multiscale (including elastic) lattice patterns. We are typically driven to separate the mechanisms creating mesoscopic structures (e.g., stripes) from modeling the signatures and functionality of those structures. I will give examples of both of these steps below.
Some useful insights can be gained from real-space Hartree–Fock (HF) numerical solutions of 3-band (M–d and O–p) M–O charge and spin models, including lattice degrees of freedom treated adiabatically (e.g., in a Su–Schrieffer–Heeger inter-site form for el–lattice coupling). For example, [15] uses such a model Hamiltonian with parameters appropriate to a Cu–O plane but allowing parameter strengths (electronic hopping, electron correlation, el–lattice coupling) to vary. A variety of broken-symmetry ground states are found numerically—including CDW, BOW, SP, AF, co-existing SP and anti-ferromagnet (AF)—as magnetism, covalency, and lattice distortion compete. In particular, as observed in Section 2, relatively weak el–lattice coupling is found to induce a zero-temperature ground state transition.
The Hamiltionian studied in [15] is
Here, creates a hole with a spin σ at the site i in the Cu or the O orbital. In the lattice part, for simplicity only, the motion of O ions along the Cu–O bonds are includeed, and it is assumed that only diagonal components of the spring constant matrix are finite, . For electron–lattice coupling, the nearest neighbor Cu–O hopping is modified by the O-ion displacement as , where the +(−) applies if the bond shrinks (stretches) with positive . The Cu-site energy is assumed to be modulated by the O-ion displacements linearly, , where the sum extends over the four surrounding O ions; here, the sign takes +(−) if the bond becomes longer (shorter) with positive uk. The other electronic matrix elements are O–O hopping for , O-site energy for , with , Cu-site and O-site repulsions for , and the nearest-neighbor Cu–O repulsion for . Parameter values are used in regimes relevant to the copper oxides from local density approximation (LDA) calculations: , , , , , and . These parameters and are used as a reference parameter set: , . , , , and are varied and with and so as to maintain a constant renormalized energy difference between Cu and O levels in the undoped case. A comparison of results for local lattice distortion and reduced Cu magnetic moments accompanied by added holes with generalized, inhomogeneous LDA calculations is consistent, e.g., with values of , , and .
It is natural to examine whether electron or hole polarons result upon doping into the various broken-symmetry ground state: a generalization of the much studied Holstein polarons (see [16]) to coupled spin–charge–lattice local quenching of the broken symmetry. As mentioned above, among the essential properties of polarons (and excitons) are the center-of-mass translation of the composite local deformation (resulting in polaronic electronic bands) and the internal (charge, lattice, spin) dynamics within the composite wave function. “Large” polarons (deforming many lattice sites coherently) have wide electronic k-space bands and incoherent internal dynamics, and they can translate (tunnel or, with temperature, diffuse) relatively easily, scattering off phonons, impurities, etc. In contrast, “small” polarons (deforming few lattice sites) have narrow electronic bands and transport very slowly from site to site by quantum tunneling or thermal hopping: they are easily pinned by the lattice’s Peierls–Nabarro barrier, weak impurities, surfaces, or fields. However, the small polaron internal dynamics exhibit coherent quantum tunneling oscillations. Again, accurate quantum simulations, even for model Hamiltonians, are limited to very small systems, despite modern computing power and efficient algorithms (e.g., [17]). Nevertheless, we can gain important insights by studying the limit of a single charge added to, e.g., a single O–M–O unit (an example of a Boson–Fermion composite and relevant to small polarons on cuprates, bismuthates, and nickelates, for example). This limit is, numerically, exactly solvable, including fully non-adiabatic (i.e., multi-quanta) treatment of lattice, charge, and spin. This limit is also relevant, since the extremely slow center-of-mass translation can be essentially decoupled. As described in detail in [18], the total energy of such a unit is a double well with two degenerate lowest energy configurations, corresponding to the added charge occupying the left or right O, and the charge oscillates (quantum tunnels) periodically between them. Figure 1 shows the numerically exact (“quantum-entangled”) ground-state wave function as the strength of el–lattice coupling is varied. As a result of el–lattice (M–O bond length) and spin coupling, the lattice and spin also oscillate. The symmetric ground state captures the double-well probability, and the gap to the anti-symmetric first excited state quantifies the tunneling frequency. We can visualize this situation as an M–O bond length oscillating between short and long M–O bond lengths as the charge tunnels (a “charged lattice vibration” in some earlier literature). This picture is useful but an oversimplification, since non-adiabaticity means that the total energy double well is effectively changing shape as the charge tunnels and thus the frequencies of charge, lattice, and spin are, although related, not the same: indeed, many interesting resonances are possible [18,19]. In fact, this is a precise description of lattice/spin-assisted C–T (i.e., dynamic polarization) in this small unit. There are many relevant issues such as polaronic excited states, decoherence, spectroscopy, etc. Ref. [18] calculates the tunneling frequencies for parameters relevant to cuprates. These frequencies are indeed similar to “anomalous” ones measured in cuprates (optical, polarizability, magnetic) and the Cu–O bond length differences from average Cu–O bond lengths are also similar to those measured by, e.g., XAFS and neutron pair-distribution functions [18,20]. These results illustrate the differences between measurement techniques as a function of their time resolution—recall Alex Müller! An important additional consideration is the dissipation of energy during tunneling through coupling to the medium in which the tunneling unit is embedded. If the tunneling is slow, the dissipation freezes the polaron into a permanent polar distortion. This is similarly important to Caldeira–Leggett [8] or Kondo singlet freeze-out, to quantum paraelectrics [9], and probably to other TMO functionalities (below).
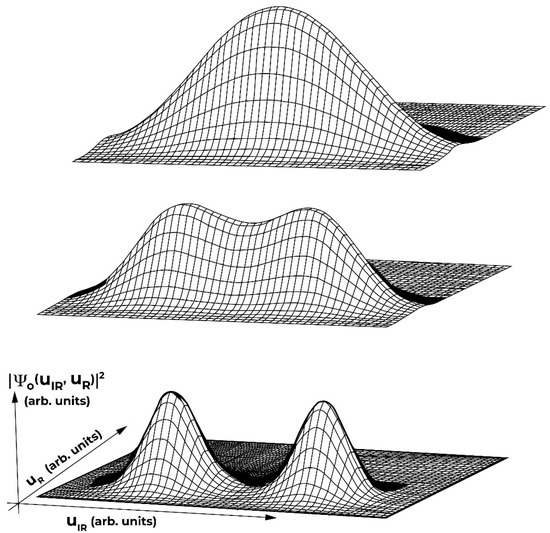
Figure 1.
Squared many-body ground-state wave function of an O–Cu–O cluster as a function of the Raman and infrared coordinates for three IR coupling strengths (weak, intermediate, strong). When the phonon coordinate is at the left bump, the extra hole is predominately on the leftmost oxygen, and vice versa. The scale of the coordinates is fixed to be 3 times the root-mean-square fluctuation of the quantum wave function, and therefore it is different for the three panels (see [18]).
Although the unit above is directly relevant to small polarons in 1D chains and quasi-1D structures embedded in higher dimensions, fully quantum, non-adiabatic calculations remain rather limited, despite continuous progress; for example, Ref [21] reports excellent advances in the first-principle characterization of a single polaron in WOx. In particular, as the doping level increases in a full M–O system, we are faced with the question of how multiple polarons interact. This is another problem beyond current analytical or simulation capability except in rather small systems [17,22]. Qualitatively, we can expect that at low density, small polarons localize independently; if they are close enough, they may bind into bi/multi-polaron clumps (depending on lattice deformation and Coulomb energies), and at densities where the average polaron spacing is near the polaron size, they transform their broken-symmetry host (probably through a sequence of commensurate–incommensurate transitions) to a metallic unbroken symmetry with a new Fermi energy (“quantum melting”).
We can again numerically explore aspects of this scenario using the same 3-band Peierls–Hubbard model (1), treated in a real-space HF approximation but now including electron or hole doping. This cannot directly describe either center-of-mass or internal tunneling dynamics. However, it is a useful guide to the (positive) feedbacks leading to polaron formation and multi-polaron patterning, and the coupled roles of lattice, charge, and spin. Reference [23] shows that single electron and hole small polarons occur in the various broken-symmetry ground states, as illustrated in Figure 2. At finite doping, bipolarons can be found [22] but also ordering into filamentary “stripes.” As discussed in [24], these filamentary patterns share oxygens and thus minimize potential energy. At sufficient doping, a hysteretic insulator to metal transition is found. Recent progress beyond HF with quantum MC simulations also suggest the possibility of multi-polaron liquid-like states [22].
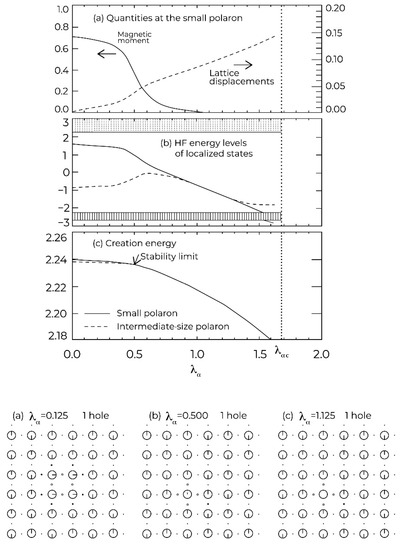
Figure 2.
Polarons calculated in a 2D 3-band Peierls–Hubbard model (see Ref.[21]). Upper Graph: (a) Magnetic moment of the central Cu site of a calculated small polaron and ratio of lattice displacement of the surrounding O to Cu–O distance (1.89 Å), (b) gap energy levels, and (c) creation energy , for the small polaron state as a function of . Other energy levels in the gap close to the bands (shaded areas) are not shown. is the total energy with i added holes and is the midgap energy. In addition, (c) also shows for the intermediate-size ferromagnetic polaron. All energies are in units of . Parameters are ,, , , , , and . The dotted line at marks the stability limit of the anti-ferromagnet (AF) ground state at stoichiometry. Lower Graph: Charge (radii of the circles) and spin (arrows) densities in the one-hole doped systems, (a) with the intermediate-size polaron; and (b,c) with the small polaron. The arrows are normalized so as to touch the circle if completely polarized. Big (small) circles are Cu (O).
Numerically, a landscape of low-energy polaron configurations can be identified, metastable but pinned by the lattice, which can be accessed by external fields, photoexcitation, impurity pinning centers, internal microstructure and interfaces, surfaces, etc. Note that the stripe interfaces are sharp on the unit-cell lattice scale: as for single small polarons, gradient energy costs are small compared to those from deviations of the undeformed broken symmetry energy. The broken symmetry host (e.g., AF moment) is locally quenched at the stripe.
We can study the lattice, spin, charge fluctuations around these polarons, and multi-polaron patterns within a real-space random field approximation (RPA) [25,26]. Since the polarons are small and the stripe interfaces sharp, the stripes are topologically “protected” and the fluctuations include ones that are spatially localized around the polarons or stripes and thus substantially separated in frequency from the band of k-space modes in the broken-symmetry host: i.e., symmetry-determined transverse and longitudinal “edge mode” vibrations of spin, charge, and lattice [25]. As illustrated in Figure 3, they are all dominated by O ion motion, resulting in Cu–O bond length fluctuations coupled to charge and spin fluctuations. Of course, any slow diffusion of polarons or stripes introduces a cut-off or broadening for the local mode frequencies, and any stripe curvature introduces a wave-vector cut-off.

Figure 3.
Lattice vibrational eigenmodes for the case of a stripe in a 20%-doped CuO2 plane computed in a 3-band Peierls–Hubbard model. The stripe is centered along the middle of the vertical Cu row. There are two branches localized at the stripe: one corresponds to the oxygen vibration parallel to the stripe (low frequency, , left), and the other corresponds to the oxygen displacements perpendicular to the stripe (high frequency, , right) (see Ref [25]).
The frequencies of these local modes are again similar to experimentally observed “anomalous” signatures in doped cuprates and also some other doped TMOs. For example, in doped nickelates, the intensity of anomalous modes observed with neutron scattering tracks the doping density [27], and interesting pressure effects have been proposed [28]. Checkerboard (“liquid crystal”) patterns have been indicated in doped cuprates [29] and are predicted to have their own signatures of specific local modes [30].
Note that the Cu–O stripes share O ions coherently in the above results (see Figure 3). If the longitudinal O vibrations are extended to strongly nonlinear amplitudes, so that there is full CT, they will correspond to a coherent filament of O–Cu–O units (the small polaron described above), periodically tunneling charge between neighboring Os, with concomitant oscillation between short and long Cu–O bond lengths. This is equivalent to a dynamical charge density wave (CDW) along the stripe. It is clear conceptually that an infinitesimal external electric field can then coherently transfer charge along the stripe—a “sliding CDW” avoiding impurity or lattice pinning (cf, [31]). In this scenario, there is no polaron center-of-mass motion, only resonant transfer of charge. In addition, the transverse O vibrations at the stripe edge provide a natural local-to-extended mode coupling with the broken-symmetry host, e.g., anti-ferromagnet (AF) [32]. These observations are intriguing in terms of conductivity mechanisms. A similar scenario applies to BixK1-xTiO3, where a window of superconductivity appears around a specific x (doping) value with a transition from a broken-symmetry CDW (i.e., charge-disproportionated) insulator to metal—in this case, polarons, stripes, and precursor local structure will be with respect to the CDW, instead of AF, host. We note that if the dissipation from the coupling to the host medium for the stripes is too strong, then the CT/bond-length vibrations will freeze into a static CDW/BOW. This sets a lower frequency limit for the CT frequency, which suggests consequences for models of superconductivity, dynamic versus static magnetic moments (e.g., in Pu [33]), etc. For instance, higher superconducting Tc would be aided by a lower CT tunneling frequency. Partially charged stripes can also be found with the above formalism by tuning the band-filling. Similarly, topological (including fractionally charged) edge states resulting from boundary conditions in finite systems, as has been extensively studied in 2D Dirac metals, can be captured.
4. Elasticity and Short–Long-Range Competitions
As suggested earlier, elasticity in TMOs (and related materials such as f-electron and many organic compounds) is very important because of their localized, directional d-orbitals. This consideration complements electronic/spin focuses and cannot be ignored. In fact, the elasticity in these materials is strong (because it is weakly screened and therefore must be integrated over long ranges) and directional, resulting in constraints and competitions for ground and metastable states. Indeed, the origin of elasticity is a coupling of optic and acoustic modes [34]: unit cell optic lattice distortions constrain next-neighbor unit cell distortions and sequentially to acoustic long-range “elastic” fields. This provides a self-consistent complex network situation, with multiscale microstructure (twinning, tweed, etc.) as intrinsic sub-grain textures, which is the result of the self-consistent short–long-range field competition. Importantly, the network adjusts globally to either local or global perturbations. Furthermore, solid–solid phase transitions are accompanied by extended regimes of lattice microstructure around the transition, as well as sensitivity to strain and external fields (electric, magnetic, etc., depending on the specific material). Recall Alex Müller!
For illustration, consider the class of materials known as ferroelastic martensites. Ferroelasticity is the existence of two or more stable orientation states of a crystal that correspond to different arrangements of the atoms but are structurally identical (enantiomorphous). These orientation states are degenerate in energy in the absence of mechanical stress. The term martensitic usually refers to a diffusionless first-order phase transition that can be described in terms of one or successive shear deformations from a parent to a product phase. Schematic illustrations of symmetry-allowed 2D transitions are shown in Figure 4. The morphology and kinetics of the transition are dominated by the strain energy, and the transition results in characteristic lamellar (twinned) microstructures. Features observed in proper ferroelastic crystals include mechanical hysteresis and mechanically switchable domain patterns. Ferroelasticity usually occurs as a result of a phase transition from a nonferroelastic high-symmetry parent phase and is associated with the softening of an elastic modulus with decreasing temperature or increasing pressure in the parent phase. The ferroelastic transition can be described by Landau theory with spontaneous strain or deviation of a given ferroelastic orientation state from the parent phase as the order parameter (OP). The strain can be coupled to other fields, such as electric polarization and magnetic moment; thus, the crystal can have more than one transition.
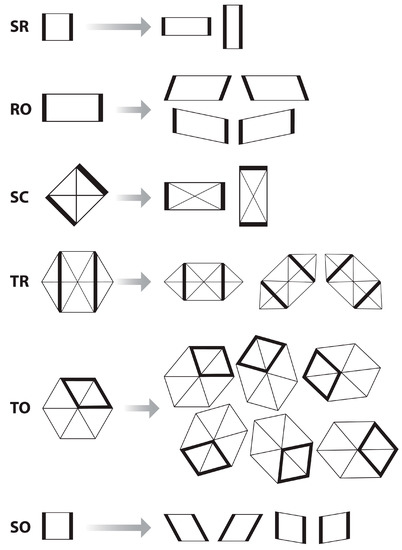
Figure 4.
Symmetry-allowed transitions in 2D for four crystal systems. (See Ref. [35]). The dark lines are visual guides to indicate deformations. There is a one-component strain order parameter (OP) for the square-to-rectangle (SR) case, driven by deviatoric strain, : the rectangle-to-oblique (RO) case, driven by ; and the square-to-centered rectangle (SC) case, driven by shear strain, . A two-component OP, or two one-component OPs, leads to the triangular-to-centered rectangle (TR) case, driven by , ; the triangle-to-oblique (TO) case, driven by , ; and the square-to-oblique (SO) case, driven by and independently. Copyright 2020 American Physical Society.
A comprehensive Ginzburg–Landau (GL) theory of this lattice elasticity can be built using so-called St. Venant lattice compatibility constraints to capture the symmetry-constrained short–long-range framework described above. This theory is detailed in [35,36] for many 2D and 3D cases. The theory successfuly describes key observed features of solid–solid phase transitions, including twins and twinning periodicity system (e.g., grain) size-dependence; twinning hierarchies at high–low symmetry interfaces and boundaries; extensive precursor (nucleation/spinodal) microstructure regimes around the solid–solid phase transition; global, multiscale structural effects of local dopants; (“local stress”); and global, multiscale, including local, structural effects of external stress and other applied fields. Figure 5 and Figure 6 show a few examples of the results, illustrating the intrinsic and sensitive landscapes of microstructure. There is some optimism that this sensitivity might be represented in statistical configuration ensembles, including the use of Machine Learning/Neural Network techniques for relevant feature capture (see [37]). The above GL theory (extended to time-dependent GL (TDGL) [35,36]) also self-consistently predicts multi-timescale dynamics and relaxation of the multi-lengthscale microstructure, including glassy phenomena.

Figure 5.
Multiscale texture evolution computed in a 2D TDGL elasicity theory (see Ref. [35]). Square-to-rectangle (Figure 4) case, showing simulated interface propagation. The rows show (left to right) temporal sequences at 40, 80, 160, and 1000 ps. Top Row: The order parameter (OP) deviatoric strain, showing domain walls propagating under the repulsive long-range lattice compatibility potential. Bottom Row: Non-OP shear strain, propagating outward with interfaces, concentrated at the corners. Copyright 2020 American Physical Society.
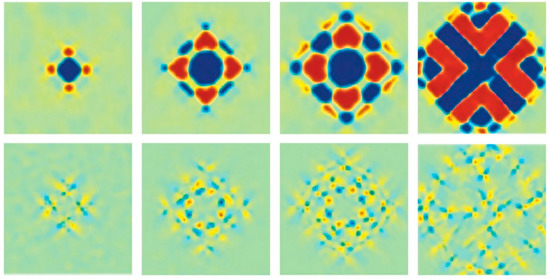
Figure 6.
Same square-to-rectangle case as Figure 5, demonstrating global effects of a local stress: simulated strain evolution, with an added fixed, time-independent, Lorentzian-profile local stress (see Ref [33]). The sequence (left to right) is shown for timet = 40, 60, 76, and 106 ps. Top Row: Dynamic texturing of deviatoric strain. The system reduces the energy from the imposed single-sign strain by elastic photocopying, or adaptive screening, of the long-range elastic interaction, generating higher multipoles. Bottom Row: The non-order parameter (OP) shear strain follows the OP propagation. Copyright 2020 American Physical Society.
There are several important lessons from this elasticity description. The precursor microstructure extends over large parameter regimes of temperature, pressure, etc., around solid–solid phase transitions—recall Alex Müller. The functionality of this microstructure is often as important as the transition itself. (For example the tetragonal-orthorhomic transition in cuprate superconducors or hierarchical ordering in shape-memory alloys.) Throughout the precursor regime, local doping sites, because of their long-range elastic effects, have significant influence on the transition and nucleate structured precursor domains of the incipient phase. We emphasize that the sensitive microstructural landscapes are intrinsic free-energy states. Attempts to eliminate the microstructure (e.g., de-twinning), especially in the extended vicinity of solid–solid transitions, are unhelpful, since they will simply reform unless pinned into non-equilibrium configurations. With this in mind, it is natural to ask whether the intrinsic microstructure provides the template on which electronic, magnetic, etc., degrees of freedom can act, i.e., can the microstructure be the driver of electronic or magnetic properties?
This question has been explored through several examples. For example, [38] examines the electronic signature of twin boundaries (TB) and anti-phase boundaries in 2D. Here, the boundary centers constitute a local (e.g., square) lattice symmetry smoothly joining domains (twins) of a different (e.g., rectangular) lattice symmetry (see Figure 4). This results in locally metallic filaments in a semiconducting host. In fact, the TB can be considered a 2D Dirac metal with flat electronic bands of edge states [39]. WOx provides an excellent example of quasi-periodic patterns of shear planes [40,41], and intriguingly, in a certain x regime, it is also a high-temperature superconductor, with the superconductivity probably strongest on the shear planes—recall the comments on possible filamentary superconductivity above, since dopant (polaronic) charges will preferentially decorate shear planes (and TBs).
In [42], the effects of long-range anisotropic elastic deformations on electronic structure in conventional BCS superconductors are analyzed within the framework of Bogoliubov–de Gennes equations. Cases of TBs and isolated defects are considered there as illustrations. The calculated local density of states suggests that the electronic structure is strongly modulated in response to lattice deformations and propagates to longer distances because of the elasticity. In particular, this allows the trapping of low-lying quasiparticle states around defects. Some of these predictions could be directly tested by scanning tunneling microscopy.
Reference [43] uses the St Venant lattice compatibility constraint theory to predict the role of elasticity in colossal magnetoresistance (CMR) perovskite manganites. The intrinsic coexistence of distinct metallic and insulating electronic phases in perovskite manganites, such as La1−x−y Pry Cax MnO3, is predicted, which presents opportunities for sensitively tuning the electronic properties. In particular, the CMR in these materials is closely related to the observed texture owing to coexisting nanometer- and micrometer-scale inhomogeneities. Extensive data from various high-resolution probes show the existence of such inhomogeneities. Experimental results also support the presence of metastable states in manganites. For example, magnetic fields or X-rays have been used to convert insulating regions into ferromagnetic metallic ones, which are stable even when the fields are removed. Explanations based on electronic mechanisms and chemical disorder have not been sufficient to describe the multiscale, multiphase coexistence within a unified picture. However, lattice distortions and strain are known to be important in the manganites [44], and indeed the resistivity transition can be tuned with pressure as well as magnetic field. In [43], it is shown how the texturing can be due to the intrinsic complexity of a system with coupling between the electronic and elastic degrees of freedom. This leads to landscapes of energetically favorable configurations and provides a self-organizing mechanism for the observed inhomogeneities. Since the domain formation is self-sustained, external stimulii such as optical lasers, X-rays, or ultrasonic standing waves can be used to sensitively manipulate patterns of metallic and insulating regions, thus making the control of nanoengineered functional structures feasible and technologically important.
The same mechanisms should be applicable to describing intrinsic inhomogeneities in other materials with strong bonding constraints, such as relaxor ferroelectrics and high transition temperature superconducting oxides, f-electron materials (including heavy-fermions), organics (including superconductors), multiferroics, and 2D Dirac materials (such as graphene, dichalcogenides), etc., where the functionalities may also be mediated through self-organized lattice distortions. We return to the probable role of polarons below. More generally, there are many materials where the above approach to coupling lattice, spin, charge and orbital degrees of freedom, including elastically driven transitions, can be applied. For instance, epitaxial oxide layers and multilayers provide extensive functional tunability [45], and magnetocalorics [46] are studied for their potential application as efficient refrigeration and waste-recovery materials. Reference [47] uses the above elasticity framework to argue that certain metal–insulator transitions are accompanied by precursor elasticity microstructure. Indeed, early neutron scattering around the metal–insulator transition in VO2 found short magnetic correlation lengths even very close to the transition, suggesting that the lattice microstructure limits the electronic/magnetic properties. Modern time-resolved crystallography can now resolve substantial lattice contributions to several M–I transitions, including VO2, as anticipated in early theory [48]. I suggest that similar roles for elastic fluctuations can be expected around many broken-symmetry transitions, including many quantum critical points [49]. Note that the elasticity discussion here was for a single grain. Multigrain interactions are beyond the scope of the present discussion and require coarser-scale (e.g., phase-field, finite-element) modeling for homogenization and constitutive equations.
Reference [50] uses an extended Holstein polaron model to suggest how elastic interactions can control the organization of small polaron patterns. This modeling leads to a landscape of filamentary (stripe) polaron patterns, similarly to those outlined in Section 3. The small polarons have very localized electronic cores but act as local impurities in the multiscale, directional elastic field, creating anisotropic elastic fields and driving the filamentary ordering. Figure 7 shows examples calculated for a 2D square lattice hosting a finite density of small polarons.
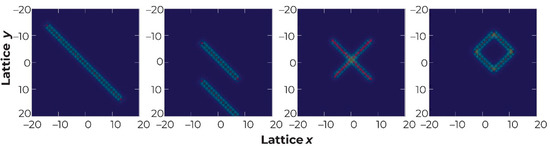
Figure 7.
Computed configurations of small polarons embedded in an elastic 2D medium, illustrating the angular dependence of the strain field favoring diagonal strings. Four examples of metastable minima are shown for different numbers of polarons (see Reference [50] for details). Copyright 2020 American Physical Society.
5. Hybridized Bands and more examples of Short–Long-Range Competitions
The coexistence of narrow (d,f) and wider (s,p) electronic bands has motivated a great variety hybridization studies. Many of these are theoretically rich, and some are surely exhibited in various TMOs and related electronic and magnetic materials. Below, we summarize a few examples but emphasize the additional features and competing phases resulting from the inclusion of lattice degrees of freedom.
Multi-band superconductivity is a natural candidate. Substantial Tc enhancement and tunability is possible, which is controlled by the interband coupling strengths and locations (in k-space) (e.g., [51]). Resonant coupling (e.g., Fermi resonance) is especially intriguing and is well-covered in this volume and elsewhere [52]. Clearly, the mesoscopic phase separation of lattice, charge, spin broken- and unbroken-symmetry regions described above provide environments for these scenarios, with stripes and TBs sources of flat electronic bands.
Intrinsic local modes (ILMs) are spatially localized lattice modes (multi-phonon bound states) resulting from sufficiently anharmonic lattice vibrations (e.g., [10]), where the anharmonicity is often the consequence of feedback from electron or spin coupling to the lattice. In fact, as discussed above, polarons are the result of such a (positive) feedback from linear coupling between charge/spin and lattice. When this coupling is strong enough to create small polarons, the lattice distortion is locally anharmonic and can create an ILM, resulting in a composite polaron–ILM state [53]. In addition, doping sites can locally distort the lattice into an anharmonic regime and create a ILM. An appealing scenario is that ILMs can be induced in this way by doping and then embedded self-consistently in an undoped background. Reference [54] uses this approach to model ferroelectrics, including anomalous phonons and glassy/relaxor phases. This approach has also been used [55] within nonlinear shell models, which, as as noted above, are an approximate but effective description of O polarizability and M–O charge transfer. For example, the quantum paraelectric phase of SrTiO3 and the onset of ferroelectricity with O18 isotope substitution are well explained [56], as are the differences between ferroelectrics BaTiO3 and EuTiO3 [57]. More generally, this approach provides an excellent basis for understanding the T-doping-strain phase-diagram of these materials—the doping-induced superconductivity phase-diagram [58] is reminiscent of cuprates. I note again that nonlinear shell models owe much to Heinz Bilz and his ability to combine insights from solid-state physics, quantum chemistry, and nonlinear statistical mechanics long before sufficient ab initio quantum methods were available.
In [59], dimerized AF (homogeneous SP) and inhomogeneous-lattice AF (inhomogeneous SP) ground states are predicted in both 1D and 2D periodic Anderson models when el–lattice coupling is included, as shown schematically in Figure 8. Coexistence and mutual enhancement of the Peierls distortion and the AF long-range order are found. The stoichiometric phase diagrams are strongly dependent on the relative hybridization and el–lattice coupling strengths. For non-stiochiometric fillings, coupled spin–charge–lattice polarons are found containing precursor textures of neighboring phases. Relations to Ce-based heavy-fermion systems, volume collapse, and inorganic SP materials are discussed in [59].
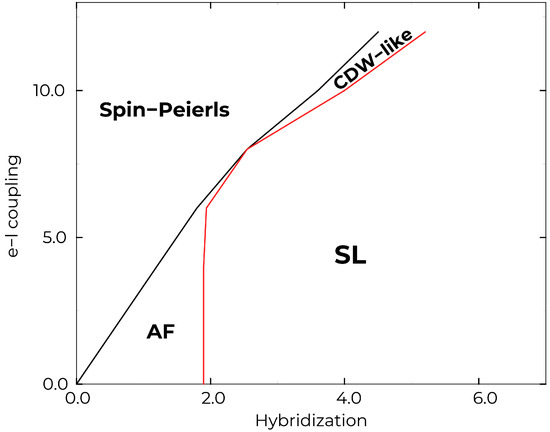
Figure 8.
Computed phase diagram in a 2D periodic Anderson model with el–lattice coupling, as a function of hybridization and el-lattice coupling strengths. (See [59]). Ground states found are: long-period spin–Peierls; antiferromagnet (AF); charge density wave (CDW); spin liquid (SL).
Returning to the importance of short–long-range field competitions (Section 4), RKKY is a familiar magnetic long-range (and oscillatory) interaction. In [60], the magnetic properties of a system of coexisting localized spins and conduction electrons are investigated within an extended version of the 1D Kondo lattice model in which effects of el–lattice and on-site Coulomb interactions are explicitly included. It is found that intrinsic inhomogeneities with the statistical scaling properties of a Griffiths phase appear and determine the spin structure of the localized impurities. The appearance of the inhomogeneities is enhanced by appropriate phonons and acts destructively on the spin ordering. The inhomogeneities appear on well-defined length scales and can be compared to the formation of intrinsic mesoscopic metastable patterns found in two-fluid phenomenologies. A mapping to an effective random field transverse field Ising model is found to be instructive. The RKKY system can indeed be viewed as intrinsically frustrated [61].
I conclude this section with a more general perspective on multiscale landscapes resulting from coexisting short–long-range interactions. In particular, the appearance of glassy filamentary phases in windows of intermediate doping concentration (“intermediate phases”) [62,63] is demonstrated in [64,65] as a model of doped 2D anti-ferromagnets. I believe these intermediate phases are very important functionally and should be realized in many materials, including doped TMOs. For example, using efficient numerical methods to handle long-range interactions, references [65,66] study a quasi-classical model for the charge ordering of holes in TMOs, in which the particles have a Coulomb repulsion and a dipolar attraction. As a function of hole density (doping), an extended soft phase comprising partially ordered filaments is found (see Figure 9). Ordered clumps form for low densities and ordered stripes (Wigner crystal-like phases) at high densities (see Figure 10). The soft filamentary structures persist to high temperatures. Within the soft phase region, there is an onset at low T of motion along the filaments: i.e., the filaments act as a template for the correlated percolation of particle motion. When the particle positions are averaged over long times, the filaments form a checkerboard pattern (see Figure 11). All of this rich multiscale patterning and dynamics arises from a deceptively simple 2D model in which the effective interaction between two holes, 1 and 2, a distance r apart is given by
Here, q = 1 is the hole charge, θ is the angle between r and a fixed axis, and 1,2 are the angles of the magnetic dipoles relative to the same fixed axis, which is allowed to take an arbitrary value. A is the strength of a short-range anisotropic interaction, and B is that of a magnetic dipolar interaction [B ≈ A/(2π ξ/2)], which were assumed to be independent variables. Here, for simplicity, we take A = 0 and assume a scaling for the magnetic correlation length ξ∼1/√n, with n the hole density. Reference [67] describes characteristic noise and hysteresis associated with the stripe, clump, and checkerboard phases. Reference [68] demonstrates how both commensurate and incommensurate checkerboard configurations are possible.
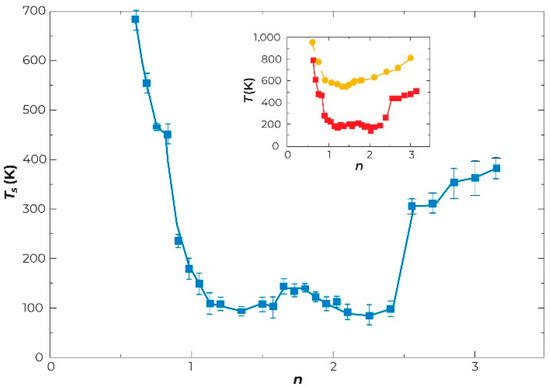
Figure 9.
Onset temperature Ts of a modulated square liquid state as a function of hole density n in model Equation (2). INSET: Melting temperature of pattern Tm (yellow circles) and Ts (red squares). Copyright 2020 American Physical Society.
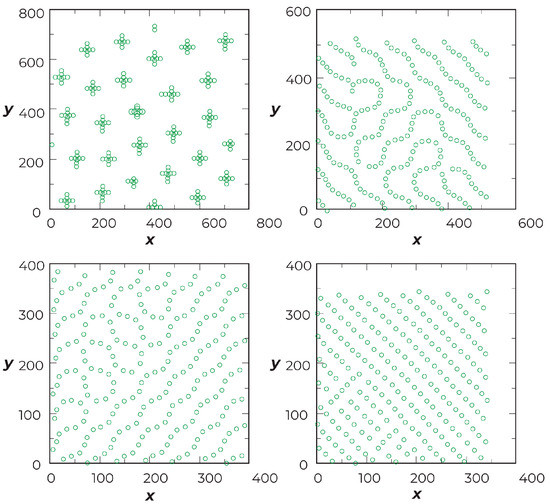
Figure 10.
Simulated static positions of holes for different densities, n, in model Equation (2): (a) clump phase, n = 0.6; (b) soft phase, density n = 1.2; (c) soft phase, n = 2.1; and (d) anisotropic Wigner crystal phase, n = 2.7. Copyright 2020 American Physical Society.

Figure 11.
Image of system above the filamentary melting transition, with lines indicating the motion of the holes between consecutive simulation frames. (a) n=0.6 in the clump phase, where the particles remain predominantly localized. (b) n=1.2, showing the square modulated liquid phase in the filamentary regime (see [65]).
TMOs, and related materials, exhibit complex interplays of spin, charge, orbital, and lattice so that a simplified model such as the above should not be overinterpreted. For instance, as noted earlier, there are essential roles of polarizable oxygen or equivalent ions [displacements, rotations, charge transfer, etc. (e.g., [5,12])]. Nevertheless, some implications are suggestive. Namely, charge-ordered states may persist up to very high temperatures, but signatures of disordered filamentary states occur at much lower temperatures with a transition to a checkerboard state at intermediate temperatures. The coexisting short- and long-range interactions will appear only upon the (polaronic) localization of holes, which happens below a characteristic temperature. Above this temperature, a more metallic-like electronic state is expected. The soft phase also shows similarities with the inhomogeneous states observed in manganite oxides (above) between the true critical temperature and a higher temperature at which short-range order first appears. In addition, as we note below, some stripe-based theories for superconductivity require fluctuating stripes. An important feature of the soft phase in Figure 9 is that the fluctuations are predominantly on (correlated) percolating filaments rather than meandering of the filaments themselves. Therefore, the fluctuating filamentary and checkerboard states should provide a reasonable starting point for introducing detailed quantum-mechanical and oxygen effects.
Although, a full simulation has not yet been performed, we should expect that similar soft intermediate phase behavior will be found for the multi-polaron patterns introduced in Section 4. Indeed, in that case, the long- and short-range fields are provided self-consistently by the same elasticity. In this context, it is worth recalling that elasticity has its origins in the total energy of a solid including the Coulomb contributions. Hence, if atomic configurations are allowed to relax self-consistently in a Coulomb field, the elasticity features above must be recovered. Finally, we note that a quite general framework for intermediate phases can be expressed in a theory describing network adaptability and rigidity transitions based on the degree of lattice connectivity and the number of bonding constraints [62,63,69]. The next material frontiers must include understanding reactive networks. Viz, the network structure adapts to the functioning (lattice, spin, charge) of (or collections of) nodes because this changes local- and multiscale network connections, and the new structure then initiates new functioning. This feedback cycle underpins the complementary aspects of learning and aging in complex materials, similarly to emerging views of hierarchical landscapes and substates in quantitative biology and other fields adopting network scenarios [70].
6. Conclusions and Discussion
The competitions among spin, charge, orbital, and lattice degrees of freedom in TMOs (and related materials with directional bonding and coupled localized/narrow band and delocalized/wide band electronic orbitals) leads to a richness of ground (and excited) states because of delicate free-energy balances. This is a wonderful situation for tunable functionality and applications, but it challenges conceptual frameworks created for simpler classes of materials. Asymptotic length and time-scaling descriptions, although certainly useful, are incomplete, and the community has yet to create a full palette of experimental, theoretical, and computational tools to understand the resulting multiscale, multiphysics landscapes of states. However, it is clear that understanding and controlling the functionality of this “dark matter”(!) will require combining techniques from many disciplines (solid state, quantum chemistry, correlated electrons, field theory, mathematical physics, nonlinear science, high-performance computing, data analytics such as ML, etc.). This is surely the interdisciplinary path to addressing the challenges and opportunities of “quantum materials” [11].
It is always true that new experimental and modeling techniques motivate new conceptual frameworks, and vice versa. This also motivates new interpretations of existing data. For example, I mentioned in Section 1 the birth of STM and its impact. It is striking to trace STM’s history since then through mesoscopics, Bose–Einstein condensates, to TMOs [71], DNA manipulation, etc. No less impressive are similar journeys for neutron and X-ray resolution, angle-resoved photoemission, nuclear magnetic resonance, resonant ultrasound, pump-probe spectroscopy, time-resolved crystallography, and more. These are all now critical tools for understanding the multiple spatial and temporal scales that Alex Müller so presciently anticipated in TMOs. They are essential capabilities to combine with equally impressive revolutions in high-performance computing, visualization, and data analytics on the path to the holy grail of understanding, controlling, and using materials’ synthesis–structure–property–performance relationships.
I finish with a few open questions.
- I have deliberately emphasized lattice, including elastic, effects in TMOs (and related d- and f- orbital materials) because these have often been under-represented in research on “strongly correlated” quantum matter. The recent workshop [2] is an encouraging community step. However, clearly, it remains to be understood when lattice, spin, charge, and orbital degrees of freedom individually dominate and then the others are slaved. There are likely to be classes of materials that should be so categorized in this fascinating collusion among degrees of freedom. This is a quantum mechanical adiabaticity question that must be addressed on appropriate spatial and temporal scales and, as with the importance of el–lattice coupling, not simply in terms of average properties. Functionality through charge, spin, and lattice at active interfaces, including between TMOs, is an important direction for applications (e.g., perovskite-based solar cells and detectors) [45,72]. Similarly, domain boundary engineering, e.g., in multiferroic materials [73], is a very attractive direction.
- The recent emphasis on quantum entanglement and the increasing recognition of geometry and topology in electronic and magnetic materials research raises important questions. For instance, (1) above in the context of when does the lattice simply renormalize parameters for quantum phases and when do topological lattice configurations act as the driving template for quantum mechanics? For example, this is an important issue in materials design for qubits and quantum information research.
- I have not focused here on high-temperature (HTC) mechanisms. The wonderful discovery of HTC in cuprates by Bednorz and Müller certainly propelled remarkable advances in synthesis, experimental, theoretical and simulation capabilities for complex electronic materials and whole new classes of materials have benefitted: multilayer TMOs [45], Dirac–Weyl materials, organic and heavy-fermions SCs, pnictides, multiferroics, over-doped HTC cuprates [74], etc. After these many years, a generally accepted theory of HTC remains elusive. Which of the multitude of measured perovskite features are directly relevant to the superconductivity mechanism has yet to be understood. However, much research falls into the framework of multiscale, coexisting charge-rich and charge-poor regions [29,75]. Inhomogeneous superconductivity is familiar, e.g., in granular superconductors. However, the possibility of inhomogeneity being an intrinsic template for the SC mechanism. For example, Reference [76] proposes micro (i.e., bond-length) strain (cf, Section 4) as a primary control parameter in cuprate SCs. The polaron patterns discussed above are also examples: precursors to CDWs and equilibria with multi-polaron (including bi-polaron) bound states. Such CDW-like phases embedded in various undoped broken-symmetry hosts are attractive scenarios, but the AF broken-symmetry host state is not unique. Rather, the main issue becomes: How do the charge-rich regions communicate? Magnetic, charge, and elastic fluctuations are all feasible [77]. There is accumulating evidence [29] for a checkerboard period-4 CDW-like configuration in cuprates. Various small perturbations can isolate such a specific periodicity for the ordering illustrated in Section 5 (e.g., [68]). However, qualitatively different origins are also interesting (e.g., [78]). The charge-transfer (polarizability) features of perovskites we have discussed lend themselves to W.A. Little’s scenario of enhanced SC from off-chain/plane polarizable material [79,80]. Finally, an intriguing consideration is that (correlated) percolating charged filaments organize fractally as doping increases, before finally over-packing and quantum melting. This would certainly be the optimal space filling to maximize percolating filamentary properties if those properties are desirable—e.g., for high Tc, as suggested for many years by J.C. Phillips [81].
Materials play fundamental roles in the health and prosperity of society. It is not accidental that many new technologies and their impacts on society are rapidly accelerating in this dynamic era of complexity science: they are results of remarkable new experimental, simulation, and visualization tools and the resulting data explosion. As throughout history, the new technologies are also producing new societal challenges—in this century for health, energy, natural resources, climate, national security, space, cyber, social media, etc., sectors—but now at a very accelerated pace. It is fortunate that this century is generating the tools for the science, technology, engineering, and mathematics workforce to play its part in addressing these societal opportunities and challenges, making this an exciting time for the historic cycle of science–society evolution. Happily, the many disciples of Alex Müller are well supplied with opportunities to conceive new ideas and create tools to test them as the future history of quantum materials is written.
Funding
This research received no external funding.
Acknowledgments
Although the views expressed in this article are personal, I have very many colleagues to thank for partnering with me through the research I have referenced, including Miklos Gulacsi and Zlatko Tesanovic who are sadly no longer with us. Since there are so many to recognize individually, I hope that the references will suffice and I apologize to all those colleagues whose important research I have not directly referenced. However, this is a tribute to Alex Müller. I wish to acknowledge him in particular for his inspiration and to mention two of his contemporaries who deeply influenced my scientific life—Heinz Bilz and Jim Krumhansl. Alex, Heinz, and Jim are wonderful icons of a great science generation.
Conflicts of Interest
The author declares no conflict of interest.
References
- Müller, K.A. Microscopic Probing of BaTiO3 Ferroelectric Phase Transitions by EPR. In Nonlinearity in Condensed Matter, Proceedings of the Sixth Annual Conference, Center for Nonlinear Studies, Los Alamos, NM, USA, 5–9 May 1986; Bishop, A.R., Campbell, D.K., Kumar, P., Trullinger, S.E., Eds.; Springer: Berlin/Heidelberg, Germany, 1987; pp. 234–245. [Google Scholar]
- Schmalian, J.; Sinova, J.; Valenti, R. Elastic Tuning and Response of Electronic Order. In Proceedings of the Spin Phenomena Interdisciplinary Center (SPICE) Workshop, Mainz, Germany, 9–11 December 2019. [Google Scholar]
- Müller, K.A.; Berlinger, W.; Tosatti, E. Indication for a novel phase in the quantum paraelectric regime of SrTiO3. Z. Phys. B Condens. Matter 1991, 84, 277–283. [Google Scholar] [CrossRef]
- Tokura, Y. Correlated-electron physics in transition-metal oxides. Phys. Today 2003, 56, 50–55. [Google Scholar] [CrossRef]
- Krumhansl, J.A. Fine Scale Mesostructures in Superconducting and Other Materials. In Proceedings of the Lattice Effects in High-Temperature Superconductors, Santa Fe, NM, USA, 13–15 January 1992. [Google Scholar]
- Migoni, R.; Bilz, H.; Bauerle, D. Origin of raman scattering and ferroelectricity in oxidic perovskites. Phys. Rev. Lett. 1976, 37, 1155. [Google Scholar] [CrossRef]
- Dernadis, K.D. The localized-to-delocalized transition in mixed-valence chemistry. J. Chem. Rev. 2001, 101, 2655–2685. [Google Scholar]
- Caldeira, A.O.; Leggett, A.J. Quantum Tunneling in a Dissipative System. Ann. Phys. 1983, 149, 374–456. [Google Scholar] [CrossRef]
- Martonák, R.; Tosatti, E. Path-integral Monte Carlo study of a model two-dimensional quantum paraelectric. Phys. Rev. B 1994, 49, 596–613. [Google Scholar] [CrossRef]
- Manley, M.E.; Lynn, J.W.; Abernathy, D.L.; Specht, E.D.; Delaire, O.; Bishop, A.R.; Sahul, R.; Budai, J.D. Phonon localization drives polar nanoregions in a relaxor ferroelectric. Nat. Commun. 2014, 5, 3683. [Google Scholar] [CrossRef]
- Awschalom, D.; Christen, H. Opportunities for basic research for next generation quantum system. In Proceedings of the Basic Energy Sciences Roundtable on Opportunities for Basic Research for Next-Generation Quantum Systems, Gaithersburg, MD, USA, 30–31 October 2017; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2017. [Google Scholar]
- Porer, M.; Fechner, M.; Kubli, M.; Neugebauer, M.J.; Parchenko, S.; Esposito, V.; Narayan, A.; Spaldin, N.A.; Huber, R.; Radovic, M.; et al. Ultrafast transient increase of oxygen octahedral rotations in a perovskite. Phys. Rev. Res. 2019, 1, 012005. [Google Scholar] [CrossRef]
- Nelson, T.R.; White, A.J.; Bjorgaard, J.A.; Sifain, A.E.; Zhang, Y.; Nebgen, B.; Fernandez-Alberti, S.; Mozyrsky, D.; Roitberg, A.E.; Tretiak, S. Non-adiabatic Excited-State Molecular Dynamics: Theory and Applications for Modeling Photophysics in Extended Molecular Materials. Chem. Rev. 2020, 120, 2215–2287. [Google Scholar] [CrossRef]
- Kreutzer, M.; Ernst, D.; Bishop, A.R.; Fehske, H.; Hager, G.; Nakajima, K.; Wellein, G. Chebyshev Filter Diagonalization on Modern Manycore Processors and GPGPUs. In High Performance Computing, Proceedings of the 33rd International Conference, ISC High Performance 2018, Frankfurt, Germany, 24–28 June 2018; Yokota, R., Weiland, M., Keyes, D., Trinitis, C., Eds.; Springer International Publishing AG: Cham, Switzerland, 2018; pp. 329–349. [Google Scholar]
- Yonemitsu, K.; Bishop, A.R.; Lorenzana, J. Sensitivity of Doping States in the Copper Oxides to Electron-Lattice Coupling. Phys. Rev. Lett. 1992, 69, 965–968. [Google Scholar] [CrossRef]
- Emin, D. Polarons; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Fehske, H.; Wellein, G.; Bishop, A.R. Spatiotemporal evolution of polaronic states in finite quantum systems. Phys. Rev. B 2011, 83, 075104. [Google Scholar] [CrossRef]
- Salkola, M.I.; Bishop, A.R.; Trugman, S.A.; de Leon, J.M. Correlation-function analysis of nonlinear and nonadiabatic systems: Polaron tunneling. Phys. Rev. B. 1995, 51, 8878. [Google Scholar] [CrossRef] [PubMed]
- Raghavan, S.; Bishop, A.R.; Kenkre, V.M. Quantum versus semiclassical description of self-trapping: Anharmonic effects. Phys. Rev. B 1999, 59, 9929–9932. [Google Scholar] [CrossRef]
- Bishop, A.R.; Mihailovic, D.; Mustre de León, J. Signatures of mesoscopic Jahn–Teller polaron inhomogeneities in high-temperature superconductors. J. Phys. Condens. Matter 2003, 15, L169–L175. [Google Scholar] [CrossRef]
- Bousquet, E.; Hamdi, H.; Aguado-Puente, P.; Salje, E.K.; Artacho, E.; Ghosez, P. First-principle characterization of single-electron polaron in WO3. Phys. Rev. Res. 2020, 2, 012052. [Google Scholar] [CrossRef]
- Li, S.; Johnston, S. Quantum Monte Carlo study of lattice polarons in the two-dimensional multi-orbital Su-Schrieffer-Heeger model. arXiv 2019, arXiv:1901.07612. [Google Scholar]
- Yonemitsu, K.; Bishop, A.R.; Lorenzana, J. Magnetism and covalency in the two-dimensional three-band Peierls-Hubbard model. Phys. Rev. B 1993, 47, 8065–8075. [Google Scholar] [CrossRef]
- Yu, Z.G.; Zang, J.; Gammel, J.T.; Bishop, A.R. Charge localization and stripes in a two-dimensional three-band Peierls-Hubbard model. Phys. Rev. B 1998, 57, R3241–R3244. [Google Scholar] [CrossRef]
- Martin, I.; Kaneshita, E.; Bishop, A.R.; McQueeney, R.J.; Yu, Z.G. Vibrational edge modes in intrinsically heterogeneous doped transition metal oxides. Phys. Rev. B 2004, 70, 224514. [Google Scholar] [CrossRef]
- Yonemitsu, K.; Batistić, I.; Bishop, A.R. Random-phase-approximation approach to collective modes around inhomogeneous Hartree-Fock states: One-dimensional doped Hubbard model. Phys. Rev. B 1991, 44, 2652–2663. [Google Scholar] [CrossRef]
- McQueeney, R.J.; Bishop, A.R.; Yi, Y.-S.; Yu, Z.G. Charge localization and phonon spectra in hole-doped La2NiO4. J. Phys. Condens. Matter 2000, 12, L317–L322. [Google Scholar] [CrossRef]
- Kaneshita, E.; Tohyama, T.; Bishop, A.R. Modeling of pressure effects in striped nickelates. Physica C 2010, 470, S247–S248. [Google Scholar] [CrossRef]
- Agterberg, D.F.; Séamus Davis, J.C.; Edkins, S.D.; Fradkin, E.; Van Harlingen, D.J.; Kivelson, S.A.; Lee, P.A.; Radzihovsky, L.; Tranquada, J.M.; Wang, Y. The Physics of Pair-Density Waves: Cuprate Superconductors and Beyond. Annu. Rev. Condens. Matter Phys. 2020, 11, 231–270. [Google Scholar] [CrossRef]
- Kaneshita, E.; Martin, I.; Bishop, A.R. Local Edge Modes in Doped Cuprates with Checkerboard Polaronic Heterogeneity. J. Phys. Soc. Jpn. 2004, 73, 3223–3226. [Google Scholar] [CrossRef][Green Version]
- Kaneshita, E.; Martin, I.; Bishop, A.R. Pressure-induced phase transition and bipolaronic sliding in a hole-doped Cu2O3-ladder system. Phys. Rev. B 2006, 73, 094514. [Google Scholar] [CrossRef]
- Chernyshev, A.L.; Castro Neto, A.H.; Bishop, A.R. Metallic Stripe in Two Dimensions: Stability and Spin-Charge Separation. Phys. Rev. Lett. 2000, 84, 4922–4925. [Google Scholar] [CrossRef]
- Janoschek, M.; Das, P.; Chakrabarti, B.; Abernathy, D.L.; Lumsden, M.D.; Lawrence, J.M.; Thompson, J.D.; Lander, G.H.; Mitchell, J.N.; Richmond, S.; et al. The valence-fluctuating ground state of plutonium. Sci. Adv. 2015, 1, e1500188. [Google Scholar] [CrossRef] [PubMed]
- Zener, C. Elasticity and Anelasticity of Metals; University of Chicago Press: Chicago, IL, USA, 1948. [Google Scholar]
- Lookman, T.; Shenoy, S.R.; Rasmussen, K.Ø.; Saxena, A.; Bishop, A.R. Ferroelastic dynamics and strain compatibility. Phys. Rev. B 2003, 67, 024114. [Google Scholar] [CrossRef]
- Planes, A.; Lloveras, P.; Castán, T.; Saxena, A.; Porta, M. Ginzburg–Landau modelling of precursor nanoscale textures in ferroelastic materials. Contin. Mech. Thermodyn. 2012, 24, 619–627. [Google Scholar] [CrossRef]
- Holm, E.A.; Cohn, R.; Gao, N.; Kitahara, A.R.; Matson, T.P.; Lei, B.; Yarasi, S.R. Overview: Computer vision and machine learning for microstructural characterization and analysis. arXiv 2020, arXiv:2005.14260. [Google Scholar]
- Ahn, K.H.; Lookman, T.; Saxena, A.; Bishop, A.R. Electronic properties of structural twin and antiphase boundaries in materials with strong electronic-lattice coupling. Phys. Rev. B 2005, 71, 212102. [Google Scholar] [CrossRef]
- Zhu, L.; Prodan, E.; Ahn, K.H. Flat energy bands within antiphase and twin boundaries and at open edges in topographical materials. Phys. Rev. B 2019, 99, 041117. [Google Scholar] [CrossRef]
- Aird, A.; Salje, E.K.H. Sheet conductivity in twin walls; experimental evidence of WO3-x. J. Phys. Cond. Matt. 1998, 10, L377–L380. [Google Scholar] [CrossRef]
- Shengelaya, A.; Conder, K.; Müller, K.A. Signatures of Filamentary Superconductivity up to 94 K in Tungsten Oxide WO2.90. J. Supercond. Nov. Magn. 2020, 33, 301–306. [Google Scholar] [CrossRef]
- Zhu, J.-X.; Ahn, K.H.; Nussinov, Z.; Lookman, T.; Balatsky, A.V.; Bishop, A.R. Elasticity-Driven Nanoscale Electronic Structure in Superconductors. Phys. Rev. Lett. 2003, 91, 057004. [Google Scholar] [CrossRef]
- Ahn, K.H.; Seman, T.F.; Lookman, T.; Bishop, A.R. Role of complex energy landscapes and strains in multiscale inhomogeneities in perovskite manganites. Phys. Rev. B 2013, 88, 144415. [Google Scholar] [CrossRef]
- Millis, A.J. Lattice effects in magnetoresistive manganese perovskites. Nature 1998, 392, 147–150. [Google Scholar] [CrossRef]
- Chen, A.; Su, Q.; Han, H.; Enriquez, E.; Jia, Q. Metal Oxide Nanocomposites: A Perspective from Strain, Defect, and Interface. Adv. Mater. 2019, 31, 1803241. [Google Scholar] [CrossRef]
- Gottschall, T.; Benke, D.; Fries, M.; Taubel, A.; Radulov, I.A.; Skokov, K.P.; Gutfleisch, O. A Matter of Size and Stress: Understanding the First-Order Transition in Materials for Solid-State Refrigeration. Adv. Funct. Mater. 2017, 27, 1606735. [Google Scholar] [CrossRef]
- Guzmán-Verri, G.G.; Brierley, R.T.; Littlewood, P.B. Cooperative elastic fluctuations provide tuning of the metal-insulator transition. Nature 2019, 576, 429–432. [Google Scholar] [CrossRef]
- Shi, J.; Bruinsma, R.; Bishop, A.R. Theory of Vanadium Dioxide. Synth. Met. 1991, 43, 3527–3530. [Google Scholar] [CrossRef]
- She, J.-H.; Zaanen, J.; Bishop, A.R.; Balatsky, A.V. Stability of Quantum Critical Points in the Presence of Competing Orders. Phys. Rev. B 2010, 82, 165128. [Google Scholar] [CrossRef]
- Maniadis, P.; Lookman, T.; Bishop, A.R. Elastically driven polaron patterns: Stripes and glass phases. Phys. Rev. B 2011, 84, 024304. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Micnas, R.; Bishop, A.R. Enhancements of the superconducting transition temperature within the two-band model. Eur. Phys. J. B 2004, 37, 345–348. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Keller, H.; Simon, A.; Bianconi, A. Multi-Band Superconductivity and the Steep Band/Flat Band Scenario. Condens. Matter 2019, 4, 4040091. [Google Scholar] [CrossRef]
- Cuevas, J.; Kevrekidis, P.G.; Frantzeskakis, D.J.; Bishop, A.R. Existence of bound states of a polaron with a breather in soft potentials. Phys. Rev. B 2006, 74, 064304. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Bishop, A.R.; Egami, T. Relaxor ferroelectrics and intrinsic inhomogeneity. Europhys. Lett. 2005, 71, 249–255. [Google Scholar] [CrossRef]
- Bishop, A.R.; Bussmann-Holder, A.; Kamba, S.; Maglione, M. Common characteristics of displacive and relaxor ferroelectrics. Phys. Rev. B 2010, 81, 064106. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Büttner, H.; Bishop, A.R. Polar-Soft-Mode-Driven Structural Phase Transition in SrTiO3. Phys. Rev. Lett. 2007, 99, 167603. [Google Scholar] [CrossRef]
- Bettis, J.L.; Whangbo, M.-H.; Köhler, J.; Bussmann-Holder, A.; Bishop, A.R. Lattice dynamical analogies and differences between SrTiO3 and EuTiO3 revealed by phonon-dispersion relations and double-well potentials. Phys. Rev. B 2011, 84, 184114. [Google Scholar] [CrossRef]
- Edge, J.M.; Kedem, Y.; Aschauer, U.; Spaldin, N.A.; Balatsky, A.V. Quantum Critical Origin of the Superconducting Dome in SrTiO3. Phys. Rev. Lett. 2015, 115, 247002. [Google Scholar] [CrossRef] [PubMed]
- Yi, Y.-S.; Bishop, A.R.; Röder, H. Spin-Peierls ground states in an electron-lattice periodic Anderson model. J. Phys. Condens. Matter 1999, 11, 3547–3554. [Google Scholar] [CrossRef]
- Gulacsi, M.; Bussman-Holder, A.; Bishop, A.R. Spin and lattice effects in the Kondo lattice model. Phys. Rev. B 2005, 71, 214415. [Google Scholar] [CrossRef]
- She, J.-H.; Bishop, A.R. RKKY Interaction and Intrinsic Frustration in Non-Fermi-Liquid Metals. Phys. Rev. Lett. 2013, 111, 017001. [Google Scholar] [CrossRef]
- Phillips, J.C.; Saxena, A.; Bishop, A.R. Pseudogaphs, dopants, and strong disorder in cuprate high-temperature superconductors. Rep. Prog. Phys. 2003, 66, 2111–2182. [Google Scholar] [CrossRef]
- Chakravarty, S.; Almutairi, B.S.; Chbeir, R.; Chakraborty, S.; Bauchy, M.; Micoulaut, M.; Boolchand, P. Progress, Challenges, and Rewards in Probing Melt Dynamics, Configurational Entropy Change, and Topological Phases of Group V- and Group IV-Based Multicomponent Sulfide Glasses. Phys. Status Solidi B 2020, 2000116. [Google Scholar] [CrossRef]
- Stojković, B.P.; Yu, Z.G.; Chernyshev, A.L.; Bishop, A.R.; Castro Neto, A.H.; Grønbech-Jensen, N. Charge ordering and long-range interactions in layered transition metal oxides: A quasiclassical continuum study. Phys. Rev. B 2000, 62, 4353–4369. [Google Scholar] [CrossRef]
- Olson Reichhardt, C.J.; Reichhardt, C.; Bishop, A.R. Fibrillar Templates and Soft Phases in Systems with Short-Range Dipolar and Long-Range Interactions. Phys. Rev. Lett. 2004, 92, 016801. [Google Scholar] [CrossRef]
- Olson Reichhardt, C.J.; Reichhardt, C.; Bishop, A.R. Structural transitions, melting, and intermediate phases for stripe- and clump-forming systems. Phys. Rev. E 2010, 82, 041502. [Google Scholar] [CrossRef]
- Reichhardt, C.; Olson Reichhardt, C.J.; Bishop, A.R. Noise and hysteresis in charged stripe, checkerboard, and clump forming systems. In SPIE Proceedings Vol. 6600, Proceedings of the SPIE 6600, Noise and Fluctuations in Circuits, Devices, and Materials, Florence, Italy, 20–24 May 2007; Macuci, M., Vandamme, L.K.J., Ciofi, C., Weissman, M.B., Eds.; SPIE: Bellingham, WA, USA, 2007; p. 66001B. [Google Scholar]
- Reichhardt, C.; Olson Reichhardt, C.J.; Bishop, A.R. Commensurate and incommensurate checkerboard charge ordered states. Physica C 2007, 460–462, 1178–1179. [Google Scholar] [CrossRef]
- Barré, J.; Bishop, A.R.; Lookman, T.; Saxena, A. Random bond models of the intermediate phase in network forming glasses. In Rigidity and Boolchand Intermediate Phases in Nanomaterials; Micolaut, M., Popescu, M., Eds.; INOE Publishing House: Bucharest, Romania, 2009; Volume 3, pp. 105–128. [Google Scholar]
- Frauenfelder, H.; Bishop, A.R.; Garcia, A.; Perelson, A.; Schuster, P.; Sherrington, D.; Swart, P.J. (Eds.) Landscape Paradigms in Physics and Biology; North-Holland: Amsterdam, The Netherlands, 1997. [Google Scholar]
- She, J.-H.; Fransson, J.; Bishop, A.R.; Balatsky, A.V. Inelastic Electron Tunneling Spectroscopy for Topological Insulators. Phys. Rev. Lett. 2013, 110, 026802. [Google Scholar] [CrossRef] [PubMed]
- Haraldsen, J.T.; Wölfle, P.; Balatsky, A.V. Understanding the electric-field enhancement of the superconducting transition temperature for complex oxide interfaces. Phys. Rev. B 2012, 85, 134501. [Google Scholar] [CrossRef]
- Salje, E.K.H. Multiferroic domain boundaries as active memory devices: Trajectories towards domain boundary engineering. Chem. Phys. Chem. 2010, 11, 940–950. [Google Scholar] [CrossRef] [PubMed]
- Conradson, S.D.; Geballe, T.H.; Jin, C.; Cao, L.; Baldinozzi, G.; Jiang, J.M.; Latimer, M.J.; Mueller, O. Local structure of Sr2CuO3.3, a 95 K cuprate superconductor without CuO2 planes. Proc. Natl. Acad. Sci. USA 2020, 117, 4565–4570. [Google Scholar] [CrossRef] [PubMed]
- Barzykin, V.; Gor’kov, L.P. Inhomogeneous stripe phase revisited for surface suoerconductivity. Phys. Rev. Lett. 2002, 89, 227002. [Google Scholar] [CrossRef]
- Agrestini, S.; Saini, N.L.; Bianconi, G.; Bianconi, A. The strain of CuO2 lattice: The second variable for the phase diagram of cuprate perovskites. J. Phys. A Math. Gen. 2003, 36, 9133. [Google Scholar] [CrossRef]
- Eroles, J.; Ortiz, G.; Balatsky, A.V.; Bishop, A.R. Inhomogeneity-induced superconductivity? Europhys. Lett. 2000, 50, 540–546. [Google Scholar] [CrossRef][Green Version]
- Mazumdar, S. Valence transition model of the pseudogap, charge order, and superconductivity in electron-doped and hole-doped copper oxides. Phys. Rev. B 2018, 98, 205153. [Google Scholar] [CrossRef]
- Bishop, A.R.; Martin, R.L.; Müller, K.A.; Tesanovic, Z. Superconductivity in oxides: Toward a unified picture. Z. Phys. B 1989, 76, 17. [Google Scholar] [CrossRef]
- Shenoy, S.R.; Subrahmanyam, V.; Bishop, A.R. Quantum paraelectric model for layered superconductor. Phys. Rev. Lett. 1997, 79, 4657. [Google Scholar] [CrossRef]
- Phillips, J.C. Ted Geballe and HTSC. J. Supercond. Nov. Mag. 2020, 33, 11–13. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).