Meetings with a Remarkable Man, Alex Müller—The Professor of SrTiO3

After my bachelor degree in chemistry with physics and mathematics (in Dutch kandidaatsexamen) at the University of Amsterdam, I chose to study for my master degree (in Dutch doctoraal) a physical chemistry direction. At the laboratory of physical chemistry, I met Ad Lagendijk (later full Professor and Spinoza laureate), who studied with the help of ESR (electron spin resonance) impurities in SrTiO₃. Together with Jan Mooij, I did research in hexaurea perchlorate, especially the 300 K phase transition. My master thesis was a theoretical study about the 105 K phase transition in SrTiO₃. In this way, I became familiar with the work of Professor K. Alex Müller (KAM), especially the structural phase transition. In 1975, I started a PhD research in SrTiO₃ in the group of Professor Max Glasbeek. In the same building, Professor Laurens Jansen (writer of a well-known book about group theory) [1] was working. He was the head of the theoretical chemistry department. Jansen had worked at the Batelle institute (Geneva-Switzerland), which is the same institute where KAM had worked. The PhD thesis of KAM (in German, English translation can be found in Reference [2] was a study of Fe-doped SrTiO₃, especially Fe³⁺ [3]. Prof. Jansen suggested that I contact KAM, and so I did. In the summer of 1976, during my vacation in Italy and Switzerland, I had a break in Rüschlikon near Zürich, the IBM research center, where I met KAM. It was a special meeting. I remember talking about my ESR study of an axial Fe⁵⁺ center in SrTiO₃, telling KAM that I did not know how to explain the rotation angle of this center below the 105K structural phase transition. The rotation angle is different and larger than the intrinsic one. After a few minutes in pin-drop silence, KAM found the solution (see also the first research article below). KAM invited me to do further experiments at the K-band spectrometer at IBM, which I did. There, I met the late Walter Berlinger and performed together with him measurements with Swiss precision. In 1976, KAM visited Amsterdam, giving lectures, and we had discussions about the research we did. We had a wonderful time visiting the Dutch beach, and we also went to classical concerts in Amsterdam. A college of mine, Henk de Jong, studied the SrTiO₃ Cr⁵⁺ center. Lagendijk had the opinion that it was an off-center system [4], but de Jong had the opinion that it was a tetragonal Jahn–Teller system [5]. He also found another Cr⁵⁺ center and attributed this center to another Jahn–Teller (JT) system, orthorhombic [6]. I had hesitations (see also the second research article below). One evening at a restaurant, I discussed this with KAM, and we found the solution to this second center: it must be an off-center system. He advised me to publish this later after writing my thesis, and so it happened [7]. At that time, KAM was writing a part of a publication about the central peak found in SrTiO₃.

Due to personal circumstances, it took a while to write my PhD thesis [8]. Alex was enthusiastic about the thesis, which was completely dedicated to impurity systems in SrTiO₃. At a summer holiday in Switzerland, meeting him in his house in the eastern part at Laax-Salums, we decided to write about the SrTiO₃ orthorhombic off-center system [7]. He also asked me to translate his thesis from German into English, which I did together with Charlotte Bolliger from the IBM laboratory. The purpose was the publication of a book with the research work of KAM before the Nobel prize and some later work. After a considerable time, Alex invited me to help him to write and edit the book and finish it. In the summer of 2008 and 2009, we were writing the book “Properties of perovskites and other oxides [2]”, which was published by World Scientific in 2010. The book contained also work of mine performed in Amsterdam and Osnabrück. The research in Osnabrück was with the late Prof. Ortwin Schirmer, who had worked at the IBM research laboratory before. This research was mainly about impurities in BaTiO₃ and explained bosonic bi-polaron behavior, which is important in the cuprate superconductors.

The discussions with Alex were not only about physics but contained a broad spectrum of mutual interest. One of his topics was the number five (in German, Zahl fünf), see reference [9].

In the following part, I will discuss some research in SrTiO₃.

The first article is about the 105 K structural phase transition. In this article, the rotation angle of the non-cubic Fe⁵⁺ is explained as mentioned above [10].

The second article is about the tetragonal off-center Cr⁵⁺ [11].

1. SrTiO₃ with the Non-Cubic Fe⁵⁺ as Local Probe and a Reinterpretation of Other Fe⁵⁺ Centers

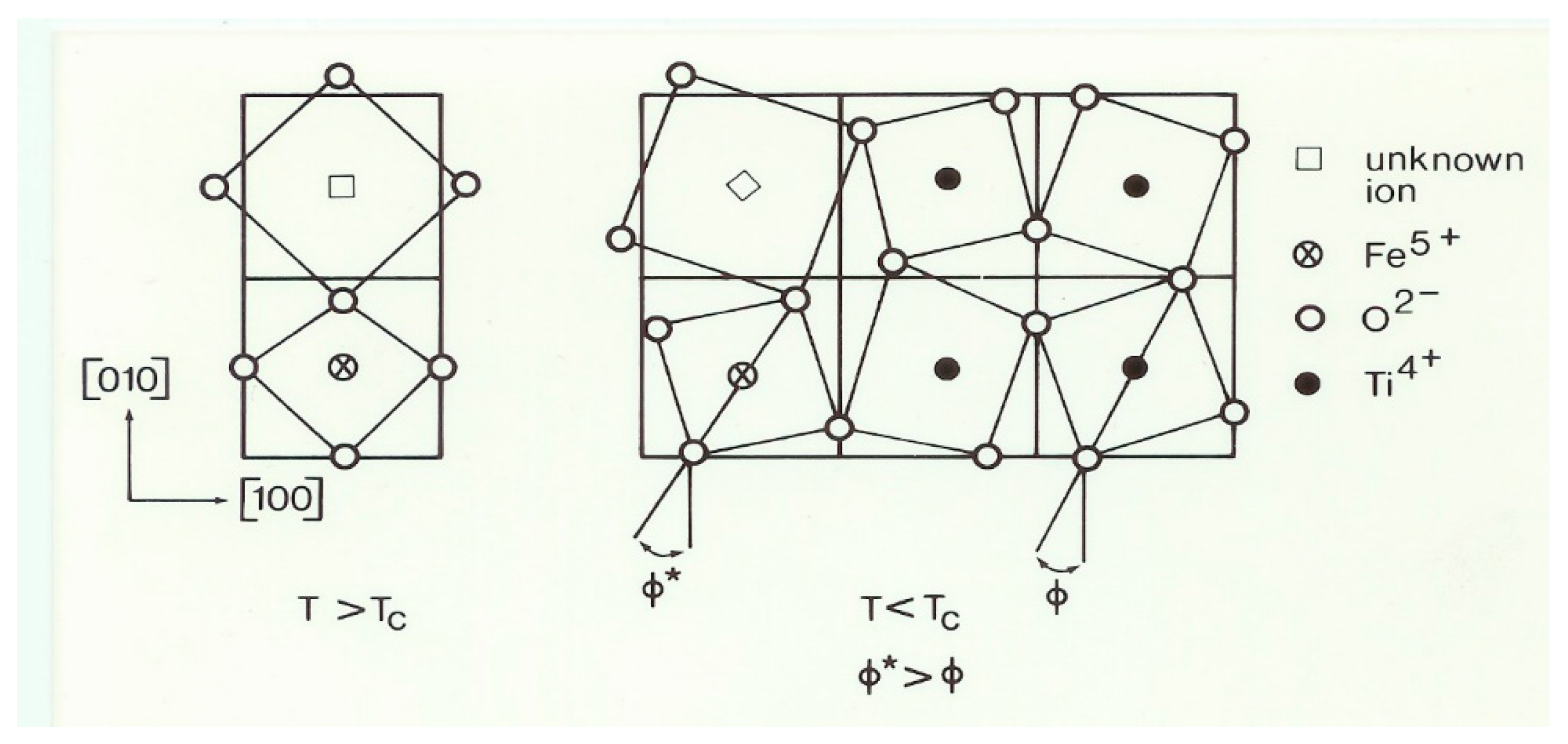
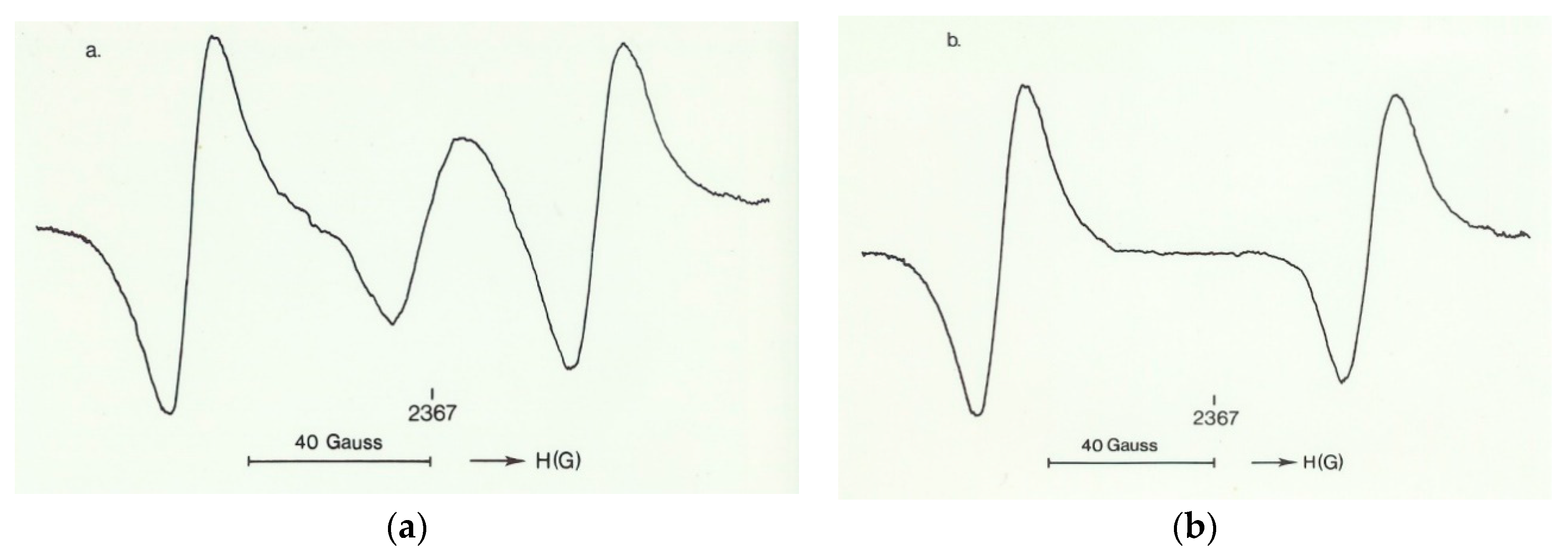
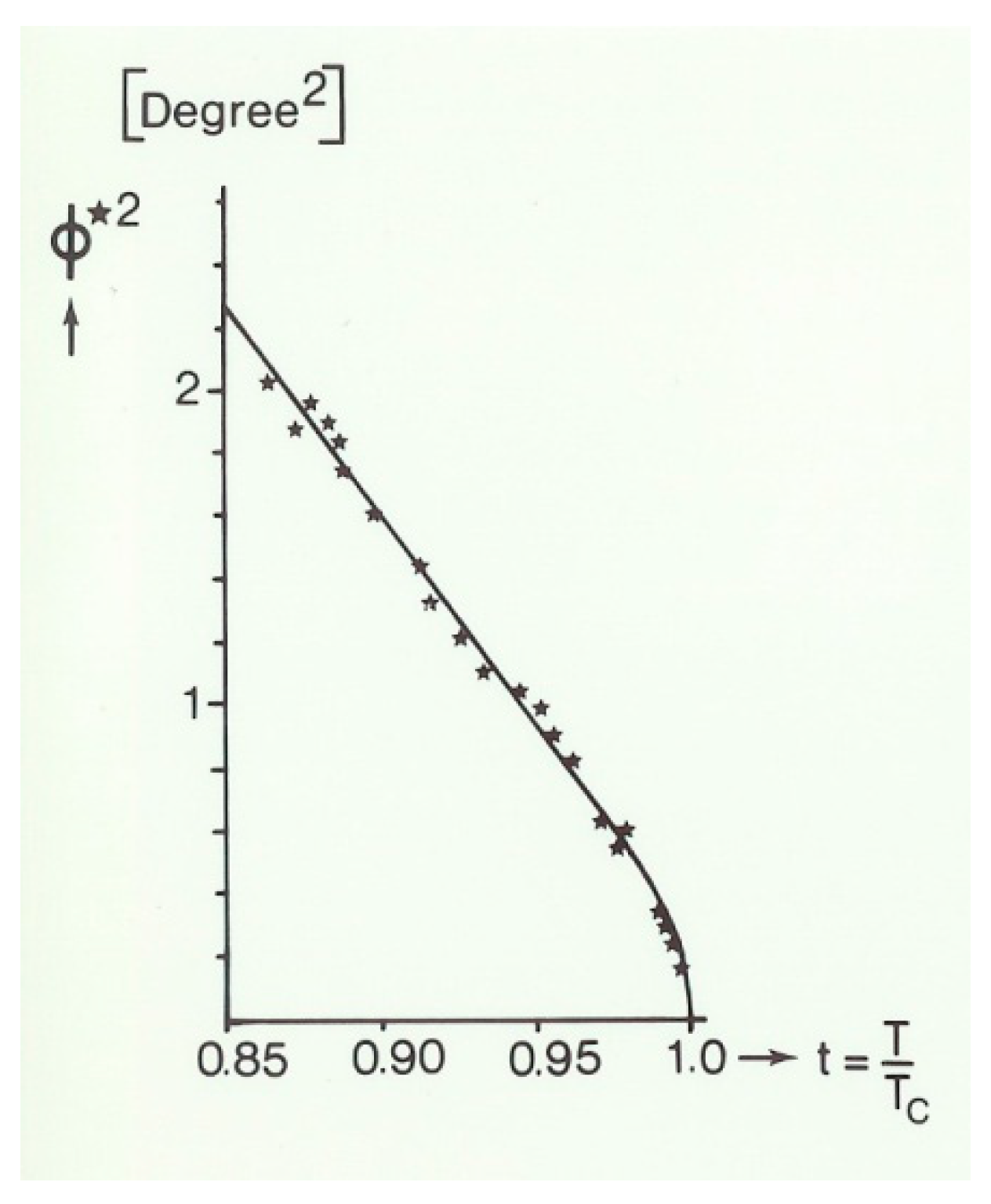
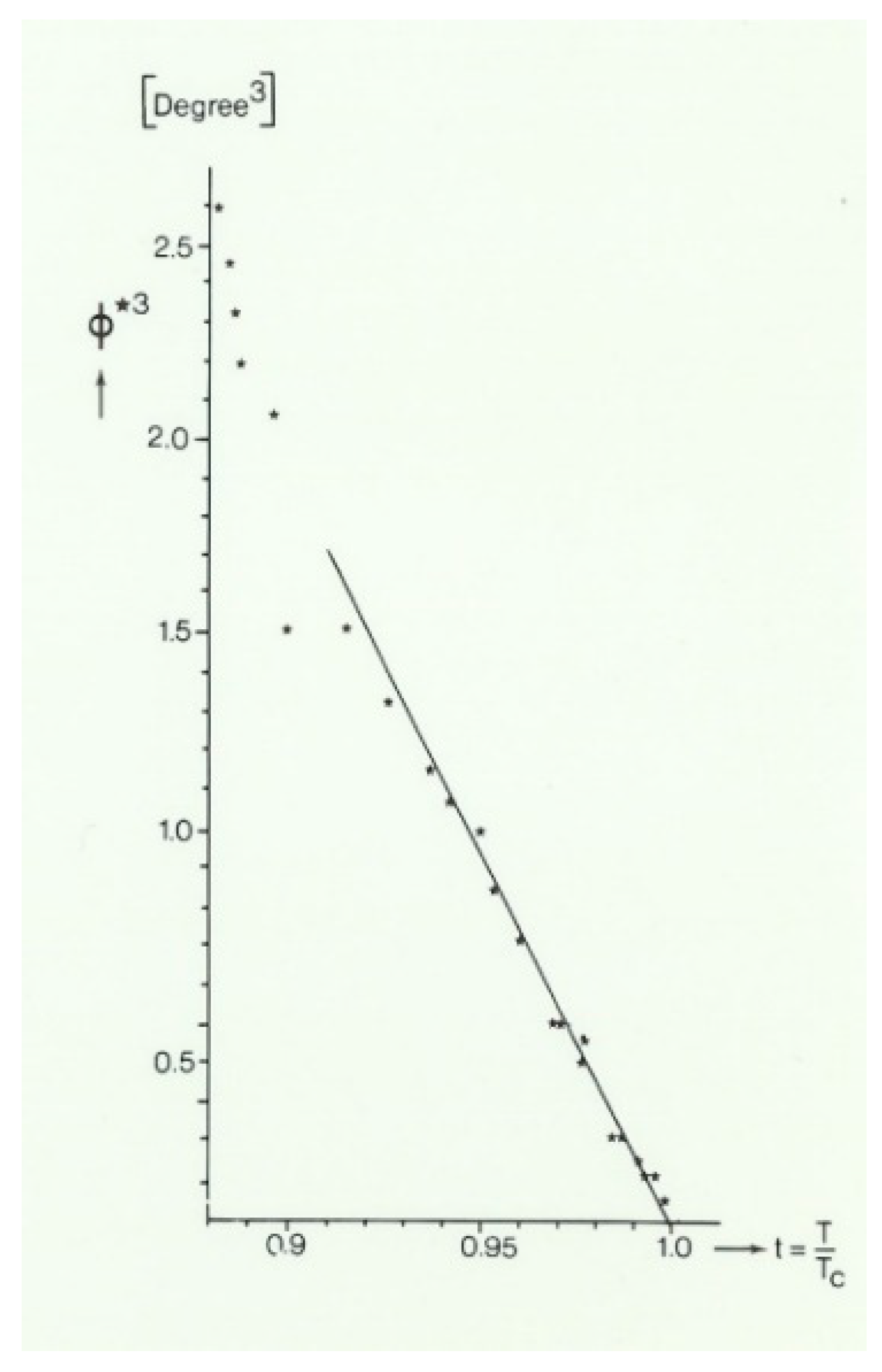
The 105 K second-order displacive phase transition of SrTiO₃ (ST) has been studied with the help of Electron Paramagnetic Resonance. The photochromic non-cubic Fe⁵⁺ center is used as local probe. Critical phenomena, characterized by an exponent β = 1/3, are presented. Line broadening effects are interpreted as stemming from time-dependent fluctuations near the phase transition point. The data are consistent with those reported earlier on the Fe³⁺-V_O pair center, indicating cooperative effects in the crystal. In addition, a model for the non-cubic Fe⁵⁺ is proposed, i.e., the ion is substitutional for Ti⁴⁺ with an empty adjacent expanded octahedron. Other Fe⁵⁺ centers in ST and BaTiO₃ (BT) are reviewed and reinterpreted.

1.1. Introduction

Displacive phase transitions were analyzed almost four decades ago with the help of classical theories such as the Landau theory [12] or with microscopic theories using the mean field approximation [13]. More specifically, a typical temperature behavior is predicted for the generalized susceptibility χ, the order parameter and the specific heat c_p of the form (−ε)^x, where ε = (T − T_c)/T_c. Values for the exponent x are:

• x = β = ½ for the order parameter,
• x = γ = −1 for the susceptibility, and
• x = 0 for the specific heat, indicating a jump at T_c, where T_c is the critical temperature of the phase transition.

Although classical theories are adequate for temperatures well outside the phase transition point, deviations or critical behavior from these theories occur near T_c. These phenomena arise from correlated fluctuations of the order parameter and become important when the length of the correlated fluctuations exceeds the range of forces. An explanation of these effects and the Electron Spin Resonance (ESR) technique used is reviewed by K. Alex Müller and J.C. Fayet [14]. This article can also be found in Chapter VII of the book: Properties of Perovskites and other oxides by K. Alex Müller and Tom W. Kool [2].

Experimentally, the critical behavior of ST near the 105 K phase transition was verified by means of the Fe³⁺ and Fe³⁺-V_O impurity centers [15]; both are substitutional for Ti⁴⁺. In this paper, we present EPR results of the 105 K second-order displacive phase transition in ST, where the non-cubic photochromic Fe⁵⁺ is used as local probe. This impurity center is a d³(S = 3/2) system, substituting for Ti⁴⁺ and is octahedrally surrounded by a cage of oxygen ions in the presence of a moderate axial field for T > T_c. For T < T_c, a weak orthorhombic perturbation due to the phase transition is added. This center has been analyzed before by Kool et al. [16].

The study of phase transitions by means of ESR and the use of different impurities situated at the same site provide more evidence of the cooperative behavior in the crystal. The non-cubic Fe⁵⁺ center in ST is adequate because of the large anisotropy of the resonance lines, ranging from g ≈ 2–4 and the very accurate measurements of the rotational order parameter φ(T).

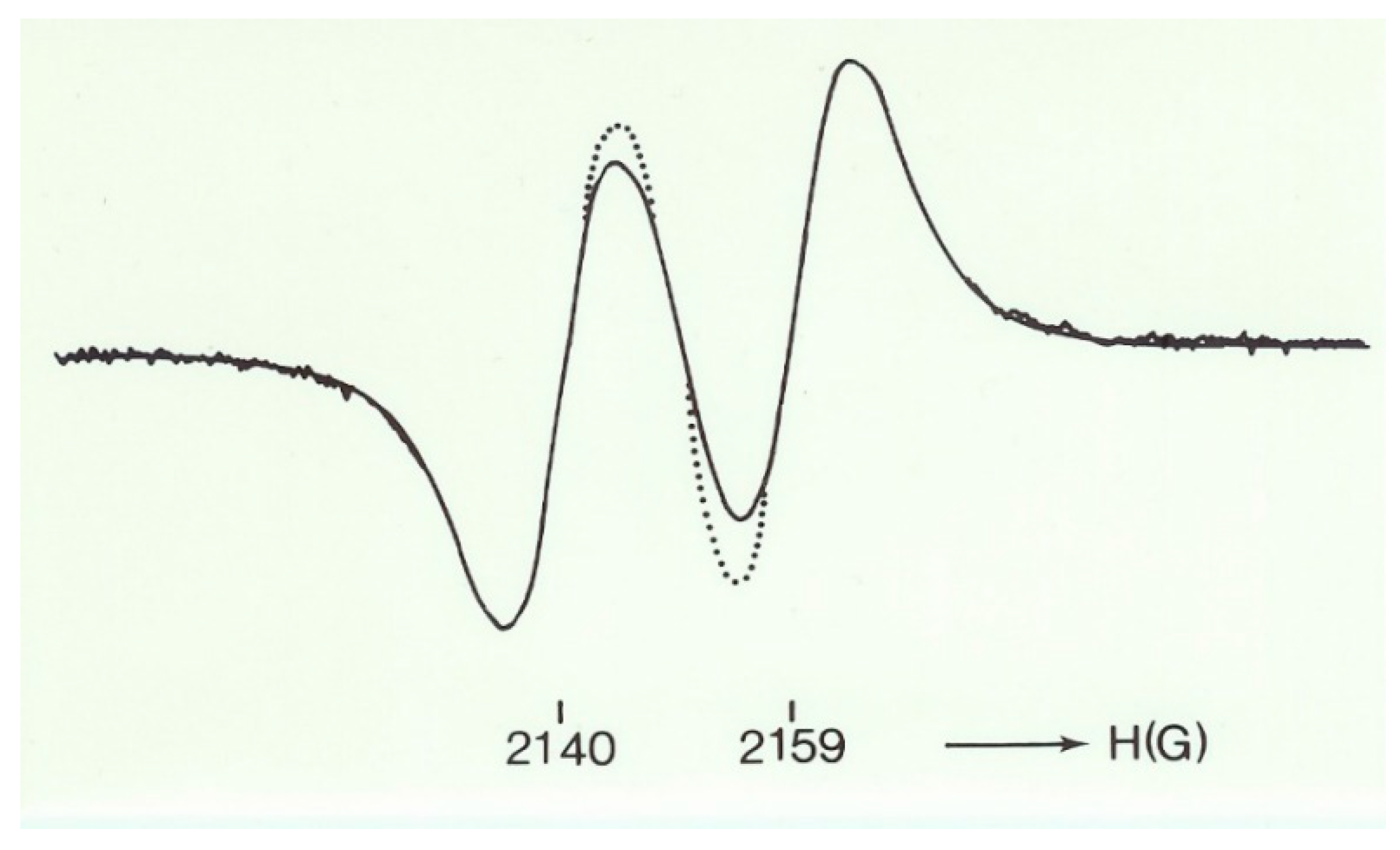
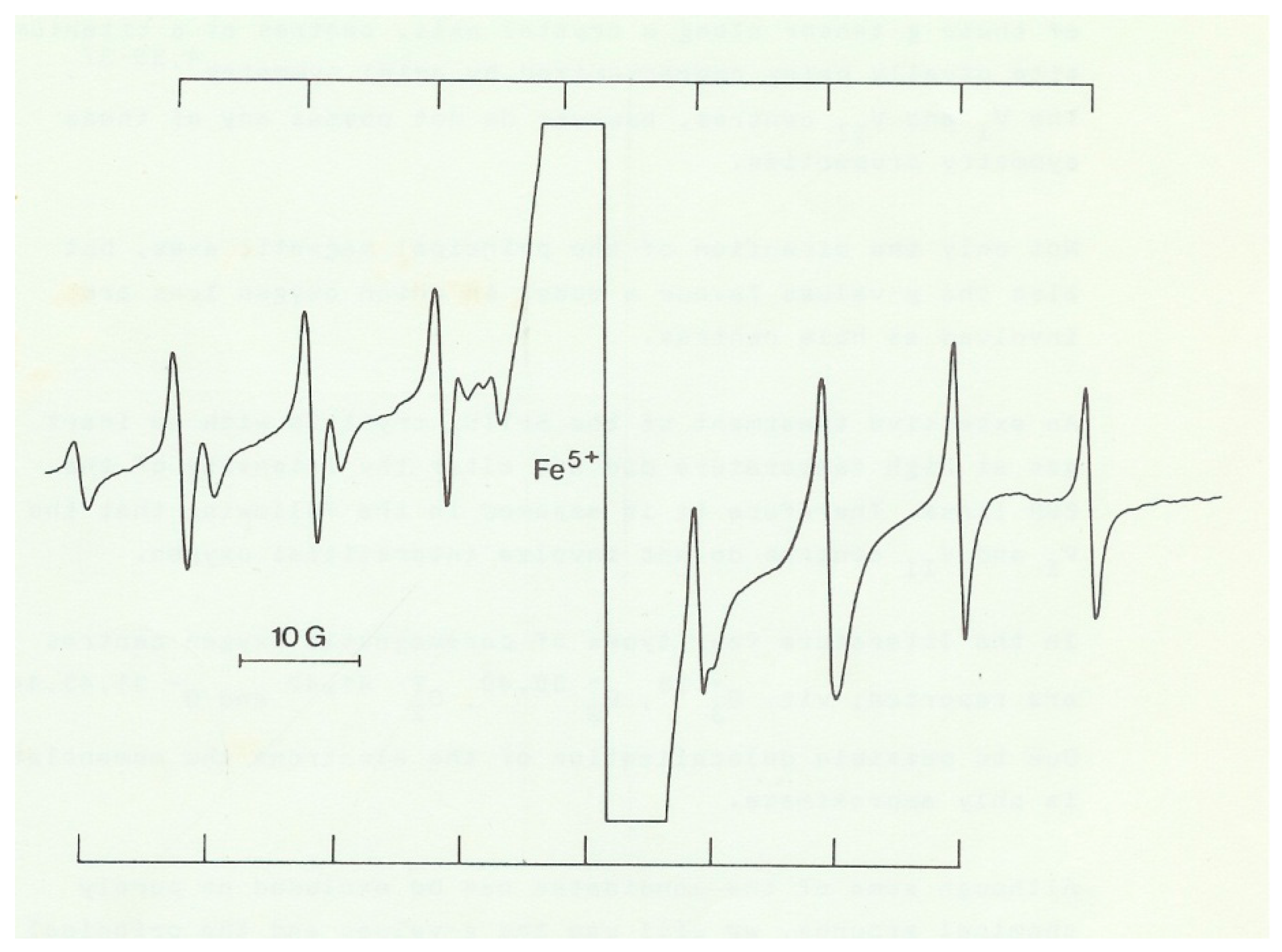
1.2. The Non-Cubic Fe⁵⁺ Centre

For axially distorted (tetragonal or trigonal) octahedrally surrounded d³ spin systems, the following spin-Hamiltonian is used [17,18,19,20]:

$$\mathscr{H}=S·\overline{D }·S+{\mu }_{B}H·\overline{g}·S.$$

(1)

The first term represents the zero-field splitting and the latter represents the Zeeman interaction. For systems with |D|»hv, with v the frequency of a typical ESR experiment, the first term is taken as zero-order Hamiltonian ${\mathscr{H}}_0$, and the Zeeman splitting is treated as a perturbation ${\mathscr{H}}_1$. For values hv/|2D| ≥ 0.25, one has to proceed with exact numerical computer calculations [21]. If the zero-field splitting $\left|2D\right|$ is much larger than the Zeeman term, only one ESR transition within the Kramers doublet with M_S = |±1/2〉 levels is observed, giving a typical g^eff ESR spectrum for S = 3/2 systems ranging from g^eff ≈ 2 to 4. The ESR spectrum of the non-cubic Fe⁵⁺ center shows these lines, too [16]. The non-cubic Fe⁵⁺ center has the following g and D values: $g_{\parallel }$ = 2.0132, $g_{\perp }$ = 2.0116, and |2D| = 0.541 cm⁻¹ at 115 K [2,16]. From depopulation measurements at helium temperatures, it could be concluded that the sign of D is negative.

Below the phase transition (T < T_c), an extra weak orthorhombic perturbation in the spin-Hamiltonian has to be added:

$$E\left(S_x^2-S_y^2\right).$$

(2)

For $\left|D\right|\ge h\nu$ and $\left|E\right|\le h\nu$, general angular expressions for d³ (S = 3/2) systems were derived [22].

At 77 K, well below T_c, |2D| = 0.551 cm⁻¹ and |E| = 0.529 × 10⁻³ cm⁻¹, indicating that D is a little temperature dependent. The rhombic parameter E is temperature dependent and is proportional to φ², with φ the intrinsic rotation angle of ST consisting of alternating rotations of neighboring oxygen octahedra below T_c [14,16].

The rotation angle φ* of the non-cubic Fe⁵⁺ is larger than the intrinsic one φ. The relative large value for φ* is interpreted as follows. As can been seen in Figure 1, the octahedron adjacent to the Fe⁵⁺ ion has been expanded. As a consequence of this expansion, the rotation angle φ* becomes larger.

This expansion can be caused by a Ti⁴⁺ vacancy or a nearby impurity substitutional for the Ti⁴⁺ ion. Simple calculations at 77 K showed that with the given intrinsic angle φ = 1.53° and φ* = 1.75° of the non-cubic Fe⁵⁺ and the distance of the lattice constant (above T_c) a = 3.9 Å, the expansion must be equal to 0.30 Å. Then, it follows that the unknown ion possesses a radius r = 0.94 Å, knowing that r(Ti⁴⁺) = 0.64 Å [23].

The impurity concentration (in ppm) in the investigated crystal obtained by spectrochemical analyses is as follows (see the

Table 1. Impurity concentration.

Fe 18	B < 10
Mo 2	Si 500–2000
Pb 500–1000	Ni 10–50
Sn 200–1000	Al < 10

Impurity concentration in ppm.

).

None of the above-mentioned impurities and their respective ions fit into the expanded cage [23]. In addition, Ti²⁺, with r(Ti²⁺) = 0.80 Å, and Sr²⁺, with r(Sr²⁺) = 1.27 Å, do not fit. Therefore, we assume that the expansion is due to a neighboring Ti⁴⁺ vacancy and is caused by the repulsion of the O²⁻ ions.

1.3. Critical Effects

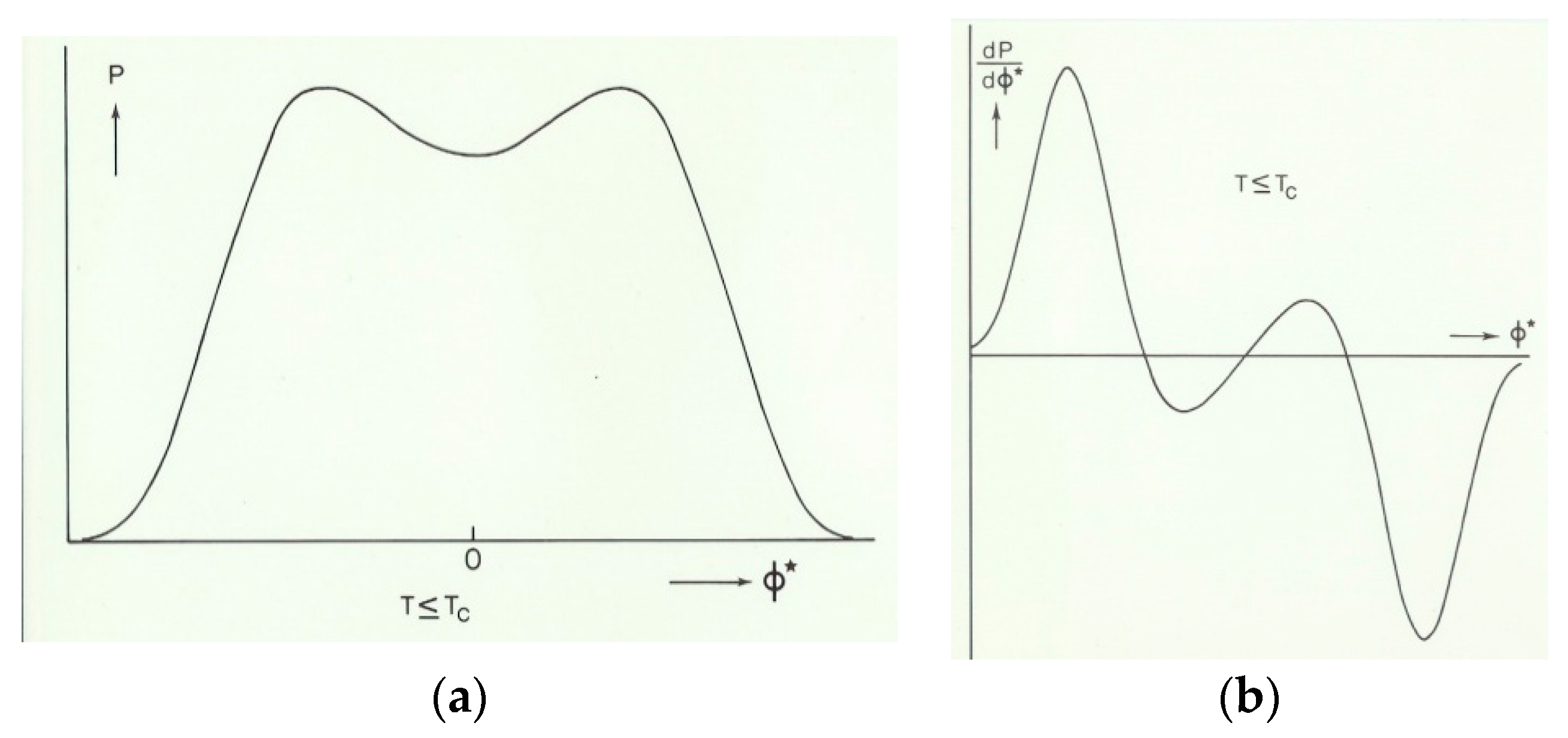
1.3.1. Static Critical Exponents

The order parameter (with critical exponent β) corresponds to the displacement parameter, which in ST is represented by the rotation angle φ. The shaping of the crystals was such that after rapid cooling, the crystals became monodomain below the structural phase transition (Figure 2). In monodomain crystals, only the ±φ* lines are present [24].

In a monodomain crystal, the rotation angle φ* can be used for the study of static critical exponents and will not be disturbed by extra ESR lines stemming from different domains. In the temperature range 30 K < T < 85 K, this rotation angle was found to be linearly proportional to the intrinsic one. The classical Landau behavior with β = 1/2 was obtained by plotting φ^*1/β = φ^*2 as a function of the reduced temperature t = T/T_c. For 0.7 < t < 0.9, we found a straight line following a Landau behavior. At t = 0.9, the bending down from a straight line becomes noticeable (Figure 3).

It is found that for 0.9 < t < 1, β = 1/3, i.e., in this temperature region, the crystal displays critical behavior. In Figure 4, φ^*1/β = φ^*3 is plotted as a function of t. Extrapolation of the plot to φ^*3 = 0 yields the phase transition temperature T_c = 103 K, which in our sample is lower than the usual value of 105 K. This is due to the presence of impurities, which can alter the phase transition temperature.

1.3.2. Asymmetric Line Shapes for T→$T_c^{-}$

Time-dependent fluctuations and line-broadening effects for the non-cubic Fe⁵⁺ have been published before by Kool et al. [2,16]. In addition, asymmetric line shapes in the critical region were found [2,25,26]. In a monodomain crystal ST, with the magnetic field H||[110] and the elongated axis of the crystal c||[001], we found outside the critical region (T«T_c) a symmetric Lorenzian line shape for each of the ±φ* lines at g^eff ≈ 3.4 On approaching T_c, the lines have at T = T_c − 0.8 K an asymmetric line shape (Figure 5).

The asymmetry is apparent from a comparison of the observed line shape with that of a simulated symmetric line shape. The dotted curve is simulated for a best fit symmetrical line composed of a mixture of 50% Gaussian line shape and a 50% Lorenzian line shape. The discrepancy in the amplitudes of the experimental and simulated curves is a measure of the asymmetry in the experimental line shape. At T_c, the fluctuations of the oxygen octahedra become very slow compared to the ESR measuring time. This means that the local rotation of each non-cubic Fe⁵⁺ center is seen at rest in the ESR experiment. At T_c, the EPR lines reflect the Gaussian line shape in the case of statistical independence. The origin of the asymmetry is related to the form of the probability distribution for φ* near T_c in the slow motion limit. Close to T_c, the classical probability distribution P(φ*) of the ensemble P(φ*,T) = c(T)exp(−ΔF(T)), where ΔF(T) is the free energy depending on the order parameter. In the Landau theory, ΔF is given by A(T)φ^*2 + Bφ^*4, where A(T) = a(T − T_c). P(φ*,T) is a double-peaked function for T < T_c (Figure 6a).

The spread in the value that φ* may adopt, of course, gives rise to an inhomogeneous broadening (spread in g^eff) of the ESR lines. In Figure 6b, it is sketched how the ESR line shape is affected by the distribution function. Additional homogeneous broadening effects result in the observed asymmetrical shaped ESR lines. All the results obtained here are similar to those obtained for the Fe³⁺-V_O center, reflecting cooperative bulk behavior of the crystal near the 105 K phase transition [15,16].

1.4. Different Fe⁵⁺ Centers

Different Fe⁵⁺ centers have been found in ST as well as in BaTiO₃ (BT). In ST:Fe⁵⁺, (g_isotropic = 2.013); only the −½↔+½ transition could be observed, even at helium temperatures [27]. The ±3/2↔±1/2 transitions are not observable due to a distribution of strain in the crystal leading to fine structure broadening. As a result of the smaller radius of this center in comparison with that of Ti⁴⁺, the ion must be off-centered in one of the <100> directions. In contrast to this, the Fe⁵⁺ center in BT goes off-centered along one of the <111> directions [28]. In previous unpublished ESR investigations of ST, a vanadium center was found, which was attributed to a V⁵⁺-O⁻ hole-like center (Figure 7) [29]. It is a tetragonal S = ½, I = 7/2 light-sensitive center with g_|| = 2.017, $g_{\perp }$ = 2.012, and A_|| = 10.3 × 10⁻⁴ cm⁻¹, $A_{\perp }$ = 9.9 × 10⁻⁴ cm⁻¹.

The interpretation of this center was largely based on arguments used for a similar center in ST, i.e., the Al³⁺-O⁻ hole center [30]. In both centers, the mean g-value is larger than the free electron one, and the hyperfine interaction is relatively small, indicating that the hole is not localized on the central ion. For instance, the localized electron in the V⁴⁺ (d¹) Jahn–Teller center in ST has much larger hyperfine values of A_|| = 147 × 10⁻⁴ cm⁻¹ and A_⊥ = 44 × 10⁻⁴ cm⁻¹ [31]. However, Schirmer et al. found a new Al³⁺-O⁻ hole center in ST with a different local symmetry [32]. Therefore, they reinterpreted the formerly found hole center to be an Fe⁵⁺-O²-Al³⁺ center, where the Al³⁺ is located in the neighboring oxygen octahedron substitutional for a Ti⁴⁺ ion. The average g-value of this center, g_av = ⅓(g_|| + 2g_⊥) = 2.013, is the same as the isotropic g-value found for the Fe⁵⁺ in ST [2,27,32]. New ESR experiments revealed that by applying [011] uniaxial stress, no change in the ESR line intensity took place, indicating that no reorientation of the axes of this center occurs [33]. In addition, also the vanadium hole center could not be reoriented by applying uniaxial [011] stress [33]. Former stress studies showed that under the influence of uniaxial externally applied stress, the hole-like centers Fe²⁺-O⁻ in ST [34] and Na⁺-O⁻ in BT [35] could be reoriented. Therefore, we ascribe this vanadium hole center to an Fe⁵⁺-O²⁻-V⁵⁺ association with a similar structure as the Fe⁵⁺-O²⁻-Al³⁺ center. The g_av = ⅓(g_|| + 2g_⊥) = 2.0137 is equal to that of the Fe⁵⁺ center in ST [2,27,32].

All the discussed iron impurity centers are non-centro symmetric systems in contrast to, for instance, the ST:Mo³⁺ [36] and ST:Cr³⁺ [2] centers with Mo³⁺ and Cr³⁺ sitting on center.

1.5. Conclusions

The non-cubic Fe⁵⁺ center in ST shows the same behavior in the vicinity of the 105 K structural phase transition as the Fe³⁺-V_O and Fe³⁺ centers, indicating cooperative effects in the ST crystal. Furthermore, the non-cubic Fe⁵⁺ is probably an Fe⁵⁺-O²⁻-V_Ti center with an expanded adjacent oxygen octahedron due to a Ti⁴⁺ vacancy. New stress experiments confirmed that the hole center Al³⁺-O^- must be an Fe⁵⁺-O²⁻-Al³⁺ center, and a previous found vanadium hole center is now attributed to an Fe⁵⁺-O²⁻-V⁵⁺ association.

2. The Tetragonal Elastic Dipole Cr⁵⁺ in SrTiO₃

We reinvestigate the tetragonal Cr⁵⁺ impurity center in single crystals of the perovskite ST. After careful analyses, we came to the conclusion that this center is an off-center system and is not a Jahn–Teller impurity system. From previous stress experiments in ESR, we calculated the linear stress coupling tensor as β = 3.56 × 10⁻³⁰ m³; which is in agreement with other stress coupling tensors of off-center systems in ST as well as BT.

The research of the Cr⁵⁺ impurity center in ST started with ESR experiments performed by Lagendijk [4]. He concluded that the Cr⁵⁺ (d¹) ion is substituted for Ti⁴⁺ sitting off-centered along one of the <100> directions. It was a logical conclusion, because the ion radius of tetragonal Cr⁵⁺ in octahedral symmetry (0.54 Å) is considerably smaller than that of the Ti⁴⁺ (0.64 Å) [23]. Furthermore, the experiments performed at 77 K revealed a rotation of the oxygen octahedral of 1.6°, which is larger than one measured by on-center impurities, i.e., 1.53 [2], indicating a shift of the center from the on-center position. The Cr⁵⁺ center in ST has also been measured by Müller and Berlinger [37].

Later, de Jong et al. performed uniaxial stress experiments on the system [5] with the help of specialized stress equipment [38]. The intensity changes under stress P showed that centers with their tetragonal axes along the stress direction were favorable to centers with their tetragonal axes perpendicular to the stress direction. Therefore, they concluded that the system is a strong Jahn–Teller (JT) ion (T_2g × e_g) with a squeezed oxygen octahedron. The research went on with static electric field experiments (E) [39]. Surprisingly, there was an increase of the ESR line intensities due to centers with their main center axes perpendicular to the E-field at the cost of those centers with main axes parallel to E. Since there was a quadratic change of the line intensities with E, they concluded that tetragonal Cr⁵⁺ is a JT ion in ST.

We make the following objections against their conclusions. First of all, by applying a static electric field, one expects that the centers parallel to E increase in intensities. This was shown for the impurity center ion V⁴⁺ (d¹) in ST [40]. V⁴⁺ has the same ion radius as the Ti⁴⁺ that it replaces, so it must be an on-center system, and therefore it must be a JT ion. In this system, the tetragonal axis of the system is directed along the applied E-field in contrast with that of Cr⁵⁺. In addition there is an E² dependence. The experiments of de Jong et al. can be explained by assuming that the observed quadratic change in intensities is due to a large electro-strictive coupling and must be a P² dependence. So, their interpretation that the ST:Cr⁵⁺ system is a JT system is in our opinion not right, and the interpretation of Lagendijk is the right one.

In the following part, we give more evidence in favor of the off-center system of tetragonal Cr⁵⁺. In a later study, Koopmans et al. studied the orthorhombic Cr⁵⁺ ion in ST. They concluded that this orthorhombic system is a T_2g × (e_g+t_2g) JT system [6,41]. However, Müller, Blazey and Kool concluded that the center must be an-off center system that is off-centered in one of the <110> directions and tetrahedrally surrounded by four O²⁻ ions [7]. The assignment was based on the g-values of the ion, which was almost the same as in other Cr⁵⁺ systems. In addition, the ionic radius of the ion (0.34 Å) is considerably smaller than that of Ti⁴⁺, which it replaces [23]. Moreover, the local rotation of the octahedra is different from that of the intrinsic one, 1.6° versus 2.0° at 4.2 K. The value of this last rotation we also found for the V⁴⁺ octahedron at 4.2 K [31]. The off-center assignment was confirmed by static electric field experiments in ESR [42]. From these measurements, an electric dipole of µ = 2.88 × 10⁻³⁰ Cm and an off-center displacement of about 0.2 Å was determined [43]. In ST, only one type of V⁴⁺ ion was found in contrast with the two Cr⁵⁺ centers, which gives further support to the off-center model. The two different Cr⁵⁺ centres were also found in the perovskite BT [44].

From Figure 2 of the article of de Jong et al. [5], we were able to calculate the elastic dipole of tetragonal Cr⁵⁺ in ST. The concept of an elastic dipole can be found in an article by Nowick and Heller [45]. From the plot of ln(2_a/I_b) versus the stress P and assuming Boltzmann distribution, the elastic dipole moment β_[100] could be determined.

ln(2_a/I_b) = ΔU/kT, with ΔU = −V_oλ^(p) σ ≡ β∙σ, with λ^(p) = ½λ₁ − ½λ₂

This results in a value of β = 3.56 × 10⁻³⁰ m³.

This value is in agreement and in the order of magnitude of other off-center systems in ST and BT (see the

Table 2. Elastic dipole values in SrTiO3 and BaTiO3.

SrTiO3	β (10−30 m3)	Reference
Fe2+-O−	3.56	[34]
Cr5+ (orthorhombic)	4.19	[42]
Cr5+ (tetragonal–this study)	3.56
BaTiO3
Ni1+ (substituted for Ba2+)	3.8	[46]
Na+-O−	1.23	[35]
Fe5+	4.13	[28]

).

As a last remark, we would like to mention that we do not agree with the conclusion of Yu-Guang Yang et al [47]. First of all, they use for Cr⁵⁺ in octahedral surroundings an ionic radius of 0.63 Å and for the Ti⁴⁺ which it replaces an ionic radius of 0.745 Å. It is better to use the values that are given in Reference [23]. Therefore, the ionic radius of Cr⁵⁺ is much smaller than the intrinsic one 0.54 Å versus 0.64 Å, as mentioned before. Furthermore, they say in their discussion: “Upon cooling, only a continuously increasing resolution is observed, and no specific effects are found in ESR when passing the 105 K phase transition.” This is not true. Lagendijk et al. observed a splitting of the ESR lines due to the tetragonal domains of ST and inferred a rotation of the oxygen octahedra of 1.6° which, as already mentioned before, is different from the intrinsic one, indicating an off-center displacement.