Abstract
Bismuth has recently attracted interest in connection with Na-ion battery anodes due to its high volumetric capacity. It reacts with Na to form NaBi which is a prototypical Dirac semimetal with a nontrivial electronic structure. Density-functional-theory based first-principles calculations are playing a key role in understanding the fascinating electronic structure of NaBi and other topological materials. In particular, the strongly-constrained-and-appropriately-normed (SCAN) meta-generalized-gradient-approximation (meta-GGA) has shown significant improvement over the widely used generalized-gradient-approximation (GGA) scheme in capturing energetic, structural, and electronic properties of many classes of materials. Here, we discuss the electronic structure of NaBi within the SCAN framework and show that the resulting Fermi velocities and s-band shift around the point are in better agreement with experiments than the corresponding GGA predictions. SCAN yields a purely spin-orbit-coupling (SOC) driven Dirac semimetal state in NaBi in contrast with the earlier GGA results. Our analysis reveals the presence of a topological phase transition from the Dirac semimetal to a trivial band insulator phase in NaBiSb alloys as the strength of the SOC varies with Sb content, and gives insight into the role of the SOC in modulating conduction properties of NaBi.
1. Introduction
Since lithium is a nonrenewable resource [1], its widespread use in Li-ion batteries can be expected to lead to increasing costs of batteries in the coming years. This has motivated extensive research on Na-ion batteries [2,3] as an alternative to Li based batteries. However, since Na ions have a larger size and greater weight compared to Li ions, they diffuse with greater difficulty through common electrode materials. It is important therefore to develop electrode materials with a high reversible capacity and good conducting properties [4]. This effort can benefit from first-principles computations within the framework of the density functional theory (DFT) [5].
The generalized gradient approximation (GGA) has been extensively used for identifying many classes of topological materials [6,7,8,9] and their novel applications [10] including electrodes for Li-ion batteries [11]. The presence of symmetry-enforced Dirac states in a topological material can provide robust carriers for high electronic conductivity, which is an important factor for improved battery performance. Despite its success in predicting the first topological insulator [12], the Dirac semimetal [13], and the Weyl semimetal [14], the GGA suffers from fundamental shortcomings in describing the structural and electronic properties of materials. In this connection, recent advances in constructing new classes of exchange-correlation functionals show that the strongly-constrained-and-appropriately-normed (SCAN) [15] meta-GGA functional provides a systematic improvement over the GGA in diversely bonded materials. SCAN is the first meta-GGA that satisfies all of the 17 exact constraints that a meta-GGA can satisfy. SCAN has been shown to yield improved modeling of metal surfaces [16], 2D atomically thin-films beyond graphene [17], the noncollinear antiferromagnetic ground state of manganese [18], magnetic states of copper oxide superconductors [19,20,21], and cathode materials for Li ion batteries [22], among others materials.
Among the various anode materials, antimony was recently shown to be a good candidate for sodium-ion batteries with strong sodium cyclability [23,24] and a high theoretical capacity of 660 mAh/g corresponding to the NaSb phase. However, DFT calculations predict that NaSb is prone to being an insulator [25]. (The electronic conductivity of the anode could be activated, for example, by using carbon matrices [26]). NaBi, on the other hand, is a three-dimensional (3D) nontrivial Dirac semimetal [27], and a number of recent studies discuss NaBi as an anode material in sodium-ion batteries [28,29,30,31,32]. Huang et al. [32] identify a variety of different phases of NaBi such as NaBi, c-NaBi (cubic), and h-NaBi (hexagonal) as being involved in the sodiation process.
Notably, h-NaBi (henceforth NaBi, for simplicity) is a 3D analog of graphene. It hosts symmetry-protected, four-fold degenerate band-touching points or nodes in its bulk energy spectrum around which the energy dispersion is linear in all momentum space directions [33,34,35,36,37]. The aforementioned nodes or Dirac points are robust in the sense that they cannot be removed without breaking space-group symmetries. NaBi is a prototypical band inversion Dirac semimetal which was predicted theoretically before its Dirac semimetal character was verified experimentally [13,38,39,40,41,42]. The Dirac points in this material are protected by rotational symmetry and lie along the hexagonal z-axis. GGA-based studies indicate that the band inversion in NaBi is driven essentially by crystal-field effects and does not require the presence of spin-orbit-coupling (SOC) effects, although the SOC is responsible for opening up gaps in the energy spectrum everywhere except at the Dirac points. However, the GGA has well-known shortcomings in predicting sizes of bandgaps and crystal-field splittings, providing motivation for investigating the topological structure of NaBi using more advanced density functionals.
Here, we revisit the topological electronic structure of NaBi using the more accurate SCAN meta-GGA exchange-correlation functional and find that NaBi is a trivial band insulator in the absence of the SOC in contrast to the GGA results. In our case, inclusion of the SOC drives the system into the topological Dirac semimetal state. We show that SCAN yields the band energetics and Fermi velocities in substantial agreement with the available experimental results on NaBi. We also discuss a topological phase transition from the Dirac semimetal to a trivial band insulator phase in NaBiSb alloys with varying Sb content. Our results establish that NaBi is an SOC-driven topological semimetal like the common topological insulators such as Bi(Se, Te). Since bismuth nano-sheets have been shown to display structural stability and good conduction properties after sodiation/desodiation cycles in sodium-ion batteries [32], our results further indicate the promise of NaBi as an anode material.
The remainder of this paper is organized as follows. In Section 2, we describe computational details and discuss the crystal structure of NaBi. The SCAN-based topological electronic properties are discussed in Section 3. In Section 4, we consider the bulk and surface electronic properties of NaBiSb alloy. Finally, we present brief concluding remarks in Section 5.
2. Methodology and Crystal Structure
Electronic structure calculations were carried out within the DFT framework with the projector augmented wave (PAW) method using the Vienna ab initio Simulation Package (VASP) [7,8,9,43,44]. We used the GGA and SCAN meta-GGA energy functionals with the Perdew–Burke–Ernzerhof (PBE) parametrization [15] to include exchange-correlation effects in computations. An energy cut-off of 400 eV was used for the plane-wave-basis set and a -centered k-mesh was employed to sample the bulk Brillouin zone (BZ). SOC effects were included self-consistently. The topological analysis was performed by employing a real-space tight-binding model Hamiltonian, which was obtained by using the VASP2WANNIER90 interface [45]. Bi p and Na s and p states were included in generating Wannier functions. The surface electronic structure was calculated using the iterative Green’s function method as implemented in the WannierTools package [46].
Figure 1a shows the hexagonal crystal structure of NaBi with lattice parameters Å and Å and space group (, No. 194). It has a layered crystal structure where Na(1) and Bi atoms in the Wyckoff positions and form a shared honeycomb structure. The Na(2) atoms with Wyckoff position and form a triangular lattice which is inserted between the honeycomb layers along the z-axis. Here, Na(1) and Na(2) represent two nonequivalent Na atoms in the unit cell. The bulk and surface BZs are shown in Figure 1b.
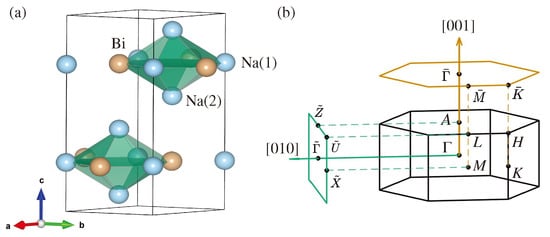
Figure 1.
(a) crystal structure of NaBi visualized using the VESTA [47] package. Na and Bi atoms are shown as blue and orange spheres. The two nonequivalent Na atoms are marked as Na(1) and Na(2); (b) bulk and (orange) and (green) surface projected Brillouin zones. The relevant high-symmetry points are marked.
3. SOC-Driven Topological Dirac Semimetal
The bulk electronic structure of NaBi without SOC obtained with GGA is shown in Figure 2a. It unveils a band inversion semimetal state in which the doubly-degenerate Bi and singly-degenerate Bi states cross along the direction and form two triply-degenerate points. At , Na s states are inverted and located eV below the Bi states. Figure 2c presents the band structure with SOC. The nodal states now become gapped everywhere except at two discrete points along the line ( rotational axis). The strength of band inversion is enhanced such that Na s states are lowered to eV below the Bi states.
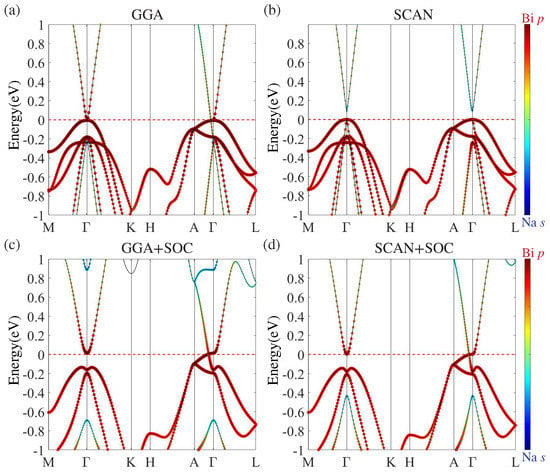
Figure 2.
Bulk band structure of NaBi obtained (without spin-orbit-coupling (SOC)) using (a) GGA and (b) SCAN meta-GGA. The Na s and Bi p states are shown as blue and red markers; (c,d) are same as (a,b) except that the SOC is included in the computations.
Figure 2b shows the energy bands without SOC calculated using SCAN. An insulating ground state with a band gap of 90 meV is seen in sharp contrast to the GGA results. When the SOC is included, SCAN yields an inverted band structure and the Dirac semimetal state with a pair of Dirac points (Figure 2d), although the band inversion strength is reduced and the Na s states are lifted to lie 0.45 eV below the Bi states. The shift of the Na s band can be verified via angle-resolved photoemission spectroscopy (ARPES) experiments. Since the band inversion in NaBi is driven by SOC, our SCAN-based results suggest that it should be possible to realize a topological phase transition from normal insulator to Dirac semimetal by modulating the strength of the SOC. In this connection, Figure 3c illustrates how the GGA and SCAN based band structures can be expected to evolve in NaBi as a function of the strength of the SOC.
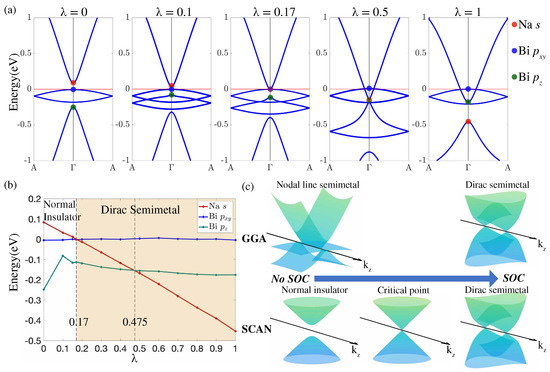
Figure 3.
(a) energy bands in NaBi along the symmetry line as the strength of the SOC is varied from 0 to 1. Red, blue, and green dots mark the Na-s, Bi-, and Bi- derived levels, respectively, at ; (b) energies of the Na s (red), Bi (blue), and Bi (green) levels at as a function of . Orange shading marks the Dirac semimetal region; (c) a schematic of how the Dirac semimetal forms in GGA (top) and SCAN (bottom) as is varied.
We turn now to discuss details of the Dirac points and the related Fermi velocities and compare our theoretical predictions with the corresponding experimental results. We obtained the Fermi velocity , where , , and are the velocities along the , , and directions in the bottom half of the Dirac cone, respectively, via a linear fit to the band structures over the momentum range of Å to 0.2 Å. The resulting values are: eV·Å for GGA and eV·Å for SCAN. The Fermi velocity obtained from ARPES measurements [38] is eV·Å.(Error bars on the experimental velocities are not reported in Ref. [38].) Locations of the Dirac points are , , from GGA and SCAN, respectively, while the corresponding experimental value is with [38]. The SCAN-based Fermi velocity is seen to be in better agreement with experiment. The locations of the Dirac points from SCAN and GGA are both within the experimental resolution.
As we already pointed out, a topological phase transition in NaBi could be realized by tuning SOC. We demonstrate this by adding a scaling factor to the SOC term in the Hamiltonian as . The resulting energy dispersion obtained self-consistently along the direction is presented in Figure 3a for a series of values. An insulator state is realized at . At , the bandgap vanishes as the Na s-derived conduction band crosses the Bi -derived valence band at the point, and the system reaches a topological critical point. As is increased further, two Dirac points start to emerge along the line at the Fermi level. At , the Na-s and Bi- bands cross in the valence band continuum region to form a second critical point. Finally, at , the Na-s band shifts down to 0.45 eV below the Fermi level, while the system preserves a pair of Dirac states at the Fermi level. Evolution of energies of the Na-s and Bi-p states at as a function of is shown in Figure 3b. The Na-s band evolves linearly as increases from 0 to 1, but the Bi states are seen to be almost independent of . In this way, the SOC realizes the band inversion by breaking the degeneracy of the doubly-degenerate Bi states and shifting up the Bi state.
In Figure 3c, we illustrate schematically how the bulk electronic structure of NaBi evolves within GGA and SCAN as the strength of the SOC is varied from 0 to 1. GGA yields a nodal-line semimetal at , which evolves into a Dirac semimetal with increasing , so that the SOC is a secondary effect that breaks the degeneracy of Bi and shifts the Bi level up to invert with Na s level. However, for the bands which form the Dirac points, the topology is dominated in the GGA by the crystal field which inverts the Bi and the Na s levels. If the symmetry is preserved, a topological phase transition in GGA can therefore only be achieved through an additional controlling parameter (other than the SOC) such as lattice strain along the c-axis [48]. In contrast, the SOC provides sufficient control within SCAN to realize a topological phase transition.
4. Topological Properties of NaBiSb
Modulation of the SOC strength could be realized experimentally in NaBi by forming NaBiSb solid solutions where the SOC will weaken as the Bi atoms are replaced by the lighter Sb atoms. Along this line, we consider the end-compound NaSb in the NaBi structure, and find NaSb to be a trivial insulator with SCAN-based optimized lattice parameters to be: Å and Å. NaSb hosts a bandgap of 0.74 eV and the electronic states around the Fermi level are derived from Na-s and Sb-p orbitals. Notably, SCAN gives a bandgap, which is larger than the GGA value of ∼0.5 eV [25]. The SCAN bandgap is in better agreement with the experimental value of ∼1.1 eV observed through absorption and photoconductivity measurements [49].
We have investigated the electronic structure of NaBiSb alloys within the virtual-crystal-approximation (VCA), which is a reasonable description for alloys in which the dopant and host atoms have similar chemical compositions [50,51,52,53]. Figure 4a shows the bulk band structure of NaBiSb alloys for various values of x. The band structure in the vicinity of the Fermi level is seen to evolve with x along the lines discussed above in connection with the evolution of the band structure in NaBi with varying SOC strength. At , there is a clear band gap between the Na-s and Bi/Sb- levels. At , the gap between the valence and conduction states vanishes and the system reaches a topological critical point. With increasing x, a Dirac semimetal state with a pair of Dirac points on the symmetry line emerges and the Na-s derived levels move down to the Fermi level. The energy variation of various levels at as a function of x is illustrated in Figure 4b.
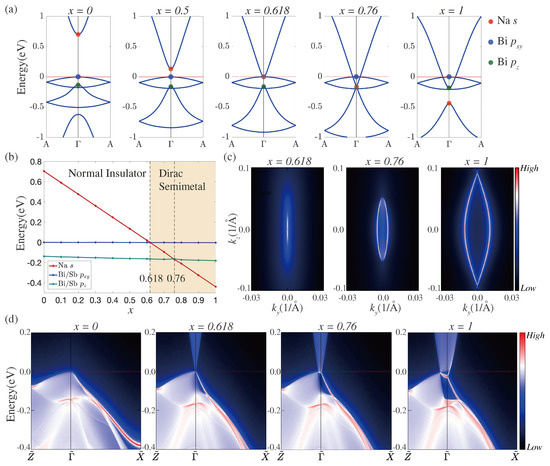
Figure 4.
(a) Bulk band structure of NaBiSb alloys along the symmetry line in the BZ for various x values. Red, blue, and green markers identify Na-s, Bi/Sb-, and Bi/Sb- derived levels, respectively; (b) evolution of the Na- and Bi/Sb-derived levels at as a function of x. Shaded region marks the Dirac semimetal phase; (c) topological double-Fermi-arcs at (left), (middle), and (right); (d) surface band structure for the [010] surface of NaBiSb alloys at , , , and .
The SCAN-based surface band structure for the [010] surface for various values of x is presented in Figure 4d. There is no surface state connecting the valence and conduction bands at as expected from the bulk band structure of NaSb. At , the system reaches a critical point. With increasing x, the critical point splits into two bulk Dirac cones along the symmetry line, and the nontrivial surface states connecting the Dirac cones emerge and can be seen for as depicted in Figure 4c. The preceding surface state results are consistent with the evolution of the bulk band topology with x. Although we have discussed the electronic structure of the NaBiSb alloys using the relatively simpler VCA scheme, a more sophisticated treatment of disorder effects using the coherent-potential-approximation (CPA) will be interesting [25,54].
5. Conclusions
We discuss the topological electronic structure of NaBi using the recently developed SCAN meta-GGA functional within the first-principles DFT framework. Our SCAN-based band structure and Fermi velocities of the Dirac states are in better accordance with the corresponding experimental results compared to the earlier GGA-based results. Nature of the Dirac states in NaBi is examined in depth by exploring effects of the strength of the SOC on the topology of the band structure. The SCAN-based Dirac semimetal state in NaBi is shown to be driven by SOC effects in contrast to the GGA where the topological phase appears even in the absence of the SOC. We also consider NaBiSb alloys and show that a topological phase transition can be realized from the Dirac semimetal state to a trivial band insulator by varying the Bi/Sb concentration. Our analysis indicates that the topological state of pristine NaBi is very robust compared to other anode materials such as NaSb [25] and MoS [55], which can undergo metal-insulator transitions. The presence of Dirac bands with high carrier velocities and the associated conductivity provide a favorable factor for battery performance.
Author Contributions
W.-C.C., B.S., B.B., C.L., and A.B. initiated the project. W.-C.C., S.M., and J.N. performed first-principles calculations and theoretical analysis with guidance from B.S., C.L., K.P., B.B., A.A., H.L., and A.B. All authors discussed the results and contributed to the planning and writing the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
The work at Northeastern University was supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences Grant No. DE-FG02-07ER46352, and benefited from Northeastern University’s Advanced Scientific Computation Center and the National Energy Research Scientific Computing Center through DOE Grant No. DE-AC02-05CH11231. J.N. is supported by the Finnish Cultural Foundation. H.L. acknowledges Academia Sinica (Taiwan) for the support under Innovative Materials and Analysis Technology Exploration (AS-iMATE-107-11). C.L. was supported by the U.S. DOE NNSA under Contract No. 89233218CNA000001 and by the Center for Integrated Nanotechnologies, a DOE BES user facility, in partnership with the LANL Institutional Computing Program for computational resources. Additional support was provided by DOE Office of Basic Energy Sciences Program E3B5.
Acknowledgments
B.B. acknowledges support from the COST Action CA16218.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Olivetti, E.A.; Ceder, G.; Gaustad, G.G.; Fu, X. Lithium-Ion Battery Supply Chain Considerations: Analysis of Potential Bottlenecks in Critical Metals. Joule 2017, 1, 229–243. [Google Scholar] [CrossRef]
- Nayak, P.K.; Yang, L.; Brehm, W.; Adelhelm, P. From Lithium-Ion to Sodium-Ion Batteries: Advantages, Challenges, and Surprises. Angew. Chem. Int. Ed. 2018, 57, 102–120. [Google Scholar] [CrossRef]
- Mukherjee, S.; Bin Mujib, S.; Soares, D.; Singh, G. Electrode Materials for High-Performance Sodium-Ion Batteries. Materials 2019, 12, 1952. [Google Scholar] [CrossRef] [PubMed]
- Luo, W.; Shen, F.; Bommier, C.; Zhu, H.; Ji, X.; Hu, L. Na-Ion Battery Anodes: Materials and Electrochemistry. Acc. Chem. Res. 2016, 49, 231–240. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Yu, B.; Li, Z.; Zhao, Y. Density Functional Theory for Battery Materials. Energy Environ. Mater. 2019, 2, 264–279. [Google Scholar] [CrossRef]
- Bansil, A.; Lin, H.; Das, T. Colloquium: Topological band theory. Rev. Mod. Phys. 2016, 88, 021004. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Savage, N. Topology Shapes a Search for New Materials. ACS Cent. Sci. 2018, 4, 523–526. [Google Scholar] [CrossRef]
- Liu, J.; Wang, S.; Sun, Q. All-carbon-based porous topological semimetal for Li-ion battery anode material. Proc. Nat. Acad. Sci. USA 2017, 114, 651–656. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Liu, C.X.; Qi, X.L.; Dai, X.; Fang, Z.; Zhang, S.C. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 438–442. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, Y.; Chen, X.Q.; Franchini, C.; Xu, G.; Weng, H.; Dai, X.; Fang, Z. Dirac semimetal and topological phase transitions in A3Bi (A = Na, K, Rb). Phys. Rev. B 2012, 85, 195320. [Google Scholar] [CrossRef]
- Xu, S.Y.; Belopolski, I.; Alidoust, N.; Neupane, M.; Bian, G.; Zhang, C.; Sankar, R.; Chang, G.; Yuan, Z.; Lee, C.C.; et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 2015, 349, 613–617. [Google Scholar] [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef] [PubMed]
- Patra, A.; Bates, J.E.; Sun, J.; Perdew, J.P. Properties of real metallic surfaces: Effects of density functional semilocality and van der Waals nonlocality. Proc. Nat. Acad. Sci. USA 2017, 114, E9188–E9196. [Google Scholar] [CrossRef]
- Buda, I.G.; Lane, C.; Barbiellini, B.; Ruzsinszky, A.; Sun, J.; Bansil, A. Characterization of Thin Film Materials using SCAN meta-GGA, an Accurate Nonempirical Density Functional. Sci. Rep. 2017, 7, 44766. [Google Scholar] [CrossRef]
- Pulkkinen, A.; Barbiellini, B.; Nokelainen, J.; Sokolovskiy, V.; Baigutlin, D.; Miroshkina, O.; Zagrebin, M.; Buchelnikov, V.; Lane, C.; Markiewicz, R.S.; et al. Coulomb correlation in noncollinear antiferromagnetic α-Mn. Phys. Rev. B 2020, 101, 075115. [Google Scholar] [CrossRef]
- Lane, C.; Furness, J.W.; Buda, I.G.; Zhang, Y.; Markiewicz, R.S.; Barbiellini, B.; Sun, J.; Bansil, A. Antiferromagnetic ground state of La2CuO4: A parameter-free ab initio description. Phys. Rev. B 2018, 98, 125140. [Google Scholar] [CrossRef]
- Furness, J.W.; Zhang, Y.; Lane, C.; Buda, I.G.; Barbiellini, B.; Markiewicz, R.S.; Bansil, A.; Sun, J. An accurate first-principles treatment of doping-dependent electronic structure of high-temperature cuprate superconductors. Commun. Phys. 2018, 1, 11. [Google Scholar] [CrossRef]
- Zhang, Y.; Lane, C.; Furness, J.W.; Barbiellini, B.; Perdew, J.P.; Markiewicz, R.S.; Bansil, A.; Sun, J. Competing stripe and magnetic phases in the cuprates from first principles. Proc. Natl. Acad. Sci. USA 2020, 117, 68–72. [Google Scholar] [CrossRef] [PubMed]
- Hafiz, H.; Suzuki, K.; Barbiellini, B.; Orikasa, Y.; Kaprzyk, S.; Tsuji, N.; Yamamoto, K.; Terasaka, A.; Hoshi, K.; Uchimoto, Y.; et al. Identification of ferrimagnetic orbitals preventing spinel degradation by charge ordering in LixMn2O4. Phys. Rev. B 2019, 100, 205104. [Google Scholar] [CrossRef]
- He, J.; Wei, Y.; Zhai, T.; Li, H. Antimony-based materials as promising anodes for rechargeable lithium-ion and sodium-ion batteries. Mater. Chem. Front. 2018, 2, 437–455. [Google Scholar] [CrossRef]
- Darwiche, A.; Fehse, M.; Mahmoud, A.; La Fontaine, C.; Fraisse, B.; Hermann, R.; Doublet, M.L.; Monconduit, L.; Sougrati, M.; Ben Yahia, M.; et al. The Electrochemical Sodiation of Sb Investigated by Operando X-ray Absorption and 121Sb Mössbauer Spectroscopy: What Does One Really Learn? Batteries 2018, 4, 25. [Google Scholar] [CrossRef]
- Narayan, A.; Di Sante, D.; Picozzi, S.; Sanvito, S. Topological Tuning in Three-Dimensional Dirac Semimetals. Phys. Rev. Lett. 2014, 113, 256403. [Google Scholar] [CrossRef]
- Nagulapati, V.M.; Kim, D.S.; Oh, J.; Lee, J.H.; Hur, J.; Kim, I.T.; Lee, S.G. Enhancing the Electrochemical Performance of SbTe Bimetallic Anodes for High-Performance Sodium-Ion Batteries: Roles of the Binder and Carbon Support Matrix. Nanomaterials 2019, 9, 1134. [Google Scholar] [CrossRef]
- Kushwaha, S.K.; Krizan, J.W.; Feldman, B.E.; Gyenis, A.; Randeria, M.T.; Xiong, J.; Xu, S.Y.; Alidoust, N.; Belopolski, I.; Liang, T.; et al. Bulk crystal growth and electronic characterization of the 3D Dirac semimetal Na3Bi. APL Mater. 2015, 3, 041504. [Google Scholar] [CrossRef]
- Sottmann, J.; Herrmann, M.; Vajeeston, P.; Hu, Y.; Ruud, A.; Drathen, C.; Emerich, H.; Fjellvåg, H.; Wragg, D.S. How Crystallite Size Controls the Reaction Path in Nonaqueous Metal Ion Batteries: The Example of Sodium Bismuth Alloying. Chem. Mater. 2016, 28, 2750–2756. [Google Scholar] [CrossRef]
- Lim, C.H.; Selvaraj, B.; Song, Y.F.; Wang, C.C.; Jin, J.T.; Huang, S.S.; Chuang, C.H.; Sheu, H.S.; Liao, Y.F.; Wu, N.L. Insight into microstructural and phase transformations in electrochemical sodiation—Desodiation of a bismuth particulate anode. J. Mater. Chem. A 2017, 5, 21536–21541. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L.; Li, F.; Cheng, F.; Chen, J. Bulk Bismuth as a High-Capacity and Ultralong Cycle-Life Anode for Sodium-Ion Batteries by Coupling with Glyme-Based Electrolytes. Adv. Mater. 2017, 29, 1702212. [Google Scholar] [CrossRef]
- Sun, J.; Li, M.; Oh, J.A.S.; Zeng, K.; Lu, L. Recent advances of bismuth based anode materials for sodium-ion batteries. Mater. Technol. 2018, 33, 563–573. [Google Scholar] [CrossRef]
- Huang, Y.; Zhu, C.; Zhang, S.; Hu, X.; Zhang, K.; Zhou, W.; Guo, S.; Xu, F.; Zeng, H. Ultrathin Bismuth Nanosheets for Stable Na-Ion Batteries: Clarification of Structure and Phase Transition by in Situ Observation. Nano Lett. 2019, 19, 1118–1123. [Google Scholar] [CrossRef] [PubMed]
- Armitage, N.P.; Mele, E.J.; Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 2018, 90, 015001. [Google Scholar] [CrossRef]
- Yang, B.J.; Nagaosa, N. Classification of stable three-dimensional Dirac semimetals with nontrivial topology. Nat. Commun. 2014, 5, 4898. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Hua, M.; Zhang, H.; Zhang, X. Classification of stable Dirac and Weyl semimetals with reflection and rotational symmetry. Phys. Rev. B 2016, 93, 205109. [Google Scholar] [CrossRef]
- Weng, H.; Dai, X.; Fang, Z. Topological semimetals predicted from first-principles calculations. J. Phys. Condens. Matter 2016, 28, 303001. [Google Scholar] [CrossRef]
- Young, S.M.; Zaheer, S.; Teo, J.C.Y.; Kane, C.L.; Mele, E.J.; Rappe, A.M. Dirac Semimetal in Three Dimensions. Phys. Rev. Lett. 2012, 108, 140405. [Google Scholar] [CrossRef]
- Liu, Z.K.; Zhou, B.; Zhang, Y.; Wang, Z.J.; Weng, H.M.; Prabhakaran, D.; Mo, S.K.; Shen, Z.X.; Fang, Z.; Dai, X.; et al. Discovery of a Three-Dimensional Topological Dirac Semimetal, Na3Bi. Science 2014, 343, 864–867. [Google Scholar] [CrossRef]
- Xu, S.Y.; Liu, C.; Kushwaha, S.K.; Sankar, R.; Krizan, J.W.; Belopolski, I.; Neupane, M.; Bian, G.; Alidoust, N.; Chang, T.R.; et al. Observation of Fermi arc surface states in a topological metal. Science 2015, 347, 294–298. [Google Scholar] [CrossRef]
- Cheng, X.; Li, R.; Sun, Y.; Chen, X.Q.; Li, D.; Li, Y. Ground-state phase in the three-dimensional topological Dirac semimetal Na3Bi. Phys. Rev. B 2014, 89, 245201. [Google Scholar] [CrossRef]
- Jenkins, G.S.; Lane, C.; Barbiellini, B.; Sushkov, A.B.; Carey, R.L.; Liu, F.; Krizan, J.W.; Kushwaha, S.K.; Gibson, Q.; Chang, T.R.; et al. Three-dimensional Dirac cone carrier dynamics in Na3Bi and Cd3As2. Phys. Rev. B 2016, 94, 085121. [Google Scholar] [CrossRef]
- Shao, D.; Ruan, J.; Wu, J.; Chen, T.; Guo, Z.; Zhang, H.; Sun, J.; Sheng, L.; Xing, D. Strain-induced quantum topological phase transitions in Na3Bi. Phys. Rev. B 2017, 96, 075112. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Marzari, N.; Vanderbilt, D. Maximally localized generalized Wannier functions for composite energy bands. Phys. Rev. B 1997, 56, 12847–12865. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, S.; Song, H.F.; Troyer, M.; Soluyanov, A.A. WannierTools: An open-source software package for novel topological materials. Comput. Phys. Commun. 2018, 224, 405–416. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Guan, S.; Yu, Z.M.; Liu, Y.; Liu, G.B.; Dong, L.; Lu, Y.; Yao, Y.; Yang, S.A. Artificial gravity field, astrophysical analogues, and topological phase transitions in strained topological semimetals. NPJ Quantum Mater. 2017, 2, 23. [Google Scholar] [CrossRef]
- Spicer, W.E. Photoemissive, Photoconductive, and Optical Absorption Studies of Alkali-Antimony Compounds. Phys. Rev. 1958, 112, 114–122. [Google Scholar] [CrossRef]
- Bansil, A. Coherent-potential and average t-matrix approximations for disordered muffin-tin alloys. I. Formalism. Phys. Rev. B 1979, 20, 4025–4034. [Google Scholar] [CrossRef]
- Bansil, A. Coherent-potential and average t-matrix approximations for disordered muffin-tin alloys. II. Application to realistic systems. Phys. Rev. B 1979, 20, 4035–4043. [Google Scholar] [CrossRef]
- Liu, J.; Vanderbilt, D. Topological phase transitions in (Bi1−xInx)2Se3 and (Bi1−xSbx)2Se3. Phys. Rev. B 2013, 88, 224202. [Google Scholar] [CrossRef]
- Huang, H.; Jin, K.H.; Liu, F. Alloy Engineering of Topological Semimetal Phase Transition in MgTa2−xNbxN3. Phys. Rev. Lett. 2018, 120, 136403. [Google Scholar] [CrossRef] [PubMed]
- Bansil, A.; Kaprzyk, S.; Mijnarends, P.E.; Toboła, J. Electronic structure and magnetism of Fe3−xVxX(X = Si, Ga, and Al) alloys by the KKR-CPA method. Phys. Rev. B 1999, 60, 13396–13412. [Google Scholar] [CrossRef]
- Lane, C.; Cao, D.; Li, H.; Jiao, Y.; Barbiellini, B.; Bansil, A.; Zhu, H. Understanding Phase Stability of Metallic 1T-MoS2 Anodes for Sodium-Ion Batteries. Condens. Matter 2019, 4, 53. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).