Polaronic States and Superconductivity in WO3-x
Abstract
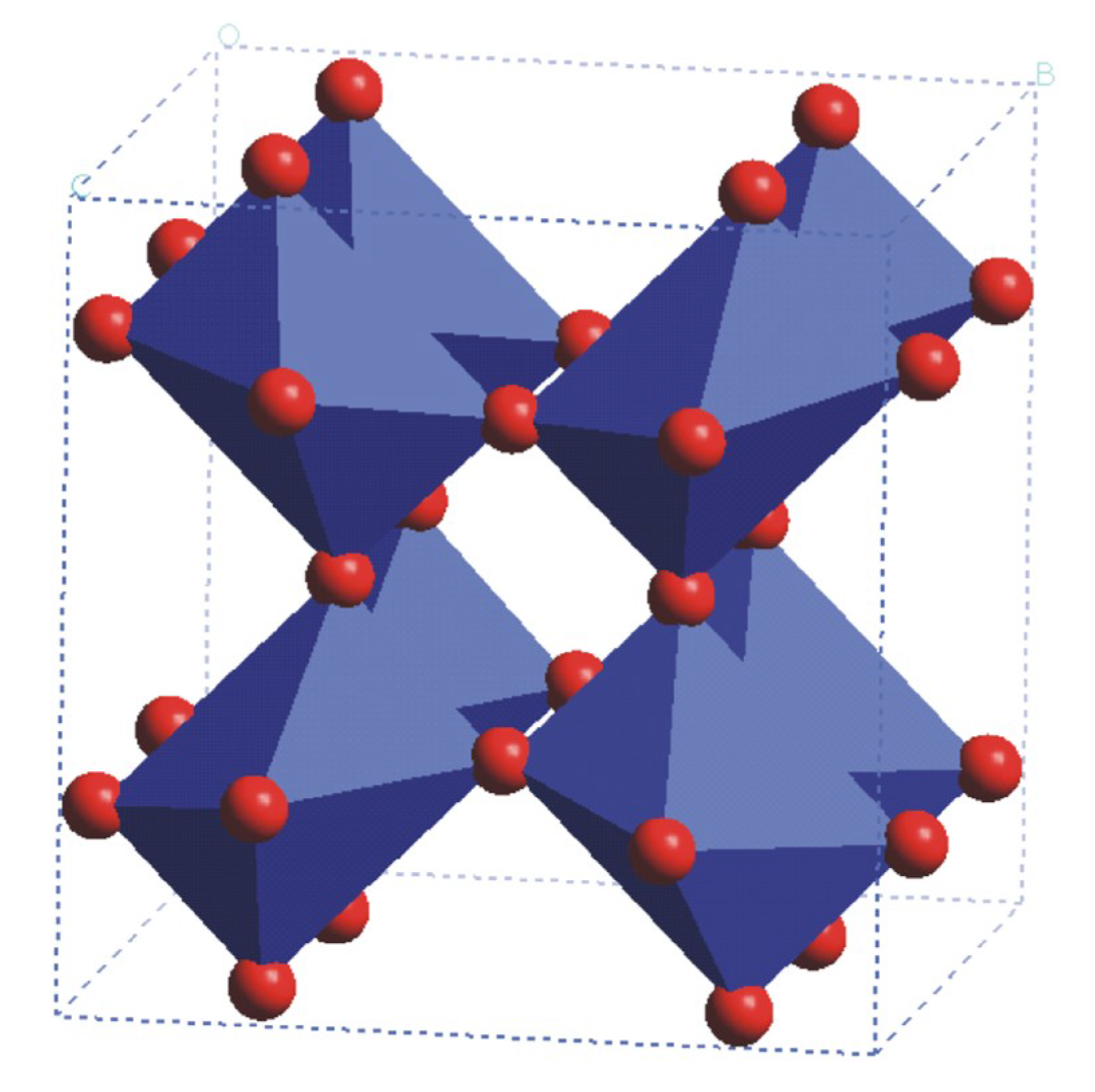
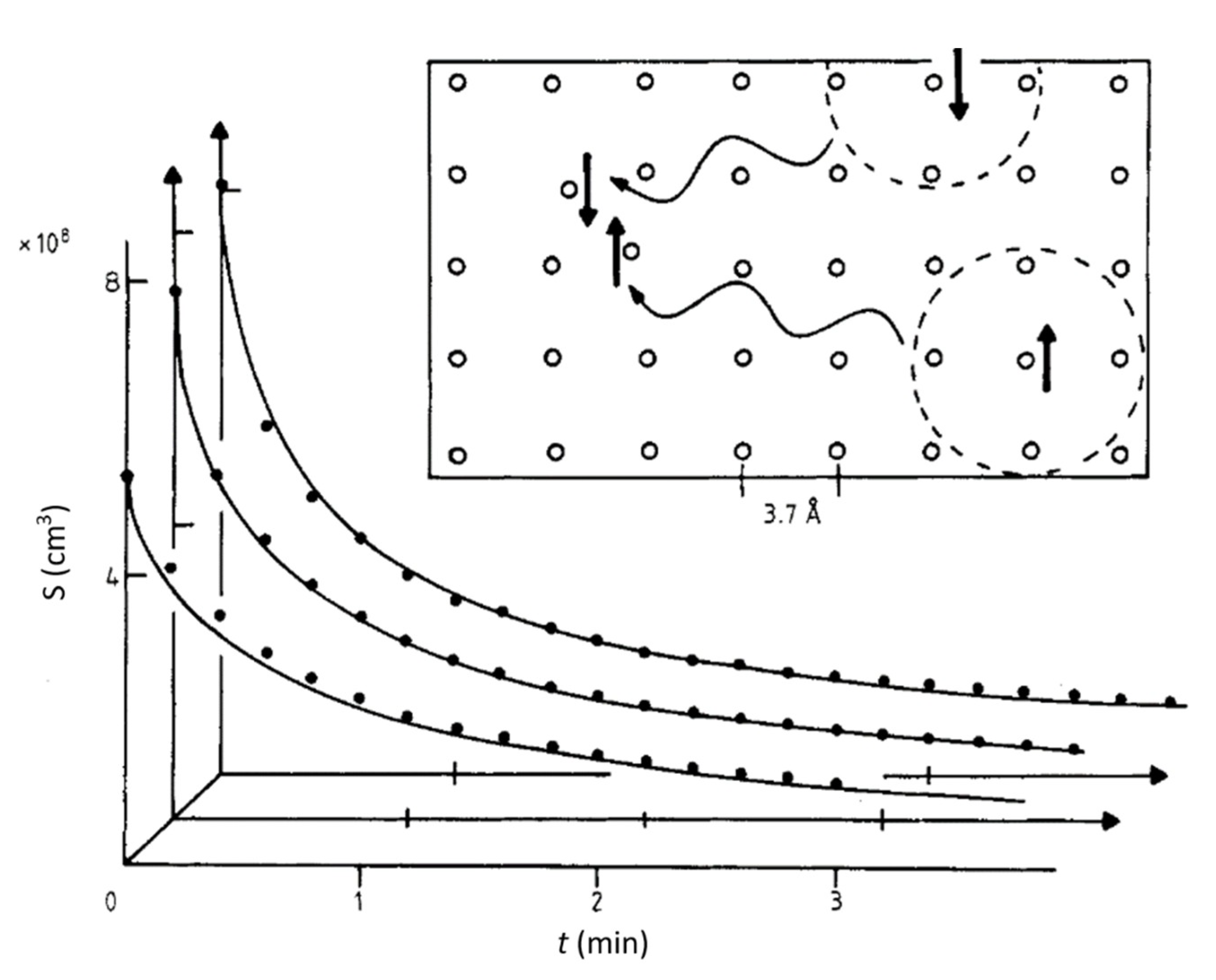
1. Introduction and Some Historic Background
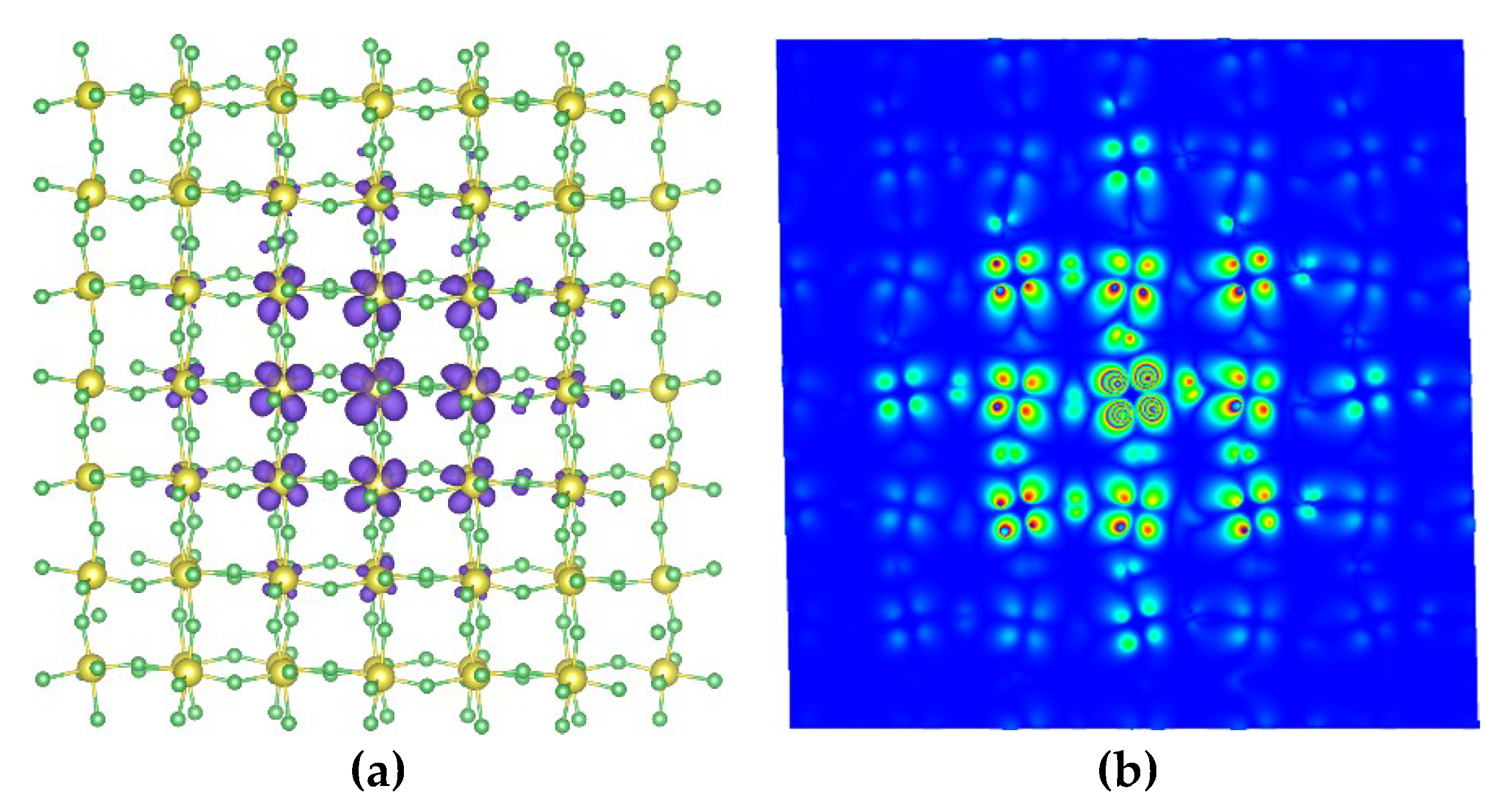
2. Results
3. Outlook
Acknowledgments
Conflicts of Interest
References
- Axe, J.D.; Shirane, G.; Mueller, K.A. Zone-boundary phonon instability in cubic LaAlO3. Bull. Am. Phys. Soc. 1969, 183, 820. [Google Scholar] [CrossRef]
- Mueller, K.A.; Burkhard, H. SrTiO3 Intrinsic quantum paraelectric below 4K. Phys. Rev. B 1979, 19, 3593–3602. [Google Scholar] [CrossRef]
- Salje, E. Non-stoichiometric tungsten compound, synthesis and lattice constants of WO3-NaWO3 mixed crystal compounds. Z. Fur Allg. Angew. Chem. 1973, 396, 267–270. [Google Scholar] [CrossRef]
- Salje, E. New type of electrooptic effect in semiconducting WO3. J. Appl. Crystallogr. 1974, 7, 615–617. [Google Scholar] [CrossRef]
- Salje, E. Viswanathan K, Physical properties and phase transitions in WO3. Acta Crystallogr. Sect. A 1975, 31, 356–359. [Google Scholar] [CrossRef]
- Salje, E. Lattice dynamics of WO3. Acta Crystallogr. Sect. A 1975, 31, 360–363. [Google Scholar] [CrossRef]
- Schirmer, O.F.; Salje, E. Conducting bi-polarons in low-temperature crystalline WO3-x. J. Phys. C 1980, 13, 1067–1072. [Google Scholar] [CrossRef]
- Schirmer, O.F.; Salje, E. W5+ polaron in low temperature crystalline WO3 Electron spin response and optical absorption. Solid State Commun. 1980, 33, 333–336. [Google Scholar] [CrossRef]
- Salje, E.K.H.; Wruck, B.; Thomas, H. Order parameter saturation and low temperature extension of Landau theory. Z. Phys. Condens. Matter 1991, 82, 399–404. [Google Scholar] [CrossRef]
- Kustov, S.; Luibimova, I.; Salje, E.K.H. Domain dynamics in quantum-paraelectric SrTiO3. Phys. Rev. Lett. 2020, 124, 016801. [Google Scholar] [CrossRef]
- Shengelaya, A.; Conder, K.; Mueller, K.A. Signatures of filamentary superconductivity up to 94K in tungsten oxide WO2.9. J. Supercond. Nov. Magn. 2020, 33, 301–306. [Google Scholar] [CrossRef]
- Locherer, K.R.; Swainson, I.P.; Salje, E.K.H. Phase transitions in WO3 at high temperatures—A new look. J. Phys. Condens. Matter 2002, 11, 6737–6756. [Google Scholar] [CrossRef]
- Howard, C.J.; Luca, V.; Knight, K.S. High-temperature phase transitions in tungsten trioxide—The last word? J. Phys. Condens. Matter 2002, 14, 377–387. [Google Scholar] [CrossRef]
- Viehland, D.D.; Salje, E.K.H. Domain boundary dominated systems, adaptive structures and functional twin boundaries. Adv. Phys. 2014, 63, 267–326. [Google Scholar] [CrossRef]
- Salje, E.K.H.; Rehmann, S.; Pobell, F.; Morris, D.; Knight, K.S.; Herrmannsdorfer, T.; Dove, M.T. Crystal structure and paramagnetic behaviour of epsilon-WO3-x. J. Phys. Condens. Matter 1997, 9, 6563–6577. [Google Scholar] [CrossRef]
- Aird, A.; Salje, E.K.H. Sheet superconductivity in twin walls: Experimental evidence of WO3-x. J. Phys. Condens. Matter 1998, 10, L377–L380. [Google Scholar] [CrossRef]
- Aird, A.; Domeneghetti, M.C.; Mazzi, F.; Salje, E.K.H. Sheet superconductivity in WO3-x: Crystal structure of the tetragonal Matrix. J. Phys. Condens. Matter 1998, 33, L569–L574. [Google Scholar] [CrossRef]
- Kim, Y.; Alexe, M.; Salje, E.K.H. Nanoscale properties of twin walls and surface layers in piezoelectric WO3-x. Appl. Phys. Lett. 2010, 96, 032904. [Google Scholar] [CrossRef]
- Seidel, J.; Maksymovych, P.; Batra, Y.; Katan, A.; Yang, S.-Y.; He, Q.; Baddorf, A.P.; Kalinin, S.V.; Yang, C.-H.; Yang, J.-C.; et al. Domain wall conductivity in La doped BiFeO3. Phys. Rev. Lett. 2010, 105, 197603. [Google Scholar] [CrossRef]
- Hamdi, H.; Salje, E.K.H.; Ghosez, P.; Bousquet, P. First-principles investigation of bulk WO3. Phys. Rev. B 2016, 94, 245124. [Google Scholar] [CrossRef]
- Bousquet, E.; Hamdi, H.; Aguado-Puente, P.; Salje, E.K.H.; Artacho, E.; Ghosez, P. First-principles characterization of single-electron polaron in WO3. Phys. Rev. Res. 2020, 2, 012052. [Google Scholar] [CrossRef]
- Reich, S.; Tsabba, Y. Possible nucleation of a 2D superconducting phase on WO3 single crystals surface doped with Na+. Eur. Phys. J. B 1999, 1, 1–4. [Google Scholar] [CrossRef]
- Salje, E.K.H. Polarons and bi-polarons in WO3-x. Eur. J. Solid State Inorg. Chem. 1994, 31, 805–821. [Google Scholar]
- Salje, E.; Gehlig, R.; Viswanathan, K. Structural phase transitions in mixed crystals WxMo1-xO3. J. Solid State Chem. 1978, 25, 239–250. [Google Scholar] [CrossRef]
- Viswanathan, K.; Salje, E. Crystal-structure and charge carrier behavior of (W12.64Mo1.36)O41 and its significance to other related compounds. Acta Cryst. 1981, 37, 4449–4456. [Google Scholar] [CrossRef]
- Viswanathan, K.; Brandt, K.; Salje, E. Crystal-structure and charge carrier concentration of W18O49. J. Solid State Chem. 1981, 36, 45–51. [Google Scholar] [CrossRef]
- Ruscher, C.; Salje, E.; Hussain, A. The effect of Nb-W distribution of polaronic transport in ternary Nb-W oxides- electrical and optical properties. J. Phys. C-Solid State 1988, 21, 4465–4480. [Google Scholar] [CrossRef]
- Ruscher, C.; Salje, E.; Hussain, A. The effect of polaron concentration on the polaron transport in NbO2.5-x Optical and electric properties. J. Phys. C-Solid State 1988, 21, 3737–3749. [Google Scholar] [CrossRef]
- Salje, E.K.H. Domain boundaries as active memory devices: Trajectories towards domain boundary engineering. ChemPhysChem 2010, 11, 940–950. [Google Scholar] [CrossRef]
- Catalan, G.; Seidel, J.; Ramesh, R.; Scott, J.F. Domain wall nanoelectronics. Rev. Mod. Phys. 2012, 84, 119–156. [Google Scholar] [CrossRef]
- Salje, E.K.H.; Ding, X.; Aktas, O. Domain glass. Phys. Status Solidi B 2014, 251, 2061–2066. [Google Scholar] [CrossRef]
- Ding, X.; Zhao, Z.; Lookman, T.; Saxena, A.; Salje, E.K.H. High junction and twin boundary densities in driven dynamical systems. Adv. Mater. 2012, 24, 5385–5389. [Google Scholar] [CrossRef] [PubMed]
- Caprara, S.; Grilli, M.; Benfatto, L.; Castellani, C. Effective medium theory for superconducting layers: A systematic analysis including space correlation effects. Phys. Rev. B 2011, 84, 014514. [Google Scholar] [CrossRef]
- Caprara, S.; Biscaras, J.; Bergeal, N.; Bucheki, D.; Hurand, S.; Feuillet-Palma, C.; Rastogi, A.; Budhani, R.C.; Lesueur, J.; Grilli, M. Multiband superconductivity and nanoscale inhomogeneity at oxide interfaces. Phys. Rev. B 2013, 88, 020504. [Google Scholar] [CrossRef]
- Scopigno, N.; Bucheli, D.; Caprara, S.; Biscaras, J.; Bergeal, N.; Lesueur, J.; Grilli, M. Phase separation from electron confinement at oxide interfaces. Phys. Rev. Lett. 2016, 116, 026804. [Google Scholar] [CrossRef]
- Dezi, G.; Scopigno, N.; Caprara, S.; Grilli, M. Negative electronic compressibility and nanoscale inhomogeneity in ionic-liquid gated two-dimensional superconductors. Phys. Rev. B 2018, 98, 214507. [Google Scholar] [CrossRef]
- Bovenzi, N.; Caprara, S.; Grilli, M.; Raimondi, R.; Scopigno, N.; Seibold, G. Density inhomogeneities and Rashba spin-orbit coupling interplay in oxide interfaces. J. Phys. Chem. Solids 2019, 128, 118–129. [Google Scholar] [CrossRef]

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salje, E.K.H. Polaronic States and Superconductivity in WO3-x. Condens. Matter 2020, 5, 32. https://doi.org/10.3390/condmat5020032
Salje EKH. Polaronic States and Superconductivity in WO3-x. Condensed Matter. 2020; 5(2):32. https://doi.org/10.3390/condmat5020032
Chicago/Turabian StyleSalje, Ekhard K. H. 2020. "Polaronic States and Superconductivity in WO3-x" Condensed Matter 5, no. 2: 32. https://doi.org/10.3390/condmat5020032
APA StyleSalje, E. K. H. (2020). Polaronic States and Superconductivity in WO3-x. Condensed Matter, 5(2), 32. https://doi.org/10.3390/condmat5020032




