Unconventional Magnetism in Layered Transition Metal Dichalcogenides
Abstract
1. Introduction
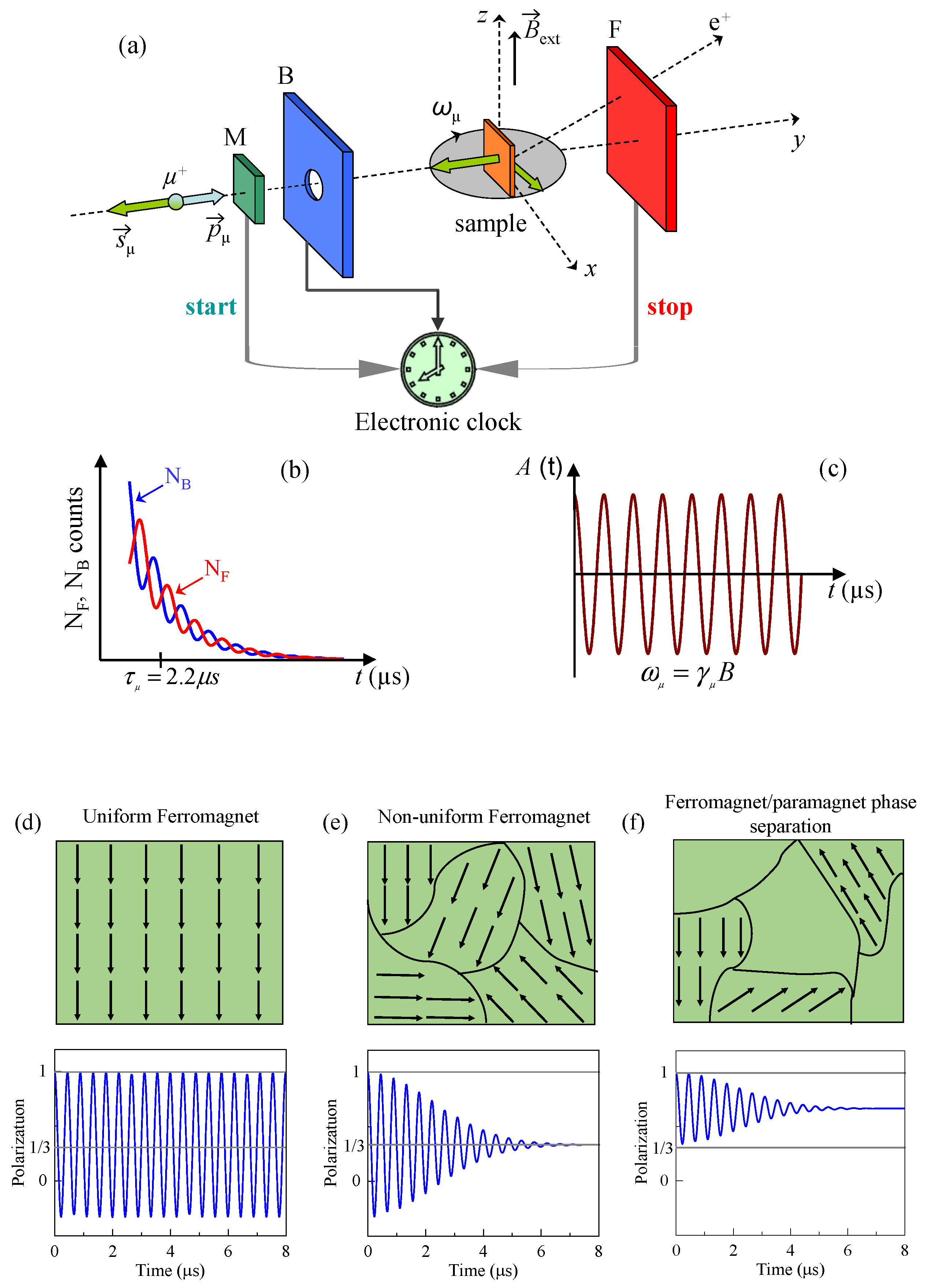
2. SR Technique: Very Sensitive Microscopic Magnetic Probe
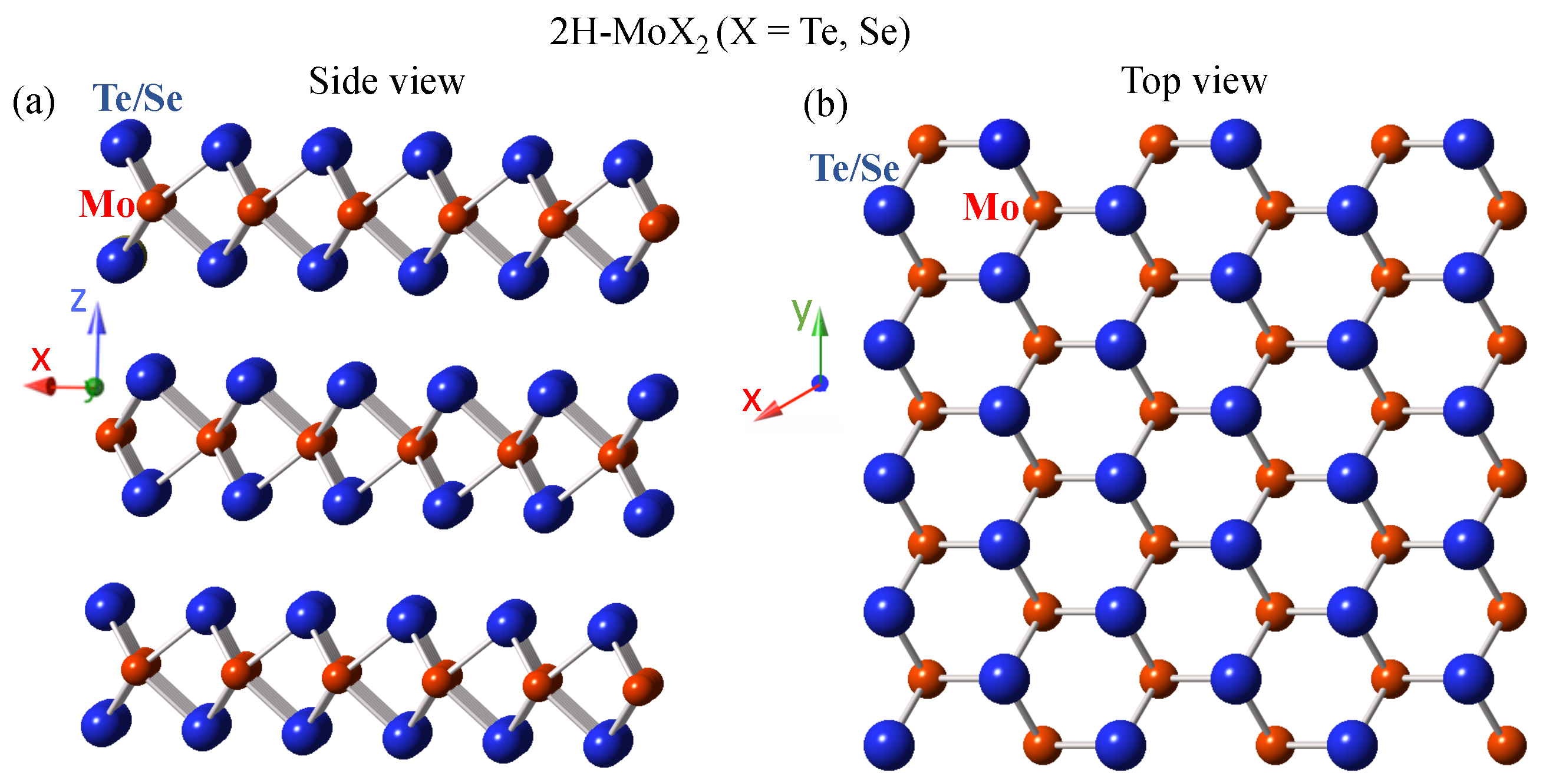
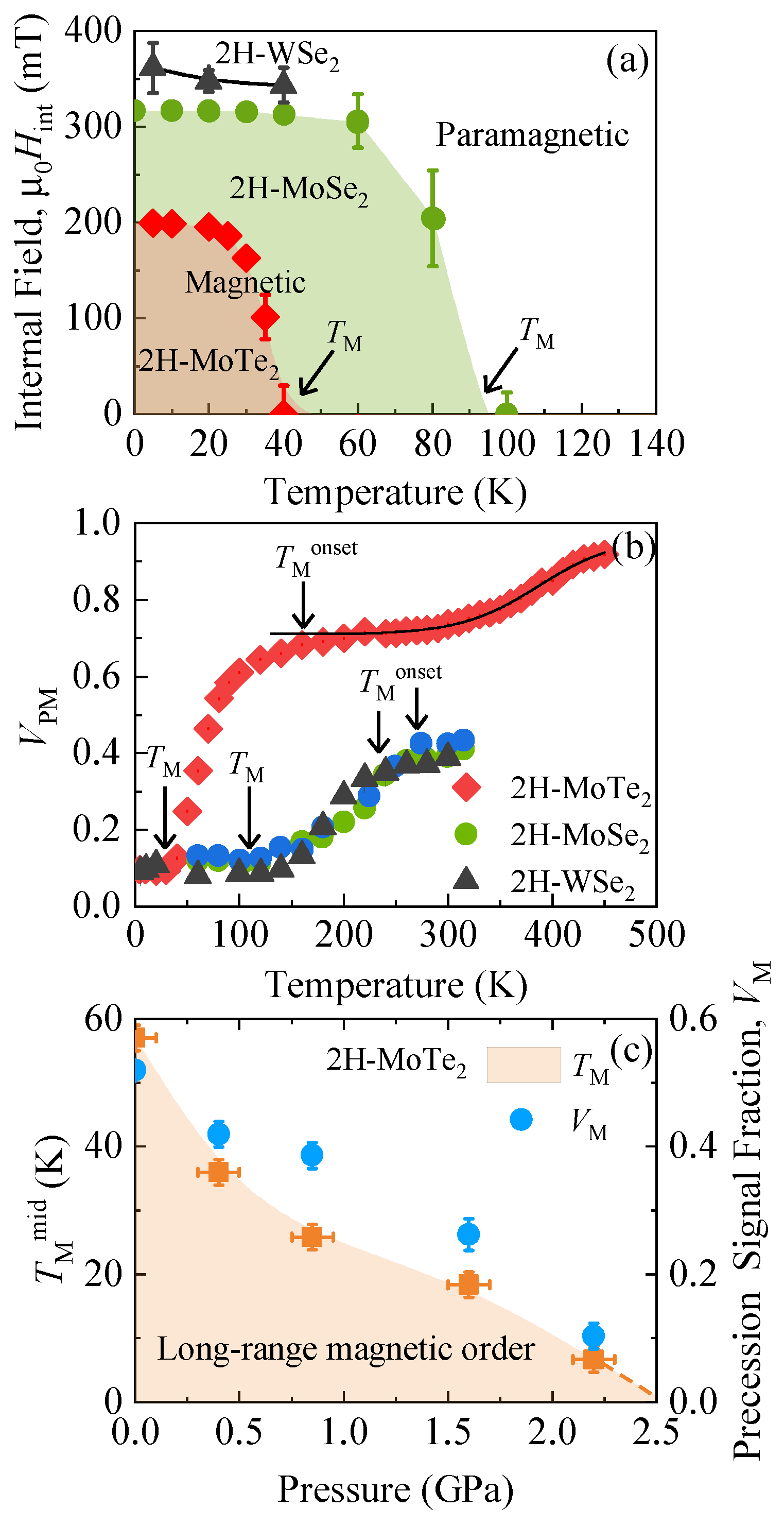
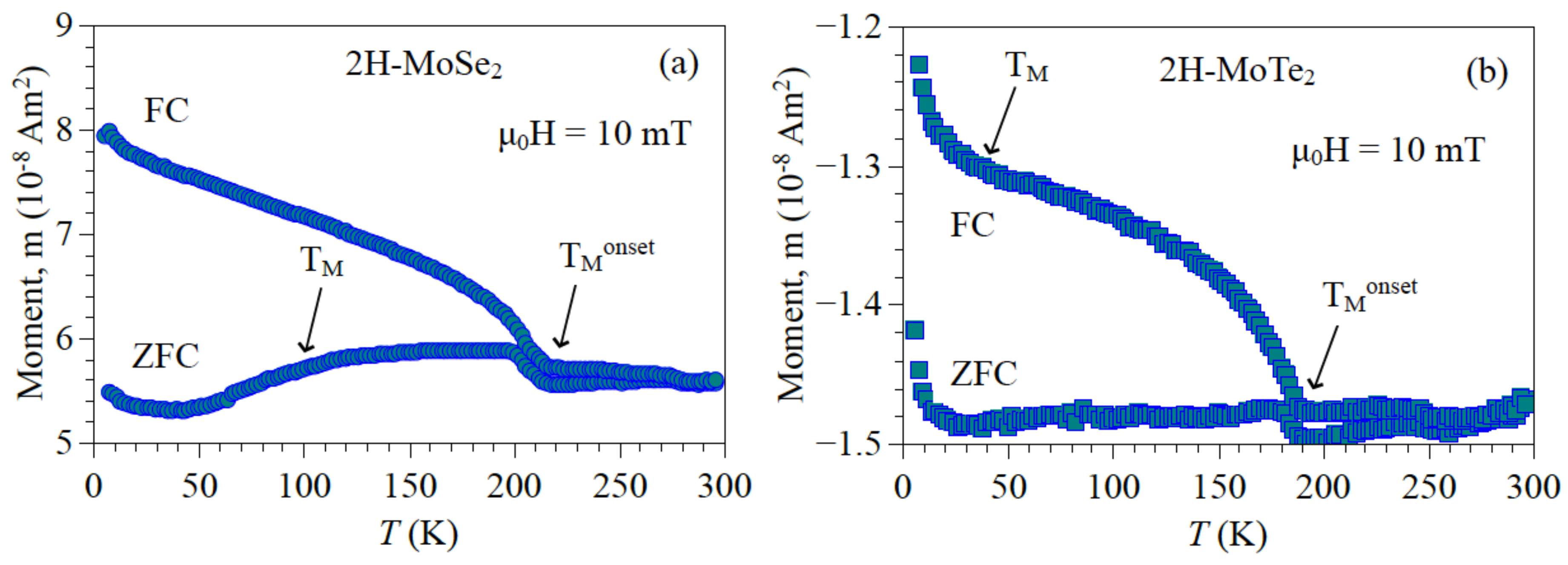
3. Results
4. Summary and Discussion
- High quality bulk samples of Mo/W-based semiconducting TMDs can be grown. The systems can be doped to make both n-type and p-type semiconductors available.
- The materials are cleavable down to a monolayer thickness and readily grown in large-area form. As it is well established in these materials, the bandgap is strongly dependent on the thickness, providing tunability over the semiconductor properties.
- The chemical potential and electric field in thin films are easily tuned by electrostatic gates, opening the possibility to tune magnetism, as demonstrated in GaAs.
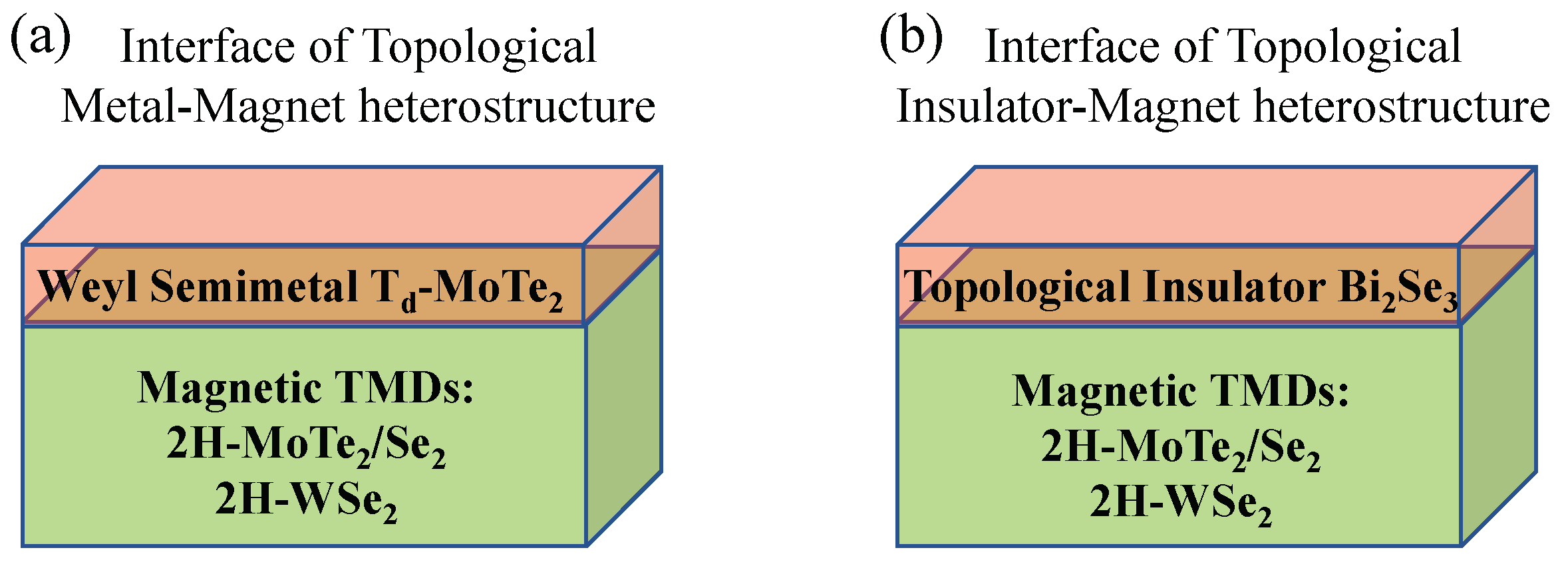
- Finally, these materials can be easily layered by van der Waals heteroepitaxy, allowing the creation of unique new device concepts. For instance, one can grow the heterostructure of the magnetic TMDs (2H-MoTe, 2H-MoSe, 2H-WSe) and superconducting Weyl semimetal [3] (-MoTe) or the heterostructure of the magnetic TMDs (2H-MoTe, 2H-MoSe, 2H-WSe) and topological insulator (TI) [59,60] (BiSe) and study exotic magnetic/superconducting properties at the interface [61,62,63]. Even though the SC in the bulk can be topologically trivial, the robust Z related topological states at the surface or at the interfaces is expected to feature helical or other exotic Cooper pairing due to spin-momentum locking [64], and the external magnet field induced vortex line can support Majorana fermions. When a topological insulator/metal is in contact with a ferromagnet, both time reversal and inversion symmetries are broken at the interface. An energy gap is formed at the TI surface, and its electrons gain a net magnetic moment through short-range exchange interactions. Magnetic/superconducting proximity effects at the interface between magnet and Weyl semimetal (Figure 7a) or magnet and topological insulators (Figure 7b) is considered to have great potential in spintronics as, in principle, it allows realizing the quantum anomalous Hall and topological magneto-electric effects. However, detailed experimental investigations of induced magnetism at the interfaces has remained a challenge. Low-energy SR [63,65] experiments, which allows to probe the magnetism and superconductivity as a function of distance from the free surface to the interface, will be crucial to address the interesting magnetic/superconducting aspects of the interfaces.
Funding
Acknowledgments
Conflicts of Interest
References
- Lombardi, G.C.; Bianchi, G.E. Spintronics: Materials, Applications and Devices; Nova Science Pub Inc.: Hauppauge, NY, USA, 2009. [Google Scholar]
- Jungwirth, T.; Marti, X.; Wadley, P.; Wunderlich, J. Antiferromagnetic spintronics. Nat. Nanotechnol. 2016, 11, 231–241. [Google Scholar] [CrossRef] [PubMed]
- Soluyanov, A.A.; Gresch, D.; Wang, Z.; Wu, Q.; Troyer, M.; Dai, X.; Bernevig, B.A. Type-II Weyl semimetals. Nature 2015, 527, 495–498. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Yao, W.; Xiao, D.; Heinz, T.F. Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 2014, 10, 343–350. [Google Scholar] [CrossRef]
- Ali, M.N.; Xiong, J.; Flynn, S.; Tao, J.; Gibson, Q.D.; Schoop, L.M.; Liang, T.; Haldolaarachchige, N.; Hirschberger, M.; Ong, N.P.; et al. Large, non-saturating magnetoresistance in WTe2. Nature 2014, 514, 205–208. [Google Scholar] [CrossRef] [PubMed]
- Qian, X.; Liu, J.; Fu, L.; Li, J. Quantum spin Hall effect in two-dimensional transition metal dichalcogenides. Science 2014, 346, 1344–1347. [Google Scholar] [CrossRef]
- Costanzo, D.; Jo, S.; Berger, H.; Morpurgo, A.F. Gate-induced superconductivity in atomically thin MoS2 crystals. Nat. Nanotechnol. 2016, 11, 339. [Google Scholar] [CrossRef]
- Guguchia, Z.; von Rohr, F.; Shermadini, Z.; Lee, A.T.; Banerjee, S.; Wieteska, A.R.; Marianetti, C.A.; Frandsen, B.A.; Luetkens, H.; Gong, Z.; et al. Signatures of topologically non-trivial s+− superconducting order parameter in type-II Weyl semimetal Td-MoTe2. Nat. Commun. 2017, 8, 1082. [Google Scholar] [CrossRef]
- Guguchia, Z.; Kerelsky, A.; Edelberg, D.; Banerjee, S.; von Rohr, F.; Scullion, D.; Augustin, M.; Scully, M.; Rhodes, D.A.; Shermadini, Z.; et al. Magnetism in Semiconducting Molybdenum Dichalcogenides. Sci. Adv. 2018, 4, eaat3672. [Google Scholar] [CrossRef]
- Tongay, S.; Varnoosfaderani, S.S.; Appleton, B.R.; Wu, J.; Hebard, A.F. Magnetic properties of MoS2: Existence of ferromagnetism. Appl. Phys. Lett. 2012, 101, 123105. [Google Scholar] [CrossRef]
- Ataca, C.; Sahin, H.; Akturk, E.; Ciraci, S. Mechanical and Electronic Properties of MoS2 Nanoribbons and Their Defects. J. Phys. Chem. C 2011, 115, 3934–3941. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Z.; Zhang, S.; Chen, Z. MoS2 nanoribbons: High stability and unusual electronic and magnetic properties. J. Am. Chem. Soc. 2008, 130, 16739–16744. [Google Scholar] [CrossRef] [PubMed]
- Krasheninnikov, A.V.; Lehtinen, P.O.; Foster, A.S.; Pyykko, P.; Nieminen, R.M. Embedding Transition-Metal Atoms in Graphene: Structure, Bonding, and Magnetism. Phys. Rev. Lett. 2009, 102, 126807. [Google Scholar] [CrossRef] [PubMed]
- Santos, E.J.G.; Sanchez-Portal, D.; Ayuela, A. Magnetism of substitutional Co impurities in graphene: Realization of single π-vacancies. Phys. Rev. B 2010, 81, 125433. [Google Scholar] [CrossRef]
- Santos, E.J.G.; Ayuela, A.; Sanchez-Portal, D. Universal magnetic properties of sp3-type defects in covalently functionalized graphene. New J. Phys. 2012, 14, 043022. [Google Scholar] [CrossRef]
- Zhang, Z.; Zou, X.; Crespi, V.H.; Yakobson, B.I. Intrinsic Magnetism of Grain Boundaries in Two-Dimensional Metal Dichalcogenides. ACS Nano 2013, 7, 10475. [Google Scholar] [CrossRef] [PubMed]
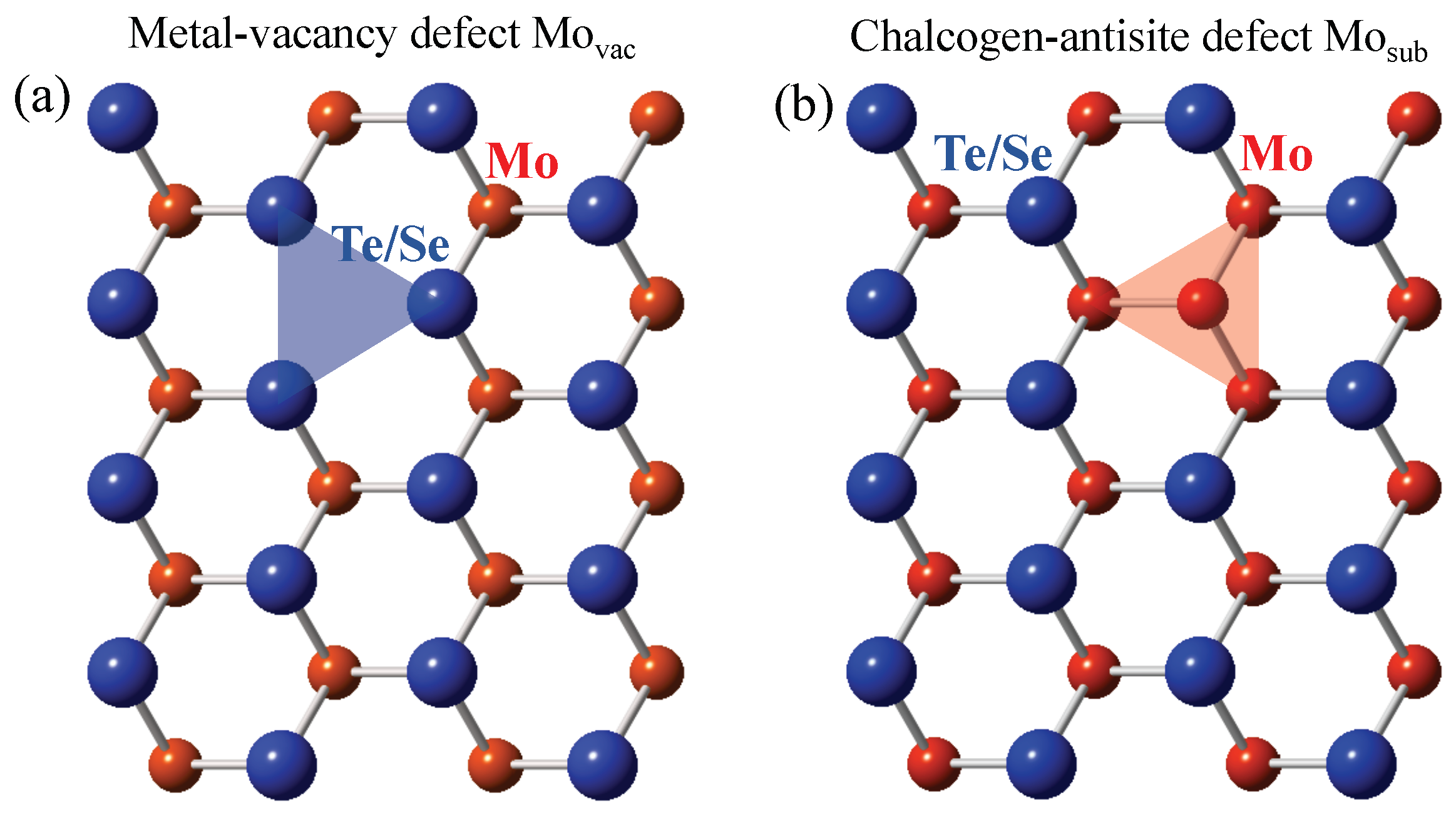
- Cai, L.; He, J.; Liu, Q.; Yao, T.; Chen, L.; Yan, W.; Hu, F.; Jiang, Y.; Zhao, Y.; Hu, T.; et al. Vacancy-Induced Ferromagnetism of MoS2 Nanosheets. J. Am. Chem Soc. 2015, 137, 2622. [Google Scholar] [CrossRef]
- Pümpin, B.; Keller, H.; Kündig, W.; Odermatt, W.; Patterson, B.D.; Schneider, J.W.; Simmler, H.; Connell, S.; Müller, K.A.; Bednorz, J.G.; et al. Internal magnetic fields in the high-temperature superconductor YBa2Cu3O7-δ from muon spin rotation experiments. Z. Phys. B—Condensed Matter 1988, 72, 175–180. [Google Scholar] [CrossRef]
- Keller, H. Muon spin rotation experiments in high-Tc superconductors. In Earlier and Recent Aspects of Superconductivity; Springer: Berlin/Heidelberg, Germany, 1990; pp. 222–239. [Google Scholar]
- Pümpin, B.; Keller, H.; Kündig, W.; Odermatt, W.; Savić, I.M.; Schneider, J.W.; Simmler, H.; Zimmermann, P.; Kaldis, E.; Rusiecki, S.; et al. Muon-spin-rotation measurements of the London penetration depths in YBa2Cu3O6.97. Phys. Rev. B 1990, 42, 8019–8029. [Google Scholar] [CrossRef]
- Morenzoni, E.; Wojek, B.M.; Suter, A.; Prokscha, T.; Logvenov, G.; Bozovic, I. The Meissner effect in a strongly underdoped cuprate above its critical temperature. Nat. Commun. 2011, 2, 272. [Google Scholar] [CrossRef]
- Uemura, Y.J.; Luke, G.M.; Sternlieb, B.J.; Brewer, J.H.; Carolan, J.F.; Hardy, W.N.; Kadono, R.; Kempton, J.R.; Kiefl, R.F.; Kreitzman, S.R.; et al. Universal Correlations between Tc and ns/m* (Carrier Density over Effective Mass) in High-Tc Cuprate Superconductors. Phys. Rev. Lett. 1989, 62, 2317. [Google Scholar] [CrossRef]
- Sonier, J.E.; Brewer, J.H.; Kiefl, R.F. μSR studies of the vortex state in type-II superconductors. Rev. Mod. Phys. 2000, 72, 769. [Google Scholar] [CrossRef]
- Khasanov, R.; Shengelaya, A.; Maisuradze, A.; La Mattina, F.; Bussmann-Holder, A.; Keller, H.; Müller, K.A. Experimental Evidence for Two Gaps in the HighTemperature La1.83Sr0.17CuO4 Superconductor. Phys. Rev. Lett. 2007, 98, 057007. [Google Scholar] [CrossRef]
- Keller, H.; Bussmann-Holder, A.; Muller, K.A. Jahn-Teller physics and high-Tc superconductivity. Mater. Today 2008, 11, 38. [Google Scholar] [CrossRef]
- Uemura, Y.J. Condensation, excitation, pairing, and superfluid density in high-Tc superconductors: Magnetic resonance mode as a roton analogue and a possible spin-mediated pairing. J. Phys. Condens. Matter 2004, 16, S4515–S4540. [Google Scholar] [CrossRef]
- Bernhard, C.; Drew, A.J.; Schulz, L.; Malik, V.K.; Rossle, M.; Niedermayer, C.; Wolf, T.; Varma, G.D.; Mu, G.; Wen, H.H.; et al. Muon spin rotation study of magnetism and superconductivity in BaFe2-xCoxAs2 and Pr1−xSrxFeAsO. New J. Phys. 2009, 11, 055050. [Google Scholar] [CrossRef]
- Luetkens, H.; Klauss, H.-H.; Kraken, M.; Litterst, F.J.; Dellmann, T.; Klingeler, R.; Hess, C.A.; Khasanov, R.; Amato, A.; Baines, C.; et al. The electronic phase diagram of the LaO1−xFxFeAs superconductor. Nature Mater. 2009, 8, 305. [Google Scholar] [CrossRef] [PubMed]
- Luke, G.M.; Fudamoto, Y.; Kojima, K.M.; Larkin, M.I.; Merrin, J.; Nachumi, B.; Uemura, Y.J.; Maeno, Y.; Mao, Z.Q.; Mori, Y.; et al. Time-Reversal Symmetry Breaking Superconductivity in Sr2RuO4. Nature 1998, 394, 558–561. [Google Scholar] [CrossRef]
- Dalmas de Reotier, P.; Yaouanc, A. Muon spin rotation and relaxation in magnetic materials. J. Phys. Condens. Matter 1997, 9, 9113. [Google Scholar] [CrossRef]
- Amato, A. Heavy-fermion systems studied by μSR technique. Rev. Modern Phys. 1997, 69, 1119. [Google Scholar] [CrossRef]
- Uemura, Y.J.; Goko, T.; Gat-Malureanu, I.M.; Carlo, J.P.; Russo, P.L.; Savici, A.T.; Aczel, A.; MacDougall, G.J.; Rodriguez, J.A.; Luke, G.M.; et al. Phase separation and suppression of critical dynamics at quantum phase transitions of MnSi and (Sr1−xCax)RuO3. Nat. Phys. 2007, 3, 29–35. [Google Scholar] [CrossRef]
- Blundell, S.J. Spin-polarized muons in condensed matter physics. Contemporary Phys. 1999, 40, 175. [Google Scholar] [CrossRef]
- Schenk, A. Muon Spin Rotation Spectroscopy: Principles and Applications in Solid State; Physics, Adam Hilger: Bristol, UK, 1985. [Google Scholar]
- Yaouanc, A.; Dalmas de Reotier, P. Muon Spin Rotation, Relaxation, and Resonance: Applications to Condensed Matter; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Amato, A. Physics with Muons: From Atomic Physics to Condensed Matter Physics. Available online: https://www.psi.ch/en/lmu/lectures (accessed on 15 June 2020).
- Amato, A.; Luetkens, H.; Sedlak, K.; Stoykov, A.; Scheuermann, R.; Elender, M.; Raselli, A.; Graf, D. The new versatile general purpose surface-muon instrument (GPS) based on silicon photomultipliers for μSR measurements on a continuous-wave beam. Rev. Sci. Instrum. 2017, 88, 093301. [Google Scholar] [CrossRef] [PubMed]
- Kubo, R.; Toyabe, T. A stochastic model for low field resonance and relaxation. In Magnetic Resonance and Relaxation; North-Holland: Amsterdam, The Netherlands, 1967; pp. 810–823. [Google Scholar]
- Guguchia, Z. Investigations of Superconductivity and Magnetism in Iron-Based and Cuprate High-Temperature Superconductors. Ph.D. Thesis, University of Zurich, Zürich, Switzerland, 2013. [Google Scholar]
- Guguchia, Z.; Amato, A. SPG Mitteilungen Nr. 60. January 2020, p. 12 ff. Available online: https://www.sps.ch/fileadmin/doc/Mitteilungen/Mitteilungen.60.pdf (accessed on 15 June 2020).
- Salman, Z.; Prokscha, T.; Amato, A.; Morenzoni, E.; Scheuermann, R.; Sedlak, K.; Suter, A. Direct spectroscopic observation of a shallow hydrogen-like donor state in insulating SrTiO3. Phys. Rev. Lett. 2014, 113, 156801. [Google Scholar] [CrossRef] [PubMed]
- Khasanov, R.; Guguchia, Z.; Maisuradze, A.; Andreica, D.; Elender, M.; Raselli, A.; Shermadini, Z.; Goko, T.; Knecht, F.; Morenzoni, E.; et al. High pressure research using muons at the Paul Scherrer Institute. High Press. Res. 2016, 36, 140–166. [Google Scholar] [CrossRef]
- Guguchia, Z.; Amato, A.; Kang, J.; Luetkens, H.; Biswas, P.K.; Prando, G.; von Rohr, F.; Bukowski, Z.; Shengelaya, A.; Keller, H.; et al. Direct evidence for a pressure-induced nodal superconducting gap in the Ba0.65Rb0.35Fe2As2 superconductor. Nat. Commun. 2015, 6, 8863. [Google Scholar] [CrossRef]
- Kerelsky, A.; Nipane, A.; Edelberg, D.; Wang, D.; Zhou, X.; Motmaendadgar, A.; Gao, H.; Xie, S.; Kang, K.; Park, J.; et al. Absence of a Band Gap at the Interface of a Metal and Highly Doped Monolayer MoS2. Nano Lett. 2017, 17, 5962–5968. [Google Scholar] [CrossRef] [PubMed]
- Santos, E.J.G.; Ayuela, A.; Sanchez-Portal, D. First-principles study of substitutional metal impurities in graphene: Structural, electronic and magnetic properties. New J. Phys. 2010, 12, 053012. [Google Scholar] [CrossRef]
- Oliva, R.; Wozniak, T.; Dybala, F.; Kopaczek, J.; Scharoch, P.; Kudrawiec, R. Hidden spin-polarized bands in semiconducting 2H-MoTe2. Mat. Res. Lett. 2020, 8, 75–81. [Google Scholar] [CrossRef]
- Avsar, A.; Ciarrocchi, A.; Pizzochero, M.; Unuchek, D.; Yazyev, O.V.; Kis, A. Defect induced, layer-modulated magnetism in ultrathin metallic PtSe2. Nat. Nanotechnol. 2019, 14, 674–678. [Google Scholar] [CrossRef]
- Bonilla, M.; Kolekar, S.; Ma, Y.; Coy Diaz, H.; Kalappattil, V.; Das, R.; Eggers, T.; Gutierrez, H.R.; Phan, M.-H.; Batzill, M. Strong room-temperature ferromagnetism in VSe2 monolayers on van der Waals substrates. Nat. Nanotechnol. 2018, 13, 289. [Google Scholar] [CrossRef]
- Zhang, F.; Zheng, B.; Sebastian, A.; Olson, H.; Liu, M.; Fujisawa, K.; Pham, Y.T.H.; Jimenez, V.O.; Kalappattil, V.; Miao, L.; et al. Monolayer Vanadium-doped Tungsten Disulfide: A Room-Temperature Dilute Magnetic Semiconductor. arXiv 2020, arXiv:2005.01965. [Google Scholar]
- Pham, Y.T.H.; Liu, M.; Jimenez, V.O.; Zhang, F.; Kalappattil, V.; Yu, Z.; Wang, K.; Williams, T.; Terrones, M.; Phan, M.-H. Tunable Ferromagnetism and Thermally Induced Spin Flip in Vanadium-doped Tungsten Diselenide Monolayers at Room Temperature. arXiv 2020, arXiv:2005.00493. [Google Scholar]
- Duong, D.L.; Yun, S.J.; Kim, Y.; Kim, S.-G.; Lee, Y.H. Long-range ferromagnetic ordering in vanadium-doped WSe2 semiconductor. Appl. Phys. Lett. 2019, 115, 242406. [Google Scholar] [CrossRef]
- Gibertini, M.; Koperski, M.; Morpurgo, A.F.; Novoselov, K.S. Magnetic 2D materials and heterostructures. Nat. Nanotechnol. 2019, 14, 408–419. [Google Scholar] [CrossRef]
- McGuire, M.A.; Dixit, H.; Cooper, V.R.; Sales, B.C. Coupling of crystal structure and magnetism in the layered, ferromagnetic insulator CrI3. Chem. Mat. 2015, 27, 612–620. [Google Scholar] [CrossRef]
- Prokscha, T.; Chow, K.H.; Stilp, E.; Suter, A.; Luetkens, H.; Morenzoni, E.; Nieuwenhuys, G.J.; Salman, Z.; Scheuermann, R. Photo-induced persistent inversion of germanium in a 200-nm-deep surface region. Sci. Rep. 2013, 3, 2569. [Google Scholar] [CrossRef]
- Ding, C.; Man, H.; Qin, C.; Lu, J.; Sun, Y.; Wang, Q.; Yu, B.; Feng, C.; Goko, T.; Arguello, C.J.; et al. (La1−xBax)(Zn1−xMnx)AsO: A two-dimensional 1111-type diluted magnetic semiconductor in bulk form. Phys. Rev. B 2013, 88, 041102. [Google Scholar] [CrossRef]
- Dietl, T. A ten-year perspective on dilute magnetic semiconductors and oxides. Nat. Mater 2010, 9, 965–974. [Google Scholar] [CrossRef]
- Masek, J.; Kudrnovsky, J.; Maca, F.; Gallagher, B.L.; Campion, R.P.; Gregory, D.H.; Jungwirth, T. Dilute Moment n-Type Ferromagnetic Semiconductor Li(Zn,Mn)As. Phys. Rev. Lett. 2007, 98, 067202. [Google Scholar] [CrossRef]
- Glasbrenner, J.K.; Zutic, I.; Mazin, I.I. Theory of Mn-doped I-II-V Semiconductors. Phys. Rev. B 2014, 90, 140403(R). [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
- Ando, Y.; Fu, L. Topological Crystalline Insulators and Topological Superconductors: From Concepts to Materials. Annu. Rev. Condens. Matter Phys. 2015, 6, 361. [Google Scholar] [CrossRef]
- Eremeev, S.V.; Otrokov, M.M.; Chulkov, E.V. New Universal Type of Interface in the Magnetic Insulator/Topological Insulator Heterostructures. Nano Lett. 2018, 18, 6521–6529. [Google Scholar] [CrossRef]
- Chen, J.; Wang, L.; Zhang, M.; Zhou, L.; Zhang, R.; Jin, L.; Wang, X.; Qin, H.; Qiu, Y.; Mei, J.; et al. Evidence for Magnetic Skyrmions at the Interface of Ferromagnet/Topological-Insulator Heterostructures. Nano Lett. 2019, 19, 6144–6151. [Google Scholar] [CrossRef]
- Krieger, J.A.; Pertsova, A.; Giblin, S.R.; Dobeli, M.; Prokscha, T.; Schneider, C.W.; Suter, A.; Hesjedal, T.; Balatsky, A.V.; Salman, Z. Proximity-induced odd-frequency superconductivity in a topological insulator. arXiv 2020, arXiv:2003.12104. [Google Scholar]
- Xu, S.-Y.; Alidoust, N.; Belopolski, I.; Richardella, A.; Liu, C.; Neupane, M.; Bian, G.; Huang, S.-H.; Sankar, R.; Fang, C.; et al. Momentum-space imaging of Cooper pairing in a half-Dirac-gas topological superconductor. Nat. Phys. 2014, 10, 943–950. [Google Scholar] [CrossRef]
- Jackson, T.J.; Riseman, T.M.; Forgan, E.M.; Gluckler, H.; Prokscha, T.; Morenzoni, E.; Pleines, M.; Niedermayer, C.; Schatz, G.; Luetkens, H.; et al. Depth-Resolved Profile of the Magnetic Field beneath the Surface of a Superconductor with a Few nm Resolution. Phys. Rev. Lett. 2000, 84, 4958. [Google Scholar] [CrossRef]
- Suter, A.; Wojek, B. Musrfit: A free platform-independent framework for μSR data analysis. Phys. Procedia. 2012, 30, 69. [Google Scholar] [CrossRef]

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guguchia, Z. Unconventional Magnetism in Layered Transition Metal Dichalcogenides. Condens. Matter 2020, 5, 42. https://doi.org/10.3390/condmat5020042
Guguchia Z. Unconventional Magnetism in Layered Transition Metal Dichalcogenides. Condensed Matter. 2020; 5(2):42. https://doi.org/10.3390/condmat5020042
Chicago/Turabian StyleGuguchia, Zurab. 2020. "Unconventional Magnetism in Layered Transition Metal Dichalcogenides" Condensed Matter 5, no. 2: 42. https://doi.org/10.3390/condmat5020042
APA StyleGuguchia, Z. (2020). Unconventional Magnetism in Layered Transition Metal Dichalcogenides. Condensed Matter, 5(2), 42. https://doi.org/10.3390/condmat5020042




