The TeraFERMI Electro-Optic Sampling Set-Up for Fluence-Dependent Spectroscopic Measurements
Abstract
1. Introduction
2. The TeraFERMI Beamline
2.1. Source
2.2. Transport System
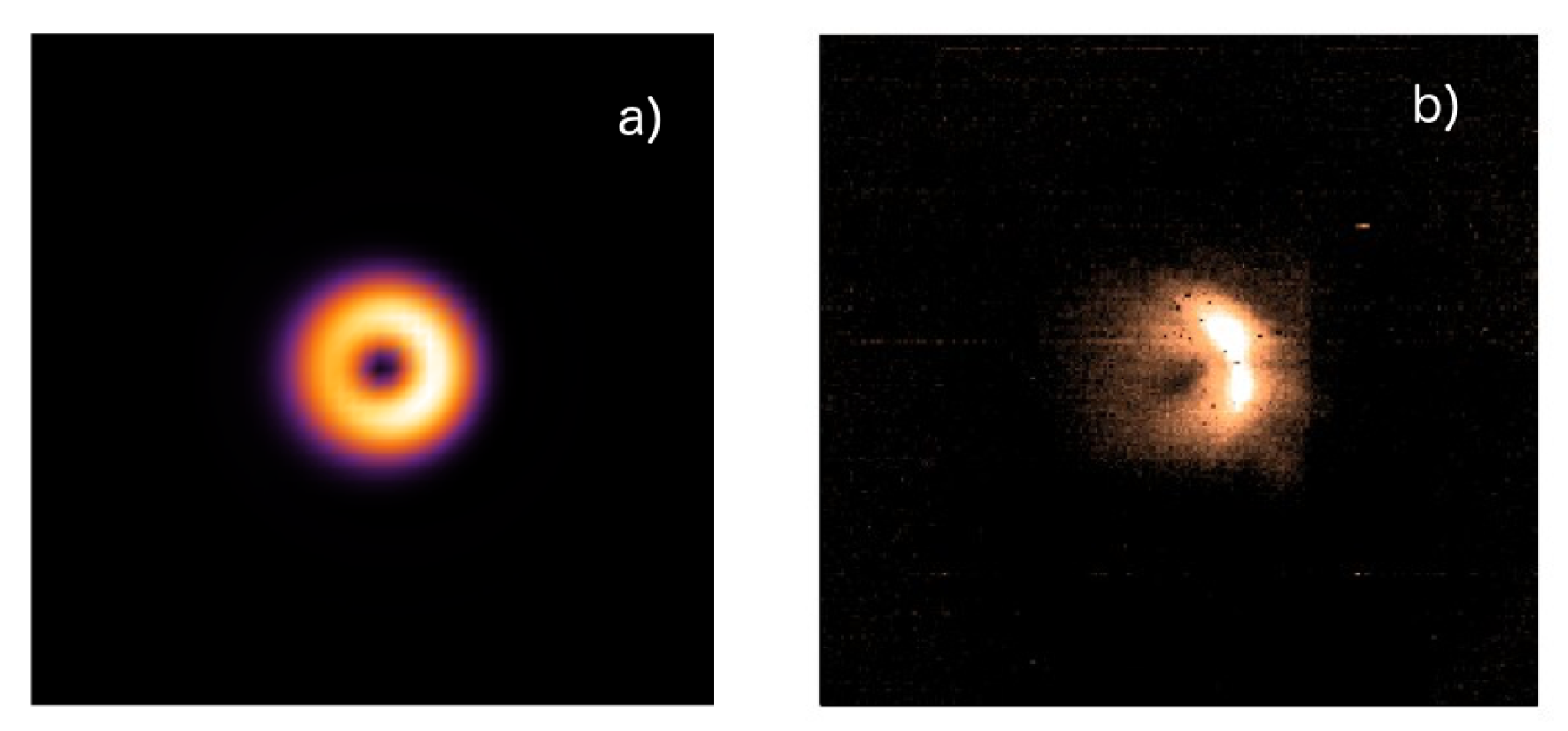
2.3. Beamline Performance
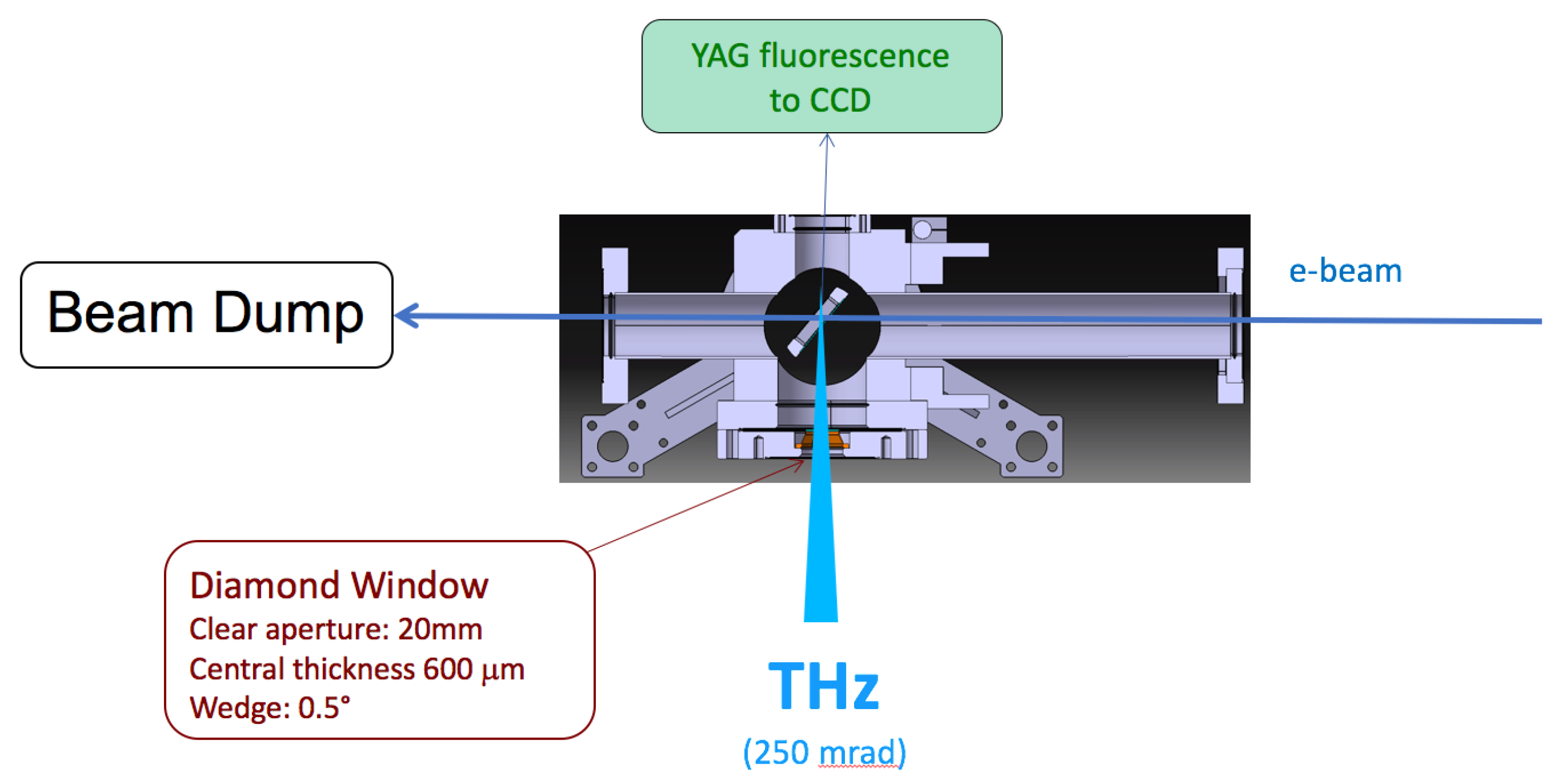
2.4. Optical Scheme
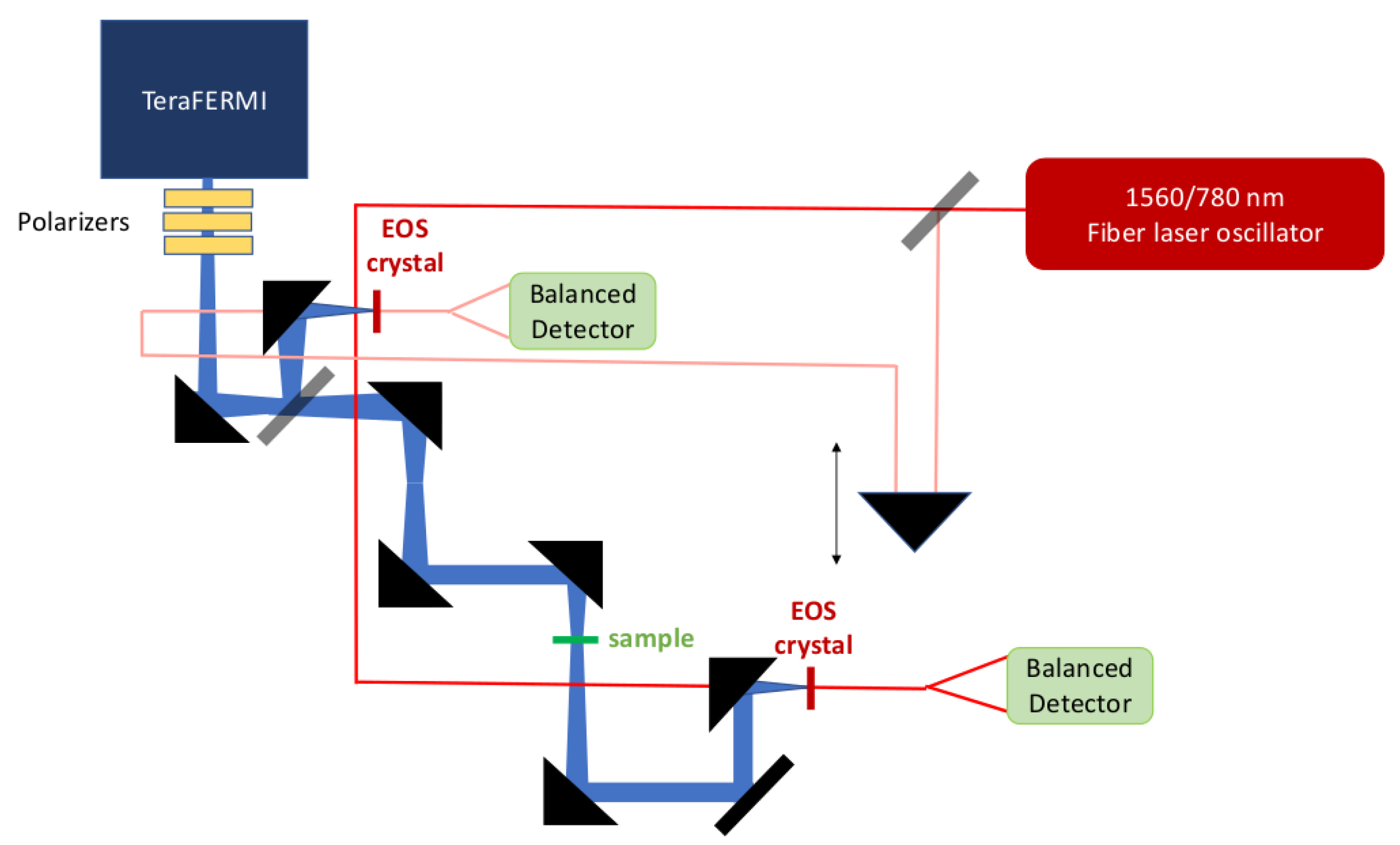
3. The TeraFERMI Electro-Optic Sampling Set-Up
3.1. Laser Synchronization
3.2. Fast Pulse Detection System
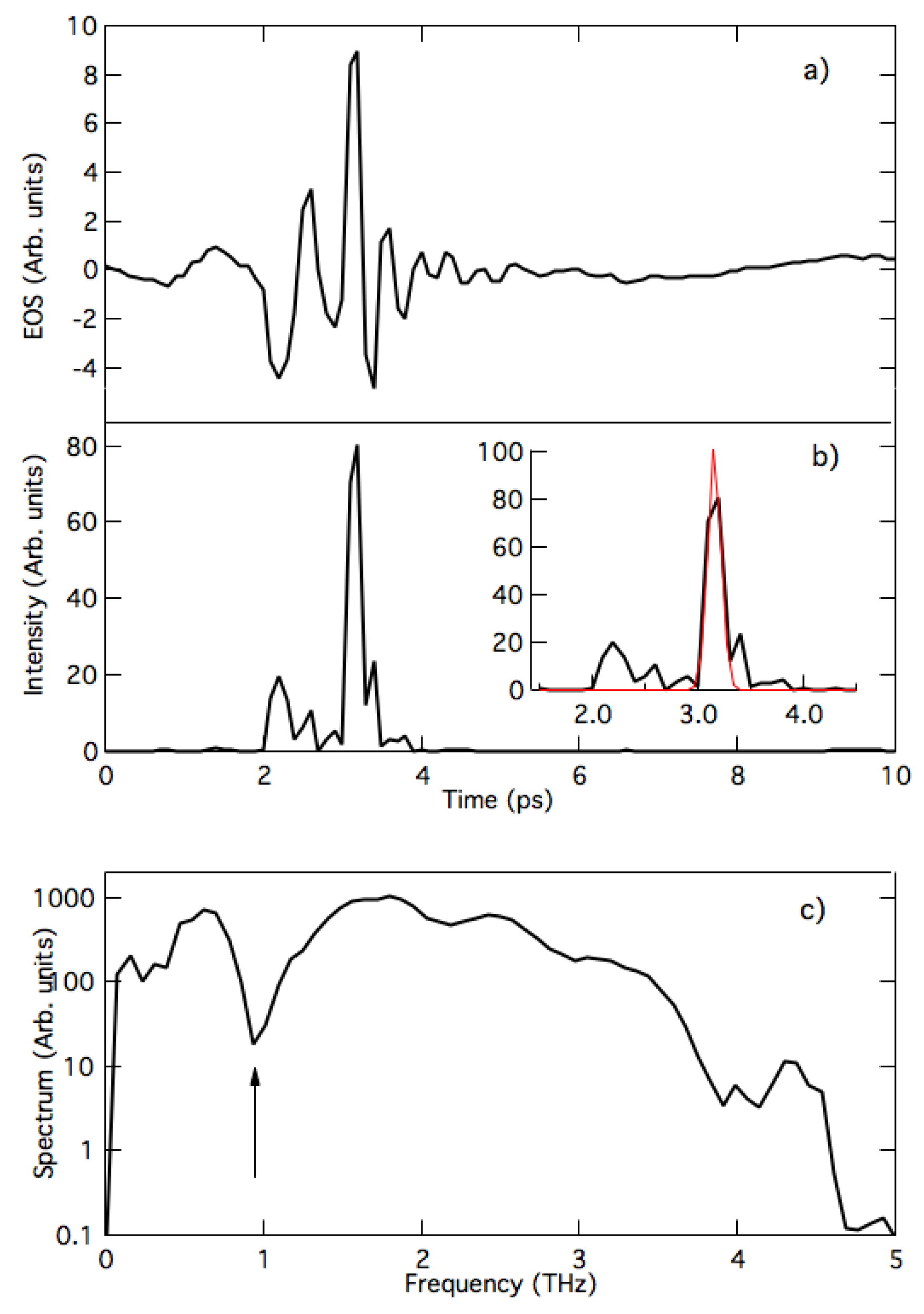
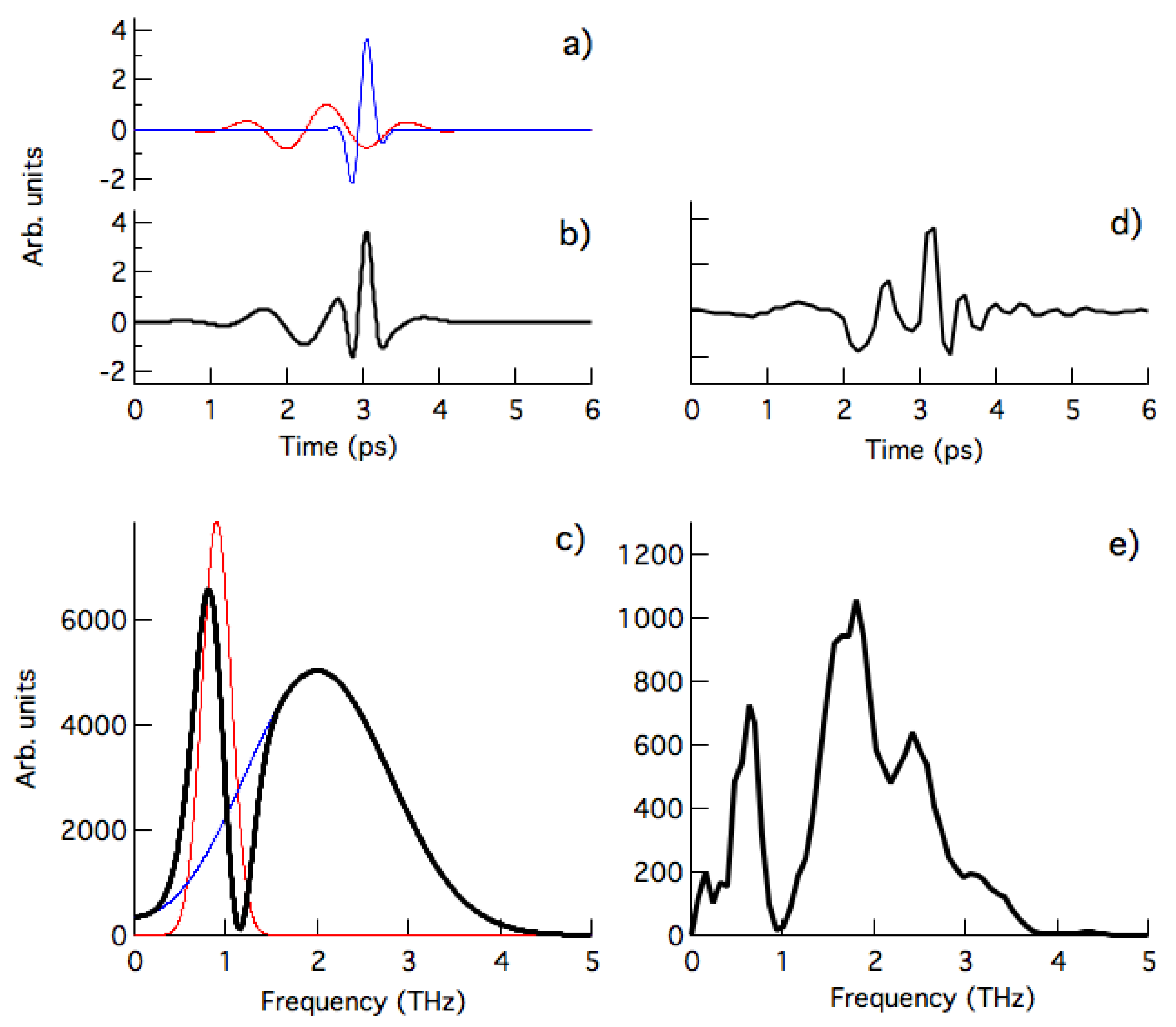
4. Electro-Optic Sampling Results
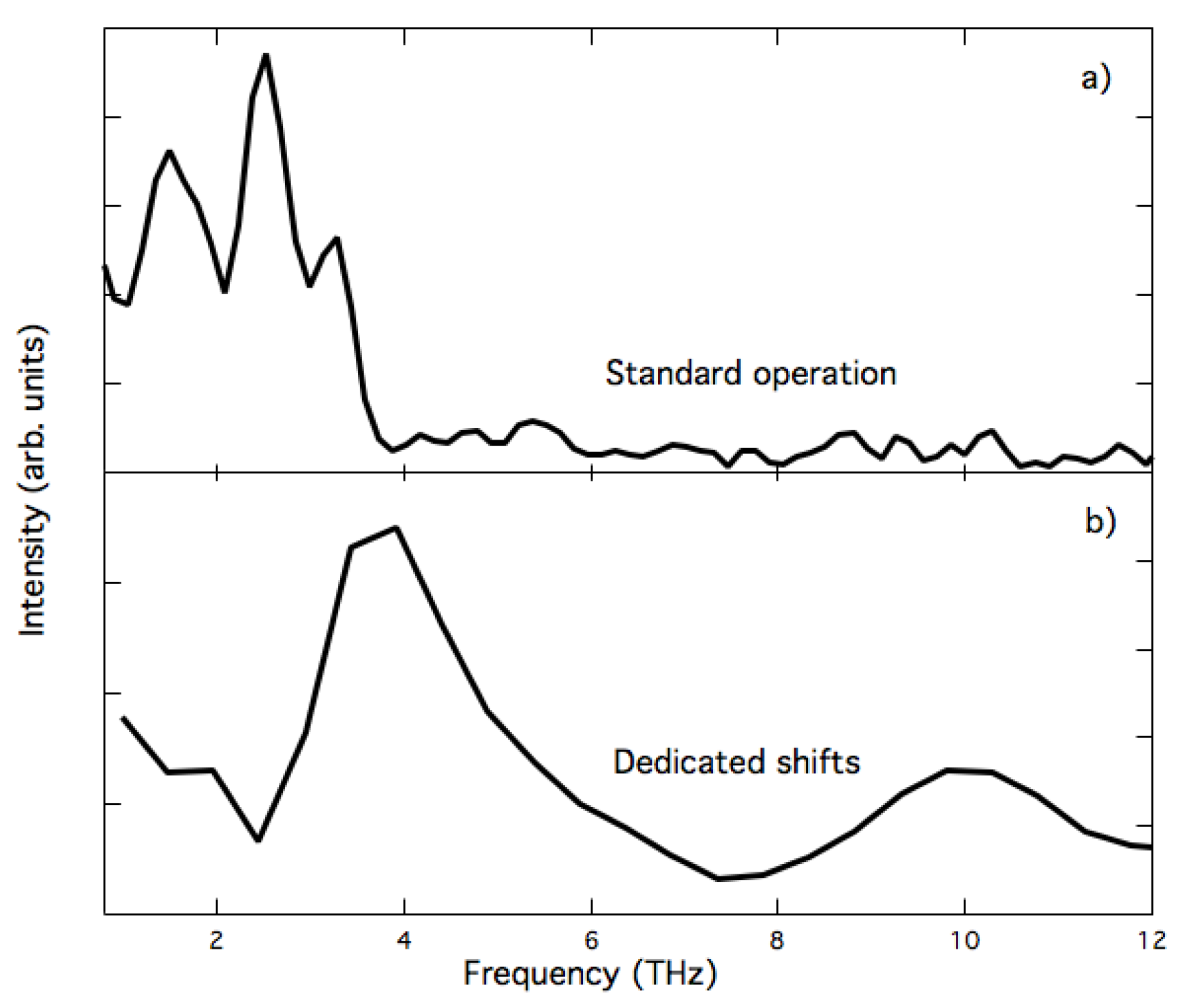
Measured Electric Field and Spectrum
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FEL | Free Electron Laser |
| EOS | Electro Optic Sampling |
| CSR | Coherent Synchrotron Radiation |
| CTR | Coherent Transition Radiation |
| YAG | Yttrium Aluminium Garnet |
| OMO | Optical Master Oscillator |
| PLL | Phase Locked Loop |
| BOCC | Balanced Optical Cross-Correlator |
| SFG | Sum Frequency Generation |
References
- Salén, P.; Basini, M.; Bonetti, S.; Hebling, J.; Krasilnikov, M.; Nikiting, A.Y.; Shamuilov, G.; Tibaid, Z.; Zhaunerchyki, V.; Goryashko, V. Matter Manipulation with Extreme Terahertz Light: Progress in the enabling THz technology. Phys. Rep. 2019, 836–837, 1–74. [Google Scholar] [CrossRef]
- Kampfrath, T.; Tanaka, K.; Nelson, K.A. Resonant and nonresonant control over matter and light by intense terahertz transients. Nat. Photonics 2013, 7, 680. [Google Scholar] [CrossRef]
- Carr, G.L.; Martin, M.C.; McKinney, W.R.; Jordan, K.; Neil, G.R.; Williams, G.P. High-power terahertz radiation from relativistic electrons. Nature 2002, 420, 153. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Watanabe, T.; Arena, D.A.; Kao, C.-C.; Murphy, J.B.; Tsang, T.Y.; Wang, X.J.; Carr, G.L. High-power terahertz radiation from relativistic electrons, Nonlinear Cross-Phase Modulation with Intense Single-Cycle Terahertz Pulses. Phys. Rev. Lett. 2007, 99, 043901. [Google Scholar] [CrossRef] [PubMed]
- Gensch, M.; Bittner, L.; Chesnov, A.; Delsim-Hashemi, H.; Drescher, M.; Faatz, B.; Feldhaus, J.; Fruehling, U.; Geloni, G.A.; Gerth, C.; et al. New infrared undulator beamline at FLASH. Infrared Phys. Technol. 2008, 51, 423. [Google Scholar] [CrossRef]
- Chiadroni, E.; Bacci, A.; Bellaveglia, M.; Boscolo, M.; Castellano, M.; Cultrera, L.; Di Pirro, G.; Ferrario, M.; Ficcadenti, L.; Filippetto, D.; et al. The SPARC linear accelerator based terahertz source. Appl. Phys. Lett. 2013, 102, 094101. [Google Scholar] [CrossRef]
- Green, B.; Kovalev, S.; Asgekar, V.; Geloni, G.; Lehnert, U.; Golz, T.; Kuntzsch, M.; Bauer, C.; Hauser, J.; Voigtlaender, J.; et al. High-Field High-Repetition-Rate Sources for the Coherent THz Control of Matter. Sci. Rep. 2016, 6, 22256. [Google Scholar] [CrossRef] [PubMed]
- Gensch, M. Super-radiant THz facilities: New opportunities for studying selective THz control of matter. Proc. SPIE 2018, 10756, 1075606. [Google Scholar]
- Zapolnova, E.; Golz, T.; Pan, R.; Klose, K.; Schreiber, S.; Stojanovic, N. THz pulse doubler at FLASH: Double pulses for pump-probe experiments at X-ray FELs. J. Synch. Rad. 2017, 25, 39. [Google Scholar] [CrossRef] [PubMed]
- Allaria, E.; Appio, R.; Badano, L.; Barletta, W.A.; Bassanese, S.; Biedron, S.G.; Borga, A.; Busetto, E.; Castronovo, D.; Cinquegrana, P.; et al. Highly coherent and stable pulses from the FERMI seeded free-electron laser in the extreme ultraviolet. Nat. Photonics 2012, 6, 699. [Google Scholar] [CrossRef]
- Perucchi, A.; Di Mitri, S.; Penco, G.; Allaria, E.; Lupi, S. The TeraFERMI terahertz source at the seeded FERMI free-electron-laser facility. Rev. Sci. Instr. 2013, 84, 2. [Google Scholar] [CrossRef] [PubMed]
- Di Mitri, S.; Perucchi, A.; Adhlakha, N.; Di Pietro, P.; Nicastro, S.; Roussel, E.; Spampinati, S.; Veronese, M.; Allaria, E.M.; Badano, L.; et al. Coherent THz Emission Enhanced by Coherent Synchrotron Radiation Wakefield. Sci. Rep. 2018, 8, 11661. [Google Scholar] [CrossRef] [PubMed]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media; Pergamon: New York, NY, USA, 1960. [Google Scholar]
- Casalbuoni, S.; Schmidt, B.; Schmüser, P.; Steffen, B. Far-Infrared Transition and Diffraction Radiation Part I: Production, Diffraction Effects and Optical Propagation. TESLA Rep. 2005, 15, 2012. [Google Scholar]
- Moreno, T.; Westfahl, H.; de Oliveira Freitas, R.; Petroff, Y.; Dumas, P. Optical layouts for large infrared beamline opening angles. J. Phys. Conf. Ser. 2013, 425, 142003. [Google Scholar] [CrossRef]
- Svetina, C.; Mahne, N.; Raimondi, L.; Perucchi, A.; Di Pietro, P.; Lupi, S.; Schmidt, B.; Zangrando, M. Photon transport of the superradiant TeraFERMI THz beamline at the FERMI free-electron laser. J. Synch. Rad. 2016, 23, 106. [Google Scholar] [CrossRef] [PubMed]
- Di Pietro, P.; Adhlakha, N.; Piccirilli, F.; Capasso, L.; Svetina, C.; Di Mitri, S.; Veronese, M.; Giorgianni, F.; Lupi, S.; Perucchi, A. TeraFERMI: A superradiant beamline for THz nonlinear studies at the FERMI free-electron-laser facility. Sync. Rad. News 2017, 30, 36–39. [Google Scholar] [CrossRef]
- Casalbuoni, S.; Schlarb, H.; Schmidt, B.; Schmüser, P.; Steffen, B.; Winter, A. Numerical Studies on the Electro-Optic Sampling of Relativistic Electron Bunches. In Proceedings of the 2005 Particle Accelerator Conference, Knoxville, TN, USA, 16–20 May 2005. [Google Scholar]
- Van Tilborg, J. Coherent terahertz radiation from laser-wakefield-accelerated electron beams. Eindhoven Tech. Univ. Eindhoven 2006. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adhlakha, N.; Di Pietro, P.; Piccirilli, F.; Cinquegrana, P.; Di Mitri, S.; Sigalotti, P.; Spampinati, S.; Veronese, M.; Lupi, S.; Perucchi, A. The TeraFERMI Electro-Optic Sampling Set-Up for Fluence-Dependent Spectroscopic Measurements. Condens. Matter 2020, 5, 8. https://doi.org/10.3390/condmat5010008
Adhlakha N, Di Pietro P, Piccirilli F, Cinquegrana P, Di Mitri S, Sigalotti P, Spampinati S, Veronese M, Lupi S, Perucchi A. The TeraFERMI Electro-Optic Sampling Set-Up for Fluence-Dependent Spectroscopic Measurements. Condensed Matter. 2020; 5(1):8. https://doi.org/10.3390/condmat5010008
Chicago/Turabian StyleAdhlakha, Nidhi, Paola Di Pietro, Federica Piccirilli, Paolo Cinquegrana, Simone Di Mitri, Paolo Sigalotti, Simone Spampinati, Marco Veronese, Stefano Lupi, and Andrea Perucchi. 2020. "The TeraFERMI Electro-Optic Sampling Set-Up for Fluence-Dependent Spectroscopic Measurements" Condensed Matter 5, no. 1: 8. https://doi.org/10.3390/condmat5010008
APA StyleAdhlakha, N., Di Pietro, P., Piccirilli, F., Cinquegrana, P., Di Mitri, S., Sigalotti, P., Spampinati, S., Veronese, M., Lupi, S., & Perucchi, A. (2020). The TeraFERMI Electro-Optic Sampling Set-Up for Fluence-Dependent Spectroscopic Measurements. Condensed Matter, 5(1), 8. https://doi.org/10.3390/condmat5010008









