Sub-THz Waveguide Spectroscopy of Coating Materials for Particle Accelerators
Abstract
1. Introduction
2. Materials and Methods
2.1. The Device under Test
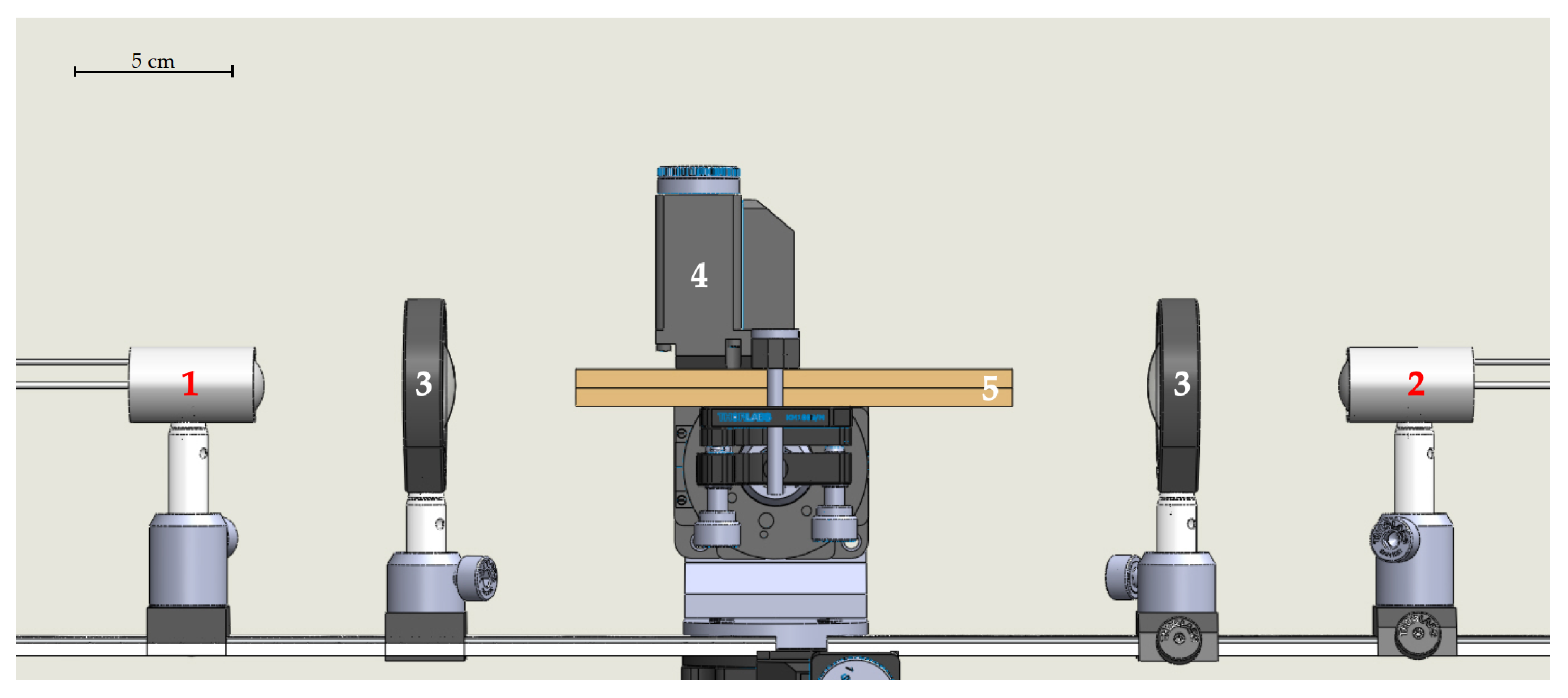
2.2. Sub-THz System
2.3. The Analytical Method
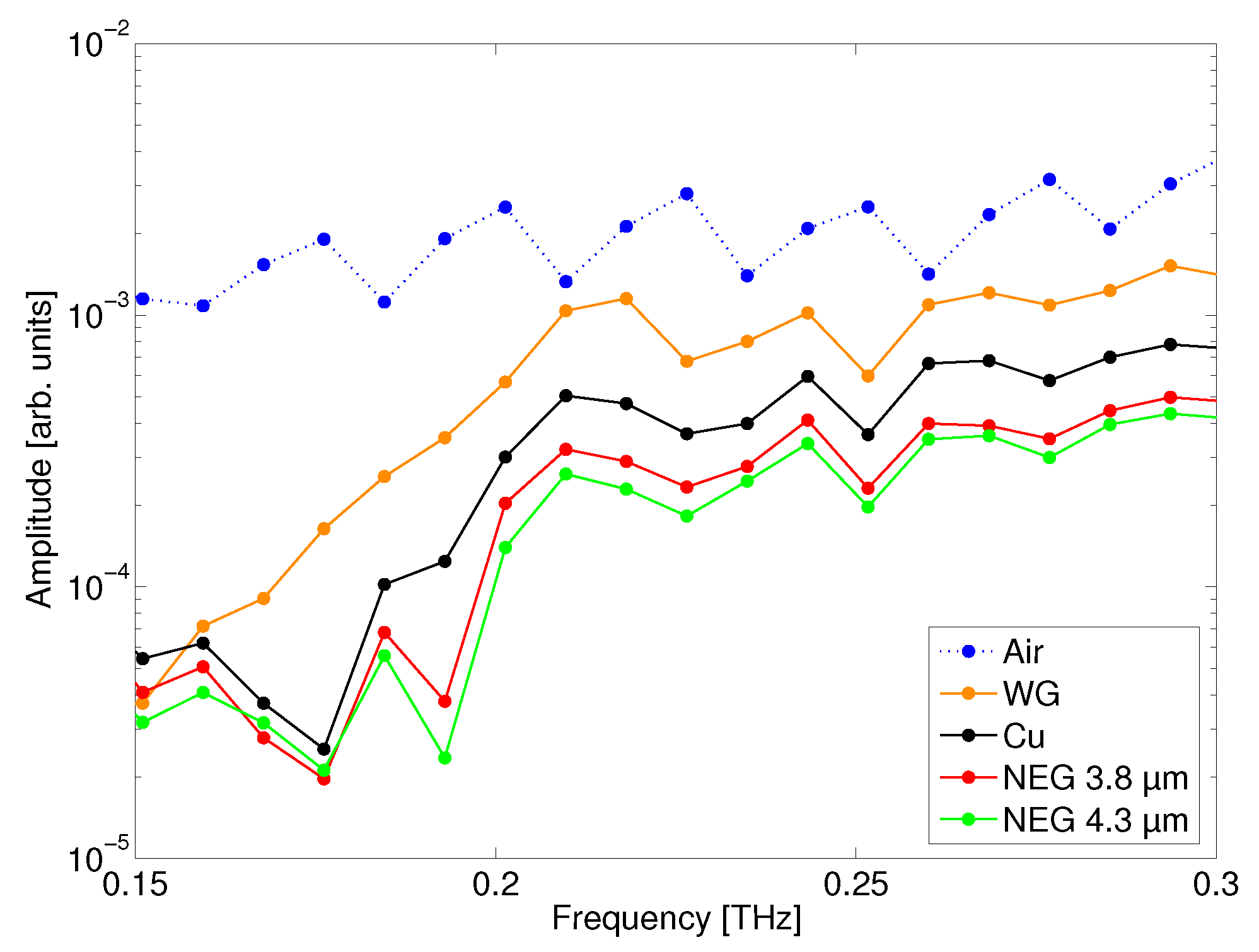
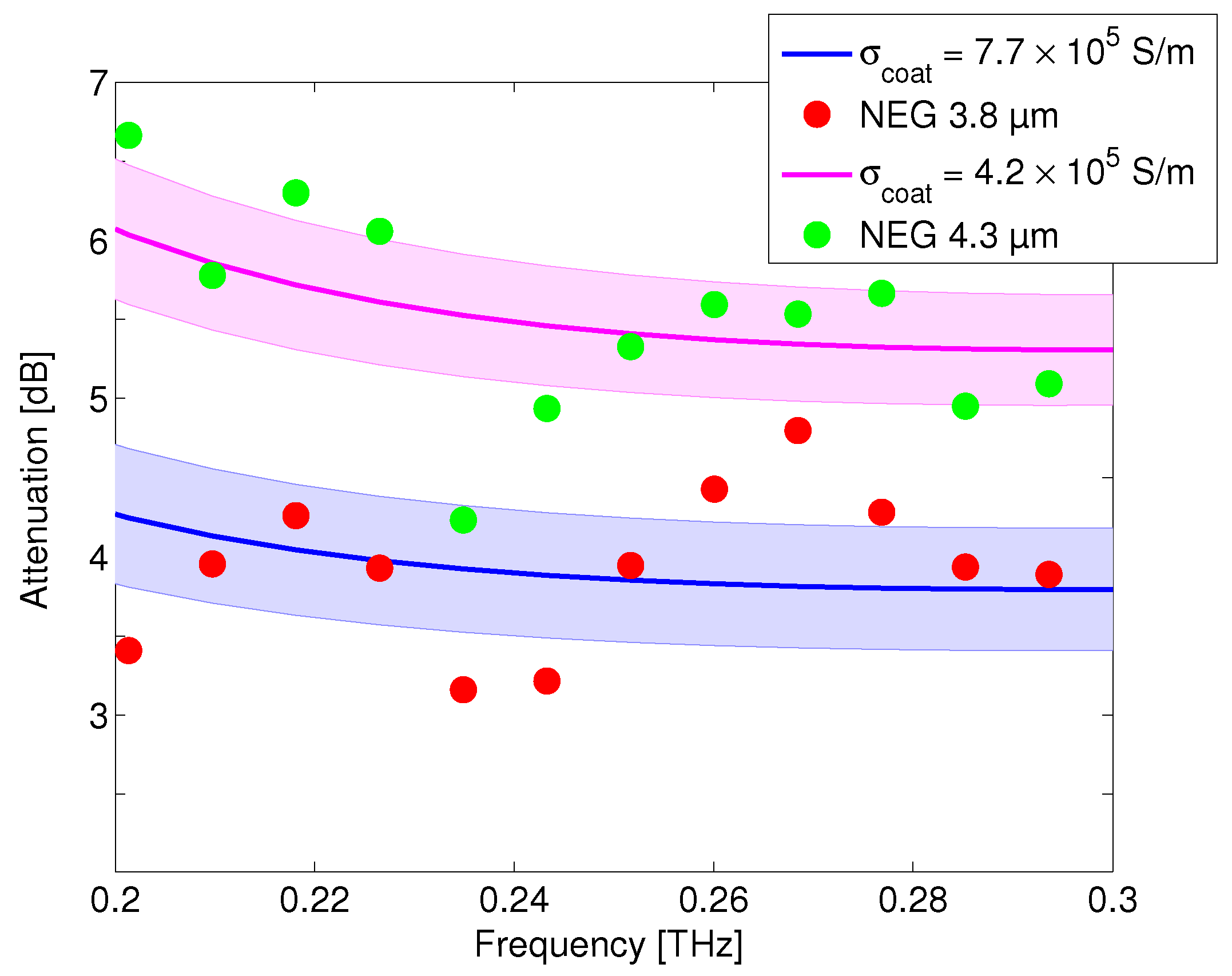
3. Results and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Furman, M.A. Electron Cloud Effects in Accelerators. arXiv 2013, arXiv:1310.1706. [Google Scholar]
- Rumolo, G.; Ruggiero, F.; Zimmermann, F. Simulation of the electron-cloud build up and its consequences on heat load, beam stability, and diagnostics. Phys. Rev. Spec. Top.-Accel. Beams 2001, 4, 012801. [Google Scholar] [CrossRef]
- Cimino, R.; Gonzalez, L.A.; Larciprete, R.; Di Gaspare, A.; Iadarola, G.; Rumolo, G. Detailed investigation of the low energy secondary electron yield of technical Cu and its relevance for the LHC. Phys. Rev. Spec. Top.-Accel. Beams 2015, 18, 051002. [Google Scholar] [CrossRef]
- Yin Vallgren, C.; Arduini, G.; Bauche, J.; Calatroni, S.; Chiggiato, P.; Cornelis, K.; Pinto, P.C.; Henrist, B.; Métral, E.; Neupert, H.; et al. Amorphous carbon coatings for the mitigation of electron cloud in the CERN Super Proton Synchrotron. Phys. Rev. Spec. Top.-Accel. Beams 2011, 14, 071001. [Google Scholar] [CrossRef]
- Taborelli, M.; Chiggiato, P.; Costa Pinto, P.; Cruikshank, P. Nine Years of Carbon Coating Development for the SPS Upgrade: Achievements and Heritage; Technical Report CERN-ACC-2016-0010; CERN: Geneva, Switzerland, 2015. [Google Scholar]
- Palmer, M.; Livezey, J.; Wolski, A.; Zwaska, R.; Sagan, D.; Savino, J.; Williams, H.; Antoniou, F.; Tan, C.Y.; Sikora, J. Electron Cloud at Low Emittance in CesrTA. In Proceedings of the International Particle Accelerator Conference, Kyoto, Japan, 23–28 May 2010. [Google Scholar]
- Benvenuti, C.; Chiggiato, P.; Pinto, P.C.; Santana, A.E.; Hedley, T.; Mongelluzzo, A.; Ruzinov, V.; Wevers, I. Vacuum properties of TiZrV non-evaporable getter films. Vacuum 2001, 60, 57–65. [Google Scholar] [CrossRef]
- Migliorati, M.; Belli, E.; Zobov, M. Impact of the resistive wall impedance on beam dynamics in the Future Circular e+e− Collider. Phys. Rev. Accel. Beams 2018, 21, 041001. [Google Scholar] [CrossRef]
- Federmann, S.; Caspers, F.; Mahner, E. Measurements of electron cloud density in the CERN Super Proton Synchrotron with the microwave transmission method. Phys. Rev. Spec. Top.-Accel. Beams 2011, 14, 012802. [Google Scholar] [CrossRef]
- Koukovini-Platia, E.; Rumolo, G.; Zannini, C. Electromagnetic characterization of nonevaporable getter properties between 220–330 and 500–750 GHz for the Compact Linear Collider damping rings. Phys. Rev. Accel. Beams 2017, 20, 011002. [Google Scholar] [CrossRef]
- Koukovini Platia, E. High Frequency Effects of Impedances and Coatings in the CLIC Damping Rings. Ph.D. Thesis, Ecole Polytechnique, Lausanne, Switzerland, 2015. [Google Scholar]
- Theuer, M.; Melinger, J.S. High Resolution Waveguide Terahertz Time-Domain Spectroscopy. J. Infrared Millim. Terahertz Waves 2011, 32, 1267–1284. [Google Scholar] [CrossRef]
- Razanoelina, M.; Kinjo, R.; Takayama, K.; Kawayama, I.; Murakami, H.; Mittleman, D.M.; Tonouchi, M. Parallel-Plate Waveguide Terahertz Time Domain Spectroscopy for Ultrathin Conductive Films. J. Infrared, Millim. Terahertz Waves 2015, 36, 1182–1194. [Google Scholar] [CrossRef]
- Khachatrian, A.; Melinger, J.S.; Qadri, S.B. Waveguide terahertz time-domain spectroscopy of ammonium nitrate polycrystalline films. J. Appl. Phys. 2012, 111, 093103. [Google Scholar] [CrossRef]
- Zhang, J.; Grischkowsky, D. Adiabatic compression of parallel-plate metal waveguides for sensitivity enhancement of waveguide THz time-domain spectroscopy. Appl. Phys. Lett. 2005, 86, 061109. [Google Scholar] [CrossRef]
- Passarelli, A.; Bartosik, H.; Rumolo, G.; Vaccaro, V.G.; Masullo, M.R.; Koral, C.; Papari, G.P.; Andreone, A.; Boine-Frankenheim, O. Novel measurement technique for the electromagnetic characterization of coating materials in the sub-THz frequency range. Phys. Rev. Accel. Beams 2018, 21, 103101. [Google Scholar] [CrossRef]
- Prodromides, A.E.; Levy, F. Non-Evaporable Getter Thin Film Coatings for Vacuum Applications. Ph.D. Thesis, Ecole Polytechnique, Lausanne, Switzerland, 1 September 2002; pp. 95–96. [Google Scholar]
- Johansson, J.F.; Whyborn, N.D. The diagonal horn as a sub-millimeter wave antenna. IEEE Trans. Microw. Theory Tech. 1992, 40, 795–800. [Google Scholar] [CrossRef]
- Lee, C.S.; Lee, S.W.; Chuang, S.L. Plot of Modal Field Distribution in Rectangular and Circular Waveguides. IEEE Trans. Microw. Theory Tech. 1985, 33, 271–274. [Google Scholar] [CrossRef]
- Papari, G.P.; Silvestri, B.; Vitiello, G.; De Stefano, L.; Rea, I.; Luciani, G.; Aronne, A.; Andreone, A. Morphological, Structural, and Charge Transfer Properties of F-Doped ZnO: A Spectroscopic Investigation. J. Phys. Chem. C 2017, 121, 16012–16020. [Google Scholar] [CrossRef]
- Marcuvitz, N. Waveguide Handbook; IEE: London, UK, 1986. [Google Scholar]
- Franceschetti, G. Electromagnetics: Theory, Techniques, and Engineering Paradigms; Springer: New York, NY, USA, 1997. [Google Scholar]
- Mendis, R.; Mittleman, D.M. Comparison of the lowest-order transverse-electric (TE1) and transverse-magnetic (TEM) modes of the parallel-plate waveguide for terahertz pulse applications. Opt. Express 2009, 17, 14839–14850. [Google Scholar] [CrossRef] [PubMed]
- Hammerstad, E.; Jensen, O. Accurate Models for Microstrip Computer-Aided Design. In Proceedings of the 1980 IEEE MTT-S International Microwave symposium Digest, Washington, DC, USA, 28–30 May 1980; pp. 407–409. [Google Scholar] [CrossRef]

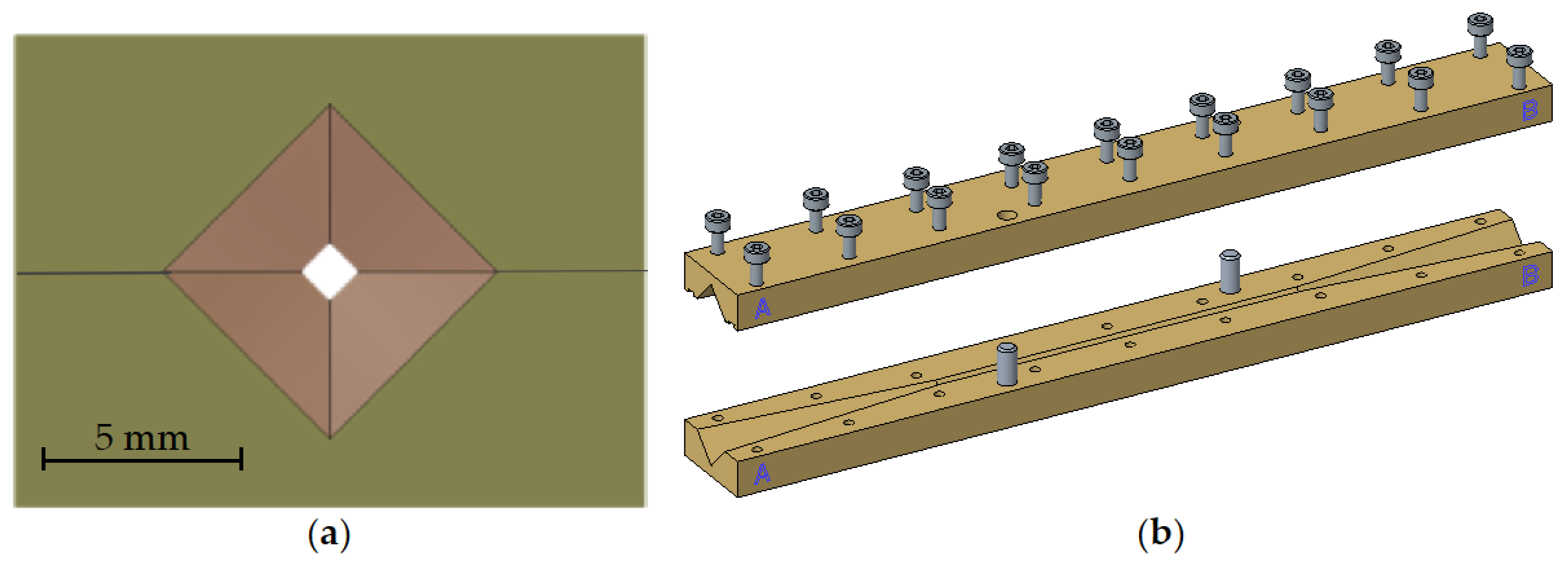

| Material | Brass (Au Plated) |
|---|---|
| Waveguide | Diagonal |
| Length [mm] | 62 |
| Side [mm] | |
| Transition | Pyramidal |
| Length [mm] | 39 |
| Side [mm] | |
| Total Length [mm] | 140 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Passarelli, A.; Koral, C.; Masullo, M.R.; Vollenberg, W.; Amador, L.L.; Andreone, A. Sub-THz Waveguide Spectroscopy of Coating Materials for Particle Accelerators. Condens. Matter 2020, 5, 9. https://doi.org/10.3390/condmat5010009
Passarelli A, Koral C, Masullo MR, Vollenberg W, Amador LL, Andreone A. Sub-THz Waveguide Spectroscopy of Coating Materials for Particle Accelerators. Condensed Matter. 2020; 5(1):9. https://doi.org/10.3390/condmat5010009
Chicago/Turabian StylePassarelli, Andrea, Can Koral, Maria Rosaria Masullo, Wilhelmus Vollenberg, Lucia Lain Amador, and Antonello Andreone. 2020. "Sub-THz Waveguide Spectroscopy of Coating Materials for Particle Accelerators" Condensed Matter 5, no. 1: 9. https://doi.org/10.3390/condmat5010009
APA StylePassarelli, A., Koral, C., Masullo, M. R., Vollenberg, W., Amador, L. L., & Andreone, A. (2020). Sub-THz Waveguide Spectroscopy of Coating Materials for Particle Accelerators. Condensed Matter, 5(1), 9. https://doi.org/10.3390/condmat5010009









