Dynamical Detection of Level Repulsion in the One-Particle Aubry-André Model
Abstract
1. Introduction
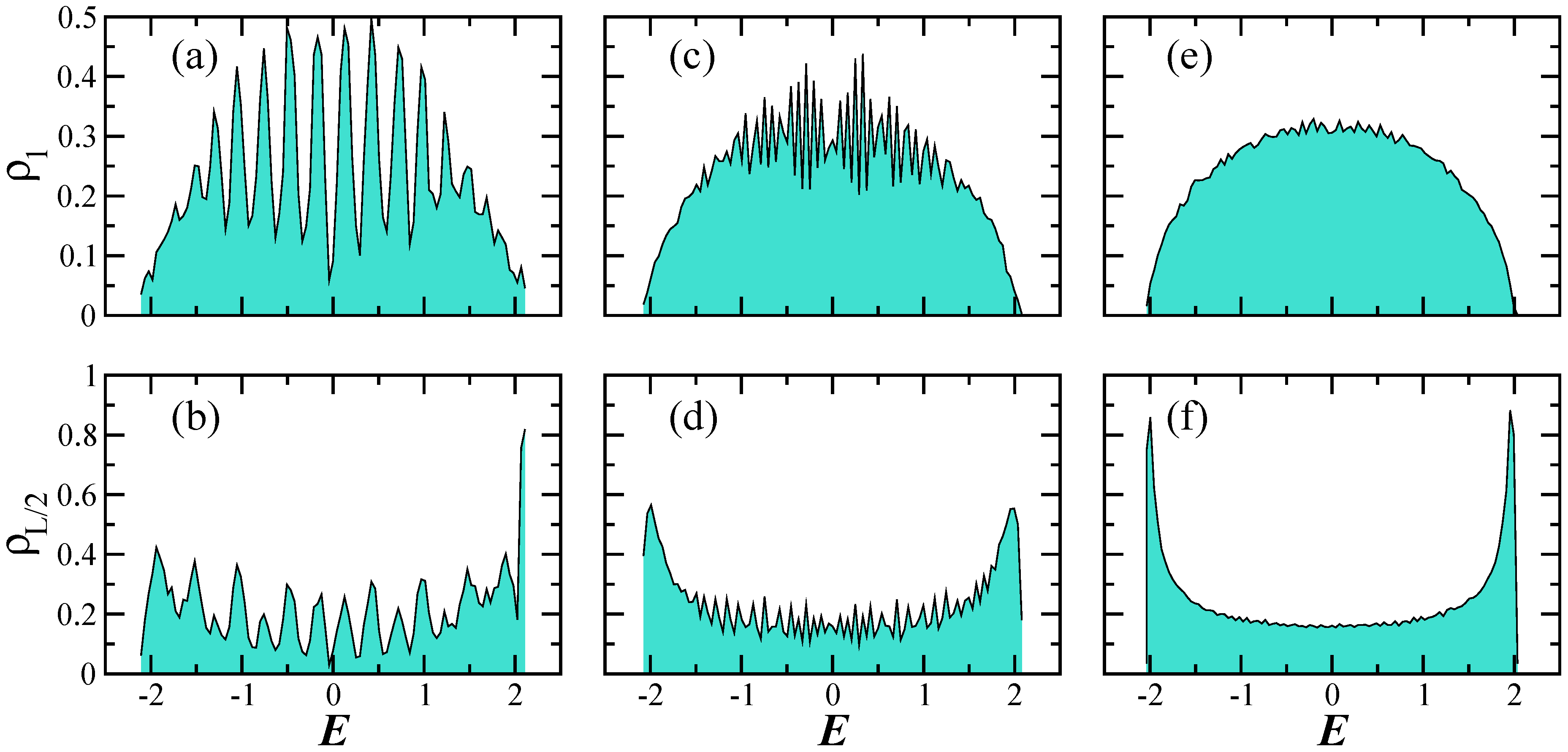
2. Finite One-Particle One-Dimension Aubry-André Model
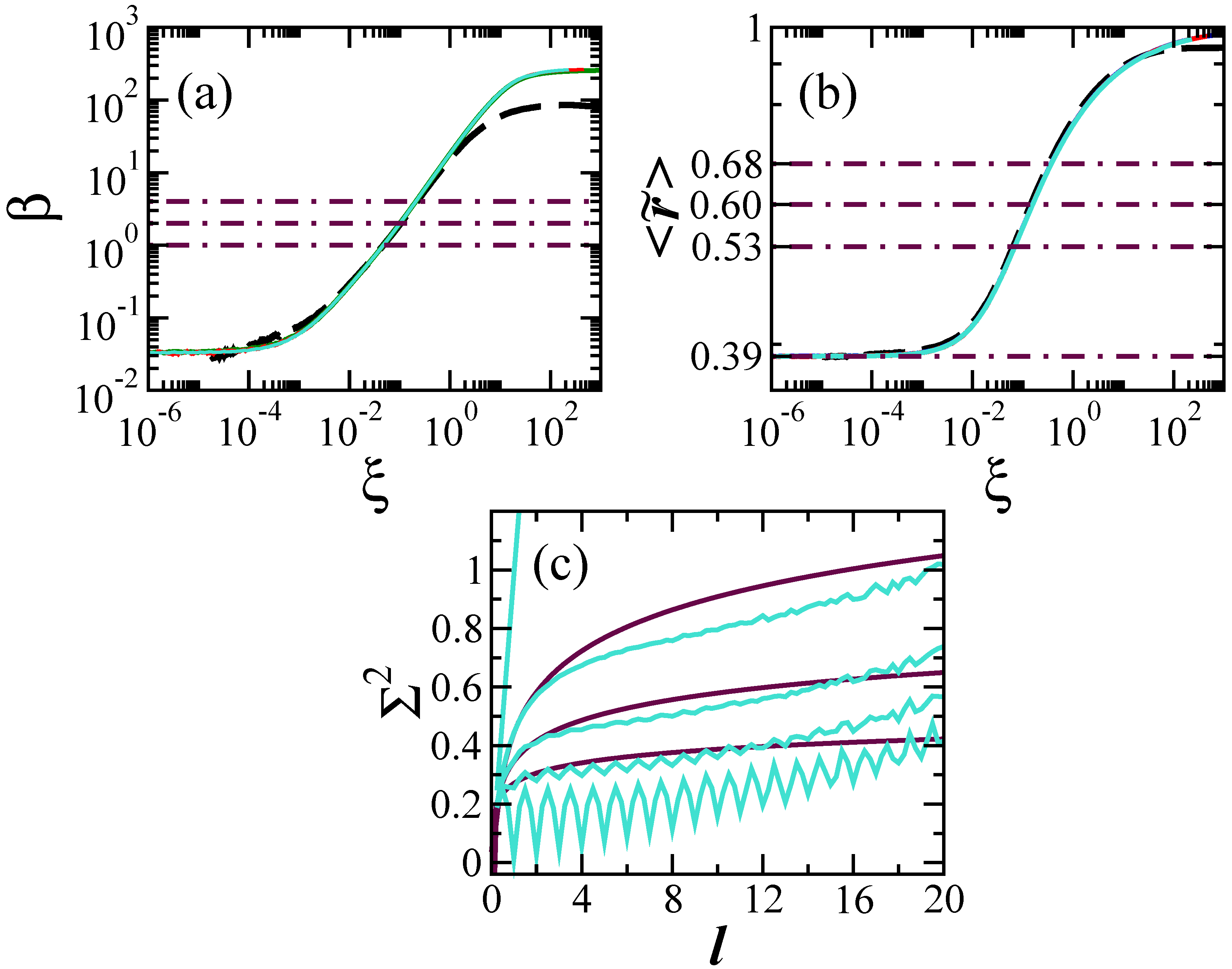
2.1. Level Statistics
2.1.1. Short-Range Correlations
2.1.2. Long-Range Correlations
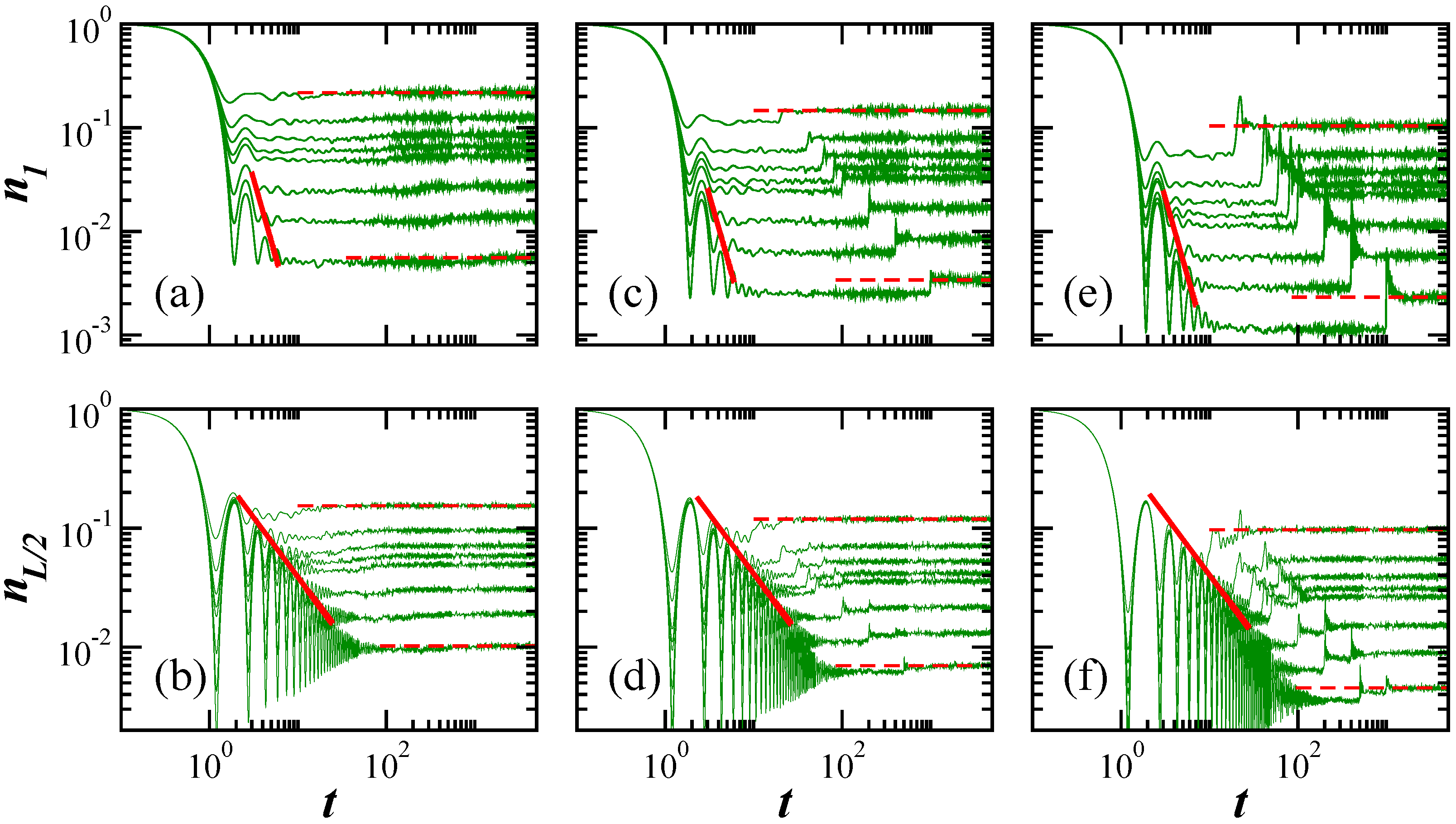
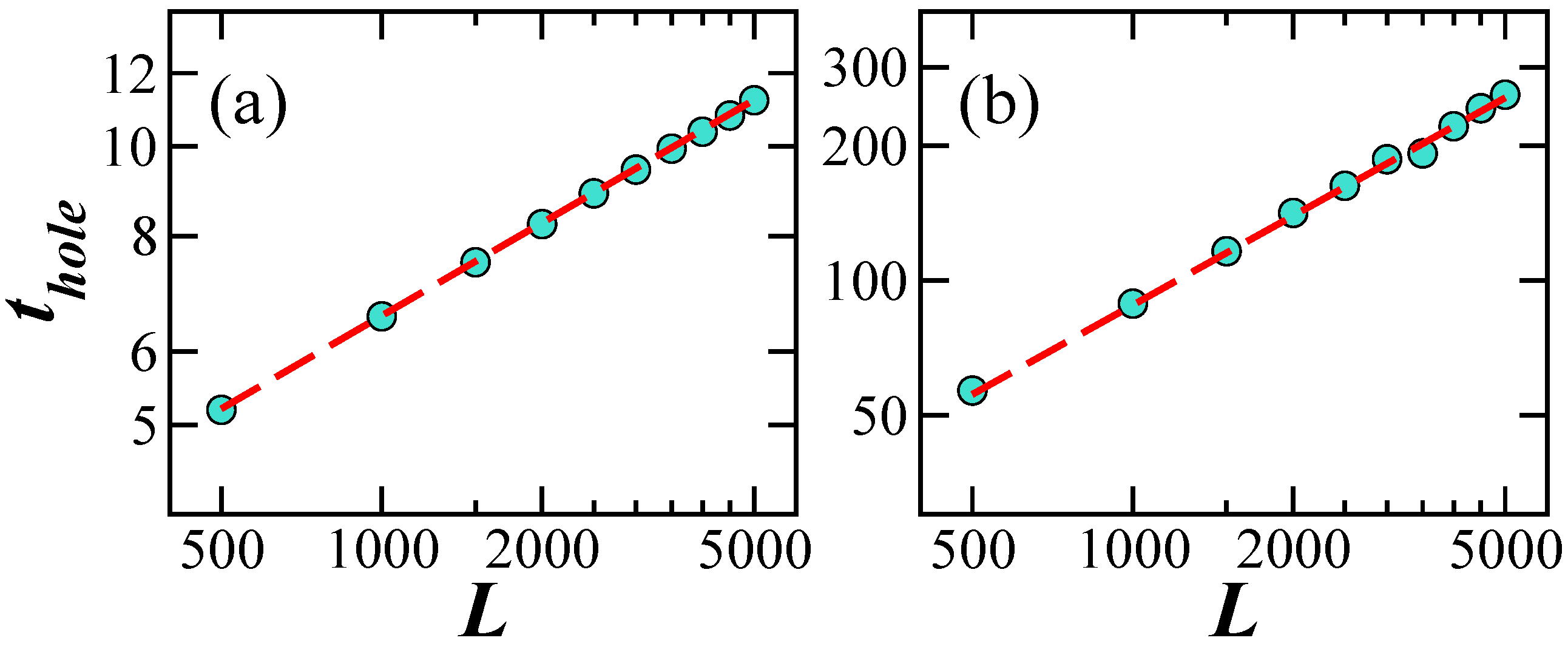
3. Evolution of the Number Operator
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kitaev, A. Kitp Talk. 2015. Available online: http://online.kitp.ucsb.edu/online/entangled15/kitaev/ (accessed on 15 June 2016).
- Maldacena, J.; Stanford, D. Remarks on the Sachdev-Ye-Kitaev model. Phys. Rev. D 2016, 94, 106002. [Google Scholar] [CrossRef]
- Maldacena, J.; Shenker, S.H.; Stanford, D. A bound on chaos. J. High Energy Phys. 2016, 2016, 106. [Google Scholar] [CrossRef]
- Daniel, A. Roberts and Douglas Stanford. Diagnosing chaos using four-point functions in two-dimensional conformal field theory. Phys. Rev. Lett. 2015, 115, 131603. [Google Scholar]
- Fan, R.; Zhang, P.; Shen, H.; Zhai, H. Out-of-time-order correlation for many-body localization. Sci. Bull. 2017, 62, 707–711. [Google Scholar] [CrossRef]
- Luitz, D.J.; Lev, Y.B. Information propagation in isolated quantum systems. Phys. Rev. B 2017, 96, 020406. [Google Scholar] [CrossRef]
- Borgonovi, F.; Izrailev, F.M.; Santos, L.F. Timescales in the quench dynamics of many-body quantum systems: Participation ratio versus out-of-time ordered correlator. Phys. Rev. E 2019, 99, 052143. [Google Scholar] [CrossRef] [PubMed]
- Yan, H.; Wang, J.; Wang, W. Similar early growth of out-of-time-ordered correlators in quantum chaotic and integrable ising chains. arXiv 2019, arXiv:1906.11775. [Google Scholar] [CrossRef]
- García-Mata, I.; Saraceno, M.; Jalabert, R.A.; Roncaglia, A.J.; Wisniacki, D.A. Chaos signatures in the short and long time behavior of the out-of-time ordered correlator. arXiv 2018, arXiv:1806.04281. [Google Scholar]
- Bohigas, O.; Giannoni, M.; Schmit, C. Spectral fluctuations of classically chaotic quantum systems. Lect. Notes Phys. 1986, 263, 18. [Google Scholar]
- Guhr, T.; Mueller-Gröeling, A.; Weidenmüller, H.A. Random matrix theories in quantum physics: Common concepts. Phys. Rep. 1998, 299, 189. [Google Scholar] [CrossRef]
- Haake, F. Quantum Signatures of Chaos; Springe: Berlin, Gremany, 1991. [Google Scholar]
- Stöckmann, H.-J. Quantum Chaos: An Introduction; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Rozenbaum, E.B.; Ganeshan, S.; Galitski, V. Lyapunov exponent and out-of-time-ordered correlator’s growth rate in a chaotic system. Phys. Rev. Lett. 2017, 118, 086801. [Google Scholar] [CrossRef] [PubMed]
- Jalabert, R.A.; García-Mata, I.; Wisniacki, D.A. Semiclassical theory of out-of-time-order correlators for low-dimensional classically chaotic systems. Phys. Rev. E 2018, 98, 062218. [Google Scholar] [CrossRef]
- Rozenbaum, E.B.; Ganeshan, S.; Galitski, V. Universal level statistics of the out-of-time-ordered operator. arXiv 2018, arXiv:1801.10591. [Google Scholar] [CrossRef]
- Chávez-Carlos, J.; López-del Carpio, B.; Bastarrachea-Magnani, M.A.; Stránský, P.; Lerma-Hernández, S.; Santos, L.F.; Hirsch, J.G. Quantum and classical Lyapunov exponents in atom-field interaction systems. Phys. Rev. Lett. 2019, 122, 024101. [Google Scholar] [CrossRef]
- Lewis-Swan, R.J.; Safavi-Naini, A.; Bollinger, J.J.; Rey, A.M. Unifying scrambling, thermalization and entanglement through measurement of fidelity out-of-time-order correlators in the Dicke model. Nat. Commun. 2019, 10, 1581. [Google Scholar] [CrossRef]
- Pappalardi, S.; Russomanno, A.; Zunkovic, B.; Iemini, F.; Silva, A.; Rosario, F. Scrambling and entanglement spreading in long-range spin chains. Phys. Rev. B 2018, 98, 134303. [Google Scholar] [CrossRef]
- Hummel, Q.; Geiger, B.; Urbina, J.D.; Richter, K. Reversible quantum information spreading in many-body systems near criticality. Phys. Rev. Lett. 2019, 123, 160401. [Google Scholar] [CrossRef]
- Pilatowsky-Cameo, S.; Chávez-Carlos, J.; Bastarrachea-Magnani, M.A.; Stránský, P.; Lerma-Hernández, S.; Santos, L.F.; Hirsch, J.G. Positive quantum Lyapunov exponents in classically regular systems. arXiv 2019, arXiv:1909.02578. [Google Scholar]
- Schreiber, M.; Hodgman, S.S.; Bordia, P.; Lüschen, H.P.; Fischer, M.H.; Vosk, R.; Altman, E.; Schneider, U.; Bloch, I. Observation of many-body localization of interacting fermions in a quasirandom optical lattice. Science 2015, 349, 842–845. [Google Scholar] [CrossRef]
- Harper, P.G. Single band motion of conduction electrons in a uniform magnetic field. Proc. Phys. Soc. A 1955, 68, 874–878. [Google Scholar] [CrossRef]
- Aubry, S.; André, G. Analyticity breaking and Anderson localization in incommensurate lattices. Ann. Isr. Phys. Soc. 1980, 3, 18. [Google Scholar]
- Sokoloff, J.B. Unusual band structure, wave functions and electrical conductance in crystals with incommensurate periodic potentials. Phys. Rep. 1985, 126, 189–244. [Google Scholar] [CrossRef]
- Domínguez-Castro, G.A.; Paredes, R. The Aubry-André model as the hobbyhorse for understanding localization phenomenon. arXiv 2018, arXiv:1812.06201. [Google Scholar] [CrossRef]
- Roy, N.; Sharma, A. Study of counterintuitive transport properties in the aubry-andré-harper model via entanglement entropy and persistent current. Phys. Rev. B 2019, 100, 195143. [Google Scholar] [CrossRef]
- Anderson, P.W. Absence of diffusion in certain random lattices. Phys. Rev. 1958, 109, 1492. [Google Scholar] [CrossRef]
- Lee, P.A.; Ramakrishnan, T.V. Disordered electronic systems. Rev. Mod. Phys. 1985, 57, 287–337. [Google Scholar] [CrossRef]
- Kramer, B.; MacKinnon, A. Localization: Theory and experiment. Rep. Prog. Phys. 1993, 56, 1469. [Google Scholar] [CrossRef]
- Lagendijk, A.; Van Tiggelen, B.; Wiersma, D.S. Fifty years of Anderson localization. Phys. Today 2009, 62, 24. [Google Scholar] [CrossRef]
- Sorathia, S.; Izrailev, F.M.; Zelevinsky, V.G.; Celardo, G.L. From closed to open one-dimensional Anderson model: Transport versus spectral statistics. Phys. Rev. E 2012, 86, 011142. [Google Scholar] [CrossRef]
- Torres-Herrera, E.J.; Méndez-Bermúdez, J.A.; Santos, L.F. Level repulsion and dynamics in the finite one-dimensional Anderson model. Phys. Rev. E 2019, 100, 022142. [Google Scholar] [CrossRef]
- Leviandier, L.; Lombardi, M.; Jost, R.; Pique, J.P. Fourier transform: A tool to measure statistical level properties in very complex spectra. Phys. Rev. Lett. 1986, 56, 2449–2452. [Google Scholar] [CrossRef]
- Guhr, T.; Weidenmüller, H.A. Correlations in anticrossing spectra and scattering theory. analytical aspects. Chem. Phys. 1990, 146, 21–38. [Google Scholar] [CrossRef]
- Wilkie, J.; Brumer, P. Time-dependent manifestations of quantum chaos. Phys. Rev. Lett. 1991, 67, 1185–1188. [Google Scholar] [CrossRef] [PubMed]
- Alhassid, Y.; Levine, R.D. Spectral autocorrelation function in the statistical theory of energy levels. Phys. Rev. A 1992, 46, 4650–4653. [Google Scholar] [CrossRef]
- Gorin, T.; Seligman, T.H. Signatures of the correlation hole in total and partial cross sections. Phys. Rev. E 2002, 65, 026214. [Google Scholar] [CrossRef] [PubMed]
- Torres-Herrera, E.J.; Santos, L.F. Extended nonergodic states in disordered many-body quantum systems. Ann. Phys. (Berlin) 2017, 529, 1600284. [Google Scholar] [CrossRef]
- Torres-Herrera, E.J.; Santos, L.F. Dynamical manifestations of quantum chaos: Correlation hole and bulge. Philos. Trans. Royal Soc. A 2017, 375, 20160434. [Google Scholar] [CrossRef]
- Torres-Herrera, E.J.; García-García, A.M.; Santos, L.F. Generic dynamical features of quenched interacting quantum systems: Survival probability, density imbalance, and out-of-time-ordered correlator. Phys. Rev. B 2018, 97, 060303. [Google Scholar] [CrossRef]
- Cotler, J.S.; Gur-Ari, G.; Hanada, M.; Polchinski, J.; Saad, P.; Shenker, S.H.; Stanford, D.; Streicher, A.; Tezuka, M. Black holes and random matrices. J. High Energy Phys. 2017, 2017, 118. [Google Scholar] [CrossRef]
- Numasawa, T. Late time quantum chaos of pure states in random matrices and in the sachdev-ye-kitaev model. Phys. Rev. D 2019, 100, 126017. [Google Scholar] [CrossRef]
- Schiulaz, M.; Torres-Herrera, E.J.; Santos, L.F. Thouless and relaxation time scales in many-body quantum systems. Phys. Rev. B 2019, 99, 174313. [Google Scholar] [CrossRef]
- Lerma-Hernández, S.; Villaseñor, D.; Bastarrachea-Magnani, M.A.; Torres-Herrera, E.J.; Santos, L.F.; Hirsch, J.G. Dynamical signatures of quantum chaos and relaxation time scales in a spin-boson system. Phys. Rev. E 2019, 100, 012218. [Google Scholar] [CrossRef] [PubMed]
- Singh, K.; Fujiwara, C.J.; Geiger, Z.A.; Simmons, E.Q.; Lipatov, M.; Cao, A.; Dotti, P.; Rajagopal, S.V.; Senaratne, R.; Shimasaki, T.; et al. Quantifying and controlling prethermal nonergodicity in interacting Floquet matter. arXiv 2018, arXiv:1809.05554. [Google Scholar] [CrossRef]
- Griniasty, M.; Fishman, S. Localization by pseudorandom potentials in one dimension. Phys. Rev. Lett. 1988, 60, 1334–1337. [Google Scholar] [CrossRef] [PubMed]
- Mehta, M.L. Random Matrices; Academic Press: Boston, MA, USA, 1991. [Google Scholar]
- Oganesyan, V.; Huse, D.A. Localization of interacting fermions at high temperature. Phys. Rev. B 2007, 75, 155111. [Google Scholar] [CrossRef]
- Atas, Y.Y.; Bogomolny, E.; Giraud, O.; Roux, G. Distribution of the ratio of consecutive level spacings in random matrix ensembles. Phys. Rev. Lett. 2013, 110, 084101. [Google Scholar] [CrossRef]
- Gómez, J.M.G.; Molina, R.A.; Relaño, A.; Retamosa, J. Misleading signatures of quantum chaos. Phys. Rev. E 2002, 66, 036209. [Google Scholar] [CrossRef]
- Berry, M.V.; Tabor, M. Level clustering in the regular spectrum. Proc. R. Soc. Lond. A 1997, 356, 375–394. [Google Scholar] [CrossRef]
- Pandey, A.; Ramaswamy, R. Level spacings for harmonic-oscillator systems. Phys. Rev. A 1991, 43, 4237–4243. [Google Scholar] [CrossRef]
- Chirikov, B.V.; Shepelyansky, D.L. Shnirelman peak in level spacing statistics. Phys. Rev. Lett. 1995, 74, 518–521. [Google Scholar] [CrossRef]
- Izrailev, F.M. Simple models of quantum chaos: Spectrum and eigenfunctions. Phys. Rep. 1990, 196, 299–392. [Google Scholar] [CrossRef]
- Wu, H.; Sprung, D.W.L.; Feng, D.H.; Vallières, M. Modeling chaotic quantum systems by tridiagonal random matrices. Phys. Rev. E 1993, 47, 4063–4066. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.-M.; Feng, D.H. Quantum nonintegrability in finite systems. Phys. Rep. 1995, 252, 1–100. [Google Scholar] [CrossRef]
- Relaño, A.; Dukelsky, J.; Gómez, J.M.G.; Retamosa, J. Stringent numerical test of the poisson distribution for finite quantum integrable hamiltonians. Phys. Rev. E 2004, 70, 026208. [Google Scholar] [CrossRef] [PubMed]
- Flambaum, V.V.; Gribakina, A.A.; Gribakin, G.F.; Kozlov, M.G. Structure of compound states in the chaotic spectrum of the ce atom: Localization properties, matrix elements, and enhancement of weak perturbations. Phys. Rev. A 1994, 50, 267–296. [Google Scholar] [CrossRef]
- Angom, D.; Ghosh, S.; Kota, V.K.B. Strength functions, entropies, and duality in weakly to strongly interacting fermionic systems. Phys. Rev. E 2004, 70, 016209. [Google Scholar] [CrossRef]
- Izrailev, F.M.; Castañeda-Mendoza, A. Return probability: Exponential versus Gaussian decay. Phys. Lett. A 2006, 350, 355–362. [Google Scholar] [CrossRef]
- Torres-Herrera, E.J.; Santos, L.F. Quench dynamics of isolated many-body quantum systems. Phys. Rev. A 2014, 89, 043620. [Google Scholar] [CrossRef]
- Távora, M.; Torres-Herrera, E.J.; Santos, L.F. Inevitable power-law behavior of isolated many-body quantum systems and how it anticipates thermalization. Phys. Rev. A 2016, 94, 041603. [Google Scholar] [CrossRef]
- Távora, M.; Torres-Herrera, E.J.; Santos, L.F. Power-law decay exponents: A dynamical criterion for predicting thermalization. Phys. Rev. A 2017, 95, 013604. [Google Scholar] [CrossRef]
- Torres-Herrera, E.J.; Kollmar, D.; Santos, L.F. Relaxation and thermalization of isolated many-body quantum systems. Phys. Scr. T 2015, 165, 014018. [Google Scholar] [CrossRef]
- Santos, L.F.; Távora, M.; Pérez-Bernal, F. Excited-state quantum phase transitions in many-body systems with infinite-range interaction: Localization, dynamics, and bifurcation. Phys. Rev. A 2016, 94, 012113. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torres-Herrera, E.J.; Santos, L.F. Dynamical Detection of Level Repulsion in the One-Particle Aubry-André Model. Condens. Matter 2020, 5, 7. https://doi.org/10.3390/condmat5010007
Torres-Herrera EJ, Santos LF. Dynamical Detection of Level Repulsion in the One-Particle Aubry-André Model. Condensed Matter. 2020; 5(1):7. https://doi.org/10.3390/condmat5010007
Chicago/Turabian StyleTorres-Herrera, Eduardo Jonathan, and Lea F. Santos. 2020. "Dynamical Detection of Level Repulsion in the One-Particle Aubry-André Model" Condensed Matter 5, no. 1: 7. https://doi.org/10.3390/condmat5010007
APA StyleTorres-Herrera, E. J., & Santos, L. F. (2020). Dynamical Detection of Level Repulsion in the One-Particle Aubry-André Model. Condensed Matter, 5(1), 7. https://doi.org/10.3390/condmat5010007




