Resonant Quantum Kicked Rotor as A Continuous-Time Quantum Walk
Abstract
1. Introduction
2. Probability Distributions of the Walks
2.1. Review of the QKR
2.2. Evolution of CTQW
3. Equivalence between Resonant QKR and CTQW
3.1. Equivalence at the Hamiltonian Level
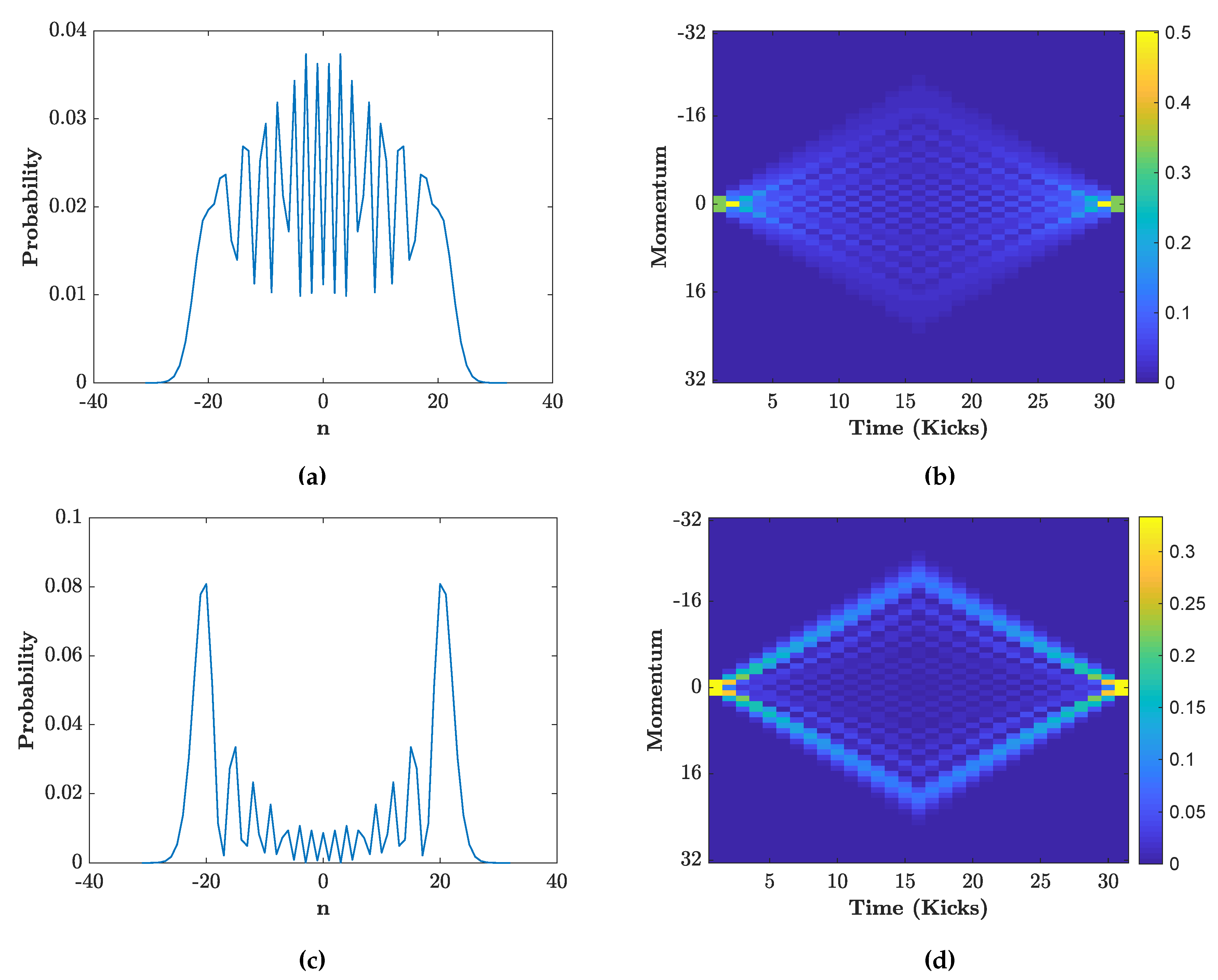
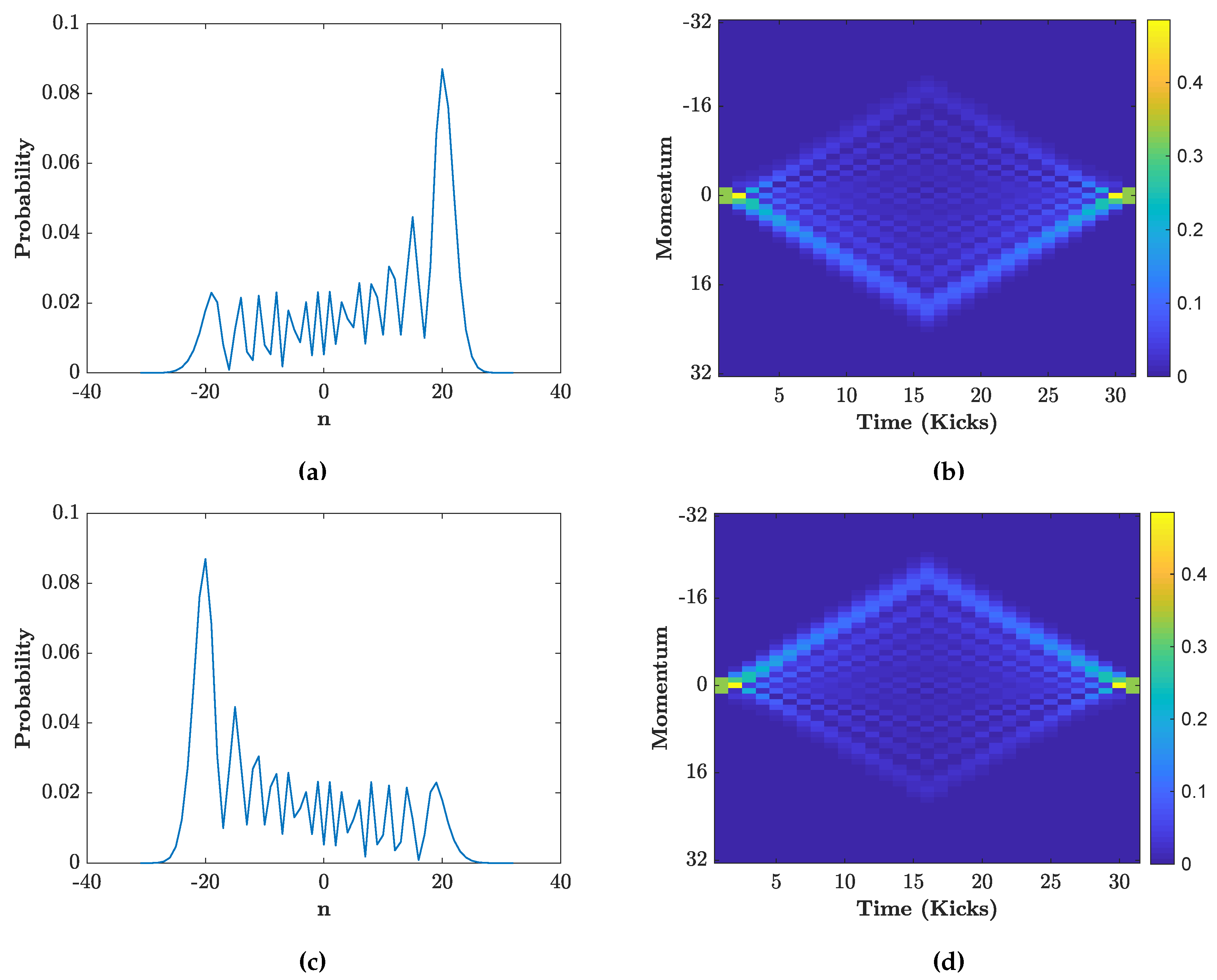
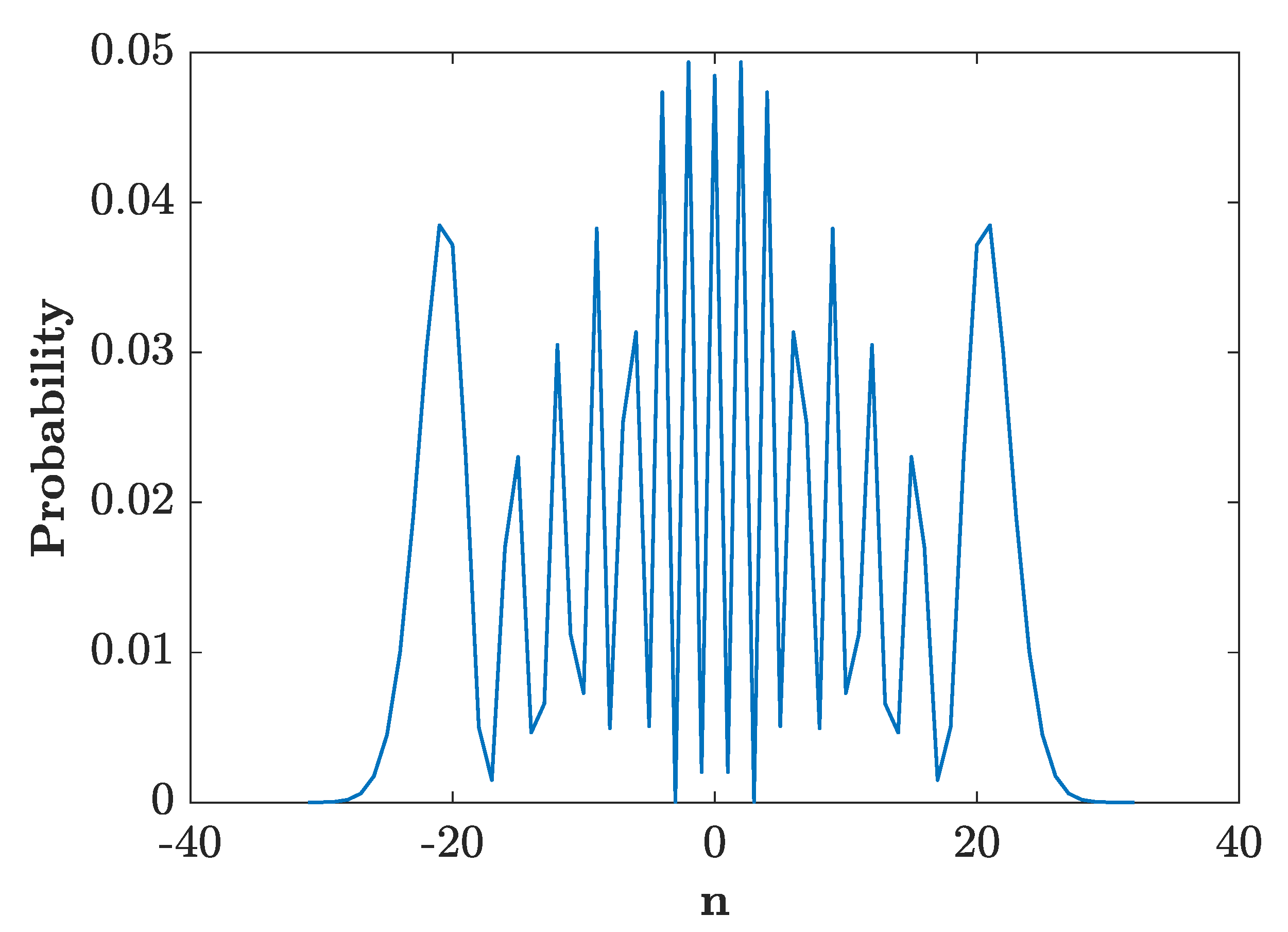
3.2. Distributions for Specific Initial States
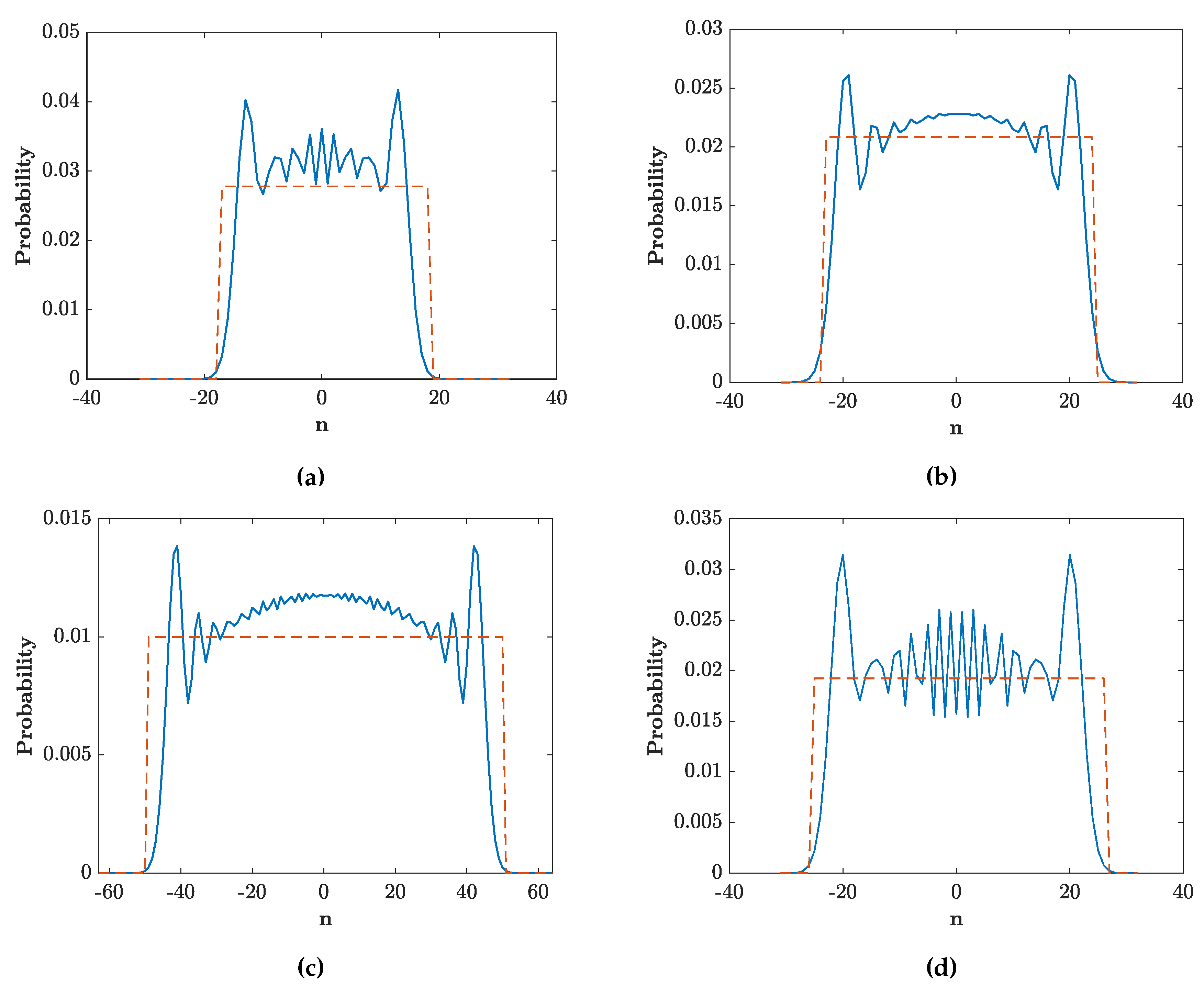
4. Engineering the Final Walk Distributions
5. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Explicit Calculations for the Distributions of CTQW
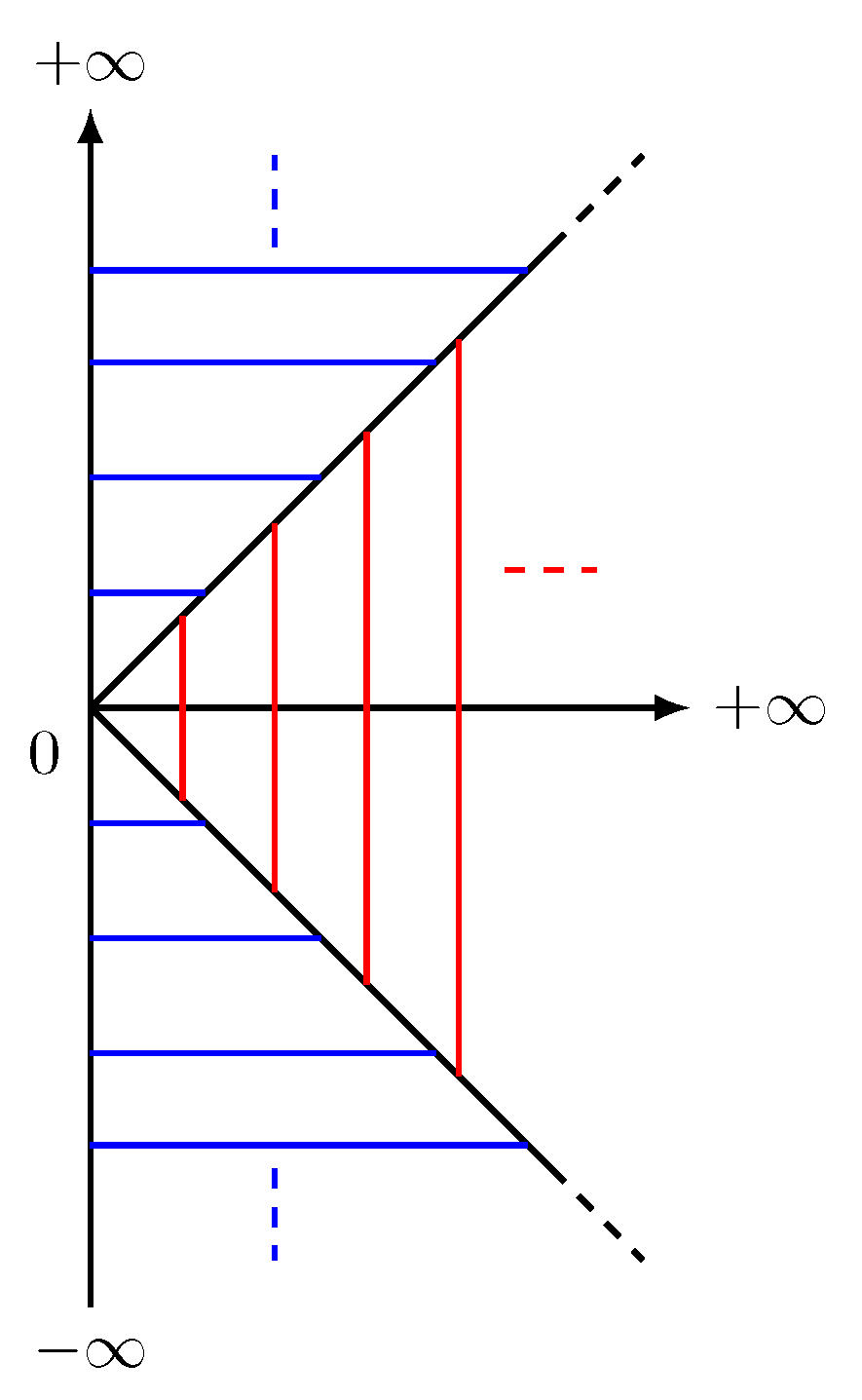
Appendix B. Bessel Identity Check
Appendix C. Modified Vandermonde’s Identity
References
- Aharonov, Y.; Davidovich, L.; Zagury, N. Quantum random walks. Phys. Rev. A 1993, 48, 1687. [Google Scholar] [CrossRef]
- Sadgrove, M.; Horikoshi, M.; Sekimura, T.; Nakagawa, K. Rectified Momentum Transport for a Kicked Bose-Einstein Condensate. Phys. Rev. Lett. 2007, 99, 043002. [Google Scholar] [CrossRef]
- Dana, I.; Ramareddy, V.; Talukdar, I.; Summy, G.S. Experimental Realization of Quantum-Resonance Ratchets at Arbitrary Quasimomenta. Phys. Rev. Lett. 2008, 100, 024103. [Google Scholar] [CrossRef] [PubMed]
- White, D.H.; Ruddell, S.K.; Hoogerland, M.D. Experimental realization of a quantum ratchet through phase modulation. Phys. Rev. A 2013, 88, 063603. [Google Scholar] [CrossRef]
- Ni, J.; Dadras, S.; Lam, W.K.; Shrestha, R.K.; Sadgrove, M.; Wimberger, S.; Summy, G.S. Hamiltonian Ratchets with Ultra-Cold Atoms. Ann. Phys. 2017, 529, 1600335. [Google Scholar] [CrossRef]
- Sadgrove, M.; Wimberger, S. A pseudoclassical method for the atom-optics kicked rotor: From theory to experiment and back. In Advances in Atomic, Molecular, and Optical Physics; Elsevier: Amsterdam, The Netherlands, 2011; Volume 60, pp. 315–369. [Google Scholar]
- Ni, J.; Lam, W.K.; Dadras, S.; Borunda, M.F.; Wimberger, S.; Summy, G.S. Initial-state dependence of a quantum resonance ratchet. Phys. Rev. A 2016, 94, 043620. [Google Scholar] [CrossRef]
- Portugal, R. Quantum Walks and Search Algorithms; Springer: Berlin, Germany, 2013. [Google Scholar]
- Delvecchio, M.; Groiseau, C.; Petiziol, F.; Summy, G.; Wimberger, S. Quantum search with a continuous-time quantum walk in momentum space. J. Phys. B 2019, in press. [Google Scholar] [CrossRef]
- Bouwmeester, D.; Marzoli, I.; Karman, G.P.; Schleich, W.; Woerdman, J.P. Optical Galton board. Phys. Rev. A 1999, 61, 013410. [Google Scholar] [CrossRef]
- Du, J.; Li, H.; Xu, X.; Shi, M.; Wu, J.; Zhou, X.; Han, R. Experimental implementation of the quantum random-walk algorithm. Phys. Rev. A 2003, 67, 042316. [Google Scholar] [CrossRef]
- Perets, H.B.; Lahini, Y.; Pozzi, F.; Sorel, M.; Morandotti, R.; Silberberg, Y. Realization of quantum walks with negligible decoherence in waveguide lattices. Phys. Rev. Lett. 2008, 100, 170506. [Google Scholar] [CrossRef]
- Tang, H.; Lin, X.F.; Feng, Z.; Chen, J.Y.; Gao, J.; Sun, K.; Wang, C.Y.; Lai, P.C.; Xu, X.Y.; Wang, Y.; et al. Experimental two-dimensional quantum walk on a photonic chip. Sci. Adv. 2018, 4. [Google Scholar] [CrossRef] [PubMed]
- Izaac, J.A.; Zhan, X.; Bian, Z.; Wang, K.; Li, J.; Wang, J.B.; Xue, P. Centrality measure based on continuous-time quantum walks and experimental realization. Phys. Rev. A 2017, 95, 032318. [Google Scholar] [CrossRef]
- Preiss, P.M.; Ma, R.; Tai, M.E.; Lukin, A.; Rispoli, M.; Zupancic, P.; Lahini, Y.; Islam, R.; Greiner, M. Strongly correlated quantum walks in optical lattices. Science 2015, 347, 1229–1233. [Google Scholar] [CrossRef] [PubMed]
- Summy, G.; Wimberger, S. Quantum random walk of a Bose-Einstein condensate in momentum space. Phys. Rev. A 2016, 93, 023638. [Google Scholar]
- Weiß, M.; Groiseau, C.; Lam, W.K.; Burioni, R.; Vezzani, A.; Summy, G.S.; Wimberger, S. Steering random walks with kicked ultracold atoms. Phys. Rev. A 2015, 92, 033606. [Google Scholar] [CrossRef]
- Dadras, S.; Gresch, A.; Groiseau, C.; Wimberger, S.; Summy, G.S. Quantum Walk in Momentum Space with a Bose-Einstein Condensate. Phys. Rev. Lett. 2018, 121, 070402. [Google Scholar] [CrossRef]
- Dadras, S.; Gresch, A.; Groiseau, C.; Wimberger, S.; Summy, G.S. Experimental realization of a momentum-space quantum walk. Phys. Rev. A 2019, 99, 043617. [Google Scholar] [CrossRef]
- Knight, P.L.; Roldán, E.; Sipe, J.E. Quantum walk on the line as an interference phenomenon. Phys. Rev. A 2003, 68, 020301. [Google Scholar] [CrossRef]
- Buerschaper, O.; Burnett, K. Stroboscopic quantum walks. arXiv 2004, arXiv:quant-ph/0406039. [Google Scholar]
- Ishkhanyan, A.M. Narrowing of interference fringes in diffraction of prepared atoms by standing waves. Phys. Rev. A 2000, 61, 063609. [Google Scholar] [CrossRef]
- Romanelli, A.; Hernández, G. Anomalous diffusion in the resonant quantum kicked rotor. Phys. A Stat. Mech. Appl. 2010, 389, 3420–3426. [Google Scholar] [CrossRef][Green Version]
- Hernández, G.; Romanelli, A. Resonant quantum kicked rotor with two internal levels. Phys. Rev. A 2013, 87, 042316. [Google Scholar] [CrossRef]
- Romanelli, A.; Hernández, G. Driving the resonant quantum kicked rotor via extended initial conditions. Eur. Phys. J. D 2011, 64, 131–136. [Google Scholar] [CrossRef]
- Matsuoka, L.; Segawa, E.; Yuki, K.; Konno, N.; Obata, N. Asymptotic behavior of a rotational population distribution in a molecular quantum-kicked rotor with ideal quantum resonance. Phys. Lett. A 2017, 381, 1773–1779. [Google Scholar] [CrossRef]
- Matsuoka, L. Unified parameter for localization in isotope-selective rotational excitation of diatomic molecules using a train of optical pulses. Phys. Rev. A 2015, 91, 043420. [Google Scholar] [CrossRef]
- Behinaein, G.; Ramareddy, V.; Ahmadi, P.; Summy, G.S. Exploring the Phase Space of the Quantum δ-Kicked Accelerator. Phys. Rev. Lett. 2006, 97, 244101. [Google Scholar] [CrossRef]
- Casati, G.; Chirikov, B.; Ford, J.; Izrailev, F. Stochastic Behavior of A Quantum Pendulum Under Periodic Perturbation. In Lecture Notes in Physics; Casati, G., Ford, J., Eds.; Springer: Berlin, Germany, 1979. [Google Scholar]
- Fishman, S. Quantum Localization. In Quantum Chaos; Casati, G., Chirikov, B.V., Eds.; School “E. Fermi” CXIX; IOS – North Holland: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Wimberger, S. Nonlinear Dynamics and Quantum Chaos; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Izrailev, F.M. Simple models of quantum chaos: Spectrum and eigenfunctions. Phys. Rep. 1990, 196, 299–392. [Google Scholar] [CrossRef]
- Raizen, M.G. Quantum chaos with cold atoms. Adv. Atom Molec. Opt. Phys. 1999, 41, 199. [Google Scholar]
- Duffy, G.J.; Parkins, S.; Müller, T.; Sadgrove, M.; Leonhardt, R.; Wilson, A.C. Experimental investigation of early-time diffusion in the quantum kicked rotor using a Bose-Einstein condensate. Phys. Rev. E 2004, 70, 056206. [Google Scholar] [CrossRef]
- Ryu, C.; Andersen, M.F.; Vaziri, A.; d’Arcy, M.B.; Grossman, J.M.; Helmerson, K.; Phillips, W.D. High-Order Quantum Resonances Observed in a Periodically Kicked Bose-Einstein Condensate. Phys. Rev. Lett. 2006, 96, 160403. [Google Scholar] [CrossRef]
- Wimberger, S.; Guarneri, I.; Fishman, S. Quantum resonances and decoherence for delta-kicked atoms. Nonlinearity 2003, 16, 1381. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Dover: New York, NY, USA, 1972. [Google Scholar]
- Farhi, E.; Gutmann, S. Quantum computation and decision trees. Phys. Rev. A 1998, 58, 915–928. [Google Scholar] [CrossRef]
- Sadgrove, M.; Wimberger, S.; Nakagawa, K. Phase-selected momentum transport in ultra-cold atoms. Eur. Phys. J. D 2012, 66, 155. [Google Scholar] [CrossRef]
- Alberti, A.; Wimberger, S. Quantum walk of a Bose-Einstein condensate in the Brillouin zone. Phys. Rev. A 2017, 96, 023620. [Google Scholar] [CrossRef]
- Ho, D.Y.H.; Gong, J. Quantized Adiabatic Transport In Momentum Space. Phys. Rev. Lett. 2012, 109, 010601. [Google Scholar] [CrossRef]
- Chen, Y.; Tian, C. Planck’s Quantum-Driven Integer Quantum Hall Effect in Chaos. Phys. Rev. Lett. 2014, 113, 216802. [Google Scholar] [CrossRef]
- Dana, I. Topological properties of adiabatically varied Floquet systems. Phys. Rev. E 2017, 96, 022216. [Google Scholar] [CrossRef]
- Zhou, L.; Gong, J. Floquet topological phases in a spin-1/2 double kicked rotor. Phys. Rev. A 2018, 97, 063603. [Google Scholar] [CrossRef]
- Groiseau, C.; Wagner, A.; Summy, G.S.; Wimberger, S. Impact of Lattice Vibrations on the Dynamics of a Spinor Atom-Optics Kicked Rotor. Condens. Matter 2019, 4, 10. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delvecchio, M.; Petiziol, F.; Wimberger, S. Resonant Quantum Kicked Rotor as A Continuous-Time Quantum Walk. Condens. Matter 2020, 5, 4. https://doi.org/10.3390/condmat5010004
Delvecchio M, Petiziol F, Wimberger S. Resonant Quantum Kicked Rotor as A Continuous-Time Quantum Walk. Condensed Matter. 2020; 5(1):4. https://doi.org/10.3390/condmat5010004
Chicago/Turabian StyleDelvecchio, Michele, Francesco Petiziol, and Sandro Wimberger. 2020. "Resonant Quantum Kicked Rotor as A Continuous-Time Quantum Walk" Condensed Matter 5, no. 1: 4. https://doi.org/10.3390/condmat5010004
APA StyleDelvecchio, M., Petiziol, F., & Wimberger, S. (2020). Resonant Quantum Kicked Rotor as A Continuous-Time Quantum Walk. Condensed Matter, 5(1), 4. https://doi.org/10.3390/condmat5010004





