Next Article in Journal / Special Issue
Time Reversal Symmetry Breaking Superconductors: Sr2RuO4 and Beyond
Previous Article in Journal
High Precision Test of the Pauli Exclusion Principle for Electrons
Previous Article in Special Issue
Multiple Electronic Components and Lifshitz Transitions by Oxygen Wires Formation in Layered Cuprates and Nickelates
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Condensed Matter
Volume 4
Issue 2
10.3390/condmat4020046
condensedmatter-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Orbital Symmetry and Orbital Excitations in High-Tc Superconductors

by
Andrzej M. Oleś
1,2,*,
Krzysztof Wohlfeld
3 and
Giniyat Khaliullin
1
1
Max Planck Institute for Solid State Research, Heisenbergstrasse 1, D-70569 Stuttgart, Germany
2
Marian Smoluchowski Institute of Physics, Jagiellonian University, Prof. S. ojasiewicza 11, PL-30348 Kraków, Poland
3
Institute of Theoretical Physics, Faculty of Physics, University of Warsaw, Pasteura 5, PL-02093 Warsaw, Poland
*
Author to whom correspondence should be addressed.
Condens. Matter 2019, 4(2), 46; https://doi.org/10.3390/condmat4020046
Submission received: 12 March 2019 / Revised: 29 April 2019 / Accepted: 2 May 2019 / Published: 6 May 2019
(This article belongs to the Special Issue From cuprates to Room Temperature Superconductors)
Browse Figures
Versions Notes

Abstract

:
We discuss a few possibilities of high- T c superconductivity with more than one orbital symmetry contributing to the pairing. First, we show that the high energies of orbital excitations in various cuprates suggest a simplified model with a single orbital of x 2 − y 2 symmetry doped by holes. Next, several routes towards involving both e g orbital symmetries for doped holes are discussed: (i) some give superconductivity in a CuO 2 monolayer on Bi2212 superconductors, Sr 2 CuO 4 − δ , Ba 2 CuO 4 − δ , while (ii) others as nickelate heterostructures or Eu 2 − x Sr x NiO 4 , could in principle realize it as well. At low electron filling of Ru ions, spin-orbital entangled states of t 2 g symmetry contribute in Sr 2 RuO 4 . Finally, electrons with both t 2 g and e g orbital symmetries contribute to the superconducting properties and nematicity of Fe-based superconductors, pnictides or FeSe. Some of them provide examples of orbital-selective Cooper pairing.

1. Introduction: Towards Superconductivity with Orbital Degrees of Freedom

Significance of the discovery of high- T c superconductivity by Bednorz and Muller [1] for recent progress in the quantum many-body theory cannot be overestimated—it triggered a huge amount of innovative research on quantum materials and unconventional superconductors, both in the experiment and in the theory. In spite of reaching a qualitative understanding of the nature of the superconducting (SC) state in different transition metal compounds, several open problems remain. Some are related to cuprates, as the astonishing complexity of the phase diagram and the physical origin of the temperature T * observed well above T c itself [2,3,4,5,6]; others are more general and include questions about the origin of pairing [7,8,9,10,11], optimal conditions for the onset of the SC state [12,13,14,15], variation under pressure [16], and the actual orbital symmetry at the Fermi surface [17].
In this short review we concentrate on the last question. After the discovery of high- T c superconductivity in cuprates it was believed that lifting of degeneracy of e g orbitals was important to obtain the SC state with a high value of T c [18,19,20]. Indeed, typically in cuprates degeneracy is quite lifted and relevance of Jahn-Teller effect is controversial. It is under discussion whether the effective model for cuprates has nondegenerate orbitals and may be represented by extended Hubbard model with on-site Coulomb and further neighbor hopping [21]. Yet, it is derived for the case of large splitting of e g orbitals, while orbital degrees of freedom might play an important role in the SC instability and the multiorbital Hubbard model is a standard model for all high- T c superconductors in general, where the dome of T c occurs by driving the chemical potential in the proximity of a Lifshitz transition [22].
We shall not address here the role played by electron-phonon coupling which is expected to contribute in cuprates and is a driving force of recently discovered superconductivity in H 3 S [23,24]. In particular, since the degenerate orbital degrees of freedom necessarily come along with strong Jahn-Teller coupling [25,26], the electron-phonon coupling seems to be essential for SC instabilities in all systems with orbital degeneracy. Nevertheless, to make this review more focused, we shall limit ourselves to the consequences of the orbital degeneracy for the models containing solely electronic degrees of freedom—thus leaving the interplay of the electron-phonon coupling and the orbital degeneracy in the high- T c superconductors for another work.
The outline of this paper is as follows. One early idea in the theory of cuprate superconductivity was that orbital excitations could contribute to the pairing mechanism, as discussed also in Section 2.1, but this was not supported by more recent developments. A usual situation is that the pairing occurs for holes in a single molecular orbital of x 2 − y 2 symmetry, see Section 2.2. But certainly an interesting question is whether allowing for the presence of holes in both e g orbitals would not lead to enhanced SC instabilities. This idea has its roots in the Jahn-Teller physics in cuprates [25,26], as well as in the observation that the propagation of a hole in a Mott (or charge-transfer) insulator is much richer when both e g orbitals can participate [27]. Partial filling of both e g orbitals could be realized in the highly overdoped CuO 2 monolayer grown on Bi 2 Sr 2 CaCu 2 O 8 + δ (Bi2212) [28,29]. We remark that the symmetry of the SC phase in Bi2212 has been extensively discussed in the literature (see, e.g., [30,31,32,33,34,35]).
Furthermore, we emphasize that two-dimensional (2D) systems are special, and possible SC instability was predicted for a layered geometry of NiO 2 planes in LaNiO 3 /LaMO 3 superlattices [36]. We follow this idea and discuss briefly remarkable similarity between overdoped cuprates and nickelates in Section 3.1 and Section 3.2. Furthermore, superconductivity occurs also in metallic systems with t 2 g degrees of freedom, i.e., in planar ruthenate Sr 2 RuO 4 (Section 3.3) and in Fe-based superconductors (Section 3.4). In the latter systems orbital fluctuations are expected to contribute [8,37]. The former systems are of particular interest as there spin-orbit interaction entangles spin-orbital degrees of freedom and the orbital states become mixed [38]. A planar iridate Sr 2 IrO 4 with an even stronger spin-orbit coupling shows much of the cuprate phenomenology [39], but no superconductivity was reported so far. This review is summarized in Section 4.

2. The Role of Orbitals in Superconducting Cuprates

2.1. Earlier Theoretical Proposals

Following the idea of Jahn-Teller physics in cuprates [25,26], a question arises how many orbital symmetries should be included in a minimal realistic model for cuprates. Already in the early years of high- T c , the idea of going beyond the single band picture by including O( 2 p ) orbitals in the three-band model has emerged [40,41,42]. Whether or not the oxygen orbitals could be fully integrated out is still not fully resolved [43,44,45]. Leaving this issue open, we shall present here an overview of the role played by the copper orbital degrees of freedom.
It has been discussed early on that multiple orbitals contribute to the physical properties of YBa 2 Cu 3 O 7 − x [46,47,48] and La 2 − x Sr x CuO 4 [49,50]. The coupling to the lattice was employed as sensitive to the orbital content of wave-functions—multiorbital components were deduced from uniaxial and hydrostatic pressure effects on the value of T c [51], and from the effect of rhombic distortion on the polarized x-ray absorption spectra in high- T c superconductors [52].
Further research on stripes and electron-lattice interactions suggested the presence of pseudo-Jahn-Teller effect in cuprates [53,54,55,56]. These phenomena follow in a natural way from orbital pseudo-degeneracy [57], and these ideas were further developed in [58,59,60,61,62]. Support for the relevance of electron-phonon interaction comes from the observation of the isotope effect on the pseudogap temperature T * [63], from strong renormalization of certain phonons by doped holes [64], and from recently observed phonon anomalies in charge density wave states in cuprates [65,66].
Already shortly after the discovery of high- T c cuprates, it was suggested by Weber [67] that an orbital excitation could be responsible for the pairing. In a typical copper oxide the nearest neighbor Coulomb interaction between holes in the oxygen p orbitals and the copper 3 z 2 − r 2 orbital is substantially smaller than between holes in the oxygen p orbitals and the Cu x 2 − y 2 orbital—such an aspherical Coulomb interaction is estimated to be of the order of 0.3-0.5 eV in the cuprates [67]. Consequently, an excitonic pairing mechanism was proposed: two oxygen holes can gain energy provided that the first one excites the Cu d hole from the x 2 − y 2 to the 3 z 2 − r 2 orbital and the second one follows, forming a pair. This mechanism was later further improved by Jarrell, Cox, and others [68,69] by including the superexchange processes between the nearest neighbor oxygen p orbitals and both Cu e g orbitals. This latter mechanism was estimated to roughly triple the strength of the coupling between the orbital exciton and the holes on oxygen.
While the above proposal is appealing, unfortunately it is not very realistic: the crucial role played by the copper spins is completely neglected and it is implicitly assumed that the doped holes go to the π -bonding oxygen orbitals. A more realistic two-orbital e g model was proposed in [27], and the onset of superconductivity in the various versions of the two-orbital Hubbard models was studied in more detail, e.g., in [70,71,72,73]. Nevertheless, in order to verify whether these models could be relevant to the cuprate superconductivity, it is crucial to include the size of the crystal-field splitting between the Cu 3 z 2 − r 2 and x 2 − y 2 orbitals—as discussed in the next subsection.

2.2. Orbital Excitations in Cuprates

In a ‘typical’ high- T c cuprate, the CuO 6 octahedra are elongated along the c axis due to apical oxygen displacements, and the degeneracy of e g orbitals is lifted. It has been established that both electron-doped and hole-doped copper oxides are strongly correlated electron systems in the vicinity of the metal to charge-transfer insulator transition [74]. One also finds large splitting of the copper 3 d states and only a single Cu( 3 d )–O( 2 p ) hybridized band crosses the Fermi surface in doped systems. This band has the x 2 − y 2 symmetry and becomes half-filled in the undoped charge-transfer insulator La 2 CuO 4 . The superexchange stabilizes then antiferromagnetic (AF) order [75] in this and other compounds of the cuprate family [2,3]. Doping generates a Fermi surface originating from a single band made of oxygen 2 p and copper 3 d states, for small hole doping x < 0.3 , as discussed by Zhang and Rice [76], see Figure 1. In this regime d-wave SC phase is found, and a high value of T c is obtained when the orbital splitting is large [18,19,20].
Interestingly, it has taken almost 20 years both for the experiment and the theory to unequivocally agree on the energies of the (local) orbital excitations on the copper ion of the undoped cuprates (“ d − d excitations” [27]). It has long been believed that, while the ground state orbital is of x 2 − y 2 character, the energy of the 3 z 2 − r 2 orbital excitation is rather low, for instance of the order of ∼0.4 eV—as suggested by the optical and resonant inelastic x-ray scattering (RIXS) measurements of La 2 CuO 4 [77,78] as well as by optical absorption for Sr 2 CuO 2 Cl 2 [77]. The latter result is particularly striking, for the most recent understanding (see Table 1 and discussion below) is that the 3 z 2 − r 2 orbital excitation is not even the lowest lying orbital excitation in Sr 2 CuO 2 Cl 2 . Though, even earlier the above result was challenged by Lorenzana and Sawatzky [79], suggesting a different interpretation of the optical absorption spectra, in which the 0.4 eV feature was assigned to the magnetic excitations. Finally, these results did not agree with the theoretical estimates giving about 0.9 eV energy for such an orbital excitation, according to the density-functional theory [20], or with the X-ray absorption spectroscopy results showing a very weak 3 z 2 − r 2 character in the ground state of the hole-doped cuprates [50].
The recent years have, however, lead to substantial advancements both in the resolution of the RIXS experiments of the cuprates [80] as well as ab-initio quantum chemistry calculations [81], and allowed for obtaining the results for cuprates [81,82] in remarkable agreement between the theory and experiment, as presented in Table 1. We emphasize that nowhere one can find the above-mentioned low values of the orbital excitation energies, for all excitations have their energies substantially above 1 eV. Finally, it is only in La 2 CuO 4 that the lowest energy orbital excitation has a 3 z 2 − r 2 character; otherwise this excitation has the highest energy. In general, a more detailed study of various other copper oxides, with/without apical ligands, suggests that the energy of the 3 z 2 − r 2 orbital correlates with the out-of-plane Cu-ligand distance h, although this relation is rather complex (cf. Figure 1 of [81]).
Table
Table 1. The energies of orbital excitations in various undoped cuprates, as obtained form the RIXS experiment [82] (quantum-chemistry calculations [81]). Note that a classical magnetic exchange energy 2 J ≃ 0.26 eV is subtracted from all given energy values. Table adopted from [81].
Table 1. The energies of orbital excitations in various undoped cuprates, as obtained form the RIXS experiment [82] (quantum-chemistry calculations [81]). Note that a classical magnetic exchange energy 2 J ≃ 0.26 eV is subtracted from all given energy values. Table adopted from [81].
Cu( 3 d ) OrbitalLa 2 CuO 4 Sr 2 CuO 2 Cl 2 CaCuO 2
3 z 2 − r 2 1.44 (1.37)1.71 (1.75)2.39 (2.38)
x y 1.54 (1.43)1.24 (1.16)1.38 (1.36)
x z / y z 1.86 (1.78)1.58 (1.69)1.69 (2.02)
This situation is somewhat more subtle in doped cuprates. Again, in the early years of high- T c research, it was expected that the occupancy of the low-lying orbital 3 z 2 − r 2 would increase upon doping [47,83,84,85]. However, as just discussed, in ‘most’ of the cuprates this orbital turns out to be the highest lying one in the undoped crystals, such a scenario now seems to be no longer relevant. Instead, (typically) the lowest lying x y orbital either hardens by about 50 meV [86], or softens by 150 meV [87] with doping, depending on the compound. Moreover, in both cases the lowest lying d − d excitation has an energy by ∼1.5 eV higher than the ground state orbital even in SC samples [88], in agreement with Table 1.
The above discussion shows that the orbital excitations in the cuprates have relatively high energies, suggesting that the electrons close to the Fermi surface are clearly of a single 3 d -band character. Surprisingly, however, some important signatures of the so-called orbital physics [89,90,91,92,93,94,95,96,97,98,99,100,101,102] are visible there: clear experimental signatures of the collective orbital excitation, the orbiton, have been observed in the quasi-one-dimensional (quasi-1D) copper oxides [97,98]. To a large extent this turned out to be possible due to the strong crystal-field splitting of the orbital excitations [99,100]. The search for similar phenomena in the quasi-2D (i.e., high- T c ) cuprates is ongoing [103].

3. Superconductivity with Orbital Degrees of Freedom

3.1. Beyond the Cuprates with the Pairing in a Single x 2 − y 2 Orbital

A way to enhance the value of T c in compounds isostructural with La 2 CuO 4 was found by Uchida et al. [104]: higher hole doping in CuO 2 planes is realized by replacing La ions by Sr ions in Sr 2 CuO 4 − δ . The SC transition temperature T c = 95 K is then almost doubled for the hole doping x ≃ 0.8 , see Figure 1. In this regime another nodeless SC phase arises, and the symmetry in the orbital space is partly restored. In fact, also the band of 3 z 2 − r 2 symmetry is partly filled, and the pairing occurs jointly for the B 1 g and A 1 g channels in Sr 2 CuO 4 − δ and also in Ba 2 CuO 4 − δ [105]. This possibility was discussed a decade ago [106], and was realized, inter alia, in a recently discovered superconductor with T c > 70 K [107]. The CuO 6 octahedra are compressed here and 3 z 2 − r 2 orbitals contribute at the Fermi surface. The pairing strength is large relative to a similar calculation for an optimally doped Hubbard model. The theory predicts that the pairing strength depends on the shape of the Fermi surface [105], see the right inset of Figure 1, with nearly square shapes of both electron and hole bands responsible for the enhanced pairing. These results seem to challenge an early view that T c is optimized when a single band with x 2 − y 2 symmetry crosses the Fermi surface [18,19,20], see also Section 2.
Condensedmatter 04 00046 g001 550
Figure 1. Schematic phase diagram for cuprates as a function of hole doping x, showing the route from the single-band SC phase with holes in x 2 − y 2 -type molecular orbitals, realized in bulk cuprates (left), to the two-orbital nodeless SC phase in the hole-rich CuO 2 /Bi2212 monolayer (right). The insets show the corresponding Fermi surface for one-orbital (left) and two-orbital { x 2 − y 2 , 3 z 2 − r 2 } (right) SC phase. Image is reproduced from [106]; right inset for the hole-rich CuO 2 monolayer is reproduced from [105].
Figure 1. Schematic phase diagram for cuprates as a function of hole doping x, showing the route from the single-band SC phase with holes in x 2 − y 2 -type molecular orbitals, realized in bulk cuprates (left), to the two-orbital nodeless SC phase in the hole-rich CuO 2 /Bi2212 monolayer (right). The insets show the corresponding Fermi surface for one-orbital (left) and two-orbital { x 2 − y 2 , 3 z 2 − r 2 } (right) SC phase. Image is reproduced from [106]; right inset for the hole-rich CuO 2 monolayer is reproduced from [105].
Condensedmatter 04 00046 g001
Another way of increasing the hole density in Cu( 3 d ) orbitals was realized for a CuO 2 monolayer grown on Bi2212 cuprate [28]. Here the CuO 2 monolayer is heavily overdoped by charge transfer at the interface and has a short bond between Cu and the apical O in the substrate. A minimal two-orbital model predicts indeed a nodeless high- T c SC state with s ± pairing [29], arising from the spin-orbital exchange a’la Kugel-Khomskii model [89].

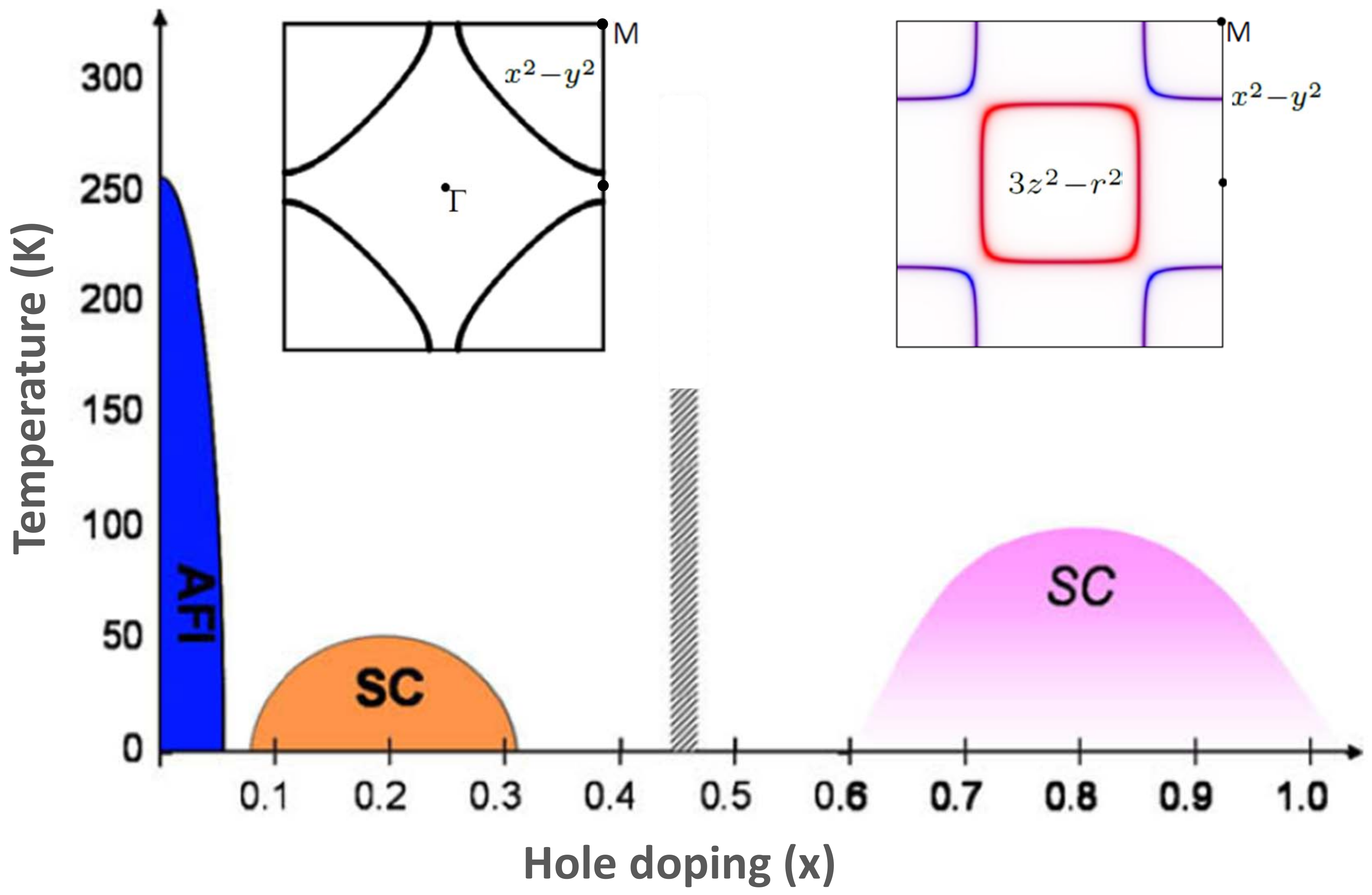
3.2. Nickelates

One expects that another route to achieve higher hole doping in Cu( 3 d ) orbitals is realized in Ni oxides, and indeed the Fermi surface very similar to that for the overdoped cuprates was observed in Eu 2 − x Sr x NiO 4 [108]. This Fermi surface is also similar to the one found for LaNiO 3 /LaAlO 3 heterostructure, where both e g symmetries contribute to the band structure obtained in local density approximation (LDA) [109], see Figure 2. Although it was argued that the 3 z 2 − r 2 symmetry would be eliminated by electron correlations, both bands were observed in the experiment [108].
The theoretical study of the electronic structure for the LaNiO 3 /LaAlO 3 heterostructure suggests that orbital engineering using heterostructuring is in principle possible. The electronic structure obtained with LDA for the heterostructure without strain, see Figure 2a, has the Fermi surface at k z = 0 very similar to that of the overdoped CuO 2 monolayer, see Figure 2b and the right inset of Figure 1. Hence, the theory predicts a SC heterostructure, if this system could be synthesized in the future. So far, widely tunable orbital configurations were indeed realized by in strongly correlated systems: LaTiO 3 /LaNiO 3 /LaAlO 3 heterostructure [110], and nickelate superlattices [111,112].
Condensedmatter 04 00046 g002 550
Figure 2. Electronic structure for the LaNiO 3 /LaAlO 3 heterostructure without strain obtained in the LDA: (a) bands of e g symmetry (black to yellow shading for orbital character), and (b) corresponding cross section of the Fermi surface with the k z = 0 plane. Images are reproduced from [109].
Figure 2. Electronic structure for the LaNiO 3 /LaAlO 3 heterostructure without strain obtained in the LDA: (a) bands of e g symmetry (black to yellow shading for orbital character), and (b) corresponding cross section of the Fermi surface with the k z = 0 plane. Images are reproduced from [109].
Condensedmatter 04 00046 g002
Also in other square-planar nickelate, Pr 4 Ni 3 O 8 , both e g orbitals contribute to the Fermi surface [113]. X-ray absorption shows that low-spin configuration with x 2 − y 2 character of the hole states is realized there [114], making these states remarkably similar to those in hole-doped cuprates. Hence, also these compounds may be considered as promising candidates for unconventional superconductivity. Recently, a family of Ni-based compounds, which contain [Ni 2 M 2 O] 2 − (M-chalcogen) layers with an antiperovskite structure constructed by mixed-anion Ni complexes, has been suggested as possible high- T c superconductors [115]. Here again both e g symmetries should contribute, and one expects strong competition between s-wave and d-wave pairing symmetries.
More complicated situations are also possible, and we mention here KNi 2 S 2 as an example of a Ni-based superconductor with three different orbital symmetries contributing at the Fermi surface and a small value of T c = 0.46 K [116]. The electronic structure is described by the multiorbital Hubbard model and this system has certain similarity to iron-based superconductors discussed in Section 3.4.

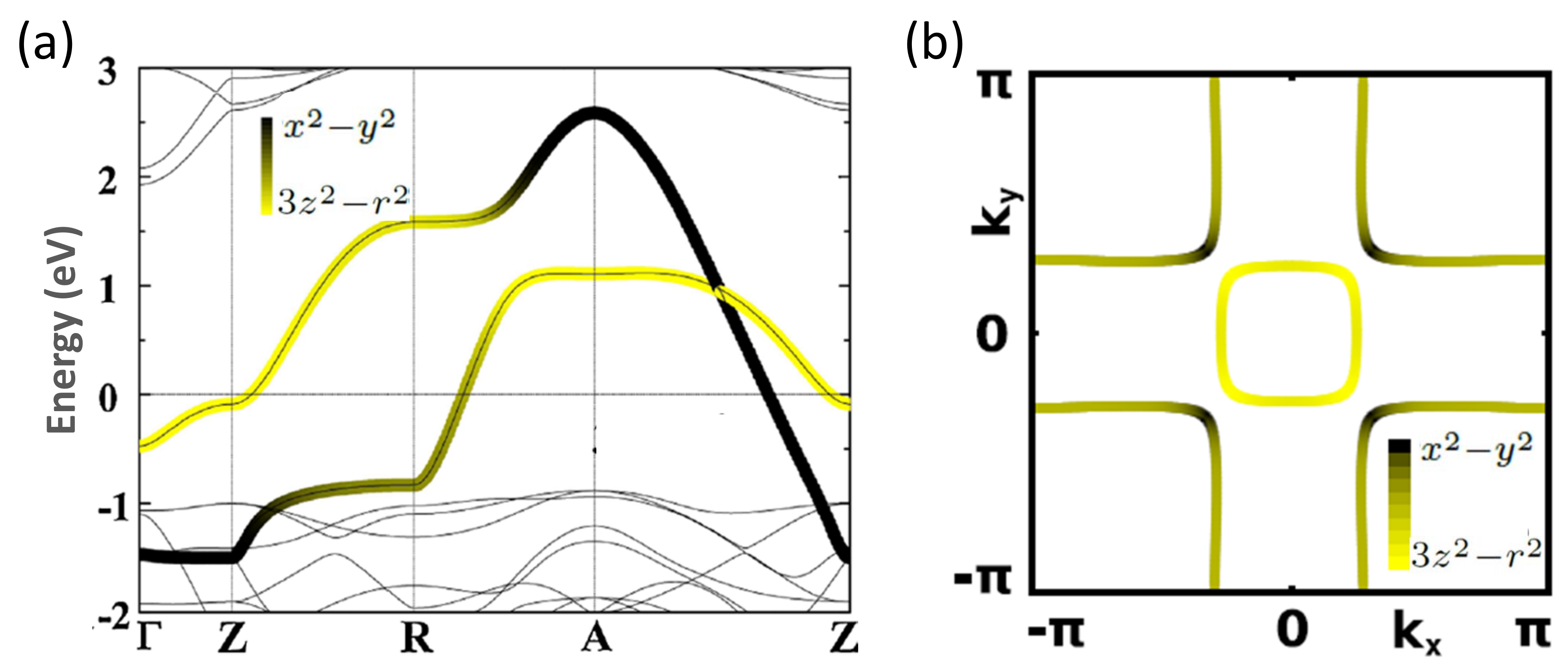
3.3. Superconducting Ruthenate Sr 2 RuO 4

The SC state of strontium ruthenate Sr 2 RuO 4 was discovered in 1994 by Maeno and his collaborators after they had succeeded in synthesizing high-quality samples of the material [117]. It was soon realized that different orbital symmetries contribute to the SC state in this unique ruthenium oxide [118]. The value of T c = 1.5 K is not particularly high, but the ruthenate structure suggests a possible relationship to the high- T c cuprate superconductors. Yet, in spite of their structural similarity, doped La 2 CuO 4 and Sr 2 RuO 4 are quite different [119].
In conventional superconductors, in high- T c copper oxides, and in Fe pnictides, the Cooper pairs have even parity. In contrast, Sr 2 RuO 4 is the candidate for odd parity superconductivity [15]. However, the pairing symmetry in this material is not yet fully established (see, e.g., [120,121]). Ruthenates have active t 2 g orbital degrees of freedom [122,123], with degenerate y z and z x orbital states. An additional complication in the theory is the presence of a sizeable spin-orbit coupling ( ζ ∼ 90 meV at the Γ point), which is much smaller than full bandwidth of ∼3 eV but nonetheless leads to important consequences by mixing the low-energy t 2 g spin-orbital states. As a result, the Fermi surface, consisting of three { α , β , γ } bands [124], changes qualitatively, see Figure 3a. In particular, the crossing points (accidental degeneracies) between the electronic β and γ bands vanish and the Fermi surface for both { β , γ } bands becomes more circular [38], while there is no phase space for mixing of hole-like α band.
For further discussion we focus on the representative β band; the mixing of t 2 g orbital states remains similar for the other bands. The most important consequence of finite spin-orbit coupling ζ is momentum-dependent spin-orbital entanglement [38] of the eigenstates near the Fermi surface. It is illustrated in Figure 3b for the β band and three representative values of momentum k z . Going along the Fermi surface for a fixed value of k z , one observes that not only the orbital character changes, but also both components of s = 1 / 2 spin mix. The latter mixing of spin components is somewhat weaker for large value of k z = 3 π / 4 . This mixing plays an important role and the challenging theoretical problem is to include orbital fluctuations in the theory of superconductivity in Sr 2 RuO 4 .
Condensedmatter 04 00046 g003 550
Figure 3. (a) and (b): Spin-orbital entanglement in Sr 2 RuO 4 ruthenate: (a) Fermi surface for bands { α , β , γ } at k z = 0 calculated without (thin black) and with (thick, color-coded) spin-orbit 〈 l → · s → 〉 coupling, and (b) momentum-dependent Ru( 4 d ) orbital projection of the wave function for the β band at selected momentum locations along the 3D Fermi surface. The orbital color represents the momentum-dependent spin 〈 s z 〉 expectation value; blue/red correspond to spin ↑ / ↓ for one state of the Kramers-degenerate pair, see the color scale at bottom right. The strongly mixed colors indicate momentum-dependent spin-orbital entanglement. Images (a) and (b) are reproduced from [38]. (c) Orbital excitations in Sr 2 IrO 4 between the entangled spin-orbital ground state (with J eff = 1 / 2 ) and the excited doublet (with J eff = 3 / 2 ), with the energy much lower than in cuprates (cf. Table 1).
Figure 3. (a) and (b): Spin-orbital entanglement in Sr 2 RuO 4 ruthenate: (a) Fermi surface for bands { α , β , γ } at k z = 0 calculated without (thin black) and with (thick, color-coded) spin-orbit 〈 l → · s → 〉 coupling, and (b) momentum-dependent Ru( 4 d ) orbital projection of the wave function for the β band at selected momentum locations along the 3D Fermi surface. The orbital color represents the momentum-dependent spin 〈 s z 〉 expectation value; blue/red correspond to spin ↑ / ↓ for one state of the Kramers-degenerate pair, see the color scale at bottom right. The strongly mixed colors indicate momentum-dependent spin-orbital entanglement. Images (a) and (b) are reproduced from [38]. (c) Orbital excitations in Sr 2 IrO 4 between the entangled spin-orbital ground state (with J eff = 1 / 2 ) and the excited doublet (with J eff = 3 / 2 ), with the energy much lower than in cuprates (cf. Table 1).
Condensedmatter 04 00046 g003
When spin-orbit coupling is large enough, it can unify the spin and orbital subspaces locally, forming the effective pseudospin J eff = 1 / 2 states that dominate low energy physics [93,125,126]. This case is particulary relevant for iridium oxides, and indeed, a perovskite compound Sr 2 IrO 4 was found to host pseudospin J eff = 1 / 2 antiferromagnetism [127,128,129], with quasi-2D magnon excitations similar to those of spin S = 1 / 2 in cuprates. It was recently found that spin-orbit entangled magnetism in iridates and ruthenates is strongly influenced by electron-lattice coupling, via pseudo-Jahn-Teller effect [130]. The remarkable analogy between layered iridates and cuprates holds also upon doping—single band Fermi surface, (pseudo)gap, and Fermi arcs have been detected [131]. However, a long-range coherent superconductivity has not been yet found in iridates. Whether this is related to the fact that spin-orbital excitation energies 0.6 eV [129] in iridates, see Figure 3c, are much lower than in cuprates, or to the Mott insulating nature of iridates, in contrast to charge-transfer insulating cuprates, remains an open question. For detailed discussion the similarities and differences between iridates and cuprates, we refer to the recent review article [39].

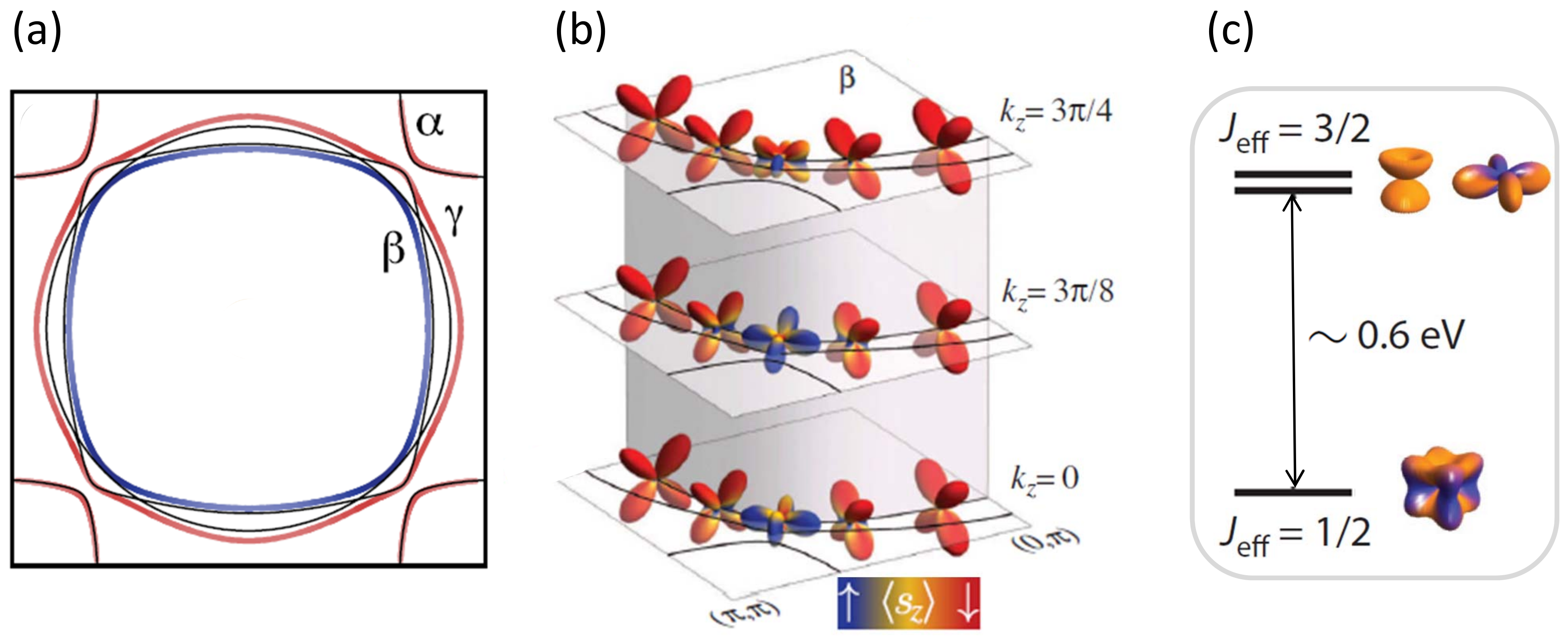
3.4. Iron-Based Superconductors

Similar to cuprates, the Fe-based superconductors have 2D lattices of 3 d transition metal ions as building blocks. However, while oxygen ions lie in the same planes as Cu ions in La 2 CuO 4 , ions of As, P, or Se lie above or below the Fe plane, in positions close to tetrahedral. For this reason, the out-of-plane As orbitals hybridize well with t 2 g orbitals of Fe ions. In addition, there is a substantial overlap between the 3 d orbitals [7,8,9,10,11,132,133,134]. Under these circumstances, the minimal models for pnictide superconductors contain at least two [135] or three [136] t 2 g orbitals per Fe atom.
In contrast to undoped cuprates, parent compounds of Fe-based superconductors are metallic [7], and the pairings of different symmetry compete in a two-band model [11,137,138,139]. The coexistence of hole-like and electron-like bands at the Fermi surface is quite generic [7,8,133]. Then Lifshitz transitions can develop for increasing external magnetic field. Such transitions were indeed found in a two-band model with intra-band pairing [140] and could explain the experimental observations in FeSe and Co-doped BaFe 2 As 2 compounds. The competition between different pairing symmetries in KFe 2 As 2 causes a change of symmetry at the critical pressure, from d-wave to s + + -wave symmetry [141].
Before discussing the nature of pairing, it is interesting to look at the strong coupling model for pnictides, including magnetic frustration [142]. A spin-orbital model for interacting Fe ions in intermediate S = 1 spin states was derived [143] in the regime of strong electron correlations. It highlights Hund’s exchange for electron correlations, recently observed experimentally [144]. Magnetic and orbital instabilities are here far richer than in cuprates, and one finds the experimentally observed spin-stripe state which could be accompanied by three different types of orbital order. This is another manifestation of substantial magnetic frustration of the superexchange [142] which may partly explain why magnetic instabilities are sometimes absent, e.g., in FeSe and LiFeAs.
The spin-orbital model [143], however, does not contain biquadratic exchange which was found to be crucial in magnetism of Fe-based superconductors [145,146,147,148]. This coupling may originate from spin-state fluctuations [149] typical for Fe-ions in systems with strong p − d covalency. While large biquadratic exchange is quite unique and essential for the description of magnetic and nematic instabilities, its implications for SC instabilities belong to open problems in the field. Indeed, the SC phase in iron-based materials occurs in the vicinity of the two above instabilities: Not only one has the usual magnetic phases [150], but also the nematic order may occur [97,151,152]. A detailed study shows that the Fermi surface of FeSe undergoes a spontaneous distortion from fourfold-symmetric to twofold-symmetric elliptical pockets, and next SC phase emerges from the nematic electronic phase.
The theory of Cooper pairing in Fe-based superconductors is rather involved and still far from complete [8,9,153]. The role played by orbital and spin fluctuations belongs to challenging open problems in the theory. It was found that the orbital fluctuations may give rise to the strong pairing interaction due to the cooperation of Coulomb and electron-phonon interactions [154,155]. The theory explains also the famous empirical relation between T c and the As-Fe-As bond angle [156].
Altogether, the pairing in iron-based superconductors involves all the five Fe( 3 d ) orbitals, and multiple orbital physics gives rise to various novel phenomena like orbital-selective Mott transition, nematicity, and orbital fluctuations that may support the SC phase. Recent theory treating spin and orbital fluctuations on equal footing predicts that, at certain conditions, a spontaneous orbital order sets in first, and then superconductivity follows [157]. The SC gap and low energy excitations in FeSe are dominated by a single x z orbital [158] which uncovers the orbital origin of the strongly anisotropic gap in the FeSe superconductor [159,160,161,162]. In LiFe 1 − x Co x As spin excitations are orbital selective: low-energy spin excitations are mostly from x y orbitals, while high-energy spin excitations arise from the y z and z x orbitals [163]. Such strongly orbital selective spin excitations in LiFeAs family might play a role in the mechanism of orbital selective Cooper pairing as well.

4. Summary

To conclude, we have presented the current status of the high- T c superconductivity in the presence of orbital degrees of freedom. As this subject is very broad, in this review we limit the presentation solely to the electronic degrees of freedom, leaving aside a detailed discussion of the role played by their coupling to the lattice. In case of cuprates large hole doping and removing octahedral distortions is necessary to activate the 3 z 2 − r 2 orbitals, and we gave examples of cuprates with two e g orbitals and higher values of T c than in La 2 − x (Sr,Ba) x CuO 4 . These orbitals contribute to almost the same Fermi surface, consisting of hole and electron parts, also in doped nickelates. But for nickelates we cannot present anything more than a theoretical suggestion that the superconducting instabilities could occur as well. Finally, very interesting superconducting states emerge in Sr 2 RuO 4 and in iron pnictides, where several t 2 g symmetries meet at the Fermi surface and participate in the Cooper pairing. Search for other transition metal compounds with SC instabilities continues—for instance, recently AgF 2 was suggested as an excellent analogue to La 2 CuO 4 [164], but no superconductivity was observed so far.
Summarizing, the presence of orbital degrees of freedom makes high- T c superconductors an even more exciting class of quantum materials where the competing quantum phases are of particular importance for superconductivity in layered compounds [165]. It seems that orbital fluctuations could enhance the superconducting transition temperature T c , but we emphasize that the role of orbital degrees of freedom in the phenomenon of pairing belongs to open problems in the theory; in particular the interplay between orbital degeneracy and the Jahn-Teller coupling to lattice—the idea that guided Bednorz and Müller in their discovery of high- T c superconductivity—has to be worked out in a greater detail.

Author Contributions

All authors selected the relevant information, participated in discussions, wrote the manuscript and contributed to the interpretation of the results.

Funding

This research was funded by Narodowe Centrum Nauki (NCN, National Science Centre, Poland) under Projects Nos. 2016/22/E/ST3/00560 and 2016/23/B/ST3/00839.

Acknowledgments

We would like to thank Mona Berciu, Antonio Bianconi, Lucio Braicovich, Jeroen van den Brink, Mario Cuoco, Maria Daghofer, Thomas P. Devereaux, Louis Felix Feiner, Jörg Fink, Andres Greco, Maurits Haverkort, Peter J. Hirschfeld, Peter Horsch, Liviu Hozoi, Huimei Liu, Andrzej Ptok, Roman Puźniak, George A. Sawatzky, Józef Spałek, Hiroyuki Yamase, Alexander N. Yaresko, Jan Zaanen, and Roland Zeyher for many insightful discussions. A. M. Oleś is grateful for the Alexander von Humboldt Foundation Fellowship (Humboldt-Forschungspreis).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Bednorz, J.G.; Muller, K.A. Possible high-Tc superconductivity in the Ba-La-Cu-O system. Z. Phys. B 1986, 64, 189–193. [Google Scholar] [CrossRef]
  2. Lee, P.A.; Nagaosa, N.; Wen, X.G. Doping a Mott insulator: Physics of high-temperature superconductivity. Rev. Mod. Phys. 2006, 78, 17–85. [Google Scholar] [CrossRef] [Green Version]
  3. Ogata, M.; Fukuyama, H. The t-J model for the oxide high-Tc superconductors. Rep. Prog. Phys. 2008, 71, 036501. [Google Scholar] [CrossRef]
  4. Vojta, M. Lattice symmetry breaking in cuprate superconductors: Stripes, nematics, and superconductivity. Adv. Phys. 2009, 58, 699–820. [Google Scholar] [CrossRef]
  5. Bianconi, A.; Poccia, N. Superstripes and complexity in High-Temperature Superconductors. J. Supercond. Nov. Magn. 2012, 25, 1403–1412. [Google Scholar] [CrossRef]
  6. Keimer, B.; Kivelson, S.A.; Norman, M.R.; Uchida, S.; Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 2015, 518, 179–186. [Google Scholar] [CrossRef]
  7. Paglione, J.; Greene, R.L. High-Temperature Tuperconductivity in Iron-Based Material. Nat. Phys. 2010, 6, 645–658. [Google Scholar] [CrossRef]
  8. Hirschfeld, P.J.; Korshunov, M.M.; Mazin, I.I. Gap symmetry and structure of Fe-based superconductors. Rep. Prog. Phys. 2011, 74, 124508. [Google Scholar] [CrossRef] [Green Version]
  9. Scalapino, D.J. A common thread: The pairing interaction for unconventional superconductors. Rev. Mod. Phys. 2012, 84, 1383–1417. [Google Scholar] [CrossRef] [Green Version]
  10. Si, Q.; Yu, R.; Abrahams, E. High-temperature superconductivity in iron pnictides and chalcogenides. Nat. Rev. Mat. 2016, 1, 16017. [Google Scholar] [CrossRef] [Green Version]
  11. Fernandes, R.M.; Chubukov, A.V. Low-energy microscopic models for iron-based superconductors: A review. Rep. Prog. Phys. 2017, 80, 014503. [Google Scholar] [CrossRef]
  12. Cava, R.J.; Takagi, H.; Zandbergen, H.W.; Krajewski, J.J.; Peck, W.F., Jr.; Siegrist, T.; Batlogg, B.; van Dover, R.B.; Felder, R.J.; Mizuhashi, K.; et al. Superconductivity in the quaternary intermetallic compounds LnNi2B2C. Nature 1994, 367, 252–253. [Google Scholar] [CrossRef]
  13. Kastner, M.A.; Birgeneau, R.J.; Shirane, G.; Endoh, Y. Magnetic, transport, and optical properties of monolayer copper oxides. Rev. Mod. Phys. 1998, 70, 897–928. [Google Scholar] [CrossRef]
  14. Imada, M.; Fujimori, A.; Tokura, Y. Metal-insulator transitions. Rev. Mod. Phys. 1998, 70, 1039–1263. [Google Scholar] [CrossRef]
  15. Mackenzie, A.P.; Maeno, Y. The superconductivity of Sr2RuO4 and the physics of spin-triplet pairing. Rev. Mod. Phys. 2003, 75, 657–712. [Google Scholar] [CrossRef]
  16. Krzton-Maziopa, A.; Svitlyk, V.; Pomjakushina, E.; Puźniak, R.; Conder, K. Superconductivity in alkali metal intercalated iron selenides. J. Phys. Condens. Mat. 2016, 28, 293002. [Google Scholar] [CrossRef]
  17. Graser, S.; Maier, T.A.; Hirschfeld, P.J.; Scalapino, D.J. Near-degeneracy of several pairing channels in multiorbital models for the Fe pnictides. New J. Phys. 2009, 21, 025016. [Google Scholar] [CrossRef]
  18. Ohta, Y.; Tohyama, T.; Maekawa, S. Apex oxygen and critical temperature in copper oxide superconductors: Universal correlation with the stability of local singlets. Phys. Rev. B 1991, 43, 2968–2982. [Google Scholar] [CrossRef]
  19. Pavarini, E.; Dasgupta, I.; Saha-Dasgupta, T.; Jepsen, O.; Andersen, O.K. Band-Structure Trend in Hole-Doped Cuprates and Correlation with Tc max. Phys. Rev. Lett. 2014, 112, 127002. [Google Scholar]
  20. Sakakibara, H.; Usui, H.; Kuroki, K.; Arita, R.; Aoki, H. Two-Orbital Model Explains the Higher Transition Temperature of the Single-Layer Hg-Cuprate Superconductor Compared to That of the La-Cuprate Superconductor. Phys. Rev. Lett. 2010, 105, 057003. [Google Scholar] [CrossRef]
  21. Feiner, L.F.; Jefferson, J.H.; Raimondi, R. Effective single-band models for the high-Tc cuprates. 1. Coulomb interactions. Phys. Rev. B 1996, 53, 8751–8773. [Google Scholar] [CrossRef]
  22. Bianconi, A. Lifshitz Transitions In Multi-band Hubbard Models for Topological Superconductivity in Complex Quantum Matter. J. Supercond. Novel Magn. 2018, 31, 603–610. [Google Scholar] [CrossRef] [Green Version]
  23. Drozdov, A.P.; Eremets, M.I.; Troyan, I.A.; Ksenofontov, V.; Shylin, S.I. Conventional superconductivity at 203 Kelvin at high pressures in the sulfur hydride system. Nature 2015, 525, 73–76. [Google Scholar] [CrossRef] [PubMed]
  24. Capitani, F.; Langerome, B.; Brubach, J.-B.; Roy, P.; Drozdov, A.; Eremets, M.I.; Nicol, E.J.; Carbotte, J.P.; Timusk, T. Spectroscopic evidence of a new energy scale for superconductivity in H3S. Nat. Phys. 2017, 13, 859–863. [Google Scholar] [CrossRef] [PubMed]
  25. Müller, K.A. Large, small, and especially Jahn-Teller polarons. J. Supercond. 1999, 12, 3–7. [Google Scholar] [CrossRef]
  26. Keller, H.; Bussmann-Holder, A.; Müller, K.A. Jahn-Teller physics and high-Tc superconductivity. Mat. Today 2008, 11, 38–46. [Google Scholar] [CrossRef]
  27. Zaanen, J.; Oleś, A.M. Carriers binding to excitons: Crystal-field excitations in doped Mott-Hubbard insulators. Phys. Rev. B 1993, 48, 7197–7215. [Google Scholar] [CrossRef] [Green Version]
  28. Zhong, Y.; Wang, Y.; Han, S.; Lv, Y.-F.; Wang, W.-L.; Zhang, D.; Ding, H.; Zhang, Y.-M.; Wang, L.; He, K.; et al. Nodeless pairing in superconducting copper-oxide monolayer films on Bi2Sr2CaCu2O8+δ. Sci. Bull. 2016, 61, 1239–1247. [Google Scholar] [CrossRef]
  29. Jiang, K.; Wu, X.; Hu, J.; Wang, Z. Nodeless High-Tc Superconductivity in the Highly Overdoped CuO2 Monolayer. Phys. Rev. Lett. 2018, 121, 227002. [Google Scholar] [CrossRef] [PubMed]
  30. Li, Q.; Tsay, Y.N.; Suenaga, M.; Klemm, R.A.; Gu, G.D.; Koshizuka, N. Bi2Sr2CaCu2O8+δ Bicrystal c-Axis Twist Josephson Junctions: A New Phase-Sensitive Test of Order Parameter Symmetry. Phys. Rev. Lett. 1999, 83, 4160–4163. [Google Scholar] [CrossRef]
  31. Misra, S.; Oh, S.; Hornbaker, D.J.; DiLuccio, T.; Eckstein, J.N.; Yazdani, A. Atomic Scale Imaging and Spectroscopy of a CuO2 Plane at the Surface of Bi2Sr2CaCu2O8+δ. Phys. Rev. Lett. 2002, 89, 087002. [Google Scholar] [CrossRef]
  32. Hoogenboom, B.W.; Kadowaki, K.; Revaz, B.; Fischer, Ø. Homogeneous samples of Bi2Sr2CaCu2O8+δ. Phys. C 2003, 391, 376–380. [Google Scholar] [CrossRef]
  33. Latyshev, Y.I.; Orlov, A.P.; Nikitina, A.M.; Monceau, P.; Klemm, R.A. c-axis transport in naturally grown Bi2Sr2CaCu2O8+δ cross-whisker junctions. Phys. Rev. B 2004, 70, 094517. [Google Scholar] [CrossRef]
  34. Klemm, R.A. The phase-sensitive c-axis twist experiments on Bi2Sr2CaCu2O8+δ and their implications. Philos. Mag. 2004, 85, 801–853. [Google Scholar] [CrossRef]
  35. Zhu, Y.; Liao, M.; Zhang, Q.; Meng, F.; Zhong, R.; Schneeloch, J.; Gu, G.; Gu, L.; Ma, X.; Zhang, D.; et al. Isotropic Josephson tunneling in c-axis twist bicrystals of Bi2Sr2CaCu2O8+δ. arXiv 2019, arXiv:1903.07965. [Google Scholar]
  36. Chaloupka, J.; Khaliullin, G. Orbital Order and Possible Superconductivity in LaNiO3/LaMO3 Superlattices. Phys. Rev. Lett. 2008, 100, 016404. [Google Scholar] [CrossRef]
  37. Knolle, J.; Eremin, I.; Moessner, R. Multiorbital spin susceptibility in a magnetically ordered state: Orbital versus excitonic spin density wave scenario. Phys. Rev. B 2011, 83, 224503. [Google Scholar] [CrossRef]
  38. Veenstra, C.N.; Zhu, Z.-H.; Raichle, M.; Ludbrook, B.M.; Nicolaou, A.; Slomski, B.; Landolt, G.; Kittaka, S.; Maeno, Y.; Dil, J.H.; et al. Spin-Orbital Entanglement and the Breakdown of Singlets and Triplets in Sr2RuO4 Revealed by Spin- and Angle-Resolved Photoemission Spectroscopy. Phys. Rev. Lett. 2014, 112, 127002. [Google Scholar] [CrossRef]
  39. Bertinshaw, J.; Kim, Y.K.; Khaliullin, G.; Kim, B.J. Square Lattice Iridates. Annu. Rev. Condens. Matter Phys. 2019, 10, 315–336. [Google Scholar] [CrossRef]
  40. Varma, C.M.; Schmitt-Rink, S.; Abrahams, E. Charge transfer excitations and superconductivity in “ionic” metals. Solid State Commun. 1987, 62, 681–685. [Google Scholar] [CrossRef]
  41. Emery, V.J. Theory of High-Tc Superconductivity in Oxides. Phys. Rev. Lett. 1987, 58, 2794–2797. [Google Scholar] [CrossRef]
  42. Oleś, A.M.; Zaanen, J.; Fulde, P. How strongly are electrons correlated in the high-Tc superconducting materials? Phys. B & C 1987, 148, 260–263. [Google Scholar]
  43. Arrigoni, E.; Aichhorn, M.; Daghofer, M.; Hanke, W. Phase diagram and single-particle spectrum of CuO2 layers within a variational cluster approach to the 3-band Hubbard model. New J. Phys. 2009, 11, 055066. [Google Scholar] [CrossRef]
  44. Hanke, W.; Kiesel, M.L.; Aichhorn, M.; Brehm, S.; Arrigoni, E. The 3-band Hubbard model versus the 1-band model for the high-Tc cuprates: Pairing dynamics, superconductivity and the ground state phase diagram. Eur. Phys. J. Spec. Top. 2010, 188, 15–32. [Google Scholar] [CrossRef]
  45. Ebrahimnejad, H.; Sawatzky, G.A.; Berciu, M. The dynamics of a doped hole in a cuprate is not controlled by spin fluctuations. Nat. Phys. 2014, 10, 951–955. [Google Scholar] [CrossRef] [Green Version]
  46. Bianconi, A.; De Santis, M.; Flank, A.; Fontaine, A.; Lagarde, P.; Marcelli, A.; Katayamayoshida, H.; Kotani, A. Determination of the symmetry of the 3d9L states by polarized Cu L3 XAS spectra of single crystal YBa2Cu3O6.9. Phys. C 1988, 153–155, 1760–1761. [Google Scholar] [CrossRef]
  47. Bianconi, A.; De Santis, M.; Di Cicco, A.; Flank, A.M.; Fontaine, A.; Lagarde, P.; Katayama-Yoshida, H.; Kotani, A.; Marcelli, A. Symmetry of the 3d9 ligand hole induced by doping in YBa2Cu3O7−x. Phys. Rev. B 1988, 38, 7196–7199. [Google Scholar] [CrossRef]
  48. Nücker, N.; Pellegrin, E.; Schweiss, P.; Fink, J.; Molodtsov, S.L.; Simmons, C.T.; Kaindl, G.; Frentrup, W.; Erb, A.; Müller-Vogt, G. Site-specific and doping-dependent electronic structure of YBa2Cu3Ox probed by O 1s and Cu 2p x-ray-absorption spectroscopy. Phys. Rev. B 1995, 51, 8529–8542. [Google Scholar] [CrossRef]
  49. Pompa, M.; Castrucci, P.; Li, C.; Udron, D.; Flank, A.M.; Lagarde, P.; Katayama-Yoshida, H.; Della Longa, S.; Bianconi, A. On the orbital angular momentum of Cu 3d hole states in superconducting La2−xSrxCuO4. Phys. C 1991, 184, 102–112. [Google Scholar] [CrossRef]
  50. Chen, C.T.; Tjeng, L.H.; Kwo, J.; Kao, H.L.; Rudolf, P.; Sette, F.; Fleming, R.M. Out-of-plane orbital characters of intrinsic and doped holes in La2−xSrxCuO4. Phys. Rev. Lett. 1992, 68, 2543–2546. [Google Scholar] [CrossRef] [PubMed]
  51. Sakakibara, H.; Suzuki, K.; Usui, H.; Kuroki, K.; Arita, R.; Scalapino, D.J.; Aoki, H. Multiorbital analysis of the effects of uniaxial and hydrostatic pressure on Tc in the single-layered cuprate superconductors. Phys. Rev. B 2012, 86, 134520. [Google Scholar] [CrossRef]
  52. Seino, Y.; Kotani, A.; Bianconi, A. Effect of Rhombic Distortion on the Polarized X-Ray Absorption Spectra in High Tc Superconductors. J. Phys. Soc. Jpn. 1990, 59, 815–818. [Google Scholar] [CrossRef]
  53. Bianconi, A.; Valletta, A.; Perali, A.; Saini, N.L. Superconductivity of a striped phase at the atomic limit. Phys. C 1998, 1998 296, 269–280. [Google Scholar] [CrossRef]
  54. Bianconi, A.; Di Castro, D.; Bianconi, G.; Pifferi, A.; Saini, N.L.; Chou, F.C.; Johnston, D.C.; Colapietro, M. Coexistence of stripes and superconductivity: Tc amplification in a superlattice of superconducting stripes. Phys. C 2000, 341, 1719–1722. [Google Scholar] [CrossRef]
  55. Bianconi, A.; Bianconi, G.; Caprara, S.; Di Castro, D.; Oyanagi, H.; Saini, N.L. The stripe critical point for cuprates. J. Phys. Condens. Matter 2000, 12, 10655–10666. [Google Scholar] [CrossRef]
  56. Bianconi, A.; Agrestini, S.; Bianconi, G.; Di Castro, D.; Saini, N.L. A quantum phase transition driven by the electron lattice interaction gives high Tc superconductivity. J. Alloys Compd. 2001, 317, 537–541. [Google Scholar] [CrossRef]
  57. Bersuker, I.B. Pseudo-Jahn-Teller effect? A two-state paradigm in formation, deformation, and transformation of molecular systems and solids. Chem. Rev. 2013, 113, 1351–1390. [Google Scholar] [CrossRef]
  58. Müller, K.A. Recent experimental insights into HTSC materials. Phys. C 2000, 341, 11–18. [Google Scholar] [CrossRef]
  59. Bussmann-Holder, A.; Keller, H.; Bishop, A.R.; Simon, A.; Micnas, R.; Müller, K.A. Unconventional isotope effects as evidence for polaron formation in cuprates. Europhys. Lett. 2005, 72, 423–429. [Google Scholar] [CrossRef]
  60. Müller, K.A. The unique properties of superconductivity in cuprates. J. Supercond. Novel Magn. 2014, 27, 2163–2179. [Google Scholar] [CrossRef]
  61. Zhou, J.S.; Bersuker, G.I.; Goodenough, J.B.. Non-adiabatic electron-lattice interactions in the copper-oxide superconductors. J. Supercond. 1995, 8, 541–544. [Google Scholar] [CrossRef]
  62. Bersuker, G.I.; Goodenough, J.B. Large low-symmetry polarons of the high-Tc copper oxides: Formation, mobility and ordering. Phys. C 1997, 274, 267–285. [Google Scholar] [CrossRef]
  63. Lanzara, A.; Zhao, G.M.; Saini, N.L.; Bianconi, A.; Conder, K.; Keller, H.; Müller, K.A. Oxygen-isotope shift of the charge-stripe ordering temperature in La2−xSrxCuO4 from x-ray absorption spectroscopy. J. Phys. Condens. Matter 1999, 11, L541–L546. [Google Scholar] [CrossRef]
  64. McQueeney, R.J.; Petrov, Y.; Egami, T.; Yethiraj, M.; Shirane, G.; Endoh, Y. Anomalous Dispersion of LO Phonons in La1.85Sr0.15CuO4 at Low Temperatures. Phys. Rev. Lett. 1999, 82, 628–631. [Google Scholar] [CrossRef]
  65. Le Tacon, M.; Bosak, A.; Souliou, S.M.; Dellea, G.; Loew, T.; Heid, R.; Bohnen, K.-P.; Ghiringhelli, G.; Krisch, M.; Keimer, B. Giant phonon anomalies and central peak due to charge density wave formation in YBa2Cu3O6.6. Nat. Phys. 2014, 10, 52–58. [Google Scholar] [CrossRef]
  66. Miao, H.; Ishikawa, D.; Heid, R.; Le Tacon, M.; Fabbris, G.; Meyers, D.; Gu, G.D.; Baron, A.Q.R.; Dean, M.P.M. Incommensurate Phonon Anomaly and the Nature of Charge Density Waves in Cuprates. Phys. Rev. X 2018, 8, 011008. [Google Scholar] [CrossRef] [Green Version]
  67. Weber, W. A Cu d-d Excitation Model for the Pairing in the High-Tc Cuprates. Z. Phys. B 1988, 70, 323–329. [Google Scholar] [CrossRef]
  68. Jarrell, M.; Krishnamurthy, H.R.; Cox, D.L. Charge-transfer mechanisms for high-Tc superconductivity. Phys. Rev. B 1988, 38, 4584–4587. [Google Scholar] [CrossRef]
  69. Cox, D.L.; Jarrell, M.; Jayaprakash, C.; Krishnamurthy, H.R.; Deisz, J. Virtual Electric Quadrupole Fluctuations: A Mechanism for High Tc. Phys. Rev. Lett. 1989, 62, 2188–2191. [Google Scholar] [CrossRef]
  70. Feiner, L.F.; Grilli, M.; Di Castro, C. Apical oxygen ions and the electronic structure of the high-Tc cuprates. Phys. Rev. B 1992, 45, 10647–10669. [Google Scholar] [CrossRef]
  71. Buda, F.; Cox, D.L.; Jarrell, M. Random-phase-approximation analysis of orbital- and magnetic-fluctuation- mediated superconductivity in a two-band Hubbard model. Phys. Rev. B 1994, 49, 1255–1268. [Google Scholar] [CrossRef]
  72. Bucci, F.; Castellani, C.; Di Castro, C.; Grilli, M. Charge fluctuations in the four-band extended Hubbard model. Phys. Rev. B 1995, 52, 6880–6893. [Google Scholar] [CrossRef]
  73. Sakakibara, H.; Suzuki, K.; Usui, H.; Miyao, S.; Maruyama, I.; Kusakabe, K.; Arita, R.; Aoki, H.; Kuroki, K. Orbital mixture effect on the Fermi-surface–Tc correlation in the cuprate superconductors: Bilayer vs. single layer. Phys. Rev. B 2014, 89, 224505. [Google Scholar] [CrossRef]
  74. Weber, C.; Haule, K.; Kotliar, G. Apical oxygens and correlation strength in electron- and hole-doped copper oxides. Phys. Rev. B 2010, 82, 125107. [Google Scholar] [CrossRef]
  75. Zaanen, J.; Oleś, A.M. Canonical Perturbation Theory and the Two-Band Model for High-Tc Superconductors. Phys. Rev. B 1988, 45, 9423–9438. [Google Scholar] [CrossRef]
  76. Zhang, F.C.; Rice, T.M. Effective Hamiltonian for the superconducting Cu Oxides. Phys. Rev. B 1988, 37, 3759–3761. [Google Scholar] [CrossRef]
  77. Perkins, J.D.; Graybeal, J.M.; Kastner, M.A.; Birgeneau, R.J.; Falck, J.P.; Greven, M. Mid-infrared optical absorption in undoped lamellar copper oxides. Phys. Rev. Lett. 1992, 71, 1621–1624. [Google Scholar] [CrossRef]
  78. Ghiringhelli, G.; Brookes, N.B.; Annese, E.; Berger, H.; Dallera, C.; Grioni, M.; Perfetti, L.; Tagliaferri, A.; Braicovich, L. Low Energy Electronic Excitations in the Layered Cuprates Studied by Copper L3 Resonant Inelastic X-Ray Scattering. Phys. Rev. Lett. 2004, 92, 117406. [Google Scholar] [CrossRef]
  79. Lorenzana, J.; Sawatzky, G.A. Phonon assisted multimagnon optical absorption and long lived two-magnon states in undoped lamellar copper oxides. Phys. Rev. Lett. 1995, 74, 1867–1870. [Google Scholar] [CrossRef]
  80. Ament, L.J.P.; van Veenendaal, M.; Devereaux, T.P.; Hil, J.P.; van den Brink, J. Resonant inelastic x-ray scattering studies of elementary excitations. Rev. Mod. Phys. 2011, 83, 705–767. [Google Scholar] [CrossRef] [Green Version]
  81. Hozoi, L.; Siurakshina, L.; Fulde, P.; van den Brink, J. Ab Initio determination of Cu 3d orbital energies in layered copper oxides. Sci. Rep. 2011, 1, 65. [Google Scholar] [CrossRef]
  82. Moretti Sala, M.; Bisogni, V.; Aruta, C.; Balestrino, G.; Berger, H.; Brookes, N.B.; de Luca, G.M.; Di Castro, D.; Grioni, M.; Guarise, M.; et al. Energy and symmetry of dd excitations in undoped layered cuprates measured by Cu L3 resonant inelastic x-ray scattering. New J. Phys. 2011, 13, 043026. [Google Scholar] [CrossRef]
  83. Bianconi, A.; Castrucci, P.; Fabrizi, A.; Pompa, M.; Flank, A.M.; Lagarde, P.; Katayama-Yoshida, H.; Calestani, G. Correlation between mixing of Cu d orbitals and Tc determined by polarized Cu L3 XAS: Experimental evidence for pairing mediated by d-d excitations. Phys. C 1989, 162, 209–210. [Google Scholar] [CrossRef]
  84. Nücker, N.; Romberg, H.; Xi, X.X.; Fink, J.; Gegenheimer, B.; Zhao, Z.X. Symmetry of holes in high-Tc superconductors. Phys. Rev. B 1989, 39, 6619–6629. [Google Scholar] [CrossRef]
  85. Khomskii, D.I.; Neimark, E.I. Orbital structure of copper in high temperature superconductors. Phys. C 1991, 173, 342–346. [Google Scholar] [CrossRef]
  86. Ellis, D.S.; Huang, Y.B.; Olalde-Velasco, P.; Dantz, M.; Pelliciari, J.; Drachuck, G.; Ofer, R.; Bazalitsky, G.; Berger, J.; Schmitt, T.; et al. Correlation of the superconducting critical temperature with spin and orbital excitations in (CaxLa1−x)(Ba1.75−xLa0.25+x)Cu3Oy as measured by resonant inelastic x-ray scattering. Phys. Rev. B 2015, 92, 104507. [Google Scholar] [CrossRef]
  87. Fumagalli, R.; Braicovich, L.; Minola, M.; Peng, Y.Y.; Kummer, K.; Betto, D.; Rossi, M.; Lefrancois, E.; Morawe, C.; Salluzzo, M. Polarization resolved Cu L3-edge resonant inelastic x-ray scattering of orbital and spin excitations in NdBa2Cu3O7-δ. arXiv 2019, arXiv:1902.05471. [Google Scholar] [CrossRef]
  88. Kang, M.; Pelliciari, J.; Krockenberger, Y.; Li, J.; McNally, D.E.; Paris, E.; Liang, R.; Hardy, W.N.; Bonn, D.A.; Yamamoto, H.; et al. Resolving the nature of electronic excitations in resonant inelastic x-ray scattering. Phys. Rev. B 2019, 99, 045105. [Google Scholar] [CrossRef]
  89. Kugel, K.I.; Khomskii, D.I. Jahn-Teller Effect and Magnetism: Transition Metal Compounds. Usp. Fiz. Nauk 1982, 25, 621–664. [Google Scholar] [CrossRef]
  90. Feiner, L.F.; Oleś, A.M.; Zaanen, J. Quantum Melting of Magnetic Order due to Orbital Fluctuations. Phys. Rev. Lett. 1997, 78, 2799–2802. [Google Scholar] [CrossRef] [Green Version]
  91. Tokura, Y.; Nagaosa, N. Orbital Physics in Transition-Metal Oxides. Science 2000, 288, 462–468. [Google Scholar] [CrossRef] [PubMed]
  92. Oleś, A.M.; Khaliullin, G.; Horsch, P.; Feiner, L.F. Fingerprints of spin-orbital physics in cubic Mott insulators: Magnetic exchange interactions and optical spectral weights. Phys. Rev. B 2005, 72, 214431. [Google Scholar] [CrossRef]
  93. Khaliullin, G. Orbital Order and Fluctuations in Mott Insulators. Prog. Theor. Phys. Suppl. 2005, 160, 155–202. [Google Scholar] [CrossRef] [Green Version]
  94. Normand, B.; Oleś, A.M. Frustration and entanglement in the t2g spin-orbital model on a triangular lattice: Valence-bond and generalized liquid states. Phys. Rev. B 2008, 78, 094427. [Google Scholar] [CrossRef]
  95. Corboz, P.; Lajkó, M.; Laüchli, A.M.; Penc, K.; Mila, F. Spin-Orbital Quantum Liquid on the Honeycomb Lattice. Phys. Rev. X 2012, 2, 041013. [Google Scholar] [CrossRef]
  96. Oleś, A.M. Fingerprints of Spin-Orbital Entanglement in Transition Metal Oxides. J. Phys. Condens. Matter 2012, 24, 313201. [Google Scholar] [CrossRef]
  97. Schlappa, J.; Wohlfeld, K.; Zhou, K.J.; Mourigal, M.; Haverkort, M.W.; Strocov, V.N.; Hozoi, L.; Monney, C.; Nishimoto, S.; Singh, S.; et al. Spin-orbital separation in the quasi-one-dimensional Mott insulator Sr2CuO3. Nature 2012, 485, 82–85. [Google Scholar] [CrossRef]
  98. Bisogni, V.; Wohlfeld, K.; Nishimoto, S.; Monney, C.; Trinckauf, J.; Zhou, K.; Kraus, R.; Koepernik, K.; Sekar, C.; Strocov, V.; et al. Orbital Control of Effective Dimensionality: From Spin-Orbital Fractionalization to Confinement in the Anisotropic Ladder System CaCu2O3. Phys. Rev. Lett. 2015, 114, 096402. [Google Scholar] [CrossRef]
  99. Wohlfeld, K.; Daghofer, M.; Nishimoto, S.; Khaliullin, G.; van den Brink, J. Intrinsic Coupling of Orbital Excitations to Spin Fluctuations in Mott Insulators. Phys. Rev. Lett. 2011, 107, 247201. [Google Scholar] [CrossRef] [PubMed]
  100. Wohlfeld, K.; Nishimoto, S.; Haverkort, M.W.; van den Brink, J. Microscopic origin of spin-orbital separation in Sr2CuO3. Phys. Rev. B 2013, 88, 195138. [Google Scholar] [CrossRef]
  101. Brzezicki, W.; Oleś, A.M.; Cuoco, M. Spin-Orbital Order Modified by Orbital Dilution in Transition-Metal Oxides: From Spin Defects to Frustrated Spins Polarizing Host Orbitals. Phys. Rev. X 2015, 5, 011037. [Google Scholar] [CrossRef]
  102. Brzezicki, W. Spin, orbital and topological order in models of strongly correlated electrons. arXiv 2019, arXiv:1904.11772. [Google Scholar]
  103. Comin, R.; Damascelli, A. Resonant X-Ray Scattering Studies of Charge Order in Cuprates. Annu. Rev. Condens. Matter Phys. 2016, 7, 369–405. [Google Scholar] [CrossRef] [Green Version]
  104. Liu, Q.Q.; Yang, H.; Qin, X.M.; Yu, Y.; Yang, L.X.; Li, F.Y.; Yu, R.C.; Jin, C.Q.; Uchida, S. Enhancement of the superconducting critical temperature of Sr2CuO3+δ up to 95K by ordering dopant atoms. Phys. Rev. B 2006, 74, 100506(R). [Google Scholar] [CrossRef]
  105. Maier, T.A.; Berlijn, T.; Scalapino, D.J. d-wave and s± Pairing Strengths in Ba2CuO3+δ. arXiv 2018, arXiv:1809.04156. [Google Scholar]
  106. Geballe, T.H.; Marezio, M. Enhanced superconductivity in Sr2CuO4-v. Phys. C 2009, 469, 680–684. [Google Scholar] [CrossRef]
  107. Li, W.M.; Cao, L.P.; Zhao, J.F.; Yu, R.Z.; Zhang, J.; Liu, Y.; Liu, Q.Q.; Zhao, G.Q.; Wang, X.C.; Hu, Z.; et al. A new superconductor of cuprates with unique features. arXiv 2018, arXiv:1808.09425. [Google Scholar]
  108. Uchida, M.; Ishizaka, K.; Hansmann, P.; Yang, X.; Sakano, M.; Miyawaki, J.; Arita, R.; Kaneko, Y.; Takata, Y.; Oura, M.; et al. Orbital characters of three-dimensional Fermi surfaces in Eu2−xSrxNiO4 as probed by soft-x-ray angle-resolved photoemission spectroscopy. Phys. Rev. B 2011, 84, 241109(R). [Google Scholar] [CrossRef]
  109. Hansmann, P.; Yang, X.; Toschi, A.; Khaliullin, G.; Andersen, O.K.; Held, K. Turning a Nickelate Fermi Surface into a Cupratelike One through Heterostructuring. Phys. Rev. Lett. 2009, 103, 016401. [Google Scholar] [CrossRef] [Green Version]
  110. Disa, A.S.; Kumah, D.P.; Malashevich, A.; Chen, H.; Arena, D.A.; Specht, E.D.; Ismail-Beigi, S.; Walker, F.J.; Ahn, C.H. Orbital Engineering in Symmetry-Breaking Polar Heterostructures. Phys. Rev. Lett. 2015, 114, 026801. [Google Scholar] [CrossRef]
  111. Wu, M.; Benckiser, E.; Haverkort, M.V.; Frano, A.; Lu, Y.; Nwanko, N.; Brück, S.; Audehm, P.; Goering, E.; Mache, S.; et al. Strain and composition dependence of the orbital polarization in nickelate superlattices. Phys. Rev. B 2013, 88, 125124. [Google Scholar] [CrossRef]
  112. Hepting, M.; Minola, M.; Frano, A.; Cristiani, G.; Logvenov, G.; Schierle, E.; Wu, M.; Bluschke, M.; Weschke, E.; Habermeier, H.-U.; et al. Tunable spin and charge order. Phys. Rev. Lett. 2014, 113, 227206. [Google Scholar] [CrossRef]
  113. Zhang, J.; Botana, A.S.; Freeland, J.W.; Phelan, D.; Zheng, H.; Pardo, V.; Norman, M.R.; Mitchell, J.F. Large orbital polarization in a metallic square-planar nickelate. Nat. Phys. 2017, 13, 864–869. [Google Scholar] [CrossRef] [Green Version]
  114. Botana, A.S.; Pardo, V.; Norman, M.R. Electron doped layered nickelates: Spanning the phase diagram of the cuprates. Phys. Rev. Mater. 2017, 1, 021801(R). [Google Scholar] [CrossRef]
  115. Le, C.; Zeng, J.; Gu, Y.; Cao, G.-H.; Hub, J. A possible family of Ni-based high temperature superconductors. Sci. Bull. 2018, 63, 957–963. [Google Scholar] [CrossRef] [Green Version]
  116. Lu, F.; Wang, W.-H.; Xie, X.; Zhang, F.-C. Correlation effects in the electronic structure of the Ni-based superconducting KNi2S2. Phys. Rev. B 2013, 87, 115131. [Google Scholar] [CrossRef]
  117. Maeno, Y.; Hashimoto, H.; Yoshida, K.; Nishizaki, S.; Fujita, T.; Bednorz, J.G.; Lichtenberg, F. Superconductivity in a layered perovskite without copper. Nature 1994, 372, 532–534. [Google Scholar] [CrossRef]
  118. Agterberg, D.F.; Rice, T.M.; Sigrist, M. Orbital Dependent Superconductivity in Sr2RuO4. Phys. Rev. Lett. 1997, 78, 3374–3377. [Google Scholar] [CrossRef]
  119. Maeno, Y.; Rice, T.M.; Sigrist, M. The Intriguing Superconductivity of Strontium Ruthenate. Phys. Today 2001, 54, 42–47. [Google Scholar] [CrossRef]
  120. Suderow, H.; Crespo, V.; Guillamon, I.; Vieira, S.; Servant, S.; Leyey, P.; Brison, J.P.; Floquet, J. A nodeless superconducting gap in Sr2RuO4 from tunneling spectroscopy. New J. Phys. 2009, 11, 093004. [Google Scholar] [CrossRef]
  121. Pustogow, A.; Yonkang, L.; Chronister, A.; Su, Y.-S.; Sokolov, D.A.; Jerzembeck, F.; Mackenzie, A.P.; Hicks, C.W.; Kikugawa, N.; Raghu, S.; et al. Pronounced drop of 17O NMR Knight shift in superconducting state of Sr2RuO4. arXiv 2019, arXiv:1904.00047. [Google Scholar]
  122. Wang, Q.H.; Platt, C.; Yang, Y.; Honerkamp, C.; Zhang, F.C.; Hanke, W.; Rice, T.M.; Thomale, R. Theory of superconductivity in a three-orbital model of Sr2RuO4. Europhys. Lett. 2013, 104, 17013. [Google Scholar] [CrossRef]
  123. Imai, Y.; Wakabayashi, K.; Sigrist, M. Topological and edge state properties of a three-band model for Sr2RuO4. Phys. Rev. B 2013, 88, 144503. [Google Scholar] [CrossRef]
  124. Akebi, S.; Kondo, T.; Nakayama, M.; Kuroda, K.; Kunisada, S.; Taniguchi, H.; Maeno, Y.; Shin, S. Low-energy electron-mode couplings in the surface bands of Sr2RuO4 revealed by laser-based angle-resolved photoemission spectroscopy. Phys. Rev. B 2019, 99, 081108(R). [Google Scholar] [CrossRef]
  125. Khaliullin, G.; Koshibae, W.; Maekawa, S. Low Energy Electronic States and Triplet Pairing in Layered Cobaltate. Phys. Rev. Lett. 2004, 93, 176401. [Google Scholar] [CrossRef] [PubMed]
  126. Jackeli, G.; Khaliullin, G. Mott Insulators in the Strong Spin-Orbit Coupling Limit: From Heisenberg to a Quantum Compass and Kitaev Models. Phys. Rev. Lett. 2009, 102, 017205. [Google Scholar] [CrossRef]
  127. Kim, B.J.; Jin, H.; Moon, S.J.; Kim, J.-Y.; Park, B.G.; Leem, C.S.; Yu, J.; Noh, T.W.; Kim, C.; Oh, S.-J.; et al. Novel Jeff=1/2 Mott State Induced by Relativistic Spin-Orbit Coupling in Sr2IrO4. Phys. Rev. Lett. 2008, 101, 076402. [Google Scholar] [CrossRef]
  128. Kim, B.J.; Ohsumi, H.; Komesu, T.; Sakai, S.; Morita, T.; Takagi, H.; Arima, T. Phase-Sensitive Observation of a Spin-Orbital Mott State in Sr2IrO4. Science 2009, 323, 1329–1332. [Google Scholar] [CrossRef]
  129. Kim, J.; Casa, D.; Upton, M.H.; Gog, T.; Kim, Y.-J.; Mitchell, J.F.; van Veenendaal, M.; Daghofer, M.; van den Brink, J.; Khaliullin, G.; et al. Magnetic Excitation Spectra of Sr2IrO4 Probed by Resonant Inelastic X-Ray Scattering: Establishing Links to Cuprate Superconductors. Phys. Rev. Lett. 2012, 108, 177003. [Google Scholar] [CrossRef]
  130. Liu, H.; Khaliullin, G. Pseudo-Jahn-Teller Effect and Magnetoelastic Coupling in Spin-Orbit Mott Insulators. Phys. Rev. Lett. 2019, 122, 057203. [Google Scholar] [CrossRef]
  131. Kim, Y.K.; Krupin, O.; Denlinger, J.D.; Bostwick, A.; Rotenberg, E.; Zhao, Q.; Mitchell, J.F.; Allen, J.W.; Kim, B.J. Fermi arcs in a doped pseudospin-1/2 Heisenberg antiferromagnet. Science 2014, 160, 1329–1332. [Google Scholar] [CrossRef]
  132. Imada, M. Universality classes of metal-insulator transitions in strongly correlated electron systems and mechanism of high-temperature superconductivity. Phys. Rev. B 2005, 72, 075113. [Google Scholar] [CrossRef]
  133. Andersen, O.K.; Boeri, L. On the multi-orbital band structure and itinerant magnetism of iron-based superconductors. Ann. Phys. 2011, 523, 8–50. [Google Scholar] [CrossRef] [Green Version]
  134. Ferber, J.; Jeschke, H.O.; Valentí, R. Fermi Surface Topology of LaFePO and LiFeP. Phys. Rev. Lett. 2012, 109, 236403. [Google Scholar] [CrossRef]
  135. Raghu, S.; Qi, X.L.; Liu, C.X.; Scalapino, D.J.; Zhang, S.C. Minimal two-band model of the superconducting iron oxypnictides. Phys. Rev. B 2013, 88, 144503. [Google Scholar] [CrossRef]
  136. Daghofer, M.; Nicholson, A.; Moreo, A.; Dagotto, E. Three orbital model for the iron-based superconductors. Phys. Rev. B 2010, 81, 014511. [Google Scholar] [CrossRef]
  137. Fernandes, R.M.; Schmalian, J. Competing order and nature of the pairing state in the iron pnictides. Phys. Rev. B 2010, 82, 014521. [Google Scholar] [CrossRef]
  138. Nicholson, A.; Ge, W.; Zhang, X.; Riera, J.; Daghofer, M.; Oleś, A.M.; Martins, G.B.; Moreo, A.; Dagotto, E. Competing Pairing Symmetries in a Generalized Two-Orbital Model for the Pnictide Superconductors. Phys. Rev. Lett. 2011, 106, 217002. [Google Scholar] [CrossRef]
  139. Nicholson, A.; Ge, W.; Riera, J.; Daghofer, M.; Moreo, A.; Dagotto, E. Pairing symmetries of a hole-doped extended two-orbital model for the pnictides. Phys. Rev. B 2012, 85, 024532. [Google Scholar] [CrossRef]
  140. Ptok, A.; Kapcia, K.J.; Cichy, A.; Oleś, A.M.; Piekarz, P. Magnetic Lifshitz transition and its consequences in multi-band iron-based superconductors. Sci. Rep. 2017, 7, 41979. [Google Scholar] [CrossRef] [Green Version]
  141. Tafti, F.F.; Juneau-Fecteau, A.; Delage, M.E.; René de Cotret, S.; Reid, J.P.; Wang, A.F.; Luo, X.G.; Chen, X.H.; Doiron-Leyraud, N.; Taillefer, L. Sudden reversal in the pressure dependence of Tc in the iron-based superconductor KFe2As2. Nat. Phys. 2013, 9, 349–352. [Google Scholar] [CrossRef]
  142. Qi, Q.; Abrahams, E. Strong Correlations and Magnetic Frustration in the High Tc Iron Pnictides. Phys. Rev. Lett. 2008, 101, 076401. [Google Scholar]
  143. Krüger, F.; Kumar, S.; Zaanen, J.; van den Brink, J. Spin-orbital frustrations and anomalous metallic state in iron-pnictide superconductors. Phys. Rev. B 2009, 79, 054504. [Google Scholar] [CrossRef]
  144. Fink, J.; Rienks, E.D.L.; Thirupathaiah, S.; Nayak, J.; van Roekeghem, A.; Biermann, S.; Wolf, T.; Adelmann, P.; Jeevan, H.S.; Gegenwart, P.; et al. Experimental evidence for importance of Hund’s exchange interaction for incoherence of charge carriers in iron-based superconductors. Phys. Rev. B 2017, 95, 144513. [Google Scholar] [CrossRef]
  145. Yaresko, A.N.; Liu, G.-Q.; Antonov, V.N.; Andersen, O.K. Interplay between magnetic properties and Fermi surface nesting in iron pnictides. Phys. Rev. B 2009, 79, 144421. [Google Scholar] [CrossRef]
  146. Wysocki, A.L.; Belashchenko, K.D.; Antropov, V.P. Consistent model of magnetism in ferropnictides. Nat. Phys. 2011, 7, 485–489. [Google Scholar] [CrossRef] [Green Version]
  147. Yu, R.; Wang, Z.; Goswami, P.; Nievidomskyy, A.H.; Si, Q.; Abrahams, E. Spin dynamics of a J1-J2-K model for the paramagnetic phase of iron pnictides. Phys. Rev. B 2012, 86, 085148. [Google Scholar] [CrossRef]
  148. Glasbrenner, J.K.; Mazin, I.I.; Jeschke, H.O.; Hirschfeld, P.J.; Valentí, R. Effect of magnetic frustration on nematicity and superconductivity in Fe chalcogenides. Nat. Phys. 2015, 11, 953–958. [Google Scholar] [CrossRef]
  149. Chaloupka, J.; Khaliullin, G. Spin-State Crossover Model for the Magnetism of Iron Pnictides. Phys. Rev. Lett. 2013, 110, 207205. [Google Scholar] [CrossRef]
  150. Dai, P.C.; Hu, J.P.; Dagotto, E. Magnetism and its microscopic origin in iron-based high-temperature superconductors. Nat. Phys. 2012, 8, 709–718. [Google Scholar] [CrossRef] [Green Version]
  151. Beak, S.-H.; Efremov, D.V.; Ok, J.M.; Kim, J.S.; van den Brink, J.; Büchner, B. Orbital-driven nematicity in FeSe. Nat. Mat. 2014, 14, 210–214. [Google Scholar] [CrossRef] [Green Version]
  152. Watson, M.D.; Kim, T.K.; Haghighirad, A.A.; Davies, N.R.; McCollam, A.; Narayanan, A.; Blake, S.F.; Chen, Y.L.; Ghannadzadeh, S.; Schofield, A.J.; et al. Emergence of nematic electronic state in FeSe. Phys. Rev. B 2015, 91, 155106. [Google Scholar] [CrossRef]
  153. Fernandes, R.M.; Chubukov, A.V.; Knolle, J.; Eremin, I.; Schmalian, J. Preemptive nematic order, pseudogap, and orbital order in the iron pnictides. Phys. Rev. B 2012, 85, 024534. [Google Scholar] [CrossRef] [Green Version]
  154. Kontani, H.; Onari, S. Orbital-Fluctuation-Mediated Superconductivity in Iron Pnictides: Analysis of the Five-Orbital Hubbard-Holstein Model. Phys. Rev. Lett. 2010, 104, 157001. [Google Scholar] [CrossRef]
  155. Onari, S.; Kontani, H. Self-consistent Vertex Correction Analysis for Iron-based Superconductors: Mechanism of Coulomb Interaction-Driven Orbital Fluctuations. Phys. Rev. Lett. 2012, 109, 137001. [Google Scholar] [CrossRef]
  156. Saito, T.; Onari, S.; Kontani, H. Orbital fluctuation theory in iron pnictides: Effects of As-Fe-As bond angle, isotope substitution, and Z2-orbital pocket on superconductivity. Phys. Rev. B 2010, 82, 144510. [Google Scholar] [CrossRef]
  157. Chubukov, A.V.; Khodas, M.; Fernandes, R.M. Magnetism, Superconductivity, and Spontaneous Orbital Order in Iron-Based Superconductors: Which Comes First and Why? Phys. Rev. X 2016, 6, 041045. [Google Scholar] [CrossRef]
  158. Liu, D.F.; Li, C.; Huang, J.W.; Lei, B.; Wang, L.; Wu, X.X.; Shen, B.; Gao, Q.; Zhang, Y.X.; Liu, X.; et al. Orbital Origin of Extremely Anisotropic Superconducting Gap in Nematic Phase of FeSe Superconductor. Phys. Rev. X 2018, 8, 031033. [Google Scholar] [CrossRef]
  159. Hashimoto, H.; Ota, Y.; Yamamoto, H.Q.; Suzuki, Y.; Shimojima, T.; Watanabe, S.; Chen, C.; Kashara, S.; Matsuda, Y.; Shibauchi, T.; et al. Superconducting gap anisotropy sensitive to nematic domains in FeSe. Nat. Commun. 2018, 9, 282. [Google Scholar] [CrossRef] [Green Version]
  160. Sprau, P.O.; Kostin, A.; Kreisel, A.; Böhmer, A.E.; Taufour, V.; Canfield, P.C.; Mukherjee, S.; Hirschfeld, P.J.; Andersen, B.M.; Séamus Davis, J.C. Discovery of orbital-selective Cooper pairing in FeSe. Science 2017, 357, 75–80. [Google Scholar] [CrossRef] [Green Version]
  161. Nica, E.M.; Yu, R.; Si, Q. Orbital-selective pairing and superconductivity in iron selenides. NPJ Quantum Mater. 2017, 2, 24. [Google Scholar] [CrossRef]
  162. Ptok, A.; Kapcia, K.J.; Piekarz, P.; Oleś, A.M. The ab initio study of unconventional superconductivity in CeCoIn5 and FeSe. New J. Phys. 2017, 19, 063039. [Google Scholar] [CrossRef]
  163. Li, Y.; Yin, Z.; Wang, X.; Tam, D.W.; Abernathy, D.L.; Podlesnyak, A.; Zhang, C.; Wang, M.; Xing, L.; Jin, C.; et al. Orbital Selective Spin Excitations and their Impact on Superconductivity of LiFe1−xCoxAs. Phys. Rev. Lett. 2016, 116, 247001. [Google Scholar] [CrossRef]
  164. Gawraczyński, J.; Kurzydłowski, D.; Ewings, R.A.; Bandaru, S.; Mazej, Z.; Ruani, G.; Bergenti, I.; Jaroń, T.; Ozarowski, A.; Hill, S.; et al. Silver route to cuprate analogs. PNAS 2019, 116, 1812857. [Google Scholar] [CrossRef]
  165. Jarlborg, T.; Bianconi, A. Multiple Electronic Components and Lifshitz Transitions by Oxygen Wires Formation in Layered Cuprates and Nickelates. Condens. Matter 2019, 4, 15. [Google Scholar] [CrossRef]

Share and Cite

MDPI and ACS Style

Oleś, A.M.; Wohlfeld, K.; Khaliullin, G. Orbital Symmetry and Orbital Excitations in High-Tc Superconductors. Condens. Matter 2019, 4, 46. https://doi.org/10.3390/condmat4020046

AMA Style

Oleś AM, Wohlfeld K, Khaliullin G. Orbital Symmetry and Orbital Excitations in High-Tc Superconductors. Condensed Matter. 2019; 4(2):46. https://doi.org/10.3390/condmat4020046

Chicago/Turabian Style

Oleś, Andrzej M., Krzysztof Wohlfeld, and Giniyat Khaliullin. 2019. "Orbital Symmetry and Orbital Excitations in High-Tc Superconductors" Condensed Matter 4, no. 2: 46. https://doi.org/10.3390/condmat4020046

APA Style

Oleś, A. M., Wohlfeld, K., & Khaliullin, G. (2019). Orbital Symmetry and Orbital Excitations in High-Tc Superconductors. Condensed Matter, 4(2), 46. https://doi.org/10.3390/condmat4020046

Article Metrics

Back to TopTop