Multiple Electronic Components and Lifshitz Transitions by Oxygen Wires Formation in Layered Cuprates and Nickelates
Abstract
1. Introduction
2. Method of Calculation
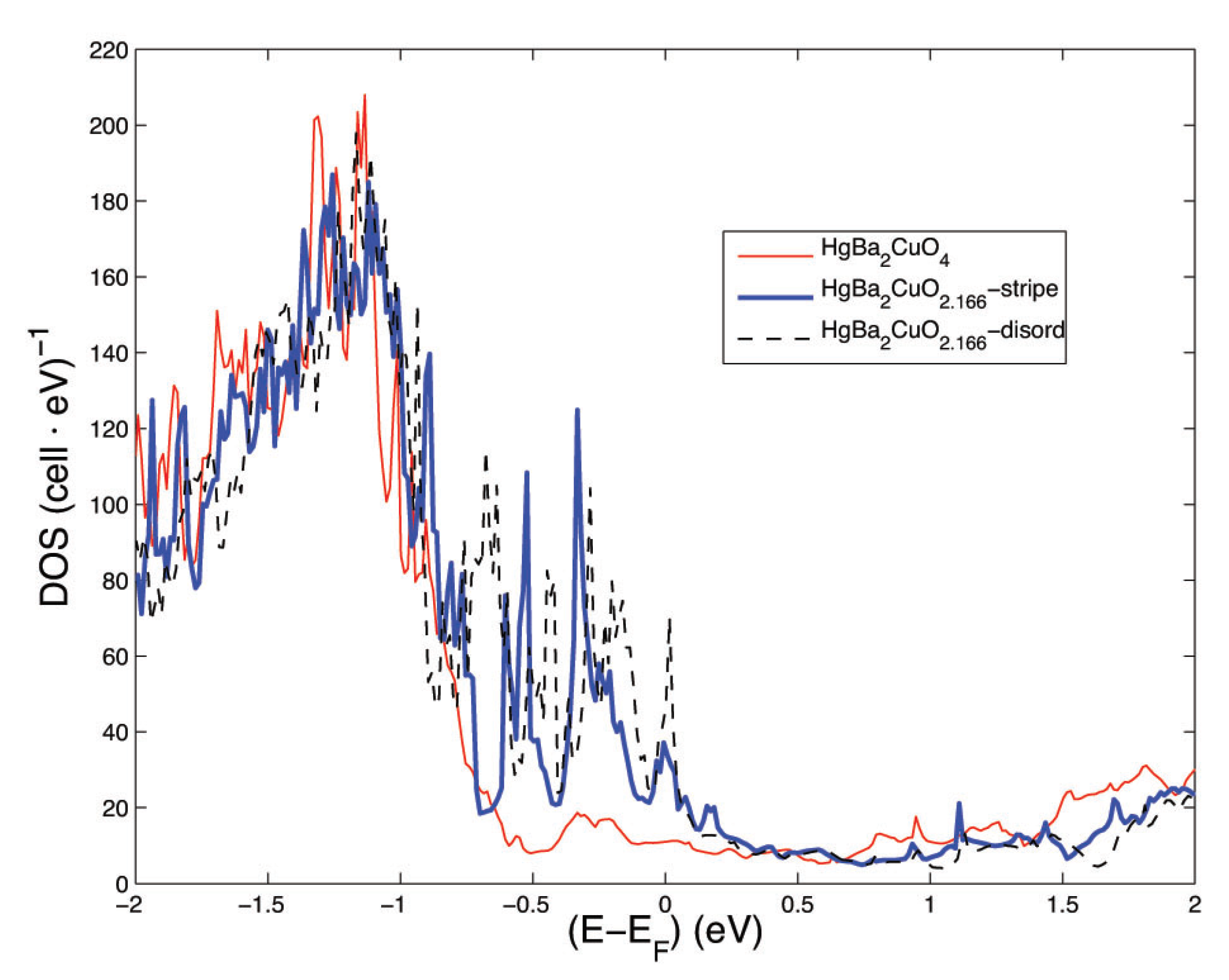
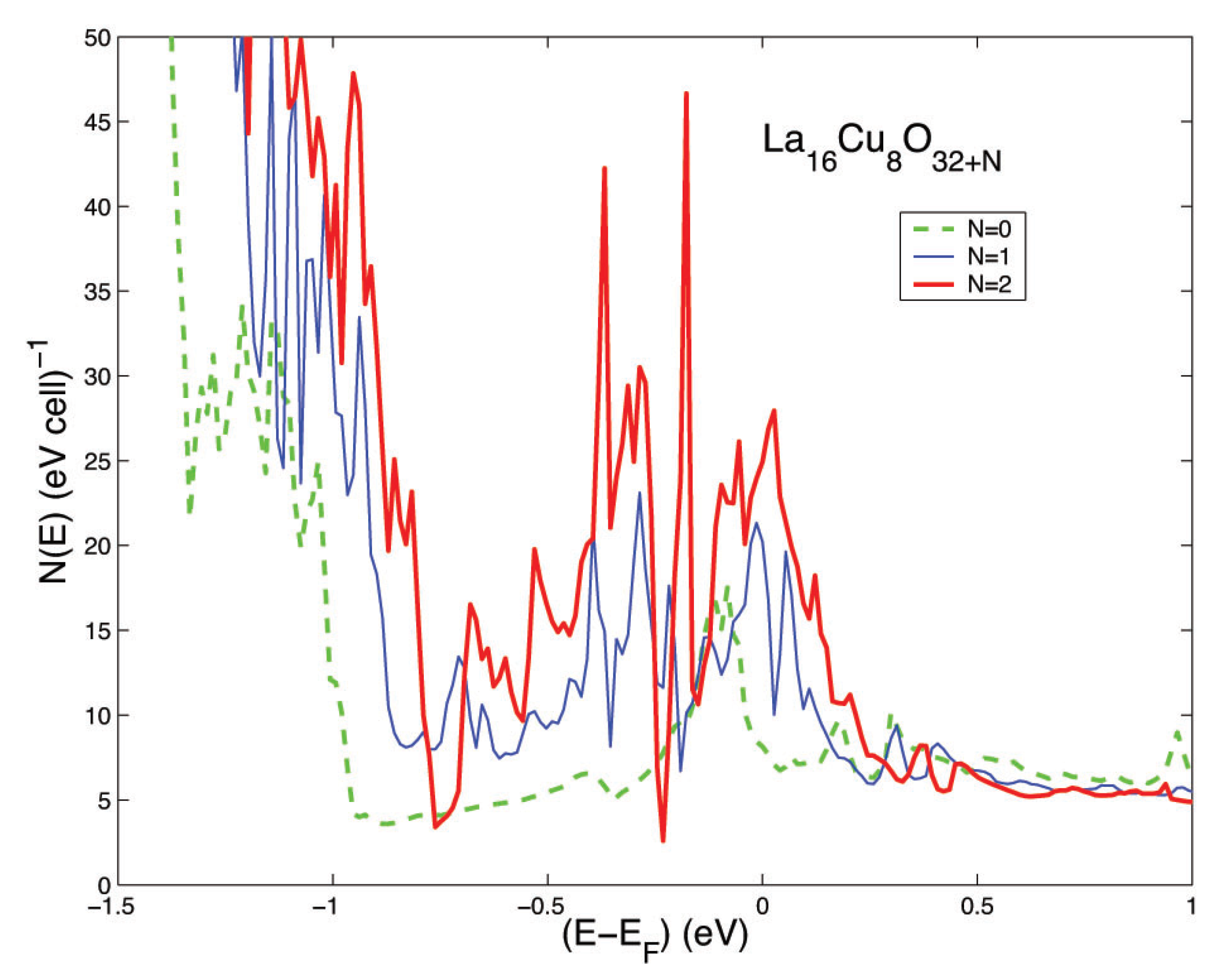
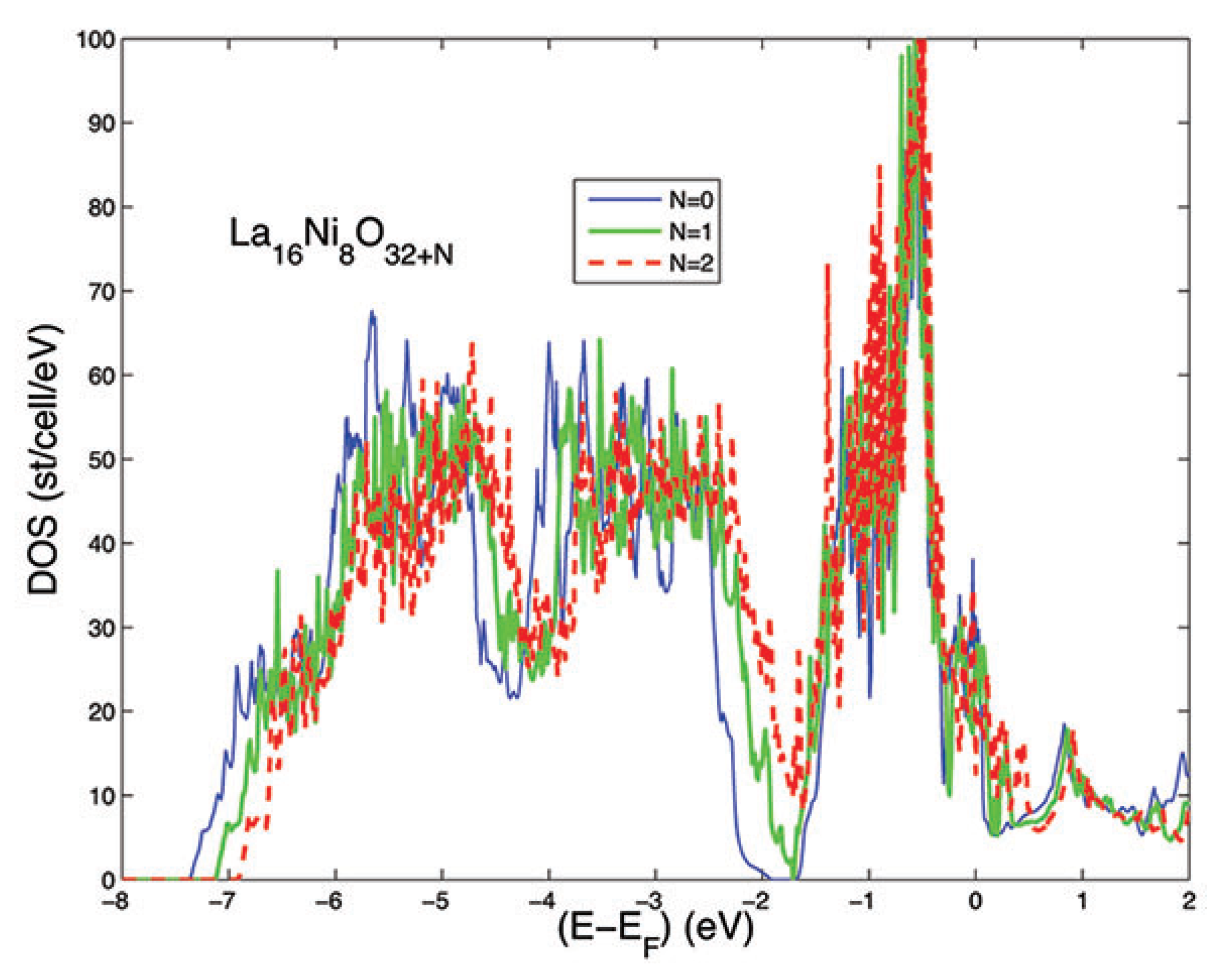
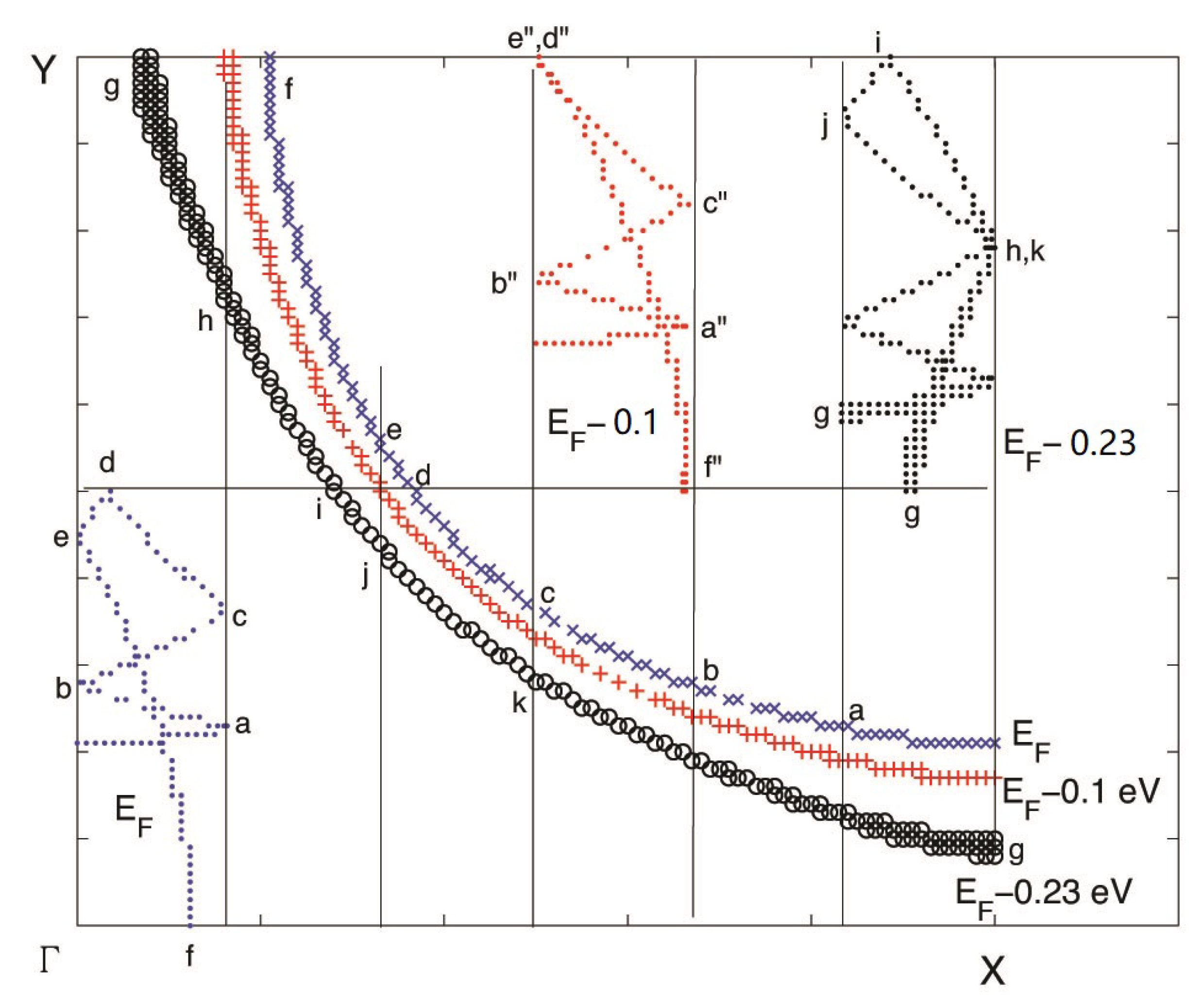
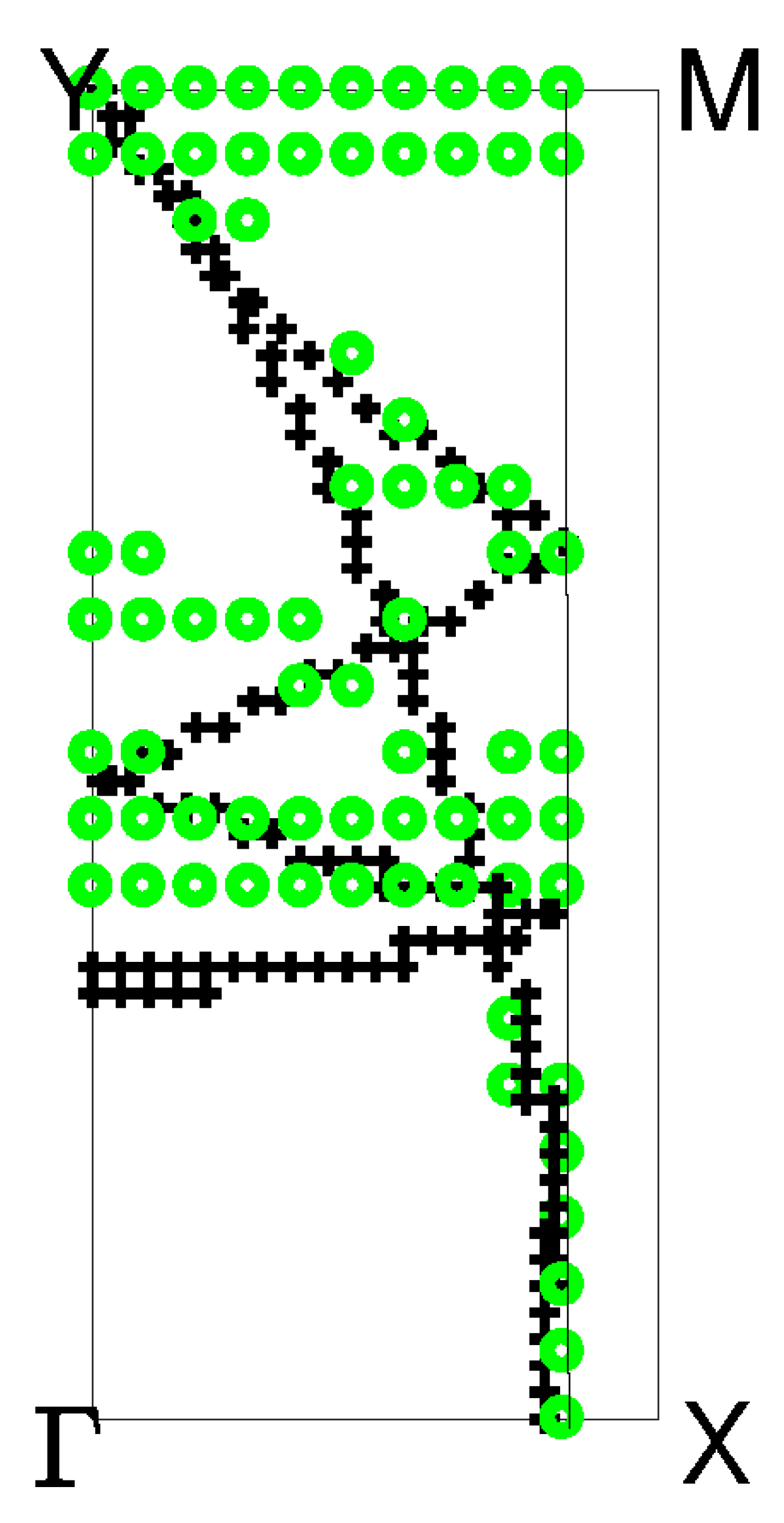
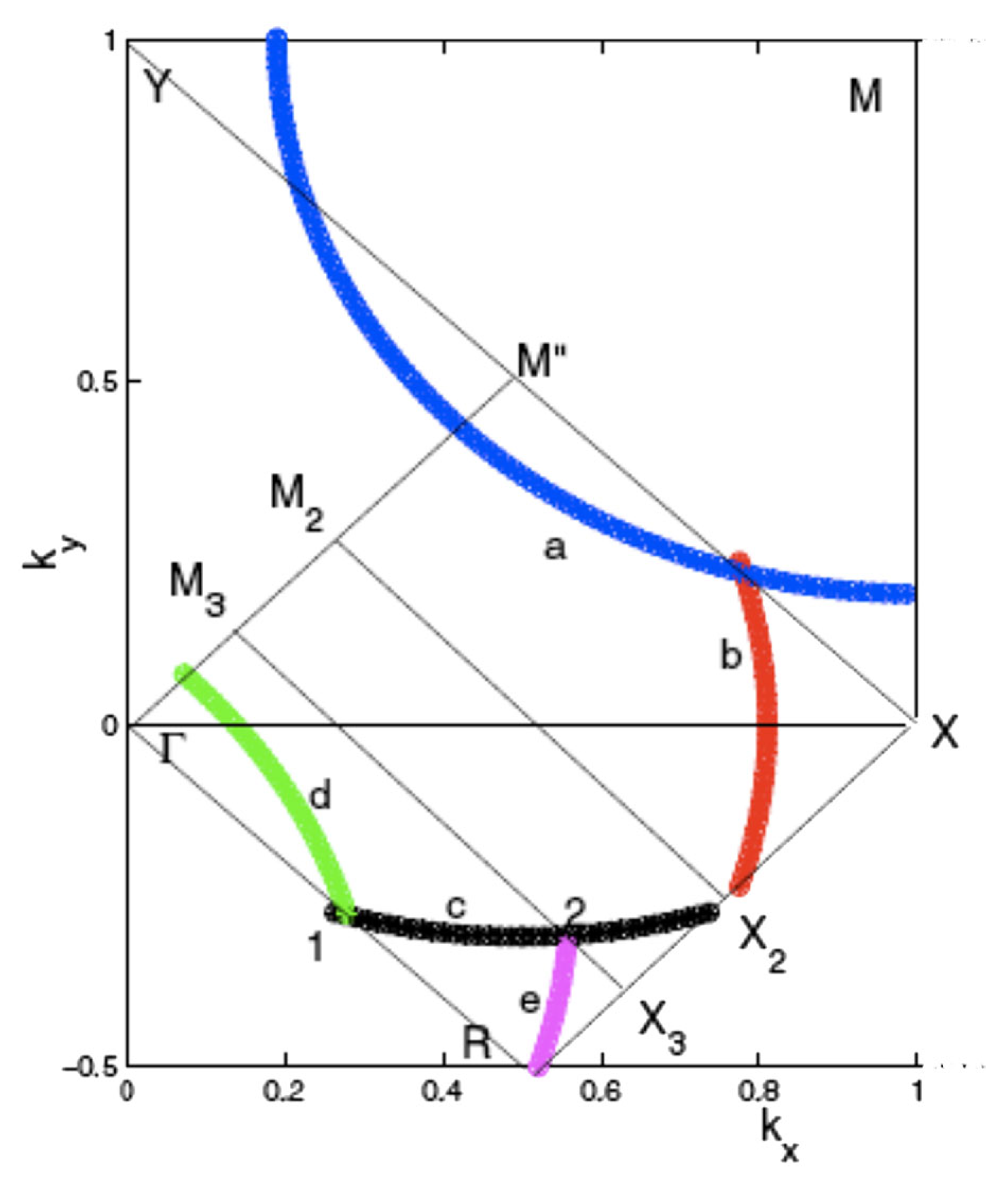
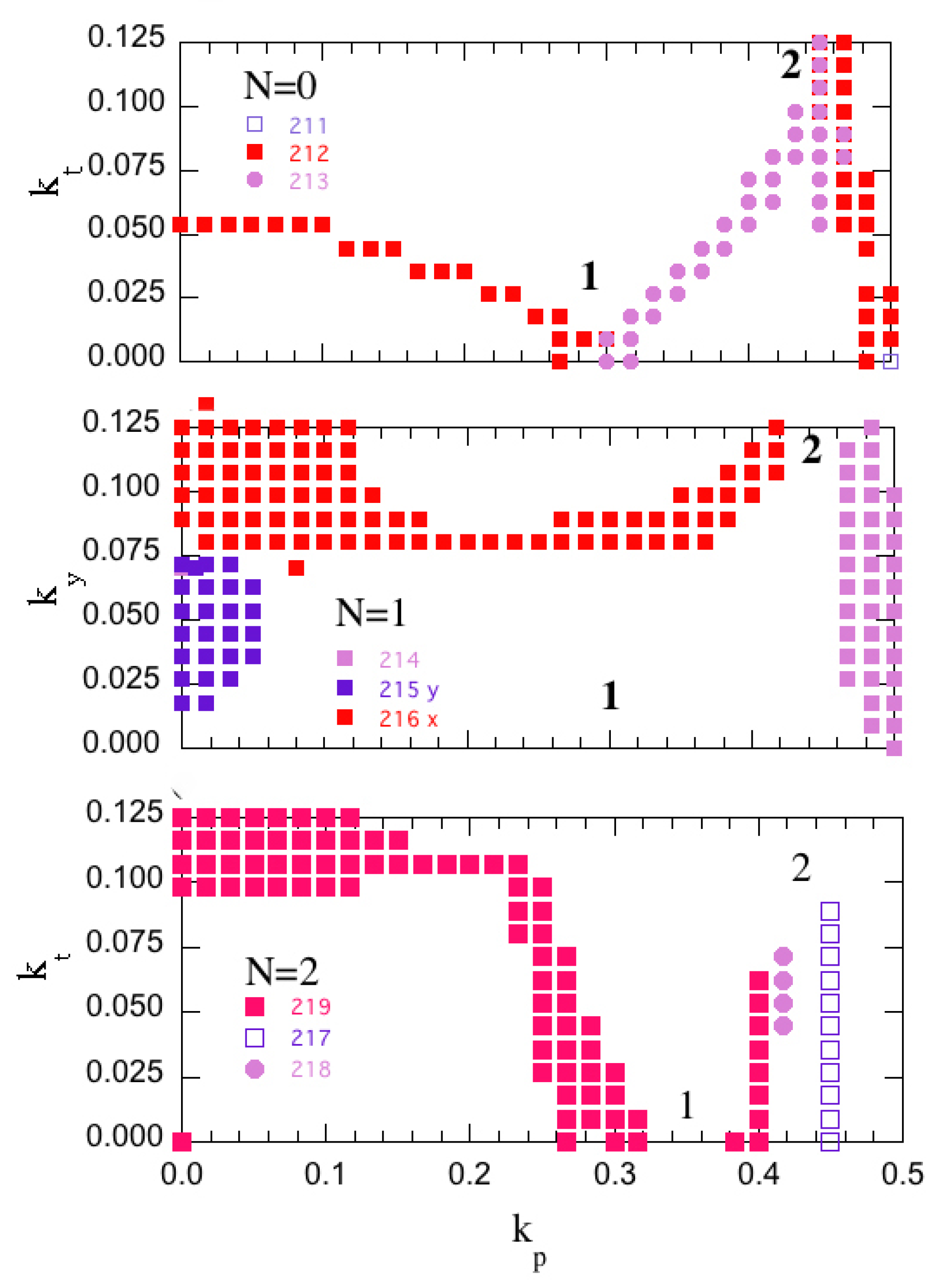
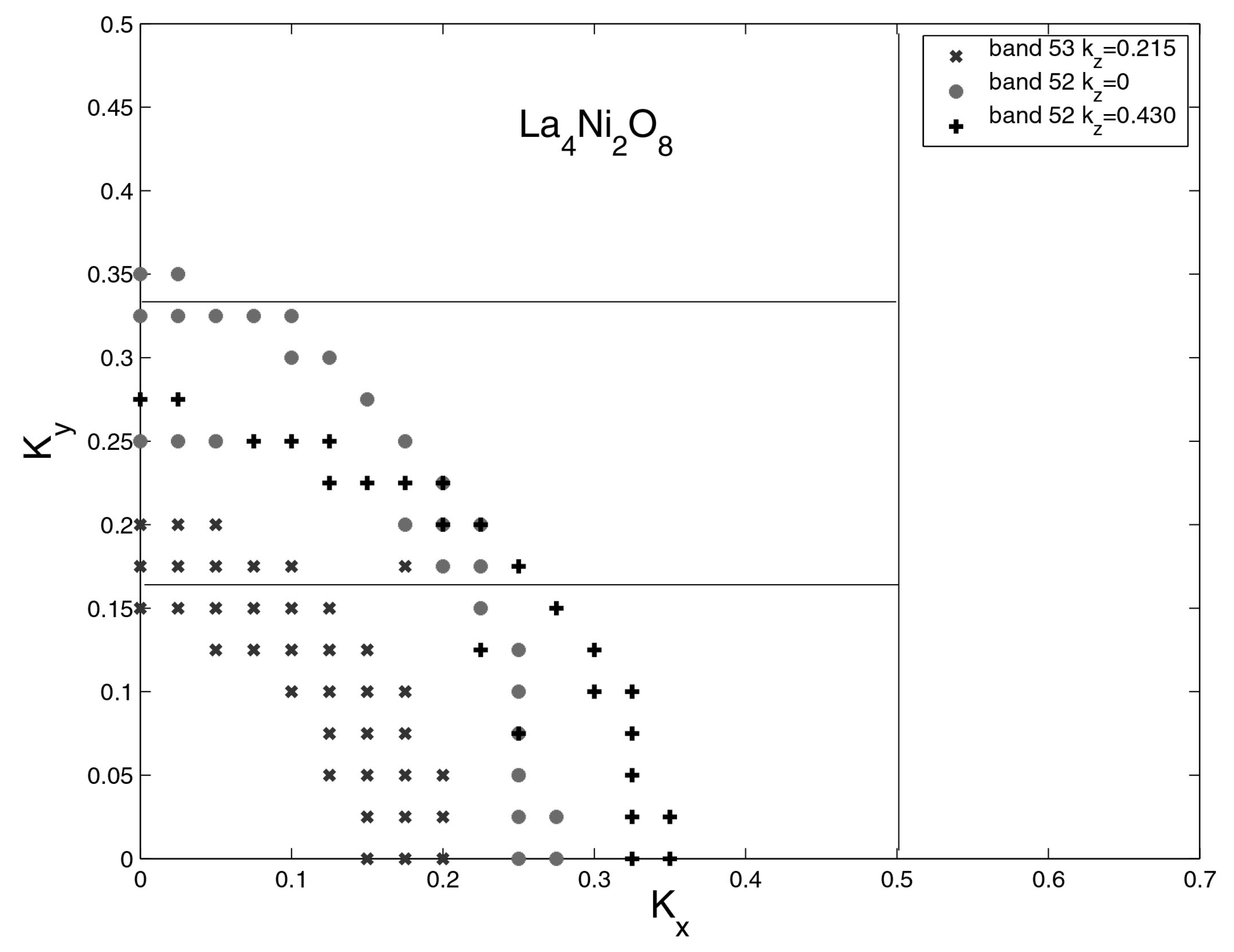
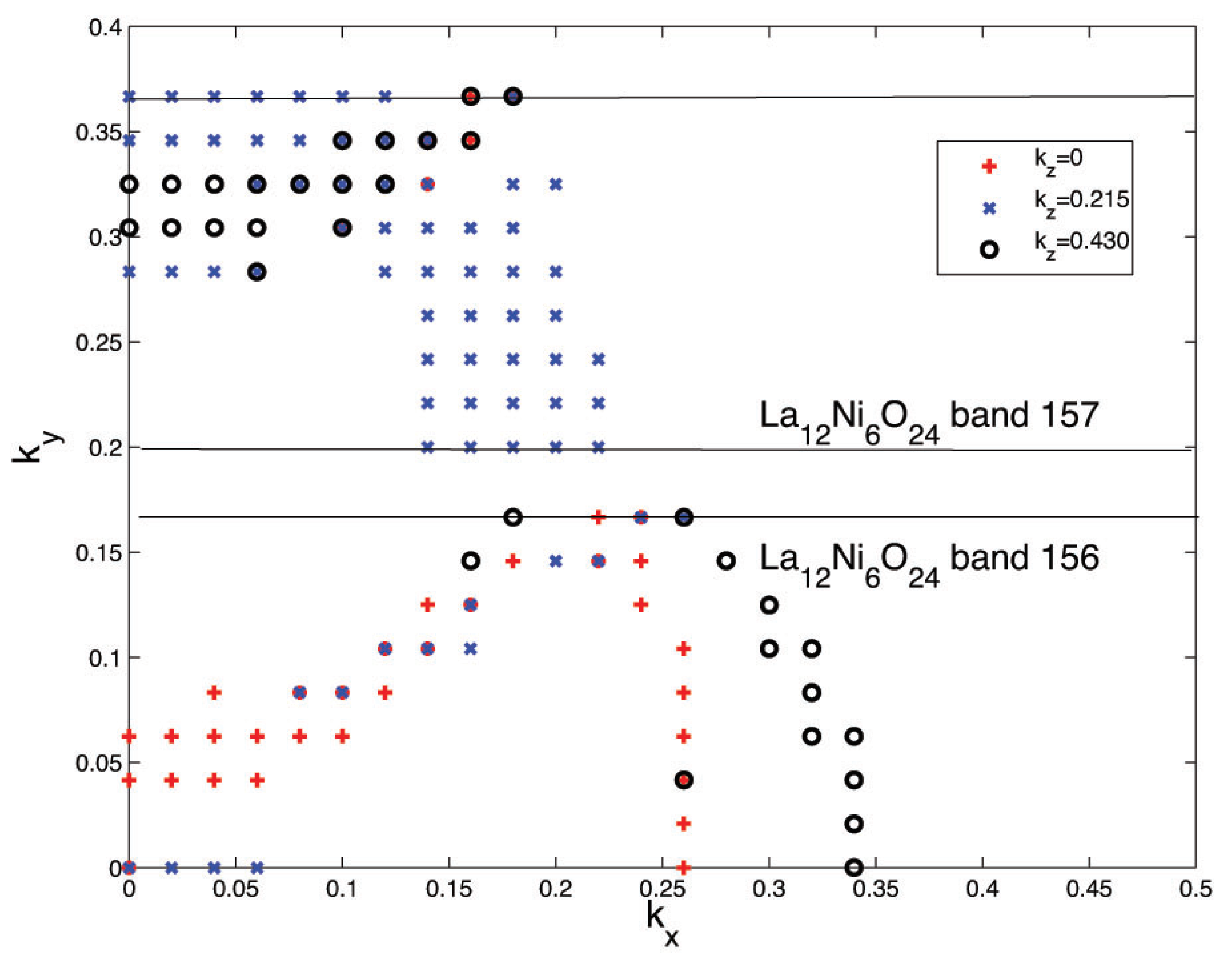
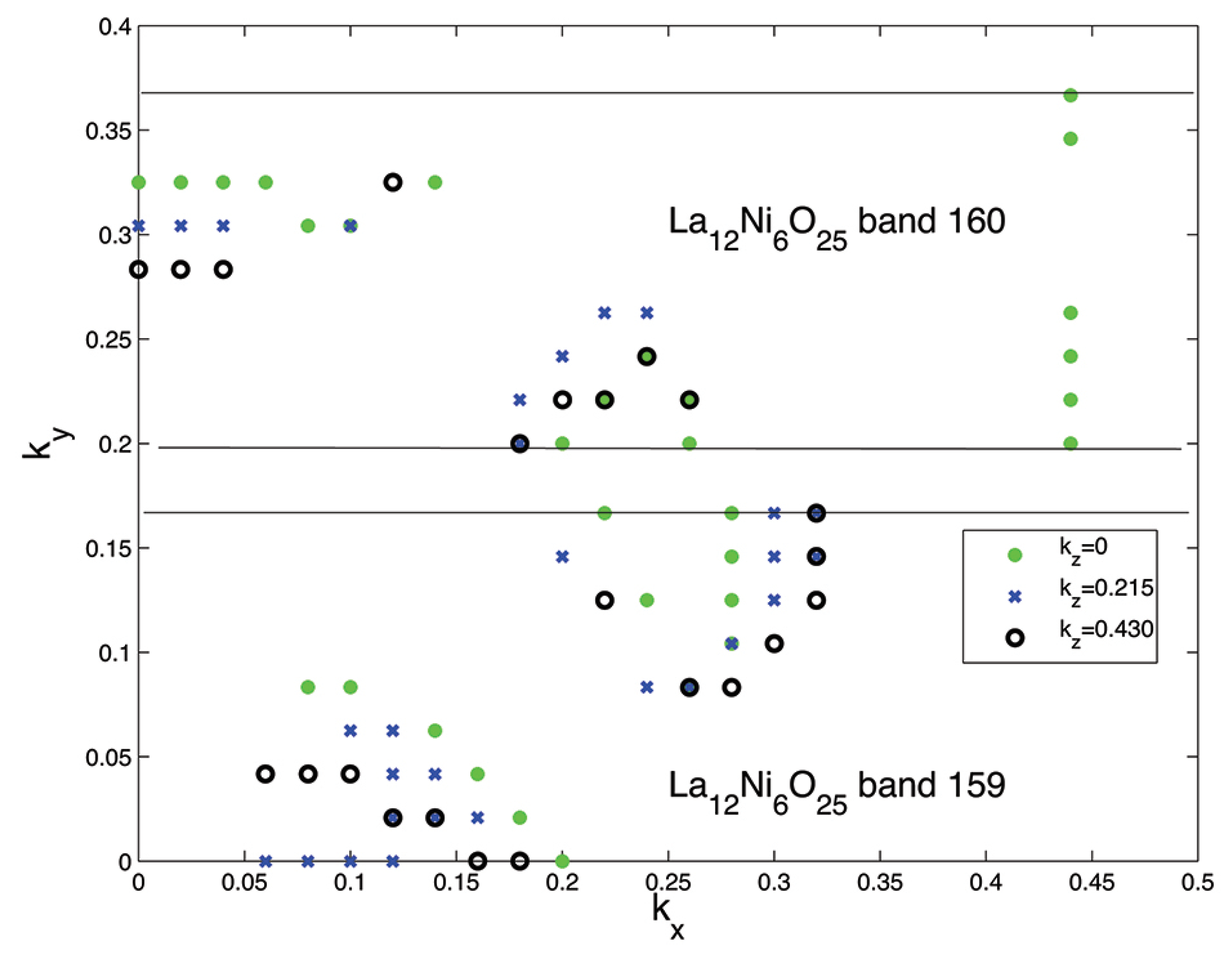
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jarlborg, T.; Bianconi, A. Breakdown of the Migdal approximation at Lifshitz transitions with giant zero-point motion in the H3S superconductor. Sci. Rep. 2016, 6, 24816. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, A.; Jarlborg, T. Lifshitz transitions and zero point lattice fluctuations in sulfur hydride showing near room temperature superconductivity. Novel Supercond. Mater. 2015, 1, 37. [Google Scholar] [CrossRef]
- Bianconi, A.; Jarlborg, T. Superconductivity above the lowest Earth temperature in pressurized sulfur hydride. Europhys. Lett. 2015, 112, 37001. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175. [Google Scholar] [CrossRef]
- Bianconi, A. Superstripes. Int. J. Mod. Phys. B 2000, 14, 3289–3297. [Google Scholar] [CrossRef]
- Bianconi, A.; Di Castro, D.; Bianconi, G.; Pifferi, A.; Saini, N.L.; Chou, F.C.; Johnston, D.C.; Colapietro, M. Coexistence of stripes and superconductivity: Tc amplification in a superlattice of superconducting stripes. Phys. C Supercond. 2000, 341, 1719–1722. [Google Scholar] [CrossRef]
- Bianconi, A. Quantum Materials: Shape Resonances in Superstripes. Nat. Phys. 2013, 9, 536. [Google Scholar] [CrossRef]
- Bianconi, A.; Castellano, A.C.; De Santis, M.; Politis, C.; Marcelli, A.; Mobilio, S.; Savoia, A. Lack of delocalized Cu p states at the Fermi level in the High Tc superconductor YBa2Cu3O∼7 by XANES spectroscopy. Zeitschrift fur Physik B Condensed Matter 1987, 67, 307–312. [Google Scholar] [CrossRef]
- Bianconi, A.; De Santis, M.; Flank, A.M.; Fontaine, A.; Lagarde, P.; Marcelli, A.; Katayama-Yoshida, H.; Kotani, A. Determination of the symmetry of the 3d9L states by polarized Cu L3 XAS spectra of single crystal YBa2Cu3O ≈ 6.9. Phys. C Supercond. 1988, 153–155, 1760–1761. [Google Scholar] [CrossRef]
- Seino, Y.; Kotani, A.; Bianconi, A.; Seino, Y.; Kotani, A.; Bianconi, A. Effect of Rhombic Distortion on the Polarized X-ray Absorption Spectra in High Tc Superconductors. J. Phys. Soc. Jpn. 1990, 59, 815–818. [Google Scholar] [CrossRef]
- Bianconi, A. Symmetry of Cu 3d holes in high Tc superconductivity by XAS spectroscopy. In Superconductivity—International Conference; Joshi, S.K., Rao, C.N.R., Subramanyam, S.V., Eds.; World Scientific: Singapore, 1990; pp. 448–469. [Google Scholar] [CrossRef]
- Pompa, M.; Turtu, S.; Bianconi, A.; Campanella, F.; Flank, A.M.; Lagarde, P.; Li, C.; Pettiti, I.; Udron, D. Coupling between the charge carriers and lattice distortions via modulation of the orbital angular momentum mℓ = 0 of the 3d holes by polarized xas spectroscopy. Phys. C Supercond. 1991, 185–189, 1061–1062. [Google Scholar] [CrossRef]
- Bianconi, A.; Agrestini, S.; Bianconi, G.; di Castro, D.; Saini, N.L. A quantum phase transition driven by the electron lattice interaction gives high Tc superconductivity. J. Alloys Compd. 2001, 317–318, 537–541. [Google Scholar] [CrossRef]
- Agrestini, S.; Saini, N.L.; Bianconi, G.; Bianconi, A. The strain of CuO2 lattice: The second variable for the phase diagram of cuprate perovskites. J. Phys. A Math. Gen. 2003, 36, 9133. [Google Scholar] [CrossRef]
- Agrestini, S.; Di Castro, D.; Sansone, M.; Saini, N.L.; Saccone, A.; De Negri, S.; Giovannini, M.; Colapietro, M.; Bianconi, A. High Tc superconductivity in a critical range of micro-strain and charge density in diborides. J. Phys. Condens. Matter 2001, 13, 11689. [Google Scholar] [CrossRef]
- Bianconi, A.; Saini, N.L.; Agrestini, S.; Castro, D.D.; Bianconi, G. The strain quantum critical point for superstripes in the phase diagram of all cuprate perovskites. Int. J. Mod. Phys. B 2000, 14, 3342–3455. [Google Scholar] [CrossRef]
- Bianconi, A.; Saini, N.L.; Rossetti, T.; Lanzara, A.; Perali, A.; Missori, M.; Oyanagi, H.; Yamaguchi, H.; Nishihara, Y.; Ha, D.H. Stripe structure in the CuO2 plane of perovskite superconductors. Phys. Rev. B 1996, 54, 12018. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A.; Poccia, N.; Bianconi, G.; Barba, L.; Arrighetti, G.; Innocenti, D.; Karpinski, J.; Zhigadlo, N.D.; Kazakov, S.M.; et al. Inhomogeneity of charge-density-wave order and quenched disorder in a High Tc superconductor. Nature 2015, 525, 359. [Google Scholar] [CrossRef] [PubMed]
- Campi, G.; Ricci, A.; Poccia, N.; Barba, L.; Arrighetti, G.; Burghammer, M.; Caporale, A.S.; Bianconi, A. Scanning micro-X-ray diffraction unveils the distribution of oxygen chain nanoscale puddles in YBa2Cu3O6.33. Phys. Rev. B 2013, 87, 014517. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A. High-Temperature superconductivity in a hyperbolic geometry of complex matter from nanoscale to mesoscopic scale. J. Supercond. Novel Magn. 2016, 29, 627. [Google Scholar] [CrossRef]
- Bianconi, G. Multilayer Networks: Structure and Function; Oxford University Press: Oxford, UK, 2018; ISBN 9780198753919. [Google Scholar]
- Bianconi, A. On the Fermi liquid coupled with a generalized Wigner polaronic CDW giving high Tc superconductivity. Solid State Commun. 1994, 91, 1–5. [Google Scholar] [CrossRef]
- Bianconi, A. Feshbach shape resonance in multiband superconductivity in heterostructures. J. Supercond. 2005, 18, 625–636. [Google Scholar] [CrossRef]
- Perali, A.; Bianconi, A.; Lanzara, A.; Saini, N.L. The gap amplification at a shape resonance in a superlattice of quantum stripes: A mechanism for High Tc. Solid State Commun. 1996, 100, 181–186. [Google Scholar] [CrossRef]
- Valletta, A.; Bianconi, A.; Perali, A.; Saini, N.L. Electronic and superconducting properties of a superlattice of quantum stripes at the atomic limit. Zeitschrift fur Physik B Condensed Matter 1997, 104, 707–713. [Google Scholar] [CrossRef]
- Simonelli, L.; Fratini, M.; Palmisano, V.; Filippi, M.; Saini, N.; Bianconi, A. The material-dependent parameter controlling the universal phase diagram of cuprates. J. Supercond. Novel Magn. 2005, 18, 773–777. [Google Scholar] [CrossRef]
- Bianconi, A.; Valletta, A.; Perali, A.; Saini, N.L. Superconductivity of a striped phase at the atomic limit. Physica C Supercond. 1998, 296, 269–280. [Google Scholar] [CrossRef]
- Fratini, M.; Poccia, N.; Ricci, A.; Campi, G.; Burghammer, M.; Aeppli, G.; Bianconi, A. Scale-free structural organization of oxygen interstitials in La2CuO4+y. Nature 2010, 466, 841. [Google Scholar] [CrossRef]
- Poccia, N.; Fratini, M.; Ricci, A.; Campi, G.; Barba, L.; Vittorini-Orgeas, A.; Bianconi, G.; Aeppli, G.; Bianconi, A. Evolution and control of oxygen order in a cuprate superconductor. Nat. Mater. 2011, 10, 733. [Google Scholar] [CrossRef]
- Littlewood, P. Superconductivity: An X-ray oxygen regulator. Nat. Mater. 2011, 10, 726. [Google Scholar] [CrossRef]
- Jarlborg, T.; Bianconi, A. Fermi surface reconstruction of superoxygenated La2CuO4 superconductors with ordered oxygen interstitials. Phys. Rev. B 2013, 87, 054514. [Google Scholar] [CrossRef]
- Jarlborg, T.; Bianconi, A. Electronic structure of superoxygenated La2NiO4 domains with ordered oxygen interstitials. J. Supercond. Novel Magn. 2016, 29, 615. [Google Scholar] [CrossRef]
- Jarlborg, T.; Bianconi, A. Electronic structure of HgBa2CuO4+δ with self-organized interstitial oxygen wires in the Hg spacer planes. Supercond. Novel Magn. 2018, 31, 689–695. [Google Scholar] [CrossRef]
- Bianconi, A.; Missori, M. The Coupling of a Wigner Polaronic Charge Density Wave with a Fermi Liquid arising from the Instability of a Wigner Polaron Crystal: A possibleI Pairing Mechanism in High Tc Superconductorsn. In Phase Separation in Cuprate Superconductors; Sigmund, E., Muller, K.A., Eds.; Springer: Berlin, Germany, 1994. [Google Scholar]
- Di Castro, D.; Bianconi, G.; Colapietro, M.; Pifferi, A.; Saini, N.L.; Agrestini, S.; Bianconi, A. Evidence for the strain critical point in High Tc superconductors. Eur. Phys. J. B 2000, 18, 617–624. [Google Scholar] [CrossRef]
- Kusmartsev, F.V.; Di Castro, D.; Bianconi, G.; Bianconi, A. Transformation of strings into an inhomogeneous phase of stripes and itinerant carriers. Phys. Lett. A 2000, 275, 118–123. [Google Scholar] [CrossRef]
- Barnes, P.; Avdeev, M.; Jorgensen, J.; Hinks, D.; Claus, H.; Short, S. Superconductivity and cobalt oxidation state in metastable NaxCoO2−δ·y H2O (x ≈ 1/3; y ≈ 4 x). Phys. Rev. B 2005, 72, 134515. [Google Scholar] [CrossRef]
- Geballe, T.H.; Marezio, M. Enhanced superconductivity in Sr2CuO4−v. Phys. C 2009, 469, 680–684. [Google Scholar] [CrossRef]
- Gao, W.B.; Liu, Q.Q.; Yang, L.X.; Yu, Y.; Li, F.Y.; Jin, Q.; Uchida, S. Out-of-plane effect on the superconductivity of Sr2−xBaxCuO3+δ with Tc up to 98 K. Phys. Rev. B 2009, 80, 094523. [Google Scholar] [CrossRef]
- Chmaissem, O.; Grigoraviciute, I.; Yamauchi, H.; Karppinen, M.; Marezio, M. Superconductivity and oxygen ordering correlations in the homologous series of (Cu, Mo) Sr2(Ce, Y)sCu2O5+2s+δ. Phys. Rev. B 2010, 82, 104507. [Google Scholar] [CrossRef]
- Marezio, M.; Chmaissem, O.; Bougerol, C.; Karppinen, M.; Yamauchi, H.; Geballe, T.H. Overdoped cuprates with high-temperature superconducting transitions. APL Mater. 2013, 1, 021103. [Google Scholar] [CrossRef]
- Giraldo-Gallo, P.; Zhang, Y.; Parra, C.; Manoharan, H.C.; Beasley, M.R.; Geballe, T.H.; Kramer, M.J.; Fisher, I.R. Stripe-like nanoscale structural phase separation in superconducting BaPb1−x BixO3. Nat. Commun. 2015, 6, 8231. [Google Scholar] [CrossRef]
- Ricci, A.; Poccia, N.; Campi, G.; Joseph, B.; Arrighetti, G.; Barba, L.; Reynolds, M.; Burghammer, M.; Takeya, H.; Mizuguchi, Y.; et al. Nanoscale phase separation in the iron chalcogenide superconductor K0.8 Fe1.6Se2 as seen via scanning nanofocused X-ray diffraction. Phys. Rev. B 2011, 84, 060511. [Google Scholar] [CrossRef]
- Ricci, A.; Poccia, N.; Joseph, B.; Arrighetti, G.; Barba, L.; Plaisier, J.; Campi, G.; Mizuguchi, Y.; Takeya, H.; Takano, Y.; et al. Intrinsic phase separation in superconducting K0.8 Fe1.6Se2 (Tc = 31.8 K) single crystals. Supercond. Sci. Technol. 2011, 24, 082002. [Google Scholar] [CrossRef]
- Ricci, A.; Poccia, N.; Campi, G.; Coneri, F.; Caporale, A.S.; Innocenti, D.; Burghammer, M.; Zimmermann, M.V.; Bianconi, A. Multiscale distribution of oxygen puddles in 1/8 doped YBa2Cu3O6.67. Sci. Rep. 2013, 3, 2383. [Google Scholar] [CrossRef] [PubMed]
- Ricci, A.; Poccia, N.; Campi, G.; Coneri, F.; Barba, L.; Arrighetti, G.; Polentarutti, M.; Burghammer, M.; Sprung, M.; Zimmermann, M.V.; et al. Networks of superconducting nano-puddles in 1/8 doped YBa2Cu3O6.5+y controlled by thermal manipulation. New J. Phys. 2014, 16, 053030. [Google Scholar] [CrossRef]
- Campi, G.; Ricci, A.; Poccia, N.; Bianconi, A. Imaging Spatial Ordering of the Oxygen Chains in YBa2Cu3O6 + y at the Insulator-to-Metal Transition. J. Supercond. Novel Magn. 2014, 27, 987. [Google Scholar] [CrossRef]
- Zeljkovic, I.; Hoffman, J.E. Interplay of chemical disorder and electronic inhomogeneity in unconventional superconductors. Phys. Chem. Chem. Phys. 2013, 15, 13462. [Google Scholar] [CrossRef] [PubMed]
- Zeljkovic, I.; Nieminen, J.; Huang, D.; Chang, T.R.; He, Y.; Jeng, H.T.; Xu, Z.; Wen, J.; Gu, G.; Lin, H.; et al. Nanoscale interplay of strain and doping in a high-temperature superconductor. Nano Lett. 2014, 14, 6749. [Google Scholar] [CrossRef] [PubMed]
- Kresin, V.; Ovchinnikov, Y.; Wolf, S. Inhomogeneous superconductivity and the pseudogap state of novel superconductors. Phys. Rep. 2006, 431, 231–259. [Google Scholar] [CrossRef]
- Bianconi, G. Superconductor-insulator transition on annealed complex networks. Phys. Rev. E 2012, 85, 061113. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, G. Enhancement of Tc in the superconductor insulator phase transition on scale free networks. J. Stat. Mech. Theory Exp. 2012, 2012, P07021. [Google Scholar] [CrossRef]
- Bianconi, G. Superconductor-insulator transition in a network of 2d percolation clusters. EPL (Europhys. Lett.) 2013, 101, 26003. [Google Scholar] [CrossRef]
- Kugel, K.I.; Rakhmanov, A.L.; Sboychakov, A.O.; Poccia, N.; Bianconi, A. Model for phase separation controlled by doping and the internal chemical pressure in different cuprate superconductors. Phys. Rev. B. 2008, 78, 165124. [Google Scholar] [CrossRef]
- Kugel, K.I.; Rakhmanov, A.L.; Sboychakov, A.O.; Kusmartsev, F.V.; Poccia, N.; Bianconi, A. A two-band model for the phase separation induced by the chemical mismatch pressure in different cuprate superconductors. Supercond. Sci. Technol. 2009, 22, 014007. [Google Scholar] [CrossRef]
- Bianconi, A.; Poccia, N.; Sboychakov, A.O.; Rakhmanov, A.L.; Kugel, K.I. Intrinsic arrested nanoscale phase separation near a topological Lifshitz transition in strongly correlated two-band metals. Supercond. Sci. Technol. 2015, 28, 024005. [Google Scholar] [CrossRef]
- Fratini, M.; Poccia, N.; Bianconi, A. The Feshbach resonance and nanoscale phase separation in a polaron liquid near the quantum critical point for a polaron Wigner crystal. J. Phys. Conf. Ser. 2008, 108, 1012036. [Google Scholar] [CrossRef]
- Bianconi, A.; Agrestini, S.; Campi, G.; Filippi, M.; Saini, N.L. Common features in high Tc cuprates and diborides. Curr. Appl. Phys. 2005, 5, 254. [Google Scholar] [CrossRef]
- Bianconi, A. Multiband superconductivity in high Tc cuprates and diborides. J. Phys. Chem. Solids 2006, 67, 567–570. [Google Scholar] [CrossRef]
- Jarlborg, T. Mechanisms for High Tc in copper oxide superconductors: Ideas from band calculations. Appl. Phys. Lett. 2009, 94, 212503. [Google Scholar] [CrossRef]
- Jarlborg, T.; Barbiellini, B.; Markiewicz, R.S.; Bansil, A. Different doping from apical and planar oxygen vacancies in Ba2CuO4−δ and La2CuO4−δ: First-principles band structure calculations. Phys. Rev. B 2012, 86, 235111. [Google Scholar] [CrossRef]
- Jarlborg, T.; Bianconi, A.; Barbiellini, B.; Markiewicz, R.S.; Bansil, A. Effects of Excess or Deficiency of Oxygen Content on the Electronic Structure of High Tc Cuprates. Journal of superconductivity and novel magnetism. J. Supercond. Novel Magn. 2013, 26, 2597. [Google Scholar] [CrossRef]
- Jarlborg, T. Spin-phonon interaction and band effects in the High Tc superconductor HgBa2CuO4. Phys. Rev. B 2003, 68, 172501. [Google Scholar] [CrossRef]
- Jarlborg, T.; Santi, G. The role of thermal disorder on the electronic structure in high-Tc compounds. Phys. C 2000, 329, 243–257. [Google Scholar] [CrossRef]
- Jarlborg, T. Bands, spin fluctuations, and traces of Fermi surfaces in angle-resolved photoemission intensities for high Tc cuprates. Phys. Rev. B 2011, 84, 064506. [Google Scholar] [CrossRef]
- Wu, Z.; Saini, N.; Bianconi, A. Hg L3 edge absorption study of the HgBa2CuO4+δ superconductor. Phys. Rev. B 2001, 64, 092507. [Google Scholar] [CrossRef]
- Lanzara, A.; Saini, N.L.; Bianconi, A.; Duc, F.; Bordet, P. Anomalous local atomic correlations in HgBa2CuO4+δ. Phys. Rev. B 1999, 59, 3851. [Google Scholar] [CrossRef]
- Bordet, P.; Duc, F.; Radaelli, P.G.; Lanzara, A.; Saini, N.; Bianconi, A.; Antipov, E.V. Structural instability around Tc observed in Hg-1201 by neutron powder diffraction and EXAFS. Phys. C Supercond. 1997, 282–287, 1081. [Google Scholar] [CrossRef]
- Bianconi, A.; Doniach, S.; Lublin, D. X-ray Ca K edge of calcium adenosine triphosphate system and of simple Ca compunds. Chem. Phys. Lett. 1978, 59, 121. [Google Scholar] [CrossRef]
- Garcia, J.; Bianconi, A.; Benfatto, M.; Natoli, C.R. Coordination geometry of transition metal ions in dilute solutions by XANES. Le Journal de Physique Colloques 1986, 47, C8-49–C8-54. [Google Scholar] [CrossRef]
- Andersen, O.K. Linear methods in band theory. Phys. Rev. B 1975, 12, 3060. [Google Scholar] [CrossRef]
- Barbiellini, B.; Dugdale, S.B.; Jarlborg, T. The EPMD-LMTO program for electron positron momentum density calculations in solids. Comput. Mater. Sci. 2003, 28, 287–301. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Gunnarsson, O.; Lundquist, B.I. Exchange and correlation in atoms, molecules, and solids by the spin-density-functional formalism. Phys. Rev. B 1976, 13, 4274. [Google Scholar] [CrossRef]
- Barbiellini, B.; Jarlborg, T. Electron and positron states in HgBa2CuO. Phys. Rev. B 1994, 50, 3239. [Google Scholar] [CrossRef]
- Jarlborg, T. Properties of high-Tc copper oxides from the nearly-free-electron model. Phys. Rev. B 2007, 76, 140504(R). [Google Scholar] [CrossRef]
- Jarlborg, T. Electronic Structure and Properties of Superconducting Materials with Simple Fermi Surfaces. J. Supercond. Novel Magn. 2015, 28, 1231. [Google Scholar] [CrossRef]
- Jarlborg, T. Spin waves and large electron-phonon coupling near the metal-insulator transition in hole-doped high-Tc oxides. Phys. Rev. B 2001, 64, 060507(R). [Google Scholar] [CrossRef]
- Jarlborg, T. Effects of spin phonon interaction within the CuO plane of high-Tc superconductors. Phys. C 2007, 454, 5. [Google Scholar] [CrossRef]
- Pickett, W.E. Electronic structure of the high-temperature oxide superconductors. Rev. Mod. Phys. 1989, 61, 433. [Google Scholar] [CrossRef]
- Damascelli, A.; Shen, Z.-X.; Hussain, Z. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 2003, 75, 473. [Google Scholar] [CrossRef]
- Barbiellini, B.; Genoud, P.; Henry, J.Y.; Hoffmann, L.; Jarlborg, T.; Manuel, A.A.; Massidda, S.; Peter, M.; Sadowski, W.; Scheel, H.J.; et al. Positron annihilation on single crystals of YBa2Cua3O7−δ. Phys. Rev. B 1991, 43, 7810. [Google Scholar] [CrossRef]
- Jarlborg, T. Role of thermal disorder for magnetism and the α-γ transition in cerium: Results from density-functional theory. Phys. Rev. B 2014, 89, 184426. [Google Scholar] [CrossRef]
- Jarlborg, T.; Moroni, E.G.; Grimvall, G. α-γ transition in Ce from temperature-dependent band-structure calculations. Phys. Rev. B 1997, 55, 1288. [Google Scholar] [CrossRef]
- Jarlborg, T. Electronic structure and properties of pure and doped ϵ-FeSi from ab initio local-density theory. Phys. Rev. B 1999, 59, 15002. [Google Scholar] [CrossRef]
- Jarlborg, T. ϵ-FeSi: A material sensitive to thermal disorder. Phys. Lett. A 1997, 236, 143. [Google Scholar] [CrossRef]
- Jarlborg, T. Spin fluctuations, electron phonon coupling and superconductivity in near-magnetic elementary metals Fe, Co, Ni and Pd. Phys. C 2003, 385, 513. [Google Scholar] [CrossRef]
- Jarlborg, T. Ferromagnetic and antiferromagnetic spin fluctuations and superconductivity in the hcp-phase of Fe. Phys. Lett. A 2002, 300, 518. [Google Scholar] [CrossRef]
- Moroni, E.G.; Jarlborg, T. Calculation of Invar anomalies. Phys. Rev. B 1990, 41, 9600. [Google Scholar] [CrossRef]
- Barbiellini, B.; Jarlborg, T. Importance of Local Band Effects for Ferromagnetism in Hole-Doped La2CuO4 Cuprate Superconductors. Phys. Rev. Lett. 2008, 101, 157002. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, A. The instability close to the 2D generalized Wigner polaron crystal density: A possible pairing mechanism indicated by a key experiment. Phys. C Supercond. 1994, 235, 269–272. [Google Scholar] [CrossRef]
- Duan, C.; Yang, J.; Ren, Y.; Thomas, S.M.; Louca, D. Appearance of superconductivity at the vacancy order-disorder boundary KxFe2−ySe2. Phys. Rev. B 2018, 97, 184502. [Google Scholar] [CrossRef]
- Ricci, A.; Poccia, N.; Joseph, B.; Innocenti, D.; Campi, G.; Zozulya, A.; Westermeier, F.; Schavkan, A.; Coneri, F.; Bianconi, A.; et al. Direct observation of nanoscale interface phase in the superconducting chalcogenide KxFe2−ySe2 with intrinsic phase separation. Phys. Rev. B 2015, 91, 020503. [Google Scholar] [CrossRef]
- Perali, A.; Innocenti, D.; Valletta, A.; Bianconi, A. Anomalous isotope effect near a 2.5 Lifshitz transition in a multi-band multi-condensate superconductor made of a superlattice of stripes. Supercond. Sci. Technol. 2012, 25, 124002. [Google Scholar] [CrossRef]
- Bendele, M.; von Rohr, F.; Guguchia, Z.; Pomjakushina, E.; Conder, K.; Bianconi, A.; Simon, A.; Bussmann-Holder, A.; Keller, H. Evidence for strong lattice effects as revealed from huge unconventional oxygen isotope effects on the pseudogap temperature in La2−xSrxCuO4. Phys. Rev. B 2017, 95, 014514. [Google Scholar] [CrossRef]
- Lanzara, A.; Zhao, G.-M.; Saini, N.L.; Bianconi, A.; Conder, K.; Keller, H.; Muller, K.A. Oxygen-isotope shift of the charge-stripe ordering temperature in La2−xSrxCuO4 from X-ray absorption spectroscopy. J. Phys. Condens. Matter 1999, 11, L541. [Google Scholar] [CrossRef]
- Saini, N.L.; Lanzara, A.; Bianconi, A.; Oyanagi, H. Local structural features of the superconducting Bi2Sr2CaCu2O8 system: A polarized Cu K-edge XAS study. Phys. Rev. B 1998, 58, 11768. [Google Scholar] [CrossRef]
- Salasnich, L.; Shanenko, A.A.; Vagov, A.; Aguiar, J.A.; Perali, A. Screening of pair fluctuations in superconductors with coupled shallow and deep bands: A route to higher temperature superconductivity. arXiv, 2018; arXiv:1810.03321. [Google Scholar]
- Kitaev, A.Y. Unpaired Majorana fermions in quantum wires. Phys. Usp. 2001, 44, 131. [Google Scholar] [CrossRef]
- Lutchyn, R.M.; Sau, J.D.; Sarma, S.D. Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures. Phys. Rev. Lett. 2010, 105, 077001. [Google Scholar] [CrossRef]
- Beenakker, C.W.J. Search for Majorana fermions in superconductors. Annu. Rev. Condens. Matter Phys. 2013, 4, 113–136. [Google Scholar] [CrossRef]
- Zhang, P.; Nori, F. Majorana bound states in a disordered quantum dot chain. New J. Phys. 2016, 18, 043033. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jarlborg, T.; Bianconi, A. Multiple Electronic Components and Lifshitz Transitions by Oxygen Wires Formation in Layered Cuprates and Nickelates. Condens. Matter 2019, 4, 15. https://doi.org/10.3390/condmat4010015
Jarlborg T, Bianconi A. Multiple Electronic Components and Lifshitz Transitions by Oxygen Wires Formation in Layered Cuprates and Nickelates. Condensed Matter. 2019; 4(1):15. https://doi.org/10.3390/condmat4010015
Chicago/Turabian StyleJarlborg, Thomas, and Antonio Bianconi. 2019. "Multiple Electronic Components and Lifshitz Transitions by Oxygen Wires Formation in Layered Cuprates and Nickelates" Condensed Matter 4, no. 1: 15. https://doi.org/10.3390/condmat4010015
APA StyleJarlborg, T., & Bianconi, A. (2019). Multiple Electronic Components and Lifshitz Transitions by Oxygen Wires Formation in Layered Cuprates and Nickelates. Condensed Matter, 4(1), 15. https://doi.org/10.3390/condmat4010015





