Scintillator Pixel Detectors for Measurement of Compton Scattering
Abstract
:1. Introduction
2. Materials and Methods
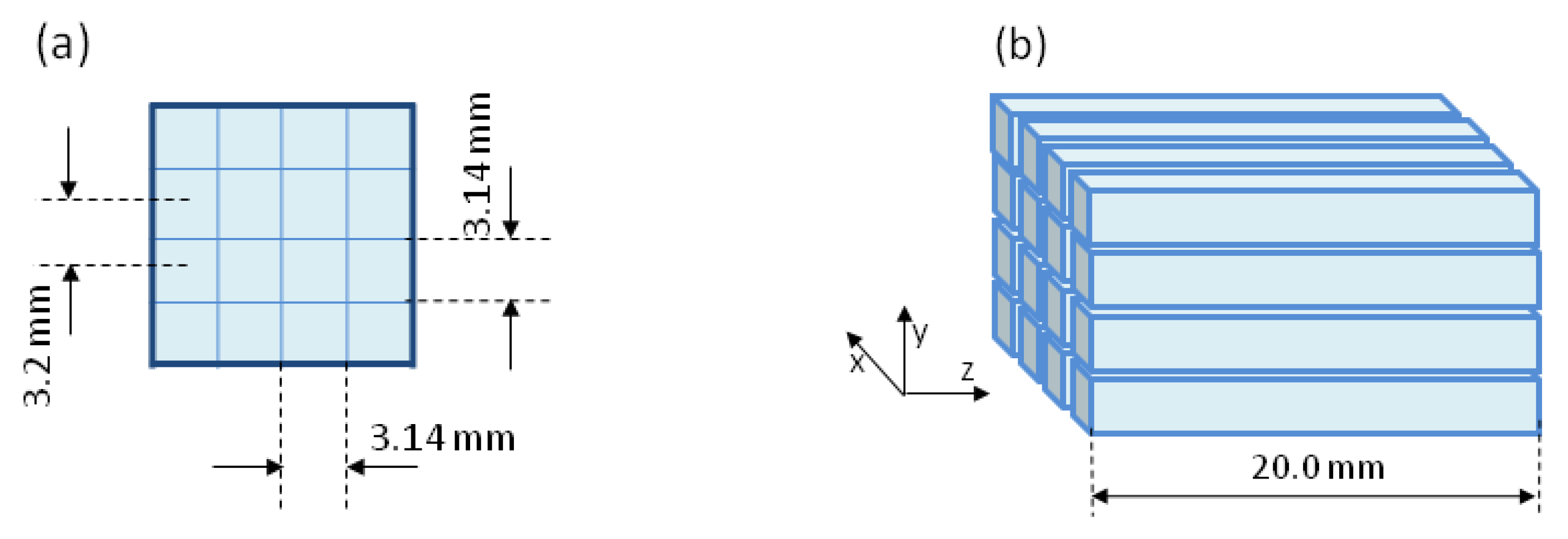
2.1. Experimental Setup
2.2. Scintillator-SiPM Optical Coupling
2.3. Signal Processing
2.4. Energy Reconstruction
2.4.1. Energy Calibration
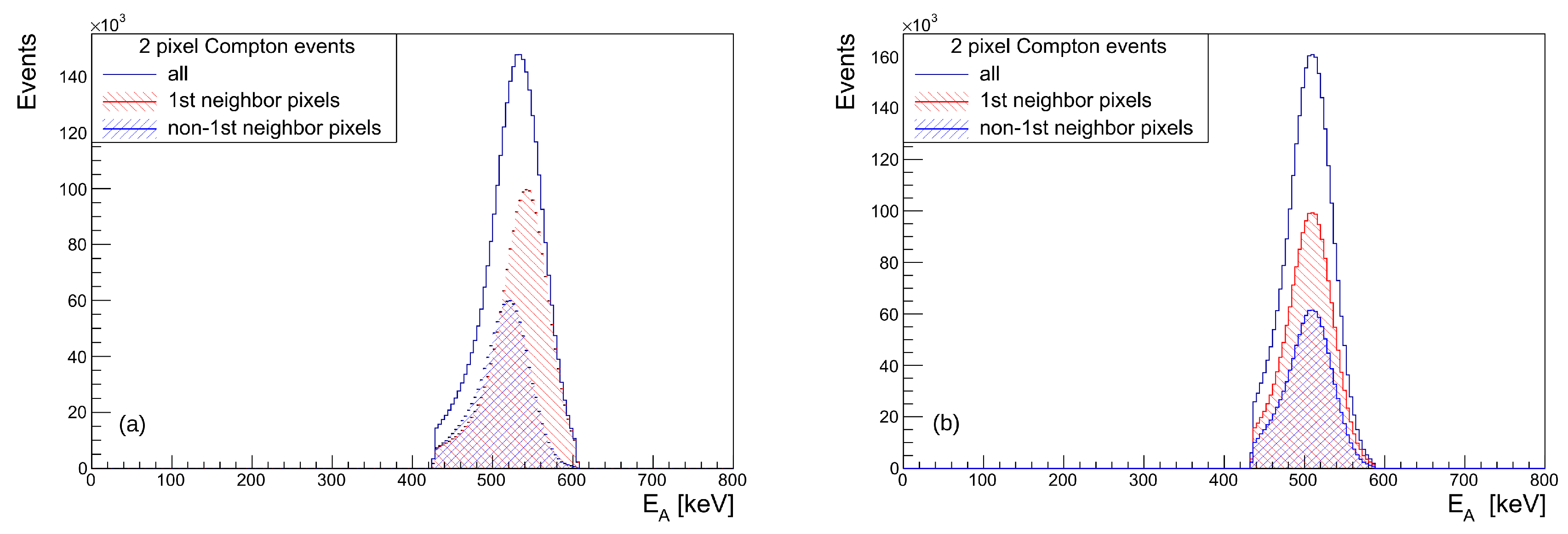
2.4.2. Light Sharing Correction
2.5. Reconstruction of Compton Scattering Angles
2.5.1. Scattering Angle
2.5.2. The Angle
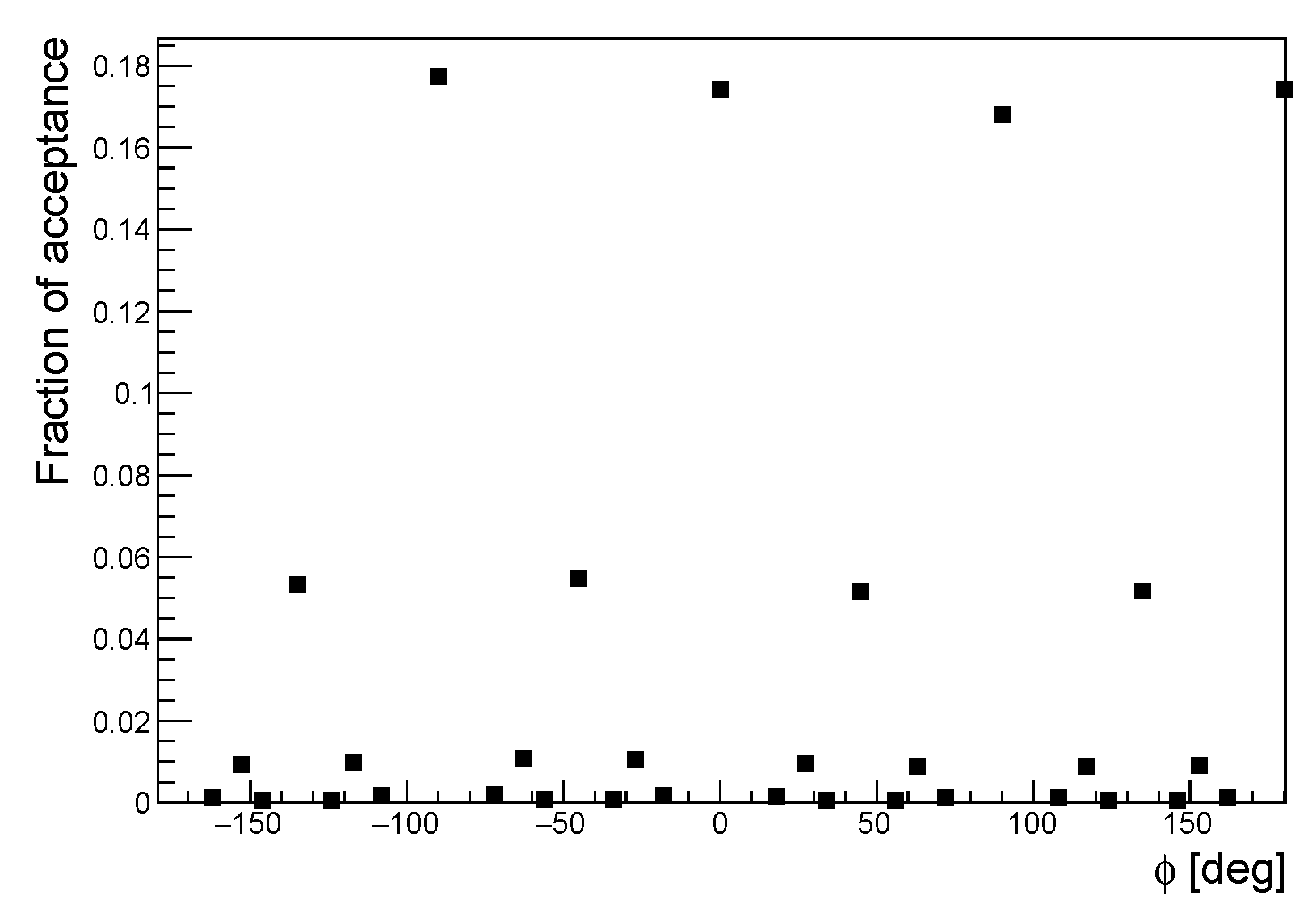
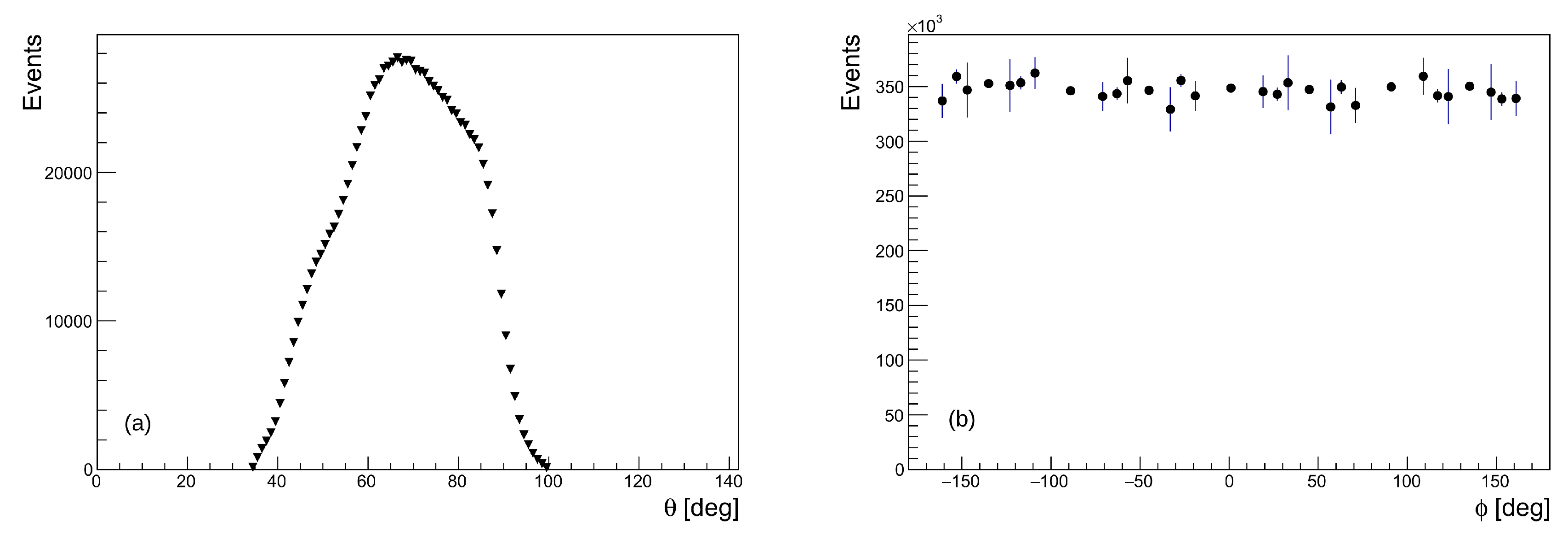
2.5.3. Acceptance Correction
2.6. Time Reconstruction
2.6.1. Channel-To-Channel Correction
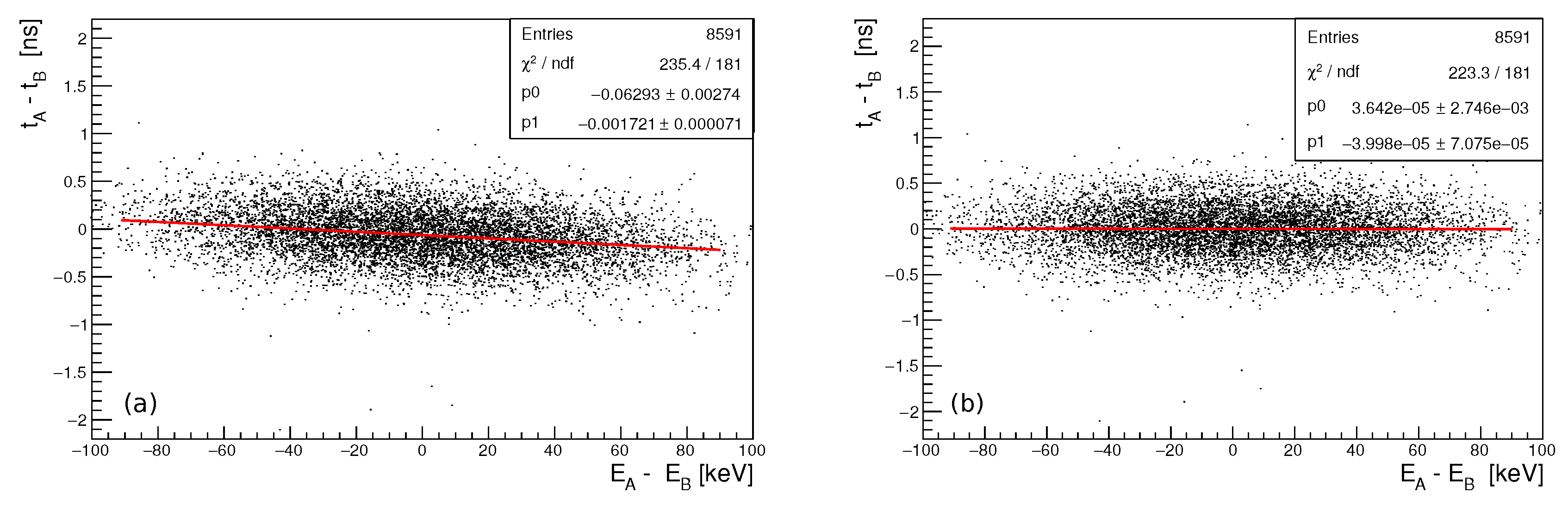
2.6.2. Walk Correction
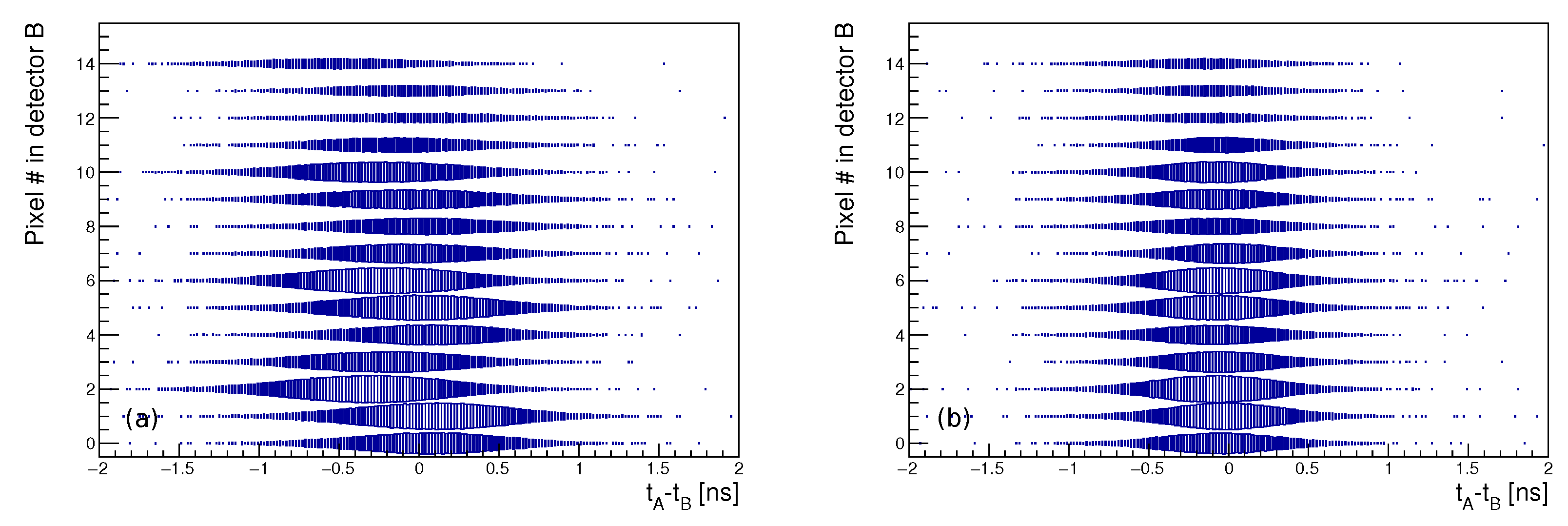
2.6.3. Timing in Two-Pixel Events
3. Results
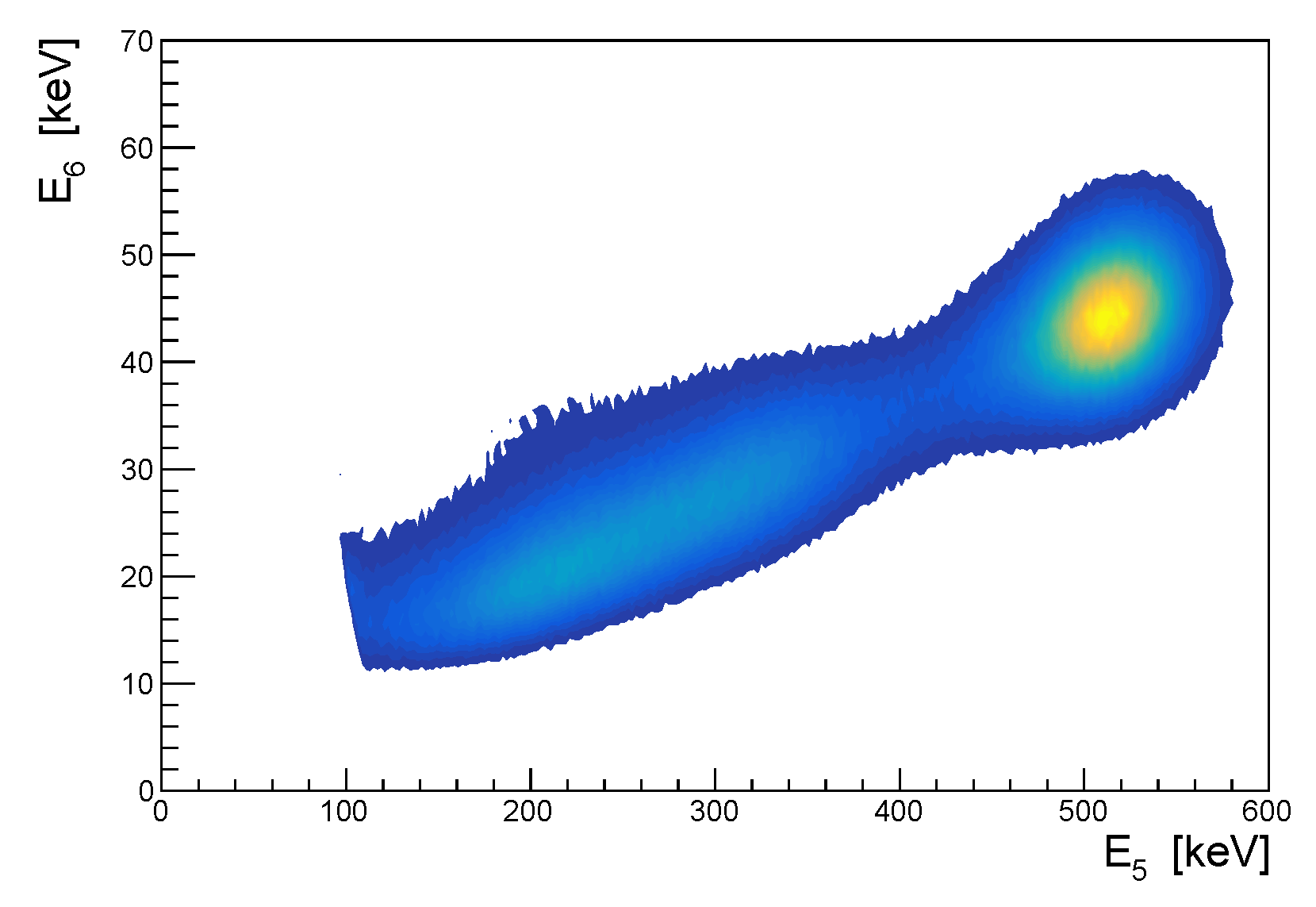
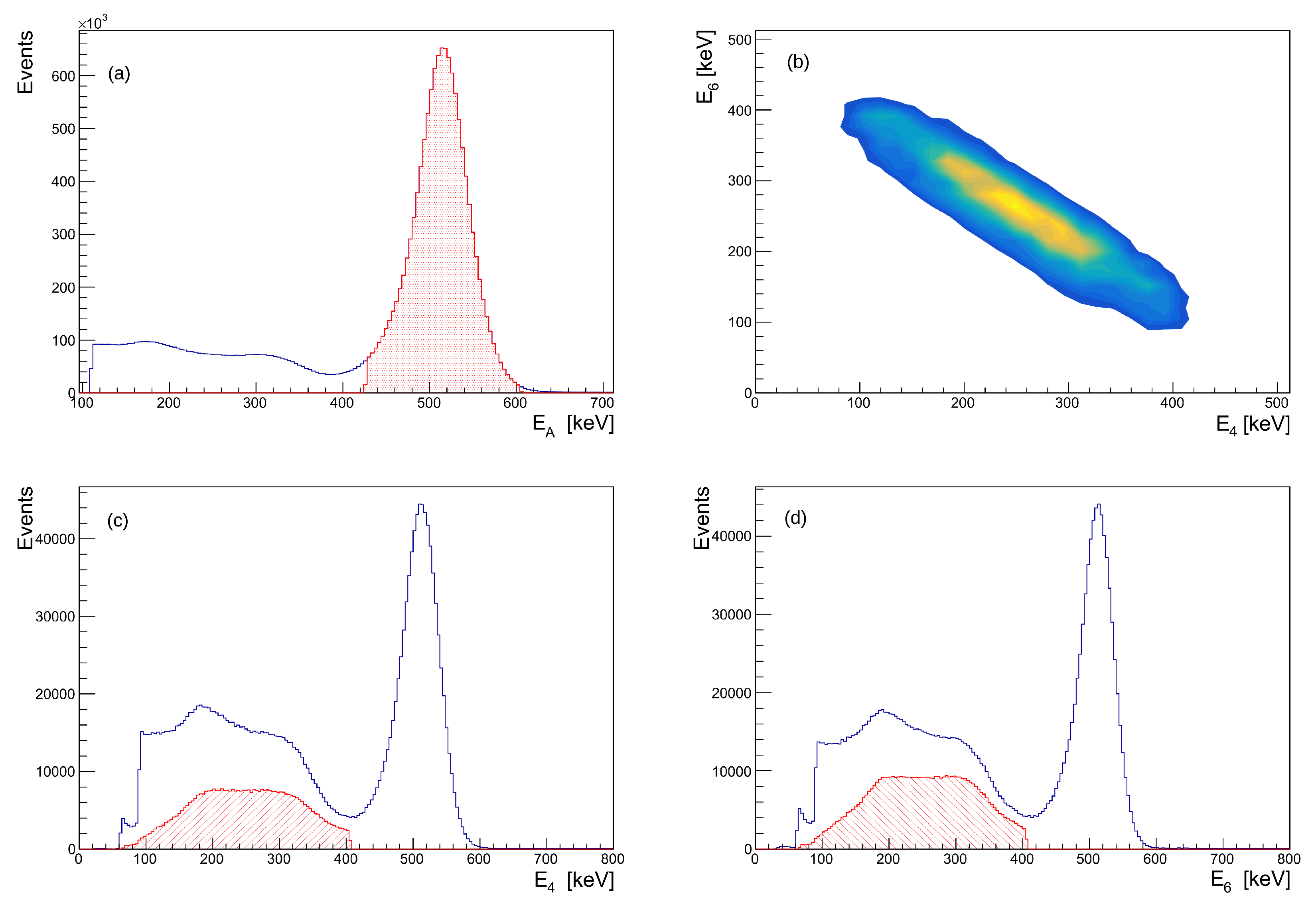
3.1. Reconstruction of Compton Events
3.2. Energy Resolution
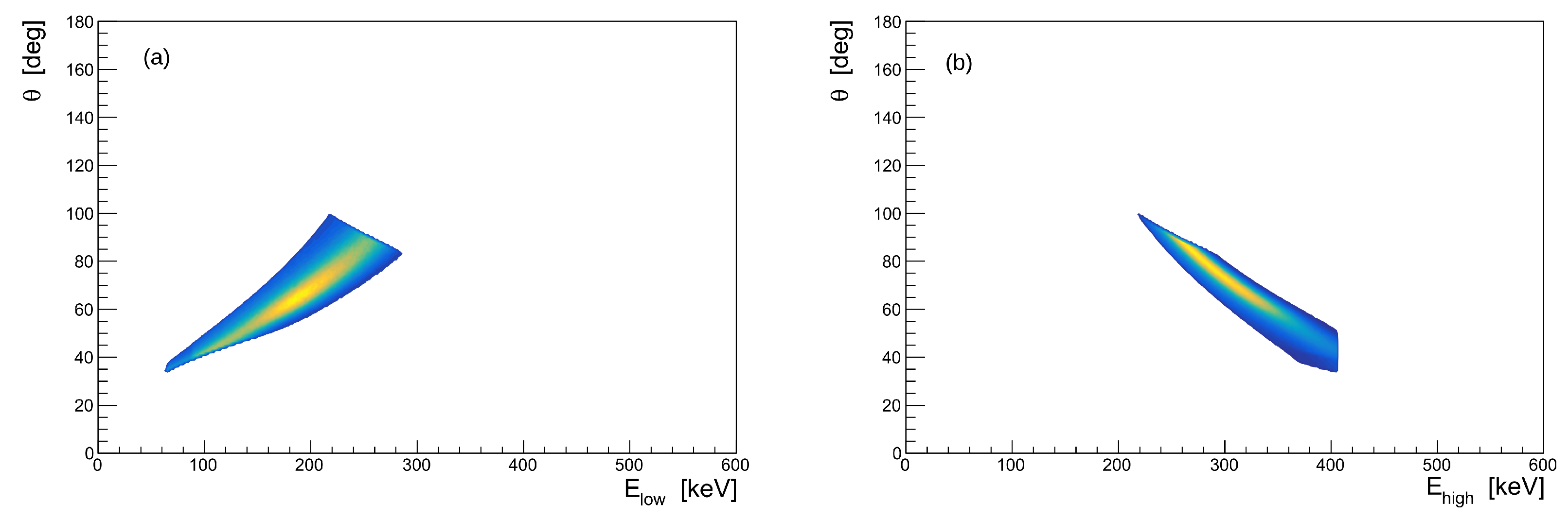
3.3. Angular Resolution
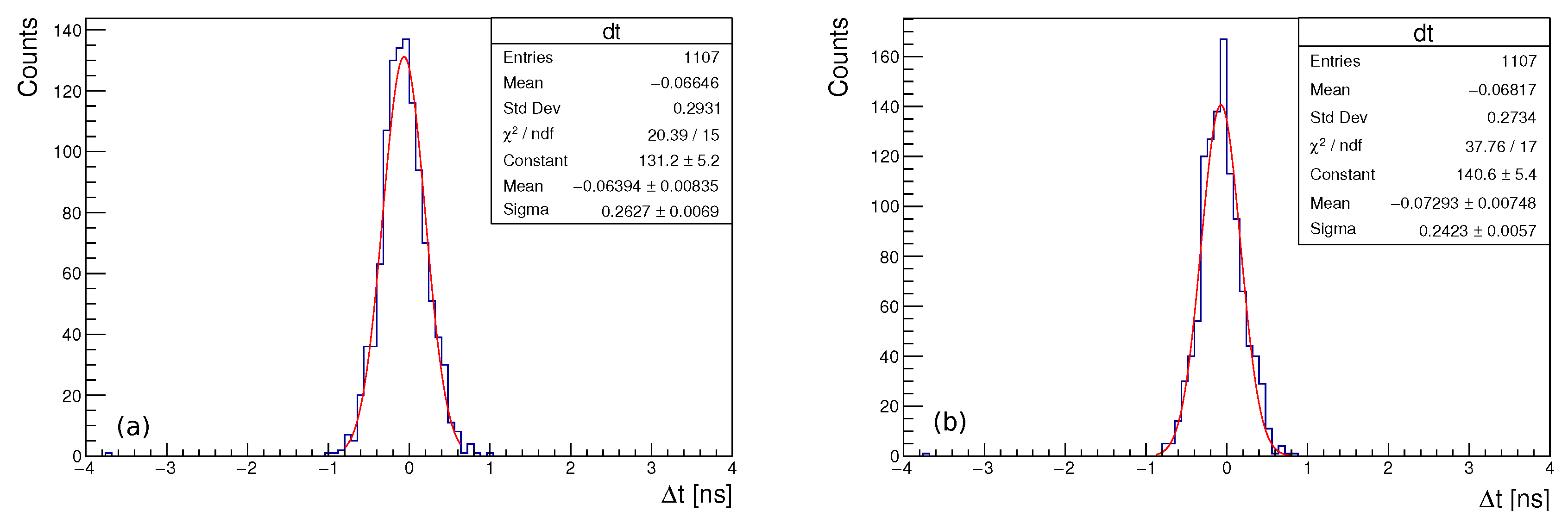
3.4. Coincidence Time Resolution
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kuncic, Z.; McNamara, A.; Wu, K.; Boardman, D. Polarization enhanced X-ray imaging for biomedicine. Nucl. Instrum. Methods Phys. Res. A 2011, 648, S208–S210. [Google Scholar] [CrossRef]
- McNamara, A.; Toghyani, M.; Gillam, J.; Wu, K.; Kuncic, Z. Towards optimal imaging with PET: An in silico feasibility study. Phys. Med. Biol. 2014, 59, 7587–7600. [Google Scholar] [CrossRef] [PubMed]
- Toghyani, M.; Gillam, J.; McNamara, A.; Kuncic, Z. Polarisation-based coincidence event discrimination: An in silico study towards a feasible scheme for Compton-PET. Phys. Med. Biol. 2016, 61, 5803–5817. [Google Scholar] [CrossRef] [PubMed]
- Mitani, T.; Tanaka, T.; Nakazawa, K.; Takahashi, T.; Takashima, T.; Tajima, H.; Nakamura, H.; Nomachi, M.; Nakamoto, T.; Fukazawa, Y. A prototype Si/CdTe Compton camera and the polarization measurement. IEEE Trans. Nucl. Sci. 2004, 51, 2432–2437. [Google Scholar] [CrossRef]
- Takeda, S.; Odaka, H.; Katsuta, J.; Ishikawa, S.; Sugimoto, S.; Koseki, Y.; Watanabe, S.; Sato, G.; Kokubun, M.; Takahashi, T.; et al. Polarimetric performance of Si/CdTe semiconductor Compton camera. Nucl. Instrum. Methods Phys. Res. A 2010, 622, 619–627. [Google Scholar] [CrossRef]
- Yonetoku, D.; Murakami, T.; Gunji, S.; Mihara, T.; Sakashita, T.; Morihara, Y.; Kikuchi, Y.; Takahashi, T.; Fujimoto, H.; Toukairin, N.; et al. Gamma-Ray Burst Polarimeter-GAP-aboard the Small Solar Power Sail Demonstrator IKAROS. Publ. Astron. Soc. Jap. 2011, 63, 625–638. [Google Scholar] [CrossRef]
- Shimazoe, K.; Yoshino, M.; Ohshima, Y.; Uenomachi, M.; Oogane, K.; Orita, T.; Takahashi, H.; Kamada, K.; Yoshikawa, A.; Takahashi, M. Development of simultaneous PET and Compton imaging using GAGG-SiPM based pixel detectors. Nucl. Instrum. Methods Phys. Res. A 2018. [Google Scholar] [CrossRef]
- Uenomachi, M.; Mizumachi, Y.; Yoshihara, Y.; Takahashi, T.; Shimazoe, K.; Yabu, G.; Yoneda, H.; Watanabe, S.; Takeda, S.; Orita, T.; et al. Double photon emission coincidence imaging with GAGG-SiPM Compton camera. Nucl. Instrum. Methods Phys. Res. A 2018. [Google Scholar] [CrossRef]
- Spillmann, U.; Bräuning, H.; Hess, S.; Beyer, H.; Stöhker, T.; Dousse, J.C.; Protic, D.; Krings, T. Performance of a Ge-microstrip imaging detector and polarimeter. Rev. Sci. Instrum. 2008, 79, 083101. [Google Scholar] [CrossRef] [PubMed]
- Bloser, P.F.; Legere, J.S.; McConnell, M.L.; Macri, J.R.; Bancroft, C.M.; Connor, T.P.; Ryan, J.M. Calibration of the Gamma-RAy Polarimeter Experiment (GRAPE) at a Polarized Hard X-Ray Beam. Nucl. Instrum. Methods Phys. Res. A 2009, 600, 424–433. [Google Scholar] [CrossRef]
- Makek, M.; Bosnar, D.; Gačić, V.; Pavelić, L.; Šenjug, P.; Žugec, P. Performance of scintillation pixel detectors with MPPC read-out and digital signal processing. Acta Phys. Pol. B 2017, 48, 1721–1726. [Google Scholar] [CrossRef]
- Gundacker, S.; Auffray, E.; Pauwels, K.; Lecoq, P. Measurement of intrinsic rise times for various L(Y)SO and LuAG scintillators with a general study of prompt photons to achieve 10 ps in TOF-PET. Phys. Med. Biol. 2016, 61, 2802–2837. [Google Scholar] [CrossRef] [PubMed]
- Berger, M.; Hubbell, J.; Seltzer, S.; Chang, J.; Coursey, J.; Sukumar, R.; Zucker, D.; Olsen, K. XCOM: Photon Cross Section Database (Version 1.5). Available online: http://physics.nist.gov/xcom (accessed on 30 January 2019).

| Neighbors | Pixel Distance d (mm) | <> | <> |
|---|---|---|---|
| 1st adjacent | 3.2 | 0.060 | 0.066 |
| 1st diagonal | 4.5 | 0.020 | 0.019 |
| 2nd direct | 6.4 | 0.013 | 0.014 |
| Pixel Distance d (mm) | ||||
|---|---|---|---|---|
| / | 1.20 | 3.2 (1st neighbors) | 1.4 | 1.7 |
| 6.4 (2nd neighbors) | 1.9 | 2.3 | ||
| / | 1.46 | 3.2 (1st neighbors) | 2.5 | 3.6 |
| 6.4 (2nd neighbors) | 6.1 | 8.9 |
| Events | Fraction of Events |
|---|---|
| Total triggered | 1 |
| Full energy deposition in the module | 0.62 |
| of which events with: | |
| 1 pixel fired | 0.46 |
| 2 pixels fired | 0.15 |
| >2 pixels fired | 0.01 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makek, M.; Bosnar, D.; Pavelić, L. Scintillator Pixel Detectors for Measurement of Compton Scattering. Condens. Matter 2019, 4, 24. https://doi.org/10.3390/condmat4010024
Makek M, Bosnar D, Pavelić L. Scintillator Pixel Detectors for Measurement of Compton Scattering. Condensed Matter. 2019; 4(1):24. https://doi.org/10.3390/condmat4010024
Chicago/Turabian StyleMakek, Mihael, Damir Bosnar, and Luka Pavelić. 2019. "Scintillator Pixel Detectors for Measurement of Compton Scattering" Condensed Matter 4, no. 1: 24. https://doi.org/10.3390/condmat4010024
APA StyleMakek, M., Bosnar, D., & Pavelić, L. (2019). Scintillator Pixel Detectors for Measurement of Compton Scattering. Condensed Matter, 4(1), 24. https://doi.org/10.3390/condmat4010024





