The Variational Reduction for Low-Dimensional Fermi Gases and Bose–Fermi Mixtures: A Brief Review
Abstract
:1. Introduction
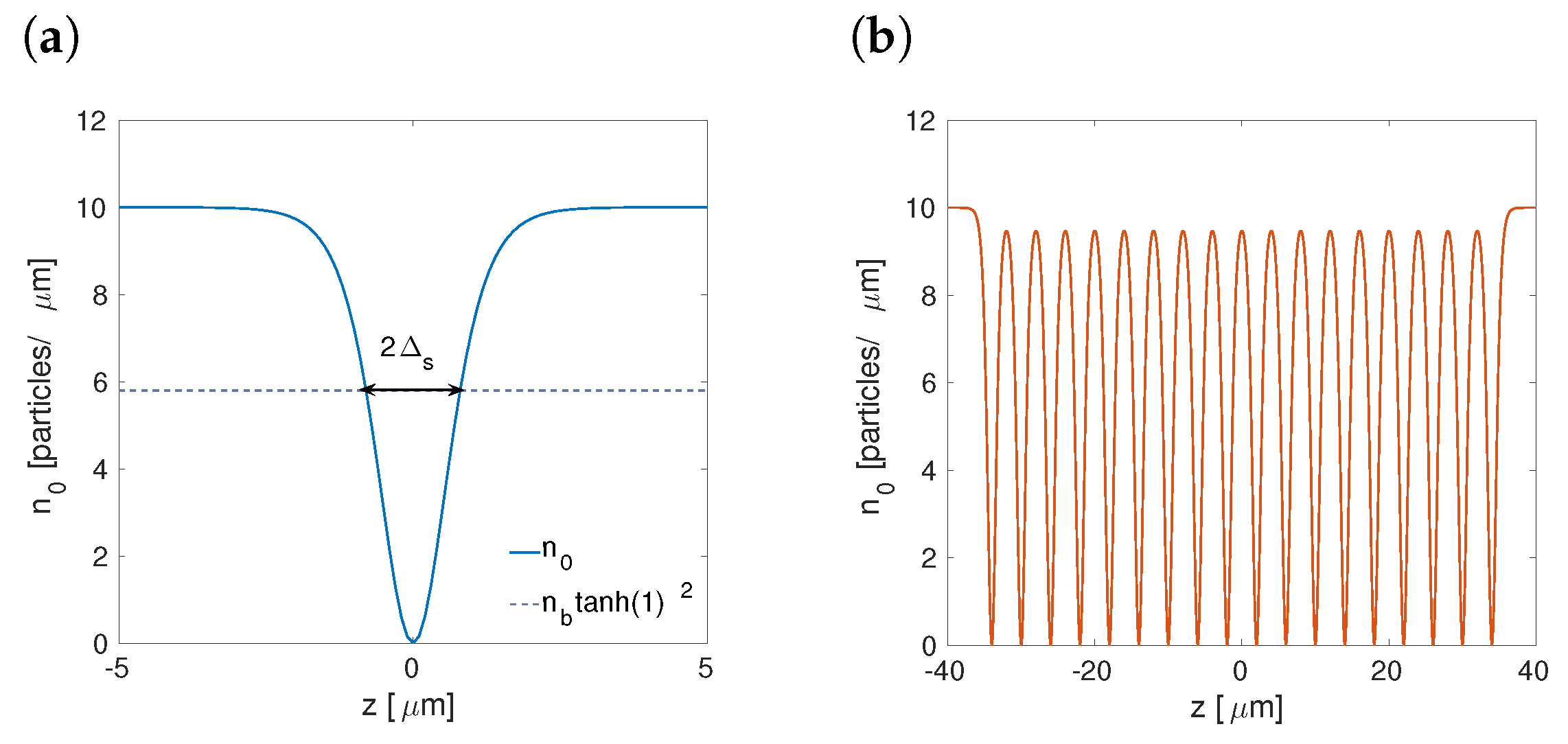
2. The Fermi Gas
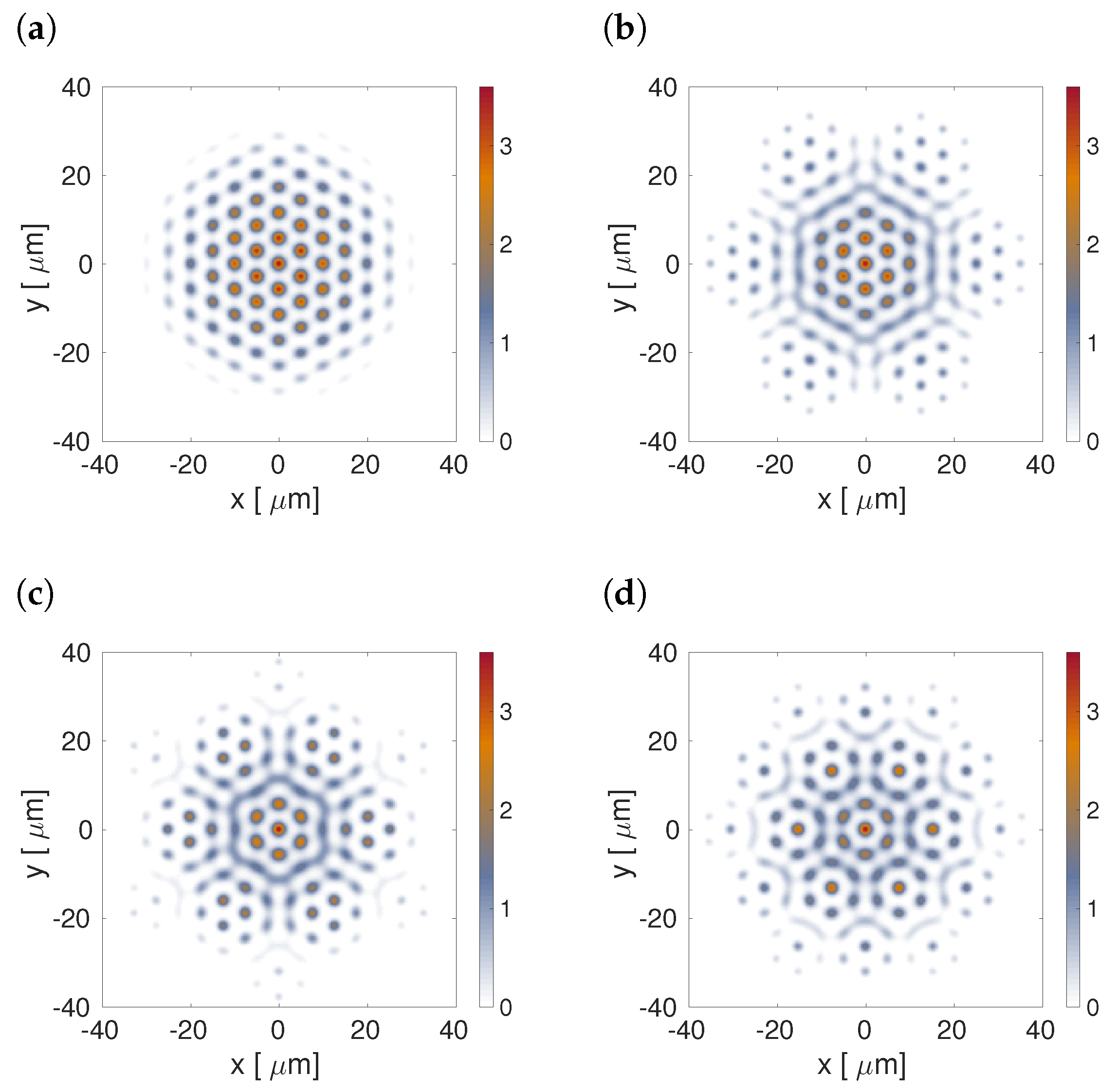
2.1. The Two-Dimensional Reduction
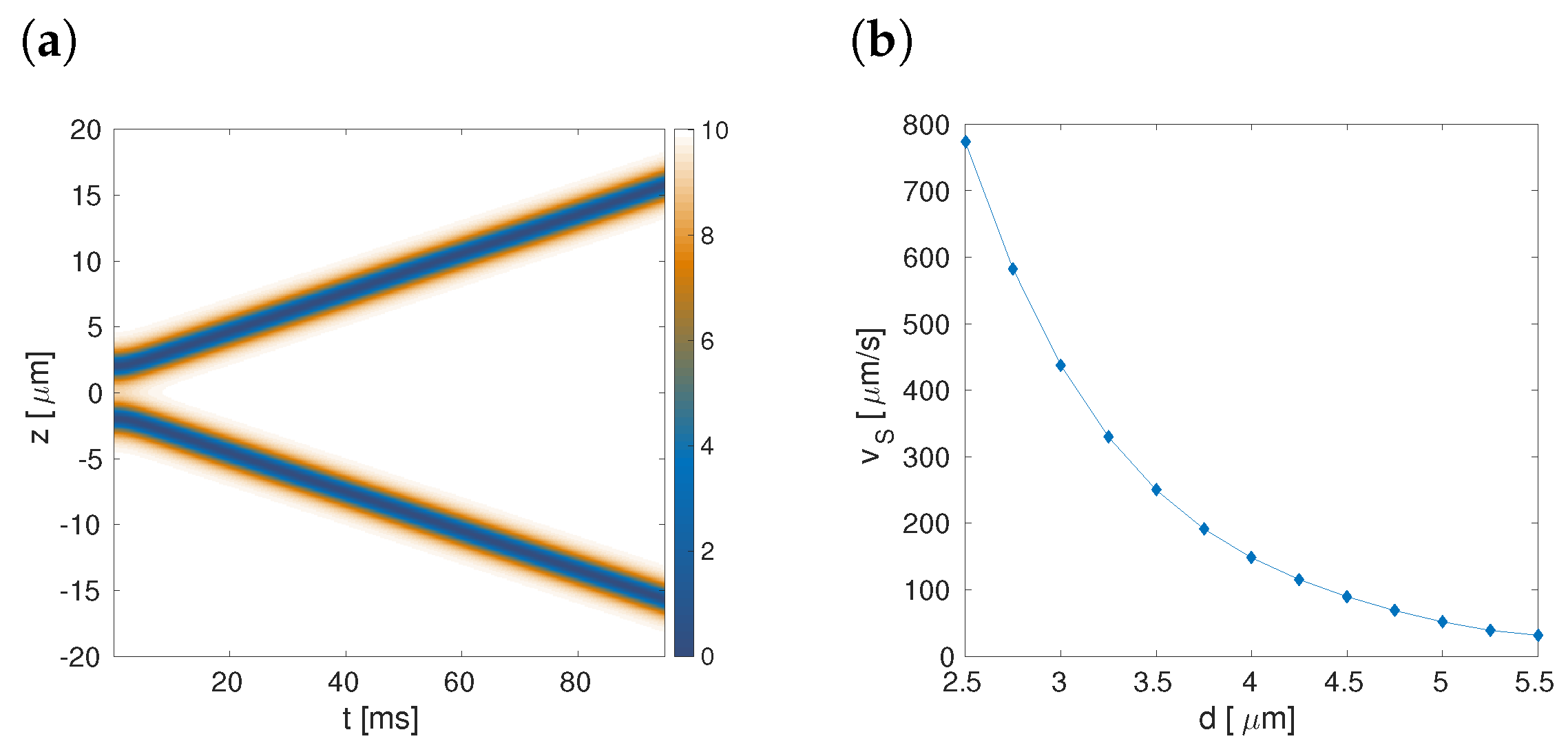
2.2. The One-dimensional Reduction
3. The Bose–Fermi Mixture
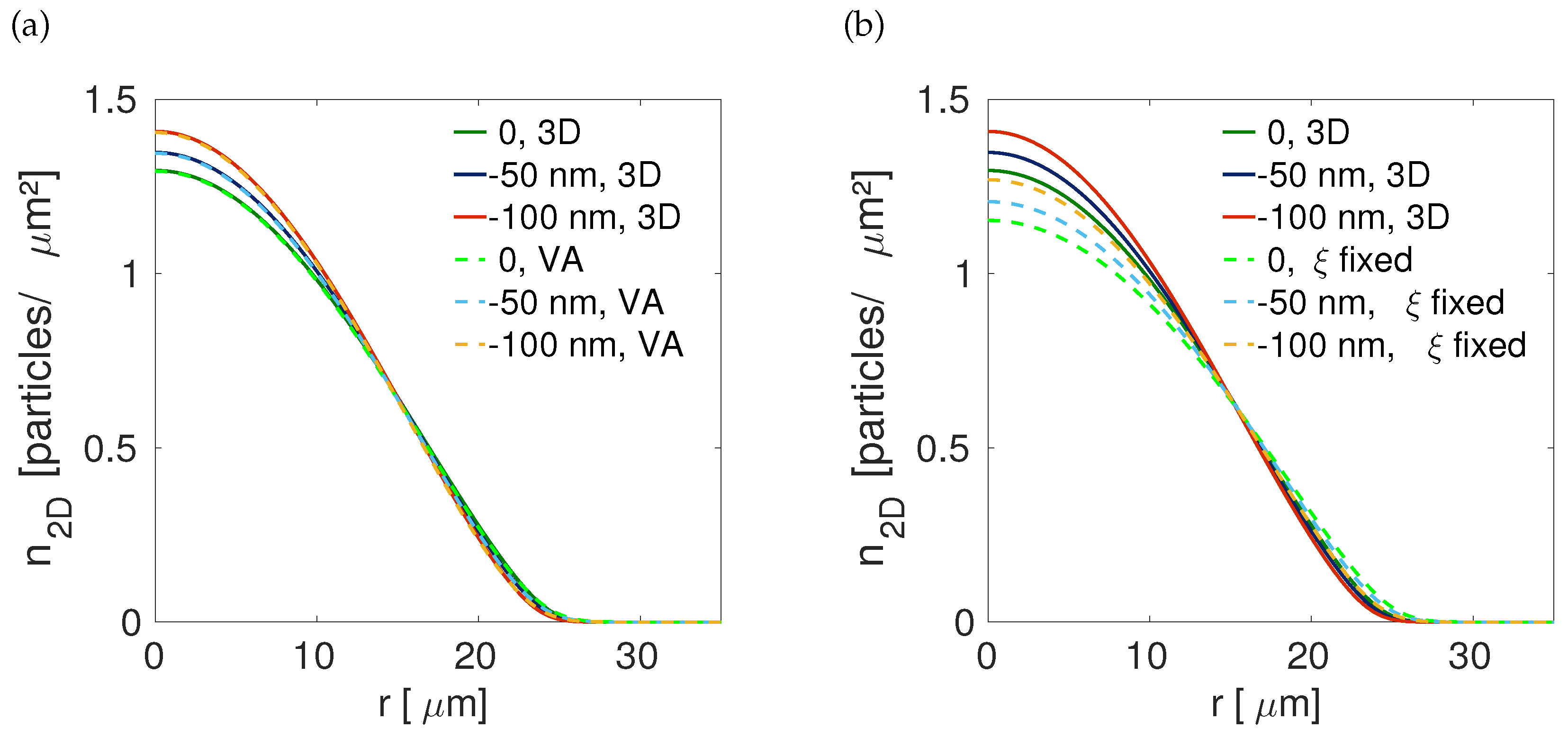
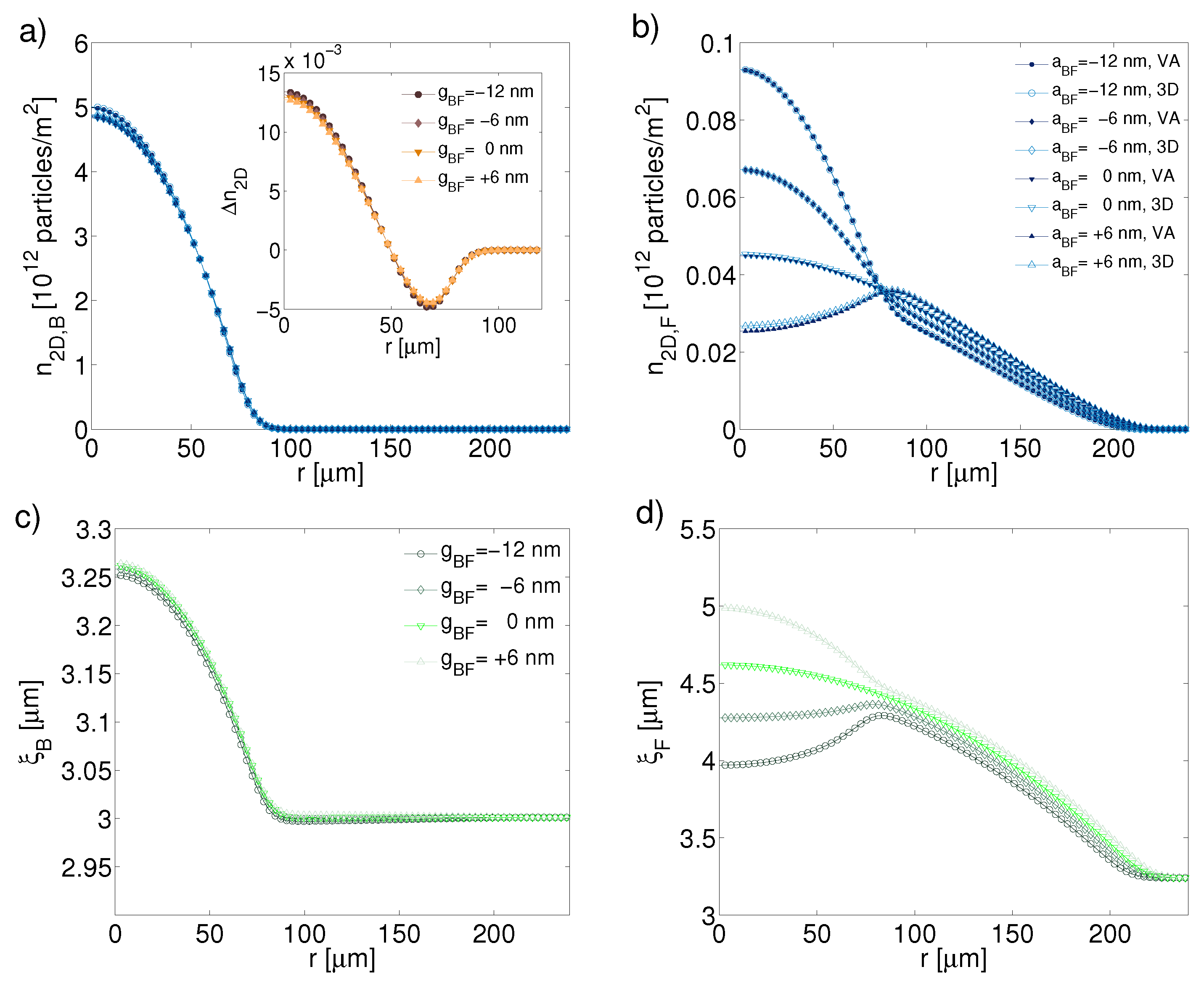
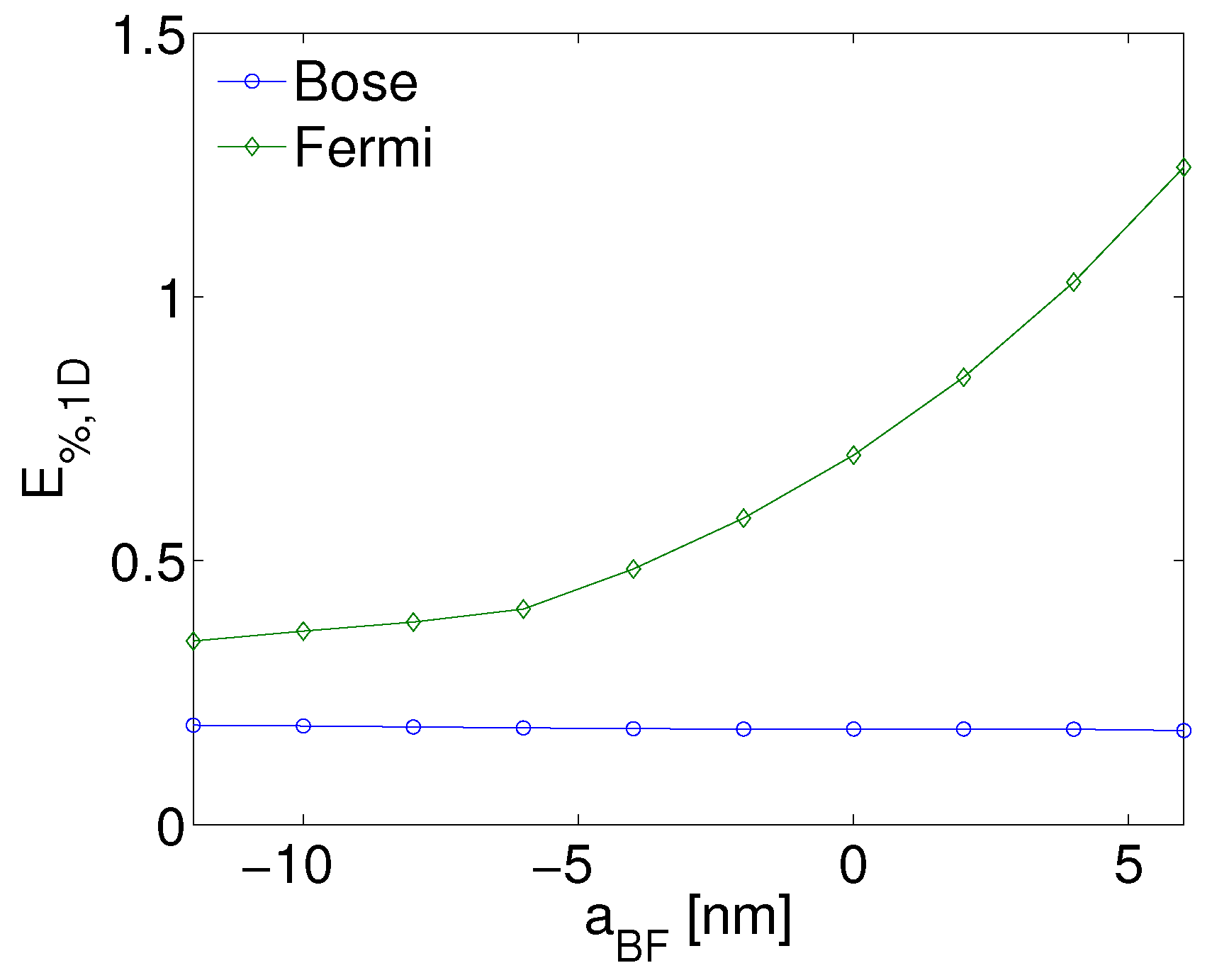
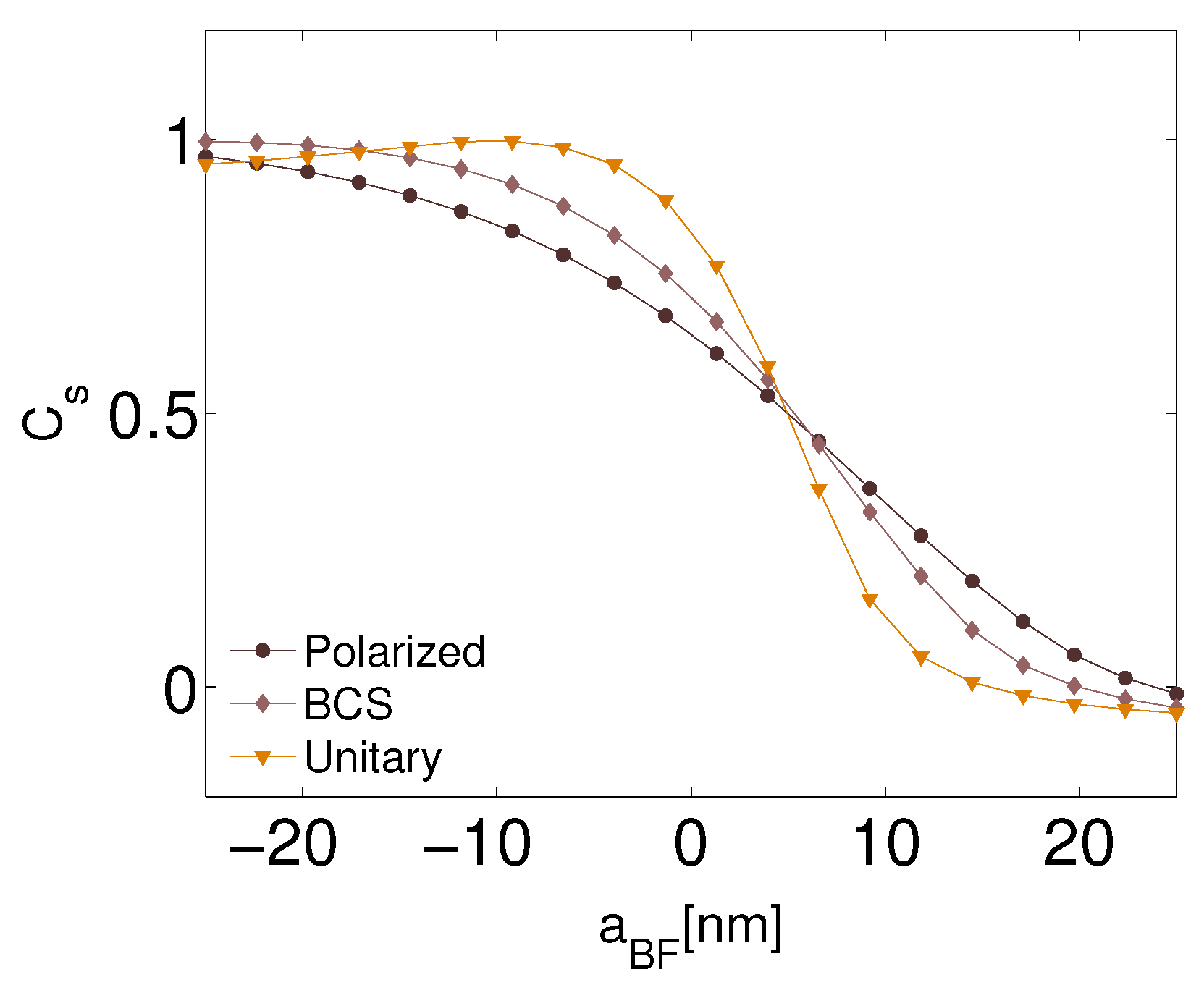
3.1. The Two-Dimensional Reduction
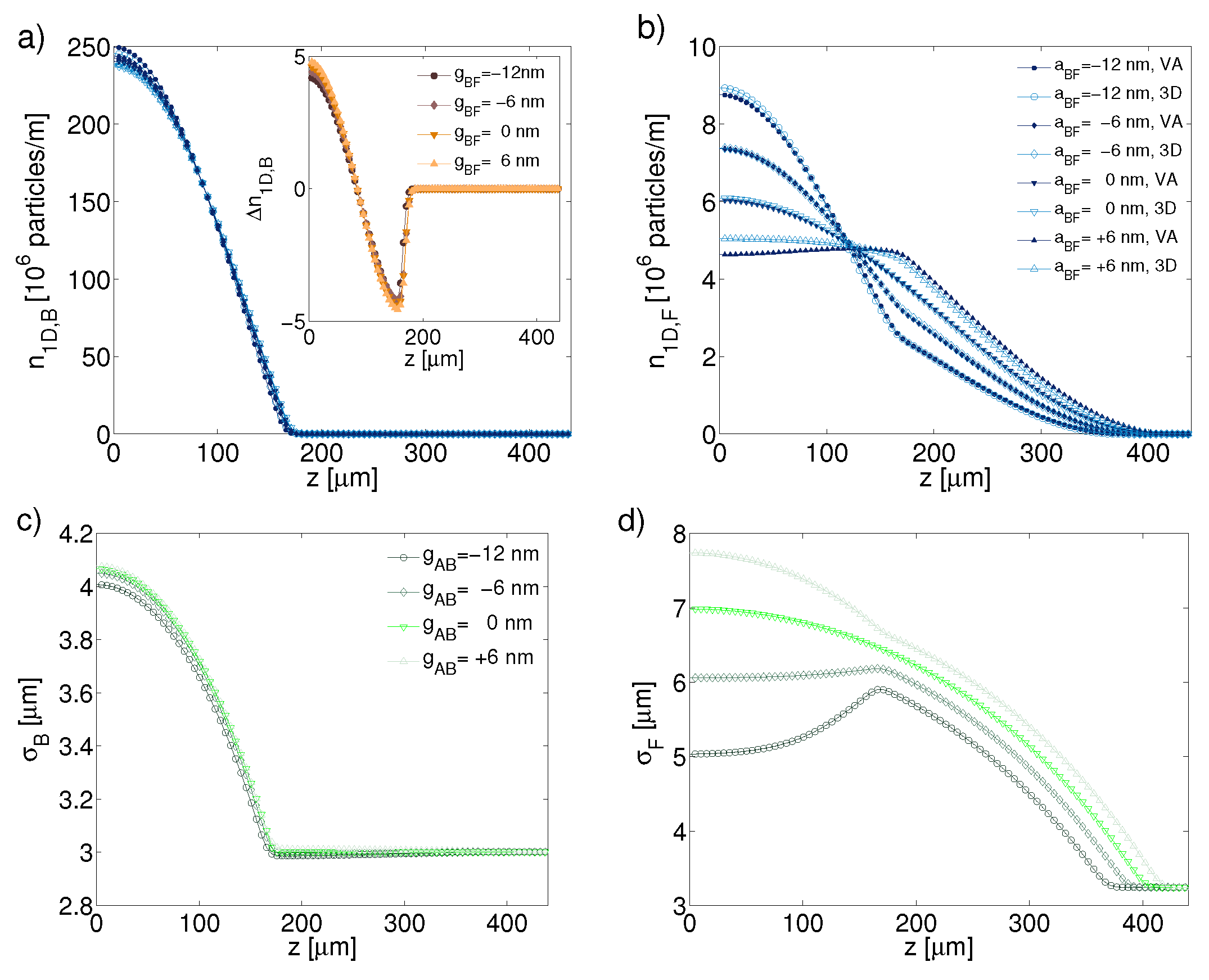
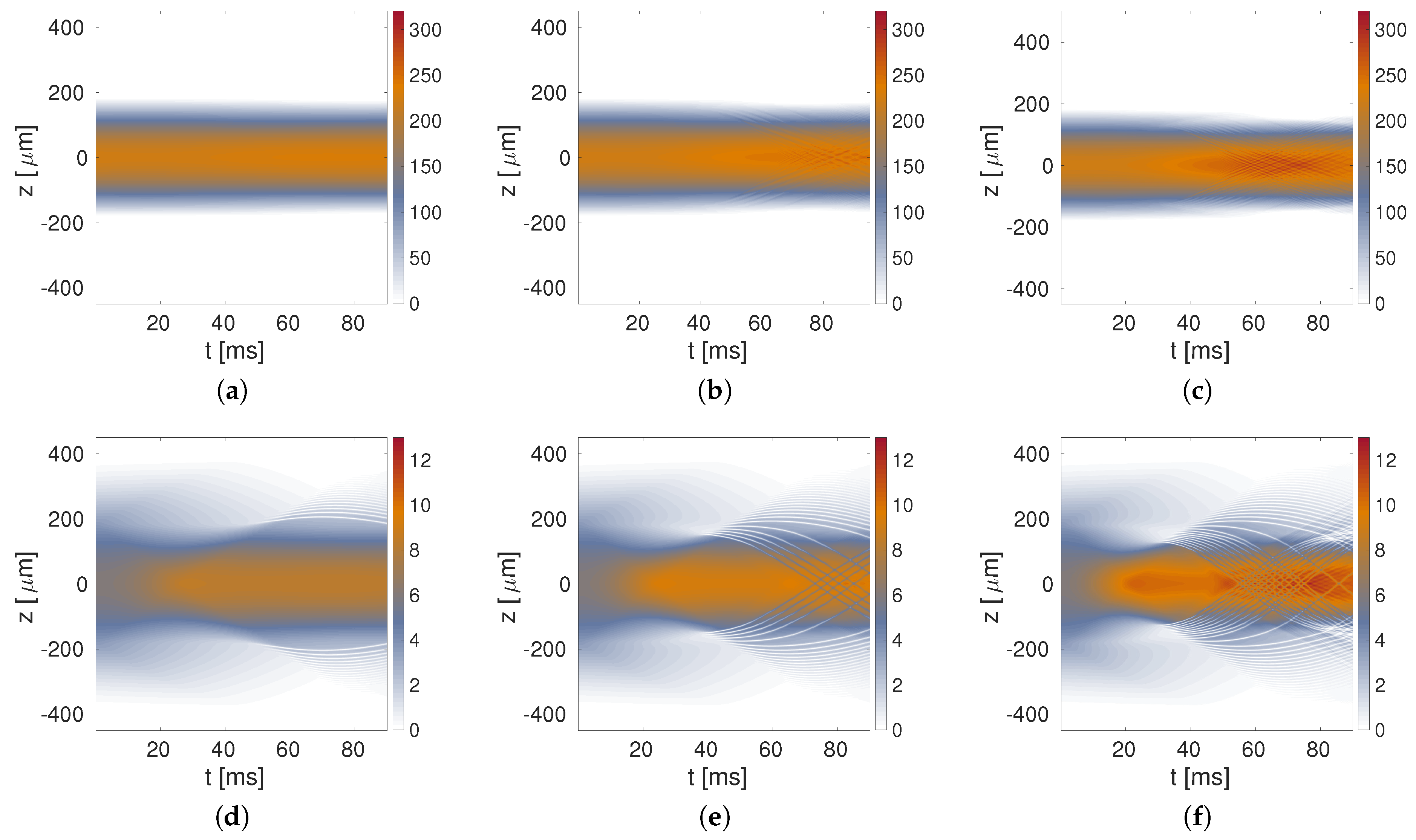
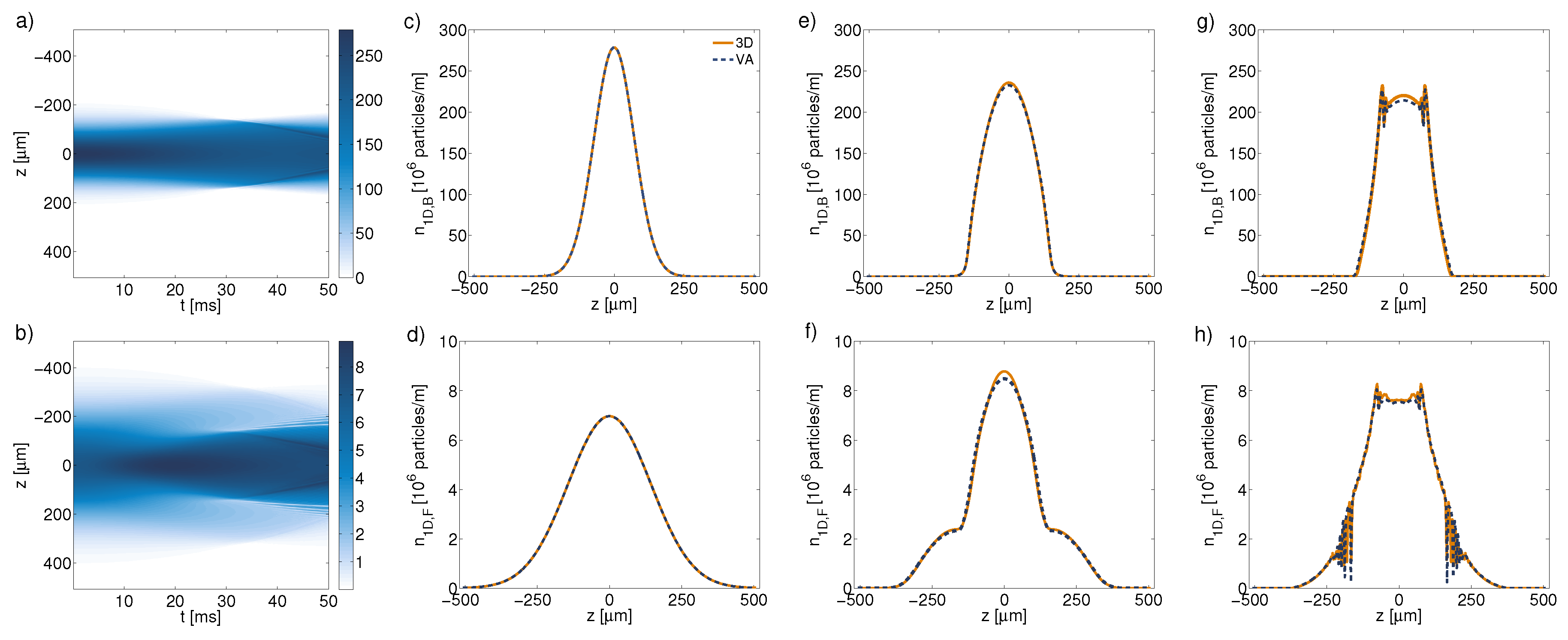
3.2. The One-Dimensional Reduction
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A Nonlinear Schrödinger Equation for the Fermionic Superfluid
References
- Bongs, K.; Sengstock, K. Physics with coherent matter waves. Rep. Prog. Phys. 2004, 67, 907. [Google Scholar] [CrossRef]
- Jaksch, D.; Zoller, P. The cold atom Hubbard toolbox. Ann. Phys. 2005, 315, 52. [Google Scholar] [CrossRef]
- Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of ultracold atomic Fermi gases. Rev. Mod. Phys. 2008, 80, 1215. [Google Scholar] [CrossRef]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 885. [Google Scholar] [CrossRef]
- Spielman, I.B. Light induced gauge fields for ultracold neutral atoms. Rev. Cold At. Mol. 2013, 1, 145. [Google Scholar]
- Goldman, N.; Juzeliūnas, G.; Öhberg, P.; Spielman, I.B. Light-induced gauge fields for ultracold atoms. Rep. Prog. Phys. 2014, 77, 126401. [Google Scholar] [CrossRef] [PubMed]
- Zhai, H. Degenerate quantum gases with spin–orbit coupling: A review. Rep. Prog. Phys. 2015, 78, 026001. [Google Scholar] [CrossRef] [PubMed]
- Malomed, B.A. Creating solitons by means of spin-orbit coupling. EPL 2018, 122, 36001. [Google Scholar] [CrossRef]
- Snoek, M.; Titvinidze, I.; Bloch, I.; Hofstetter, W. Effect of interactions on harmonically confined Bose-Fermi mixtures in optical lattices. Phys. Rev. Lett. 2011, 106, 155301. [Google Scholar] [CrossRef] [PubMed]
- Fröhlich, B.; Feld, M.; Vogt, E.; Koschorreck, M.; Zwerger, W.; Köhl, M. Radio-frequency spectroscopy of a strongly interacting two-dimensional Fermi gas. Phys. Rev. Lett. 2011, 106, 105301. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.-J.; Jimenez-Garcia, K.; Spielman, I.B. Spin–orbit-coupled Bose–Einstein condensates. Nature 2011, 471, 83. [Google Scholar] [CrossRef] [PubMed]
- Sakaguchi, H.; Li, B.; Malomed, B.A. Creation of two-dimensional composite solitons in spin-orbit-coupled self-attractive Bose-Einstein condensates in free space. Phys. Rev. E 2014, 89, 032920. [Google Scholar] [CrossRef] [PubMed]
- Díaz, P.; Laroze, D.; Ávila, A.; Malomed, B.A. Two-dimensional composite solitons in a spin-orbit-coupled Fermi gas in free space. Commun. Nonlinear Sci. Numer. Simul. 2019, 70, 372–383. [Google Scholar] [CrossRef]
- Salasnich, L.; Parola, A.; Reatto, L. Effective wave equations for the dynamics of cigar-shaped and disk-shaped Bose condensates. Phys. Rev. A 2002, 65, 043614. [Google Scholar] [CrossRef]
- Salasnich, L.; Parola, A.; Reatto, L. Condensate bright solitons under transverse confinement. Phys. Rev. A 2002, 66, 043603. [Google Scholar] [CrossRef]
- Salasnich, L.; Malomed, B.A. Solitons and solitary vortices in pancake-shaped Bose-Einstein condensates. Phys. Rev. A 2009, 79, 053620. [Google Scholar] [CrossRef]
- Young-S, L.E.; Salasnich, L.; Adhikari, S.K. Dimensional reduction of a binary Bose-Einstein condensate in mixed dimensions. Phys. Rev. A 2010, 82, 053601. [Google Scholar] [CrossRef]
- Adhikari, S.K.; Malomed, B.A. Miscibility in a degenerate fermionic mixture induced by linear coupling. Phys. Rev. A 2006, 74, 053620. [Google Scholar] [CrossRef]
- Adhikari, S.K. Superfluid fermi-fermi mixture: Phase diagram, stability, and soliton formation. Phys. Rev. A 2007, 76, 053609. [Google Scholar] [CrossRef]
- Adhikari, S.K.; Malomed, B.A. Gap solitons in a model of a superfluid fermion gas in optical lattices. Physica D 2009, 238, 1402–1412. [Google Scholar] [CrossRef]
- Díaz, P.; Laroze, D.; Schmidt, I.; Malomed, B.A. One-and two-dimensional reductions of the mean-field description of degenerate Fermi gases. J. Phys. B: At. Mol. Opt. Phys. 2012, 45, 145304. [Google Scholar] [CrossRef]
- Burger, S.; Bongs, K.; Dettmer, S.; Ertmer, W.; Sengstock, K.; Sanpera, A.; Shlyapnikov, G.V.; Lewenstein, M. Dark solitons in Bose-Einstein condensates. Phys. Rev. Lett. 1999, 83, 5198. [Google Scholar] [CrossRef]
- Becker, C.; Stellmer, S.; Soltan-Panahi, P.; Dörscher, S.; Baumert, M.; Richter, E.-M.; Kronjäger, J.; Bongs, K.; Sengstock, K. Oscillations and interactions of dark and dark–bright solitons in Bose-Einstein condensates. Nat. Phys. 2008, 4, 496. [Google Scholar] [CrossRef]
- Weller, A.; Ronzheimer, J.; Gross, C.; Esteve, J.; Oberthaler, M.; Frantzeskakis, D.; Theocharis, G.; Kevrekidis, P. Experimental observation of oscillating and interacting matter wave dark solitons. Phys. Rev. Lett. 2008, 101, 130401. [Google Scholar] [CrossRef] [PubMed]
- Stellmer, S.; Becker, C.; Soltan-Panahi, P.; Richter, E.-M.; Dörscher, S.; Baumert, M.; Kronjäger, J.; Bongs, K.; Sengstock, K. Collisions of dark solitons in elongated Bose-Einstein condensates. Phys. Rev. Lett. 2008, 101, 120406. [Google Scholar] [CrossRef] [PubMed]
- Antezza, M.; Dalfovo, F.; Pitaevskii, L.P.; Stringari, S. Dark solitons in a superfluid Fermi gas. Phys. Rev. A 2007, 76, 043610. [Google Scholar] [CrossRef]
- Scott, R.; Dalfovo, F.; Pitaevskii, L.; Stringari, S. Dynamics of dark solitons in a trapped superfluid Fermi gas. Phys. Rev. Lett. 2011, 106, 185301. [Google Scholar] [CrossRef] [PubMed]
- Liao, R.; Brand, J. Traveling dark solitons in superfluid Fermi gases. Phys. Rev. A 2011, 83, 041604. [Google Scholar] [CrossRef]
- Yefsah, T.; Sommer, A.T.; Ku, M.J.; Cheuk, L.W.; Ji, W.; Bakr, W.S.; Zwierlein, M.W. Heavy solitons in a fermionic superfluid. Nature 2013, 499, 426. [Google Scholar] [CrossRef] [PubMed]
- Ku, M.J.; Mukherjee, B.; Yefsah, T.; Zwierlein, M.W. Cascade of solitonic excitations in a superfluid fermi gas: From planar solitons to vortex rings and lines. Phys. Rev. Lett. 2016, 116, 045304. [Google Scholar] [CrossRef] [PubMed]
- Syrwid, A.; Delande, D.; Sacha, K. Emergence of dark soliton signatures in a one-dimensional unpolarized attractive Fermi gas on a ring. Phys. Rev. A 2018, 98, 023616. [Google Scholar] [CrossRef]
- Van Alphen, W.; Lombardi, G.; Klimin, S.N.; Tempere, J. Dark soliton collisions in superfluid Fermi gases. New J. Phys. 2018, 20, 053052. [Google Scholar] [CrossRef]
- Truscott, A.G.; Strecker, K.E.; McAlexander, W.I.; Partridge, G.B.; Hulet, R.G. Observation of Fermi pressure in a gas of trapped atoms. Science 2001, 291, 2570–2572. [Google Scholar] [CrossRef] [PubMed]
- Schreck, F.; Khaykovich, L.; Corwin, K.L.; Ferrari, G.; Bourdel, T.; Cubizolles, J.; Salomon, C. Quasipure Bose-Einstein Condensate Immersed in a Fermi Sea. Phys. Rev. Lett. 2001, 87, 080403. [Google Scholar] [CrossRef] [PubMed]
- Hansen, A.H.; Khramov, A.; Dowd, W.H.; Jamison, A.O.; Ivanov, V.V.; Gupta, S. Quantum degenerate mixture of Ytterbium and Lithium atoms. Phys. Rev. A 2011, 84, 011606. [Google Scholar] [CrossRef]
- Heinze, J.; Götze, S.; Krauser, J.; Hundt, B.; Fläschner, N.; Lühmann, D.-S.; Becker, C.; Sengstock, K. Multiband spectroscopy of ultracold fermions: Observation of reduced tunneling in attractive Bose-Fermi mixtures. Phys. Rev. Lett. 2011, 107, 135303. [Google Scholar] [CrossRef] [PubMed]
- Tey, M.K.; Stellmer, S.; Grimm, R.; Schreck, F. Double-degenerate Bose-Fermi mixture of Strontium. Phys. Rev. A 2010, 82, 011608. [Google Scholar] [CrossRef]
- Best, T.; Will, S.; Schneider, U.; Hackermüller, L.; Van Oosten, D.; Bloch, I.; Lühmann, D.-S. Role of interactions in 87Rb–40K Bose-Fermi mixtures in a 3D optical lattice. Phys. Rev. Lett. 2009, 102, 030408. [Google Scholar] [CrossRef] [PubMed]
- Cumby, T.D.; Shewmon, R.A.; Hu, M.-G.; Perreault, J.D.; Jin, D.S. Feshbach-molecule formation in a Bose-Fermi mixture. Phys. Rev. A 2013, 87, 012703. [Google Scholar] [CrossRef]
- Deh, B.; Gunton, W.; Klappauf, B.; Li, Z.; Semczuk, M.; Van Dongen, J.; Madison, K. Giant Feshbach resonances in Li 6 - Rb 85 mixtures. Phys. Rev. A 2010, 82, 020701. [Google Scholar] [CrossRef]
- Tung, S.-K.; Parker, C.; Johansen, J.; Chin, C.; Wang, Y.; Julienne, P.S. Ultracold mixtures of atomic 6 Li and 133 Cs with tunable interactions. Phys. Rev. A 2013, 87, 010702. [Google Scholar] [CrossRef]
- Park, J.W.; Wu, C.-H.; Santiago, I.; Tiecke, T.G.; Will, S.; Ahmadi, P.; Zwierlein, M.W. Quantum degenerate Bose-Fermi mixture of chemically different atomic species with widely tunable interactions. Phys. Rev. A 2012, 85, 051602. [Google Scholar] [CrossRef]
- Wu, C.-H.; Santiago, I.; Park, J.W.; Ahmadi, P.; Zwierlein, M.W. Strongly interacting isotopic Bose-Fermi mixture immersed in a Fermi sea. Phys. Rev. A 2011, 84, 011601. [Google Scholar] [CrossRef]
- Lelas, K.; Jukić, D.; Buljan, H. Ground-state properties of a one-dimensional strongly interacting Bose-Fermi mixture in a double-well potential. Phys. Rev. A 2009, 80, 053617. [Google Scholar] [CrossRef]
- Watanabe, T.; Suzuki, T.; Schuck, P. Bose-fermi pair correlations in attractively interacting Bose-Fermi atomic mixtures. Phys. Rev. A 2008, 78, 033601. [Google Scholar] [CrossRef]
- Kain, B.; Ling, H.Y. Singlet and triplet superfluid competition in a mixture of two-component Fermi and one-component dipolar Bose gases. Phys. Rev. A 2011, 83, 061603. [Google Scholar] [CrossRef]
- Mering, A.; Fleischhauer, M. Multiband and nonlinear hopping corrections to the three-dimensional Bose-Fermi-Hubbard model. Phys. Rev. A 2011, 83, 063630. [Google Scholar] [CrossRef]
- Song, J.-L.; Zhou, F. Anomalous dimers in quantum mixtures near broad resonances: Pauli blocking, Fermi surface dynamics, and implications. Phys. Rev. A 2011, 84, 013601. [Google Scholar] [CrossRef]
- Ludwig, D.; Floerchinger, S.; Moroz, S.; Wetterich, C. Quantum phase transition in Bose-Fermi mixtures. Phys. Rev. A 2011, 84, 033629. [Google Scholar] [CrossRef]
- Bertaina, G.; Fratini, E.; Giorgini, S.; Pieri, P. Quantum Monte Carlo study of a resonant Bose-Fermi mixture. Phys. Rev. Lett. 2013, 110, 115303. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, S.K.; Salasnich, L. Superfluid Bose-Fermi mixture from weak coupling to unitarity. Phys. Rev. A 2008, 78, 043616. [Google Scholar] [CrossRef]
- Maruyama, T.; Yabu, H. Quadrupole oscillations in Bose-Fermi mixtures of ultracold atomic gases made of Yb atoms in the time-dependent Gross-Pitaevskii and Vlasov equations. Phys. Rev. A 2009, 80, 043615. [Google Scholar] [CrossRef]
- Iskin, M.; Freericks, J. Dynamical mean-field theory for light-fermion–heavy-boson mixtures on optical lattices. Phys. Rev. A 2009, 80, 053623. [Google Scholar] [CrossRef]
- Nishida, Y.; Son, D.T. Effective field theory of boson-fermion mixtures and bound fermion states on a vortex of boson superfluid. Phys. Rev. A 2006, 74, 013615. [Google Scholar] [CrossRef]
- Salasnich, L.; Toigo, F. Fermi-bose mixture across a Feshbach resonance. Phys. Rev. A 2007, 75, 013623. [Google Scholar] [CrossRef]
- Gautam, S.; Muruganandam, P.; Angom, D. Position swapping and pinching in Bose-Fermi mixtures with two-color optical Feshbach resonances. Phys. Rev. A 2011, 83, 023605. [Google Scholar] [CrossRef]
- Díaz, P.; Laroze, D.; Malomed, B.A. Correlations and synchronization in a Bose–Fermi mixture. J. Phys. B: At. Mol. Opt. Phys. 2015, 48, 075301. [Google Scholar] [CrossRef]
- Tylutki, M.; Recati, A.; Dalfovo, F.; Stringari, S. Dark–bright solitons in a superfluid Bose–Fermi mixture. New J. Phys. 2016, 18, 053014. [Google Scholar] [CrossRef]
- Manini, N.; Salasnich, L. Bulk and collective properties of a dilute fermi gas in the BCS-BEC crossover. Phys. Rev. A 2005, 71, 033625. [Google Scholar] [CrossRef]
- Salasnich, L.; Toigo, F. Extended Thomas-Fermi density functional for the unitary Fermi gas. Phys. Rev. A 2008, 78, 053626; ibod Erratum: Extended thomas-fermi density functional for the unitary fermi gas. Phys. Rev. A 2010, 82, 059902. [Google Scholar] [CrossRef]
- Ancilotto, F.; Salasnich, L.; Toigo, F. Dc Josephson effect with fermi gases in the Bose-Einstein regime. Phys. Rev. A 2009, 79, 033627. [Google Scholar] [CrossRef]
- Ancilotto, F.; Salasnich, L.; Toigo, F. Shock waves in strongly interacting Fermi gas from time-dependent density functional calculations. Phys. Rev. A 2012, 85, 063612. [Google Scholar] [CrossRef]
- Andreev, P.A. Spin current contribution in the spectrum of collective excitations of degenerate partially polarized spin-1/2 fermions at separate dynamics of spin-up and spin-down fermions. Laser Phys. Lett. 2018, 15, 105501. [Google Scholar] [CrossRef]
- Kim, Y.E.; Zubarev, A.L. Time-dependent density-functional theory for trapped strongly interacting fermionic atoms. Phys. Rev. A 2004, 70, 033612. [Google Scholar] [CrossRef]
- Adhikari, S.K. Mixing-demixing in a trapped degenerate fermion-fermion mixture. Phys. Rev. A 2006, 73, 043619. [Google Scholar] [CrossRef]
- Bragard, J.; Boccaletti, S.; Mendoza, C.; Hentschel, H.; Mancini, H. Synchronization of spatially extended chaotic systems in the presence of asymmetric coupling. Phys. Rev. E 2004, 70, 036219. [Google Scholar] [CrossRef] [PubMed]
- Shomroni, I.; Lahoud, E.; Levy, S.; Steinhauer, J. Evidence for an oscillating soliton/vortex ring by density engineering of a Bose–Einstein condensate. Nat. Phys. 2009, 5, 193. [Google Scholar] [CrossRef]
- Cardoso, W.B.; Zeng, J.; Avelar, A.T.; Bazeia, D.; Malomed, B.A. Bright solitons from the nonpolynomial Schrödinger equation with inhomogeneous defocusing nonlinearities. Phys. Rev. E 2013, 88, 025201. [Google Scholar] [CrossRef] [PubMed]
- Sacha, K.; Delande, D. Proper phase imprinting method for a dark soliton excitation in a superfluid Fermi mixture. Phys. Rev. A 2014, 90, 021604. [Google Scholar] [CrossRef]
- Donadello, S.; Serafini, S.; Tylutki, M.; Pitaevskii, L.P.; Dalfovo, F.; Lamporesi, G.; Ferrari, G. Observation of solitonic vortices in Bose-Einstein condensates. Phys. Rev. Lett. 2014, 113, 065302. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.D.; Huang, K.; Yang, C.N. Eigenvalues and eigenfunctions of a Bose system of hard spheres and its low-temperature properties. Phys. Rev. 1957, 106, 1135. [Google Scholar] [CrossRef]
- Kim, Y.E.; Zubarev, A.L. Three-body losses in trapped Bose-Einstein-Condensed gases. Phys. Rev. A 2004, 69, 023602. [Google Scholar] [CrossRef]
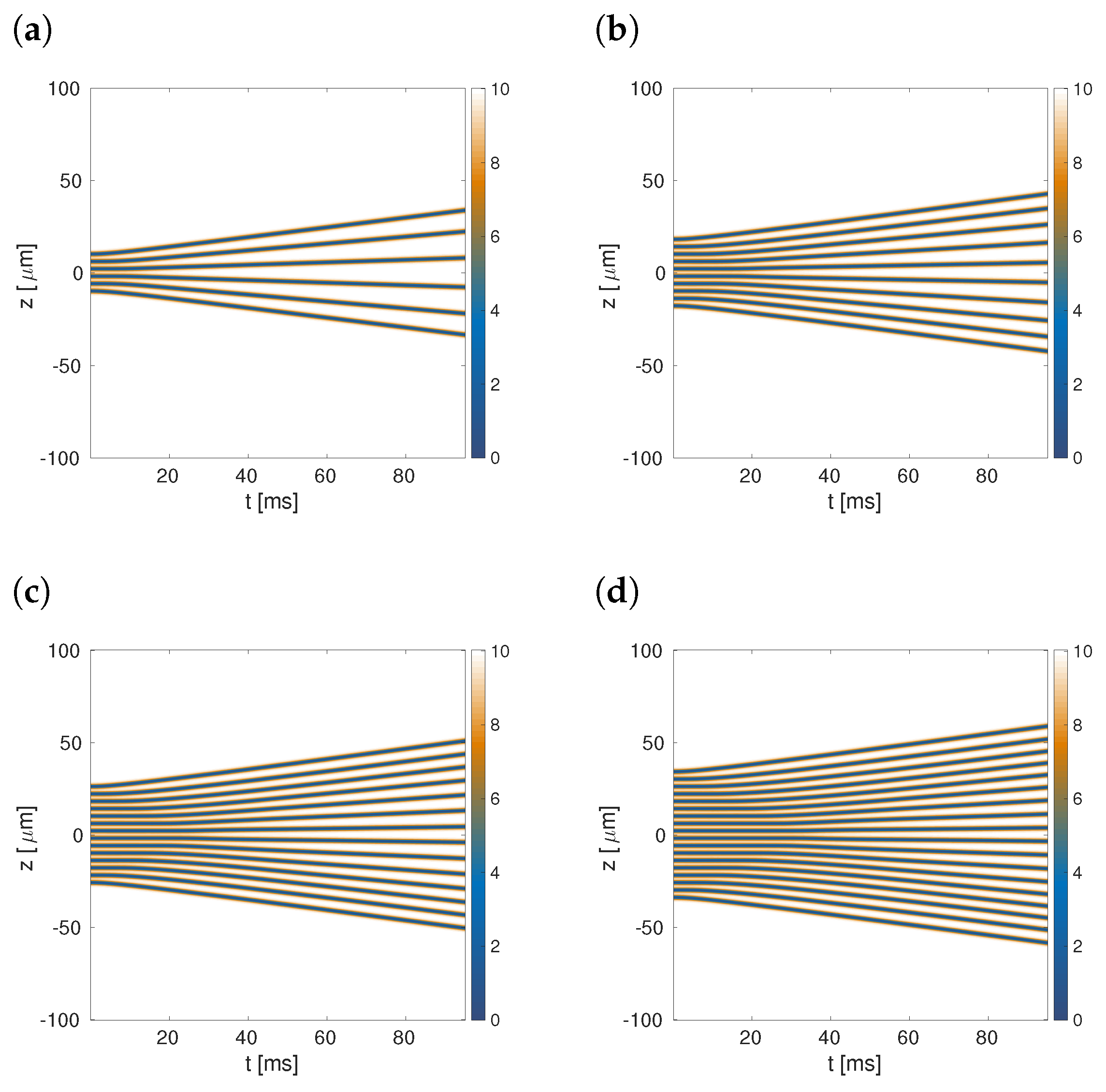
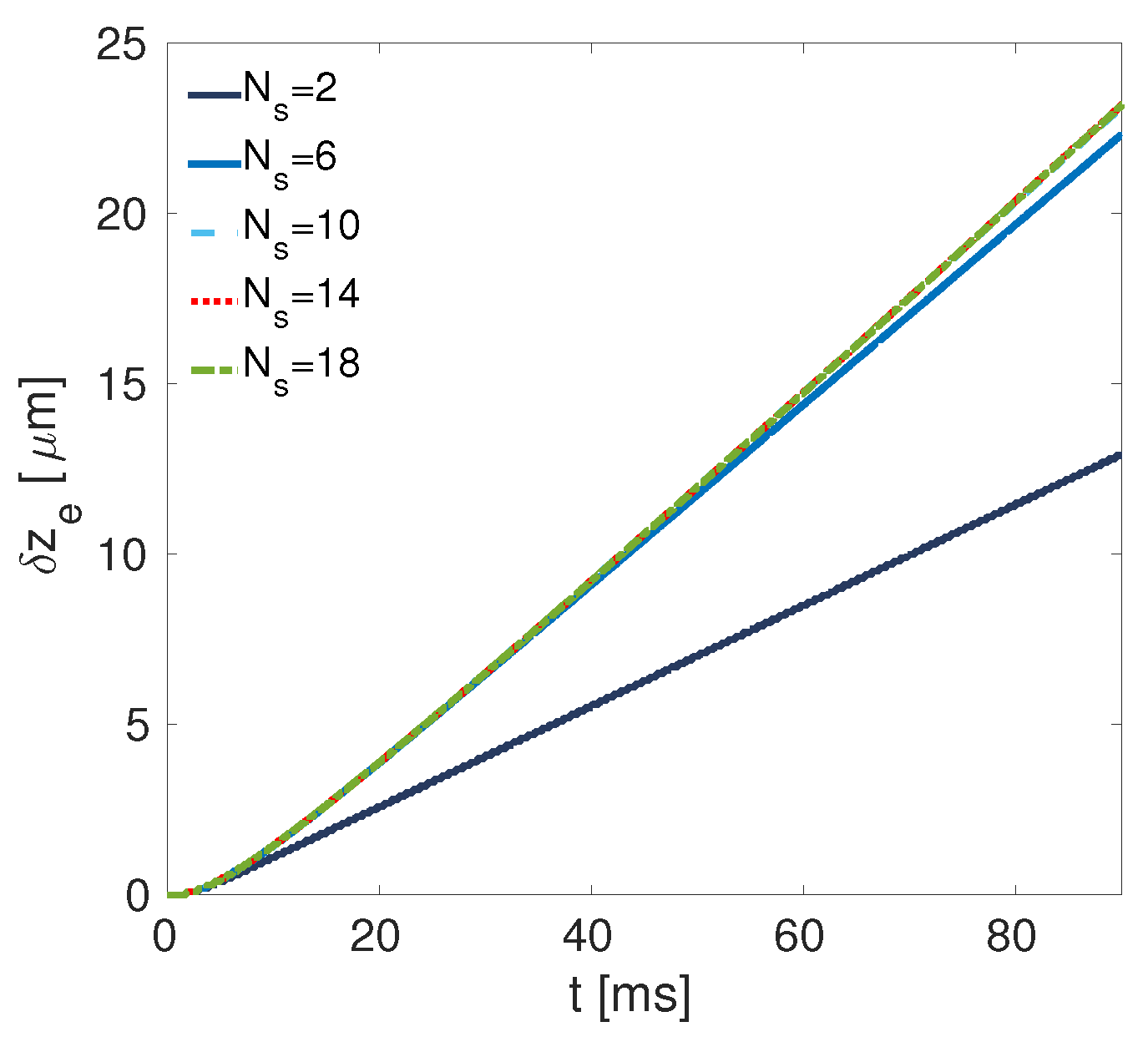
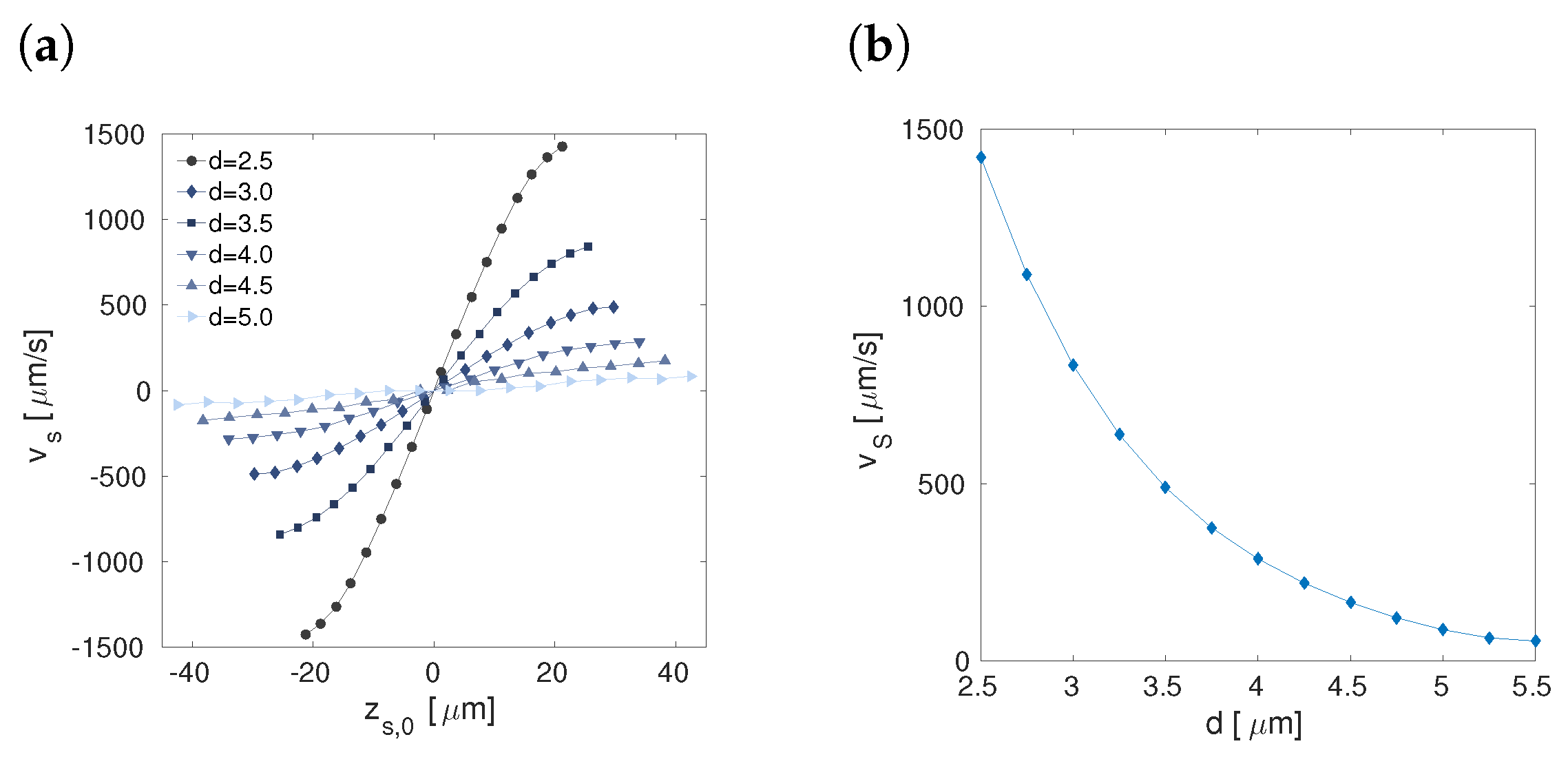
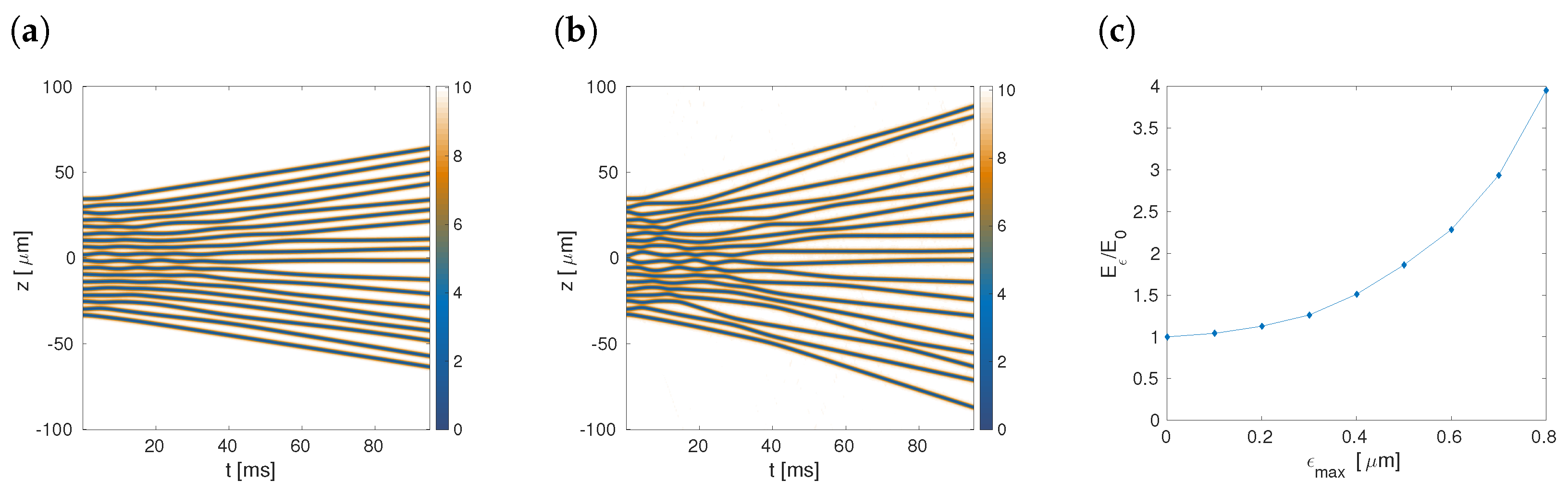
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Díaz, P.; Laroze, D.; Malomed, B.A. The Variational Reduction for Low-Dimensional Fermi Gases and Bose–Fermi Mixtures: A Brief Review. Condens. Matter 2019, 4, 22. https://doi.org/10.3390/condmat4010022
Díaz P, Laroze D, Malomed BA. The Variational Reduction for Low-Dimensional Fermi Gases and Bose–Fermi Mixtures: A Brief Review. Condensed Matter. 2019; 4(1):22. https://doi.org/10.3390/condmat4010022
Chicago/Turabian StyleDíaz, Pablo, David Laroze, and Boris A. Malomed. 2019. "The Variational Reduction for Low-Dimensional Fermi Gases and Bose–Fermi Mixtures: A Brief Review" Condensed Matter 4, no. 1: 22. https://doi.org/10.3390/condmat4010022
APA StyleDíaz, P., Laroze, D., & Malomed, B. A. (2019). The Variational Reduction for Low-Dimensional Fermi Gases and Bose–Fermi Mixtures: A Brief Review. Condensed Matter, 4(1), 22. https://doi.org/10.3390/condmat4010022






