Abstract
Crystallization is a generic phenomenon in classical and quantum mechanics arising in a variety of physical systems. In this work, we focus on a specific platform, ultracold dipolar bosons, which can be realized in experiments with dilute gases. We reviewed the relevant ingredients leading to crystallization, namely the interplay of contact and dipole–dipole interactions and system density, as well as the numerical algorithm employed. We characterized the many-body phases investigating correlations and superfluidity.
1. Introduction
Cluster phases are ubiquitous in diverse systems, from biological structures [1] to soft matter [2,3] to ultra-cold atomic and molecular condensates [4]. In many respects, particle aggregates display fascinating properties, whose features can be mainly described microscopically by means of effective two-body potentials. In a simple mean field picture, a cluster crystalline phase (or, more formally, a spontaneous breaking of translational symmetry) appears when the Fourier transform (when it exists) of the particle–particle interaction exhibits a negative region with a local minima. The cluster phase has then a density modulation with wavelength corresponding to those minima. The validity of this condition has been investigated also in the quantum regime, and it holds also if one considers fermionic or bosonic quantum gases [5]. In particular, having potentials displaying a soft-shoulder-like shape at short distance is a crucial ingredient for designing novel quantum phases. As an example, alkaline atoms off-resonantly excited to Rydberg states display an effective interaction with a soft-core at short distances that causes a supersolid phase [6,7,8,9]. A supersolid is a phase of matter that simultaneously accommodates diagonal as well as off-diagonal long-range order, which means that particles self-assemble into a rigid, regular crystal but at the same time can they can rotate with a corresponding reduced moment of inertia, which is an indication of the presence of a finite superfluid fraction [5,10,11,12,13,14].
Recently, ground-breaking experiments with bosonic dipolar condensates (Dysprosium and Erbium) demonstrated the existence of self-bound droplets in trapped configurations as well as in free space [15,16]. These experiments provides a useful isolated system to probe general quantum-mechanical properties related to cluster phases. A mean-field treatment mainly based on a generalized nonlocal nonlinear Schrödinger equation reveal a good agreement with the density distribution and the excitation spectra observed in the laboratory [17]. The same methodology has been successfully implemented to Bose–Bose mixtures [18,19]. In addition, quantum Monte Carlo simulations (QMC) have investigated the zero temperature phase diagram of bosons interacting via dipolar interactions in three dimensions in free space [20]. Other theoretical works have shown how the physical nature of self-bound droplets smoothly evolves from classical to quantum mechanical as the range of the repulsive two-body potential increases [21,22].
In the present paper, by means of first-principles numerical simulations, we characterize the many-body physics of bosons interacting via anisotropic dipole–dipole potentials with different densities and interaction strengths. In particular, here we propose an original work, which aims to understand the regime of low density, where a quantum phase transition from superfluid to cluster is expected. For this reason, we carries out simulations in order to support recent experimental findings about the stability of droplet phases in free space.
The rest of the paper is organized as follows: In Section 2, we introduce the microscopic potential that describes the physics of dipolar systems in three-dimension, whereas in Section 3 we present the details of the many-body properties known in literature.In Section 4, we illustrate our results, outlining our conclusions in Section 5.
2. Two-Body Physics of Dipole–Dipole Interactions
The two body-potential describing a short-range and an anisotropic long-range dipolar interaction reads
where m is the particle mass, is the s-wave scattering length and is the dipolar length representing the characteristic length of the dipole interactions [23]. denotes the angle between the vector and the polarization axis of the dipoles is the z-axis. Equation (1) applies to vertically aligned dipoles interacting via magnetic or electric dipole moments [23]. The pseudo-potential was discussed by Yi and Yu [24,25] making use of the Born approximation. More realistic model potentials, which include also a van der Walls short range potentials, are recently considered in [26] for a more detailed description of Dy two-body collisions. These potentials eventually lead to the same effective potential as in [24,25], with a dipolar length depending on the short range scattering length.
In our first-principle simulations based on a QMC technique (see Section 3), and were defined in terms of a unit length , being the corresponding energy with the effective pairwise potential :
describes a short-range hard core with cut-off at and the usual anisotropic dipolar component. The authors of [27,28] computed numerically the full low-energy scattering amplitude for the same model potential in Equation (2). A comparison with Equation (1) found a quite good agreement.
As a useful example, we now consider the Dysprosium’s isotopes Dy (, being the Bohr radius) and Dy (), relevant to the experimental observations by Kadau et al. [15]. In addition, the background scattering lengths were recently measured for both isotopes [15]: and , for Dy and Dy, respectively.
In [27], the authors extracted the relation between the dipolar length and the scattering length for the model potential , as shown in Figure 1. For and , we observe two resonances at which the scattering length diverges. Moreover, one also extracts the value of as a function of the corresponding ratios and (see Figure 2). From the calculation of for the two isotopes, we can also compute the value of the parameter . In particular, for Dy, we have , while considering Dy we get .
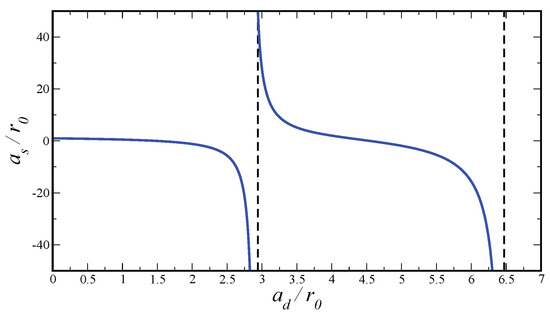
Figure 1.
Relation between scattering length and dipolar length in units of , see text.
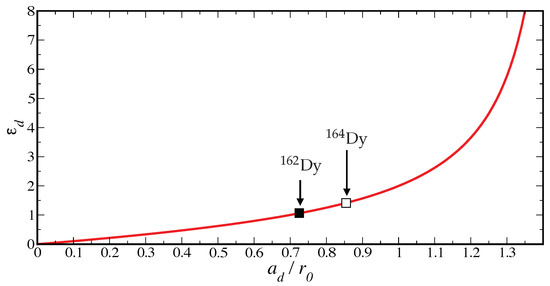
Figure 2.
Ratio vs. . filled and open square and correspond to experimental parameters for Dy and Dy, respectively, with their background scattering length ( and , respectively).
3. Many-Body Properties
The present section is devoted to discussing many-body properties of bosons interacting via a dipolar interaction. The quantum-mechanical Hamiltonian of an ensemble of N interacting identical bosons reads
The Hamiltonian is reported in units of and . It is important to note that the zero-temperature physics is exclusively controlled by the dimensionless interaction strength and the dimensionless density . Recently, the zero-temperature phase diagram of Equation (3) has been throughly investigated applying QMC techniques [20]. In particular, considering low (that is, ≲2.1 in the present units), simulations agree with the mean-field phase boundary predicted by standard Bogoliubov analysis. Upon increasing the dipole–dipole interaction, we can distinguish two different phases. At low densities (), the system displays a cluster phase with vanishing superfluidity and characterized by droplet structures with few particles. For higher densities, one observes a phase marked by elongated filaments with an anisotropic superfluid fraction; that is, whereas the superfluidity is observed along the direction of the filaments, it results greatly suppressed on the corresponding orthogonal plane, excluding then the occurrence of a global supersolid phase. In addition, finite-temperature calculations confirmed the stability of the filament phase against thermal fluctuations and provide an estimate of the superfluid fraction in the weak coupling limit in the framework of the Landau two-fluid model. It is important to stress that both cluster phase and filament phase extend from a small positive induced contact potential (), corresponding to the experimentally relevant regime in [15], to the strongly coupled limit of large dipolar interactions.
Theoretical results obtained solving the Hamiltonian in Equation (3) can be compared with recent experiments with Dy and Dy making use of the following condition:
As an example, setting an average density m, and with , taking [15], we showed in our previous work [20] that experimental results lie in the transition region (within the error bars) from superfluid to cluster phase by tuning the scattering length.
4. Results
4.1. Methodology
The low-temperature equilibrium properties of the systems described via the Hamiltonian in Equation (3) have been investigated employing first-principle computer simulations based on the worm algorithm in the continuous-space path integral representation [29], which allows one to essentially obtain the exact thermodynamics properties of Bose systems. Over the last ten years, this computational technique has been successfully tested on a large variety of bosonic systems, including, for instance, He [30], Rydberg atoms [4] and dipolar systems [31,32,33,34,35]. For the details of the implementation of the worm algorithm, the reader may refer to Boninsegni et al. [29]. Due to the intrinsic anisotropy of the potential in Equation (2), we implemented in this work the so-called primitive approximation for the imaginary time propagator, which requires a greater number of time slices with respect to more complex propagators, such as the pair-product ansatz [36] or the fourth-order one [37]. All the results reported below were extrapolated to the limit of zero temperature. In this work, we studied the equilibrium properties of scaled average density and different interaction strengths . We worked with N atoms in a cubic box of linear dimension L (fixing the density ) and using periodic boundary conditions. We performed simulations with N between 100 and 400. Keeping the system’s density constant when N increases, simulations showed a corresponding growth of the number of filaments or clusters. From these simulations, we obtained density profiles, radial correlation functions, and the superfluid fraction. The limit of zero temperature was obtained lowering the temperature until observables (e.g., energy, or superfluid fraction) do not change on further decreasing T.
4.2. Density Profile of the Filament Phase
In this section, we present results applying the QMC method discussed in Section 4.1. We consider for now a regime of high density such as . For this peculiar case, our calculations obtained a stable filament phase at temperature much lower then the transition temperature from normal to superfluid liquid. Figure 3a shows to a filament phase with and , P being the number of imaginary-time slices. This snapshot displays the projection of the single-particle imaginary-time evolution onto the real space. This representation of the condensate provides information of the delocalization of particles in the box, and therefore of their probability distribution.
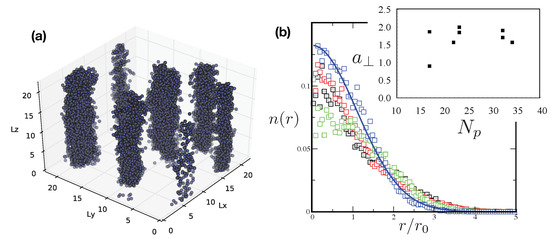
Figure 3.
(a) QMC density distribution of a filament phase for . The number of filaments for these parameters is equal to four. Periodic boundary conditions have been employed. (b) Particle density within a filament as a function of . Different colors represent different filament distributions with respect to filaments of (a). For these filaments, the average particle number is about (see text).
The system shapes in four different well defined filaments, which we now characterize. We fit the single-filament density with a Gaussian
and extract the average number of particles within each filament. The inset in Figure 3b shows the width of the Gaussian in units of , as a function of the particle number . The four different colored squares refer to the distribution for each filament of Figure 3a. The estimate of the average inter-particle distance with a gaussian wave packet in the radial direction and a cylinder of length L along z yields
for the data in Figure 3a, where is the density of the filament. From the fit of the parameters above, we get and . For sake of clearness, one Gaussian fit is only reported in Figure 3b (see blue line).
4.3. Weakly Interacting Regime
With the many-body Hamiltonian in Equation (3), one can also investigate the weakly interacting regime. To do that, we consider a limit where and length scales are much smaller than the inter-particle distance. This corresponds to maintain the general conditions and simultaneously fulfilled. Quantitatively, as already discussed in Reference [20], both inequalities hold keeping and .
We present QMC data at . Figure 4 (top) reports snapshot configurations at a rescaled low temperature equal to , being the critical temperature of the ideal Bose gas ; whereas the bottom panels show their corresponding radial distribution functions . In addition, in this case, simulations were obtained with , , keeping a fixed density of .
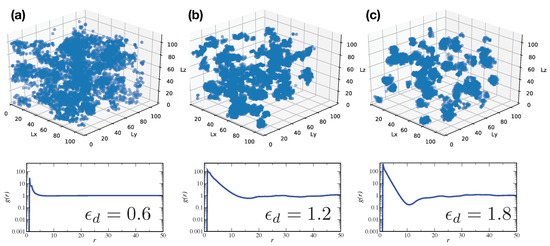
Figure 4.
(top) QMC density distribution at different strengths = 0.6 (a), 1.2 (b), 1.8 (c), considering a rescaled density ; and (bottom) radial distribution functions for the corresponding configurations.
For (Figure 4a), the condensate appears modified by the dipolar strength only marginally. Radial distribution functions display strong correlations at short distances, presenting a typical fluid behavior at large r. Upon increasing the dipolar interaction, for (e.g., Figure 4b,c), we observed a stabilization of clusters. As expected, their emergence exhibits a with stronger correlations at short r if compared to Figure 4a. However, the same observable in Figure 4b,c shows a gentle modulation at long distances, excluding long range crystalline order at larger r, and therefore any cluster crystal phase. In addition, contrary to the prediction of mean field theory for the simulation parameters, this phase is not globally superfluid. To illustrate this point, we show the computed the frequency of the occurrence of permutation cycles involving n particles () for the system with (see Figure 5). The important point here is that permutations extend only along cycles that remain confined within the single cluster or most close by clusters, supporting the interpretation that locally particles exchange and quantum droplets are locally superfluid. Finally, increasing further (Figure 4c), we observed nothing but the stabilization of the cluster phase. This completely excludes the existence of the filament regime discussed at higher densities.
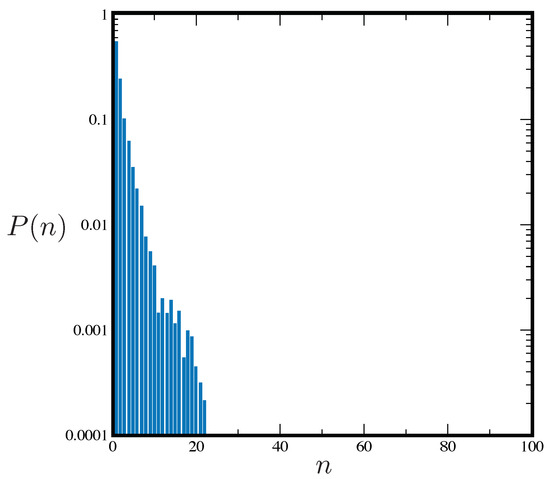
Figure 5.
Frequency of occurrence of cycles comprising n particles at low (see text) for a system of particles and .
5. Conclusions
We discussed the appearance of cluster phases in ultracold dipolar bosons. We reviewed the relevant pairwise interactions among dipoles, leading to the formation of clusters and filaments, as well as the numerical algorithm employed. We characterized the many-body phases varying the strength of the potential as well as the density of the system via extensive QMC calculations.
Author Contributions
Both authors contributed equally to mean-field and quantum Monte Carlo calculations, to analyse the results as well as to the preparation of the manuscript.
Funding
T.M. acknowledges for support CAPES through the Project CAPES/Nuffic n. 88887.156521/2017-00 and CNPq through Bolsa de produtividade em Pesquisa n. 311079/2015-6.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Butenko, S.; Chaovalitwongse, W.A.; Pardalos, P.M. Clustering Challenges in Biological Networks; World Scientific Publishers: Singapore, 2009. [Google Scholar]
- Likos, C.N. Effective interactions in soft condensed matter physics. Phys. Rep. 2001, 348, 267–439. [Google Scholar] [CrossRef]
- Díaz-Méndez, R.; Mezzacapo, F.; Lechner, W.; Cinti, F.; Babaev, E.; Pupillo, G. Glass Transitions in Monodisperse Cluster-Forming Ensembles: Vortex Matter in Type-1.5 Superconductors. Phys. Rev. Lett. 2017, 118, 067001. [Google Scholar] [CrossRef]
- Cinti, F.; Macrì, T.; Lechner, W.; Pupillo, G.; Pohl, T. Defect-induced supersolidity with soft-core bosons. Nat. Commun. 2014, 5, 3235. [Google Scholar] [CrossRef] [PubMed]
- Cinti, F.; Jain, P.; Boninsegni, M.; Micheli, A.; Zoller, P.; Pupillo, G. Supersolid Droplet Crystal in a Dipole-Blockaded Gas. Phys. Rev. Lett. 2010, 105, 135301. [Google Scholar] [CrossRef] [PubMed]
- Henkel, N.; Cinti, F.; Jain, P.; Pupillo, G.; Pohl, T. Supersolid Vortex Crystals in Rydberg-Dressed Bose-Einstein Condensates. Phys. Rev. Lett. 2012, 108, 265301. [Google Scholar] [CrossRef] [PubMed]
- Macrì, T.; Saccani, S.; Cinti, F. Ground State and Excitation Properties of Soft-Core Bosons. J. Low Temp. Phys. 2014, 177, 59–71. [Google Scholar] [CrossRef]
- Macrì, T.; Maucher, F.; Cinti, F.; Pohl, T. Elementary excitations of ultracold soft-core bosons across the superfluid-supersolid phase transition. Phys. Rev. A 2013, 87, 061602. [Google Scholar] [CrossRef]
- Cinti, F.; Boninsegni, M.; Pohl, T. Exchange-induced crystallization of soft-core bosons. New J. Phys. 2014, 16, 033038. [Google Scholar] [CrossRef]
- Saccani, S.; Moroni, S.; Boninsegni, M. Excitation Spectrum of a Supersolid. Phys. Rev. Lett. 2012, 108, 175301. [Google Scholar] [CrossRef]
- Saccani, S.; Moroni, S.; Boninsegni, M. Phase diagram of soft-core bosons in two dimensions. Phys. Rev. B 2011, 83, 092506. [Google Scholar] [CrossRef]
- Boninsegni, M. Supersolid Phases of Cold Atom Assemblies. J. Low Temp. Phys. 2012, 168, 137–149. [Google Scholar] [CrossRef]
- Moroni, S.; Boninsegni, M. Coexistence, Interfacial Energy, and the Fate of Microemulsions of 2D Dipolar Bosons. Phys. Rev. Lett. 2014, 113, 240407. [Google Scholar] [CrossRef] [PubMed]
- Boninsegni, M.; Prokof’ev, N.V. Colloquium: Supersolids: What and where are they? Rev. Mod. Phys. 2012, 84, 759–776. [Google Scholar] [CrossRef]
- Kadau, H.; Schmitt, M.; Wenzel, M.; Wink, C.; Maier, T.; Ferrier-Barbut, I.; Pfau, T. Observing the Rosensweig instability of a quantum ferrofluid. Nature 2016, 530, 194–197. [Google Scholar] [CrossRef] [PubMed]
- Chomaz, L.; Baier, S.; Petter, D.; Mark, M.J.; Wächtler, F.; Santos, L.; Ferlaino, F. Quantum-Fluctuation-Driven Crossover from a Dilute Bose-Einstein Condensate to a Macrodroplet in a Dipolar Quantum Fluid. Phys. Rev. X 2016, 6, 041039. [Google Scholar] [CrossRef]
- Wächtler, F.; Santos, L. Quantum filaments in dipolar Bose-Einstein condensates. Phys. Rev. A 2016, 93, 061603. [Google Scholar] [CrossRef]
- Cappellaro, A.; Macrì, T.; Salasnich, L. Collective modes across the soliton-droplet crossover in binary Bose mixtures. Phys. Rev. A 2018, 97, 053623. [Google Scholar] [CrossRef]
- Cappellaro, A.; Macrì, T.; Bertacco, G.F.; Salasnich, L. Equation of state and self-bound droplet in Rabi-coupled Bose mixtures. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef]
- Cinti, F.; Cappellaro, A.; Salasnich, L.; Macrì, T. Superfluid Filaments of Dipolar Bosons in Free Space. Phys. Rev. Lett. 2017, 119, 215302. [Google Scholar] [CrossRef]
- Cinti, F.; Boninsegni, M. Classical and quantum filaments in the ground state of trapped dipolar Bose gases. Phys. Rev. A 2017, 96, 013627. [Google Scholar] [CrossRef]
- Cidrim, A.; dos Santos, F.E.A.; Henn, E.A.L.; Macrì, T. Vortices in self-bound dipolar droplets. Phys. Rev. A 2018, 98, 023618. [Google Scholar] [CrossRef]
- Lahaye, T.; Menotti, C.; Santos, L.; Lewenstein, M.; Pfau, T. The physics of dipolar bosonic quantum gases. Rep. Prog. Phys. 2009, 72, 126401. [Google Scholar] [CrossRef]
- Yi, S.; You, L. Trapped atomic condensates with anisotropic interactions. Phys. Rev. A 2000, 61, 041604. [Google Scholar] [CrossRef]
- Yi, S.; You, L. Trapped condensates of atoms with dipole interactions. Phys. Rev. A 2001, 63, 053607. [Google Scholar] [CrossRef]
- Ołdziejewski, R.; Jachymski, K. Properties of strongly dipolar Bose gases beyond the Born approximation. Phys. Rev. A 2016, 94, 063638. [Google Scholar] [CrossRef]
- Bortolotti, D.C.E.; Ronen, S.; Bohn, J.L.; Blume, D. Scattering Length Instability in Dipolar Bose-Einstein Condensates. Phys. Rev. Lett. 2006, 97, 160402. [Google Scholar] [CrossRef] [PubMed]
- Ronen, S.; Bortolotti, D.C.E.; Bohn, J.L. Radial and Angular Rotons in Trapped Dipolar Gases. Phys. Rev. Lett. 2007, 98, 030406. [Google Scholar] [CrossRef] [PubMed]
- Boninsegni, M.; Prokof’ev, N.; Svistunov, B. Worm Algorithm for Continuous-Space Path Integral Monte Carlo Simulations. Phys. Rev. Lett. 2006, 96, 070601. [Google Scholar] [CrossRef] [PubMed]
- Boninsegni, M.; Prokof’ev, N.V.; Svistunov, B.V. Worm algorithm and diagrammatic Monte Carlo: A new approach to continuous-space path integral Monte Carlo simulations. Phys. Rev. E 2006, 74, 036701. [Google Scholar] [CrossRef] [PubMed]
- Cinti, F. Incommensurability Effects on Dipolar Bosons in Optical Lattices. J. Low Temp. Phys. 2015, 182, 153–161. [Google Scholar] [CrossRef]
- Cinti, F.; Wang, D.W.; Boninsegni, M. Phases of dipolar bosons in a bilayer geometry. Phys. Rev. A 2017, 95, 023622. [Google Scholar] [CrossRef]
- Lechner, W.; Cinti, F.; Pupillo, G. Tunable defect interactions and supersolidity in dipolar quantum gases on a lattice potential. Phys. Rev. A 2015, 92, 053625. [Google Scholar] [CrossRef]
- Díaz-Méndez, R.; Mezzacapo, F.; Cinti, F.; Lechner, W.; Pupillo, G. Monodisperse cluster crystals: Classical and quantum dynamics. Phys. Rev. E 2015, 92, 052307. [Google Scholar] [CrossRef] [PubMed]
- Jain, P.; Cinti, F.; Boninsegni, M. Structure, Bose-Einstein condensation, and superfluidity of two-dimensional confined dipolar assemblies. Phys. Rev. B 2011, 84, 014534. [Google Scholar] [CrossRef]
- Ceperley, D.M. Path integrals in the theory of condensed helium. Rev. Mod. Phys. 1995, 67, 279–355. [Google Scholar] [CrossRef]
- Jang, S.; Jang, S.; Voth, G.A. Applications of higher order composite factorization schemes in imaginary time path integral simulations. J. Chem. Phys. 2001, 115, 7832–7842. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).