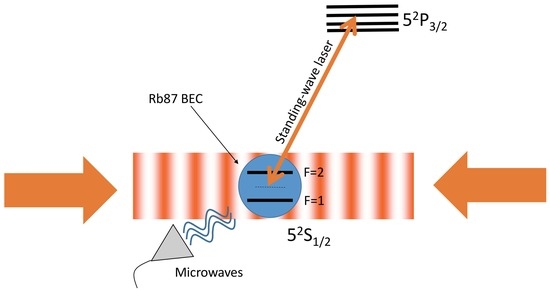
Impact of Lattice Vibrations on the Dynamics of a Spinor Atom-Optics Kicked Rotor †
Abstract
1. Introduction
2. Discrete-Time Quantum Walk in Momentum Space
2.1. Quantum Walk Evolution
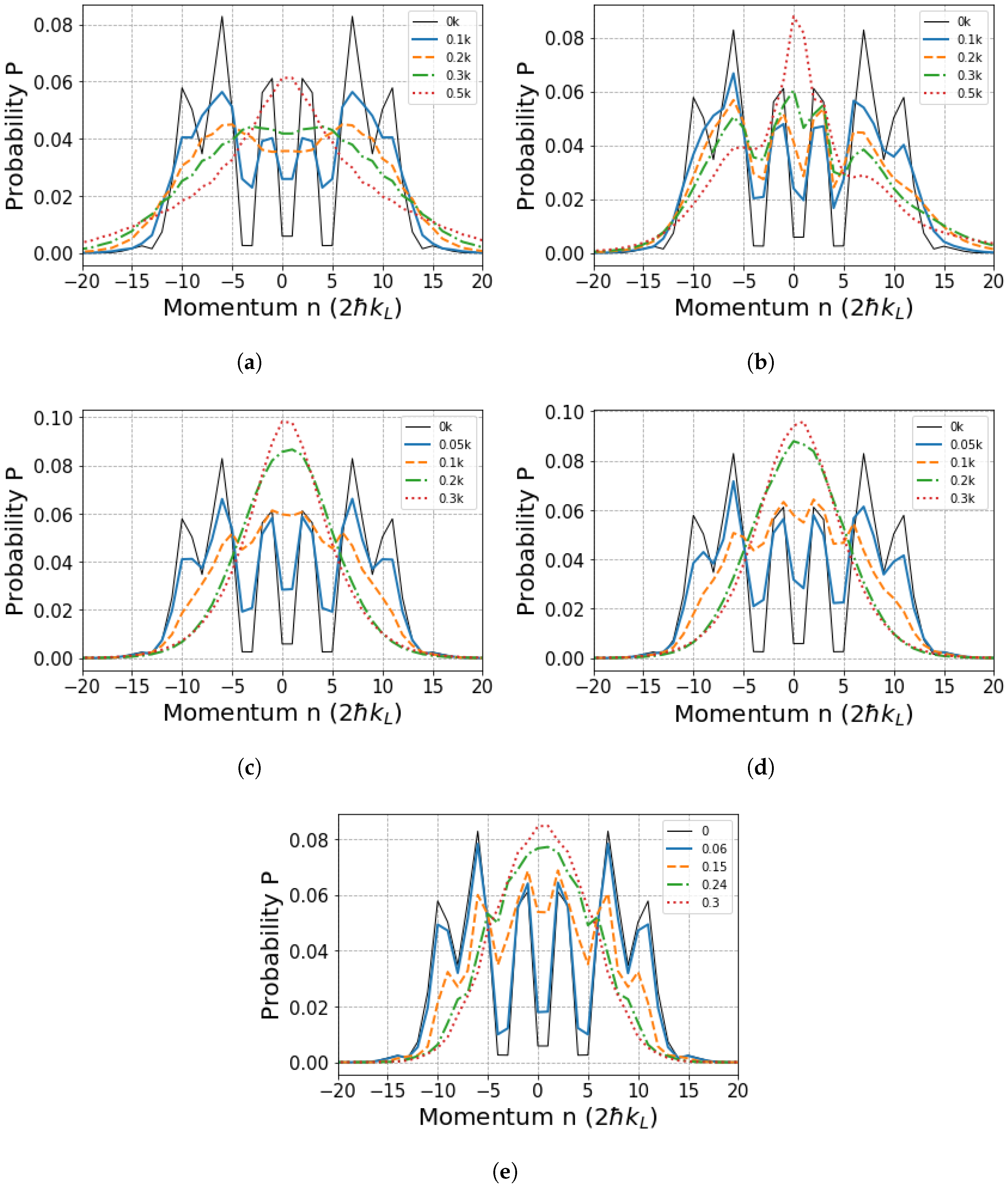
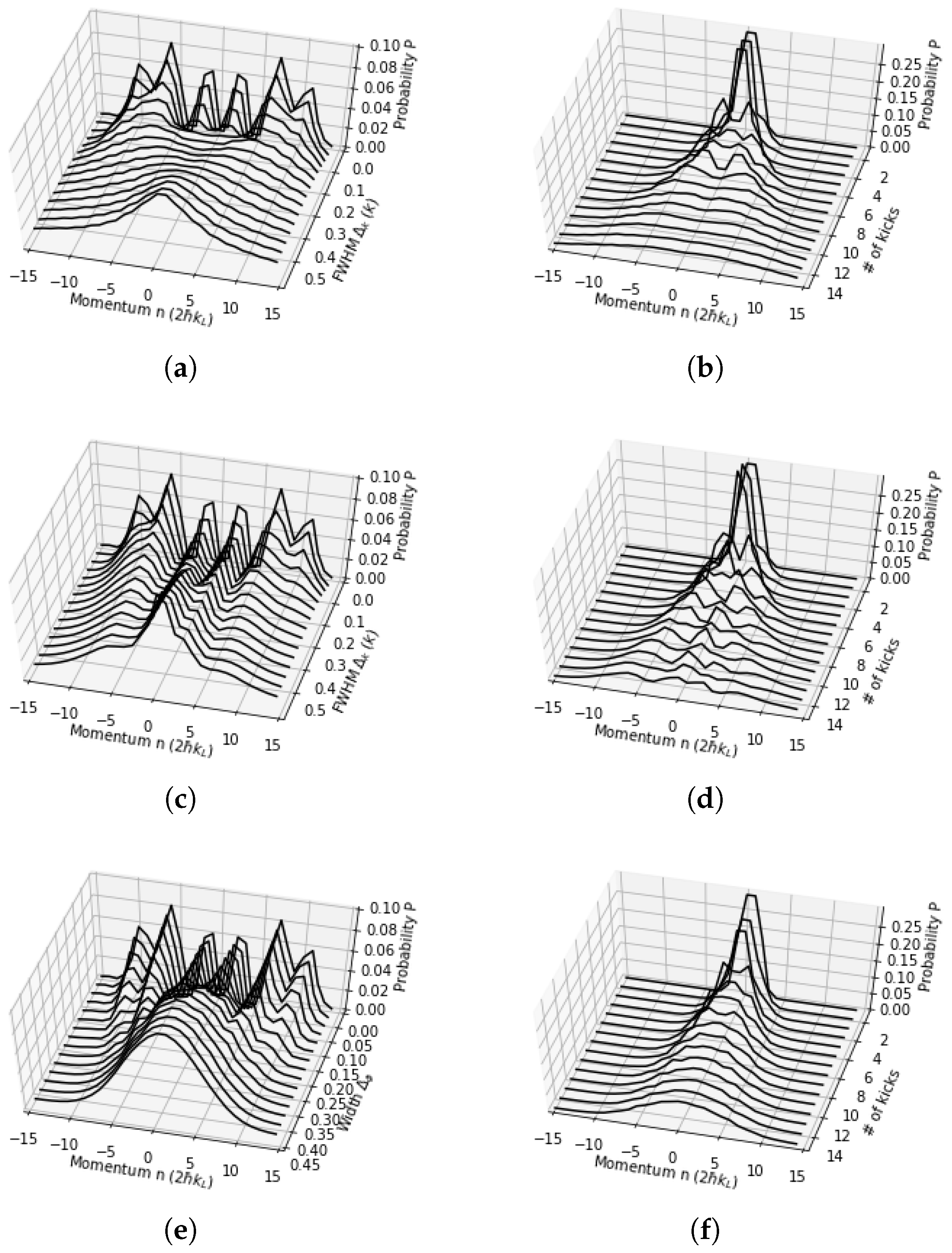
2.2. Lattice Vibrations
2.3. Numerical Simulations: Quantum-to-Classical Transitions
3. Double Kicked Rotor Evolution
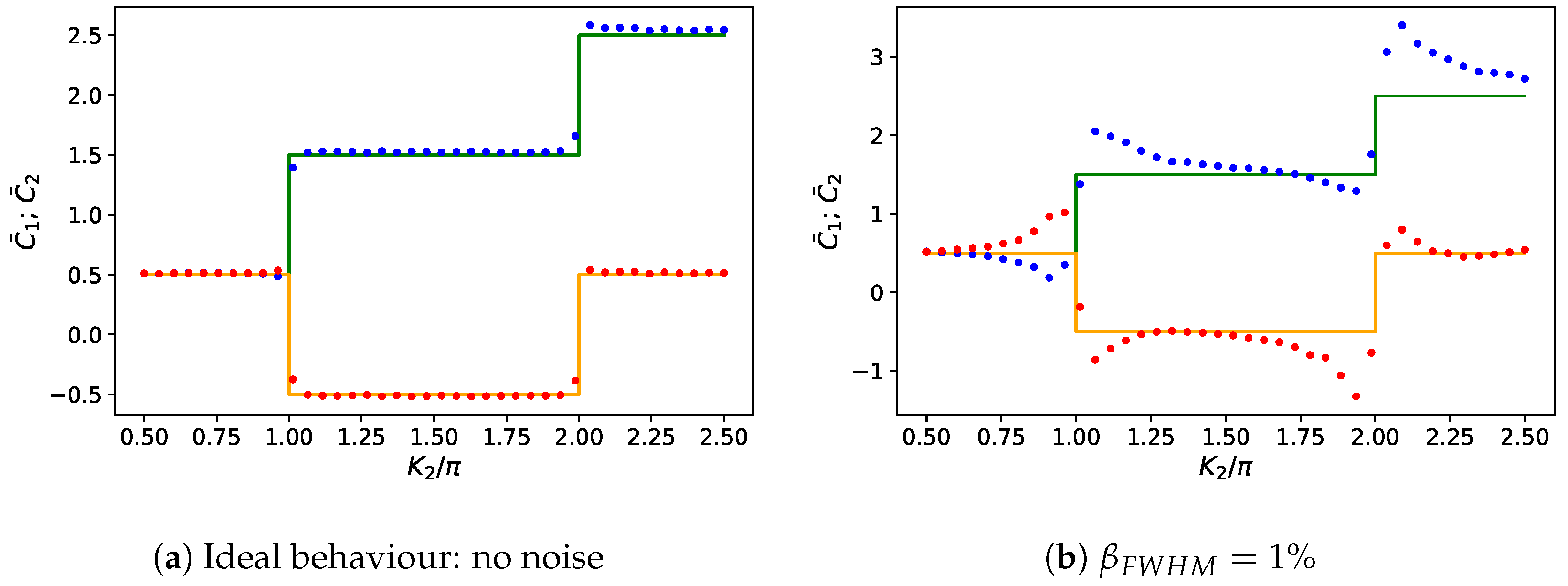
3.1. Proposal
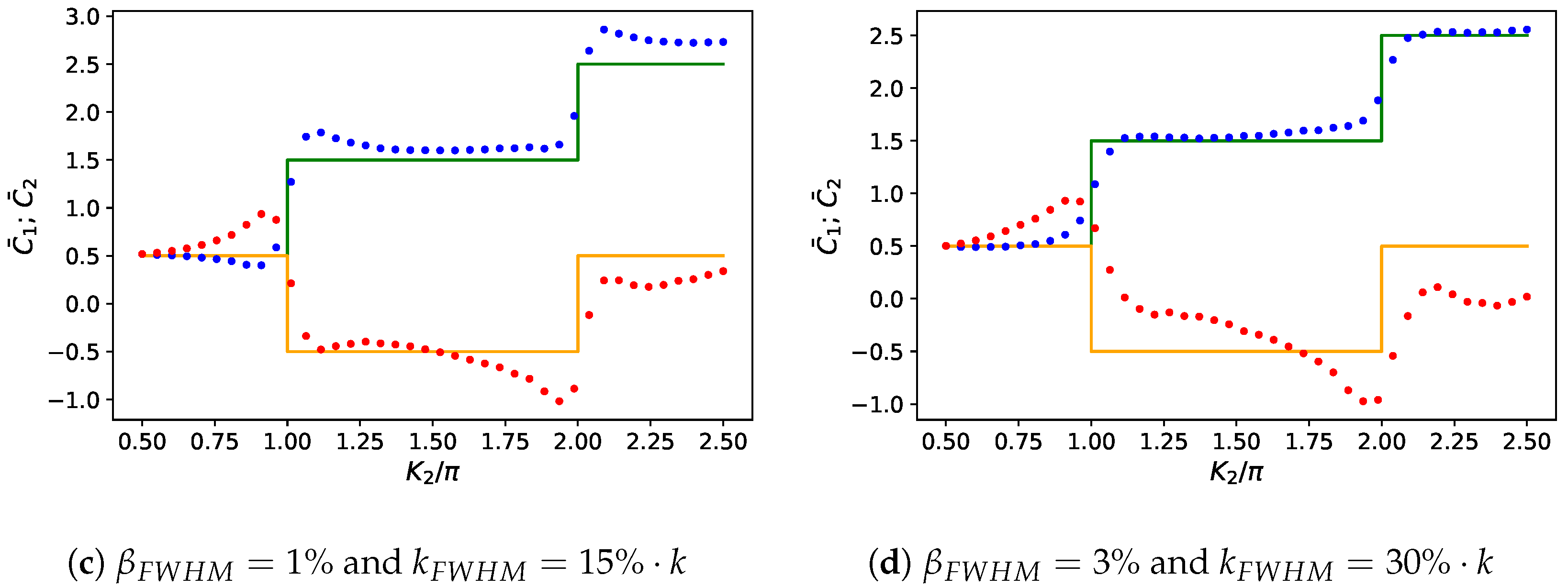
3.2. Stability with Respect to Noise
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Graham, R.; Schlautmann, M.; Zoller, P. Dynamical localization of atomic-beam deflection by a modulated standing light wave. Phys. Rev. A 1992, 45, R19–R22. [Google Scholar] [CrossRef] [PubMed]
- Raizen, M.G. Quantum Chaos with Cold Atoms. Adv. At. Mol. Opt. Phys. 1999, 41, 43–81. [Google Scholar] [CrossRef]
- Bharucha, C.F.; Robinson, J.C.; Moore, F.L.; Sundaram, B.; Niu, Q.; Raizen, M.G. Dynamical localization of ultracold sodium atoms. Phys. Rev. E 1999, 60, 3881–3895. [Google Scholar] [CrossRef]
- Sadgrove, M.; Wimberger, S. A pseudo-classical method for the atom-optics kicked rotor: From theory to experiment and back. Adv. At. Mol. Opt. Phys. 2011, 60, 315–369. [Google Scholar]
- Klappauf, B.G.; Oskay, W.H.; Steck, D.A.; Raizen, M.G. Observation of Noise and Dissipation Effects on Dynamical Localization. Phys. Rev. Lett. 1998, 81, 1203–1206. [Google Scholar] [CrossRef]
- Chabé, J.; Lemarié, G.; Grémaud, B.; Delande, D.; Szriftgiser, P.; Garreau, J.C. Experimental Observation of the Anderson Metal-Insulator Transition with Atomic Matter Waves. Phys. Rev. Lett. 2008, 101, 255702. [Google Scholar] [CrossRef]
- Lopez, M.; Clément, J.F.; Szriftgiser, P.; Garreau, J.C.; Delande, D. Experimental Test of Universality of the Anderson Transition. Phys. Rev. Lett. 2012, 108, 095701. [Google Scholar] [CrossRef]
- Tian, C.; Altland, A. Field theory of Anderson transition of the kicked rotor. Phys. Scr. 2012, 2012, 014049. [Google Scholar] [CrossRef]
- Sadgrove, M.; Wimberger, S.; Parkins, S.; Leonhardt, R. Ballistic and Localized Transport for the Atom Optics Kicked Rotor in the Limit of a Vanishing Kicking Period. Phys. Rev. Lett. 2005, 94, 174103. [Google Scholar] [CrossRef]
- Ryu, C.; Andersen, M.F.; Vaziri, A.; d’Arcy, M.B.; Grossman, J.M.; Helmerson, K.; Phillips, W.D. High-Order Quantum Resonances Observed in a Periodically Kicked Bose-Einstein Condensate. Phys. Rev. Lett. 2006, 96, 160403. [Google Scholar] [CrossRef]
- Kanem, J.F.; Maneshi, S.; Partlow, M.; Spanner, M.; Steinberg, A.M. Observation of High-Order Quantum Resonances in the Kicked Rotor. Phys. Rev. Lett. 2007, 98, 083004. [Google Scholar] [CrossRef] [PubMed]
- Ammann, H.; Gray, R.; Shvarchuck, I.; Christensen, N. Quantum Delta-Kicked Rotor: Experimental Observation of Decoherence. Phys. Rev. Lett. 1998, 80, 4111–4115. [Google Scholar] [CrossRef]
- d’Arcy, M.B.; Godun, R.M.; Oberthaler, M.K.; Cassettari, D.; Summy, G.S. Quantum Enhancement of Momentum Diffusion in the Delta-Kicked Rotor. Phys. Rev. Lett. 2001, 87, 074102. [Google Scholar] [CrossRef] [PubMed]
- Sadgrove, M.; Hilliard, A.; Mullins, T.; Parkins, S.; Leonhardt, R. Observation of robust quantum resonance peaks in an atom optics kicked rotor with amplitude noise. Phys. Rev. E 2004, 70, 036217. [Google Scholar] [CrossRef] [PubMed]
- Chai, S.; Fekete, J.; McDowall, P.; Coop, S.; Lindballe, T.; Andersen, M.F. Survival resonances in an atom-optics system driven by temporally and spatially periodic dissipation. Phys. Rev. A 2018, 97, 033616. [Google Scholar] [CrossRef]
- Wu, S.; Tonyushkin, A.; Prentiss, M.G. Observation of Saturation of Fidelity Decay with an Atom Interferometer. Phys. Rev. Lett. 2009, 103, 034101. [Google Scholar] [CrossRef] [PubMed]
- Talukdar, I.; Shrestha, R.; Summy, G.S. Sub-Fourier Characteristics of a δ-kicked-rotor Resonance. Phys. Rev. Lett. 2010, 105, 054103. [Google Scholar] [CrossRef] [PubMed]
- Shrestha, R.K.; Wimberger, S.; Ni, J.; Lam, W.K.; Summy, G.S. Fidelity of the quantum δ-kicked accelerator. Phys. Rev. E 2013, 87, 020902. [Google Scholar] [CrossRef] [PubMed]
- Duffy, G.J.; Parkins, S.; Müller, T.; Sadgrove, M.; Leonhardt, R.; Wilson, A.C. Experimental investigation of early-time diffusion in the quantum kicked rotor using a Bose-Einstein condensate. Phys. Rev. E 2004, 70, 056206. [Google Scholar] [CrossRef]
- Behinaein, G.; Ramareddy, V.; Ahmadi, P.; Summy, G.S. Exploring the Phase Space of the Quantum δ-Kicked Accelerator. Phys. Rev. Lett. 2006, 97, 244101. [Google Scholar] [CrossRef] [PubMed]
- White, D.H.; Ruddell, S.K.; Hoogerland, M.D. Experimental realization of a quantum ratchet through phase modulation. Phys. Rev. A 2013, 88, 063603. [Google Scholar] [CrossRef]
- Sadgrove, M.; Horikoshi, M.; Sekimura, T.; Nakagawa, K. Rectified Momentum Transport for a Kicked Bose-Einstein Condensate. Phys. Rev. Lett. 2007, 99, 043002. [Google Scholar] [CrossRef] [PubMed]
- Dana, I.; Ramareddy, V.; Talukdar, I.; Summy, G.S. Experimental Realization of Quantum-Resonance Ratchets at Arbitrary Quasimomenta. Phys. Rev. Lett. 2008, 100, 024103. [Google Scholar] [CrossRef] [PubMed]
- Sadgrove, M.; Schell, T.; Nakagawa, K.; Wimberger, S. Engineering quantum correlations to enhance transport in cold atoms. Phys. Rev. A 2013, 87, 013631. [Google Scholar] [CrossRef]
- Ni, J.; Dadras, S.; Lam, W.K.; Shrestha, R.K.; Sadgrove, M.; Wimberger, S.; Summy, G.S. Hamiltonian Ratchets with Ultra-Cold Atoms. Annalen der Physik 2017, 529, 1600335. [Google Scholar] [CrossRef]
- Hainaut, C.; Rançon, A.; Clément, J.F.M.C.; Garreau, J.C.; Szriftgiser, P.; Chicireanu, R.; Delande, D. Ratchet effect in the quantum kicked rotor and its destruction by dynamical localization. Phys. Rev. A 2018, 97, 061601. [Google Scholar] [CrossRef]
- Eltschka, C.; Schlagheck, P. Resonance- and Chaos-Assisted Tunneling in Mixed Regular-Chaotic Systems. Phys. Rev. Lett. 2005, 94, 014101. [Google Scholar] [CrossRef] [PubMed]
- Shrestha, R.K.; Ni, J.; Lam, W.K.; Summy, G.S.; Wimberger, S. Dynamical tunneling of a Bose-Einstein condensate in periodically driven systems. Phys. Rev. E 2013, 88, 034901. [Google Scholar] [CrossRef]
- Dadras, S.; Gresch, A.; Groiseau, C.; Wimberger, S.; Summy, G.S. Quantum Walk in Momentum Space with a Bose-Einstein Condensate. Phys. Rev. Lett. 2018, 121, 070402. [Google Scholar] [CrossRef]
- Wang, J.; Gong, J. Proposal of a cold-atom realization of quantum maps with Hofstadter’s butterfly spectrum. Phys. Rev. A 2008, 77, 031405. [Google Scholar] [CrossRef]
- Ho, D.Y.H.; Gong, J. Quantized Adiabatic Transport In Momentum Space. Phys. Rev. Lett. 2012, 109, 010601. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Ho, D.Y.H.; Lawton, W.; Wang, J.; Gong, J. Kicked-Harper model versus on-resonance double-kicked rotor model: From spectral difference to topological equivalence. Phys. Rev. E 2013, 88, 052920. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Tian, C. Planck’s Quantum-Driven Integer Quantum Hall Effect in Chaos. Phys. Rev. Lett. 2014, 113, 216802. [Google Scholar] [CrossRef] [PubMed]
- Dana, I. Topological properties of adiabatically varied Floquet systems. Phys. Rev. E 2017, 96, 022216. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Gong, J. Floquet topological phases in a spin-1/2 double kicked rotor. Phys. Rev. A 2018, 97, 063603. [Google Scholar] [CrossRef]
- Scharf, R. Kicked rotator for a spin-1/2 particle. J. Phys. A: Math. Gen. 1989, 22, 4223. [Google Scholar] [CrossRef]
- Hernández, G.; Romanelli, A. Resonant quantum kicked rotor with two internal levels. Phys. Rev. A 2013, 87, 042316. [Google Scholar] [CrossRef]
- Summy, G.; Wimberger, S. Quantum random walk of a Bose-Einstein condensate in momentum space. Phys. Rev. A 2016, 93, 023638. [Google Scholar] [CrossRef]
- Kitagawa, T. Topological phenomena in quantum walks: elementary introduction to the physics of topological phases. Quantum Inf. Process. 2012, 11, 1107–1148. [Google Scholar] [CrossRef]
- Sadgrove, M.; Wimberger, S.; Parkins, S.; Leonhardt, R. Scaling law and stability for a noisy quantum system. Phys. Rev. E 2008, 78, 025206. [Google Scholar] [CrossRef]
- Izrailev, F.M. Simple models of quantum chaos: Spectrum and eigenfunctions. Phys. Rep. 1990, 196, 299–392. [Google Scholar] [CrossRef]
- Groiseau, C.; Gresch, A.; Wimberger, S. Quantum walks of kicked Bose? Einstein condensates. J. Phys. A: Math. Theor. 2018, 51, 275301. [Google Scholar] [CrossRef]
- Wimberger, S. Nonlinear Dynamics and Quantum Chaos: An Introduction; Graduate Texts in Physics; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C++; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Weiß, M.; Groiseau, C.; Lam, W.K.; Burioni, R.; Vezzani, A.; Summy, G.S.; Wimberger, S. Steering random walks with kicked ultracold atoms. Phys. Rev. A 2015, 92, 033606. [Google Scholar] [CrossRef]
- Asbóth, J.K. Symmetries, topological phases, and bound states in the one-dimensional quantum walk. Phys. Rev. B 2012, 86, 195414. [Google Scholar] [CrossRef]
- Ho, D.Y.H.; Gong, J. Topological effects in chiral symmetric driven systems. Phys. Rev. B 2014, 90, 195419. [Google Scholar] [CrossRef]
- Cayssol, J.; Dora, B.; Simon, F.; Moessner, R. Floquet topological insulators. Phys. Status Solidi (RRL) 2013, 7, 101–108. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Groiseau, C.; Wagner, A.; Summy, G.S.; Wimberger, S. Impact of Lattice Vibrations on the Dynamics of a Spinor Atom-Optics Kicked Rotor. Condens. Matter 2019, 4, 10. https://doi.org/10.3390/condmat4010010
Groiseau C, Wagner A, Summy GS, Wimberger S. Impact of Lattice Vibrations on the Dynamics of a Spinor Atom-Optics Kicked Rotor. Condensed Matter. 2019; 4(1):10. https://doi.org/10.3390/condmat4010010
Chicago/Turabian StyleGroiseau, Caspar, Alexander Wagner, Gil S. Summy, and Sandro Wimberger. 2019. "Impact of Lattice Vibrations on the Dynamics of a Spinor Atom-Optics Kicked Rotor" Condensed Matter 4, no. 1: 10. https://doi.org/10.3390/condmat4010010
APA StyleGroiseau, C., Wagner, A., Summy, G. S., & Wimberger, S. (2019). Impact of Lattice Vibrations on the Dynamics of a Spinor Atom-Optics Kicked Rotor. Condensed Matter, 4(1), 10. https://doi.org/10.3390/condmat4010010