Tuning Nanoscale Friction by Applying Weak Magnetic Fields to Reorient Adsorbed Oxygen Molecules
Abstract
1. Introduction
2. Experimental
3. Results
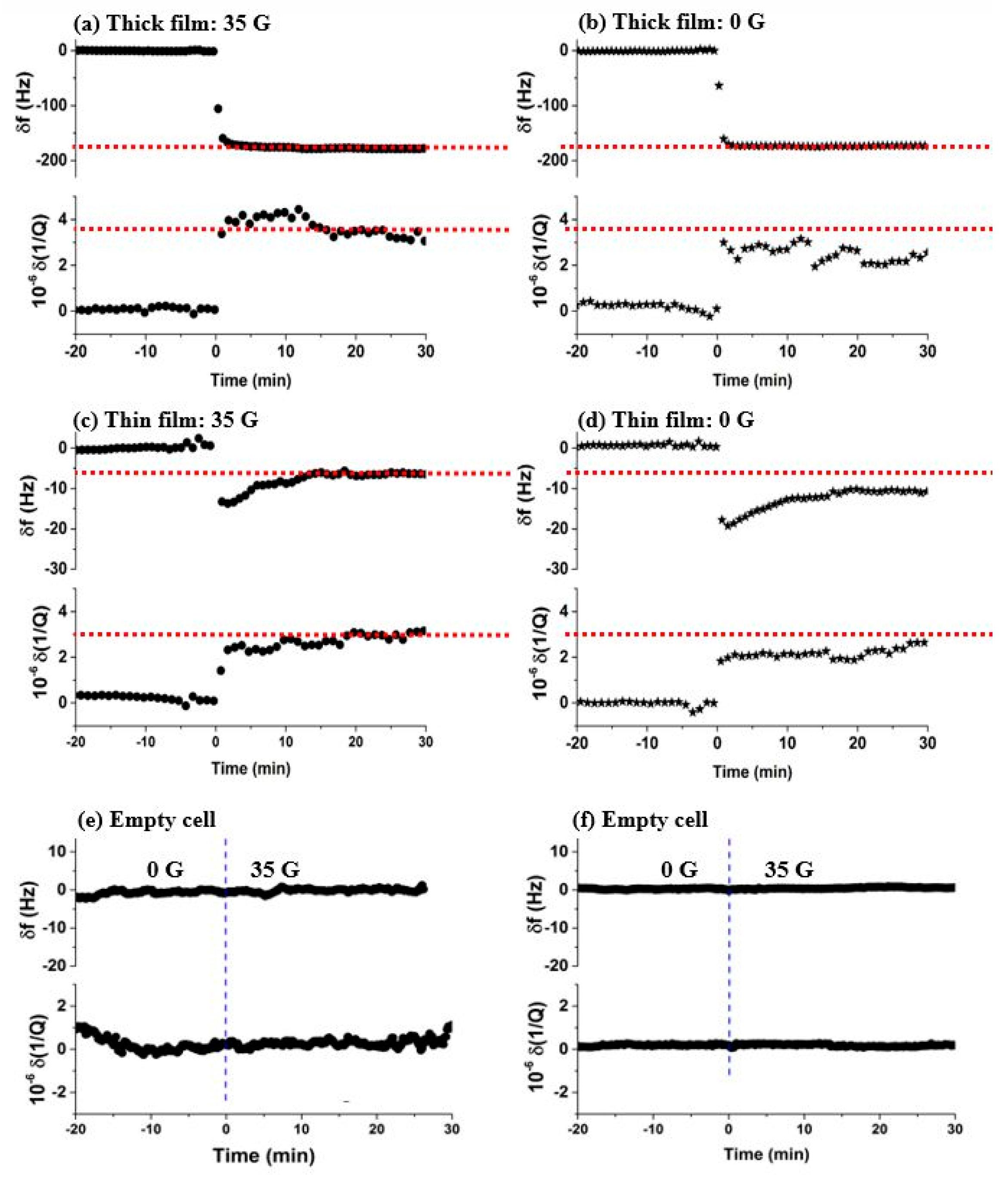
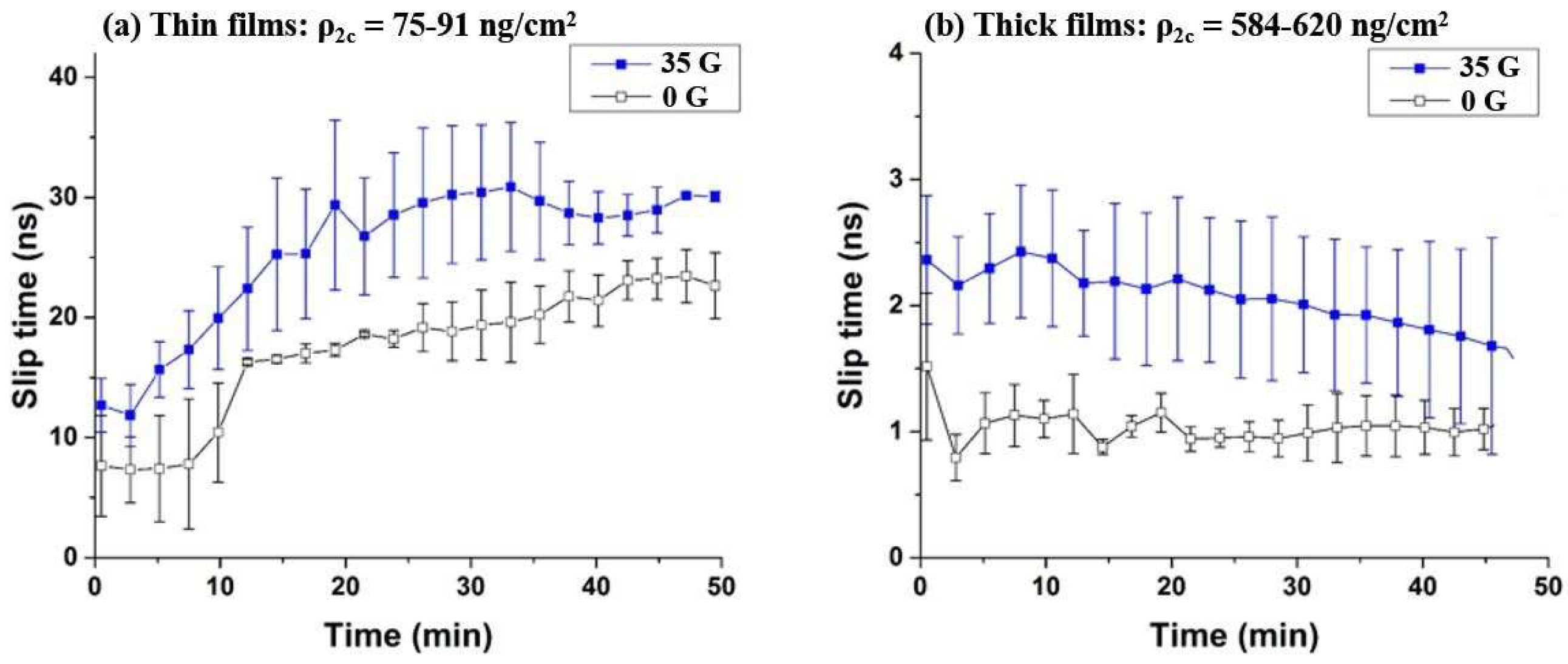
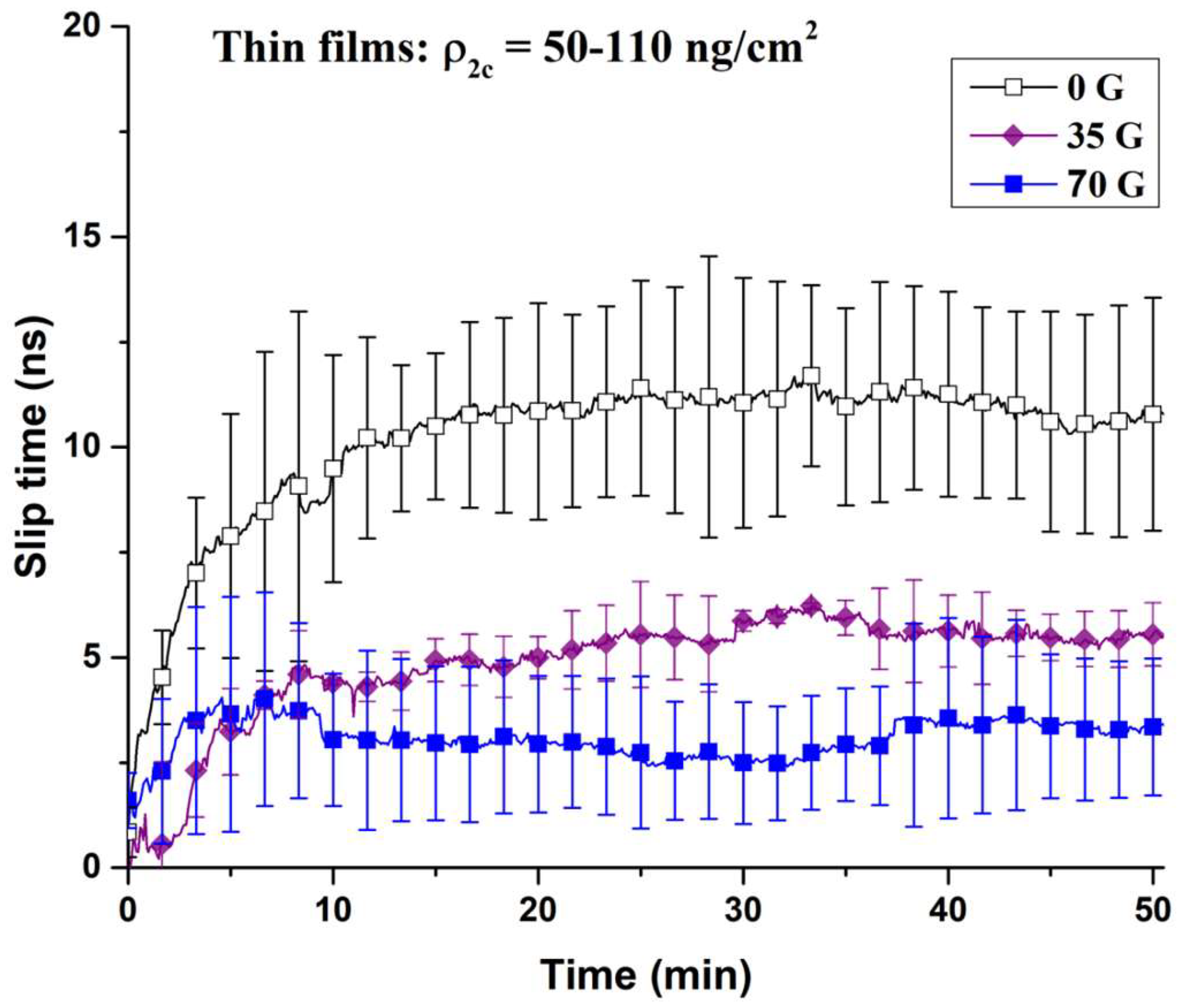
3.1. Oxygen Films on Nickel
3.2. Oxygen Films on Gold
4. Analysis of Friction Levels from Various Contribution Mechanisms.
4.1. Magnetostriction and Magnetic Spin Effects
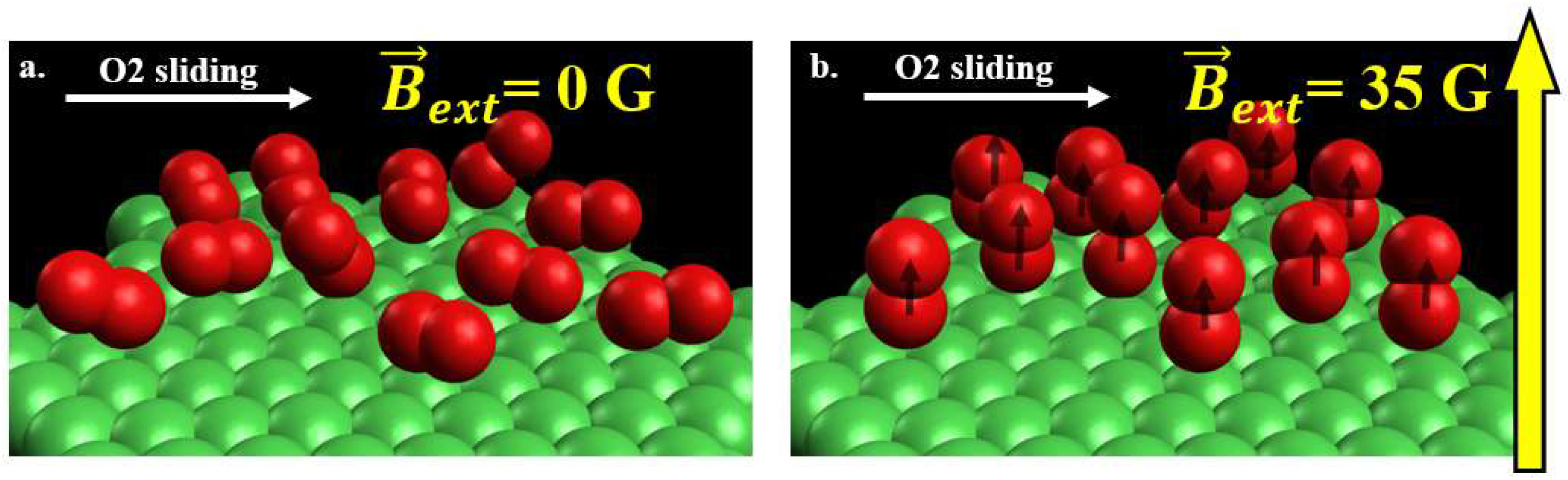
4.2. Impact of Molecular Orientation on Friction Levels.
4.3. Eddy Current and Conduction Electron Effects.
5. Summary and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Holmberg, K.; Andersson, P.; Erdemir, A. Global energy consumption due to friction in passenger cars. Tribol. Int. 2012, 47, 221–234. [Google Scholar] [CrossRef]
- Krim, J. Friction and energy dissipation mechanisms in adsorbed molecules and molecularly thin films. Adv. Phys. 2012, 61, 155–323. [Google Scholar] [CrossRef]
- Park, J.Y.; Salmeron, M. Fundamental aspects of energy dissipation in friction. Chem. Rev. 2014, 114, 677–711. [Google Scholar] [CrossRef] [PubMed]
- Robbins, M.O.; Krim, J. Energy Dissipation in Interfacial Friction. MRS Bull. 1998, 23, 23–26. [Google Scholar] [CrossRef]
- Bruch, L. Ohmic damping of center-of-mass oscillations of a molecular monolayer. Phys. Rev. B 2000, 61, 16201–16206. [Google Scholar] [CrossRef]
- Highland, M.; Krim, J. Superconductivity dependent friction of water, nitrogen, and superheated he films adsorbed on Pb(111). Phys. Rev. Lett. 2006, 96, 226107. [Google Scholar] [CrossRef]
- Persson, B.N.J. Surface resistivity and vibrational damping in adsorbed layers. Phys. Rev. B 1991, 44, 3277–3296. [Google Scholar] [CrossRef]
- Park, J.Y.; Ogletree, D.F.; Thiel, P.A.; Salmeron, M. Electronic Control of Friciton in Silicon pn junctions. Science 2006, 313, 5784. [Google Scholar] [CrossRef]
- Yao, L.; Guo, W. Spin friction in two-dimensional antiferromagnetic crystals. Phys. Rev. B 2018, 97, 104302. [Google Scholar]
- Gzik-Szumiata, M.; Szumiata, T.; Morozow, D. Modelling of Spin-Dependent Mechanical Friction at Atomic Level. Acta Phys. Pol. A 2018, 133, 713–715. [Google Scholar] [CrossRef]
- Kadau, D.; Hucht, A.; Wolf, D.E. Magnetic friction in Ising spin systems. Phys. Rev. Lett. 2008, 101, 13. [Google Scholar] [CrossRef]
- Wolter, B.; Yoshida, Y.; Kubetzka, A.; Hla, S.W.; Von Bergmann, K.; Wiesendanger, R. Spin friction observed on the atomic scale. Phys. Rev. Lett. 2012, 109, 11. [Google Scholar] [CrossRef] [PubMed]
- Lehtinen, P.O.; Foster, A.S.; Ayuela, A.; Krasheninnikov, A.; Nordlund, K.; Nieminen, R.M. Magnetic Properties and Diffusion of Adatoms on a Graphene Sheet. Phys. Rev. Lett. 2003, 91, 17202. [Google Scholar] [CrossRef] [PubMed]
- Valencia, A.M.; Caldas, M.J. Single vacancy defect in graphene: Insights into its magnetic properties from theoretical modeling. Phys. Rev. B 2017, 96, 125431. [Google Scholar] [CrossRef]
- Ouazi, S.; Kubetzka, A.; von Bergmann, K.; Wiesendanger, R. Enhanced Atomic-Scale Spin Contrast due to Spin Friction. Phys. Rev. Lett. 2014, 112, 076102. [Google Scholar] [CrossRef]
- Weinberger, B.R.; Lynds, L.; Hull, J.R.; Balachandran, U. Low friction in high temperature superconductor bearings. Appl. Phys. Lett. 1991, 59, 1132–1134. [Google Scholar] [CrossRef]
- Magiera, M.P.; Brendel, L.; Wolf, D.E.; Nowak, U. Spin waves cause non-linear friction. Europhys. Lett. 2011, 95, 17010. [Google Scholar] [CrossRef]
- Fusco, C.; Wolf, D.E.; Nowak, U. Magnetic friction of a nanometer-sized tip scanning a magnetic surface: Dynamics of a classical spin system with direct exchange and dipolar interactions between the spins. Phys. Rev. B 2008, 77, 174426. [Google Scholar] [CrossRef]
- She, J.H.; Balatsky, A.V. Noncontact friction and relaxational dynamics of surface defects. Phys. Rev. Lett. 2012, 108, 136101. [Google Scholar] [CrossRef]
- Hoffmann, B.; Houbertz, R.; Hartmann, U. Eddy current microscopy. Appl. Phys. 1998, 66, 409–413. [Google Scholar] [CrossRef]
- Gabureac, M.; Viret, M.; Ott, F.; Fermon, C. Magnetoresistance in nanocontacts induced by magnetostrictive effects. Phys. Rev. B 2004, 69, 2–5. [Google Scholar] [CrossRef]
- Nielsen, M.; McTague, J.P. Oxygen monolayers adsorbed on graphite studied by neutron scattering. Phys. Rev. B 1979, 19, 3096–3106. [Google Scholar] [CrossRef]
- Barylnik, A.S.; Prokhvatilov, A.I. Spontaneous magnetostriction effects in alpha-phases and beta-phases of oxygen. Fiz. Nizk. Temp. 1994, 20, 912–917. [Google Scholar]
- Chen, C.Y.; Hong, C.Y.; Wang, S.W. Magnetic flows in a tube with the effects of viscosity variation. J. Magn. Magn. Mater. 2002, 252, 253–255. [Google Scholar] [CrossRef]
- Murakami, Y.; Suematsu, H. Magnetic and melting transitions of oxygen monolayers and multilayers physisorped on exfoliated graphite. Phys. Rev. B 1996, 54, 4146–4154. [Google Scholar] [CrossRef]
- Altman, I.S.; Pikhitsa, P.V.; Kim, Y.-J.; Choi, M. Magnetism of adsorbed oxygen at low coverage. Phys. Rev. B 2003, 67, 144410. [Google Scholar] [CrossRef]
- Marx, R.; Christoffer, B. Magnetocaloric effects of 2D adsorbed O2. J. Phys. C 1985, 18, 2849–2858. [Google Scholar] [CrossRef]
- Bhethanabotla, V.R.; Steele, W.A. Computer-simulation study of melting in dense oxygen layers on graphite. Phys. Rev. B 1990, 41, 9480–9487. [Google Scholar] [CrossRef]
- Krim, J.; Coulomb, J.P.; Bouzidi, J. Triple-point wetting and surface melting of oxygen films adsorbed on graphite. Phys. Rev. Lett. 1987, 58, 583–586. [Google Scholar] [CrossRef] [PubMed]
- Chiarello, R.; Coulomb, J.P.; Krim, J.; Wang, C.L. Surface melting of multilayer oxygen films on graphite studied by neutron diffraction. Phys. Rev. B 1988, 38, 8967–8973. [Google Scholar] [CrossRef]
- Bhethanabotla, V.; Steele, W. Simulations of O2 adsorbed on graphite at 45 K: The monolayer to bilayer transition. Can. J. Chem. 1988, 66, 866–874. [Google Scholar] [CrossRef]
- Ulbricht, H.; Moos, G.; Hertel, T. Physisorption of molecular oxygen on single-wall carbon nanotube bundles and graphite. Phys. Rev. B 2002, 66, 75404. [Google Scholar] [CrossRef]
- Aoki, M.; Taoka, H.; Kamada, T.; Masuda, S. Local electronic states of oxygen on a Ni(111) surface studied by metastable atom electron spectroscopy. J. Electron Spectrosc. Relat. Phenom. 2001, 114–116, 507–512. [Google Scholar] [CrossRef]
- Yamagishi, S.; Jenkins, S.J.; King, D.A. First principles studies of chemisorbed O on Ni{1 1 1}. Surf. Sci. 2003, 543, 12–18. [Google Scholar] [CrossRef]
- Kazama, Y.; Matsumoto, M.; Sugimoto, T.; Okano, T.; Fukutani, K. Low-temperature surface phase and phase transition of physisorbed oxygen on the Ag(111) surface. Phys. Rev. B 2011, 84, 064128. [Google Scholar] [CrossRef]
- Kurahashi, M.; Sun, X.; Yamauchi, Y. Magnetic properties of O2 adsorbed on Cu(100): A spin polarized metastable He beam study. Phys. Rev. B 2012, 86, 245421. [Google Scholar] [CrossRef]
- Gnecco, E.; Meyer, E. (Eds.) Fundamentals of Friction and Wear on the Nanoscale; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Daly, C.; Krim, J. Sliding Friction of Solid Xenon Monolayers and Bilayers on Ag(111). Phys. Rev. Lett. 1996, 76, 803–806. [Google Scholar] [CrossRef]
- Johannsmann, D. Viscoelastic, mechanical, and dielectric measurements on complex samples with the quartz crystal microbalance. Phys. Chem. Chem. Phys. 2008, 10, 4516. [Google Scholar] [CrossRef]
- Krim, J.; Widom, A. Damping of a crystal oscillator by an adsorbed monolayer and its relation to interfacial viscosity. Phys. Rev. B 1988, 38, 12184–12189. [Google Scholar] [CrossRef]
- Watts, E.T.; Krim, J.; Widom, A. Experimental observation of interfacial slippage at the boundary of molecularly thin films with gold substrates. Phys. Rev. B 1990, 41, 3466–3472. [Google Scholar] [CrossRef]
- Sokoloff, J.B.; Krim, J.; Widom, A. Determination of an atomic-scale frictional force law through quartz-crystal microbalance measurements. Phys. Rev. B 1993, 48, 9134–9137. [Google Scholar] [CrossRef]
- Hanke, S.; Petri, J.; Johannsmann, D. Partial slip in mesoscale contacts: Dependence on contact size. Phys. Rev. E 2013, 88, 32408. [Google Scholar] [CrossRef] [PubMed]
- Smith, E.D.; Robbins, M.O.; Cieplak, M. Friction on adsorbed monolayers. Phys. Rev. B 1996, 54, 8252–8260. [Google Scholar] [CrossRef]
- Tomassone, M.S.; Sokoloff, J.B.; Widom, A.; Krim, J. Dominance of Phonon Friction for a Xenon Film on a Silver(111) Surface. Phys. Rev. Lett. 1997, 79, 4798–4801. [Google Scholar] [CrossRef]
- Franchini, A.; Bortolani, V.; Santoro, G.; Brigazzi, M. Sliding friction of N 2 on Pb(111). J. Phys. Condens. Matter 2010, 22, 304002. [Google Scholar] [CrossRef]
- Mak, C.; Krim, J. Quartz-crystal microbalance studies of the velocity dependence of interfacial friction. Phys. Rev. B 1998, 58, 5157–5159. [Google Scholar] [CrossRef]
- Bruschi, L.; Carlin, A.; Mistura, G. Depinning of Atomically Thin Kr Films on Gold. Phys. Rev. Lett. 2002, 88, 46105. [Google Scholar] [CrossRef]
- Reviakine, I.; Morozov, A.N.; Rossetti, F.F. Effects of finite crystal size in the quartz crystal microbalance with dissipation measurement system: Implications for data analysis. J. Appl. Phys. 2004, 95, 7712–7716. [Google Scholar] [CrossRef]
- Cassiède, M.; Paillol, J.H.; Pauly, J.; Daridon, J.-L. Electrical behaviour of AT-cut quartz crystal resonators as a function of overtone number. Sens. Actuators A Phys. 2010, 159, 174–183. [Google Scholar] [CrossRef]
- Edwards, R.L. The magnetic properties of evaporated nickel and iron films. Phys. Rev. 1927, 29, 321–331. [Google Scholar] [CrossRef]
- Sorensen, A.J. Magnetic Properties of Thin Films of Ferromagnetic Metals Produced by the Evaporation Method. Phys. Rev. 1924, 24, 658–665. [Google Scholar] [CrossRef]
- Mittendorfer, F.; Eichler, A.; Hafner, J. Structural, electronic and magnetic properties of nickel surfaces. Surf. Sci. 1999, 423, 1–11. [Google Scholar] [CrossRef]
- Bruschi, L.; Fois, G.; Pontarollo, A.; Mistura, G.; Torre, B.; de Mongeot, F.B.; Boragno, C.; Buzio, R.; Valbusa, U. Structural depinning of Ne monolayers on Pb at T < 6.5 K. Phys. Rev. Lett. 2006, 96, 216101. [Google Scholar] [PubMed]
- Bruschi, L.; Pierno, M.; Fois, G.; Ancilotto, F.; Mistura, G.; Boragno, C.; de Mongeot, F.B.; Valbusa, U. Friction reduction of Ne monolayers on preplated metal surfaces. Phys. Rev. B 2010, 81, 115419. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Blundell, S.; Thouless, D. Magnetism in Condensed Matter. Am. J. Phys. 2003, 71, 94. [Google Scholar] [CrossRef]
- Toney, M.F.; Fain, S.C. Low-energy electron diffraction determination of the structure of the phase of oxygen physisorbed on graphite. Phys. Rev. B 1984, 30, 1115–1118. [Google Scholar] [CrossRef]
- Freiman, Y.A.; Jodl, H.J. Solid oxygen. Phys. Rep. 2004, 401, 1–4. [Google Scholar] [CrossRef]
- Toney, M.F.; Fain, S.C. Low-energy electron diffraction study of molecular oxygen physisorbed on graphite. Phys. Rev. B 1987, 36, 1248–1258. [Google Scholar] [CrossRef]
- Herzberg, G. Molecular Spectra and Molecular Structure I. Diatomic Molecules; Prentice Hall: New York, NY, USA, 1966. [Google Scholar]
- Coffey, T.; Krim, J. Impact of substrate corrugation on the sliding friction levels of adsorbed films. Phys. Rev. Lett. 2005, 95, 076101. [Google Scholar] [CrossRef] [PubMed]
- Rose, J.H.; Tai, C.C.; Moulder, J.C. Extreme sensitivity of eddy-currents to the surface conditions of nickel. In Review of Progress in Quantitative Nondestructive Evaluation; Springer: Boston, MA, USA, 1997; pp. 249–255. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fredricks, Z.B.; Stevens, K.M.; Kenny, S.G.; Acharya, B.; Krim, J. Tuning Nanoscale Friction by Applying Weak Magnetic Fields to Reorient Adsorbed Oxygen Molecules. Condens. Matter 2019, 4, 1. https://doi.org/10.3390/condmat4010001
Fredricks ZB, Stevens KM, Kenny SG, Acharya B, Krim J. Tuning Nanoscale Friction by Applying Weak Magnetic Fields to Reorient Adsorbed Oxygen Molecules. Condensed Matter. 2019; 4(1):1. https://doi.org/10.3390/condmat4010001
Chicago/Turabian StyleFredricks, Z. B., K. M. Stevens, S. G. Kenny, B. Acharya, and J. Krim. 2019. "Tuning Nanoscale Friction by Applying Weak Magnetic Fields to Reorient Adsorbed Oxygen Molecules" Condensed Matter 4, no. 1: 1. https://doi.org/10.3390/condmat4010001
APA StyleFredricks, Z. B., Stevens, K. M., Kenny, S. G., Acharya, B., & Krim, J. (2019). Tuning Nanoscale Friction by Applying Weak Magnetic Fields to Reorient Adsorbed Oxygen Molecules. Condensed Matter, 4(1), 1. https://doi.org/10.3390/condmat4010001





