You are currently on the new version of our website. Access the old version .
MDPIMDPI
Search all articles
Condensed MatterCondensed Matter
Download PDF
  • Review
  • Open Access

20 December 2018

Nematic Superconductivity in Doped Bi2Se3 Topological Superconductors

Department of Physics, Graduate School of Science, Kyoto University, Kyoto 606-8502, Japan
Condens. Matter2019, 4(1), 2;https://doi.org/10.3390/condmat4010002
This article belongs to the Special Issue Majorana Fermions and Topological Materials Science
Version Notes
Order Reprints

Abstract

Nematic superconductivity is a novel class of superconductivity characterized by spontaneous rotational-symmetry breaking in the superconducting gap amplitude and/or Cooper-pair spins with respect to the underlying lattice symmetry. Doped Bi 2 Se 3 superconductors, such as Cu x Bi 2 Se 3 , Sr x Bi 2 Se 3 , and Nb x Bi 2 Se 3 , are considered as candidates for nematic superconductors, in addition to the anticipated topological superconductivity. Recently, various bulk probes, such as nuclear magnetic resonance, specific heat, magnetotransport, magnetic torque, and magnetization, have consistently revealed two-fold symmetric behavior in their in-plane magnetic-field-direction dependence, although the underlying crystal lattice possesses three-fold rotational symmetry. More recently, nematic superconductivity was directly visualized using scanning tunneling microscopy and spectroscopy. In this short review, we summarize the current research on the nematic behavior in superconducting doped Bi 2 Se 3 systems and discuss issues and perspectives.

1. Introduction

In the last decade, the research field on topological materials, which possess a non-trivial topology in their electronic-state wave functions in the reciprocal space, has been expanding substantially [1,2,3]. As a counterpart of topological insulators, it has been recognized that certain superconductors can have a non-trivial topological nature in their wavefunctions [2,4,5]. Superconductivity with such a non-trivial wavefunction topology is now called topological superconductivity. It has been predicted that topological superconductivity can lead to various novel phenomena. In particular, the Majorana quasiparticles with non-Abelian zero-energy modes, hosted in topologically-protected edge states or vortex cores, are quite intriguing [6]. The realization and utilization of such Majorana modes comprise one of the holy grails of this research field.
There are a number of superconductors that seemingly exhibit topological superconductivity in bulk [7]. Such bulk topological superconductors are the prototype of topological superconductivity, although there are now other recipes to induce topological superconductivity by making use of the proximity effect. Recently, a candidate for a bulk topological superconductor, doped Bi 2 Se 3 , has been found to exhibit unusual rotational-symmetry breaking in the superconducting (SC) gap amplitude, as well as in the SC spin degree of freedom [8,9,10,11]. This phenomena, called “nematic” superconductivity [12], has been attracting much attention as a new species in the superconductor zoo, accompanied by a novel class of symmetry breaking in its SC wave function. The shape and topology of the SC wave function are closely related. Indeed, in A x Bi 2 Se 3 , it is theoretically known that the nematic superconductivity is accompanied by a non-trivial topological SC gap [5,13,14,15]. Therefore, these new experimental observations of the nematic SC gap and spin have been providing firm bulk evidence for topological superconductivity, and thus establish strong bases toward realization and manipulation of Majorana states in this class of compounds.
In this short review, we summarize recent observations of the nematic behavior in superconducting doped Bi 2 Se 3 systems. After a brief introduction of nematic superconductivity in Section 2, we explain experimental and theoretical understandings of superconductivity in A x Bi 2 Se 3 in Section 3. Section 4 is devoted to explaining recent experimental findings of nematic superconductivity. Then, we discuss several known issues in Section 5, before summarizing the content in Section 6.

2. Nematic Superconductivity: Rotational Symmetry Breaking in the Gap Amplitude

2.1. Symmetry Breaking in Superconductivity

The concept of spontaneous symmetry breaking has fundamental importance in superconductivity. In the Bardeen–Cooper–Schrieffer (BCS) theory [16], the SC state spontaneously breaks the U ( 1 ) gauge symmetry, even for the ordinary s-wave superconductivity (Figure 1a). It has been then an interesting and long-standing question whether SC states with additional symmetry breaking exist or not. Such superconductivity with additional symmetry breaking is called unconventional superconductivity.
Figure 1. Schematic comparison of various known superconductivity and gap/spin nematic superconductivity, for the case of a tetragonal-lattice system.
For example, superconductivity with spontaneous time-reversal symmetry breaking in the orbital part of the SC order parameter (Figure 1b) is called as “chiral” superconductivity and is believed to be realized in several materials such as Sr 2 RuO 4 [17,18], URu 2 Si 2 [19,20], and UPt 3 [21]. Odd parity superconductivity, which exhibits π phase shift under spacial inversion (see again Figure 1b), has been an interesting topic for fairly a long time [22,23]. Odd-parity superconductivity (and superfluidity) is confirmed in superfluid 3 He [24,25] and is very probably realized in Sr 2 RuO 4 [26,27,28] and UPt 3 [29]. Moreover, odd-parity superconductivity is now recognized as a key ingredient to realize topological superconductivity [13,30].
Another fundamentally important symmetry is rotational symmetry. The symmetry behavior under rotation provides a basis of the classification of superconductivity into s-wave, p-wave, d-wave, f-wave, etc. However, the infinitesimal rotational symmetry C ∞ is already broken in superconductors because of the crystal lattice. Thus, in reality, what actually matters is the breaking/invariance of the discrete C n rotational symmetry of the underlying lattice. For example, in d-wave superconductivity in a tetragonal system (Figure 1c), the phase factor for one k direction and for its perpendicular direction differs by π . Therefore, the four-fold rotation C 4 symmetry is broken in the phase factor of the SC order parameter.

2.2. Gap-Nematic and Spin-Nematic Superconductivity

Such a rotational symmetry breaking in the phase degree of freedom in non-s-wave superconductivity is intriguing, but the experimental detection of such symmetry breaking is actually very difficult. This is because the SC gap amplitude, which governs most of the superconducting properties, is actually invariant under the C n rotation. To detect the rotational symmetry breaking in the phase factor, one has to utilize sophisticated interference techniques, as performed in cuprate d-wave superconductors [31,32]. In contrast, if the rotational-symmetry breaking occurs in the SC gap amplitude as shown in Figure 1d, the rotational symmetry breaking would be more robust and be detectable in principle in any bulk quantities. Such superconductivity with broken rotational symmetry in the gap amplitude was named as “nematic superconductivity” first by Fu [12] and has been attracting much attention as a new class of superconductivity accompanied by a novel spontaneous symmetry breaking.
The word “nematic”, originally used in the research field of liquid crystals, refers to the states with the spontaneous rotational symmetry breaking of the bar-shaped liquid crystal molecules, but without breaking the translational symmetry. Now, this word is imported to solid-state physics, and the “nematic electron liquid” with spontaneous rotational symmetry breaking in the conduction electron without losing conductivity has been attracting much attention and has actually been found in various systems such as cuprates [33,34], iron pnictides [35,36], and a ruthenate [37]. The nematic superconductivity is a superconducting version of such nematic electron liquids, but occurring as a consequence of Cooper-pair formation.
In the case of spin-triplet superconductivity, the spin part of the order parameter, i.e., the d vector, can also exhibit rotational symmetry breaking. Here, we should be careful that there are two different levels of the spin-rotational-symmetry breaking. Firstly, the S O ( 3 ) symmetry of the spin space breaks in the presence of spin-orbit interaction. In this case, the spin susceptibility exhibits anisotropic behavior, but still obeys the symmetry of the lattice. This first kind of spin-rotational symmetry breaking has not been observed in a leading candidate spin-triplet superconductor Sr 2 RuO 4 [38] and was weakly observed in another candidate UPt 3 [39]. A more exotic phenomenon is that the spin part even breaks the C n lattice rotational symmetry (but without spin polarization). In this case, spin susceptibility exhibits rotational-symmetry breaking, as schematically shown in Figure 1e. We shall call this phenomenon “spin-nematic superconductivity”; and to distinguish it, the nematic superconductivity with the rotational symmetry breaking in the gap amplitude is called “gap-nematic superconductivity” in this review. Spin-nematic superconductivity has never been known in any material before its discovery in Cu x Bi 2 Se 3 [8].

3. Superconductivity in Doped Bi 2 Se 3

In this section, SC and normal-state properties of doped Bi 2 Se 3 , as well as theoretically-proposed SC states are described. For more detailed information, refer to the nice reviews found in [5,14,15].

3.1. Crystal Structure of the Mother Compound Bi 2 Se 3

Bi 2 Se 3 , the mother compound of the doped Bi 2 Se 3 superconductors, has been extensively studied as a prototypical topological insulator [40,41]. This compound has a rhombohedral (or trigonal) crystal structure, as shown in Figure 2, with the space group of R 3 ¯ m ( D 3 d 5 ) [42]. The crystal structure contains three equivalent a axes. Strictly speaking, the situations with H parallel to the a axis and − a axis are different because of the trigonal symmetry and the pseudo-vector nature of the magnetic field. Nevertheless, practically, H ∥ a and H ∥ ( − a ) are almost equivalent in most cases, and thus, many physical quantities are expected to exhibit pseudo-six-fold rotational symmetry as a function of the in-plane field direction. The a ∗ axis is perpendicular to the a axis within the a b plane. Importantly, the a ∗ -c plane is a mirror-symmetry plane, whereas the a-c plane is not, as clearly seen in Figure 2b. This existence/absence of the mirror symmetry is closely related to the stability of the gap nodes in the nematic SC state, as will be discussed in Section 3.3. Throughout this paper, we define the x axis along one of the three a axes. In most cases, we choose x to be along the “special” a axis due to the nematic SC order (e.g., the a axis with maximal or minimal H c 2 ). Then, the y axis is defined so that it is perpendicular to the x axis within the a b plane, as explained in Figure 2b.
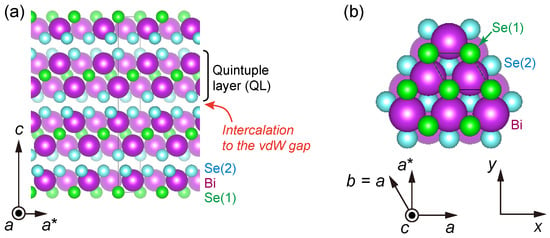
Figure 2. Schematic description of the crystal structure of the mother compound Bi 2 Se 3 [42]. The purple spheres are the Bi atoms, and the green and light-blue spheres are the Se(1) and (2) atoms, respectively. The colors of the spheres are modified depending on the depth along the view direction: atoms closer to the view point have thicker colors. (a) View from the a axis direction. The intercalated metallic ions most likely sit in the van der Waals (vdW) gap between the quintuple layers (QL). (b) View from the c axis direction. The crystal structure figures were made using the software VESTA-3 [44].
The crystal structure consists of Se-Bi-Se-Bi-Se layers, as shown in Figure 2a. This set of layers is called the quintuple layer (QL). Between the QLs, there is a van-der Waals (vdW) gap, through which metallic ions penetrate the sample during the synthesis process. Thus, the ions are most likely to be intercalated into a certain site within the vdW gap. For Sr-doped Bi 2 Se 3 , Sr ions may also sit in an interstitial site [43]. The precise position of the doped ions, in particular that for superconducting samples, has not been fully clarified.

3.2. Basic Properties of Doped Bi 2 Se 3 Superconductors

In 2010, the pioneering work by Hor et al. revealed that Cu x Bi 2 Se 3 exhibits superconductivity below the critical temperature T c of around 3 K [45]. This is truly the beginning of the research field of superconducting doped Bi 2 Se 3 systems, but the initial samples grown by the ordinary melt-grown technique exhibited a superconducting shielding fraction of about 20% and did not show complete vanishing of resistivity. One year later, Kriener et al. found that, with the electrochemical intercalation of Cu and with a suitable annealing process, Cu x Bi 2 Se 3 indeed exhibits bulk superconductivity with clear zero resistivity and volume fractions reaching 60–70% evaluated from specific-heat and magnetization measurements [46,47]. In 2015, Sr doping or Nb doping were also found to drive Bi 2 Se 3 to superconduct, with T c again around 3 K [48,49,50]. In contrast to the Cu-doped material, Sr x Bi 2 Se 3 and Nb x Bi 2 Se 3 exhibit bulk superconductivity with a fairly large shielding fraction close to 100% even with melt-grown samples.
These three compounds exhibit similar SC behavior, but there are several significant differences, as well. Firstly, the normal-state electronic state is different. In Cu x Bi 2 Se 3 , an ellipsoidal or cylindrical Fermi surface, depending on the carrier density, has been revealed by angle-resolved photoemission spectroscopy (ARPES) and quantum oscillation experiments [51]. Superconducting Cu x Bi 2 Se 3 typically has a carrier density n of around 10 20 cm − 3 [45,46,51]. Furthermore, n is known to be rather insensitive to the Cu concentration [47]. In Sr x Bi 2 Se 3 , n tends to be even lower than that in Cu x Bi 2 Se 3 : n for superconducting Sr x Bi 2 Se 3 is consistently reported to be ∼2 × 10 19 cm − 3 [48,49]. For Nb x Bi 2 Se 3 , the quantum oscillation consists of oscillations with different frequencies and with different field-angular dependence, indicating that the Fermi surface is not a simple ellipsoid or cylinder, but is composed of multiple pockets [52]. This is crucially different from the single Fermi surface in Cu x Bi 2 Se 3 and Sr x Bi 2 Se 3 . In addition, Nb x Bi 2 Se 3 has some controversy on the magnetism: in the initial report, it was argued that Nb x Bi 2 Se 3 exhibits long-range magnetic order in the superconducting state and that this magnetic order assists the formation of a chiral SC state [50]. In later reports, however, such magnetism has not been reported [11,53]. Secondly, a practical difference among the three compounds is that Sr x Bi 2 Se 3 and Nb x Bi 2 Se 3 are stable in air, whereas superconductivity in Cu x Bi 2 Se 3 is known to diminish if a sample is kept in air [45]. We should comment here that single-crystalline Cu x Bi 2 Se 3 prepared by electrochemical intercalation might not be as air-sensitive as melt-grown samples [54]. Because of the higher stability, Sr and Nb-doped Bi 2 Se 3 have been extensively studied since their discoveries, as reviewed below.
The normal-state electronic state of Cu x Bi 2 Se 3 was investigated with ARPES and quantum oscillation experiments [51]. It was found that the electronic band structure of Cu x Bi 2 Se 3 is essentially the same as that of Bi 2 Se 3 and that the surface state originating from the topological-insulator nature of Bi 2 Se 3 still exists even after the Cu doping. As expected, Cu x Bi 2 Se 3 is heavily electron doped compared to the mother compound: the chemical potential is located 0.2–0.5 eV above the Dirac point of the topological surface state. Still, the surface state was clearly observed even at the chemical potential, well distinguishable from the bulk band. This means that the bulk conduction electrons on the Fermi surface of Cu x Bi 2 Se 3 inherit the “twisted” nature of the bulk electronic state of the mother compound. Once superconductivity sets in, the Cooper pairs are formed among bulk electrons in such a non-trivial topological state. Such a situation is favorable for the realization of odd-parity and topological SC states even for simple pairing interactions, as described in the next subsection. The preserved topological-insulator surface state after doping was also confirmed in Sr x Bi 2 Se 3 via quantum oscillation and scanning tunneling microscope (STM) experiments [48,55]

3.3. Possible Superconducting States

Just after the discovery of superconductivity in Cu x Bi 2 Se 3 [45], Fu et al. performed theoretical analysis on possible SC states realized in this compound [13]. The result is quite surprising since odd-parity topological superconductivity was predicted even with a simple pairing interaction. Previously, it had been believed that an unconventional pairing glue such as ferromagnetic spin fluctuation is required to realize bulk odd-parity superconductivity. Very naively, the odd-parity superconductivity in this model originates from strong orbital mixing on the Fermi surface; when a Cooper pair is formed among electrons in different orbitals, odd-parity superconductivity is rather easily realized.
Let us review the result of this theory in a bit more detail. Fu et al. considered the D 3 d point group of Bi 2 Se 3 and assumed Cooper pairing of electrons in two p z orbitals localized nearly at the top and bottom of a QL. On the other hand, the pairing interaction was assumed to be point-like. Then, six possible pairing states Δ 1 a , Δ 1 b , Δ 2 , Δ 3 , Δ 4 x , and Δ 4 y were proposed as listed in Table 1. Here, the pairing potential in the orbital bases is expressed with Pauli matrices in the orbital and spin spaces, σ μ and s μ ( μ = x , y , z ); thus, those with off-diagonal terms in the orbital matrices σ , i.e., those containing σ x or σ y , are inter-orbital pairing states, and σ y characterizes an orbital-singlet state [15]. Among them, Δ 1 a and Δ 1 b are even-parity states, and the others, Δ 2 , Δ 3 , Δ 4 x , and Δ 4 y , are the odd-parity states. All of these odd-parity states belong to topological superconductivity, because odd-parity superconductivity is proven to have a non-trivial topological nature if the Fermi surface encloses an odd number of high-symmetry points in the Brillouin zone [13,30]. The states Δ 2 , Δ 4 x , and Δ 4 y contain s matrices in the pairing potential and thus are fundamentally spin-triplet SC states even in the absence of the spin-orbit interaction. In contrast, Δ 3 in the absence of the spin-orbit interaction is a spin-singlet state in spite of the odd-parity nature (notice that d = 0 for λ = 0 ), since the Pauli principle is satisfied together with the orbital degree of freedom [56]. Nevertheless, with finite spin-orbit interaction, Δ 3 , also acquires the spin-triplet nature.
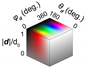
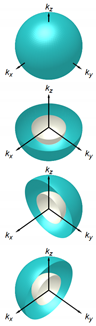
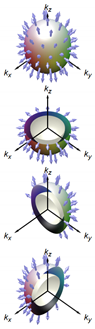
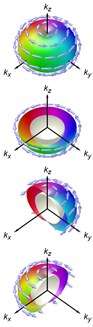
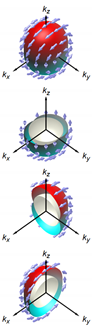
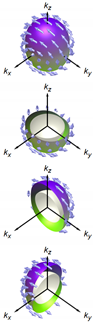
Table 1. Proposed superconducting states for doped Bi 2 Se 3 [13,14,15,56,57]. The d vector structures in the band bases are from [56,57]. Here, λ represents the strength of the spin-orbit coupling; and ε represents the gap minima for the Δ 4 y state (see the text). In the bottom row, schematic gap and d-vector structures of each state are shown, together with various cut views. The λ value is chosen to be 0.5, and the ε value is just set to be 0.1. The sphere at the center of a cut view is the Fermi surface. The gap structure is expressed with colored surfaces, whose distance from the Fermi surface corresponds to the SC gap amplitude | d | normalized by its maximal value d 0 . The color of this surface also depicts the gap value, as well as the d-vector direction, as explained in the left bottom cell: The hue and lightness of the color indicate the azimuthal and polar angles of the d vector, ϕ d and θ d , respectively; whereas the grayness of the color depicts the normalized gap, with 50% gray corresponding to | d | = 0 .
To evaluate the SC-gap and d -vector structures in the reciprocal space, the pair potential in the orbital bases has to be converted to the SC order parameter in the band bases. In the work by Hashimoto et al. [56,57], the d vector for the lowest order in k was evaluated as listed in Table 1. Here, the d vector depends on the ratio λ between the spin-orbit interaction (denoted as v in [56]) and the coefficient v z describing the k z -linear term in the bulk electronic band dispersion. These values are estimated to be v = 4.1 eV Å and v z = 9.5 eV Å [40,56,57]; thus, λ is roughly 0.5. In addition, there is a small gapping term ε to express the disappearance of the point nodes in the Δ 4 y pairing [12]. Experimentally, this term is expected to be fairly small [9]. In the bottom row of Table 1, the d vector structure in the k space, as well as the gap | d ( k ) | are schematically shown for a spherical Fermi surface and with the parameters λ = 0.5 and ε = 0.1 . The d -vector structure of each odd-parity state has a complicated texture on the Fermi surface, being similar to the d -vector structure in the Balian–Werthamer (BW) state (the B phase of superfluid 3 He) [23], but quite different from a k-uniform d vector in, e.g., Sr 2 RuO 4 [26,27].
One can easily notice in the figures that the Δ 4 x and Δ 4 y states have quite characteristic gap structures: The Δ 4 x state has a pair of point nodes ( | d ( k ) | = 0 ) along the ± k y direction and Δ 4 y has a pair of point-like gap minima along the ± k x direction. This existence of a pair of gap node/minima violates the C 3 rotational symmetry of the crystal structure of Bi 2 Se 3 . Thus, the Δ 4 x and Δ 4 y states are both gap-nematic SC states. The nodes in Δ 4 x are protected by the mirror symmetry along the a ∗ -c plane, whereas the nodes initially existing in Δ 4 y are gapped out to become gap minima because there is no symmetry protecting the nodes [12]. In addition to the gap amplitude, the d -vector structures of these Δ 4 states also have nematic natures: On the whole Fermi surface, the d vectors preferentially align along the k x direction in the Δ 4 x state and along the k y direction in the Δ 4 y state. Reminding that a d vector is perpendicular to the Cooper-pair spin and the spin susceptibility should be small along the d vector, it is expected that the spin susceptibility of the Δ 4 states exhibits a two-fold behavior, with minima along the x direction for Δ 4 x and y for Δ 4 y [56]. Thus, the Δ 4 x and Δ 4 y states are spin nematic as well.
We should comment on the robustness of the proposed odd-parity states against non-magnetic impurity scattering. Ordinarily, unconventional superconductivity is rather fragile against non-magnetic impurity scatterings, and such a strong reduction of superconductivity has been found in various non-s-wave superconductors [58,59,60,61]. In doped Bi 2 Se 3 superconductors, because of the ion doping, impurity scattering is inevitably stronger than those of stoichiometric unconventional superconductors and can suppress the predicted odd-parity ( Δ 2 , Δ 3 , and Δ 4 ) states. However, theories by Michaeli et al. [62] and Nagai et al. [63] proposed that these odd-parity states are rather robust against impurity scatterings because of strong spin-momentum locking in the normal-state Fermi surface. Thus, odd-parity superconductivity itself, as well as the nodal gap structure can still be stable in doped Bi 2 Se 3 .

3.4. Early Experiments on the Superconducting State in Doped Bi 2 Se 3

After the discovery of superconductivity in Cu x Bi 2 Se 3 , various experiments were performed on the SC nature of this compound. As a bulk probe, the temperature dependence of the electronic specific heat of Cu x Bi 2 Se 3 was studied and was found to be different from the ordinary weak-coupling BCS behavior [46]. A theoretical calculation revealed that this T dependence can be fitted well either with Δ 2 - or Δ 4 -state models [56]. Anomalous suppression of the superfluid density evaluated from the lower critical field H c 1 upon the change of the amount of Cu has been also attributed to the topological superconducting nature [64]. The T dependence of the upper critical field H c 2 was investigated, and from the shape of the H c 2 ( T ) curve, the possibility of unconventional pairing was claimed [65]. However, in general, the shape of a H c 2 ( T ) curve can vary merely due to changes in the Fermi-surface shape [66].
Several surface-sensitive experiments, seeking for topological Majorana surface states, were also performed. The soft-point-contact spectroscopy was the first experiment revealing the possible topological nature of the SC state [67]. A zero-bias peak in the differential conductivity as a function of the bias voltage was found, and was attributed to topologically-protected surface states. Indeed, a theoretical calculation revealed that the observed conductivity is consistent with the odd-parity states [68]. However, shortly after, an STM study on Cu x Bi 2 Se 3 was performed, and spectra resembling those of fully-gapped s-wave superconductivity were observed. This apparent discrepancy may be due to the dimensionality of the system: if the Fermi surface of Cu x Bi 2 Se 3 is a quasi-two-dimensional cylinder rather than an ellipsoid (as indeed suggested by the ARPES and quantum oscillation experiment [51]), an STM spectrum on the a b surface should be indistinguishable from the ordinary s-wave behavior. In contrast, a soft-point contact spectroscopy is expected to collect a certain average of conductivity of various directions, resulting in detecting the zero-bias anomaly in the a b -plane conductivity. It was also claimed that STM spectra for s-wave superconductivity with an ellipsoidal Fermi surface should form a double peak structure, one originating from the coherence peak of the s-wave gap and the other from the surface state of the topological-insulator nature of Bi 2 Se 3 [69].
Summarizing the experimental situation before the discovery of nematic superconductivity, there has been evidence for topologically non-trivial superconductivity in Cu x Bi 2 Se 3 , but the debate was yet far from convergence. It has been required to uncover more robust and reproducible properties evidencing an interesting SC state.

4. Recent Experiments on Nematic Superconducting Behavior

In this section, we briefly review recent experimental findings on the nematic superconductivity in doped Bi 2 Se 3 superconductors. As summarized in Table 2, nematic SC features have been reported quite consistently in all of Cu-, Sr, and Nb-doped Bi 2 Se 3 superconductors, as well as in related compounds and have been observed with various bulk probes such as nuclear magnetic resonance (NMR) Knight shift, specific heat, resistivity, and magnetization. More recently, the STM technique has been successfully utilized to observe nematic features, adding microscopic evidence for the nematic superconductivity.
Table 2. Comparison of experimental reports on nematic superconductivity in doped Bi 2 Se 3 and related systems.

4.1. Beginning of the Story: Nuclear Magnetic Resonance

The pioneering work on the nematic superconductivity in doped Bi 2 Se 3 systems was performed by Matano et al., who investigated the spin susceptibility in the SC state of Cu x Bi 2 Se 3 with the NMR technique [8]. The spin susceptibility in the SC state is in general rather difficult to measure, because of the strong Meissner screening. The NMR Knight shift is one of the few techniques that can measure the spin susceptibility directly, and it has been utilized for various superconductors [78,79,80,81].
Matano et al. used the 77 Se nucleus (nuclear spin: 1/2) for NMR and investigated the spin susceptibility for various field directions within the a b plane. They used a set of four single crystals of Cu x Bi 2 Se 3 with a Cu content x of 0.29–0.31. Usually, the Knight shift contains the spin part and the other parts, and the latter was evaluated using NMR of non-doped Bi 2 Se 3 . It was then found that the spin susceptibility decreases by nearly 80% in the SC state for field directions parallel to one of the three equivalent crystalline a axes, but does not change at all for other field directions, as shown in Figure 3a. Overall, the spin susceptibility exhibits 180 ° periodicity as a function of in-plane field direction in spite of the trigonal crystalline lattice, evidencing that the spin part of the SC order parameter in Cu x Bi 2 Se 3 is actually nematic. This is not only the first clear observation of S O ( 3 ) spin-rotational symmetry breaking in a SC state, but also the first observation of the spin-nematic superconductivity in any known superconductors.
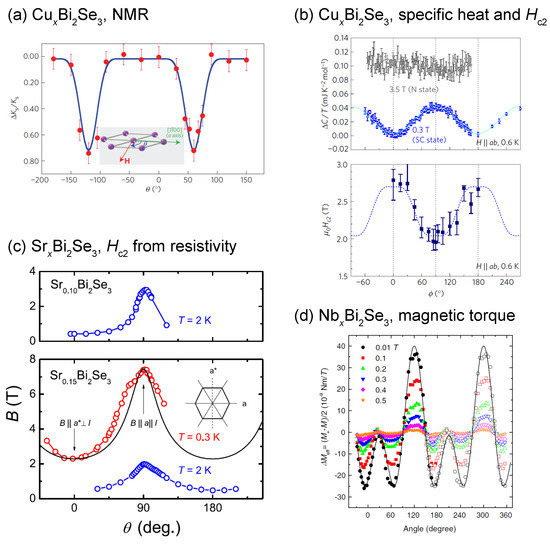
Figure 3. Representative experiments on the nematic superconductivity in A x Bi 2 Se 3 . (a) In-plane field-angle dependence of the NMR Knight shift of Cu x Bi 2 Se 3 [8]. (b) In-plane field-angle dependence of the specific heat and H c 2 of Cu x Bi 2 Se 3 [9]. (c) In-plane angular dependence of H c 2 evaluated from magnetoresistance measurements on Sr x Bi 2 Se 3 [10]. (d) In-plane field-angle dependence of the irreversible component of the magnetic torque of Nb x Bi 2 Se 3 [11]. We should be careful for the definition of the field angle: in (a,b), 0 ° corresponds to H ∥ a ; whereas in (c,d), it corresponds to H ∥ a ∗ . The panels (a,b) are respectively quoted from [8,9] with the permission of Springer Nature; (c,d) are respectively from [10,11] under the Creative Commons License.
The results of this NMR work were actually known in the community long before the final publication in 2016 and stimulated subsequent studies. In theory, Nagai et al. already in 2012 pointed out that bulk superconducting properties such as thermal conductivity can exhibit rotational symmetry breaking if one of the Δ 4 states is realized [82]. In 2014, Fu introduced the term “nematic superconductivity” in [12], and this suitable name seems to have contributed significantly to the expansion of the research field.

4.2. Pioneering Reports of Bulk Properties

In early 2016, three subsequent works reporting the nematic bulk SC nature in doped Bi 2 Se 3 were independently and almost simultaneously submitted to the arXiv server and were later published in 2016–2017 [9,10,11]. As briefly reviewed below, these three works by different groups consistently revealed the nematic nature of different dopants (Cu, Sr, and Nb) and using different experimental probes, demonstrating that the nematic superconductivity is a robust and ubiquitous feature in doped Bi 2 Se 3 superconductors.
The present author and coworkers performed specific-heat measurements of Cu x Bi 2 Se 3 single crystals under precise two-axis field-direction control [9]. Since the electronic specific heat is quite small in doped Bi 2 Se 3 because of low carrier concentration and weak electron correlation, it was necessary to measure the specific heat with high resolution. To achieve this goal, a small and low-background calorimeter was built utilizing the AC technique [83], which has the highest resolution among the standard heat-capacity measurement techniques. To apply magnetic fields, a vector magnet system was used [84], allowing the performance two-axis field-direction control. With this system, together with a careful field-alignment process, field misalignment effects were minimized. It was then found that the specific heat as a function of the in-plane field angle exhibited a two-fold symmetric behavior (Figure 3b), clearly breaking the lattice C 3 rotational symmetry. This nematicity in a bulk thermodynamic quantity is only possible if the SC gap amplitude has a nematic nature. Thus, this specific-heat result provides the first thermodynamic evidence for the gap-nematic superconductivity. From a comparison between the observed specific-heat oscillation and theoretical calculation, it was concluded that the Δ 4 y state was realized. In addition, the upper critical field H c 2 was also found to exhibit two-fold behavior with in-plane anisotropy of 20%, as shown in Figure 3b, providing additional evidence for the nematic superconductivity.
Pan et al. measured the in-plane resistivity of Sr x Bi 2 Se 3 under in-plane magnetic fields and observed in-plane H c 2 anisotropy of around 400% [10], as plotted in Figure 3c. In this experiment, strictly speaking, the applied electric current explicitly breaks the in-plane rotational symmetry. Nevertheless, the observed anisotropy is huge and cannot be explained by the anisotropy due to the applied current. Indeed, the absence of the role of the electric current direction on the SC nematicity was later confirmed by c-axis resistivity measurements [72], as well as by in-plane resistivity measurements upon varying the current direction [74]. This work has another important aspect for demonstrating that a simple technique such as resistivity can probe the nematicity. Shortly thereafter, Nikitin et al. (the same group as Pan et al.) reported that the nematic SC feature was robust even under hydrostatic pressure [71].
Asaba et al. investigated Nb x Bi 2 Se 3 single crystals by means of torque magnetometry under various in-plane field directions [11]. They studied the size of the hysteresis between the field-up and down sweep torque signals. They found that this hysteresis size exhibited clear breaking of the expected six-fold symmetric behavior as a function of the in-plane field angle (Figure 3d). The hysteresis size is actually not a thermodynamic quantity, but is rather related to the vortex pinning and the critical current density of the sample. Thus, it is not very straightforward how this quantity is related to the nematic SC gap. Nevertheless, it is also difficult to come up with other extrinsic origins on this nematic hysteresis. The mechanism of this interesting appearance of nematicity in the hysteresis should be clarified in the future.

4.3. Recent Reports

More recently, many other groups reported nematic superconductivity in doped Bi 2 Se 3 . In particular, many works have been performed for Sr-doped Bi 2 Se 3 . Du et al. measured c-axis resistance under a magnetic field to avoid the symmetry breaking due to the external current and found that the nematicity was still there; thus the external current was not the origin of the observed two-fold behavior in the in-plane resistivity [72]. More interestingly, they investigated the sample dependence of the nematic behavior and found that the anisotropy of the upper critical field, depicting the nematicity, was actually sample dependent: among the three samples investigated, two have a large H c 2 for the x direction, but the other has a large H c 2 for the y direction. Such a sample dependence implies that the ground state ( Δ 4 x or Δ 4 y ) is also sample dependent. This issue will be discussed in more detail in the next section. Smylie et al. investigated the in-plane field-angle dependence of resistivity and magnetization [73]. The observed two-fold behavior in the magnetization provides the first thermodynamic evidence of the gap-nematic superconductivity in the Sr-doped compound. They also investigated the crystal structure using X-ray diffraction and concluded that there was no detectable crystalline distortion in their sample. Kuntsevich et al. reported in-plane resistivity anisotropy using samples grown with the Bridgman method [74]. They cut two kinds of samples from the same batch: ones cut along the a axis and the others cut along the a ∗ axis, to check the current-direction dependence of the nematicity. It was found that the nematicity was independent of the current direction. However, the nematicity was actually dependent on batches, confirming the sample-dependent nematicity reported in [72]. They also reported a tiny crystal deformation, as well as two-fold resistivity anisotropy even in the normal state. This possible “normal-state nematicity” will be discussed in Section 5.2. Willa et al. succeeded in measuring the specific heat of Sr x Bi 2 Se 3 [75]. Calorimetry of Sr x Bi 2 Se 3 is more challenging than that of Cu x Bi 2 Se 3 , because the carrier density and resulting electronic specific heat tend to be much lower in Sr x Bi 2 Se 3 [48,49]. Nevertheless, they used a micro-structured calorimeter to achieve sensitivity high enough for a Sr x Bi 2 Se 3 single crystal and resolved a specific-heat jump of around 0.25 mJ/K 2 mol, which is only a fraction of that observed in Cu x Bi 2 Se 3 [9,46]. The two-fold specific-heat behavior was then observed, which was attributed to large H c 2 anisotropy rather than the gap anisotropy.
For Nb-doped Bi 2 Se 3 , Shen et al. reported in-plane field-angle dependence of magnetization and resistivity [53]. They found nematicity in both quantities, providing the first thermodynamic and transport evidence for the gap-nematic superconductivity in Nb x Bi 2 Se 3 . We should also mention that a penetration-depth measurement was performed on Nb x Bi 2 Se 3 [85]. The penetration depth was found to exhibit a T 2 -temperature dependence down to T / T c ∼ 0.12 . This behavior is consistent with the existence of point-nodes or point-like very small gap minima. This result provides an indirect support for the nematic Δ 4 states. It was also found that the T 2 dependence is robust against the increase of the impurity concentration. This robustness is consistent with theoretical proposals [62,63].
Quite recently, Andersen et al. reported that Cu-intercalated (PbSe) 5 (Bi 2 Se 3 ) 6 , which is a “naturally-made heterostructure” of PbSe and Bi 2 Se 3 layers and exhibits superconductivity below T c ∼ 2.5 K after intercalation [86], exhibited two-fold anisotropy in the SC state via resistivity and specific-heat measurements [76]. Strictly speaking, the global crystal symmetry of this compound is orthorhombic and does not have three-fold rotational symmetry due to the neighboring PbSe layer. Nevertheless, the Bi 2 Se 3 layer of this compound, as well as its electronic structure, almost preserves the three-fold symmetry [86,87]. Therefore, the observed two-fold anisotropy in the SC state is most likely due to a nematic SC gap, rather than the conventional origin such as Fermi-velocity anisotropy. It is worth commenting that Cu x (PbSe) 5 (Bi 2 Se 3 ) 6 substantially differs from A x Bi 2 Se 3 in various aspects: Cu x (PbSe) 5 (Bi 2 Se 3 ) 6 has a highly two-dimensional electronic structure because of the separation of the conductive Bi 2 Se 3 layers by insulating PbSe layers and exhibits line-nodal SC behavior [86]. This observation implies that the nematic superconductivity is quite robust irrespective of the dimensionality and gap structure of the system, thus providing important information on the origin and nature of nematic superconductivity.

4.4. Direct Visualization

Recently, direct visualization of nematic superconductivity by STM has been reported. Chen et al. investigated Bi 2 Te 3 thin films (with a typical thickness of 2QL) grown on a FeSe 0.55 Te 0.45 single-crystal substrate via molecular-beam epitaxy (MBE) [77]. This system is a bit different from doped Bi 2 Se 3 , because the Bi 2 Te 3 thin film exhibits superconductivity due to the proximity effect from the substrate, whereas doped Bi 2 Se 3 exhibits bulk superconductivity. On the other hand, the surface of Bi 2 Te 3 /FeSe 0.55 Te 0.45 can be cleaner than A x Bi 2 Se 3 because no ion doping is necessary to induce superconductivity, being more suited for STM investigations. In the quasiparticle interference spectra of Bi 2 Te 3 /FeSe 0.55 Te 0.45 at zero field, the quasiparticle excitation in the intermediate energy range below the SC gap was found to exhibit two-fold anisotropy. The excitation is stronger along the ± k x direction, indicating that the SC gap is smaller for this field direction, thus suggesting the Δ 4 y state. In addition, they found that the magnetic vortices under H ∥ c have an ellipsoidal shape elongating along the x (a) direction, although a nearly isotropic vortex shape is expected for the trigonal crystal structure. Such a vortex core shape provides microscopic evidence for two-fold anisotropy in the penetration depth and in the coherence length.
Independently, an STM study of Cu x Bi 2 Se 3 was reported by Tao et al. [70]. In spite of difficulties in finding good surfaces for STM, they succeeded in obtaining STM spectra under magnetic fields. Under the c axis field, they observed ellipsoidal vortex cores elongating along the y ( a ∗ ) direction, breaking the C 3 rotational symmetry. Moreover, they investigated the dependence of the gap amplitude on the in-plane field directions. They directly observed that the SC gap amplitude exhibited a two-fold field-angle dependence. The gap is larger for H ∥ y than for H ∥ x at 0.5 T, in favor of the Δ 4 x state. At higher fields, the large-gap axis rotates by ∼20 ° . The origin of this rotation is not clear yet.
These STM studies are significant in providing clear microscopic evidence for gap-nematic superconductivity. Furthermore, they are the first observations of nematicity in the absence of an in-plane magnetic field; it is now confirmed that the nematic superconductivity is the ground state even at zero in-plane field.

5. Known Issues

Although the nematic feature in the SC state has been consistently and reproducibly observed in A x Bi 2 Se 3 , as well as in a related compound, there are several controversial or unresolved issues. These issues are addressed in this section.

5.1. Which of Δ 4 x or Δ 4 y Is Realized?

One of the most important, but puzzling issues is which of Δ 4 x or Δ 4 y is realized in actual samples. As listed in Table 2, the NMR [8] and STM [70] studies on Cu x Bi 2 Se 3 suggested the Δ 4 x state, but the specific heat study [9] on the same compound suggested the Δ 4 y state. Moreover, the H c 2 anisotropy, an indicator of the nematic direction, significantly varies: some reports suggest a large H c 2 for H ∥ x and others for H ∥ y . Works on multiple samples indicate that the H c 2 anisotropy is actually sample dependent [72,74]. Thus, the variation in the H c 2 anisotropy is not an artifact, but is an intrinsic property of A x Bi 2 Se 3 .
This fact very likely suggests that the Δ 4 x and Δ 4 y states are nearly degenerate and are chosen depending on the in-plane symmetry breaking fields. Such a situation is described in Figure 4: the nematic SC order parameter, which is reflected in, e.g., in-plane H c 2 anisotropy, exhibits multiple branches as a function of the in-plane symmetry breaking field, such as in-plane uniaxial strain [88], crystal deformation, or some arrangement of doped ions. This coupling between the order parameter and the symmetry-breaking field resembles the coupling between ferromagnetism and external magnetic fields.
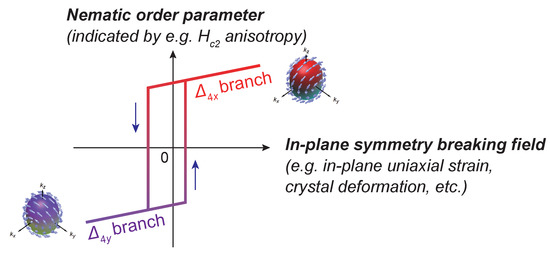
Figure 4. Schematic figure of the coupling between the nematic order parameter and the in-plane symmetry breaking field.
The schematic model in Figure 4 explains the reason for the variation in the large H c 2 direction: for some samples, Δ 4 x is favored because of a tiny, but positive symmetry breaking field, and for others, Δ 4 y is realized due to the negative field. This also explains the absence of the random switching of nematicity orientation upon different coolings: so far, there are no reports that the nematic behavior is altered by different cooling histories across T c . Thus, all the samples seem to have finite symmetry-breaking fields that pin the nematicity.

5.2. Normal-State and Superconducting-State Nematicities

This model also explain the relation between the SC nematicity and the possible lattice distortion. Because it is quite important whether the trigonal lattice symmetry is preserved even after the doping, the existence of lattice symmetry breaking has been investigated. Until recently, there has been no positive evidence for the lattice distortion, as well as for nematic behavior in the normal state [8,9,73]. Recently, Kuntsevich et al. reported that their samples grown using the Bridgman method (in which crystals tend to grow along one direction) had a tiny lattice distortion (0.02% orthorhombic distortion and 0.005 ° c-axis inclination) [74]. These samples exhibit in-plane H c 2 anisotropies ranging from 300–800%. Such large anisotropy cannot be explained at all by the electronic anisotropy caused by the observed tiny lattice distortion. Therefore, SC nematicity is mostly caused by the Cooper-pair formation, and the concept of nematic superconductivity should still be valid in the presence of explicit breaking of the trigonal symmetry. These samples with relatively large SC anisotropy and detectable lattice distortion are probably located in the region far from the origin in the schematic in Figure 4.
The nematic SC features observed in Cu x (PbSe) 5 (Bi 2 Se 3 ) 6 [76] and Bi 2 Te 3 Fe(Se, Te) [77] are also regarded as nematic superconductivity in explicit symmetry-breaking fields. In these systems, the global crystal structures do not possess trigonal rotational symmetry due to the neighboring non-trigonal layers. Thus, there are finite symmetry breaking fields in these compounds. Still, anisotropies in their normal states are rather small and are not sufficient to explain the sizable two-fold anisotropies in their SC states.

5.3. Nematic Domains

If the symmetry-breaking field is rather weak, the formation of multiple nematic domains is expected. In the specific-heat study in [9], one sample with possible nematic domains was reported (see the Supplementary Information of [9]). This sample exhibited very weak H c 2 anisotropy, as well as weak and distorted specific-heat oscillation as a function of in-plane magnetic field direction, in contrast to the sample mainly focused on in [9]. Angular magnetoresistance (AMR) is more sensitive to the existence of domains. Indeed, complicated structures in AMR curves attributable to domains were observed in [72,74].
However, in most of the other studies, samples seem to be in single-domain states. For example, in the NMR study [8], multiple domains would result in multiple sets of dips in the Knight shift as a function of in-plane field angle. In the actual experiment, only one set of dips was observed, suggesting a single-domain sample. Such dominance of single-domain samples indicates that the in-plane symmetry breaking field is in most cases strong enough to avoid the formation of multiple domains.
A nematic domain wall, if existing, is a fascinating object, forming naturally a junction between topological pairing states. This may host novel Majorana quasiparticles and may be controllable by an external symmetry breaking field. Investigation of detailed order-parameter structures near the domain wall would be quite interesting.

5.4. Possible Nematic Superconductivity in Other Systems

In principle, gap-nematic superconductivity can occur in any type of superconductivity, even in ordinary s-wave superconductivity. Nevertheless, a straightforward way to realize nematic superconductivity is to bring a multi-component superconductor (i.e., a superconductor with a multi-dimensional irreducible representation) and to stabilize one of the SC-order-parameter components. In such multi-component superconductivity, each component is in most cases nematic. However, usually, the components form a complex linear combination to satisfy the rotational symmetry of the underlying lattice. For example, in the chiral p x ± i p y -wave superconductivity on a tetragonal lattice (Figure 1b), each p x or p y component breaks the tetragonal symmetry, thus possessing the nematic nature. However, they form the complex (chiral) combination p x ± i p y to satisfy the tetragonal symmetry except in the SC phase degree of freedom. If, however, the formation of such a chiral state is unfavored, one of the nematic components can be stabilized.
Actually, in doped Bi 2 Se 3 , the predicted nematic Δ 4 x and Δ 4 y states both belong to the two-dimensional E u representation, as described in Table 1. The two components thus in principle can form complex (chiral) combinations. However, in the present case, the strong spin-momentum locking forces a non-unitary SC state to emerge when the chiral superconductivity is realized [89]. Notice that the d vector of the chiral state d chiral = d 4 x ± i d 4 y ∼ ( k z ± i ε k x , ∓ i k z , λ ( k x ± i k y ) ) has a complex spin component: see, for example, along the k z axis, d chiral ∼ ± k z ( x ^ − i y ^ ) is non-unitary ( d × d ∗ ≠ 0 ). Generally, non-unitary states have spin-dependent excitation gaps, and usually, one spin component has a significantly smaller gap than the other. Thus, non-unitary states are expected to have smaller condensation energies than the ordinary unitary SC states. This inevitable formation of non-unitary gaps in chiral states prevents the formation of the complex linear combination of d 4 x and d 4 y and favors the realization of single-component nematic superconductivity in this system.
From the discussion above, a multi-component superconductor is a promising platform to probe nematic superconductivity. Indeed, in UPt 3 with a trigonal crystal structure P 3 ¯ m 1 [90], multi-component superconductivity is believed to be realized [29] with one of the components relatively stabilized by the short-ranged antiferromagnetic ordering [91]. In the in-plane field-angle dependence of the thermal conductivity, two-fold symmetric behavior was observed in the C phase [29,92]. This phenomenon can be considered as a consequence of nematic superconductivity with a finite in-plane symmetry-breaking field (see Figure 4). In PrOs 4 Sb 12 with a cubic structure I m 3 ¯ , similar two-fold behavior in the field-angle-dependent heat transport was observed in a part of the H-T phase diagram [93]. Strictly speaking, two-fold symmetry in the magneto-transport is allowed in the space group I m 3 ¯ . Nevertheless, it seems difficult to explain the clear two-fold anisotropy just due to the electronic-state anisotropy, and gap nematicity due to a multi-component order parameter may be playing an important role. On the other hand, two-fold behavior has not been observed in the specific heat of both superconductors [94,95]. Thus, the nematic feature of these compounds, if existing, is subtle compared with those observed in doped Bi 2 Se 3 superconductors. Theoretically, several other multi-comoment-superconductor candidates such as U 1 − x Th x Be 13 [96] and half-Heusler compounds [97,98] were proposed to exhibit nematic superconductivity, and experimental verification is strongly called for.
We also comment on another leading candidate of multi-component superconductivity, Sr 2 RuO 4 , seemingly exhibiting quasi-two-dimensional chiral p x ± i p y -wave superconductivity. Theoretically, it has been predicted that a non-chiral single-component p x (or p y ) state [99] should be realized under the in-plane magnetic field or in-plane uniaxial strain. Such non-chiral states may be regarded as a symmetry-breaking field-induced nematic state, or a “meta-nematic” state in an analogy to the metamagnetic transition (field-induced ferromagnetism) in a paramagnet. Although clear experimental observation has not been achieved yet [100,101,102,103], it is worth seriously investigating the nematic features of Sr 2 RuO 4 under in-plane symmetry breaking fields. Lastly, we mention that nematic superconductivity in Sr 2 RuO 4 at ambient condition was theoretically proposed very recently in [104].

6. Summary and Perspectives

To summarize, we have reviewed recent researches on nematic superconductivity in doped Bi 2 Se 3 topological superconductors and in related compounds. The two-fold symmetric behavior in many quantities, breaking the trigonal symmetry of the underlying lattice, has been reported by more than ten groups, with excellent reproducibility. These experimental works demonstrate that the nematic superconductivity is a common and robust feature among the A x Bi 2 Se 3 family. In addition, observation of nematic gap structures in turn provide bulk evidence for topological superconductivity in this family [13]. However, there are several issues unresolved; in particular, apparent inconsistency in the nematic direction and its relation to the possibly existing in-plane symmetry-breaking field are the most important subjects to be investigated next. Furthermore, predicted novel phenomena originating from nematic superconductivity, such as the superconductivity-fluctuation-induced nematic order above T c [105], the chiral Higgs mode in the electromagnetic response [106], spin polarization of Majorana quasiparticles in a vortex core [107], and the nematic Skyrmion texture near half-quantum vortices [108], would be worth seeking.
The nematic SC state in A x Bi 2 Se 3 is qualitatively unique compared with other nematic systems in liquid crystals or normal-state electron systems: The nematic superconductivity is realized by a macroscopically-coherent quantum-mechanical wavefunction, accompanied by an odd-parity nature, non-trivial topology, and an active spin degree of freedom. We believe that this new class of nematic states stimulates further researches both in the fields of nematic liquids and unconventional topological superconductivity.

Funding

This research was funded by the Japanese Society for Promotion of Science (JSPS) Grant Numbers KAKENHI JP15H05851, JP15H05852, JP15K21717, JP26287078, and JP17H04848.

Acknowledgments

The author acknowledges collaboration with K.T., S.N., I.K., Y.M. at Kyoto University, Z.W. and Y.A. at the University of Köln, K.S. at Kyoto Sangyo University, and Y.N. at Japan Atomic Energy Agency. The author also thanks M.K. for valuable comments to improve the manuscript, and K.I., Y.M., T.M., M.S., L.F., K.M., G.-Q.Z., and D.A. for valuable discussion and support.

Conflicts of Interest

The author declares no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
AMRAngular magnetoresistance
ARPESAngle-resolved photoemission spectroscopy
BCSBardeen–Cooper–Schrieffer
BGBridgman method
BWBalian–Werthamer
ECIElectrochemical intercalation
MBEMolecular-beam epitaxy
MGMelt growth
NMRNuclear magnetic resonance
QLQuintuple layer
SCSuperconducting
STMScanning tunneling microscope
vdWvan der Waals

References

  1. Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef]
  2. Qi, X.L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef]
  3. Ando, Y. Topological Insulator Materials. J. Phys. Soc. Jpn. 2013, 82, 102001. [Google Scholar] [CrossRef]
  4. Schnyder, A.P.; Brydon, P.M.R. Topological surface states in nodal superconductors. J. Phys. Condens. Matter 2015, 27, 243201. [Google Scholar] [CrossRef] [PubMed]
  5. Sato, M.; Ando, Y. Topological superconductors: A review. Rep. Prog. Phys. 2017, 80, 076501. [Google Scholar] [CrossRef]
  6. Wilczek, F. Majorana returns. Nat. Phys. 2009, 5, 614. [Google Scholar] [CrossRef]
  7. Yonezawa, S. Bulk Topological Superconductors. AAPPS Bull. 2016, 26, 3. [Google Scholar] [CrossRef]
  8. Matano, K.; Kriener, M.; Segawa, K.; Ando, Y.; Zheng, G.-Q. Spin-rotation symmetry breaking in the superconducting state of CuxBi2Se3. Nat. Phys. 2016, 12, 852. [Google Scholar] [CrossRef]
  9. Yonezawa, S.; Tajiri, K.; Nakata, S.; Nagai, Y.; Wang, Z.; Segawa, K.; Ando, Y.; Maeno, Y. Thermodynamic evidence for nematic superconductivity in CuxBi2Se3. Nat. Phys. 2017, 13, 123. [Google Scholar] [CrossRef]
  10. Pan, Y.; Nikitin, A.M.; Araizi, G.K.; Huang, Y.K.; Matsushita, Y.; Naka, T.; de Visser, A. Rotational symmetry breaking in the topological superconductor SrxBi2Se3 probed by upper-critical field experiments. Sci. Rep. 2016, 6, 28632. [Google Scholar] [CrossRef]
  11. Asaba, T.; Lawson, B.; Tinsman, C.; Chen, L.; Corbae, P.; Li, G.; Qiu, Y.; Hor, Y.; Fu, L.; Li, L. Rotational Symmetry Breaking in a Trigonal Superconductor Nb-doped Bi2Se3. Phys. Rev. X 2017, 7, 011009. [Google Scholar] [CrossRef]
  12. Fu, L. Odd-parity topological superconductor with nematic order: Application to CuxBi2Se3. Phys. Rev. B 2014, 90, 100509(R). [Google Scholar] [CrossRef]
  13. Fu, L.; Berg, E. Odd-Parity Topological Superconductors: Theory and Application to CuxBi2Se3. Phys. Rev. Lett. 2010, 105, 097001. [Google Scholar] [CrossRef] [PubMed]
  14. Ando, Y.; Fu, L. Topological Crystalline Insulators and Topological Superconductors: From Concepts to Materials. Annu. Rev. Condens. Matter Phys. 2015, 6, 361. [Google Scholar] [CrossRef]
  15. Sasaki, S.; Mizushima, T. Superconducting doped topological materials. Physica C 2015, 514, 206. [Google Scholar] [CrossRef]
  16. Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of superconductivity. Phys. Rev. 1957, 108, 1175. [Google Scholar] [CrossRef]
  17. Luke, G.M.; Fudamoto, Y.; Kojima, K.M.; Larkin, M.I.; Merrin, J.; Nachumi, B.; Uemura, Y.J.; Maeno, Y.; Mao, Z.Q.; Mori, Y.; et al. Time-reversal symmetry-breaking superconductivity in Sr2RuO4. Nature 1998, 394, 558. [Google Scholar] [CrossRef]
  18. Xia, J.; Maeno, Y.; Beyersdorf, P.T.; Fejer, M.M.; Kapitulnik, A. High Resolution Polar Kerr Effect Measurements of Sr2RuO4: Evidence for Broken Time-Reversal Symmetry in the Superconducting State. Phys. Rev. Lett. 2006, 97, 167002. [Google Scholar] [CrossRef] [PubMed]
  19. Yamashita, T.; Shimoyama, Y.; Haga, Y.; Matsuda, T.D.; Yamamoto, E.; Onuki, Y.; Sumiyoshi, H.; Fujimoto, S.; Levchenko, A.; Shibauchi, T.; et al. Colossal thermomagnetic response in the exotic superconductor URu2Si2. Nat. Phys. 2015, 11, 17. [Google Scholar] [CrossRef]
  20. Schemm, E.R.; Baumbach, R.E.; Tobash, P.H.; Ronning, F.; Bauer, E.D.; Kapitulnik, A. Evidence for broken time-reversal symmetry in the superconducting phase of URu2Si2. Phys. Rev. B 2015, 91, 140506(R). [Google Scholar] [CrossRef]
  21. Schemm, E.R.; Gannon, W.J.; Wishne, C.M.; Halperin, W.P.; Kapitulnik, A. Observation of broken time-reversal symmetry in the heavy-fermion superconductor UPt3. Science 2014, 345, 190. [Google Scholar] [CrossRef] [PubMed]
  22. Anderson, P.W.; Morel, P. Generalized Bardeen-Cooper-Schrieffer States and the Proposed Low-Temperature Phase of Liquid 3He. Phys. Rev. 1961, 123, 1911–1934. [Google Scholar] [CrossRef]
  23. Balian, R.; Werthamer, N.R. Superconductivity with Pairs in a Relative p Wave. Phys. Rev. 1963, 131, 1553. [Google Scholar] [CrossRef]
  24. Leggett, A.J. A theoretical description of the new phases of liquid 3He. Rev. Mod. Phys. 1975, 47, 331. [Google Scholar] [CrossRef]
  25. Mizushima, T.; Tsutsumi, Y.; Kawakami, T.; Sato, M.; Ichioka, M.; Machida, K. Symmetry-Protected Topological Superfluids and Superconductors—From the Basics to 3He. J. Phys. Soc. Jpn. 2016, 85, 022001. [Google Scholar] [CrossRef]
  26. Mackenzie, A.P.; Maeno, Y. The superconductivity of Sr2RuO4 and the physics of spin-triplet pairing. Rev. Mod. Phys. 2003, 75, 657–712. [Google Scholar] [CrossRef]
  27. Maeno, Y.; Kittaka, S.; Nomura, T.; Yonezawa, S.; Ishida, K. Evaluation of Spin-Triplet Superconductivity in Sr2RuO4. J. Phys. Soc. Jpn. 2012, 81, 011009. [Google Scholar] [CrossRef]
  28. Mackenzie, A.P.; Scaffidi, T.; Hicks, C.W.; Maeno, Y. Even odder after twenty-three years: The superconducting order parameter puzzle of Sr2RuO4. npj Quantum Mater. 2017, 2, 40. [Google Scholar] [CrossRef]
  29. Izawa, K.; Machida, Y.; Itoh, A.; So, Y.; Ota, K.; Haga, Y.; Yamamoto, E.; Kimura, N.; Onuki, Y.; Tsutsumi, Y.; et al. Pairing Symmetry of UPt3 Probed by Thermal Transport Tensors. J. Phys. Soc. Jpn. 2014, 83, 061013. [Google Scholar] [CrossRef]
  30. Sato, M. Topological odd-parity superconductors. Phys. Rev. B 2010, 81, 220504(R). [Google Scholar] [CrossRef]
  31. Van Harlingen, D.J. Phase-sensitive tests of the symmetry of the pairing state in the high-temperature superconductors—Evidence for dx2−y2 symmetry. Rev. Mod. Phys. 1995, 67, 515. [Google Scholar] [CrossRef]
  32. Tsuei, C.C.; Kirtley, J.R. Pairing symmetry in cuprate superconductors. Rev. Mod. Phys. 2000, 72, 969. [Google Scholar] [CrossRef]
  33. Ando, Y.; Segawa, K.; Komiya, S.; Lavrov, A.N. Electrical Resistivity Anisotropy from Self-Organized One Dimensionality in High-Temperature Superconductors. Phys. Rev. Lett. 2002, 88, 137005. [Google Scholar] [CrossRef] [PubMed]
  34. Vojta, M. Lattice symmetry breaking in cuprate superconductors: Stripes, nematics, and superconductivity. Adv. Phys. 2009, 58, 699–820. [Google Scholar] [CrossRef]
  35. Kasahara, S.; Shi, H.J.; Hashimoto, K.; Tonegawa, S.; Mizukami, Y.; Shibauchi, T.; Sugimoto, K.; Fukuda, T.; Terashima, T.; Nevidomskyy, A.H.; et al. Electronic nematicity above the structural and superconducting transition in BaFe2(As1−xPx)2. Nature 2012, 486, 382. [Google Scholar] [CrossRef] [PubMed]
  36. Fernandes, R.M.; Chubukov, A.V.; Schmalian, J. What drives nematic order in iron-based superconductors? Nat. Phys. 2014, 10, 97. [Google Scholar] [CrossRef]
  37. Borzi, R.A.; Grigera, S.A.; Farrell, J.; Perry, R.S.; Lister, S.J.S.; Lee, S.L.; Tennant, D.A.; Maeno, Y.; Mackenzie, A.P. Formation of a Nematic Fluid at High Fields in Sr3Ru2O7. Science 2007, 315, 214. [Google Scholar] [CrossRef] [PubMed]
  38. Murakawa, H.; Ishida, K.; Kitagawa, K.; Mao, Z.Q.; Maeno, Y. Measurement of the 101Ru-Knight Shift of Superconducting Sr2RuO4 in a Parallel Magnetic Field. Phys. Rev. Lett. 2004, 93, 167004. [Google Scholar] [CrossRef] [PubMed]
  39. Tou, H.; Kitaoka, Y.; Ishida, K.; Asayama, K.; Kimura, N.; Ōnuki, Y.; Yamamoto, E.; Haga, Y.; Maezawa, K. Nonunitary Spin-Triplet Superconductivity in UPt3: Evidence from 195Pt Knight Shift Study. Phys. Rev. Lett. 1998, 80, 3129. [Google Scholar] [CrossRef]
  40. Zhang, H.; Liu, C.X.; Qi, X.L.; Dai, X.; Fang, Z.; Zhang, S.C. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 438. [Google Scholar] [CrossRef]
  41. Xia, Y.; Qian, D.; Hsieh, D.; Wray, L.; Pal, A.; Lin, H.; Bansil, A.; Grauer, D.; Hor, Y.S.; Cava, R.J.; et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 398. [Google Scholar] [CrossRef]
  42. Nakajima, S. The crystal structure of Bi2Te3−xSex. J. Phys. Chem. Solids 1963, 24, 479. [Google Scholar] [CrossRef]
  43. Li, Z.; Wang, M.; Zhang, D.; Feng, N.; Jiang, W.; Han, C.; Chen, W.; Ye, M.; Gao, C.; Jia, J.; et al. Possible structural origin of superconductivity in Sr-doped Bi2Se3. Phys. Rev. Materials 2018, 2, 014201. [Google Scholar] [CrossRef]
  44. Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272. [Google Scholar] [CrossRef]
  45. Hor, Y.S.; Williams, A.J.; Checkelsky, J.G.; Roushan, P.; Seo, J.; Xu, Q.; Zandbergen, H.W.; Yazdani, A.; Ong, N.P.; Cava, R.J. Superconductivity in CuxBi2Se3 and its Implications for Pairing in the Undoped Topological Insulator. Phys. Rev. Lett. 2010, 104, 057001. [Google Scholar] [CrossRef] [PubMed]
  46. Kriener, M.; Segawa, K.; Ren, Z.; Sasaki, S.; Ando, Y. Bulk Superconducting Phase with a Full Energy Gap in the Doped Topological Insulator CuxBi2Se3. Phys. Rev. Lett. 2011, 106, 127004. [Google Scholar] [CrossRef]
  47. Kriener, M.; Segawa, K.; Ren, Z.; Sasaki, S.; Wada, S.; Kuwabata, S.; Ando, Y. Electrochemical synthesis and superconducting phase diagram of CuxBi2Se3. Phys. Rev. B 2011, 84, 054513. [Google Scholar] [CrossRef]
  48. Liu, Z.; Yao, X.; Shao, J.; Zuo, M.; Pi, L.; Tan, S.; Zhang, C.; Zhang, Y. Superconductivity with Topological Surface State in SrxBi2Se3. J. Am. Chem. Soc. 2015, 137, 10512. [Google Scholar] [CrossRef]
  49. Shruti; Maurya, V.K.; Neha, P.; Srivastava, P.; Patnaik, S. Superconductivity by Sr intercalation in the layered topological insulator Bi2Se3. Phys. Rev. B 2015, 92, 020506(R). [Google Scholar] [CrossRef]
  50. Qiu, Y.; Sanders, K.N.; Dai, J.; Medvedeva, J.E.; Wu, W.; Ghaemi, P.; Vojta, T.; Hor, Y.S. Time reversal symmetry breaking superconductivity in topological materials. arXiv, 2015; arXiv:1512.03519. [Google Scholar]
  51. Lahoud, E.; Maniv, E.; Petrushevsky, M.S.; Naamneh, M.; Ribak, A.; Wiedmann, S.; Petaccia, L.; Salman, Z.; Chashka, K.B.; Dagan, Y.; et al. Evolution of the Fermi surface of a doped topological insulator with carrier concentration. Phys. Rev. B 2013, 88, 195107. [Google Scholar] [CrossRef]
  52. Lawson, B.J.; Corbae, P.; Li, G.; Yu, F.; Asaba, T.; Tinsman, C.; Qiu, Y.; Medvedeva, J.E.; Hor, Y.S.; Li, L. Multiple Fermi surfaces in superconducting Nb-doped Bi2Se3. Phys. Rev. B 2016, 94, 041114. [Google Scholar] [CrossRef]
  53. Shen, J.; He, W.Y.; Yuan, N.F.Q.; Huang, Z.; Cho, C.-W.; Lee, S.H.; Hor, Y.S.; Law, K.T.; Lortz, R. Nematic topological superconducting phase in Nb-doped Bi2Se3. npj Quantum Mater. 2017, 2, 59. [Google Scholar] [CrossRef]
  54. Kriener, M.; (Center for Emergent Matter Science (CEMS), Riken, Wako-shi, Saitama, Japan). Private communication, 2018.
  55. Du, G.; Shao, J.; Yang, X.; Du, Z.; Fang, D.; Wang, J.; Ran, K.; Wen, J.; Zhang, C.; Yang, H.; et al. Drive the Dirac electrons into Cooper pairs in SrxBi2Se3. Nat. Commun. 2017, 8, 14466. [Google Scholar] [CrossRef]
  56. Hashimoto, T.; Yada, K.; Yamakage, A.; Sato, M.; Tanaka, Y. Bulk Electronic State of Superconducting Topological Insulator. J. Phys. Soc. Jpn. 2013, 82, 044704. [Google Scholar] [CrossRef]
  57. Hashimoto, T.; Yada, K.; Yamakage, A.; Sato, M.; Tanaka, Y. Effect of Fermi surface evolution on superconducting gap in superconducting topological insulator. Supercond. Sci. Technol. 2014, 27, 104002. [Google Scholar] [CrossRef]
  58. Sun, Y.; Maki, K. Impurity effects in d-wave superconductors. Phys. Rev. B 1995, 51, 6059. [Google Scholar] [CrossRef]
  59. Mackenzie, A.P.; Haselwimmer, R.K.W.; Tyler, A.W.; Lonzarich, G.G.; Mori, Y.; Nishizaki, S.; Maeno, Y. Extremely Strong Dependence of Superconductivity on Disorder in Sr2RuO4. Phys. Rev. Lett. 1998, 80, 161. [Google Scholar] [CrossRef]
  60. Joo, N.; Auban-Senzier, P.; Pasquier, C.R.; Monod, P.; Jérome, D.; Bechgaard, K. Suppression of superconductivity by non-magnetic disorder in the organic superconductor (TMTSF)2(ClO4)(1−x)(ReO4)x. Eur. Phys. J. B 2004, 40, 43. [Google Scholar] [CrossRef]
  61. Yonezawa, S.; Marrache-Kikuchi, C.A.; Bechgaard, K.; Jérome, D. Crossover from impurity-controlled to granular superconductivity in (TMTSF)2ClO4. Phys. Rev. B 2018, 97, 014521. [Google Scholar] [CrossRef]
  62. Michaeli, K.; Fu, L. Spin-Orbit Locking as a Protection Mechanism of the Odd-Parity Superconducting State against Disorder. Phys. Rev. Lett. 2012, 109, 187003. [Google Scholar] [CrossRef]
  63. Nagai, Y. Robust superconductivity with nodes in the superconducting topological insulator CuxBi2Se3: Zeeman orbital field and nonmagnetic impurities. Phys. Rev. B 2015, 91, 060502(R). [Google Scholar] [CrossRef]
  64. Kriener, M.; Segawa, K.; Sasaki, S.; Ando, Y. Anomalous suppression of the superfluid density in the CuxBi2Se3 superconductor upon progressive Cu intercalation. Phys. Rev. B 2012, 86, 180505. [Google Scholar] [CrossRef]
  65. Bay, T.; Naka, T.; Huang, Y.K.; Luigjes, H.; Golden, M.S.; de Visser, A. Superconductivity in the Doped Topological Insulator CuxBi2Se3 under High Pressure. Phys. Rev. Lett. 2012, 108, 057001. [Google Scholar] [CrossRef]
  66. Kita, T.; Arai, M. Ab initio calculations of Hc2 in type-II superconductors: Basic formalism and model calculations. Phys. Rev. B 2004, 70, 224522. [Google Scholar] [CrossRef]
  67. Sasaki, S.; Kriener, M.; Segawa, K.; Yada, K.; Tanaka, Y.; Sato, M.; Ando, Y. Topological Superconductivity in CuxBi2Se3. Phys. Rev. Lett. 2011, 107, 217001. [Google Scholar] [CrossRef]
  68. Yamakage, A.; Yada, K.; Sato, M.; Tanaka, Y. Theory of tunneling conductance and surface-state transition in superconducting topological insulators. Phys. Rev. B 2012, 85, 180509(R). [Google Scholar] [CrossRef]
  69. Mizushima, T.; Yamakage, A.; Sato, M.; Tanaka, Y. Dirac-fermion-induced parity mixing in superconducting topological insulators. Phys. Rev. B 2014, 90, 184516. [Google Scholar] [CrossRef]
  70. Tao, R.; Yan, Y.J.; Liu, X.; Wang, Z.W.; Ando, Y.; Wang, Q.H.; Zhang, T.; Feng, D.L. Direct Visualization of the Nematic Superconductivity in CuxBi2Se3. Phys. Rev. X 2018, 8, 041024. [Google Scholar] [CrossRef]
  71. Nikitin, A.M.; Pan, Y.; Huang, Y.K.; Naka, T.; de Visser, A. High-pressure study of the basal-plane anisotropy of the upper critical field of the topological superconductor SrxBi2Se3. Phys. Rev. B 2016, 94, 144516. [Google Scholar] [CrossRef]
  72. Du, G.; Li, Y.; Schneeloch, J.; Zhong, R.D.; Gu, G.; Yang, H.; Lin, H.; Wen, H.H. Superconductivity with two-fold symmetry in topological superconductor SrxBi2Se3. Sci. China Phys. Mech. Astron. 2017, 60, 037411. [Google Scholar] [CrossRef]
  73. Smylie, M.P.; Willa, K.; Claus, H.; Koshelev, A.E.; Song, K.W.; Kwok, W.K.; Islam, Z.; Gu, G.D.; Schneeloch, J.A.; Zhong, R.D.; et al. Superconducting and normal-state anisotropy of the doped topological insulator Sr0.1Bi2Se3. Sci. Rep. 2018, 8, 7666. [Google Scholar] [CrossRef] [PubMed]
  74. Kuntsevich, A.; Bryzgalov, M.A.; Prudkoglyad, V.A.; Martovitskii, V.P.; Selivanov, Y.G.; Chizhevskii, E.G. Structural distortion behind the nematic superconductivity in SrxBi2Se3. New J. Phys. 2018, 20, 103022. [Google Scholar] [CrossRef]
  75. Willa, K.; Willa, R.; Song, K.W.; Gu, G.D.; Schneeloch, J.A.; Zhong, R.; Koshelev, A.E.; Kwok, W.K.; Welp, U. Nanocalorimetric evidence for nematic superconductivity in the doped topological insulator Sr0.1Bi2Se3. Phys. Rev. B 2018, 98, 184509. [Google Scholar] [CrossRef]
  76. Andersen, L.; Wang, Z.; Lorenz, T.; Ando, Y. Nematic Superconductivity in Cu1.5(PbSe)5(Bi2Se3)6. arXiv, 2018; arXiv:1811.00805. [Google Scholar]
  77. Chen, M.; Chen, X.; Yang, H.; Du, Z.; Wen, H.H. Superconductivity with twofold symmetry in Bi2Te3/FeTe0.55Se0.45 heterostructures. Sci. Adv. 2018, 4. [Google Scholar] [CrossRef] [PubMed]
  78. Tou, H.; Kitaoka, Y.; Asayama, K.; Kimura, N.; Ōnuki, Y.; Yamamoto, E.; Maezawa, K. Odd-Parity Superconductivity with Parallel Spin Pairing in UPt3: Evidence from 195Pt Knight Shift Study. Phys. Rev. Lett. 1996, 77, 1374. [Google Scholar] [CrossRef] [PubMed]
  79. Ishida, K.; Mukuda, H.; Kitaoka, Y.; Asayama, K.; Mao, Z.Q.; Mori, Y.; Maeno, Y. Spin-triplet superconductivity in Sr2RuO4 identified by 17O Knight shift. Nature 1998, 396, 658. [Google Scholar] [CrossRef]
  80. Tien, C.; Jiang, I.M. Magnetic resonance of heavy-fermion superconductors and high-Tc superconductors. Phys. Rev. B 1989, 40, 229. [Google Scholar] [CrossRef]
  81. Shinagawa, J.; Kurosaki, Y.; Zhang, F.; Parker, C.; Brown, S.E.; Jérome, D.; Bechgaard, K.; Christensen, J.B. Superconducting State of the Organic Conductor (TMTSF)2ClO4. Phys. Rev. Lett. 2007, 98, 147002. [Google Scholar] [CrossRef]
  82. Nagai, Y.; Nakamura, H.; Machida, M. Rotational isotropy breaking as proof for spin-polarized Cooper pairs in the topological superconductor CuxBi2Se3. Phys. Rev. B 2012, 86, 094507. [Google Scholar] [CrossRef]
  83. Sullivan, P.F.; Seidel, G. Steady-State, ac-Temperature Calorimetry. Phys. Rev. 1968, 173, 679. [Google Scholar] [CrossRef]
  84. Deguchi, K.; Ishiguro, T.; Maeno, Y. Field-orientation dependent heat capacity measurements at low temperatures with a vector magnet system. Rev. Sci. Instrum. 2004, 75, 1188. [Google Scholar] [CrossRef]
  85. Smylie, M.P.; Willa, K.; Claus, H.; Snezhko, A.; Martin, I.; Kwok, W.K.; Qiu, Y.; Hor, Y.S.; Bokari, E.; Niraula, P.; et al. Robust odd-parity superconductivity in the doped topological insulator NbxBi2Se3. Phys. Rev. B 2017, 96, 115145. [Google Scholar] [CrossRef]
  86. Sasaki, S.; Segawa, K.; Ando, Y. Superconductor derived from a topological insulator heterostructure. Phys. Rev. B 2014, 90, 220504(R). [Google Scholar] [CrossRef]
  87. Nakayama, K.; Kimizuka, H.; Tanaka, Y.; Sato, T.; Souma, S.; Takahashi, T.; Sasaki, S.; Segawa, K.; Ando, Y. Observation of two-dimensional bulk electronic states in the superconducting topological insulator heterostructure Cux(PbSe)5(Bi2Se3)6: Implications for unconventional superconductivity. Phys. Rev. B 2015, 92, 100508(R). [Google Scholar] [CrossRef]
  88. Venderbos, J.W.F.; Kozii, V.; Fu, L. Identification of nematic superconductivity from the upper critical field. Phys. Rev. B 2016, 94, 094522. [Google Scholar] [CrossRef]
  89. Venderbos, J.W.F.; Kozii, V.; Fu, L. Odd-parity superconductors with two-component order parameters: Nematic and chiral, full gap, and Majorana node. Phys. Rev. B 2016, 94, 180504. [Google Scholar] [CrossRef]
  90. Walko, D.A.; Hong, J.I.; Rao, T.V.C.; Wawrzak, Z.; Seidman, D.N.; Halperin, W.P.; Bedzyk, M.J. Crystal structure assignment for the heavy-fermion superconductor UPt3. Phys. Rev. B 2001, 63, 054522. [Google Scholar] [CrossRef]
  91. Aeppli, G.; Bucher, E.; Broholm, C.; Kjems, J.K.; Baumann, J.; Hufnagl, J. Magnetic order and fluctuations in superconducting UPt3. Phys. Rev. Lett. 1988, 60, 615. [Google Scholar] [CrossRef]
  92. Machida, Y.; Itoh, A.; So, Y.; Izawa, K.; Haga, Y.; Yamamoto, E.; Kimura, N.; Onuki, Y.; Tsutsumi, Y.; Machida, K. Twofold Spontaneous Symmetry Breaking in the Heavy-Fermion Superconductor UPt3. Phys. Rev. Lett. 2012, 108, 157002. [Google Scholar] [CrossRef]
  93. Izawa, K.; Nakajima, Y.; Goryo, J.; Matsuda, Y.; Osaki, S.; Sugawara, H.; Sato, H.; Thalmeier, P.; Maki, K. Multiple Superconducting Phases in New Heavy Fermion Superconductor PrOs4Sb12. Phys. Rev. Lett. 2003, 90, 117001. [Google Scholar] [CrossRef]
  94. Sakakibara, T.; Yamada, A.; Custers, J.; Yano, K.; Tayama, T.; Aoki, H.; Machida, K. Nodal Structures of Heavy Fermion Superconductors Probed by the Specific-Heat Measurements in Magnetic Fields. J. Phys. Soc. Jpn. 2007, 76, 051004. [Google Scholar] [CrossRef]
  95. Kittaka, S.; An, K.; Sakakibara, T.; Haga, Y.; Yamamoto, E.; Kimura, N.; Ōnuki, Y.; Machida, K. Anomalous Field-Angle Dependence of the Specific Heat of Heavy-Fermion Superconductor UPt3. J. Phys. Soc. Jpn. 2013, 82, 024707. [Google Scholar] [CrossRef]
  96. Machida, K. Spin Triplet Nematic Pairing Symmetry and Superconducting Double Transition in U1−xThxBe13. J. Phys. Soc. Jpn. 2018, 87, 033703. [Google Scholar] [CrossRef]
  97. Roy, B.; Ghorashi, S.A.A.; Foster, M.S.; Nevidomskyy, A.H. Topological superconductivity of spin-3/2 carriers in a three-dimensional doped Luttinger semimetal. arXiv, 2017; arXiv:1708.07825. [Google Scholar]
  98. Venderbos, J.W.F.; Savary, L.; Ruhman, J.; Lee, P.A.; Fu, L. Pairing States of Spin-3/2 Fermions: Symmetry-Enforced Topological Gap Functions. Phys. Rev. X 2018, 8, 011029. [Google Scholar] [CrossRef]
  99. Agterberg, D.F. Vortex Lattice Structures of Sr2RuO4. Phys. Rev. Lett. 1998, 80, 5184. [Google Scholar] [CrossRef]
  100. Yonezawa, S.; Kajikawa, T.; Maeno, Y. First-Order Superconducting Transition of Sr2RuO4. Phys. Rev. Lett. 2013, 110, 077003. [Google Scholar] [CrossRef]
  101. Yonezawa, S.; Kajikawa, T.; Maeno, Y. Specific-Heat Evidence of the First-Order Superconducting Transition in Sr2RuO4. J. Phys. Soc. Jpn. 2014, 83, 083706. [Google Scholar] [CrossRef]
  102. Hicks, C.W.; Brodsky, D.O.; Yelland, E.A.; Gibbs, A.S.; Bruin, J.A.N.; Barber, M.E.; Edkins, S.D.; Nishimura, K.; Yonezawa, S.; Maeno, Y.; et al. Strong Increase of Tc of Sr2RuO4 Under Both Tensile and Compressive Strain. Science 2014, 344, 283. [Google Scholar] [CrossRef]
  103. Steppke, A.; Zhao, L.; Barber, M.E.; Scaffidi, T.; Jerzembeck, F.; Rosner, H.; Gibbs, A.S.; Maeno, Y.; Simon, S.H.; et al. Strong peak in Tc of Sr2RuO4 under uniaxial pressure. Science 2017, 355, eaaf9398. [Google Scholar] [CrossRef] [PubMed]
  104. Huang, W.; Yao, H. Possible Three-Dimensional Nematic Odd-Parity Superconductivity in Sr2RuO4. Phys. Rev. Lett. 2018, 121, 157002. [Google Scholar] [CrossRef]
  105. Hecker, M.; Schmalian, J. Vestigial nematic order and superconductivity in the doped topological insulator CuxBi2Se3. npj Quantum Mater. 2018, 3, 26. [Google Scholar] [CrossRef]
  106. Uematsu, H.; Mizushima, T.; Tsuruta, A.; Fujimoto, S.; Sauls, J.A. Chiral Higgs Mode in Nematic Superconductors. arXiv, 2018; arXiv:1809.06989. [Google Scholar]
  107. Nagai, Y.; Nakamura, H.; Machida, M. Spin-Polarized Majorana Bound States inside a Vortex Core in Topological Superconductors. J. Phys. Soc. Jpn. 2014, 83, 064703. [Google Scholar] [CrossRef]
  108. Zyuzin, A.A.; Garaud, J.; Babaev, E. Nematic Skyrmions in Odd-Parity Superconductors. Phys. Rev. Lett. 2017, 119, 167001. [Google Scholar] [CrossRef] [PubMed]

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Download PDF
Tuning Nanoscale Friction by Applying Weak Magnetic Fields to Reorient Adsorbed Oxygen Molecules
Previous
Geometric Effects of a Quarter of Corrugated Torus
Next