Effect and Characterization of Stone–Wales Defects on Graphene Quantum Dot: A First-Principles Study
Abstract
:1. Introduction
2. Computational Details
3. Structural Modifications
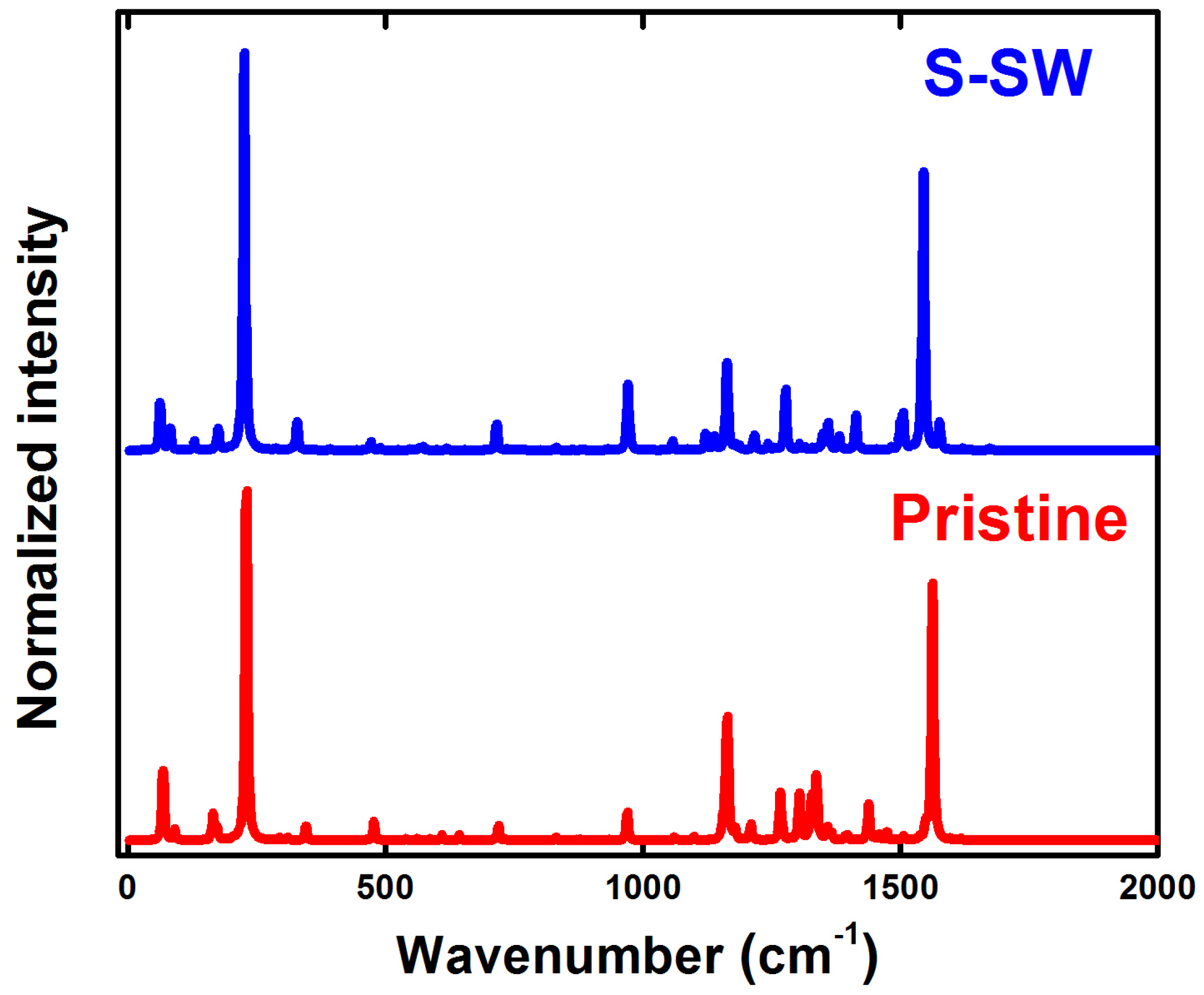
4. Raman Spectra
5. IR Spectra
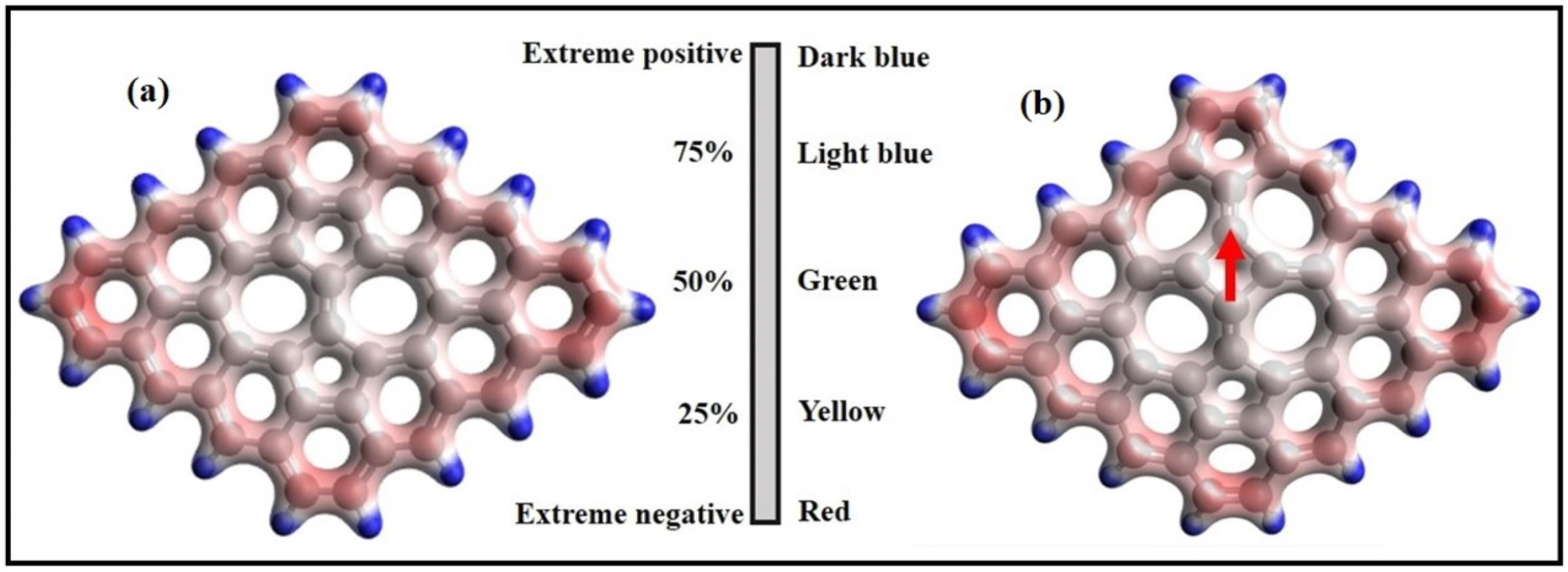
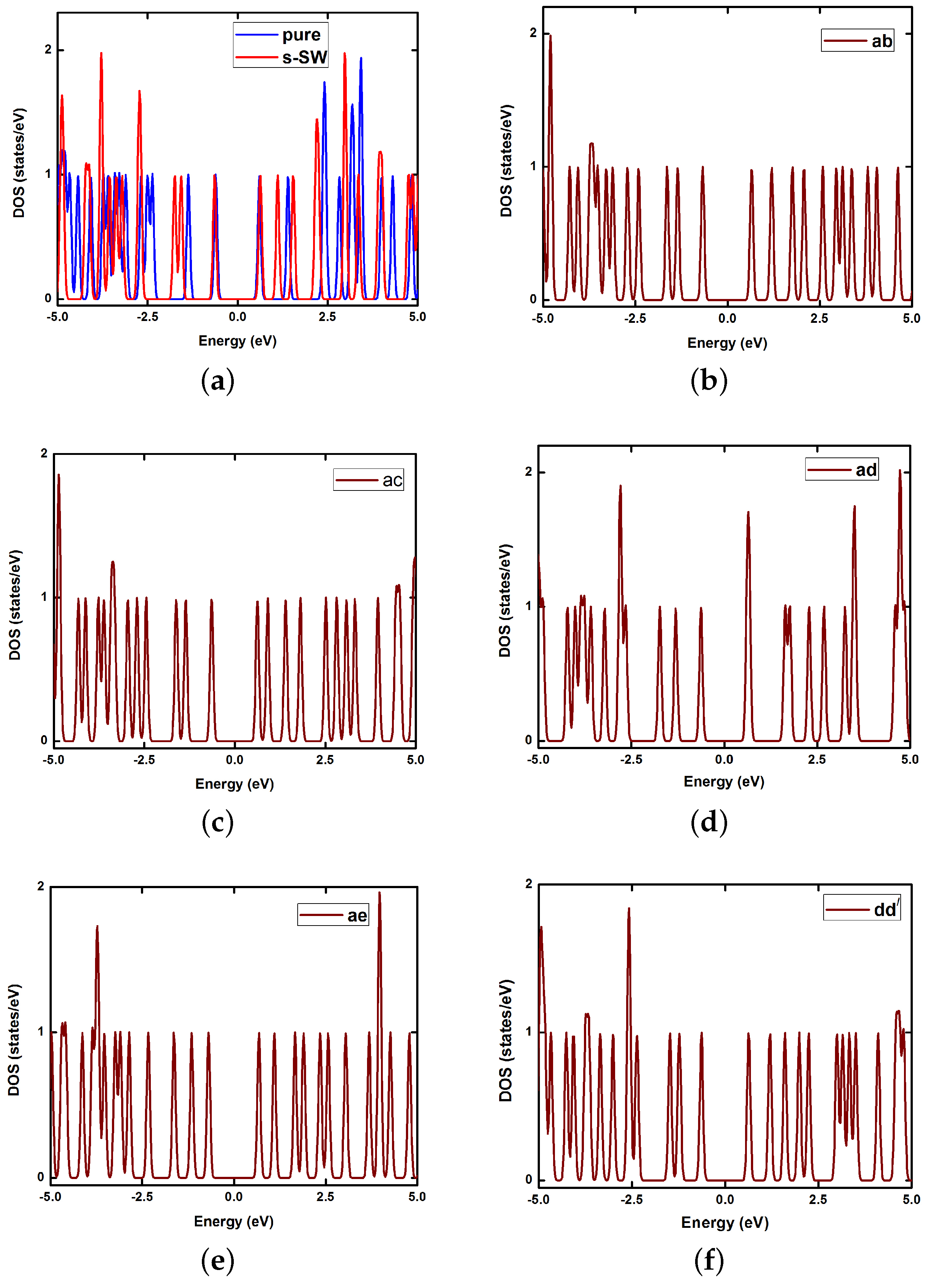
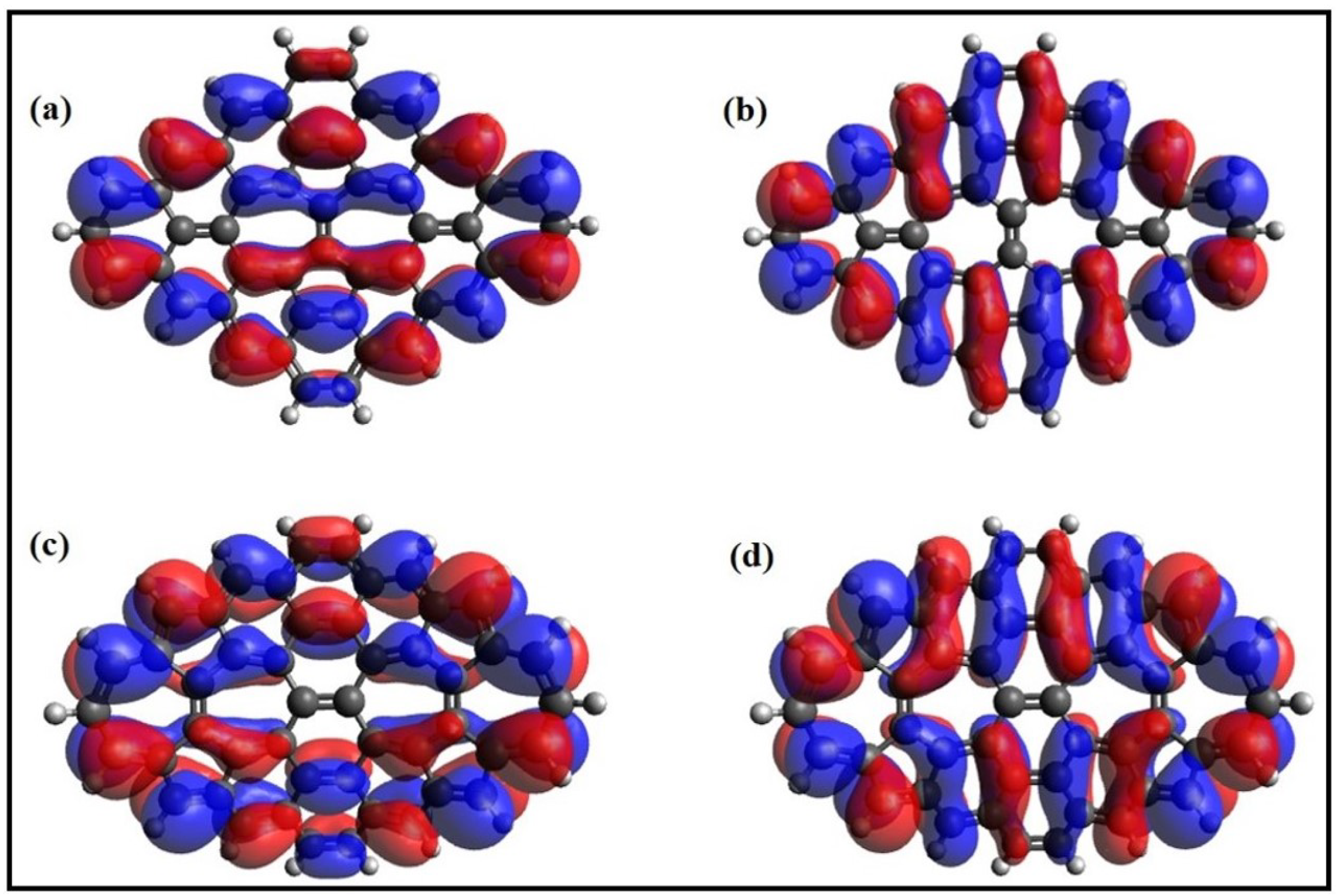
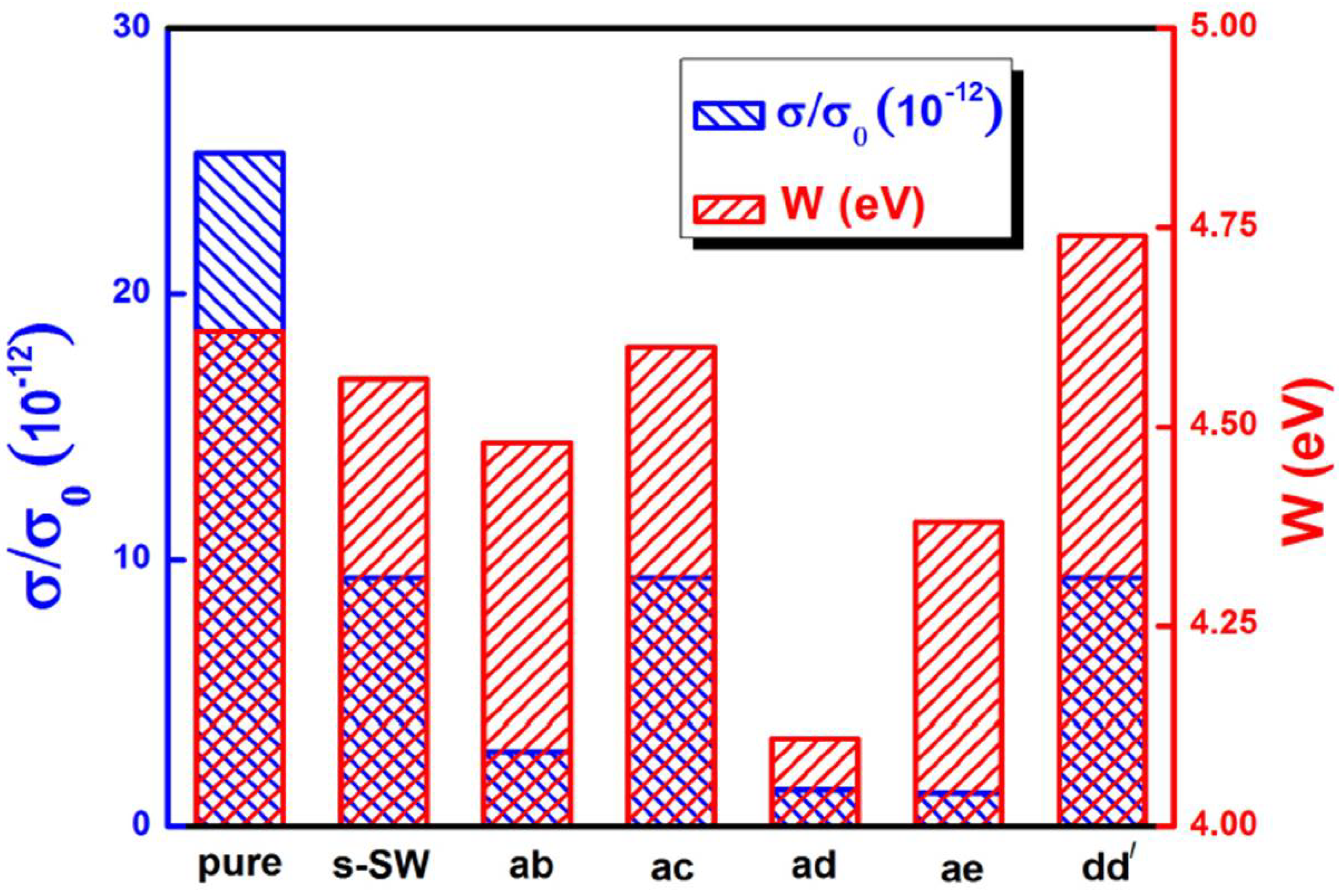
6. Electronic Properties
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183. [Google Scholar] [CrossRef] [PubMed]
- Neto, A.H.C.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Nath, P.; Chowdhury, S.; Sanyal, D.; Jana, D. Ab-initio calculation of electronic and optical properties of nitrogen and boron doped graphene nanosheet. Carbon 2014, 73, 275. [Google Scholar] [CrossRef]
- Gui, G.; Li, J.; Zhong, J. Band structure engineering of graphene by strain: First-principles calculations. Phys. Rev. B 2008, 78, 075435. [Google Scholar] [CrossRef]
- Nath, P.; Sanyal, D.; Jana, D. Semi-metallic to semiconducting transition in graphene nanosheet with site specific co-doping of boron and nitrogen. Phys. E 2014, 56, 64. [Google Scholar] [CrossRef]
- Jana, D.; Nath, P.; Sanyal, D. Modifications of electronic properties of graphene by boron (B) and nitrogen (N) substitution. In Graphene Science Handbook, Nanostructure and Atomic Arrangements; Aliofkhazraei, M., Ali, N., Milne, W.I., Ozkan, C.S., Mitura, S., Gervasoni, J.L., Eds.; CRC Press: New York, NY, USA, 2016. [Google Scholar]
- Chowdhury, S.; Das, R.; Nath, P.; Sanyal, D.; Jana, D. Electronic and optical properties of boron and nitrogen functionalizad graphene nanosheet. In Chemical Functionalization of Carbon Nano-Materials: Chemistry and Applications; Thakur, V.K., Thakur, M.K., Eds.; CRC Publications: New York, NY, USA, 2015. [Google Scholar]
- Chowdhury, S.; Jana, D. A theoretical review on electronic, magnetic and optical properties of silicene. Rep. Prog. Phys. 2016, 79, 126501. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, S.; Bandyopadhyay, A.; Dhar, N.; Jana, D. Optical and magnetic properties of free-standing silicene, germanene and T-graphene system. Phys. Sci. Rev. 2017, 2, 0102. [Google Scholar]
- Yan, X.; Cui, X.; Li, L.-S. Synthesis of large, stable colloidal graphene quantum dots with tunable size. J. Am. Chem. Soc. 2010, 132, 5944. [Google Scholar] [CrossRef]
- Li, X.L.; Wang, X.R.; Zhang, L.; Lee, S.W.; Dai, H.J. Chemically derived, ultrasmooth graphene nanoribbon semiconductors. Science 2008, 319, 1229. [Google Scholar] [CrossRef]
- Cai, J.M.; Ruffieux, P.; Jaafar, R.; Bieri, M.; Braun, T.; Blankenburg, S.; Muoth, M.; Seitsonen, A.P.; Saleh, M.; Feng, X.; et al. Atomically precise bottom-up fabrication of graphene nanoribbons. Nature 2010, 466, 470. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Nandy, A.; Chakrabarti, A.; Jana, D. Optical properties and magnetic flux-induced electronic band tuning of a T-graphene sheet and nanoribbon. Phys. Chem. Chem. Phys. 2017, 19, 21584. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Hwang, S.W.; Kim, M.K.; Shin, D.Y.; Shin, D.H.; Kim, C.O.; Yang, S.B.; Park, J.H.; Hwang, E.; Choi, S.-H.; et al. Anomalous behaviors of visible luminescence from graphene quantum dots: Interplay between size and shape. ACS Nano 2012, 6, 8203. [Google Scholar] [CrossRef] [PubMed]
- Ritter, K.A.; Lyding, J.W. The influence of edge structure on the electronic properties of graphene quantum dots and nanoribbons. Nat. Mater. 2009, 8, 235. [Google Scholar] [CrossRef] [PubMed]
- Das, R.; Dhar, N.; Bandyopadhyay, A.; Jana, D. Size dependent magnetic and optical properties in diamond shaped graphene quantum dots: A DFT study. J. Phys. Chem. Solids. 2016, 99, 34. [Google Scholar] [CrossRef]
- Hamilton, I.P.; Li, B.; Yan, X.; Li, L. Alignment of colloidal graphene quantum dots on polar surfaces. Nano Lett. 2011, 11, 1524. [Google Scholar] [CrossRef]
- Pan, D.; Xi, C.; Li, Z.; Wang, L.; Chen, Z.; Lu, B.; Wu, M. Electrophoretic fabrication of highly robust, efficient, and benign heterojunction photoelectrocatalysts based on graphene-quantum-dot sensitized TiO2 nanotube arrays. J. Mater. Chem. 2013, 1, 3551. [Google Scholar] [CrossRef]
- Gupta, V.; Chaudhary, N.; Srivastava, R.; Sharma, G.D.; Bhardwaj, R.; Chand, S. Luminscent graphene quantum dots for organic photovoltaic devices. J. Am. Chem. Soc. 2011, 133, 9960. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, Y.; Cheng, H.; Hu, Y.; Shi, G.; Dai, L.; Qu, L. Nitrogen-Doped Graphene Quantum Dots with Oxygen-Rich Functional Groups. J. Am. Chem. Soc. 2012, 134, 15. [Google Scholar] [CrossRef]
- Dong, Y.; Chen, C.; Zheng, X.; Gao, L.; Cui, Z.; Yang, H.; Guo, C.; Chi, Y.; Li, C.M. One-step and high yield simultaneous preparation of single-and multi-layer graphene quantum dots from CX-72 carbon black. J. Mater. Chem. 2012, 22, 8764. [Google Scholar] [CrossRef]
- Sun, H.; Wu, L.; Gao, N.; Ren, J.; Qu, X. Improvement of photoluminescence of graphene quantum dots with a biocompatible photochemical reduction pathway and its bioimaging application. ACS Appl. Mater. Interfaces 2013, 5, 1174. [Google Scholar] [CrossRef]
- Zhao, H.; Chang, Y.; Liu, M.; Gao, S.; Yu, H.; Quan, X. A universal immunosensing strategy based on regulation of the interaction between graphene and graphene quantum dots. Chem. Commun. 2013, 49, 234. [Google Scholar] [CrossRef]
- Ran, X.; Sun, H.; Pu, F.; Ren, J.; Qu, X. Ag nanoparticle-decorated graphene quantum dots for label-free, rapid and sensitive detection of Ag+ and biothiols. Chem. Commun. 2013, 49, 1079. [Google Scholar] [CrossRef]
- Bai, J.M.; Zhang, L.; Liang, R.P.; Qiu, J.D. Graphene quantum dots combined with europium ions as photoluminescent probes for phosphate sensing. Chem. Eur. J. 2013, 19, 3822. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, A.; Suenaga, K.; Gloter, A.; Urita, K.; Iijima, S. Direct evidence for atomic defects in graphene layers. Nature 2004, 430, 870. [Google Scholar] [CrossRef]
- Meyer, J.C.; Geim, A.K.; Katsnelson, M.I.; Novoselov, K.S.; Booth, T.J.; Roth, S. The structure of suspended graphene sheets. Nature 2007, 446, 60. [Google Scholar] [CrossRef] [PubMed]
- Fasolino, A.; Los, J.H.; Katsnelson, M.I. Intrinsic ripples in graphene. Nat. Mater. 2007, 6, 858. [Google Scholar] [CrossRef] [PubMed]
- Alam, A.; Sanyal, B.; Mookerjee, A. Effect of disorder on the electronic properties of graphene: A theoretical approach. Phys. Rev. B 2012, 86, 085454. [Google Scholar] [CrossRef]
- Sadhukhan, B.; Nayak, A.; Mookerjee, A. Effect of random vacancies on the electronic properties of graphene and T graphene: A theoretical approach. Indian J. Phys. 2017, 91, 1541. [Google Scholar] [CrossRef]
- Chowdhury, S.; Baidya, S.; Nafday, D.; Halder, S.; Kabir, M.; Sanyal, B.; Saha-Dasgupta, T.; Jana, D.; Mookerjee, A. A real-space study of random extended defects in solids: Application to disordered Stone–Wales defects in graphene. Phys. E 2014, 61, 191. [Google Scholar] [CrossRef]
- Kotakoski, J.; Meyer, J.C.; Kurasch, S.; Santos-Cottin, D.; Kaiser, U.; Krasheninnikov, A.V. Stone–Wales-type transformations in carbon nanostructures driven by electron irradiation. Phys. Rev. B 2011, 83, 245420. [Google Scholar] [CrossRef]
- Jana, D.; Sun, C.L.; Chen, L.C.; Chen, K.H. Effect of chemical doping of boron and nitrogen on the electronic, optical, and electrochemical properties of carbon nanotubes. Prog. Mater. Sci. 2013, 58, 565. [Google Scholar] [CrossRef]
- Zhang, W.X.; He, C.; Lia, T.; Gonga, S.B. Tuning electronic and magnetic properties of zigzag graphene nanoribbons with a Stone–Wales line defect by position and axis tensile strain. RSC Adv. 2015, 5, 33407. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, Y.; Yakobson, B.I. Fullerene shape transformations via Stone–Wales bond rotations. Phys. Rev. B 2003, 68, 233403. [Google Scholar] [CrossRef]
- Kotakoski, J.; Krasheninnikov, A.V.; Kaiser, U.; Meyer, J.C. From point defects in graphene to two-dimensional amorphous carbon. Phys. Rev. Lett. 2011, 106, 105505. [Google Scholar] [CrossRef] [PubMed]
- Vicarelli, L.; Heerema, S.J.; Dekker, C.; Zandbergen, H.W. Controlling defects in graphene for optimizing the electrical properties of graphene nanodevices. ACS Nano 2015, 9, 3428. [Google Scholar] [CrossRef] [PubMed]
- Xia, F.; Farmer, D.B.; Lin, Y.; Avouris, P. Graphene field-effect transistors with high on/off current ratio and large transport band gap at room temperature. Nano Lett. 2010, 10, 715. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.; Bang, J.; Ryu, B.; Chang, K.J. Effect of atomic-scale defects on the low-energy electronic structure of graphene: Perturbation theory and local-density-functional calculations. Phys. Rev. B 2008, 77, 115453. [Google Scholar] [CrossRef]
- Carlsson, J.M.; Scheffler, M. Structural, electronic, and chemical properties of nanoporous carbon. Phys. Rev. Lett. 2006, 96, 046806. [Google Scholar] [CrossRef]
- Lu, J.; Yeo, P.S.E.; Gan, C.K.; Wu, P.; Loh, K.P. Transforming C60 molecules into graphene quantum dots. Nat. Nanotechnol. 2011, 6, 247. [Google Scholar] [CrossRef]
- Malard, L.M.; Pimenta, M.A.; Dresselhaus, G.; Dresselhaus, M.S. Raman spectroscopy in graphene. Phys. Rep. 2009, 473, 51. [Google Scholar] [CrossRef]
- Dresslhaus, M.S.; Jorio, A.; Saito, R. Characterizing Graphene, Graphite, and Carbon Nanotubes by Raman Spectroscopy. Annu. Rev. Condens. Matter Phys. 2010, 108, 1. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Paria, S.; Jana, D. Tetragonal graphene nanodot as carbon monoxide gas sensor and current rectification device. J. Phys. Chem. Solids 2018, 123, 172. [Google Scholar] [CrossRef]
- Cancado, L.G.; Pimenta, M.A.; Neves, B.R.A.; Dantas, M.S.; Jorio, A. Influence of the Atomic Structure on the Raman Spectra of Graphite Edges. Phys. Rev. Lett 2004, 93, 247401. [Google Scholar] [CrossRef] [PubMed]
- Krauss, B.; Nemes-Incze, P.; Skakalova, V.; Biro, L.P.; von Klitzing, K.; Smet, J.H. Raman scattering at pure graphene zigzag edges. Nano Lett. 2010, 10, 4544. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B. Gaussian 09 Manual. Available online: http://gaussian.com (accessed on 14 December 2018).
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef]
- Miehlich, B.; Savin, A.; Stoll, H.; Preuss, H. Results obtained with the correlation energy density functionals of Becke and Lee, Yang and Parr. Chem. Phys. Lett. 1989, 157, 200. [Google Scholar] [CrossRef]
- Scott, A.P.; Radom, L. Harmonic Vibrational Frequencies: An Evaluation of Hartree–Fock, Møller–Plesset, Quadratic Configuration Interaction, Density Functional Theory, and Semiempirical Scale Factors. J. Phys. Chem. 1996, 100, 16502. [Google Scholar] [CrossRef]
- Boyle, N.O. GaussSum 3.0 Home Page. Available online: http://www.gausssum.sf.net (accessed on 13 December 2018).
- Ugarte, D. Curling and closure of graphitic networks under electron-beam irradiation. Nature 1992, 359, 707. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Pal, P.; Chowdhury, S.; Jana, D. First principles Raman study of boron and nitrogen doped planar T-graphene clusters. Mater. Res. Express 2015, 2, 95603. [Google Scholar] [CrossRef]
- Shirodkar, S.N.; Waghmare, U.V. Electronic and vibrational signatures of Stone–Wales defects in graphene: First-principles analysis. Phys. Rev. B 2012, 86, 165401. [Google Scholar] [CrossRef]
- Chopra, S.; McGuire, K.; Gothard, N.; Rao, A.M. Selective gas detection using a carbon nanotube sensor. Appl. Phys. Lett. 2003, 83, 2280. [Google Scholar] [CrossRef]
- Nagarajan, V.; Chandiramouli, R. Investigation on adsorption properties of CO and NO gas molecules on aluminene nanosheet: A density functional application. Mater. Sci. Eng. B 2018, 229, 193. [Google Scholar] [CrossRef]
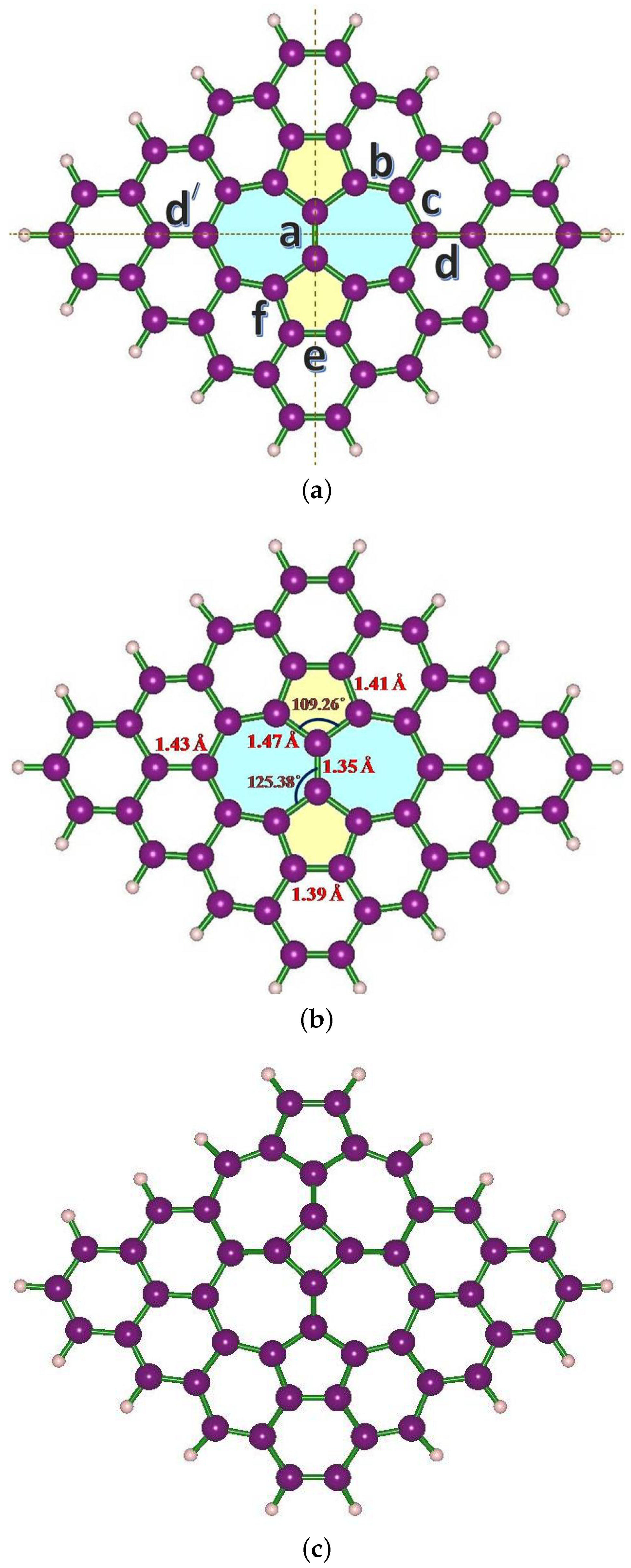
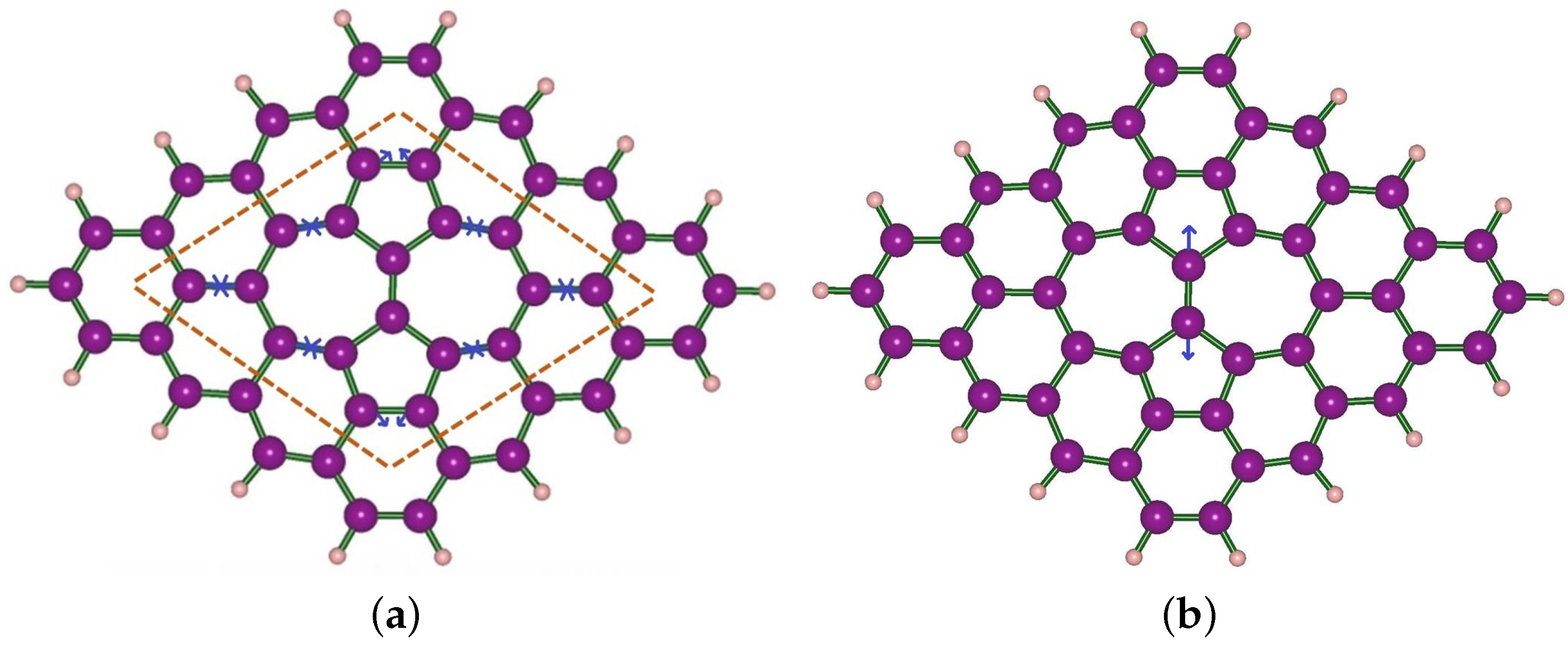
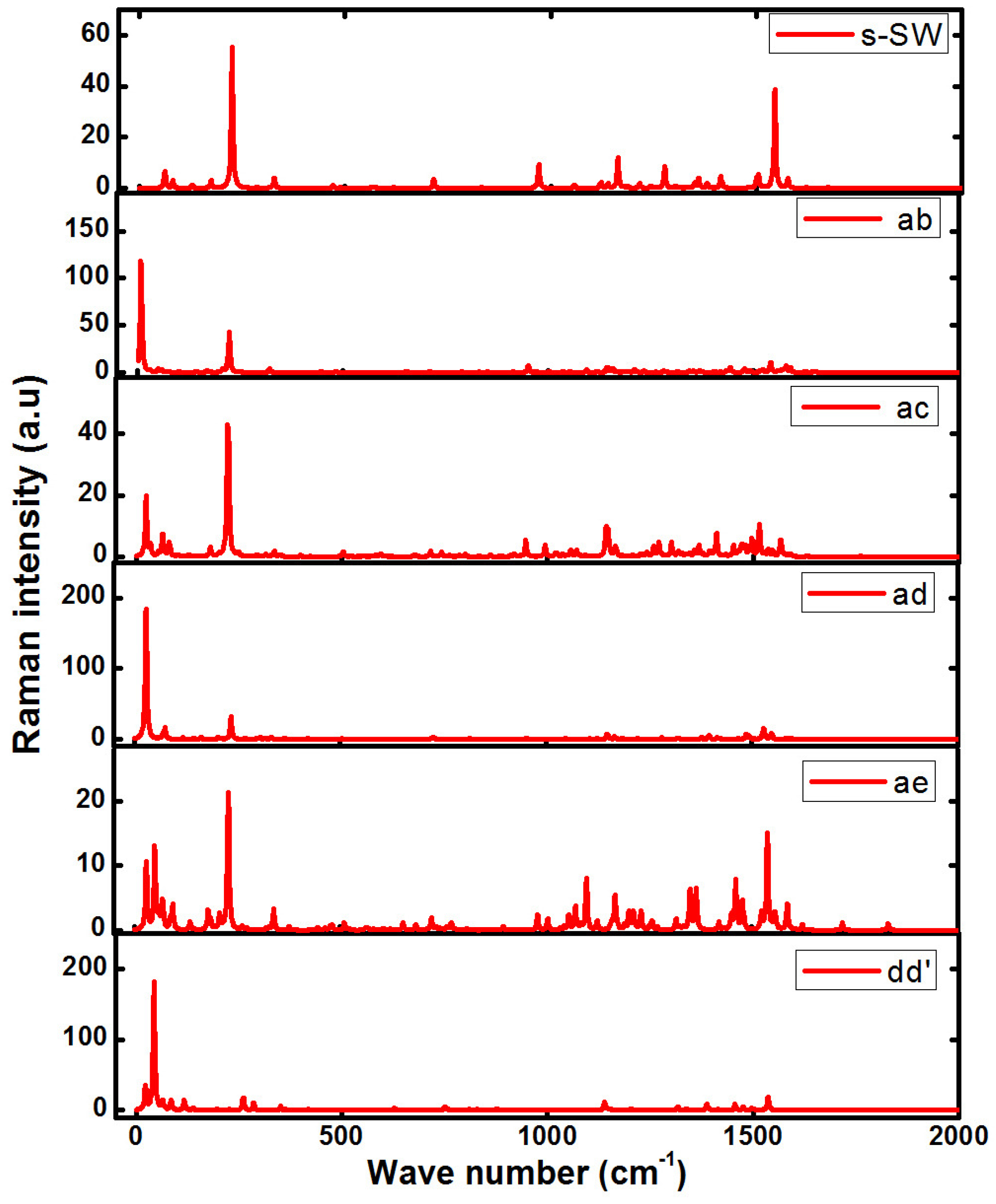
| Systems | Tetragon | Pentagon | Heptagon | Octagon | Distance (Å) | E (eV) |
|---|---|---|---|---|---|---|
| pristine | 0 | 0 | 0 | 0 | - | −50,074.06 |
| s-SW | 0 | 2 | 2 | 0 | - | −50,070.92 |
| ab | 0 | 2 | 2 | 0 | 2.36 | −50,069.59 |
| ac | 0 | 3 | 3 | 0 | 3.00 | −50,069.01 |
| ad | 0 | 4 | 2 | 1 | 3.99 | −50,068.48 |
| ae | 1 | 2 | 4 | 0 | 2.82 | −50,067.24 |
| dd | 0 | 4 | 4 | 0 | 7.98 | −50,068.52 |
| Systems | D (debye) | E (eV) | E (eV) | E (eV) | E (eV) | W (eV) |
|---|---|---|---|---|---|---|
| pristine | 0 | 0.46 | −2.94 | −4.16 | 1.22 | 4.62 |
| s-SW | 0.0013 | 0.47 | −2.82 | −4.09 | 1.27 | 4.56 |
| ab | 0.8619 | 0.29 | −2.86 | −4.19 | 1.33 | 4.48 |
| ac | 0.9864 | 0.45 | −2.88 | −4.15 | 1.27 | 4.60 |
| ad | 0.4654 | 0.02 | −2.84 | −4.09 | 1.25 | 4.11 |
| ae | 1.4739 | 0.13 | −2.88 | −4.25 | 1.37 | 4.38 |
| dd | 0.1537 | 0.54 | −2.93 | −4.20 | 1.27 | 4.74 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chakraborti, G.; Bandyopadhyay, A.; Jana, D. Effect and Characterization of Stone–Wales Defects on Graphene Quantum Dot: A First-Principles Study. Condens. Matter 2018, 3, 50. https://doi.org/10.3390/condmat3040050
Chakraborti G, Bandyopadhyay A, Jana D. Effect and Characterization of Stone–Wales Defects on Graphene Quantum Dot: A First-Principles Study. Condensed Matter. 2018; 3(4):50. https://doi.org/10.3390/condmat3040050
Chicago/Turabian StyleChakraborti (Banerjee), Gargi, Arka Bandyopadhyay, and Debnarayan Jana. 2018. "Effect and Characterization of Stone–Wales Defects on Graphene Quantum Dot: A First-Principles Study" Condensed Matter 3, no. 4: 50. https://doi.org/10.3390/condmat3040050
APA StyleChakraborti, G., Bandyopadhyay, A., & Jana, D. (2018). Effect and Characterization of Stone–Wales Defects on Graphene Quantum Dot: A First-Principles Study. Condensed Matter, 3(4), 50. https://doi.org/10.3390/condmat3040050




