Fluctuation Theory in Chemical Kinetics
Abstract
:1. Introduction
2. Reaction Mechanisms and Kinetic Rates
2.1. Chemical Equilibrium
2.2. Fluctuation Theory
3. Chemical Equilibrium Formation
3.1. Flow Components
3.2. Concentration Capacity
3.3. Concentration Correlation
3.4. Equilibrium Stability
3.4.1. Local Stability
3.4.2. Global Stability
4. Discussion of the Results
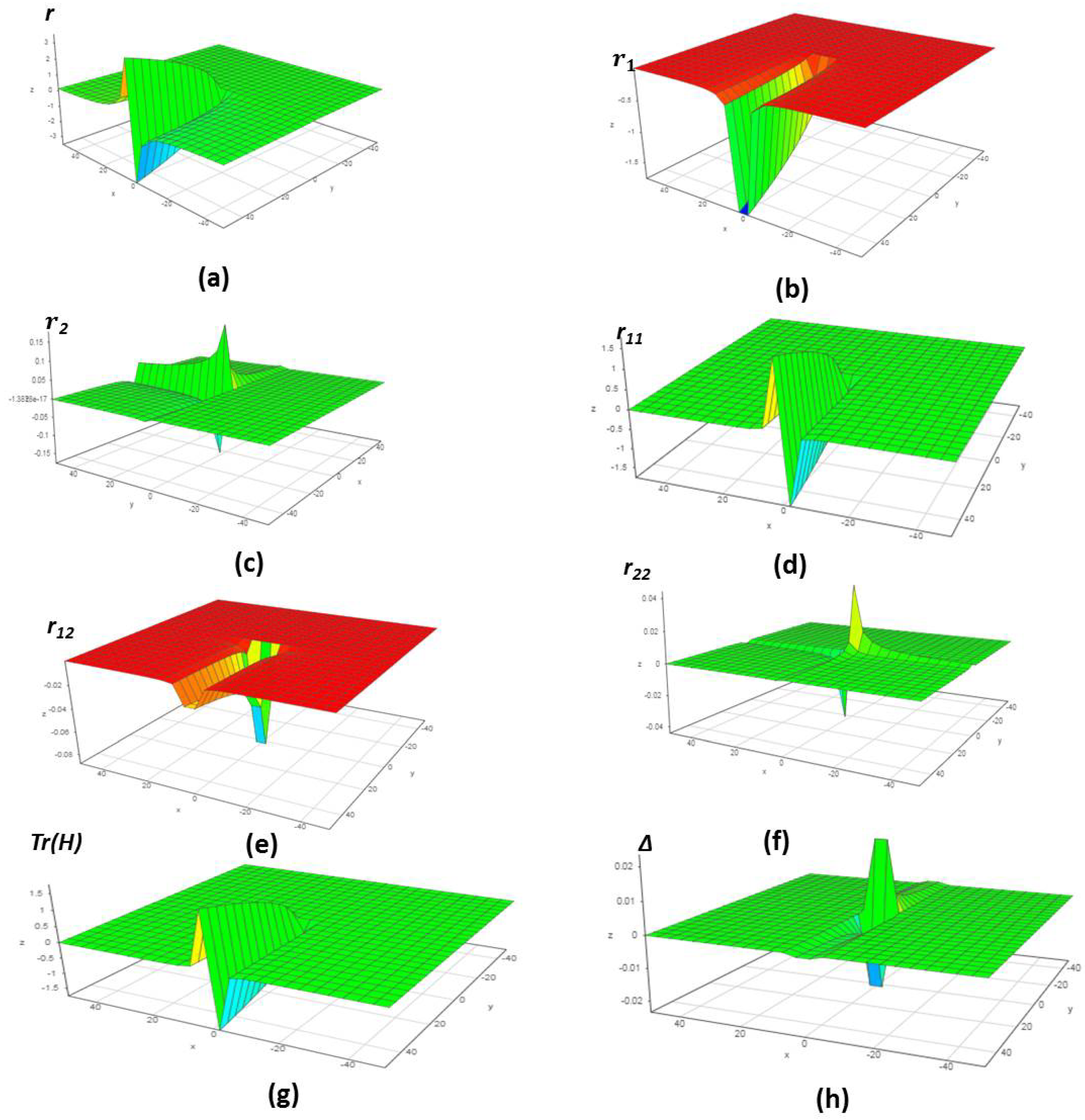
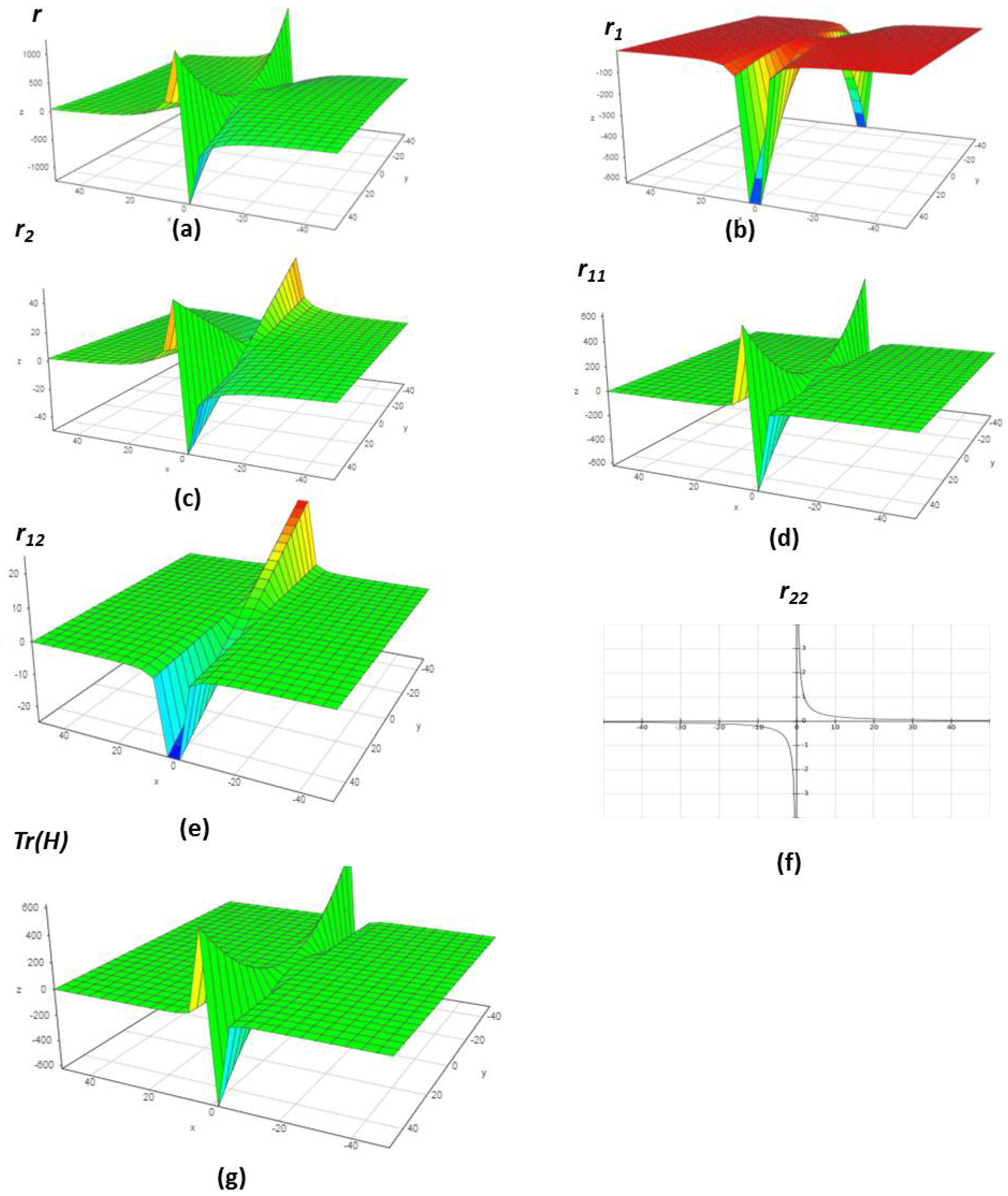
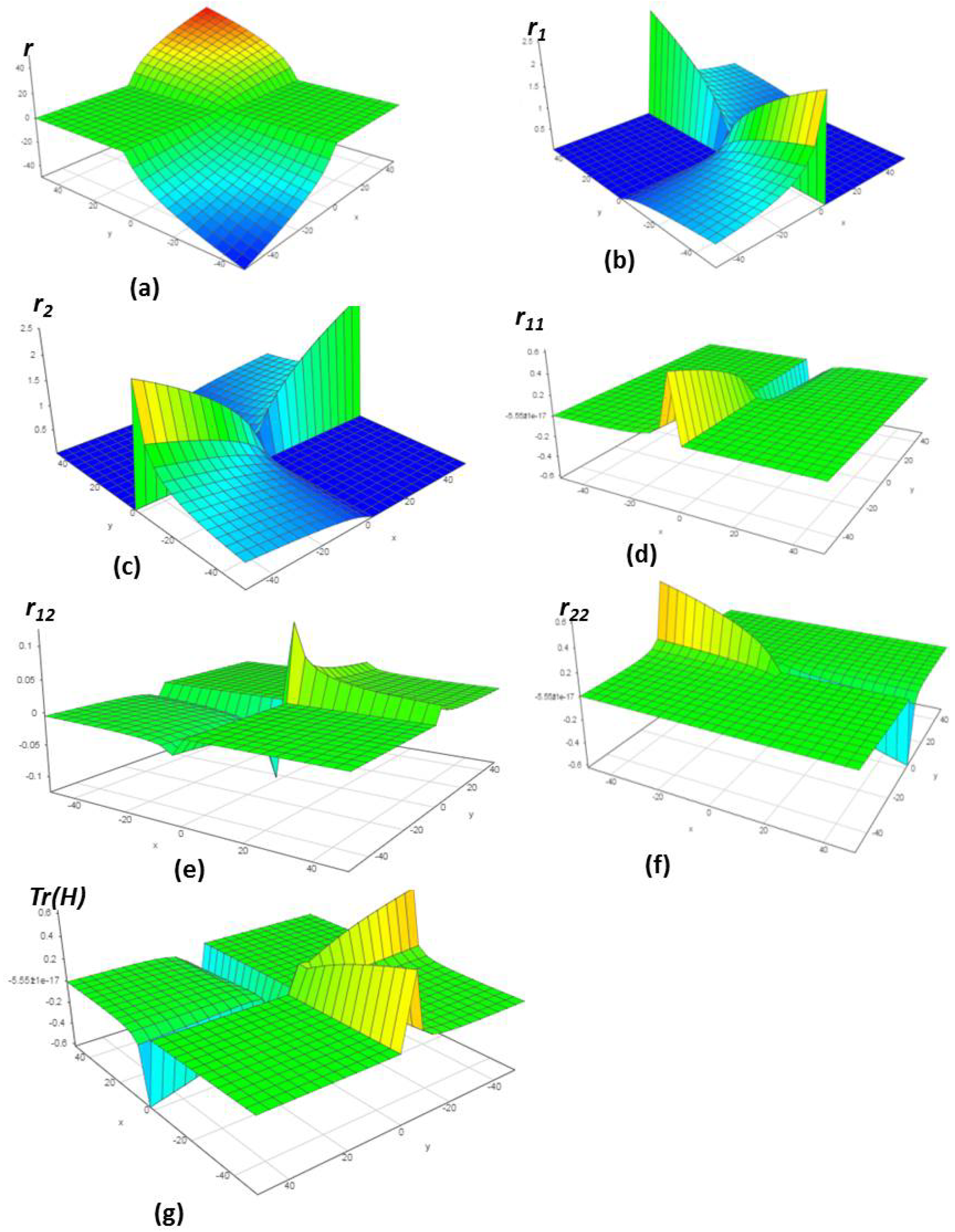
4.1. Chemical Reactions with Orders
4.2. Chemical Reactions with Orders
4.3. Chemical Reactions with Orders
4.4. Chemical Reactions with Orders
4.5. Chemical Reactions with Orders
4.6. Chemical Reactions with Orders
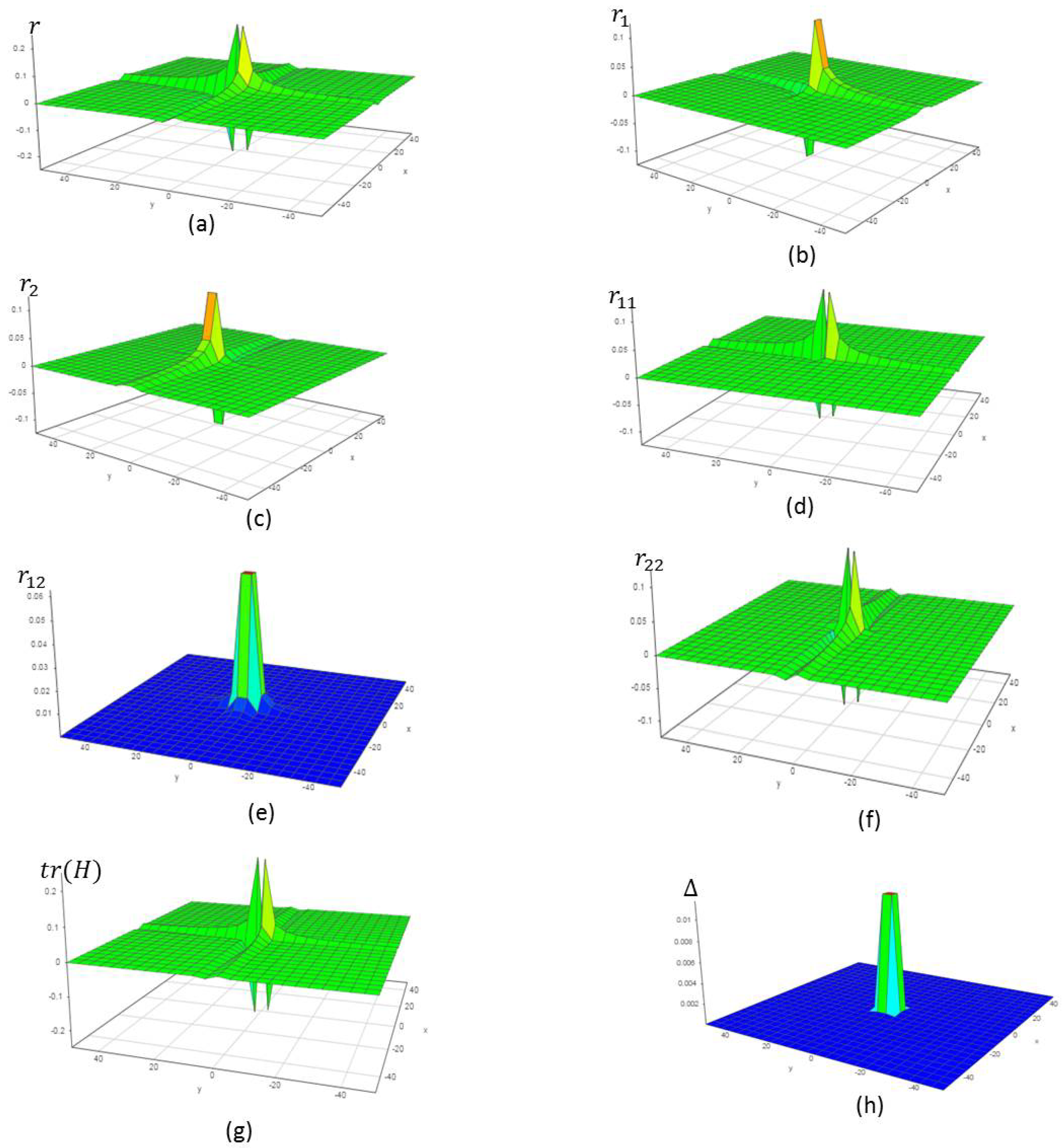
5. Verification of the Model
5.1. An Inorganic Equilibrium Formation
5.2. An Organic Equilibrium Formation
5.3. A Catalytic Oxidation of Mixtures
6. Future Scope of the Work
6.1. Proton Donor-Acceptor Equilibrium
6.2. Fall of the Proton
6.3. Buffer Capacity
6.4. Acid Raining
7. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Blinder, S.M.; Nordman, C.E. Collision theory of chemical reactions. J. Chem. Educ. 1974, 51, 790. [Google Scholar] [CrossRef]
- Scribed, Kinetics: Rates and Mechanisms of Chemical Reactions. Available online: https://www.scribd.com/document/85038774/Chapter-16 (accessed on 10 January 2017).
- Miller, W.H. Quantum mechanical transition state theory and a new semiclassical model for reaction rate constants. J. Chem. Phys. 1974, 61, 1823–1834. [Google Scholar] [CrossRef]
- Atkins, P.; de Paula, J. Physical Chemistry, 10th ed.; W. H. Freeman: New York, NY, USA, 2014; ISBN 13-978-1429290197. [Google Scholar]
- Eyring, H. Quantum Mechanics and Chemical Reactions. Chem. Rev. 1932, 10, 103–123. [Google Scholar] [CrossRef]
- Boudart, M. Kinetics of Chemical Processes; Brenner, H., Ed.; Butterworth-Heinemann: Oxford, UK, 1991; pp. 13–16. ISBN 9780750690065. [Google Scholar]
- Bransden, B.H.; Joachain, C.J. Physics of Atoms and Molecules, Pearson, 2nd ed.; Pearson Education: Delhi, India, 2003. [Google Scholar]
- Karplus, M.; Porter, R.N. Atoms and Molecules: An Introduction for Students of Physical Chemistry; Benjamin Cummings: San Francisco, CA, USA, 1970; ISBN 0-8053-5218-8. [Google Scholar]
- Haas, E.; Katchalski-Katzir, E.; Steinberg, I.Z. Effect of the orientation of donor and acceptor on the probability of energy transfer involving electronic transitions of mixed polarization. Biochemistry 1978, 17, 5064–5070. [Google Scholar] [CrossRef] [PubMed]
- Espenson, J.H. Chemical Kinetics and Reaction Mechanisms, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2002; ISBN 13-978-0072883626. [Google Scholar]
- DeCoursey, W.J.; Thring, R.W. Effects of unequal diffusivities on enhancement factors for reversible and irreversible reaction. Chem. Eng. Sci. 1989, 44, 1715–1721. [Google Scholar] [CrossRef]
- Pokrovsky, O.S.; Schott, J. Experimental study of brucite dissolution and precipitation in aqueous solutions: Surface speciation and chemical affinity control. Geochim. Cosmochim. Acta 2004, 68, 31–45. [Google Scholar] [CrossRef]
- Califano, S. Pathways to Modern Chemical Physics; Springer: Berlin/Heidelberg, Germany, 2012; ISBN 978-3-642-28180-8. [Google Scholar]
- Huang, K. Statistical Mechanics, 2nd ed.; Wiley: Hoboken, NJ, USA, 1987; ISBN 13-978-0471815181. [Google Scholar]
- Pathria, R.K. Statistical Mechanics, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1996; ISBN 13-978-0750624695. [Google Scholar]
- Bigeleisen, J.; Wolfsberg, M. Theoretical and experimental aspects of isotope effects in chemical kinetics. Adv. Chem. Phys. 2007, 1, 15–76. [Google Scholar]
- Ruppeiner, G. Reimannian geometry in thermodynamic fluctuation theory. Rev. Mod. Phys. 1995, 67, 605. [Google Scholar] [CrossRef]
- Bellucci, S.; Tiwari, B.N. On the microscopic perspective of black brans thermodynamic geometry. Entropy 2010, 12, 2097–2143. [Google Scholar] [CrossRef]
- Weinhold, F. Metric geometry of equilibrium thermodynamics. J. Chem. Phys. 1975, 63, 2479. [Google Scholar] [CrossRef]
- Weinhold, F. Metric geometry of equilibrium thermodynamics: Scaling, homogeneity and generalized Gibbs-Duhem relations. J. Chem. Phys. 1975, 63, 2484. [Google Scholar] [CrossRef]
- Tiwari, B.N. Geometric Perspective of Entropy Function: Embedding, Spectrum and Convexity; LAMBERT Academic Publishing: Riga, Latvia, 2011; ISBN 13-978-3845431789. [Google Scholar]
- Tiwari, B.N.; Kuipo, J.K.; Bellucci, S.; Marina, N. On Extensions of the Optical Optimization. Am. Sci. Res. J. Eng. Technol. Sci. 2016, 26, 302–313. [Google Scholar]
- Diercks, C.S.; Yaghi, O.M. The atom, the molecule, and the covalent organic framework. Science 2017, 355, eaal1585. [Google Scholar] [CrossRef] [PubMed]
- Espenson, J.H. Chemical Kinetics and Reaction Mechanisms; McGraw-Hill: New York, NY, USA, 1995; Volume 102. [Google Scholar]
- Laidler, K.J. Chemical Kinetics, 3rd ed.; Harper & Row: Manhattan, NY, USA, 1987; ISBN 9780060438623. [Google Scholar]
- Denbigh, K.G. The Principles of Chemical Equilibrium: With Applications in Chemistry and Chemical Engineering; Cambridge University Press: Cambridge, UK, 1981; ISBN 13-978-0521281508. [Google Scholar]
- Sandler, S.I. Chemical, Biochemical, and Engineering Thermodynamics, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006; ISBN 13-978-0471661740. [Google Scholar]
- Voit, E.O.; Martens, H.A.; Omholt, S.W. 150 years of the mass action law. PLoS Comput. Biol. 2015, 11, e1004012. [Google Scholar] [CrossRef] [PubMed]
- Alberto, M.E.; Russo, N.; Grand, A.; Galano, A. A physicochemical examination of the free radical scavenging activity of Trolox: Mechanism, kinetics and influence of the environment. Phys. Chem. Chem. Phys. 2013, 15, 4642–4650. [Google Scholar] [CrossRef] [PubMed]
- IUPAC. Compendium of Chemical Terminology—The Gold Book. Available online: https://goldbook.iupac.org/ (accessed on 24 June 2017).
- Nguyen, D.A.; Iwaniw, M.A.; Fogler, H.S. Kinetics and mechanism of the reaction between ammonium and nitrite ions: Experimental and theoretical studies. Chem. Eng. Sci. 2003, 58, 4351–4362. [Google Scholar] [CrossRef]
- Chemical Kinetics. Chapter 14. Available online: https://www.sas.upenn.edu/~mcnemar/apchem/ch14.pdf (accessed on 21 October 2018).
- Petrucci, R.H.; Herring, F.G.; Madura, J.D.; Bissonnette, C. General Chemistry: Principles and Modern Applications; Pearson: London, UK, 2017. [Google Scholar]
- Freeman, S.; Sharp, J.C.; Harrington, M. Biological Science; Prentice Hall: Upper Saddle River, NJ, USA, 2002; Volume 1. [Google Scholar]
- Pedrero, C.; Waku, T.; Iglesia, E. Oxidation of CO in H2-CO mixtures catalyzed by platinum: Alkali effects on rates and selectivity. J. Catal. 2005, 233, 242–255. [Google Scholar] [CrossRef]
- Morokuma, K. Why do molecules interact? The origin of electron donor-acceptor complexes, hydrogen bonding and proton affinity. Acc. Chem. Res. 1977, 10, 294–300. [Google Scholar] [CrossRef]
- Musto, P.; Ragosta, G.; Mascia, L. Vibrational spectroscopy evidence for the dual nature of water sorbed into epoxy resins. Chem. Mater. 2000, 12, 1331–1341. [Google Scholar] [CrossRef]
- Lower, S.K. Acid-Base Equilibria and Calculations. Available online: http://www.chem1.com/acad/pdf/c1xacid2.pdf (accessed on 14 December 2018).
- Connors, K.A. Thermodynamics of Pharmaceutical Systems: An Introduction for Students of Pharmacy; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2002; Chapter 12; pp. 157–158. [Google Scholar]
- Agmon, N.; Bakker, H.J.; Campen, R.K.; Henchman, R.H.; Pohl, P.; Roke, S.; Thamer, M.; Hassanali, A. Protons and hydroxide ions in aqueous systems. Chem. Rev. 2016, 116, 7642–7672. [Google Scholar] [CrossRef]
- Peeters, H. (Ed.) Protides of the Biological Fluids: Proceedings of the Twentieth Colloquium, Brugge, 1976; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Harris, D.C. Quantitative Chemical Analysis, 7th ed.; Freeman and Company: New York, NY, USA, 2007. [Google Scholar]
- Butler, J.N. Ionic Equilibrium: A Mathematical Approach; Addison-Wesley: Boston, MA, USA, 1964; p. 151. ISBN 13-978-0201007305. [Google Scholar]
- Hulanicki, A. Reactions of Acids and Bases in Analytical Chemistry; Masson, M.R.H., Translator; Halsted Press: Ultimo, Australia, 1987. [Google Scholar]
- Rajagopalan, R. Environmental Studies: From Crisis to Cure, 3rd ed.; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Solé, A.; Miró, L.; Barreneche, C.; Martorell, I.; Cabeza, L.F. Corrosion of metals and salt hydrates used for thermochemical energy storage. Renew. Energy 2015, 75, 519–523. [Google Scholar]
- Dillmann, P.; Beranger, G.; Piccardo, P.; Matthiessen, H. Corrosion of Metallic Heritage Artefacts: Investigation, Conservation and Prediction of Long Term Behaviour; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
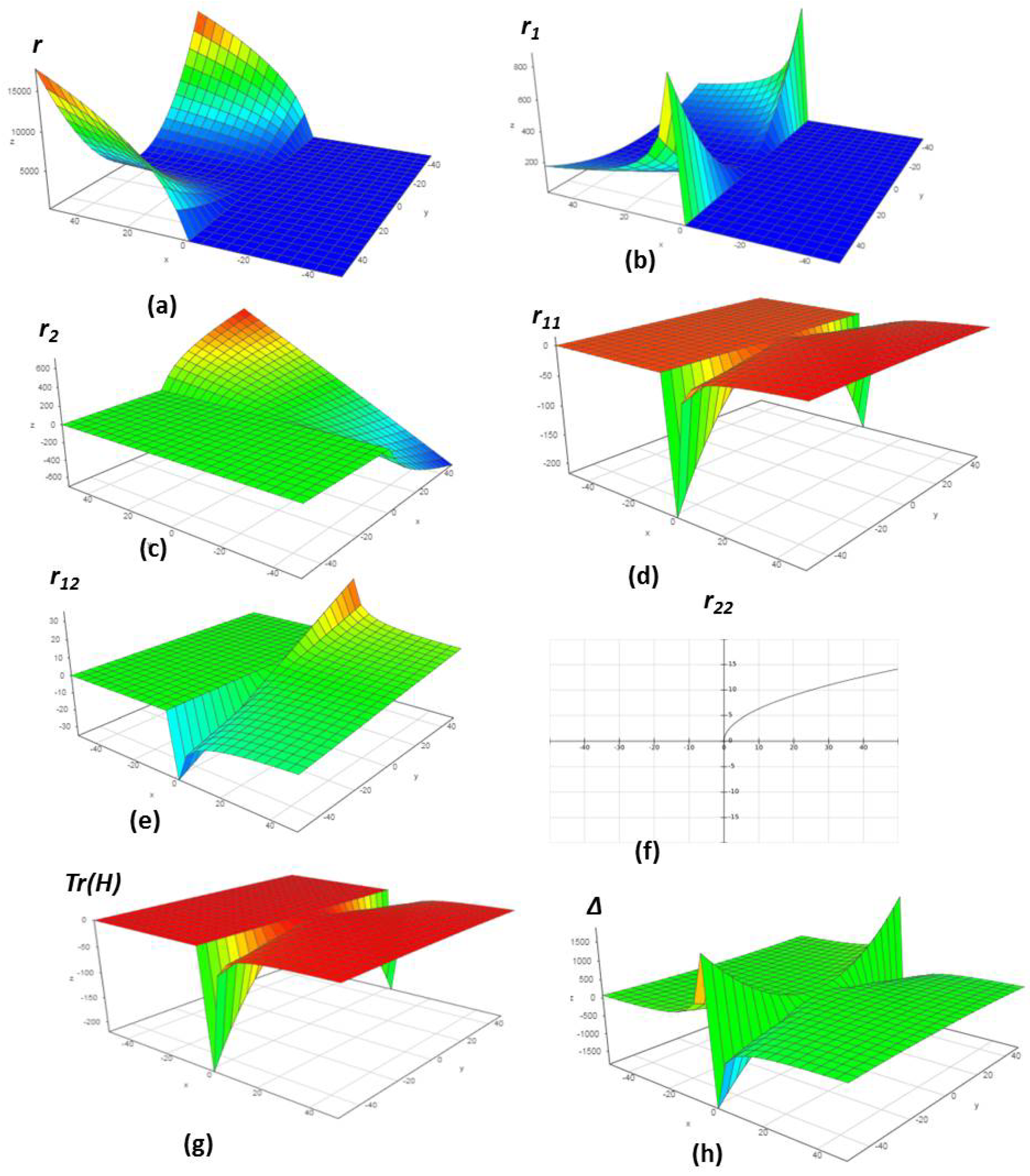
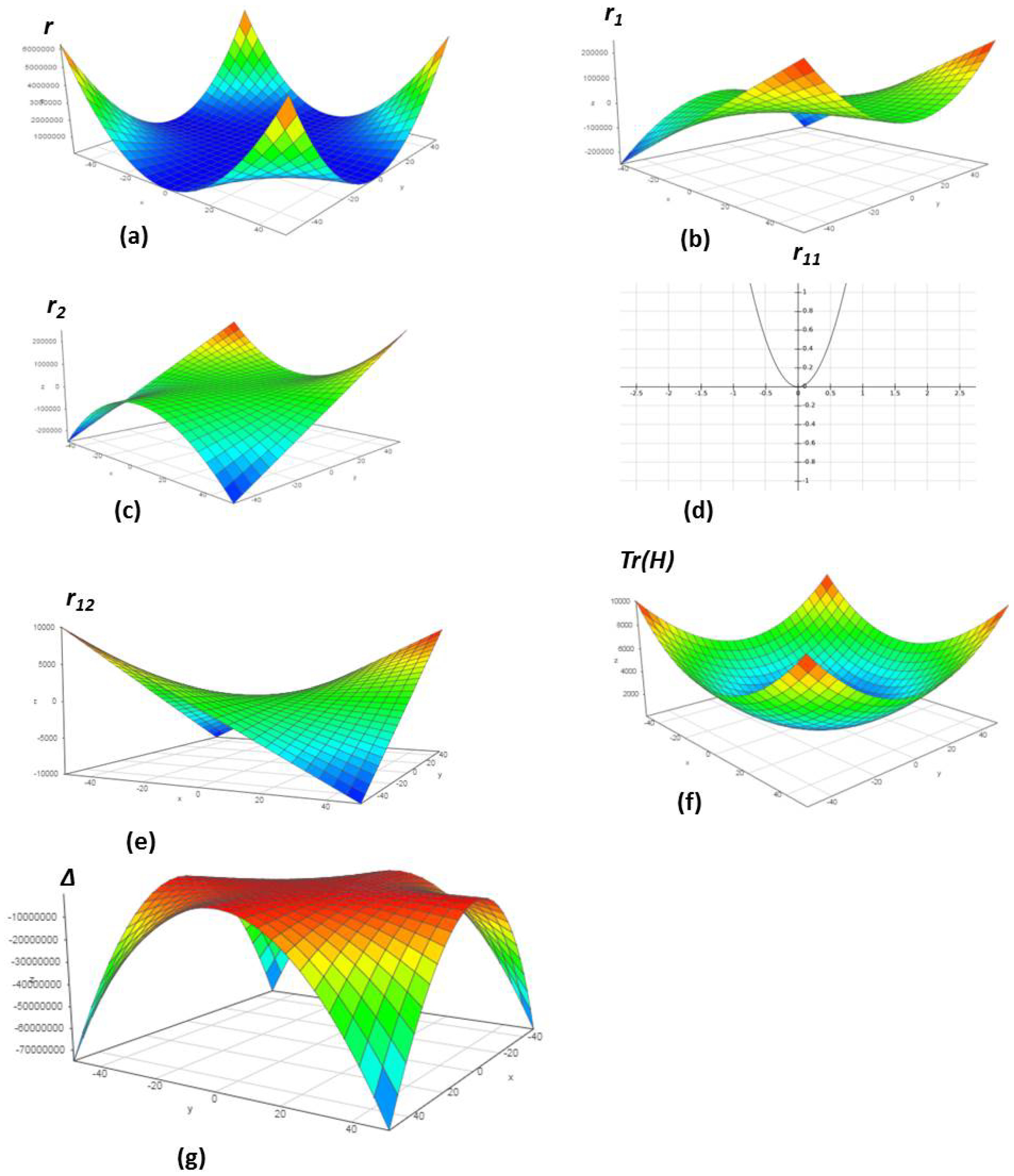
| SN | m | n | = m + n | Δ | |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0 | 1 | 0 | 0 |
| 3 | 0 | 1 | 0 | 0 | 0 |
| 4 | 1 | 1 | 2 | - | - |
| 5 | 1 | 2 | 3 | - | - |
| 6 | 2 | 1 | 3 | - | - |
| 7 | 2 | 2 | 4 | - | - |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tiwari, B.N.; Kishore, S.C.; Marina, N.; Bellucci, S. Fluctuation Theory in Chemical Kinetics. Condens. Matter 2018, 3, 49. https://doi.org/10.3390/condmat3040049
Tiwari BN, Kishore SC, Marina N, Bellucci S. Fluctuation Theory in Chemical Kinetics. Condensed Matter. 2018; 3(4):49. https://doi.org/10.3390/condmat3040049
Chicago/Turabian StyleTiwari, Bhupendra Nath, S. Chandra Kishore, Ninoslav Marina, and Stefano Bellucci. 2018. "Fluctuation Theory in Chemical Kinetics" Condensed Matter 3, no. 4: 49. https://doi.org/10.3390/condmat3040049
APA StyleTiwari, B. N., Kishore, S. C., Marina, N., & Bellucci, S. (2018). Fluctuation Theory in Chemical Kinetics. Condensed Matter, 3(4), 49. https://doi.org/10.3390/condmat3040049






