Abstract
Fractal analysis is a powerful method for the morphological study of complex systems that is increasingly applied to biomedical images. Spatial resolution and image segmentation are crucial for the discrimination of tissue structures at the multiscale level. In this work, we have applied fractal analysis to high-resolution X-ray phase contrast micro-tomography (XrPCμT) images in both uninjured and injured tissue of a mouse spinal cord. We estimated the fractal dimension (FD) using the box-counting method on tomographic slices segmented at different threshold levels. We observed an increased FD in the ipsilateral injured hemicord compared with the contralateral uninjured tissue, which was almost independent of the chosen threshold. Moreover, we found that images exhibited the highest fractality close to the global histogram threshold level. Finally, we showed that the FD estimate largely depends on the image histogram regardless of tissue appearance. Our results demonstrate that the pre-processing of XrPCμT images is critical to fractal analysis and the estimation of FD.
1. Introduction
Fractal analysis is increasingly popular in many different fields among natural and life sciences, such as, for example, materials science [1] and neuroscience [2,3,4,5,6,7,8,9,10]. A variety of complex systems exhibit fractal features (e.g., self-similarity and space-filling capacity) in a limited range of spatial scales. As an illustration, irregularly shaped biological organisms and tissues are better characterized by fractal dimension (FD) than by traditional morphometric measures based on Euclidean geometry. Fractal geometry features have been found in the morphology of tissue and in the vascular pattern around tumor cells [11,12] as well as in brain [2,3,13] and bone [14,15] structures and in protein aggregates [16]. All these systems cannot be considered “true” geometrical fractals as they do not scale to infinity but rather at many biologically relevant scales. For these systems, irregular shapes, self-similarity, and non-integer dimensions are defined from a statistical point of view as the units making the motif are similar rather than identical to the whole, and their repetition is limited to a defined spatial scaling window [10]. FD has been employed for quantitative analysis of shape complexity in a number of biomedical applications, including magnetic resonance imaging (MRI) and computed tomography studies [2,3,7,8,9,10,12,17,18,19]. In the human brain, fractal analysis has been utilized to detect structural changes in white matter (WM) [4,20,21] and grey matter (GM) [5,22,23] in a variety of clinical settings [2,3,7,8].
Noticeably, the limited spatial resolution, normally used in clinical settings, with MRI techniques (in the order of millimeters) makes it difficult to identify local variations of fractality induced by structural tissue alterations, including but not limited to glial activation, invading immune cells, or rearrangements of blood vessels. A spatial resolution of a few tens of micrometers can be obtained by magnetic resonance microscopy performed at high magnetic fields and strong gradient systems in intact mouse brain and ex vivo specimens of human brain [19,24]. However, these techniques cannot resolve cellular or subcellular elements, which is especially relevant to pathological conditions (e.g., cell damage or glia activation). Major developments in high-resolution tomographic techniques have allowed the production of three-dimensional images of intact biological samples with a micrometric or sub-micrometric spatial resolution, thereby allowing the distinction of different fine shapes in biological tissues [9,10]. We have recently demonstrated that X-ray phase contrast micro-tomography (XrPCμT) enables the study of the vascular and neuronal networks simultaneously without sample sectioning [25]. In particular, XrPCμT imaging is a multiscale (spanning from mm to <μm) 3D imaging technique that can be used to evaluate morphological alterations in central nervous system (CNS) tissue [26]. However, XrPCμT images are characterized by small intensity variations which make the segmentation process challenging.
In particular, the FD estimate largely depends on the threshold level (or levels, in the case of multilevel thresholding) used to segment the images [27,28]. To the best of our knowledge, the choice of an optimal threshold level is still a subject of investigation. In the present work, we used a single-threshold binarization approach and performed FD analysis at different threshold levels (spanning the entire range between 0–1) on high-resolution XrPCμT images of a unilaterally injured mouse spinal cord. The aim of this work was to highlight the role of image pre-processing in the capability of FD to discriminate between injured and uninjured tissue.
2. Materials and Methods
2.1. Spinal Cord Injury Model
The animal study protocol was conducted according to the European Guidelines for Animal Experiments (2010/63/EU, 86/609/EEC and 87–848/EEC) and was approved by the Animal Ethics Committee of University of Namur (UN 17-284). Spinal cord injury (i.e., ipsilateral hemicord) was induced in a mouse as previously described [29]. Briefly, a unilateral, right-sided, spinal contusion was applied, under anesthetized condition, at the C5 level using a computer-controlled spinal impactor with an impact force set at 50 kDyn (IH400, Infinite Horizon).
2.2. Sample Preparation and Histology
One week after injury, the mouse was anesthetized with ketamine (100 mg/kg) and xylazine (5 mg/kg) and euthanatized by exsanguination and intracardiac perfusion with 0.9% NaCl followed by buffered 4% paraformaldehyde. The cervical spinal cord was harvested, post-fixed overnight in paraformaldehyde, and subsequently dehydrated in Sakura-Tissue Tek–VIP for paraffin-embedding. Spinal cord slices (10 μm thick) were obtained by microtomy and were stained with Eriochrome R cyanine (Sigma-Aldrich) and Red neutral (Thermofischer, Germany) according to standard staining procedure [30]. The slices were imaged (representative single slice in Figure 1) on a Leica 2450 microscope using LAS acquisition software.
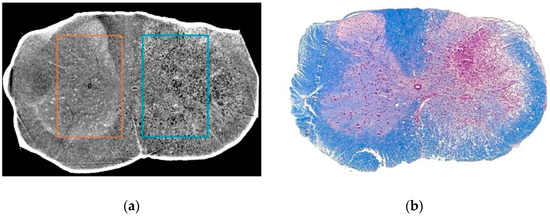
Figure 1.
Representative slices from the tomographic reconstruction (a) and histology (b) of the unilaterally–injured mouse spinal cord. The rectangles in (a) represent selected regions of interest (ROIs) from contralateral uninjured hemicord (1, orange) and ipsilateral injured hemicord (2, cyan). The choice of ROI position was performed on the basis of the histological images (see also Section 2). In (b): The spinal cord slice at the same rostrocaudal level as the tomographic reconstruction stained with Eriochrome R cyanine and Red neutral showing affinity respectively for myelin (in blue) and nervous cell bodies (in pink).
2.3. Synchrotron X-ray Microtomography
XrPCμT measurements were carried out at the TOmographic Microscopy and Coherent rAdiology experimentTs (TOMCAT) beamline of The Paul Scherrer Institute (PSI) in Zurich. High-quality images were obtained using the in-line free-space propagation method, as it ensures high image contrast of hard X-rays in transparent specimens due to the sensitivity of a coherent or partially coherent beam to the phase shift induced by the object [31,32,33,34]. Tomographic images were acquired at 17 keV using a PCO.5.5 camera and an optics combination resulting in a pixel size of 0.65 μm. The tomographic projections resulting from the measurements were reconstructed using Syrmep Tomo Project (STP), an ad hoc software [35] tuned up for phase contrast computed tomography experiments.
2.4. Fractal Analysis
Two ROIs of 1044 × 1620 pixels (approximately 700 μm2) were selected from the bidimensional slices (Figure 1) in both uninjured and injured tissue of the mouse spinal cord. ROI size were chosen to avoid spinal cord borders while maximizing the internal tissue surface area across the 850 images from a single mouse (~550 μm along the rostrocaudal axis) at the location of the injury. The contrast of the images was adjusted by saturating 1% of the top and bottom pixels values before further analysis.
After the preprocessing steps, images were binarized by either applying the image-based global histogram threshold determined using Otsu’s method [36] or defining twenty equally-spaced fixed threshold levels (eighteen excluding 0, or all-white, and 1, or all-black). FD analysis was performed in each ROI using an implementation of the box-counting 2D algorithm running on MATLAB (The Mathworks, Inc., Natick, MA, USA) version 2016b. In particular, the box-counting method is the most commonly used computational tool for the calculation of the FD in complex systems. The idea is to consider a set of points and to find the minimum number of boxes of edge length needed to cover all the points in the set. The box size is then changed to determine the dependence of on the length , i.e., . The fractal dimension can be calculated as , which represents the slope of versus .
The box sizes are powers of 2 and the cut off for the box size, 2048 pixels, has been evaluated on the basis of the image size (within-box pixels outside the image have been zero-filled). Finally, values of the FD for the contralateral uninjured hemicord and ipsilateral injured hemicord tissue were obtained by averaging across slices. Fractality of the images was estimated as the goodness of linear fit between the number of boxes and box size. Gaussian normalization of the ROI image histogram (i.e., pixel intensity distribution) was performed using rank-based inverse normal transformation. Values are expressed as mean ± standard deviation (SD).
3. Results
First, we calculated FD after employing a commonly used approach for image segmentation, i.e., estimate of global histogram threshold using Otsu’s method. Figure 2 shows the result of binarization in a representative slice for both ROIs corresponding to the contralateral uninjured (Figure 2a,b) and the ipsilateral injured (Figure 2d,e) hemicord, with a threshold of on average 0.47 and 0.51, respectively. Figure 2 also shows the application of the box-counting algorithm to the binarized images. The log–log plots of the number of boxes versus the side size of the box for both ROIs exhibited a linear trend (Figure 2c,f), which is a signature of the fractality of the system. The FD values of the contralateral and ipsilateral tissue were 1.79 ± 0.15 and 1.82 ± 0.15, respectively.
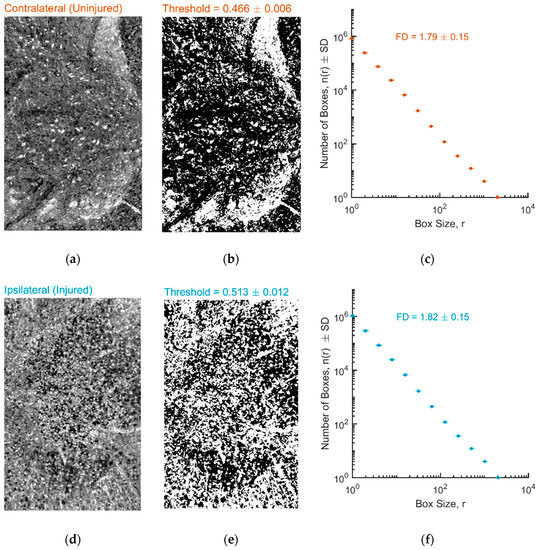
Figure 2.
(a,b) Representative preprocessed and binarized X-ray phase contrast micro-tomography (XrPCμT) image from a ROI located in the contralateral uninjured hemicord. (d,e) Representative preprocessed and binarized XrPCμT image from a ROI located in the ipsilateral injured hemicord. All images have been thresholded using the Otsu’s method. (c,f) Estimate of fractal dimension (d,f) using the box-counting method for contralateral and ipsilateral ROIs.
Next, we determined FD for different threshold levels spanning the full threshold range. In Figure 3, we report the same representative images of Figure 2, each binarized using a different threshold value, for both the contralateral uninjured (Figure 3a) and the ipsilateral injured hemicord (Figure 3b), along with the fractal dimension as a function of the threshold level averaged across all slices (Figure 3c). The FD of the contralateral uninjured hemicord was lower than that of the ipsilateral injured hemicord for all threshold levels, with the difference being very clear for threshold levels larger than about 0.3 (e.g., maximum difference of ~6% for a threshold level of 0.63; Figure 3c inset).
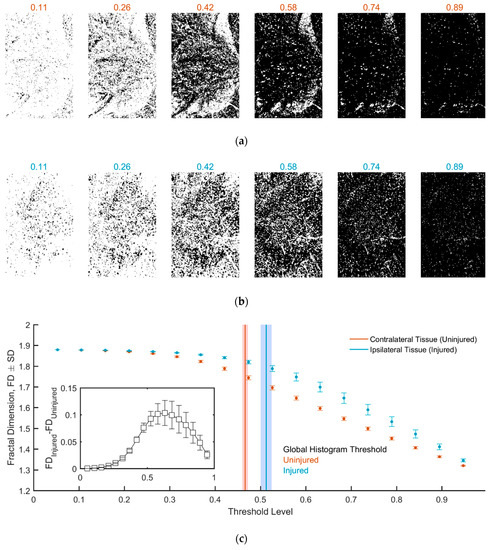
Figure 3.
(a,b) Image binarization at different threshold levels for the contralateral and ipsilateral ROIs. (c) Fractal dimension as a function of the threshold level. The vertical bars in red and blue represent the global histogram threshold (as in Figure 2; shaded areas correspond to SD). The difference in FD between uninjured and injured tissue is shown in the inset.
In addition, we examined image fractality (Figure 4a,c). Interestingly, the system was found to be more fractal for threshold levels below 0.58, while there was a departure from the linear trend at small box sizes when using thresholds >0.6. The best linear fit for the contralateral and ipsilateral ROI was obtained for a threshold level of 0.42 and 0.53, respectively, and the values were close to those obtained using Otsu’s method.
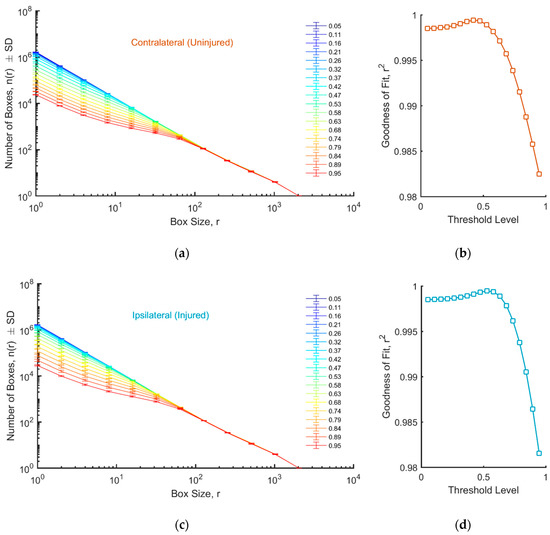
Figure 4.
(a,c) Log–log plots of the number of boxes as a function of the box size, for different threshold levels, for uninjured (a) and injured (c) tissue. (b,d) Goodness of fit as a function of the threshold level for uninjured (b) and injured (d) tissue.
Finally, we investigated how image histogram influences FD (Figure 5). In particular, we found that Gaussian normalization completely abolished the difference in FD between uninjured and injured ROIs. Similarly, different FD values were obtained when individual ROIs (either uninjured or injured) were pre-processed with or without Gaussian normalization.
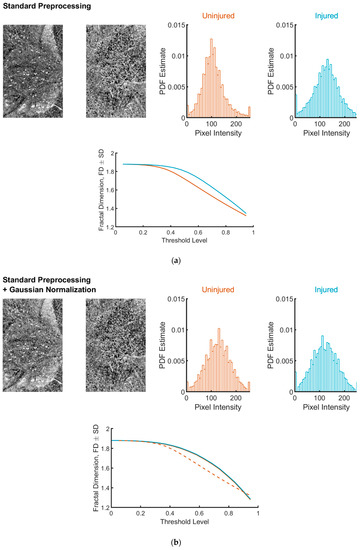
Figure 5.
Representative ROIs and FD analysis after standard pre-processing (a) or standard pre-processing plus Gaussian normalization (b). The representative images are the same as those shown in Figure 2 and Figure 3. The application of the Gaussian normalization adjusts both the appearance of the images (left on each panel) and the pixel distributions (right on each panel). FD estimates for uninjured and injured tissues are nearly indistinguishable (compare plots at the bottom of each panel). For comparison, in (b), the FD estimate for the untransformed images (uninjured condition) is shown (dashed line).
4. Discussion
Fractal geometry offers the possibility to elucidate the complexity of biological tissue either in normal or pathological conditions. For example, Esteban and colleagues found that the FD of both lesioned and normally appearing brain WM in patients with multiple sclerosis (MS) was significantly lower than in healthy controls (conversely, FD was higher in the patients’ GM of the brain) [2,3]. Moreover, fractal analysis revealed changes in FD of the brain WM/GM boundary and/or cortical folding in aged subjects [8] as well as in patients affected by schizophrenia and dyslexia [6,7,37]. FD was also found to be increased in mouse brain microvascular network around tumors compared with healthy tissue [12]. These and other studies suggest that fractal analysis can be particularly useful for preclinical and future clinical applications.
In this study, we examined several pre-processing steps relevant to FD analysis that must be taken into account to exploit the capability of FD for detecting CNS damage. We have shown that high-resolution XrPCμT images of mouse spinal cord tissue are fractal (i.e., exhibit fractal features allowing a robust determination of FD as computed through the box-counting method) across a wide range of threshold levels used for binarization. The choice of the threshold does not appreciably affect the ability of FD to discriminate uninjured from injured tissue in a mouse model of spinal cord contusion. Under the conditions of our experiment, the utilization of the image-based global histogram threshold (Otsu’s method) was sufficient to allow for discrimination of the injured hemicord. Notably, the threshold levels determined by image-based methods can be substantially different for different classes of images (in our case, they were distinct even in the same sample depending on tissue condition, whether injured or not). Our findings strengthen the importance of threshold analysis prior to FD determination. We found that the FD estimate is strongly dependent on the image histogram (i.e., pixel intensity distribution of the images). The number of voxels surviving a given threshold parallels the cumulative distribution function of the image histogram, and the latter determines FD as calculated using the box-counting method. Remarkably, the appearance of the tissue (i.e., uninjured versus injured) did not predict FD, as we clearly showed using Gaussian normalization. In other words, FD and its threshold dependence can be identical in images looking very different but with the same image histogram. Vice versa, FD and its threshold dependence can be different in images looking identical but with a distinct image histogram.
The increase in FD that we report for injured tissue of the spinal cord sample is likely the result of substantial structural changes taking place following the injury. In particular, based on histology and other preliminary results, we suggest that a potential contribution to the increased FD in the injured hemicord is an altered neuron/glia ratio, possibly due to neuronal loss and/or recruitment or activation of glial cells (i.e., reactive astrocytes and microglia). Our interpretation is in agreement with that advanced by Esteban and colleagues [3] who attributed the increased FD values in the GM of MS patients to the higher structural complexity of GM than WM in terms of possible pathological mechanisms (e.g., inflammatory component and cellular changes).
The present study had several limitations, primarily the fact that the analysis was carried out on a single spinal cord. Another important limitation is that we did not examine the effect of post-processing filters, e.g., for enhancement of specific features, on FD determination. Application of different filter types that can be tailored for specific needs might substantially change the estimate of FD. For example, edge detectors can be useful when applying the box-counting method to binarized images if one does not consider filled areas (as we did in the present study) but only the corresponding perimeters (e.g., WM/GM boundaries). Of course, when the box-counting method is applied to filled areas, it is important to define what bright pixels represent. In our images, bright pixels roughly match cellular elements, while dark pixels reflect extracellular space. Accordingly, our finding of increased FD in the injured tissue compared with uninjured tissue, entails an increase in complexity of cellular elements and a concomitant decrease in complexity of extracellular space. As an obvious consequence, we obtained the opposite results if we determined FD on the complement images (data not shown). Finally, we only performed a 2D fractal analysis, i.e., FD was determined on tissue slices, which did not entirely exploit the capabilities of the XrPCμT technique. Future studies would consider these issues by performing 3D fractal analysis on spinal cord samples from more animals.
5. Conclusions
We used different threshold-based pre-processing approaches for FD analysis of XrPCμT images from a single mouse spinal cord. We demonstrated the capability of FD analysis to discriminate injured from uninjured tissue in a manner almost independent of the threshold chosen to binarize the images. In spite of the limitations of the present study (see Section 4 above), our results provide methodological strategies that can be useful for FD analysis of XrPCμT images aimed at evaluating topological complexity and revealing structural changes in biological tissues, a very active and prompting field of research [38,39].
Author Contributions
Conceptualization, M.F.; Methodology, L.M., M.D.; Analysis, M.D.; Manuscript Draft Preparation, L.M., M.D., M.M.; Writing-Review & Editing, L.M., M.D., M.M., C.N., I.B., F.M., F.G., A.C., M.F.; Supervision, M.F.; Funding Acquisition, M.F., A.C.
Funding
The present work was supported by the The Italian Ministry of Health Young Researcher Grant 2013 (GR-2013-02358177) to M.F. Part of research reported in this publication was also supported by the European project VOXEL (HORIZON 2020-Fet Open; 665207). The content is solely the responsibility of the authors and does not necessarily represent the official views of the funding bodies.
Acknowledgments
Authors wish to thank the TOMCAT beamline at the Paul Scherrer Institute for providing beamtime. They are also grateful to the beamline staff for its technical support. In addition, they would like to thank Francesco Brun for the precious scientific and technical support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fratini, M.; Poccia, N.; Ricci, A.; Campi, G.; Burghammer, M.; Aeppli, G.; Bianconi, A. Scale-free structural organization of oxygen interstitials in La2CuO4+y. Nature 2010, 466, 841–844. [Google Scholar]
- Esteban, F.J.; Sepulcre, J.; de Mendizabal, N.V.; Goni, J.; Navas, J.; de Miras, J.R.; Bejarano, B.; Masdeu, J.C.; Villoslada, P. Fractal dimension and white matter changes in multiple sclerosis. NeuroImage 2007, 36, 543–549. [Google Scholar]
- Esteban, F.J.; Sepulcre, J.; de Miras, J.R.; Navas, J.; de Mendizabal, N.V.; Goni, J.; Quesada, J.M.; Bejarano, B.; Villoslada, P. Fractal dimension analysis of grey matter in multiple sclerosis. J. Neurolog. Sci. 2009, 282, 67–71. [Google Scholar] [CrossRef] [PubMed]
- Free, S.L.; Sisodiya, S.M.; Cook, M.J.; Fish, D.R.; Shorvon, S.D. Three-Dimensional Fractal Analysis of the White Matter Surface from Magnetic Resonance Images of the Human Brain. Cereb. Cortex 1996, 6, 830–836. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.Z.; Zhang, L.D.; Yue, G.H. Fractal Dimension in Human Cerebellum Measured by Magnetic Resonance Imaging. Biophys. J. 2003, 85, 4041–4046. [Google Scholar] [CrossRef]
- Majumdar, S.; Prasad, R.R. Fractal dimension of cerebral surfaces using magnetic resonance images. Comput. Phys. 1988, 2. [Google Scholar] [CrossRef]
- Sandu, A.L.; Rasmussen, I.A.; Lundervold, A.; Kreuder, F.; Neckelmann, G.; Hugdahl, K.; Specht, K. Fractal dimension analysis of MR images reveals grey matter structure irregularities in schizophrenia. Comput. Med. Imaging Graph. 2008, 32, 150–158. [Google Scholar] [CrossRef]
- Zhang, L.; Dean, D.; Liu, J.Z.; Sahgal, V.; Wang, X.F.; Yue, G.H. Quantifying degeneration of white matter in normal aging using fractal dimension. Neurobiol. Aging 2007, 28, 1543–1555. [Google Scholar] [CrossRef]
- Di Ieva, A.; Esteban, F.J.; Grizzi, F.; Klonowski, W.; Martín-Landrove, M. Fractals in the Neurosciences, Part II: Clinical Applications and Future Perspectives. Neuroscientist 2013, 21, 30–43. [Google Scholar] [CrossRef]
- Di Ieva, A.; Grizzi, F.; Jelinek, H.; Pellionisz, A.J.; Losa, G.A. Fractals in the Neurosciences, Part I: General Principles and Basic Neurosciences. Neuroscientist 2013, 20, 403–417. [Google Scholar] [CrossRef]
- Lang, S.; Müller, B.; Dominietto, M.; Cattin, P.; Zanette, I.; Weitkamp, T.; Hieber, S. Three-dimensional quantification of capillary networks in healthy and cancerous tissues of two mice. Microvasc. Res. 2012, 84, 314–322. [Google Scholar] [CrossRef] [PubMed]
- Risser, L.; Plouraboué, F.; Steyer, A.; Cloetens, P.; Le Duc, G.; Fonta, C. From homogeneous to fractal normal and tumour microvascular networks in the brain. J. Cereb. Blood Flow Metab. 2007, 27, 293–303. [Google Scholar] [CrossRef] [PubMed]
- Ulloa Severino, F.P.; Ban, J.; Song, Q.; Tang, M.; Bianconi, G.; Cheng, G.; Torre, V. The role of dimensionality in neuronal network dynamics. Sci. Rep. 2016, 6, 29640. [Google Scholar] [CrossRef] [PubMed]
- Mawatari, T.; Miura, H.; Higaki, H.; Kurata, K.; Moro-Oka, T.; Murakami, T.; Iwamoto, Y. Quantitative analysis of three-dimensional complexity and connectivity changes in trabecular microarchitecture in relation to aging, menopause, and inflammation. J. Orthop. Sci. 1999, 4, 431–438. [Google Scholar] [CrossRef]
- Campi, G.; Pezzotti, G.; Fratini, M.; Ricci, A.; Burghammer, M.; Cancedda, R.; Mastrogiacomo, M.; Bukreeva, I.; Cedola, A. Imaging regenerating bone tissue based on neural networks applied to micro-diffraction measurements. Appl. Phys. Lett. 2013, 103, 253703. [Google Scholar] [CrossRef]
- De Spirito, M.; Brunelli, R.; Mei, G.; Bertani, F.R.; Ciasca, G.; Greco, G.; Papi, M.; Arcovito, G.; Ursini, F.; Parasassi, T. Low Density Lipoprotein Aged in Plasma Forms Clusters Resembling Subendothelial Droplets: Aggregation via Surface Sites. Biophys. J. 2006, 90, 4239–4247. [Google Scholar] [CrossRef]
- Grizzi, F.; Castello, A.; Qehajaj, D.; Russo, C.; Lopci, E. The Complexity and Fractal Geometry of Nuclear Medicine Images. Mol. Imaging Biol. 2018, 1–9. [Google Scholar] [CrossRef]
- Peng, L.; Ju, Y.; Gao, F.; Ranjith, P.G.; Zhang, Q. CT Identification and Fractal Characterization of 3-D Propagation and Distribution of Hydrofracturing Cracks in Low-Permeability Heterogeneous Rocks. J. Geophys. Res. 2018, 123, 2156–2173. [Google Scholar]
- Wu, D.; Xu, J.D.; McMahon, M.T.; van Zijl, P.C.M.; Mori, S.; Northington, F.J.; Zhang, J.Y. In vivo high-resolution diffusion tensor imaging of the mouse brain. NeuroImage 2013, 83, 18–26. [Google Scholar] [CrossRef]
- Bullmore, E.; Brammer, M.; Harvey, I.; Persaud, R.; Murray, R.; Ron, M. Fractal analysis of the boundary between white matter and cerebral cortex in magnetic resonance images: A controlled study of schizophrenic and manic-depressive patients. Psychol. Med. 2009, 24, 771–781. [Google Scholar] [CrossRef]
- Cook, M.J.; Free, S.L.; Manford, M.R.A.; Fish, D.R.; Shorvon, S.D.; Stevens, J.M. Fractal Description of Cerebral Cortical Patterns in Frontal Lobe Epilepsy. Eur. Neurol. 1995, 35, 327–335. [Google Scholar] [CrossRef] [PubMed]
- Blanton, R.E.; Levitt, J.G.; Thompson, P.M.; Narr, K.L.; Capetillo-Cunliffe, L.; Nobel, A.; Singerman, J.D.; McCracken, J.T.; Toga, A.W. Mapping cortical asymmetry and complexity patterns in normal children. Psychiatry Res. Neuroimaging 2001, 107, 29–43. [Google Scholar] [CrossRef]
- Lee, J.M.; Yoon, U.; Kim, J.J.; Kim, I.Y.; Lee, D.S.; Kwon, J.S.; Kim, S.I. Analysis of the hemispheric asymmetry using fractal dimension of a skeletonized cerebral surface. IEEE Transa. Biomed. Eng. 2004, 51, 1494–1498. [Google Scholar]
- Tyszka, J.M.; Fraser, S.E.; Jacobs, R.E. Magnetic resonance microscopy: Recent advances and applications. Curr. Opin. Biotechnol. 2005, 16, 93–99. [Google Scholar] [CrossRef] [PubMed]
- Fratini, M.; Bukreeva, I.; Campi, G.; Brun, F.; Tromba, G.; Modregger, P.; Bucci, D.; Battaglia, G.; Spanò, R.; Mastrogiacomo, M.; et al. Simultaneous submicrometric 3D imaging of the micro-vascular network and the neuronal system in a mouse spinal cord. Sci. Rep. 2015, 5, 8514. [Google Scholar] [CrossRef] [PubMed]
- Cedola, A.; Bravin, A.; Bukreeva, I.; Fratini, M.; Pacureanu, A.; Mittone, A.; Massimi, L.; Cloetens, P.; Coan, P.; Campi, G.; et al. X-Ray Phase Contrast Tomography Reveals Early Vascular Alterations and Neuronal Loss in a Multiple Sclerosis Model. Sci. Rep. 2017, 7, 5890. [Google Scholar] [CrossRef]
- Backes, A.R.; Bruno, O.M. A New Approach to Estimate Fractal Dimension of Texture Images. In Image and Signal Processing; Springer: Berlin, Germay, 2008. [Google Scholar]
- Majumdar, S.; Weinstein, R.S.; Prasad, R.R. Erratum: “Application of fractal geometry techniques to the study of trabecular bone”. Med. Phys. 1994, 21, 491. [Google Scholar] [CrossRef]
- Nicaise, C.; Putatunda, R.; Hala, T.J.; Regan, K.A.; Frank, D.M.; Brion, J.P.; Leroy, K.; Pochet, R.; Wright, M.C.; Lepore, A.C. Degeneration of Phrenic Motor Neurons Induces Long-Term Diaphragm Deficits following Mid-Cervical Spinal Contusion in Mice. J. Neurotrauma 2012, 29, 2748–2760. [Google Scholar] [CrossRef]
- Bouchat, J.; Couturier, B.; Marneffe, C.; Gankam-Kengne, F.; Balau, B.; De Swert, K.; Brion, J.P.; Poncelet, L.; Gilloteaux, J.; Nicaise, C. Regional oligodendrocytopathy and astrocytopathy precede myelin loss and blood-brain barrier disruption in a murine model of osmotic demyelination syndrome. GLIA 2018, 66, 606–622. [Google Scholar] [CrossRef]
- Olivo, A.; Castelli, E. X-ray phase contrast imaging: From synchrotrons to conventional sources. La Rivista Del Nuovo Cimento 2014, 37, 467–508. [Google Scholar] [CrossRef]
- Mayo, S.C.; Davis, T.J.; Gureyev, T.E.; Miller, P.R.; Paganin, D.; Pogany, A.; Stevenson, A.W.; Wilkins, S.W. X-ray phase-contrast microscopy and microtomography. Opt. Express 2003, 11, 2289–2302. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.A.; Brahme, A. Development of phase-contrast X-ray imaging techniques and potential medical applications. Phys. Med. 2008, 24, 129–148. [Google Scholar] [CrossRef]
- Cloetens, P.; Barrett, R.; Baruchel, J.; Guigay, J.-P.; Schlenker, M. Phase objects in synchrotron radiation hard x-ray imaging. J. Phys. D Appl. Phys. 1996, 29, 133. [Google Scholar] [CrossRef]
- Brun, F.; Massimi, L.; Fratini, M.; Dreossi, D.; Bille, F.; Accardo, A.; Pugliese, R.; Cedola, A. SYRMEP Tomo Project: A graphical user interface for customizing CT reconstruction workflows. Adv. Struct. Chem. Imaging 2017, 3, 4. [Google Scholar] [CrossRef] [PubMed]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Transa. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Sandu, A.-L.; Specht, K.; Beneventi, H.; Lundervold, A.; Hugdahl, K. Sex-differences in grey–white matter structure in normal-reading and dyslexic adolescents. Neurosci. Lett. 2008, 438, 80–84. [Google Scholar] [CrossRef] [PubMed]
- Campi, G.; Di Gioacchino, M.; Poccia, N.; Ricci, A.; Burghammer, M.; Ciasca, G.; Bianconi, A. Nanoscale correlated disorder in out-of-equilibrium myelin ultrastructure. ACS Nano 2018, 12, 729–739. [Google Scholar] [CrossRef]
- Chialvo, D.R. Life at the edge: Complexity and criticality in biological function. arXiv, 2018; arXiv:1810.11737. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).