Fermionic Properties of Two Interacting Bosons in a Two-Dimensional Harmonic Trap
Abstract
1. Introduction
2. The Hamiltonian
3. Analytic Wave Functions to Compare with the Ground State
3.1. First-order Perturbation Theory
3.2. The Non-Interacting Two-Fermion System
3.3. Bosonized Two-fermion System
4. The Interaction Effect in the Ground State Energy
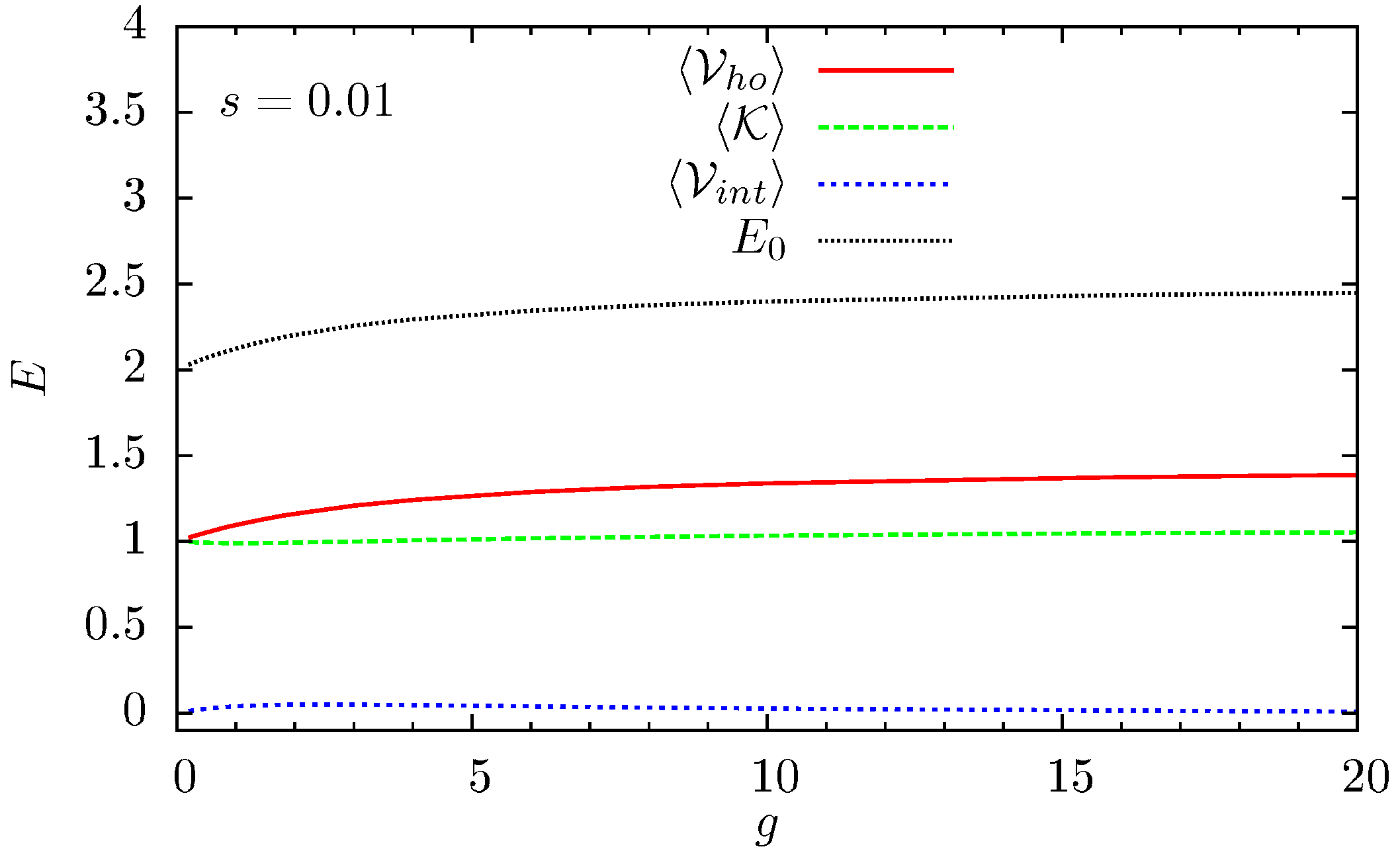
4.1. The Energy Contributions
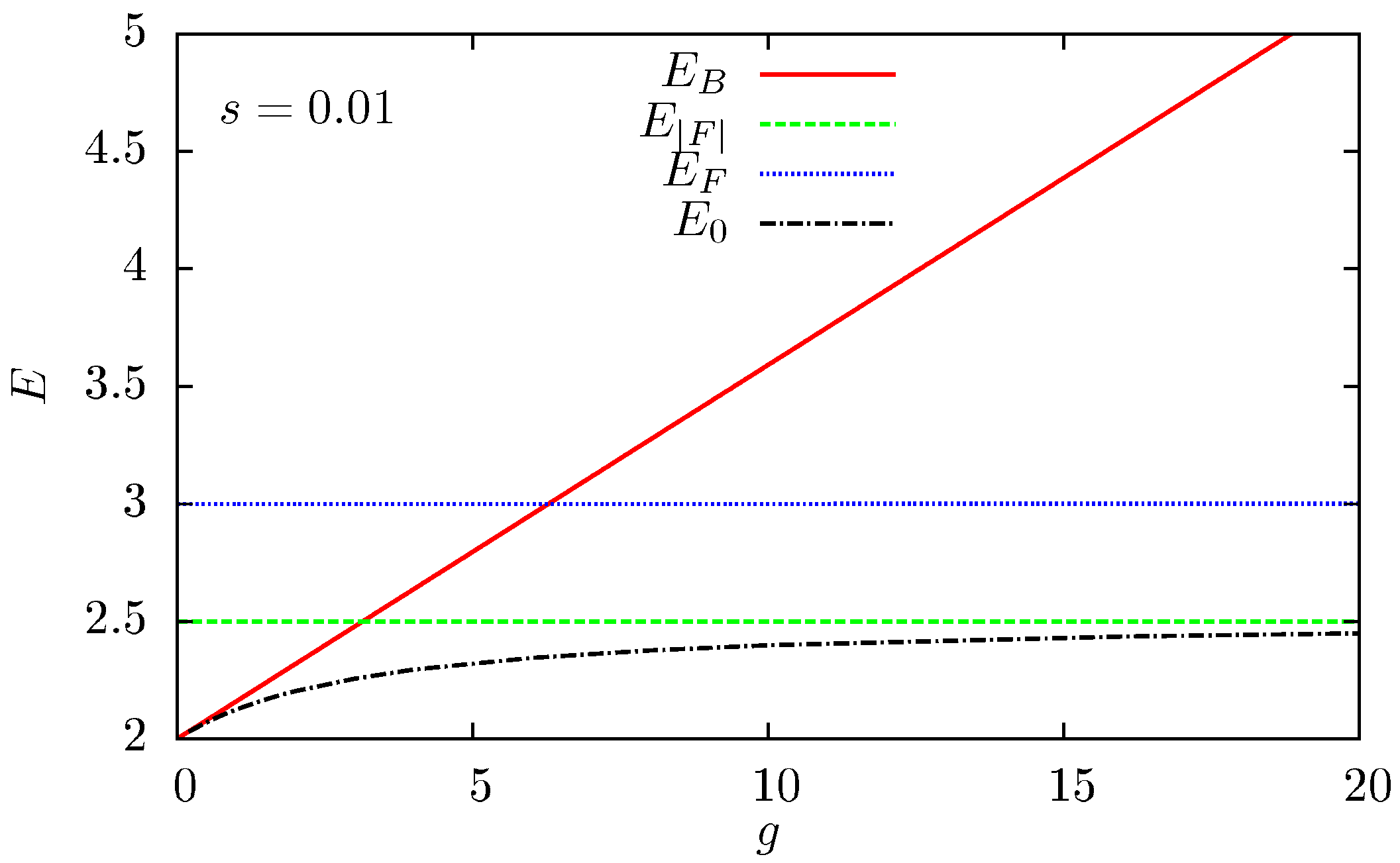
4.2. Exploring the Strongly Interacting Limit for a Short-range Interaction
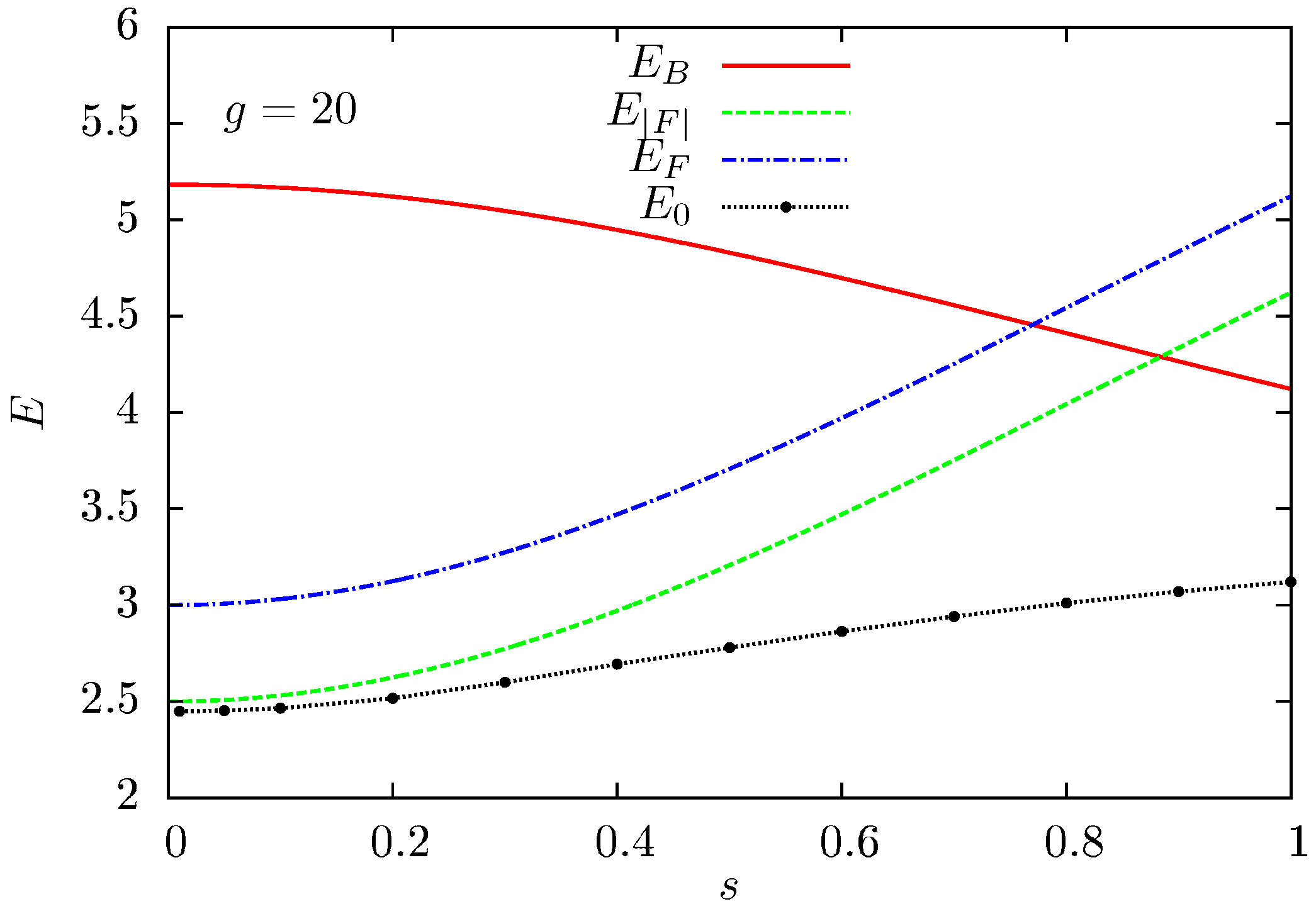
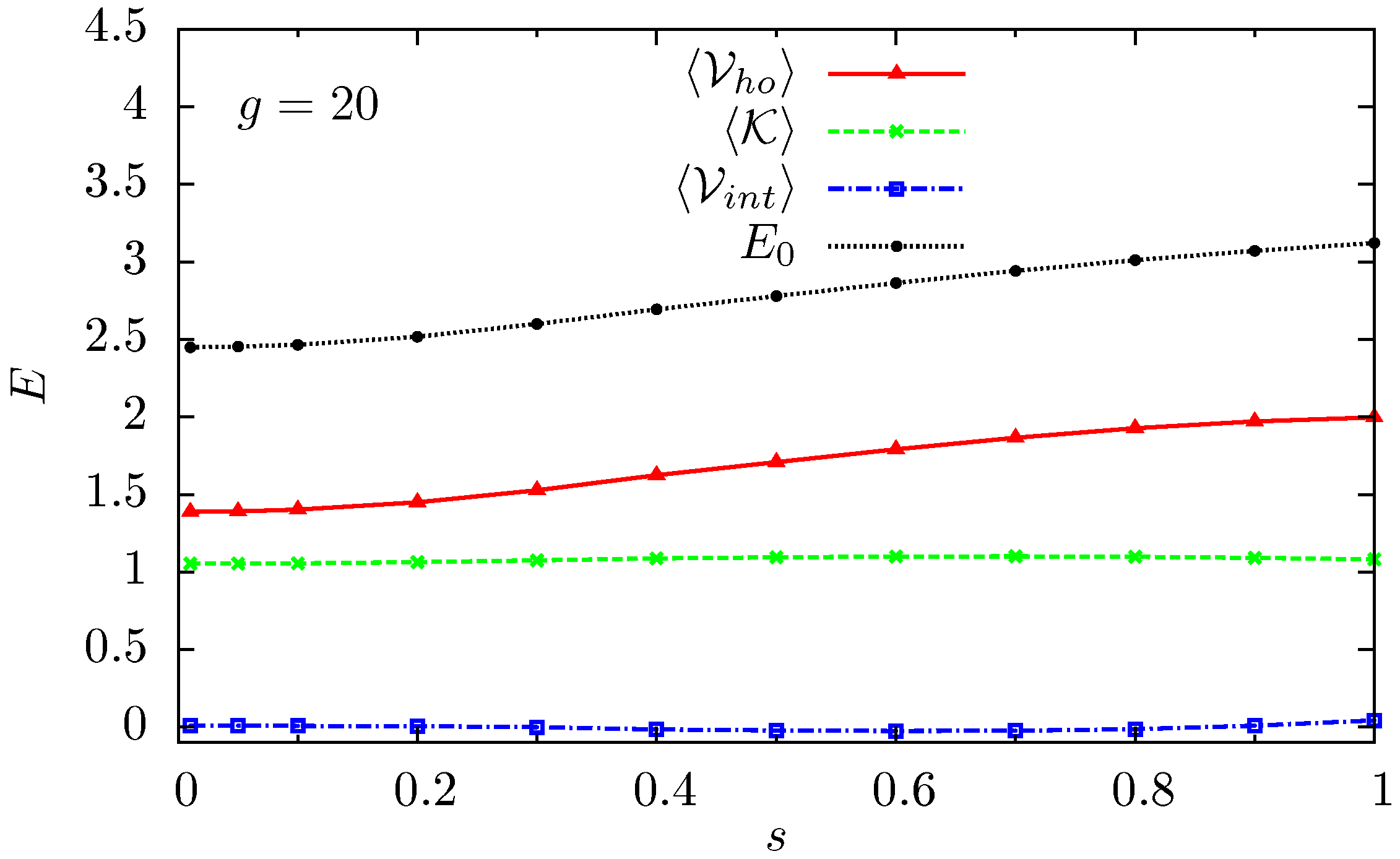
4.3. Exploring the Short-Range Limit for a Strong Interaction Strength
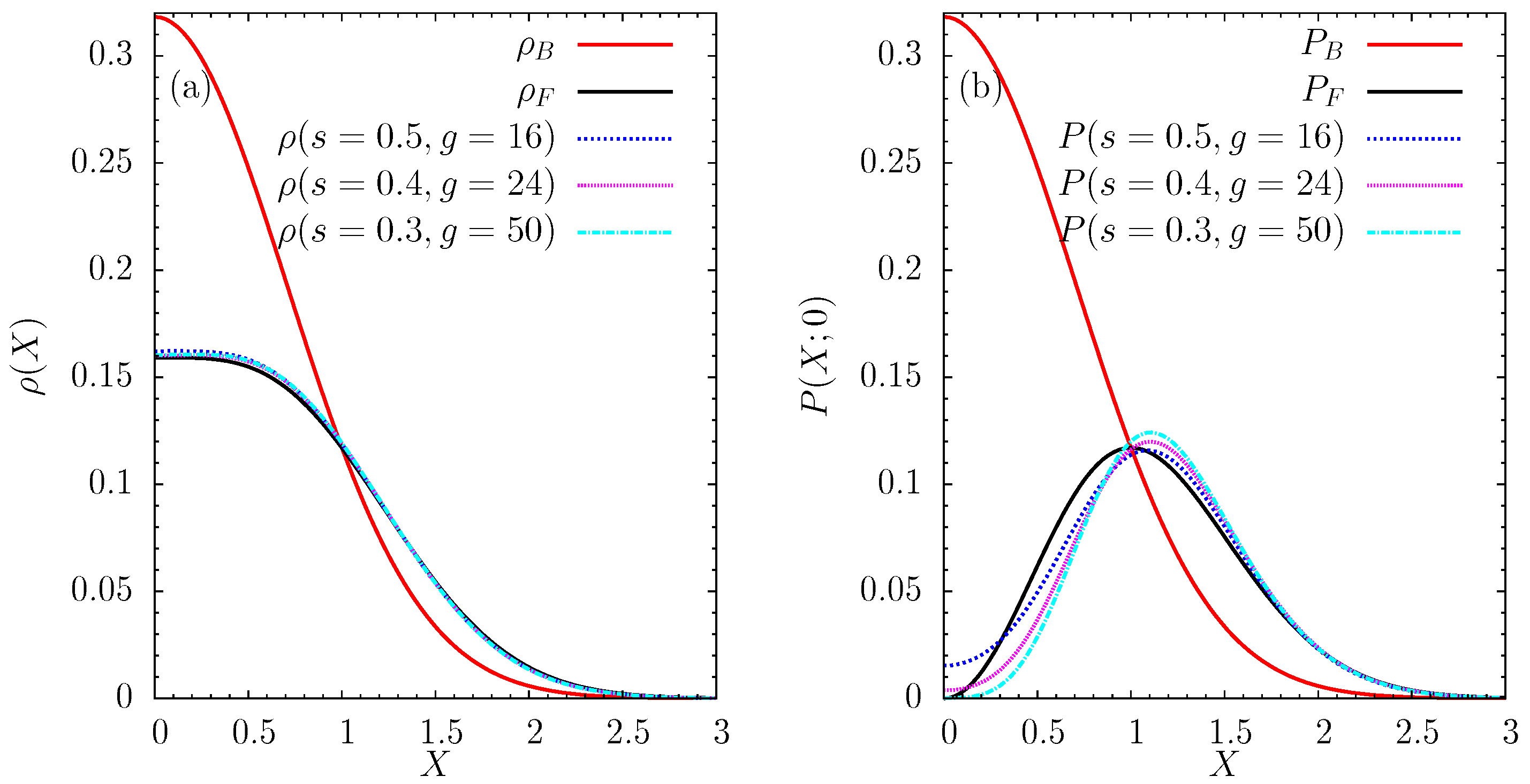
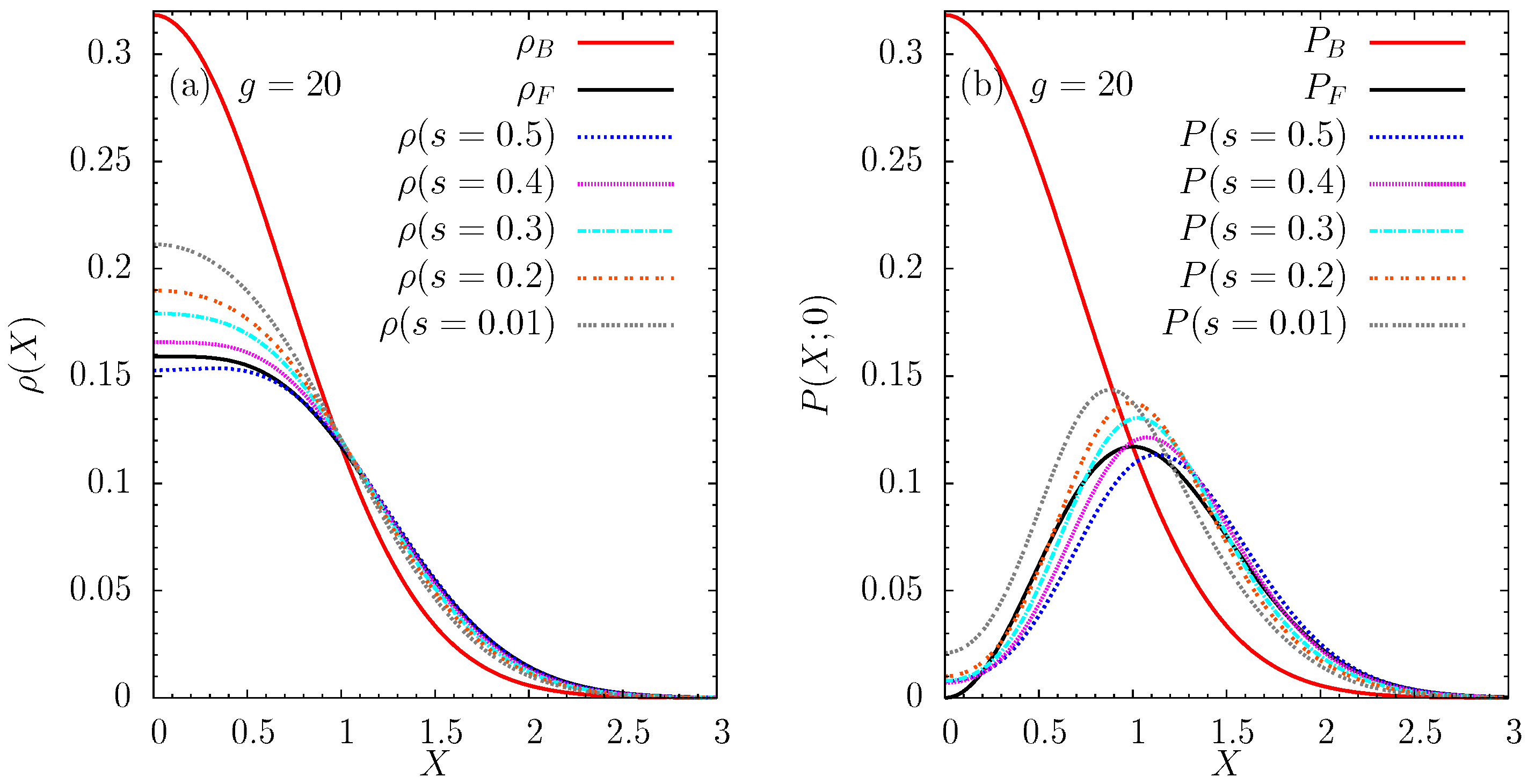
5. The Density Profile and the Two-body Correlations
6. Numerical Method
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Girardeau, M. Relationship between systems of impenetrable bosons and fermions in one dimension. J. Math. Phys. 1960, 1, 516. [Google Scholar] [CrossRef]
- Busch, T.; Englert, B.G.; Rzazewski, K.; Wilkens, M. Two cold atoms in a harmonic trap. Found. Phys. 1998, 28, 549. [Google Scholar] [CrossRef]
- Girardeau, M.D.; Wright, E.M.; Triscari, J.M. Ground-state properties of a one-dimensional system of hard-core bosons in a harmonic trap. Phys. Rev. A 2001, 63, 033601. [Google Scholar] [CrossRef]
- Paredes, B.; Widera, A.; Murg, V.; Mandel, O.; Fölling, S.; Cirac, I.; Shlyapnikov, G.V.; Hänsch, T.W.; Bloch, I. Tonks-Girardeau gas of ultracold atoms in an optical lattice. Nature 2004, 429, 277. [Google Scholar] [CrossRef] [PubMed]
- Kinoshita, T.; Wenger, T.; Weiss, D.S. Observation of a one-dimensional Tonks-Girardeau Gas. Science 2004, 305, 1125. [Google Scholar] [CrossRef] [PubMed]
- Pupillo, G.; Rey, A.M.; Williams, C.J.; Clark, C.W. Extended fermionization of 1D bosons in optical lattices. New J. Phys. 2006, 8, 161. [Google Scholar] [CrossRef]
- Tempfli, E.; Zöllner, S.; Schmelcher, P. Excitations of attractive 1d bosons: Binding versus fermionization. New J. Phys. 2008, 10, 103021. [Google Scholar] [CrossRef]
- Bakr, W.S.; Peng, A.; Tai, M.E.; Ma, R.; Simon, J.; Gillen, J.I.; Fölling, S.; Pollet, L.; Greiner, M. Probing the superfluid-to-Mott insulator transition at the single-atom level. Science 2010, 329, 547. [Google Scholar] [CrossRef] [PubMed]
- Sherson, J.F.; Weitenberg, C.; Endres, M.; Cheneau, M.; Bloch, I.; Khur, S. Single-atom-resolved fluorescence imaging of an atomic Mott insulator. Nature 2010, 467, 68. [Google Scholar] [CrossRef] [PubMed]
- Deuretzbacher, F.; Cremon, J.C.; Reimann, S.M. Ground-state properties of few dipolar bosons in a quasi-one-dimensional harmonic trap. Phys. Rev. A 2010, 81, 063616. [Google Scholar] [CrossRef]
- Kościk, P. Quantum correlations of a few bosons within a harmonic trap. Few-Body Syst. 2012, 52, 49. [Google Scholar] [CrossRef]
- Brouzos, I.; Schmelcher, P. Construction of analytical many-body wave functions for correlated bosons in a harmonic trap. Phys. Rev. Lett. 2012, 108, 045301. [Google Scholar] [CrossRef] [PubMed]
- García-March, M.A.; Juliá-Díaz, B.; Astrakharchik, G.E.; Busch, Th.; Boronat, J.; Polls, A. Sharp crossover from composite fermionization to phase separation in microscopic mixtures of ultracold bosons. Phys. Rev. A 2013, 88, 063604. [Google Scholar] [CrossRef]
- García-March, M.A.; Juliá-Díaz, B.; Astrakharchik, G.E.; Boronat, J.; Polls, A. Distinguishability, degeneracy, and correlations in three harmonically trapped bosons in one dimension. Phys. Rev. A 2014, 90, 063605. [Google Scholar] [CrossRef]
- Wilson, B.; Foerster, A.; Kuhn, C.C.N.; Roditi, I.; Rubeni, D. A geometric wave function for a few interacting bosons in a harmonic trap. Phys. Lett. A 2014, 378, 1065. [Google Scholar] [CrossRef]
- García-March, M.A.; Juliá-Díaz, B.; Astrakharchik, G.E.; Busch, Th.; Boronat, J.; Polls, A. Quantum correlations and spatial localization in one-dimensional ultracold bosonic mixtures. New J. Phys. 2014, 16, 103004. [Google Scholar] [CrossRef]
- Barfknecht, R.E.; Dehkharghani, A.S.; Foerster, A.; Zinner, N.T. Correlation properties of a three-body bosonic mixture in a harmonic trap. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 135301. [Google Scholar] [CrossRef]
- Pyzh, M.; Krönke, S.; Weitenberg, C.; Schmelcher, P. Spectral properties and breathing dynamics of a few-body Bose-Bose mixture in a 1d harmonic trap. arXiv, 2017; arXiv:1707.03758. [Google Scholar]
- Kościk, P.; Sowiński, T. Exactly solvable model of two trapped quantum particles interacting via finite-range soft-core interactions. Sci. Rep. 2018, 8, 48. [Google Scholar] [CrossRef] [PubMed]
- Mujal, P.; Sarlé, E.; Polls, A.; Juliá-Díaz, B. Quantum correlations and degeneracy of identical bosons in a two-dimensional harmonic trap. Phys. Rev. A 2017, 96, 043614. [Google Scholar] [CrossRef]
- Blume, D. Few-body physics with ultracold atomic and molecular systems in traps. Rep. Prog. Phys. 2012, 75, 046401. [Google Scholar] [CrossRef] [PubMed]
- Kartavtsev, O.I.; Malykh, A.V. Universal low-energy properties of three two-dimensional bosons. Phys. Rev. A 2006, 74, 042506. [Google Scholar] [CrossRef]
- Christensson, J.; Forssén, C.; Åberg, S.; Reimann, S.M. Effective-interaction approach to the many-boson problem. Phys. Rev. A 2009, 79, 012707. [Google Scholar] [CrossRef]
- Shea, P.; van Zyl, B.P.; Bhaduri, R.K. The two-body problem of ultra-cold atoms in a harmonic trap. Am. J. Phys. 2009, 77, 511. [Google Scholar] [CrossRef]
- Liu, X.J.; Hu, H.; Drummond, P.D. Exact few-body results for strongly correlated quantum gases in two dimensions. Phys. Rev. B 2010, 82, 054524. [Google Scholar] [CrossRef]
- Farrell, A.; van Zyl, B.P. Universality of the energy spectrum for two interacting harmonically trapped ultra-cold atoms in one and two dimensions. J. Phys. A Math. Theor. 2010, 43, 015302. [Google Scholar] [CrossRef]
- Zinner, N.T. Universal two-body spectra of ultracold harmonically trapped atoms in two and three dimensions. J. Phys. A Math. Theor. 2012, 45, 205302. [Google Scholar] [CrossRef]
- Daily, K.M.; Yin, X.Y.; Blume, D. Occupation numbers of the harmonically trapped few-boson system. Phys. Rev. A 2012, 85, 053614. [Google Scholar] [CrossRef]
- Doganov, R.A.; Klaiman, S.; Alon, O.E.; Streltsov, A.I.; Cederbaum, L.S. Two trapped particles interacting by a finite-range two-body potential in two spatial dimensions. Phys. Rev. A 2013, 87, 033631. [Google Scholar] [CrossRef]
- Whitehead, T.M.; Schonenberg, L.M.; Kongsuwan, N.; Needs, R.J.; Conduit, G.J. Pseudopotential for the two-dimensional contact interaction. Phys. Rev. A 2016, 93, 042702. [Google Scholar] [CrossRef]
- Romanovsky, I.; Yannouleas, C.; Landman, U. Cristalline boson phases in harmonic traps: Beyond the Gross-Pitaevskii mean field. Phys. Rev. Lett. 2004, 93, 230405. [Google Scholar] [CrossRef] [PubMed]
- Klaiman, S.; Lode, A.U.J.; Streltsov, A.I.; Cederbaum, L.S.; Alon, O.E. Breaking the resilience of a two-dimensional Bose-Einstein condensate to fragmentation. Phys. Rev. A 2014, 90, 043620. [Google Scholar] [CrossRef]
- Katsimiga, G.C.; Mistakidis, S.I.; Koutentakis, G.M.; Kevrekidis, P.G.; Schmelcher, P. Many-body quantum dynamics in the decay of bent dark solitons of Bose-Einstein condensates. New J. Phys. 2017, 19, 123012. [Google Scholar] [CrossRef]
- Bolsinger, V.J.; Krönke, S.; Schmelcher, P. Beyond mean-field dynamics of ultra-cold bosonic atoms in higher dimensions: Facing the challenges with a multi-configurational approach. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 034003. [Google Scholar] [CrossRef]
- Jeszenski, P.; Cherny, A.Y.; Brand, J. The s-wave scattering length of a Gaussian potential. arXiv, 2018; arXiv:1802.07063. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mujal, P.; Polls, A.; Juliá-Díaz, B. Fermionic Properties of Two Interacting Bosons in a Two-Dimensional Harmonic Trap. Condens. Matter 2018, 3, 9. https://doi.org/10.3390/condmat3010009
Mujal P, Polls A, Juliá-Díaz B. Fermionic Properties of Two Interacting Bosons in a Two-Dimensional Harmonic Trap. Condensed Matter. 2018; 3(1):9. https://doi.org/10.3390/condmat3010009
Chicago/Turabian StyleMujal, Pere, Artur Polls, and Bruno Juliá-Díaz. 2018. "Fermionic Properties of Two Interacting Bosons in a Two-Dimensional Harmonic Trap" Condensed Matter 3, no. 1: 9. https://doi.org/10.3390/condmat3010009
APA StyleMujal, P., Polls, A., & Juliá-Díaz, B. (2018). Fermionic Properties of Two Interacting Bosons in a Two-Dimensional Harmonic Trap. Condensed Matter, 3(1), 9. https://doi.org/10.3390/condmat3010009



