Abstract
The correct detection of the Berezinskii-Kosterlitz-Thouless (BKT) transition in quasi-two-dimensional superconductors still remains a controversial issue. Its main signatures, indeed, are often at odds with the theoretical expectations. In a recent work (Maccari, I.; Benfatto, L.; Castellani, C. Phys. Rev. B 2017, 96, 060508), we have shown that the presence of spatially correlated disorder plays a key role in this sense because it is the reason underlying the experimentally-observed smearing of the universal superfluid-density jump. In the present paper we closely investigate the effects of correlated disorder on the BKT transition, specifically addressing the issue of whether or not it changes the BKT universality class.
1. Introduction
Despite its age, the Berezinskii [1]-Kosterlitz and Thouless [2,3] (BKT) transition still constitutes a very active field of research from both an experimental and a theoretical perspective. Actually, a wide range of phenomena belongs to its universality class: from the quantum metal-insulator transition in one dimension to the Coulomb-gas screening transition in 2D, and of course the metal-to-superfluid transition in 2D [4]. Since its first experimental detection in He films [5], the BKT transition has been investigated in many different real systems such as cold-atoms systems made of bosons [6], neutral fermions [7] and also in quasi-two-dimensional (2D) superconductors (SC). The latter case includes not only thin films of conventional [8,9,10,11,12,13,14,15,16,17] and unconventional [18,19,20,21,22] superconductors, but also artificially confined 2D electron gas at the interface between two insulators in artificial heterostructures [23,24], or in the top-most layer of ion-gated superconducting (SC) systems [25]. However, the experimental observations made so far on 2D superconductors have raised new questions as to the nature of the transition occurring in such systems because they are often at odds with the BKT theoretical predictions.
A typical example is the temperature dependence of the superfluid density which gives access to the most spectacular signature of the BKT transition: as soon as the system reaches the BKT critical temperature (), the proliferation of free topological defects (vortices) within the system leads the superfluid density to jump suddenly to zero, causing, at the same time, the vanishing of the SC state. Nonetheless, as reported by several experimental results [8,9,10,11,12,13,14,15,16,17], such a sharp jump at the critical temperature results in being significantly smeared out around , revealing a smooth downturn definitely broader than what is observed in the case of superfluid helium films [5]. This effect is even more dramatic in ultrathin films of cuprate superconductors [21], where the BKT jump is completely lost by underdoping. In addition, a long-term discussion exists also on the possibility to observe or not quasi-2D BKT physics in bulk cuprate crystals (see, e.g., [26] and references therein). Indeed, with the presence of a weak interlayer coupling one could expect to see a quasi-2D behavior. While this could be ultimately true, the temperature scale where it occurs could move away from the universal one expected in the purely 2D case [26,27]. In the following we will focus, however, only on the purely 2D case, restricting our attention to the case of thin films, and we refer the reader to [22,26,27] for a discussion on the occurrence of BKT physics in bulk crystals of layered cuprates.
Beyond the well-known differences between superfluid and superconducting systems, the latter ones exhibit as a common characteristic a pronounced spatial inhomogeneity of the SC order parameter. Such SC-state fragmentation, which occurs on a mesoscopic scale, might be due to the presence of strong disorder as is the case for thin disordered films of conventional superconductors. It might also be due to the artificial optical confinement, as in the SC interfaces, or to the intrinsic nature of the system, as seen in cuprate superconductors. Indeed, as shown theoretically [28,29,30,31,32,33], the formation of a “granular” inhomogeneous SC state is the way out of superconductivity, which requires phase coherence, to survive in the presence of disorder-induced charge localisation. From these observations, it is natural to wonder whether the observed broadening of the BKT transition could be due to the presence of such spatially correlated disorder within the system.
In a recent paper [34], we have addressed this interesting issue by means of Monte Carlo simulations on the classical 2D XY model:
where models the SC phase and are the random couplings between neighbouring sites , mimicking the random Josephson-like couplings between coarse-grained adjacent SC islands. The granular inhomogeneity of the SC order parameter is thus embedded in the couplings , whose disordered structure has been generated by the mean-field solution of the (quantum) pseudo-spin 1/2 model in random transverse field (RTF) [33,34,35,36]:
recently proven to model disordered superconductors with a non-trivial space structure [30,33,35]. In the pseudo-spin language, corresponds to a site occupied or unoccupied by a Cooper pair, while superconductivity corresponds to a spontaneous in-plane magnetization, e.g., , controlled by the coupling J. The random transverse field , box distributed between and W, simulates the effect of disorder, which tends to localize the Cooper pair on each site or, in terms of spins, to align them out of the x-y plane. This competition is well captured by the mean-field solution of the model (2), obtained by determining the value of the in-plane local magnetization . While at small everywhere, as increases the pseudo-spins partly orient along the direction suppressing the in-plane component, i.e., the local value of the SC order parameter. It can also be shown [34,35] that the SC phase fluctuations on top of this granular SC ground state are controlled by an inhomogeneous local stiffness between neighboring sites.
In the following we will make use exactly of such inhomogeneous local stiffness as couplings constants for the classical disordered 2D XY model (1). In particular, we will refer to these spatially-correlated disordered couplings as RTF, while with we will indicate spatially uncorrelated couplings extracted randomly from the same probability distribution which represents the RTF maps. Finally, the label will indicate the considered disorder level (see [34] for more details).
The main results of our numerical study, the technical details of which are discussed at the end of the paper, are reported in Figure 1. The BKT critical temperature, used here to properly rescale the temperatures, has been computed by means of the Nelson-Kosterlitz [37] universal relation:
which indicates the critical point at which the superfluid-stiffness jump is expected to occur.
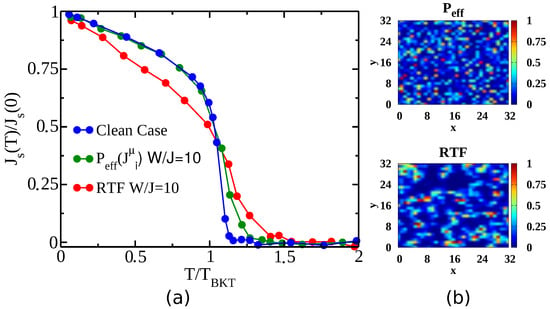
Figure 1.
(a) Rescaled curves of the superfluid stiffness by its zero-temperature value for the clean case, the uncorrelated and correlated random transverse field (RTF) disordered case at . The temperature axis has also been rescaled by the value of the Berezinskii-Kosterlitz-Thouless (BKT) critical temperature obtained from the intersection between the critical line and the superfluid-stiffness itself [34]. Despite the strong disorder, the curve shows only a small finite-size effect above , while the RTF stiffness is dramatically modified above and below the transition. (b) Maps of the couplings for both the spatially uncorrelated () and correlated (RTF) disorder. The disorder level has been fixed to while the linear size of the system is .
This study, largely discussed in [34], have revealed that for uncorrelated disorder the Harris criterion [38] is guaranteed not only at the critical point, but even away from it. Indeed, not only does the superfluid-stiffness jump remain as sharp as in the homogeneous case (green curve in Figure 1a), but even the low-temperature trend before the jump is unchanged once the suppression of the stiffness is accounted by rescaling the curve with . On the other hand, for the RTF case, the fragmentation of the SC state at strong disorder leads to a smoothening of the BKT jump (red curve in Figure 1a), which is symmetrically smeared out with respect to the expected transition, in strong analogy with the experimental observations in thin SC films [10,11,12,13,14,15,16,17].
This result has been explained in terms of an unconventional vortex-pairs nucleation in the granular SC state. Indeed, the formation of large regions with low couplings (Figure 1b), allows the system to nucleate several vortex-antivortex pairs already well below , leading to the superfluid-stiffness suppression.
In the present manuscript we want to investigate more closely these results in order to understand whether or not the correlated disorder changes the universality class of the BKT transition.
2. Results
In order to investigate the critical properties of the model (1), we need to extrapolate the thermodynamic behavior of the system via a proper finite-size scaling analysis. In the following, we will compare the well known homogeneous case () with the RTF model for a given disorder level, fixed here to .
First of all, as shown in Figure 2, the superfluid-stiffness jump expected in the thermodynamic limit is approached very slowly as a function of the size both for the homogeneous and for the RTF disordered case. This is exactly what one would expect from a BKT physics since the correlation length , instead of diverging as a power-law for , diverges exponentially as:
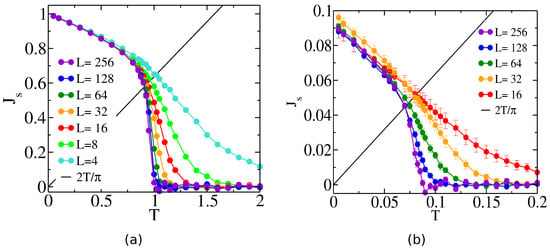
Figure 2.
Temperature dependence of the superfluid stiffness for different values of the linear sizes L. The panel (a) corresponds to the homogeneous case, while panel. (b) to the disordered case at . The solid black line in both the panels is the critical line whose intersection with would correspond to the critical point where the superfluid-stiffness jump is expected to occur.
As a consequence, since finite-size effects become relevant when , the finite-size correction to decrease logarithmically with the linear size of the system L [39,40,41,42]:
It also appears to be clear from Figure 2 that the superfluid stiffness scales differently with L below and above . Following [40] we will study separately the two different regimes: in the first part of this section and in the second one.
2.1. Scaling from
The scaling of in the homogeneous XY model below have been discussed in several papers [39,40,41,42]. They essentially follow from the analysis of the perturbative equations near the BKT critical point:
where is the rescaled coupling constant and the vortex fugacity, with vortex-core energy . When the critical line is approached from below (), the solution for the coupling x is simply [39]:
where c is a constant connected with the initial values of the flow and . From Equation(7), by the use of the Nelson-Kosterlitz universal relation [37]:
we can derive the dependence between the finite-size value of the superfluid stiffness and its thermodynamic limit at the critical point [39,40,41,42]:
This means that, by rescaling the superfluid stiffness with Equation (9), all the rescaled curves corresponding to different L will assume the same value at criticality. As a consequence, the crossing point of all of the curves will indicate the thermodynamic value of the critical temperature itself. The rescaled , obtained by tuning the value of the parameter in Equation (9) in such a way to obtain the best crossing point at finite temperature, are shown in Figure 3.
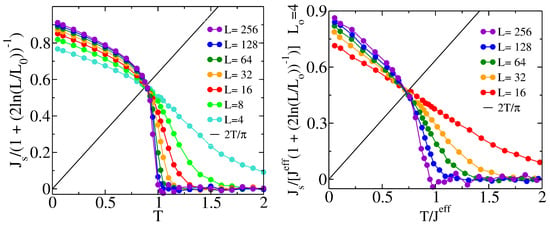
Figure 3.
Rescaling of the superfluid stiffness curves by means of Equation (9) both for (a) the clean case, (b) the disordered case with . In the presence of disorder, for a better comparison with the clean case, one can rescale both the superfluid stiffness and the temperature by .
This procedure allows us to derive the critical temperature of the RTF disordered model as well as its critical line. For the homogeneous case (Figure 3a), the best crossing point is obtained with , from which we extrapolate in good agreement with [39].
On the other hand, for the RTF disordered case (Figure 3b), the best crossing point has been found for . The first result to be highlighted is that the presence of correlated disorder does not change the universality class of the model, because the crossing point is still on the critical line . However, despite having rescaled both the superfluid stiffness and the temperature with respect to (for the clean case: ), the RTF disorder does change the critical temperature of the rescaled model to a lower value:
Quite interestingly, this result can be physically interpreted in terms of a decrease of the effective vortex-core energy , due to the presence of spatially correlated disorder. Indeed, for the homogeneous system it is well known [26] that a small implies a larger renormalization of before the transition, and as a consequence a smaller value of the critical temperature. Another remarkable effect of the presence of spatially correlated disorder is the magnification of the finite-size effects with respect to the homogeneous case. For instance, the curve of the clean case in Figure 3a relative to shows a tail similar for extension to the one correspondent to of the disordered case see Figure 3b, which is eight times bigger than the homogeneous case. This result is due to a larger scaling parameter in Equation (9) which makes the finite-size effects stronger for the disordered case.
2.2. Scaling from
In the high temperature regime, the thermodynamic limit of the superfluid stiffness is obviously zero. The finite size effects in this region are essentially due to the correlation length , whose divergence for is cut off by the system size L. By means of the finite-size scaling hypothesis [41,43], we can write the rescaled superfluid stiffness as a function of the ratio between L and :
Taking thus the logarithm of the argument of the scaling function , Equation (11) can be written in terms of another function , so that:
Hence, the rescaled superfluid stiffness will have the same functional dependence on for each value of the system size considered.
The collapsed curves of the rescaled stiffness, obtained from our numerical data, are shown in Figure 4, where we have used for the clean case and the previously-derived critical temperature for the RTF disordered case.
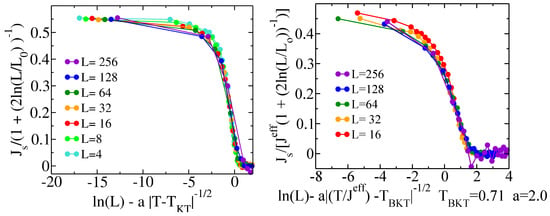
Figure 4.
Superfluid stiffness curves of different linear size L, renormalised and collapsed on the same universal curve relative to the high temperature regime: . (a) Clean case (b) RTF disordered case with .
The parameter to be fixed in this study is the factor a in Equation (4), which is chosen in such way to obtain the best collapse of all the curves. For the clean case it is known [41] to be , while in the presence of correlated disorder we have obtained the best collapse for: . The increase of the parameter a, by means of the presence of corraleted disorder, which is reflected in the scale of the x-axis, is much smaller in the case Figure 4b with respect to the homogeneous one in Figure 4a.
This physically means that the length of the correlations diverges faster in the presence of correlated disorder than without it, in agreement with the previously observed increase of the finite size effects (Figure 3). Let us also highlight that, from the limit in Figure 4, which in terms of the function corresponds to , we can extrapolate the value of the superfluid stiffness expected at the critical point.
Both for the clean and the disordered case, this confirms the Nelson-Kosterlitz relation (3):
as expected since both the critical points are crossed by the universal line .
Hence, this study confirms that in both the cases the universality class is the BKT one, showing, at the same time, that even in the presence of correlated disorder, the correlation length diverges exponentially in the reduced critical temperature. Moreover, it sheds light on the two main differences, with respect to the clean case, introduced by the spatially correlated disorder: the reduction of the critical temperature and the faster increase of the correlation length as .
Finally, a very interesting issue to be addressed in future work is whether the presence of this kind of granular disorder could also affect the low-temperature power-law decay of the two-point correlations function, whose exponent in the clean case is known to be as soon as .
3. Methods
In our simulations, each Monte Carlo step consists of five Metropolis spin flips of the whole lattice, needed to probe the correct canonical distribution of the system, followed by ten Over-relaxation sweeps of all the spins, which help the thermalization. For each temperature, we performed 5000 Monte Carlo steps, and we computed a given quantity as an average after discarding the transient regime, occurring in the first 2000 steps. Finally, the average of the disorder is calculated with 15 independent configurations for each disorder level. Where not shown, the error bars are smaller than the point size.
4. Discussion
The present paper completes the study started in [34] on the 2D model in the presence of spatially correlated couplings, which mimics the mesoscopic inhomogeneity experimentally observed in two-dimensional superconducting systems.
From the finite-size scaling analysis, we have shown that the presence of disordered couplings with spatial correlations does not change the universality class of the BKT transition, affecting nonetheless both the critical temperature and the exponential divergence of the correlation length. More specifically, the critical temperature of the RTF model is found to be lower with respect to the homogeneous case, as a consequence of an effective smaller vortex-core energy. This result appears to be perfectly in agreement with the conclusions drawn in [44], where it was shown that for a correct identification of the typical BKT signatures in NbN thin films it is needed to account for values smaller than what is expected from the standard homogeneous XY model.
Our work has also revealed that the presence of a spatially-correlated disorder makes the finite-size effects much stronger than in the homogeneous case, as reflected, e.g., in the divergence of the correlation length as the transition is approached from above . This result opens interesting perspectives for the understanding of the extended tails usually observed in the sheet resistance curves in 2D superconducting interfaces [24]. Indeed, since the resistivity tends to zero as in the BKT transition [45], the enhanced finite-size effects found in our numerical study could provide a microscopic derivation for the phenomenological models of inhomogeneity proposed so far [46,47].
In addition, the presence of SC inhomogeneity at the mesoscopic level could account for the suppression of the zero-temperature stiffness with respect to its BCS estimate recently reported in / [48]. A quantitative analysis of these effects could provide more insight into the space structure of disorder in these SC 2D materials, whose high tunability constitutes an excellent prerequisite for potential device applications.
Acknowledgments
This work has been supported by MAECI under the Italian-India collaborative project SUPERTOP-PGR04879.
Author Contributions
All the authors contributed to the design of the project. Ilaria Maccari performed the numerical simulations, all the authors analyzed the results and wrote the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Berezinsky, V.L. Destruction of long-range order in one-dimensional and two-dimensional systems possessing a continuous symmetry group. JETP 1972, 34, 610. [Google Scholar]
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C 1973, 6, 1181. [Google Scholar] [CrossRef]
- Kosterlitz, J.M. The critical properties of the two-dimensional xy model. J. Phys. C 1974, 7, 1046. [Google Scholar] [CrossRef]
- José, J.V. 40 Years of Berezinskii-Kosterlitz-Thouless Theory; World Scientific: Singapore, 2013. [Google Scholar]
- McQueeney, D.; Agnolet, G.; Reppy, J.D. Surface superfluidity in dilute 4He-3He mixtures. Phys. Rev. Lett. 1984, 52, 1325. [Google Scholar] [CrossRef]
- Hadzibabic, Z.; Krüger, P.; Cheneau, M.; Battelier, B.; Dalibard, J. Berezinskii-Kosterlitz-Thouless crossover in a trapped atomic gas. Nature 2006, 44, 1118. [Google Scholar] [CrossRef] [PubMed]
- Murthy, P.A.; Boettcher, I.; Bayha, L.; Holzmann, M.; Kedar, D.; Neidig, M.; Ries, M.G.; Wenz, A.N.; Zürn, G.; Jochim, S. Observation of the Berezinskii-Kosterlitz-Thouless phase transition in an ultracold Fermi gas. Phys. Rev. Lett. 2015, 115, 010401. [Google Scholar] [CrossRef] [PubMed]
- Epstein, K.; Goldman, A.M.; Kadin, A.M. Vortex-antivortex pair dissociation in two-dimensional superconductors. Phys. Rev. Lett 1981, 47, 534. [Google Scholar] [CrossRef]
- Kadin, A.M.; Epstein, K.; Goldman, A.M. Renormalization and the Kosterlitz-Thouless transition in a two-dimensional superconductor. Phys. Rev. B 1983, 27, 6691. [Google Scholar] [CrossRef]
- Fiory, A.T.; Hebard, A.F.; Glaberson, W.I. Superconducting phase transitions in indium/indium-oxide thin-film composites. Phys. Rev. B 1983, 28, 5075. [Google Scholar] [CrossRef]
- Turneaure, S.J.; Lemberger, T.R.; Graybeal, J.M. Effect of thermal phase fluctuations on the superfluid density of two-dimensional superconducting films. Phys. Rev. Lett. 2000, 84, 987. [Google Scholar] [CrossRef] [PubMed]
- Crane, R.W.; Armitage, N.P.; Johansson, A.; Sambandamurthy, G.; Shahar, D.; Gruner, G. Fluctuations, dissipation, and nonuniversal superfluid jumps in two-dimensional superconductors. Phys. Rev. B 2007, 75, 094506. [Google Scholar] [CrossRef]
- Liu, W.; Kim, M.; Sambandamurthy, G.; Armitage, N.P. Dynamical study of phase fluctuations and their critical slowing down in amorphous superconducting films. Phys. Rev. B 2011, 84, 024511. [Google Scholar] [CrossRef]
- Mondal, M.; Kumar, S.; Chand, M.; Kamlapure, A.; Saraswat, G.; Seibold, G.; Benfatto, L.; Raychaudhuri, P. Role of the vortex-core energy on the Berezinskii-Kosterlitz-Thouless transition in thin films of NbN. Phys. Rev. Lett. 2011, 107, 217003. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.H.; Nelson, J.; Goldman, A.M. Suppression of the Berezinskii-Kosterlitz-Thouless transition in 2D superconductors by macroscopic quantum tunneling. Phys. Rev. Lett. 2012, 109, 017002. [Google Scholar] [CrossRef] [PubMed]
- Misra, S.; Urban, L.; Kim, M.; Sambandamurthy, G.; Yazdani, A. Measurements of the magnetic-field-tuned conductivity of disordered two-dimensional Mo43Ge57 and InOx superconducting films: Evidence for a universal minimum superfluid response. Phys. Rev. Lett 2013, 110, 037002. [Google Scholar] [CrossRef] [PubMed]
- Kamlapure, A.; Mondal, M.; Chand, M.; Mishra, A.; Jesudasan, J.; Bagwe, V.; Benfatto, L.; Tripathi, V.; Raychaudhuri, P. Measurement of magnetic penetration depth and superconducting energy gap in very thin epitaxial NbN films. Appl. Phys. Lett. 2010, 96, 072509. [Google Scholar] [CrossRef]
- Corson, J.; Mallozzi, R.; Orenstein, J.; Eckstein, J.N.; Bozovic, I. Vanishing of phase coherence in underdoped Bi2Sr2CaCu2O8+δ. Nature 1999, 398, 221. [Google Scholar] [CrossRef]
- Broun, D.M.; Huttema, W.A.; Turner, P.J.; Ozcan, S.; Morgan, B.; Liang, R.; Hardy, W.N.; Bonn, D.A. Superfluid density in a highly underdoped YBa2Cu3O6+y superconductor. Phys. Rev. Lett. 2007, 99, 237003. [Google Scholar] [CrossRef] [PubMed]
- Hetel, I.; Lemberger, T.R.; Randeria, M. Quantum critical behaviour in the superfluid density of strongly underdoped ultrathin copper oxide films. Nat. Phys. 2007, 3, 700. [Google Scholar] [CrossRef]
- Yong, J.; Hinton, M.J.; McCray, A.; Randeria, M.; Naamneh, M.; Kanigel, A.; Lemberger, T.R. Evidence of two-dimensional quantum critical behavior in the superfluid density of extremely underdoped Bi2Sr2CaCu2O8+x. Phys. Rev. B 2012, 85, 180507. [Google Scholar] [CrossRef]
- Baity, P.G.; Shi, X.; Shi, Z.; Benfatto, L.; Popović, D. Effective two-dimensional thickness for the Berezinskii-Kosterlitz-Thouless-like transition in a highly underdoped La2−xSrxCuO4. Phys. Rev. B 2016, 93, 024519. [Google Scholar] [CrossRef]
- Bert, J.A.; Nowack, K.C.; Kalisky, B.; Noad, H.; Kirtley, J.R.; Bell, C.; Sato, H.K.; Hosoda, M.; Hikita, Y.; Hwang, H.Y.; et al. Gate-tuned superfluid density at the superconducting LaAlO3/SrTiO3 interface. Phys. Rev. B 2012, 86, 060503. [Google Scholar] [CrossRef]
- Daptary, G.N.; Kumar, S.; Kumar, P.; Dogra, A.; Mohanta, N.; Taraphder, A.; Bid, A. Correlated non-Gaussian phase fluctuations in LaAlO3/SrTiO3 heterointerfaces. Phys. Rev. B 2016, 94, 085104. [Google Scholar] [CrossRef]
- Saito, Y.; Kasahara, Y.; Ye, J.; Iwasa, Y.; Nojima, T. Metallic ground state in an ion-gated two-dimensional superconductor. Science 2015, 350, 409. [Google Scholar] [CrossRef] [PubMed]
- Benfatto, L.; Castellani, C.; Giamarchi, T. Berezinskii-Kosterlitz-Thouless Transition within the Sine-Gordon Approach: The Role of the Vortex-Core Energy. In 40 Years of Berezinskii-Kosterlitz-Thouless Theory; José, J.V., Ed.; World Scientific: Singapore, 2013. [Google Scholar]
- Benfatto, L.; Castellani, C.; Giamarchi, T. Kosterlitz-thouless behavior in layered superconductors: The role of the vortex core energy. Phys. Rev. Lett. 2007, 98, 117008. [Google Scholar] [CrossRef] [PubMed]
- Ghosal, A.; Randeria, M.; Trivedi, N. Inhomogeneous pairing in highly disordered s-wave superconductors. Phys. Rev. B 2001, 65, 014501. [Google Scholar] [CrossRef]
- Dubi, Y.; Meir, Y.; Avishai, Y. Nature of the superconductor-insulator transition in disordered superconductors. Nature 2007, 449, 876. [Google Scholar]
- Ioffe, L.B.; Mezard, M. Disorder-driven quantum phase transitions in superconductors and magnets. Phys. Rev. Lett. 2010, 105, 037001. [Google Scholar] [CrossRef] [PubMed]
- Bouadim, K.; Loh, Y.L.; Randeria, M.; Trivedi, N. Single-and two-particle energy gaps across the disorder-driven superconductor–insulator transition. Nat. Phys. 2011, 7, 884. [Google Scholar] [CrossRef]
- Seibold, G.; Benfatto, L.; Castellani, C.; Lorenzana, J. Superfluid density and phase relaxation in superconductors with strong disorder. Phys. Rev. Lett. 2012, 108, 207004. [Google Scholar] [CrossRef] [PubMed]
- Lemarie, G.; Kamlapure, A.; Bucheli, D.; Benfatto, L.; Lorenzana, J.; Seibold, G.; Ganguli, S.C.; Raychaudhuri, P.; Castellani, C. Universal scaling of the order-parameter distribution in strongly disordered superconductors. Phys. Rev. B 2013, 87, 184509. [Google Scholar] [CrossRef]
- Maccari, I.; Benfatto, L.; Castellani, C. Broadening of the Berezinskii-Kosterlitz-Thouless transition by correlated disorder. Phys. Rev. B 2017, 96, 060508. [Google Scholar] [CrossRef]
- Cea, T.; Bucheli, D.; Seibold, G.; Benfatto, L.; Lorenzana, J.; Castellani, C. Optical excitation of phase modes in strongly disordered superconductors. Phys. Rev. B 2014, 89, 174506. [Google Scholar] [CrossRef]
- Ma, M.; Lee, P.A. Localized superconductors. Phys. Rev. B 1985, 32, 5658. [Google Scholar] [CrossRef]
- Nelson, D.R.; Kosterlitz, J.M. Universal jump in the superfluid density of two-dimensional superfluids. Phys. Rev. Lett. 1977, 19, 1201. [Google Scholar] [CrossRef]
- Harris, A.B. Effect of random defects on the critical behaviour of Ising models. J. Phys. C 1974, 7, 1671. [Google Scholar] [CrossRef]
- Hasenbusch, M. The two-dimensional XY model at the transition temperature: A high-precision Monte Carlo study. J. Phys. Gen. A Math. 2005, 38, 5869. [Google Scholar] [CrossRef]
- Schultka, N.; Manousakis, E. Finite-size scaling in two-dimensional superfluids. Phys. Rev. B 1994, 49, 12071. [Google Scholar] [CrossRef]
- Sandvick, A.W. Computational studies of quantum spin systems. AIP Conf. Proc. 2010, 1297, 135. [Google Scholar]
- Weber, H.; Minnhagen, P. Monte Carlo determination of the critical temperature for the two-dimensional XY model. Phys. Rev. B 1988, 37, 5986. [Google Scholar] [CrossRef]
- Fisher, M.E.; Barber, M.N. Scaling theory for finite-size effects in the critical region. Phys. Rev. Lett. 1972, 28, 1516. [Google Scholar] [CrossRef]
- Mondal, M.; Kamlapure, A.; Chand, M.; Saraswat, G.; Kumar, S.; Jesudasan, J.; Benfatto, L.; Tripathi, V.; Raychaudhuri, P. Phase fluctuations in a strongly disordered s-wave NbN superconductor close to the metal-insulator transition. Phys. Rev. Lett. 2011, 106, 047001. [Google Scholar] [CrossRef] [PubMed]
- Halperin, B.I.; Nelson, D.R. Resistive transition in superconducting films. J. Low Temp. Phys. 1979, 36, 599. [Google Scholar] [CrossRef]
- Benfatto, L.; Castellani, C.; Giamarchi, T. Broadening of the Berezinskii-Kosterlitz-Thouless superconducting transition by inhomogeneity and finite-size effects. Phys. Rev. B 2009, 80, 214506. [Google Scholar] [CrossRef]
- Caprara, S.; Grilli, M.; Benfatto, L.; Castellani, C. Effective medium theory for superconducting layers: A systematic analysis including space correlation effects. Phys. Rev. B 2011, 84, 014514. [Google Scholar] [CrossRef]
- Singh, G.; Jouan, A.; Benfatto, L.; Couedo, F.; Kumar, P.; Dogra, A.; Budhani, R.; Caprara, S.; Grilli, M.; Lesne, E.; et al. Competition between electron pairing and phase coherence in superconducting interfaces. arXiv, 2017; arXiv:1704.03365. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).