Orbital-Nematic and Two-Fluid Superconductivity in Hole-Doped NdNiO2
Abstract
1. Introduction
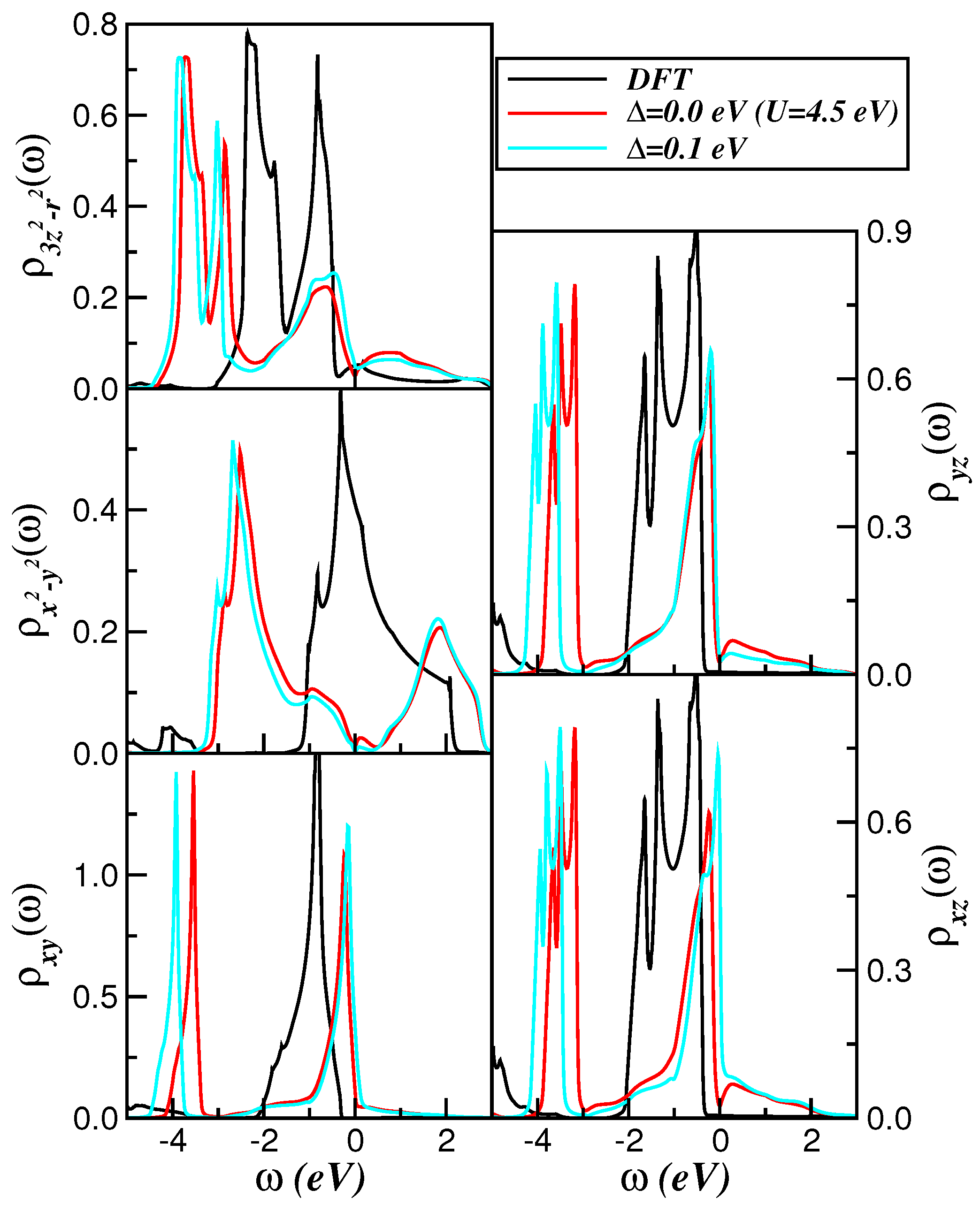
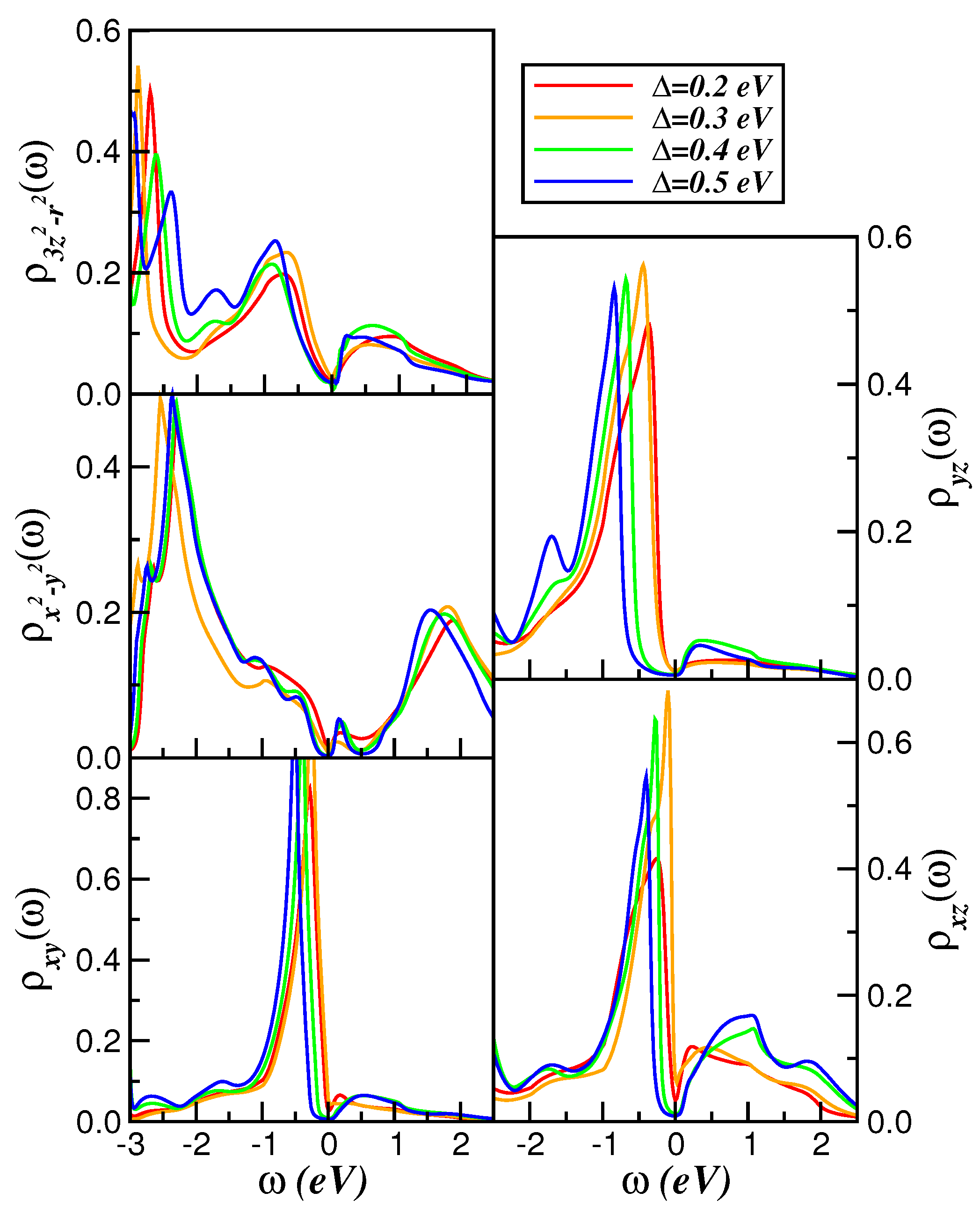
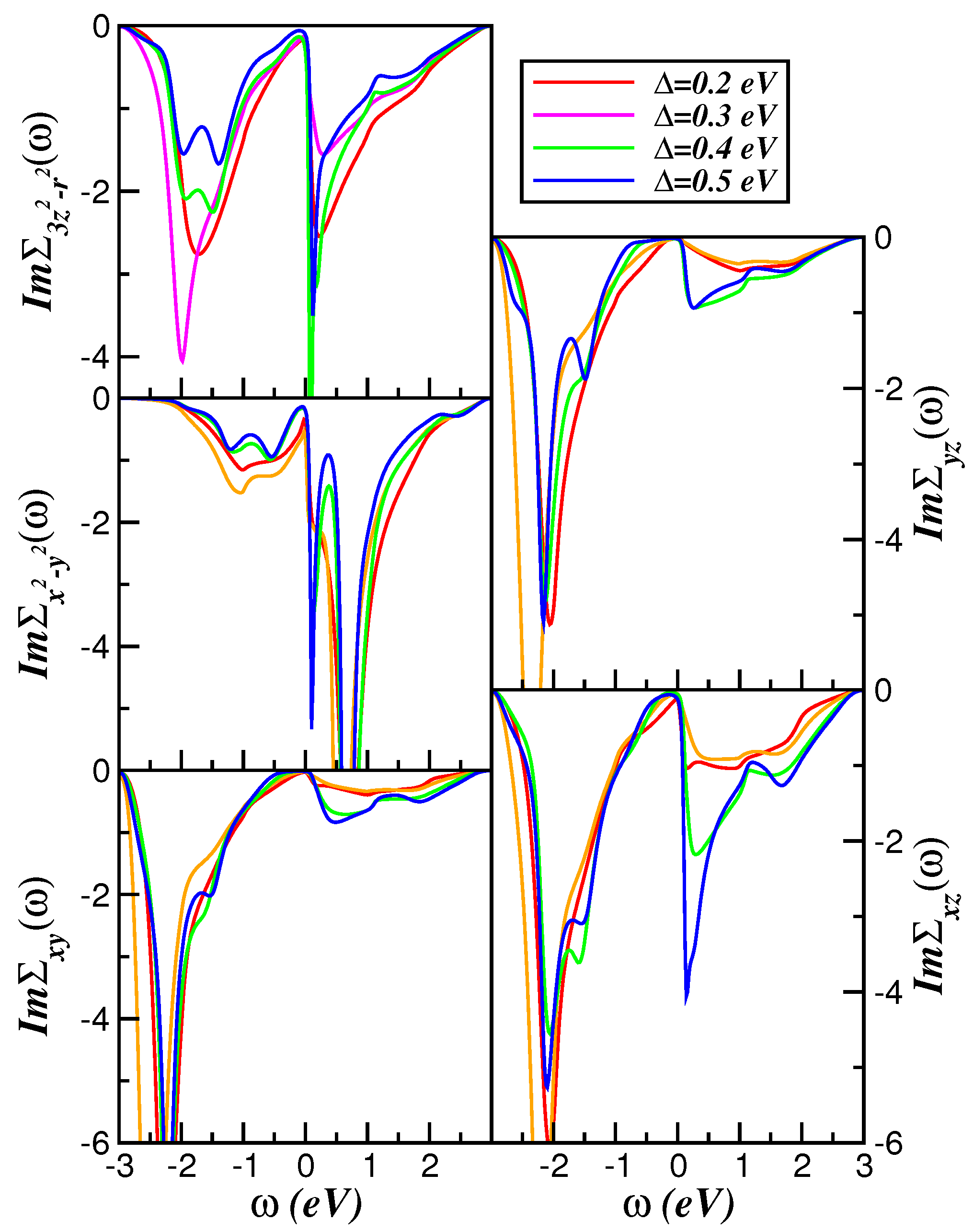
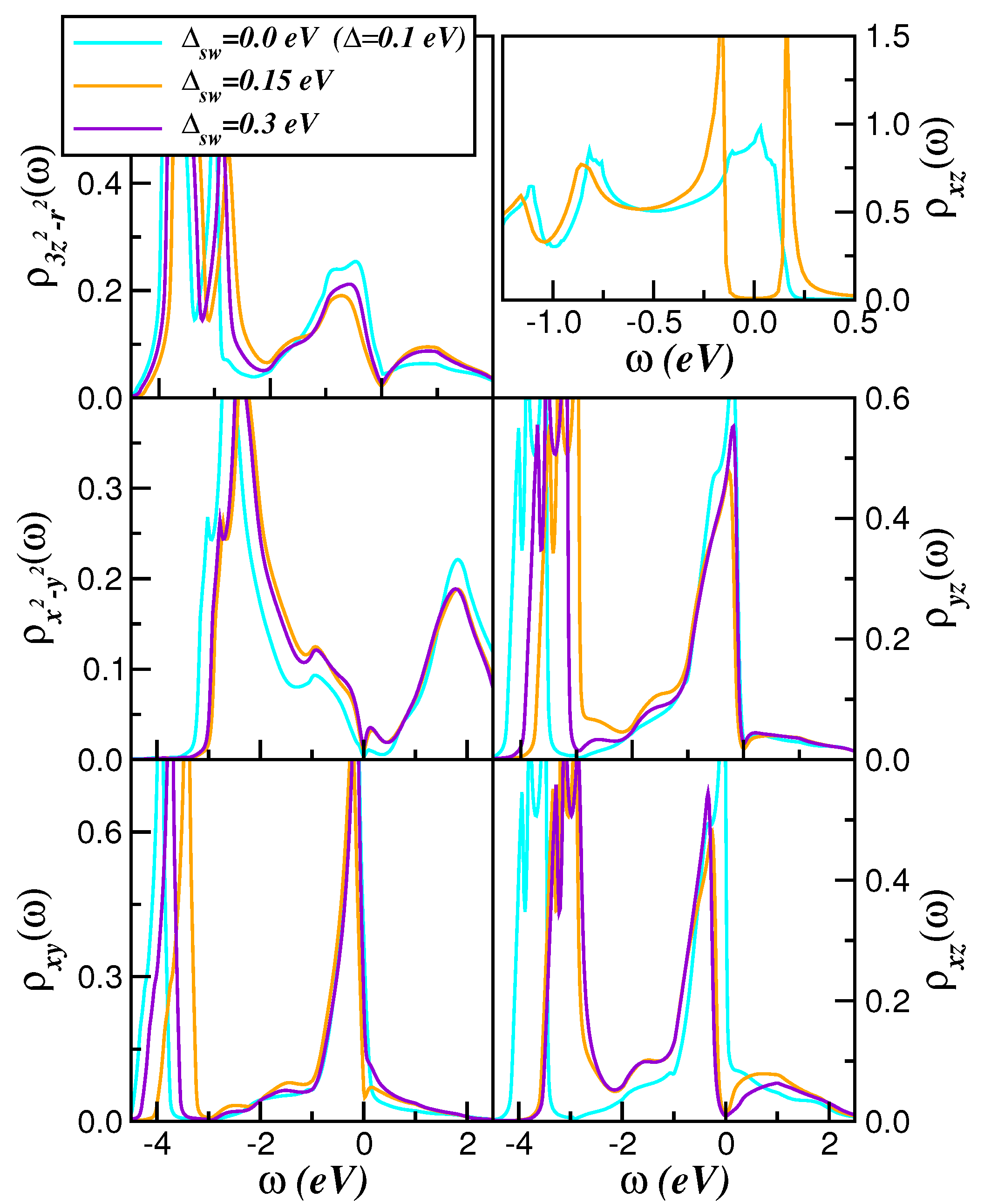
2. Theory and Results
3. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dagotto, E. Complexity in strongly correlated electronic systems. Science 2005, 309, 257. [Google Scholar] [CrossRef] [PubMed]
- Tranquada, J.M.; Sternlieb, B.J.; Axe, D.J.; Nakamura, Y.; Uchida, S. Evidence for stripe correlations of spins and holes in copper oxide superconductors. Nature 1995, 375, 561. [Google Scholar]
- Glasbrenner, J.K.; Mazin, I.I.; Jeschke, H.O.; Hirschfeld, P.J.; Fernandes, R.M.; Valenti, R. Effect of magnetic frustration on nematicity and superconductivity in iron chalcogenides. Nat. Phys. 2015, 11, 953. [Google Scholar]
- Imada, M.; Fujimori, A.; Tokura, Y. Metal-insulator transitions. Rev. Mod. Phys. 1998, 70, 1039. [Google Scholar]
- Zhang, R.; Lane, C.; Nokelainen, J.; Singh, B.; Barbiellini, B.; Markiewicz, R.S.; Bansil, A.; Sun, J. Emergence of competing stripe phases in undoped Infinite-layer nickelates. Phys. Rev. Lett. 2024, 133, 066401. [Google Scholar]
- Zhuge, H.; Si, L.; Jiang, M. Impactof rotational symmetry breaking on d-wave superconductivity in Hubbard models for cuprate and nickelate superconductors. Phys. Rev. B 2024, 110, L020501. [Google Scholar] [CrossRef]
- Zhang, Y.-H.; Vishwanath, A. Type-II t-J model in superconducting nickelate Nd1-xSrxNiO2. Phys. Rev. Res. 2020, 2, 023112. [Google Scholar] [CrossRef]
- Sakakibara, H.; Usui, H.; Suzuki, K.; Kotani, T.; Aoki, H.; Kuroki, K. Model construction and a possibility of cupratelike pairing in a new d9 nickelate superconductor. Phys. Rev. Lett. 2020, 125, 077003. [Google Scholar] [CrossRef]
- Kreisel, A.; Andersen, B.M.; Romer, A.T.; Eremin, I.M.; Lechermann, F. Superconducting instabilities in strongly correlated infinite-layer nickelates. Phys. Rev. Lett. 2022, 129, 077002. [Google Scholar] [CrossRef]
- Li, D.; Lee, K.; Wang, B.Y.; Osada, M.; Crossley, S.; Lee, H.R.; Cui, Y.; Hikita, Y.; Hwang, H.Y. Superconductivity in an infinite-layer nickelate. Nature 2019, 572, 624. [Google Scholar] [CrossRef]
- Yu, Y.; Ma, L.; Cai, P.; Zhong, R.; Ye, C.; Shen, J.; Gu, G.D.; Chen, X.H.; Zhang, Y. High-temperature superconductivity in monolayer Bi2Sr2CaCu2O8+δ. Nature 2019, 575, 156. [Google Scholar] [CrossRef] [PubMed]
- Yuan, H.Q.; Singleton, J.; Balakirev, F.F.; Baily, S.A.; Chen, G.F.; Luo, J.L.; Wang, N.L. Nearly isotropic superconductivity in (Ba,K)Fe2As2. Nature 2009, 457, 565. [Google Scholar] [CrossRef] [PubMed]
- Talantsev, E.F. Intrinsic coherence length anisotropy in nickelates and some iron-based superconductors. Materals 2023, 16, 4367. [Google Scholar] [CrossRef] [PubMed]
- Vojta, M. Lattice symmetry breaking in cuprate superconductors. Adv. Phys. 2009, 58, 699. [Google Scholar] [CrossRef]
- Chow, L.E.; Rubi, K.K.; Yip, K.Y.; Pierre, M.; Leroux, M.; Liu, X.; Luo, Z.; Zeng, S.; Li, C.; Goiran, M.; et al. Dimensionality control and rotational symmetry breaking superconductivity in square-planar layered nickelates. arXiv 2023, arXiv:2301.07606. [Google Scholar]
- Lechermann, F. Late transition metal oxides with infinite-layer structure: Nickelates versus cuprates. Phys. Rev. B 2020, 101, 081110(R). [Google Scholar] [CrossRef]
- Botana, A.S.; Norman, M.R. Similarities and differences between LaNiO2 and CaCuO2 and implications for superconductivity. Phys. Rev. X 2020, 10, 011024. [Google Scholar] [CrossRef]
- Liu, L.; Xu, C.; Cao, C.; Zhu, W.; Wang, Z.F.; Yang, J. Doping dependence of electronic structure of infinite-layer NdNiO2. Phys. Rev. B 2021, 103, 045103. [Google Scholar] [CrossRef]
- Worm, P.; Si, L.; Kitatani, M.; Arita, R.; Tomczak, J.M.; Held, K. Correlations tune the electronic structure of pentalayer nickelates into the superconducting regime. Phys. Rev. Mater. 2022, 6, L091801. [Google Scholar] [CrossRef]
- Wang, Y.; Kang, C.-J.; Miao, H.; Kotliar, G. Hund’s metal physics: From SrNiO2 to LaNiO2. Phys. Rev. B 2020, 102, 161118(R). [Google Scholar] [CrossRef]
- Ryee, S.; Yoon, H.; Kim, T.J.; Jeong, M.Y.; Han, M.J. Induced magnetic two-dimensionality by hole doping in the superconducting infinite-layer nickelate. Phys. Rev. B 2020, 101, 064513. [Google Scholar] [CrossRef]
- Goodge, B.H.; Li, D.; Lee, K.; Osada, M.; Wang, B.Y.; Sawatzky, G.A.; Hwang, H.Y.; Kourkoutis, L.F. Doping evolution of the Mott–Hubbard landscape in infinite-layer nickelates. Proc. Natl. Acad. Sci. USA 2021, 118, e2007683118. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.Y.; Wang, T.C.; Hsu, Y.-T.; Osada, M.; Lee, K.; Jia, C.; Duffy, C.; Li, D.; Fowlie, J.; Beasley, M.R.; et al. Effects of rare-earth magnetism on the superconducting upper critical field in infinite-layer nickelates. Sci. Adv. 2023, 9, adf665. [Google Scholar] [CrossRef] [PubMed]
- Ji, H.; Li, Y.; Liu, Y.; Ding, X.; Xie, Z.; Qi, S.; Qiao, L.; Yang, Y.-F.; Zhang, G.-M.; Wang, J. Rotational symmetry breaking in superconducting nickelate Nd0.8Sr0.2NiO2 films. Nat. Commun. 2023, 14, 7155. [Google Scholar] [CrossRef]
- Sun, W.; Li, Y.; Liu, R.; Yang, J.; Li, J.; Yan, S.; Sun, H.; Guo, W.; Gu, Z.; Deng, Y.; et al. Evidence for anisotropic superconductivity beyond Pauli limit in infinite-layer lanthanum nickelates. Adv. Matter. 2023, 35, 2303400. [Google Scholar] [CrossRef]
- Russell, R.R.; Nair, H.P.; Shen, K.M.; Schlom, D.G.; Harter, J.W. Electronic nematic order in the normal state of strontium ruthenate. Phys. Rev. B 2023, 108, L081105. [Google Scholar] [CrossRef]
- Laad, M.S.; Craco, L. Theory of the unusual high-temperature anisotropic resistivity of underdoped iron arsenide superconductors: Evidence for an orbital nematic order. Phys. Rev. B 2021, 84, 054530. [Google Scholar] [CrossRef]
- Zhao, D.; Zhou, Y.B.; Fu, Y.; Wang, L.; Zhou, X.F.; Cheng, H.; Li, J.; Song, D.W.; Li, S.J.; Kang, B.L.; et al. Intrinsic spin susceptibility and pseudogaplike behavior in infinite-layer LaNiO2. Phys. Rev. Lett. 2021, 126, 197001. [Google Scholar] [CrossRef]
- Craco, L.; de Arruda, A.S.; Leoni, S. Emergent normal-state Mottness in the infinite-layer NdNiO2 superconductor. Phys. Rev. Res. 2022, 4, 043036. [Google Scholar] [CrossRef]
- Baek, S.-H.; Efremov, D.V.; Ok, J.M.; Kim, J.S.; van den Brink, J.; Büchner, B. Orbital-driven nematicity in FeSe. Nat. Mat. 2015, 14, 210. [Google Scholar] [CrossRef]
- Cao, R.X.; Hu, J.; Dong, J.; Zhang, J.B.; Ye, X.S.; Xu, Y.F.; Chareev, D.A.; Vasiliev, A.N.; Wu, B.; Zeng, X.H. Observation of orbital ordering and origin of the nematic order in FeSe. New J. Phys. 2019, 21, 103033. [Google Scholar] [CrossRef]
- Wang, Z.; Nevidomskyy, A.H. Orbital nematic order and interplay with magnetism in the two-orbital Hubbard model. J. Phys. Condens. Matter 2015, 27, 225602. [Google Scholar] [CrossRef] [PubMed]
- Gu, Q.; Li, Y.; Wan, S.; Li, H.; Guo, W.; Yang, H.; Li, Q.; Zhu, X.; Pan, X.; Nie, Y.; et al. Single particle tunneling spectrum of superconducting Nd1-xSrxNiO2 thin films. Nat. Commun. 2020, 11, 6027. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, G.-M.; Yang, Y.-F.; Zhang, F.-C. Distinct pairing symmetries of superconductivity in infinite-layer nickelates. Phys. Rev. B 2020, 102, 220501(R). [Google Scholar] [CrossRef]
- Wu, X.; Jiang, K.; Di Sante, D.; Hanke, W.; Schnyder, A.P.; Hu, J.; Thomale, R. Surface s-wave superconductivity for oxide-terminated infinite-layer nickelates. arXiv 2020, arXiv:2008.06009. [Google Scholar]
- Occhialini, C.A.; Sanchez, J.J.; Song, Q.; Fabbris, G.; Choi, Y.; Kim, J.-W.; Ryan, P.J.; Comin, R. Spontaneous orbital polarization in the nematic phase of FeSe. Nat. Mat. 2023, 22, 985. [Google Scholar] [CrossRef]
- Lee, C.-C.; Yin, W.-G.; Ku, W. Ferro-orbital order and strong magnetic anisotropy in the parent compounds of iron-pnictide superconductors. Phys. Rev. Lett. 2009, 103, 267001. [Google Scholar] [CrossRef]
- Chen, C.-C.; Maciejko, J.; Sorini, A.P.; Moritz, B.; Singh, R.R.P.; Devereaux, T.P. Orbital order and spontaneous orthorhombicity in iron pnictides. Phys. Rev. B 2010, 82, 100504(R). [Google Scholar] [CrossRef]
- Fernandes, R.M.; Chubukov, A.V.; Schmalian, J. What drives nematic order in iron-based superconductors? Nat. Phys. 2014, 10, 97. [Google Scholar] [CrossRef]
- Kotliar, G.; Savrasov, S.Y.; Haule, K.; Oudovenko, V.S.; Parcollet, O.; Marianetti, C.A. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 2006, 78, 865. [Google Scholar] [CrossRef]
- Craco, L.; Leoni, S. Orbital-selective mixed-valent Mott/metal phase coexistence in NdNiO2 films. Phys. Rev. Mater. 2023, 7, 044802. [Google Scholar] [CrossRef]
- Brito, W.H.; Aguiar, M.C.O.; Haule, H.; Kotliar, G. Metal-insulator transition in VO2: A DFT + DMFT perspective. Phys. Rev. Lett. 2016, 117, 056402. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.-f.; Zhang, G.-M. Self-doping and the Mott-Kondo scenario for infinite-layer nickelate superconductors. Front. Phys. 2022, 9, 801236. [Google Scholar] [CrossRef]
- Craco, L.; Laad, M.S.; Leoni, S. Unconventional Mott transition in KxFe2-ySe2. Phys. Rev. B 2011, 84, 224520. [Google Scholar] [CrossRef]
- Freelon, B.; Liu, Y.H.; Chen, J.-L.; Craco, L.; Laad, M.S.; Leoni, S.; Chen, J.; Tao, L.; Wang, H.; Flauca, R.; et al. Mott-Kondo insulator behavior in the iron oxychalcogenides. Phys. Rev. B 2015, 92, 155139. [Google Scholar] [CrossRef]
- Werner, P.; Millis, A.J. High-spin to low-spin and orbital polarization transitions in multiorbital Mott systems. Phys. Rev. Lett. 2007, 99, 126405. [Google Scholar] [CrossRef]
- Ni, Y.; Quan, Y.-M.; Liu, J.; Song, Y.; Zou, L.-Z. Electronic correlation-driven orbital polarization transitions in the o orbital-selective Mott compound Ba2CuO4-δ. Phys. Rev. B 2021, 103, 214510. [Google Scholar] [CrossRef]
- Pascut, G.L.; Cosovanu, L.; Haule, K.; Quader, K.F. Correlation-temperature phase diagram of prototypical infinite layer rare earth nickelates. Commun. Phys. 2023, 6, 45. [Google Scholar] [CrossRef]
- Karp, J.; Hampel, A.; Millis, A.J. Dependence of DFT +DMFT results on the construction of the correlated orbitals. Phys. Rev. B 2011, 103, 195101. [Google Scholar] [CrossRef]
- Lechermann, F. Doping-dependent character and possible magnetic ordering of NdNiO2. Phys. Rev. Mater. 2021, 5, 044803. [Google Scholar] [CrossRef]
- Hayward, M.A.; Rosseinsky, M.J. Synthesis of the infinite layer Ni(I) phase NdNiO2+x by low temperature reduction of NdNiO3 with sodium hydride. Solid State Sci. 2003, 5, 839. [Google Scholar] [CrossRef]
- Craco, L. Quantum orbital entanglement: A view from the extended periodic Anderson model. Phys. Rev. B 2008, 77, 125122. [Google Scholar] [CrossRef]
- Craco, L.; Leoni, S. two-fluid metallicity in superconducting FeSe at high pressure. Phys. Rev. B 2019, 100, 121101(R). [Google Scholar] [CrossRef]
- Rossi, M.; Lu, H.; Nag, A.; Li, D.; Osada, M.; Lee, K.; Wang, B.Y.; Agrestini, S.; Garcia-Fernandez, M.; Kas, J.J.; et al. Orbital and spin character of doped carriers in infinite-layer nickelates. Phys. Rev. B 2021, 104, L220505. [Google Scholar] [CrossRef]
- Xie, T.Y.; Liu, Z.; Cao, C.; Wang, Z.F.; Yang, J.L.; Zhu, W. Microscopic theory of superconducting phase diagram in infinite-layer nickelates. Phys. Rev. B 2022, 106, 035111. [Google Scholar] [CrossRef]
- Acharya, S.; Pashov, D.; van Schilfgaarde, M. Role of nematicity in controlling spin fluctuations and superconducting Tc in bulk FeSe. Phys. Rev. B 2022, 105, 144507. [Google Scholar] [CrossRef]
- Laad, M.S.; Freelon, B.; Craco, L. Microscopic description of unconventional nodal superconductivity in FeSe. arXiv 2018, arXiv:1805.09628. [Google Scholar]
- Worasaran, T.; Ikeda, M.S.; Straquadine, J.A.; Kivelson, S.A.; Fisher, I.A. Nematic quantum criticality in an Fe-based superconductor revealed by strain-tuning. Science 2021, 372, 973. [Google Scholar] [CrossRef]
- Leonov, I. Effect of lattice strain on the electronic structure and magnetic correlations in infinite-layer. J. Alloy. Compd. 2021, 883, 160888. [Google Scholar] [CrossRef]
- Choubey, P.; Eremin, I.M. Electronic theory for scanning tunneling microscopy spectra in infinite-layer nickelate superconductors. Phys. Rev. B 2021, 104, 144504. [Google Scholar] [CrossRef]
- Craco, L.; Laad, M.S.; Leoni, S. Microscopic description of insulator-metal transition in high-pressure oxygen. Sci. Rep. 2017, 7, 2632. [Google Scholar] [CrossRef] [PubMed]
- Craco, L.; Carara, S.S.; Leoni, S. Landau-Fermi liquidness and s-wave superconducting properties of pressurized gray phosphorus. Eur. Phys. J. B 2021, 94, 115. [Google Scholar] [CrossRef]
- Bardeen, J. Two-fluid model of superconductivity. Phys. Rev. Lett. 1958, 1, 399. [Google Scholar] [CrossRef]
- Yuan, N.F.Q.; Fu, L. Zeeman-induced gapless superconductivity with a partial Fermi surface. Phys. Rev. B 2018, 97, 115139. [Google Scholar] [CrossRef]
- Laad, M.S.; Craco, L. Theory of multiband superconductivity in iron pnictides. Phys. Rev. Lett. 2009, 103, 017002. [Google Scholar] [CrossRef]
- Gu, Q.; Wen, H.-H. Superconductivity in nickel-based 112 systems. Innovation 2022, 3, 100202. [Google Scholar] [CrossRef]
- Craco, L. Correlated nature of hybrid s-wave superconducting and Rashba lattices. Phys. Rev. B 2021, 104, 064509. [Google Scholar] [CrossRef]
- Lei, X.L. Balance Equation Approach to Electron Transport in Semiconductors; World Scientific Publishing Co., Pte. Ltd.: Singapore, 2008. [Google Scholar]
- Dzero, M. Collisionless dynamics of the pairing amplitude in disordered superconductors. Phys. Rev. B 2024, 109, L100503. [Google Scholar] [CrossRef]
- Sulangi, M.A.; Zaanen, J. Self-energies and quasiparticle scattering interference. Phys. Rev. B 2018, 98, 094518. [Google Scholar] [CrossRef]
- Chow, S.L.E.; Ariando, A. Nickel age of high-temperature superconductivity. Adv. Mater. Interfaces 2025, 12, 2400717. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Craco, L. Orbital-Nematic and Two-Fluid Superconductivity in Hole-Doped NdNiO2. Condens. Matter 2025, 10, 18. https://doi.org/10.3390/condmat10010018
Craco L. Orbital-Nematic and Two-Fluid Superconductivity in Hole-Doped NdNiO2. Condensed Matter. 2025; 10(1):18. https://doi.org/10.3390/condmat10010018
Chicago/Turabian StyleCraco, Luis. 2025. "Orbital-Nematic and Two-Fluid Superconductivity in Hole-Doped NdNiO2" Condensed Matter 10, no. 1: 18. https://doi.org/10.3390/condmat10010018
APA StyleCraco, L. (2025). Orbital-Nematic and Two-Fluid Superconductivity in Hole-Doped NdNiO2. Condensed Matter, 10(1), 18. https://doi.org/10.3390/condmat10010018





