Automated Monitoring of Bluefin Tuna Growth in Cages Using a Cohort-Based Approach
Abstract
1. Introduction
2. Materials and Methods
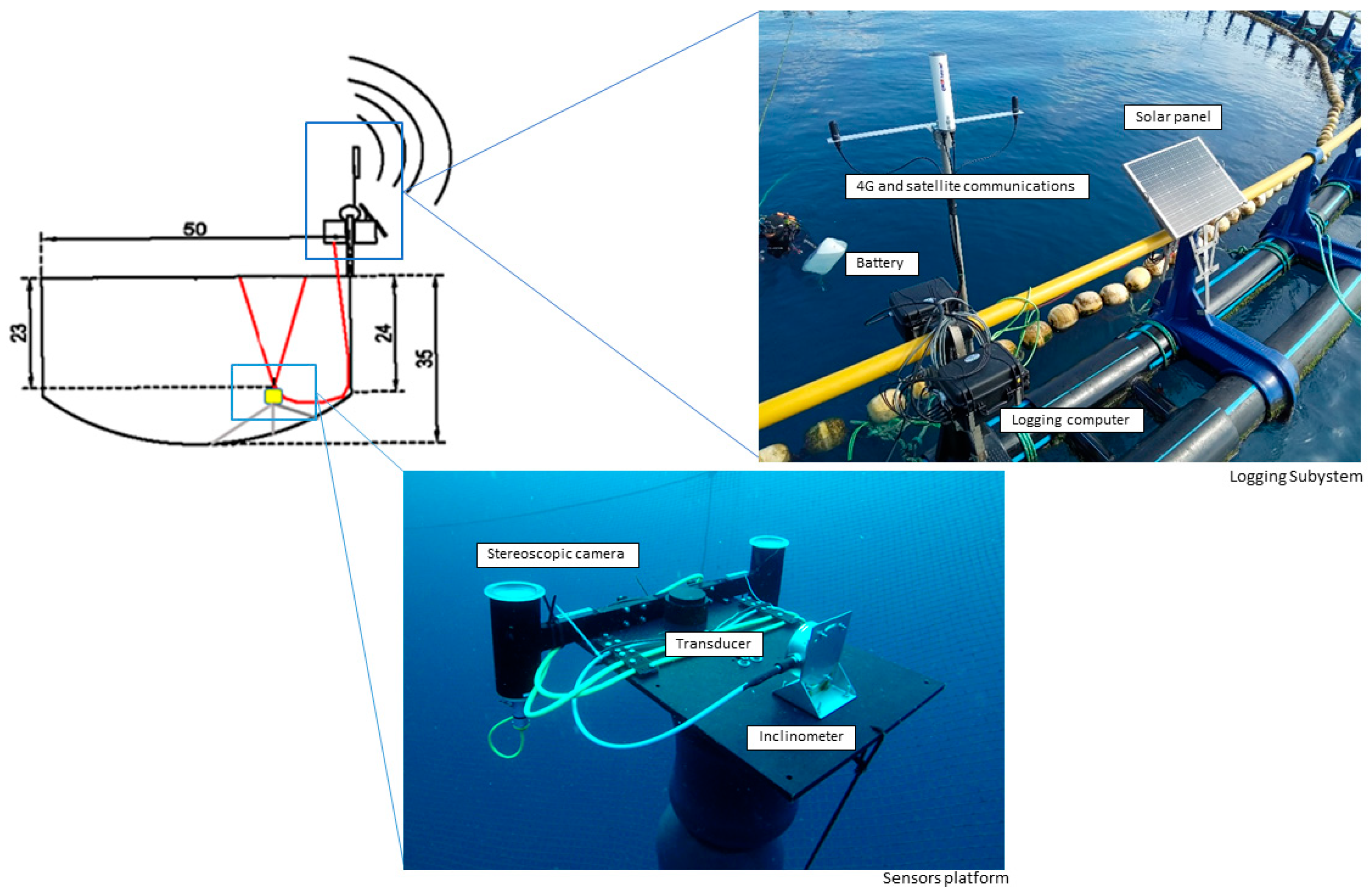
2.1. Description of the Subsea Monitoring System
2.2. Computer Vision Algorithms for Fish Width and Length Estimation
2.3. Bhattacharya’s Method for Modal Analysis
- SI (separation index) values between successive cohorts should be similar in different analyses, with a minimum value of 2 considered as a general reference, occasionally accepting slightly lower values in older cohorts.
- SD (standard deviation) values of identified modal groups should fall within the range of 3 to 7 cm, considering background information about the variability within annual cohorts.
- The proportions of specimens belonging to given cohorts should be consistent among different analyses.
3. Results
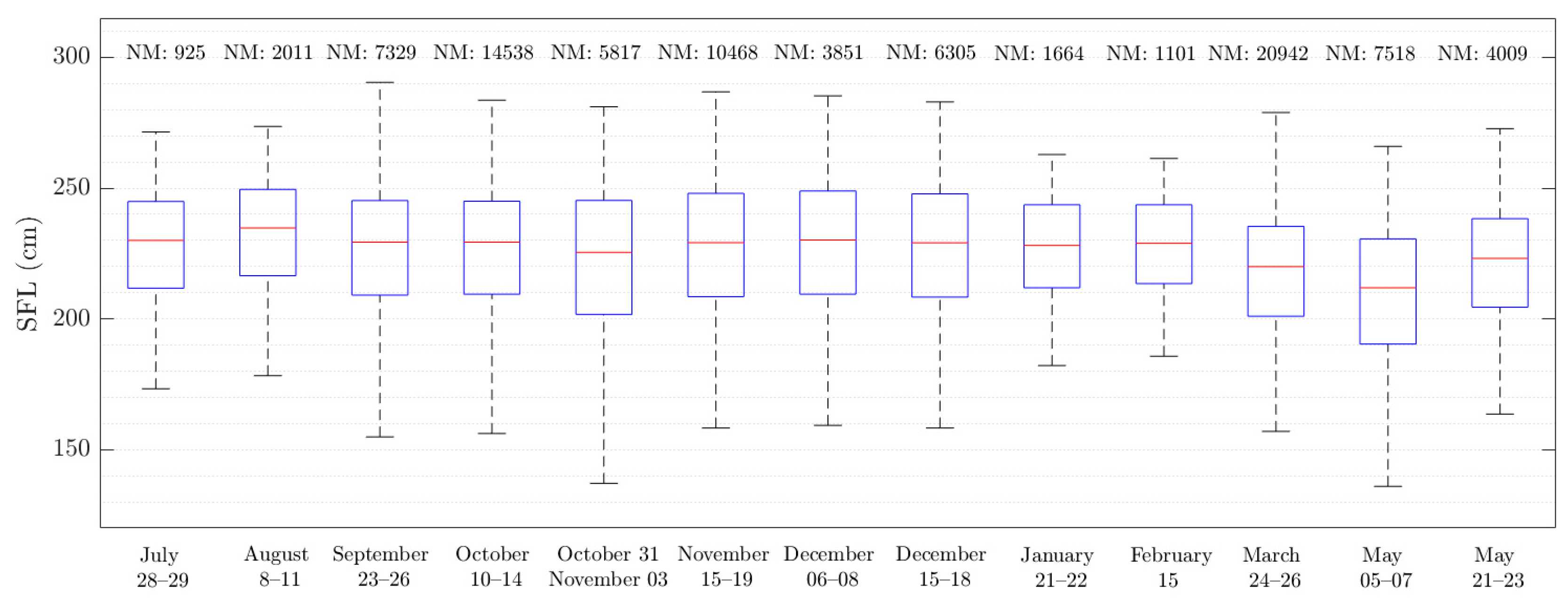
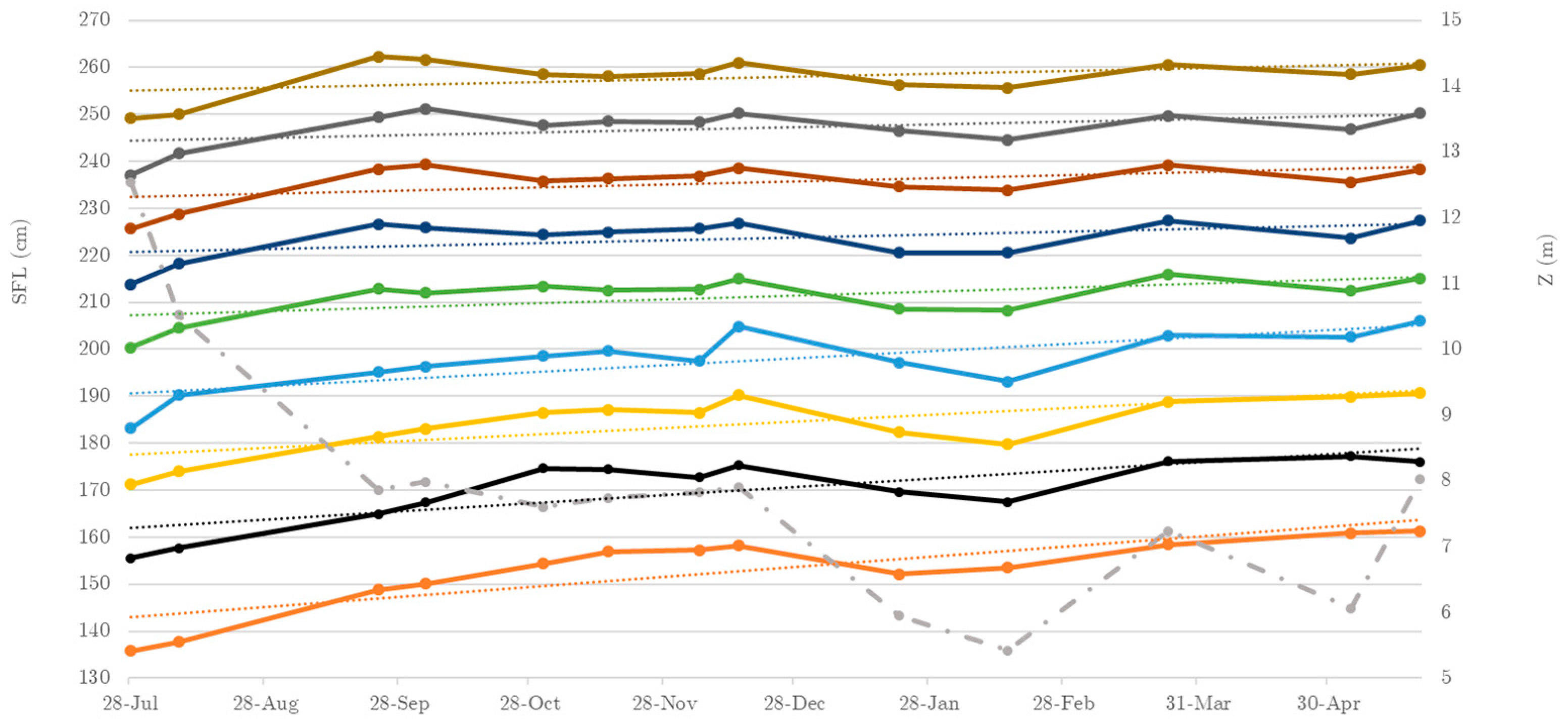
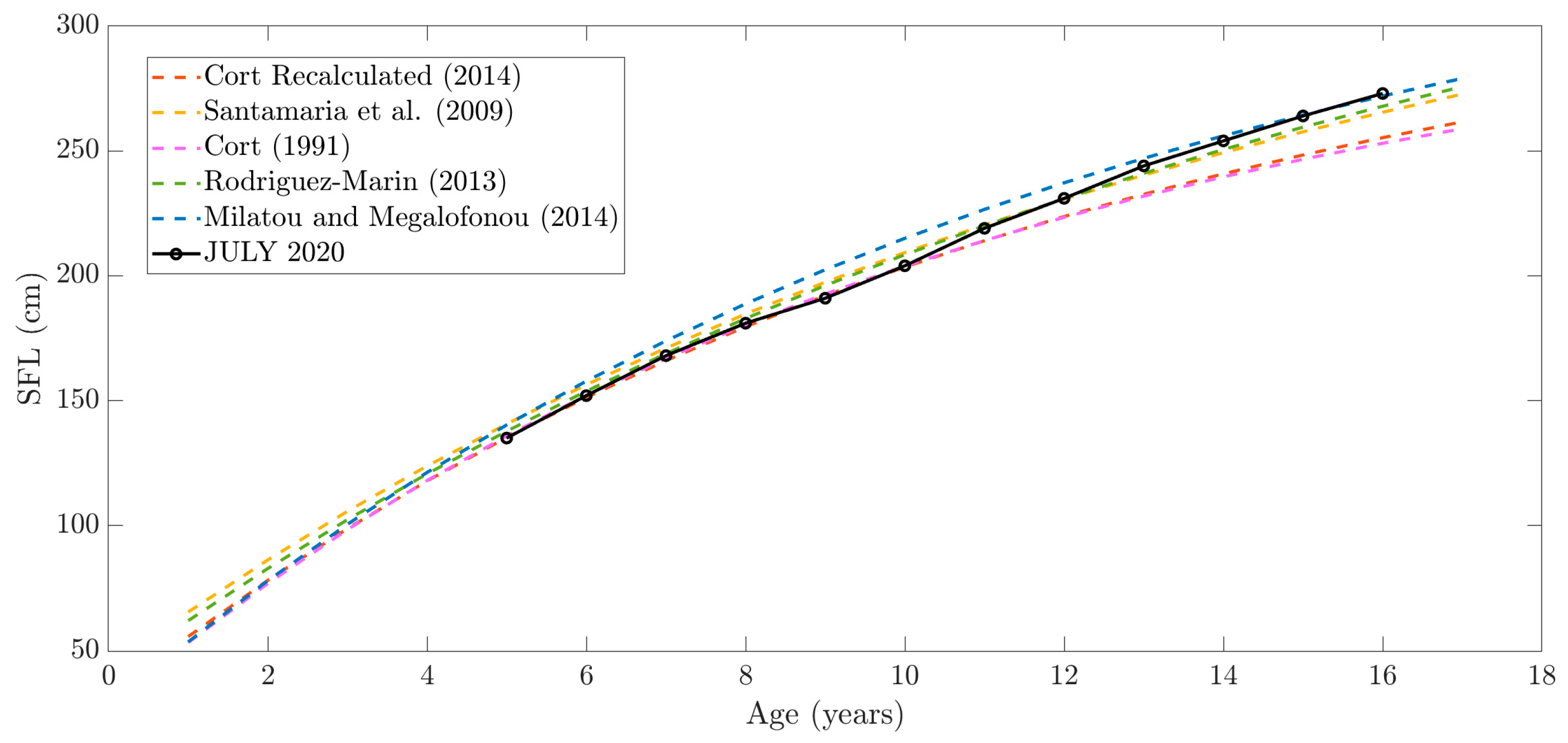
3.1. Straight Fork Length (SFL) Evolution
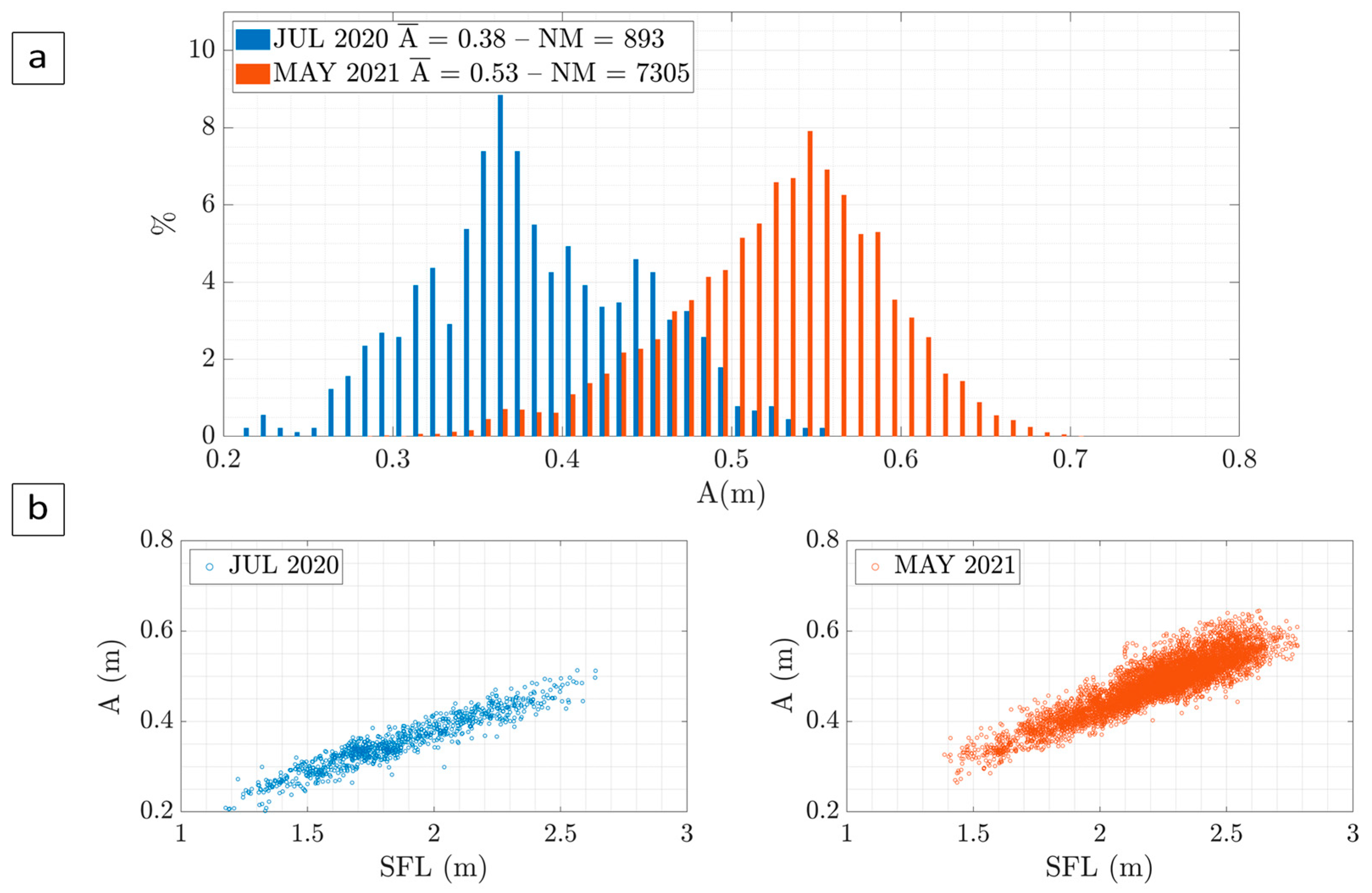
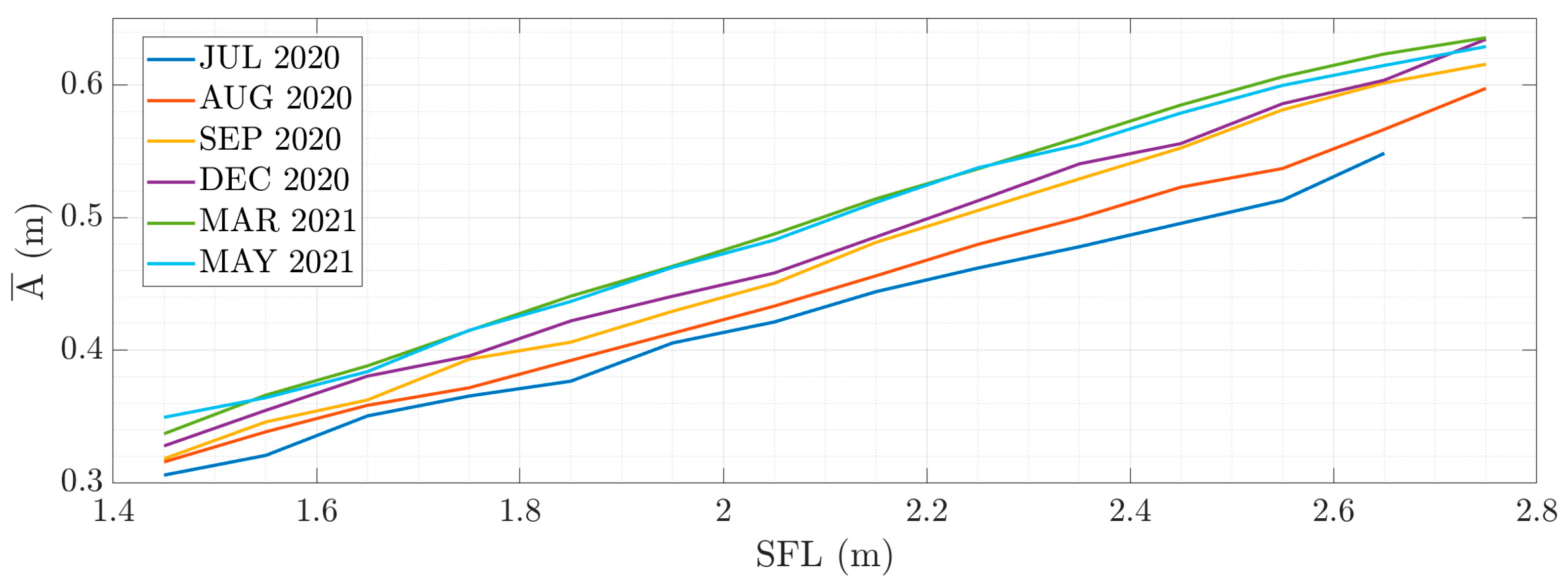
3.2. Width Evolution
3.3. Condition Factor Evolution
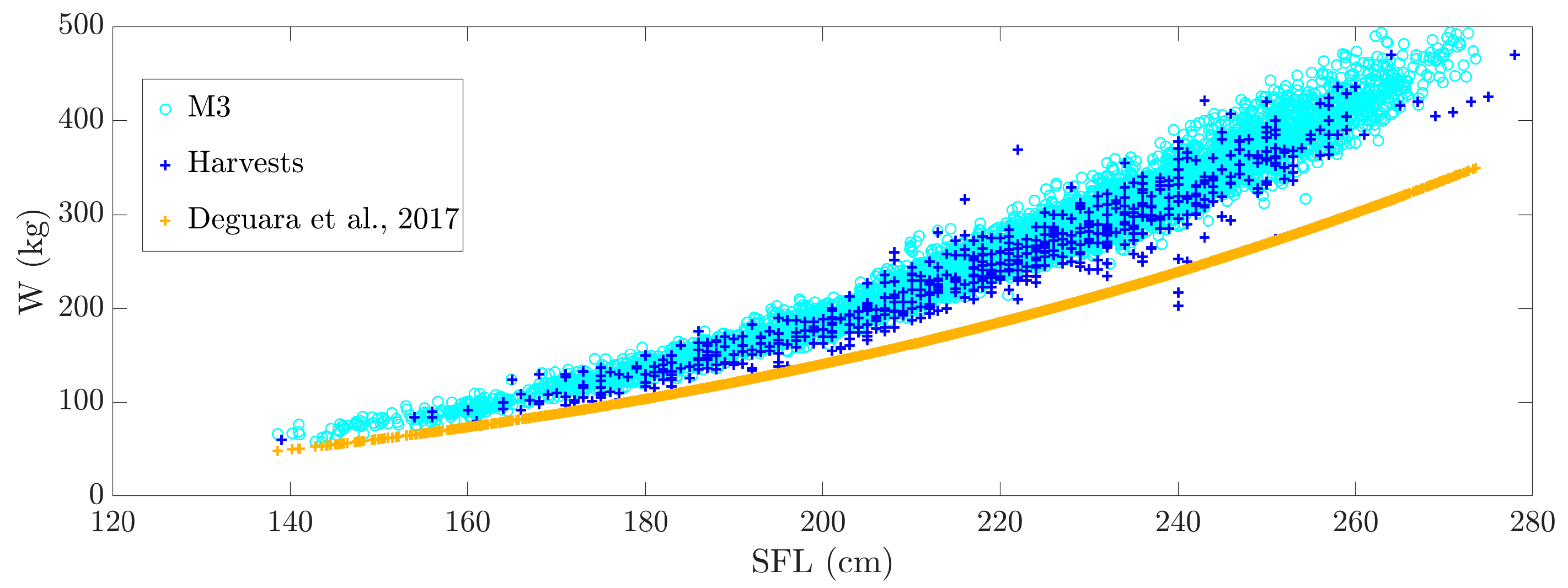
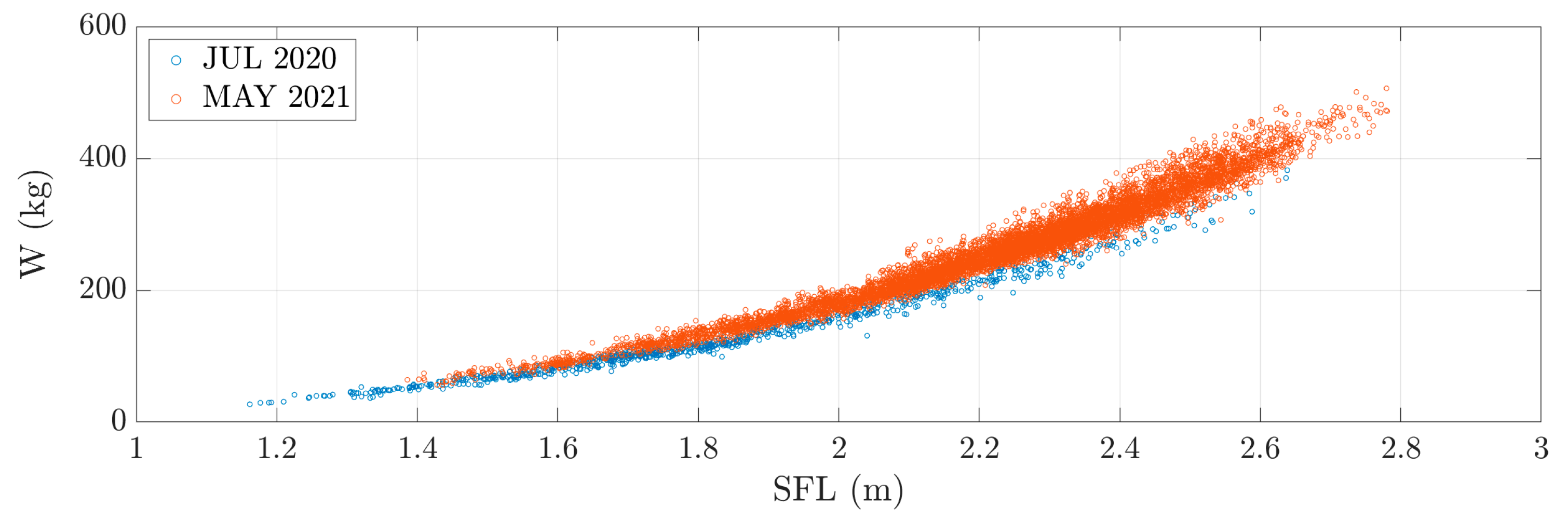
3.4. Tuna Weight Estimation
4. Conclusions and Further Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Cohorts | 1 * | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | Total Samples | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 28–29 July | SFL | 122 | 136 | 156 | 171 | 183 | 200 | 214 | 226 | 237 | 249 | 266 | 925 |
| NM | 13 | 54 | 166 | 181 | 141 | 156 | 61 | 82 | 43 | 24 | 4 | ||
| NI | 10 | 42 | 130 | 141 | 111 | 122 | 47 | 64 | 34 | 19 | 3 | ||
| 8–11 August | SFL | 128 | 138 | 158 | 174 | 190 | 205 | 218 | 229 | 242 | 250 | 260 | 2011 |
| NM | 37 | 152 | 371 | 458 | 298 | 229 | 271 | 102 | 70 | 13 | 10 | ||
| NI | 13 | 55 | 134 | 165 | 107 | 83 | 98 | 37 | 25 | 5 | 4 | ||
| 23–26 September | SFL | 149 | 165 | 181 | 195 | 213 | 227 | 238 | 249 | 262 | 272 | 7329 | |
| NM | 23 | 46 | 179 | 206 | 341 | 547 | 383 | 301 | 185 | 30 | |||
| NI | 7 | 15 | 58 | 67 | 110 | 177 | 124 | 97 | 60 | 10 | |||
| 10–14 October | SFL | 139 | 150 | 167 | 183 | 196 | 212 | 226 | 239 | 251 | 262 | 272 | 14,538 |
| NM | 32 | 263 | 422 | 1137 | 1032 | 2255 | 3267 | 2920 | 1867 | 1047 | 264 | ||
| NI | 2 | 13 | 21 | 57 | 51 | 113 | 163 | 146 | 93 | 52 | 13 | ||
| 31 October–3 November | SFL | 150 | 154 | 175 | 187 | 199 | 213 | 224 | 236 | 248 | 259 | 268 | 5817 |
| NM | 48 | 80 | 415 | 378 | 736 | 809 | 902 | 918 | 821 | 538 | 178 | ||
| NI | 6 | 10 | 52 | 47 | 91 | 101 | 112 | 114 | 102 | 67 | 22 | ||
| 15–19 November | SFL | 141 | 157 | 174 | 187 | 200 | 213 | 225 | 236 | 249 | 258 | 268 | 10,468 |
| NM | 19 | 159 | 369 | 739 | 837 | 1301 | 2066 | 1853 | 1754 | 932 | 402 | ||
| NI | 1 | 11 | 26 | 51 | 58 | 90 | 143 | 129 | 122 | 65 | 28 | ||
| 6–8 December | SFL | 143 | 157 | 173 | 186 | 197 | 213 | 226 | 237 | 248 | 259 | 269 | 3851 |
| NM | 7 | 86 | 96 | 266 | 255 | 662 | 574 | 704 | 645 | 367 | 152 | ||
| NI | 1 | 16 | 18 | 50 | 48 | 126 | 109 | 134 | 123 | 70 | 29 | ||
| 15–18 December | SFL | 143 | 158 | 175 | 190 | 205 | 215 | 227 | 239 | 250 | 261 | 271 | 6305 |
| NM | 7 | 91 | 178 | 315 | 422 | 468 | 826 | 587 | 671 | 355 | 93 | ||
| NI | 1 | 16 | 32 | 57 | 76 | 84 | 149 | 106 | 121 | 64 | 17 | ||
| 21–22 January | SFL | 152 | 170 | 182 | 197 | 209 | 221 | 235 | 246 | 256 | 1664 | ||
| NM | 32 | 49 | 174 | 212 | 330 | 327 | 352 | 162 | 23 | ||||
| NI | 14 | 21 | 76 | 92 | 144 | 142 | 153 | 70 | 10 | ||||
| 15 February | SFL | 147 | 153 | 168 | 180 | 193 | 208 | 221 | 234 | 245 | 256 | 1101 | |
| NM | 16 | 45 | 63 | 159 | 217 | 202 | 240 | 111 | 48 | 8 | |||
| NI | 10 | 29 | 41 | 104 | 142 | 132 | 157 | 72 | 32 | 5 | |||
| 24–26 March | SFL | 143 | 158 | 176 | 189 | 203 | 216 | 227 | 239 | 250 | 261 | 270 | 20,942 |
| NM | 83 | 431 | 1072 | 1692 | 2704 | 4004 | 4344 | 3095 | 2376 | 1031 | 100 | ||
| NI | 3 | 15 | 37 | 59 | 94 | 138 | 150 | 107 | 82 | 36 | 3 | ||
| 5–7 May | SFL | 148 | 161 | 176 | 191 | 206 | 215 | 227 | 238 | 250 | 260 | 272 | 7518 |
| NM | 58 | 163 | 318 | 607 | 1023 | 969 | 1773 | 1278 | 1043 | 244 | 35 | ||
| NI | 6 | 16 | 31 | 59 | 99 | 93 | 171 | 123 | 100 | 23 | 3 | ||
| 21–23 May | SFL | 148 | 163 | 180 | 194 | 208 | 219 | 229 | 241 | 252 | 263 | 4009 | |
| NM | 197 | 467 | 442 | 755 | 549 | 731 | 486 | 235 | 65 | 197 | |||
| NI | 15 | 36 | 84 | 80 | 136 | 99 | 132 | 88 | 42 | 12 | |||
| Growth in length | 26 | 27 | 24 | 23 | 25 | 19 | 15 | 15 | 15 | 14 | - | ||
| 28 July | 8 August | 23 September | 4 October | 31 October | 15 November | 6 December | 15 December | 21 January | 15 February | 24 March | 5 May | 21 May | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cohort #2 SFL (cm) | 136 | 138 | 149 | 150 | 154 | 157 | 157 | 158 | 152 | 153 | 158 | 161 | 161 |
| Cohort #3 SFL (cm) | 156 | 158 | 165 | 167 | 175 | 174 | 173 | 175 | 170 | 168 | 176 | 177 | 176 |
| Cohort #4 SFL (cm) | 171 | 174 | 181 | 183 | 187 | 187 | 186 | 190 | 182 | 180 | 189 | 190 | 191 |
| Cohort #5 SFL (cm) | 183 | 190 | 195 | 196 | 199 | 200 | 197 | 205 | 197 | 193 | 203 | 203 | 206 |
| Cohort #6 SFL (cm) | 200 | 205 | 213 | 212 | 213 | 213 | 213 | 215 | 209 | 208 | 216 | 212 | 215 |
| Cohort #7 SFL (cm) | 214 | 218 | 227 | 226 | 224 | 225 | 226 | 227 | 221 | 221 | 227 | 224 | 227 |
| Cohort #8 SFL (cm) | 226 | 229 | 238 | 239 | 236 | 236 | 237 | 239 | 235 | 234 | 239 | 236 | 238 |
| Cohort #9 SFL (cm) | 237 | 242 | 249 | 251 | 248 | 249 | 248 | 250 | 246 | 245 | 250 | 247 | 250 |
| Cohort #10 SFL (cm) | 249 | 250 | 262 | 262 | 259 | 258 | 259 | 261 | 256 | 256 | 261 | 259 | 260 |
| SFL Range | July 2020 | August 2020 | September 2020 | December 2020 | March 2021 | May 2021 | July 2020–May 2021 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NM | NM | NM | NM | NM | NM | ||||||||
| [140,150] | 28.2 | 46 | 29.0 | 89 | 29.3 | 45 | 30.2 | 11 | 31.0 | 84 | 32.1 | 36 | 3.9 (14%) |
| [150,160] | 29.5 | 75 | 31.1 | 171 | 31.8 | 46 | 32.7 | 59 | 33.7 | 254 | 33.5 | 69 | 4.0 (14%) |
| [160,170] | 32.3 | 113 | 33.0 | 252 | 33.3 | 136 | 35.0 | 38 | 35.7 | 264 | 35.3 | 119 | 3.0 (9%) |
| [170,180] | 33.6 | 128 | 34.2 | 253 | 36.2 | 223 | 36.4 | 89 | 38.2 | 656 | 38.2 | 232 | 4.6 (14%) |
| [180,190] | 34.6 | 115 | 36.1 | 215 | 37.4 | 421 | 38.8 | 179 | 40.6 | 1204 | 40.2 | 307 | 5.6 (16%) |
| [190,200] | 37.3 | 72 | 38.0 | 171 | 39.5 | 453 | 40.6 | 236 | 42.6 | 1486 | 42.5 | 472 | 5.2 (14%) |
| [200,210] | 38.8 | 73 | 39.9 | 187 | 41.4 | 450 | 42.1 | 255 | 44.9 | 1845 | 44.4 | 619 | 5.6 (14%) |
| [210,220] | 40.9 | 67 | 42.0 | 179 | 44.3 | 824 | 44.6 | 437 | 47.3 | 3134 | 47.0 | 1031 | 6.1 (15%) |
| [220,230] | 42.5 | 65 | 44.1 | 159 | 46.5 | 1203 | 47.2 | 536 | 49.4 | 3615 | 49.5 | 1316 | 7.0 (16%) |
| [230,240] | 44.0 | 46 | 46.0 | 67 | 48.7 | 1082 | 49.7 | 573 | 51.6 | 2986 | 51.1 | 1318 | 7.1 (16%) |
| [240,250] | 45.6 | 23 | 48.1 | 57 | 50.9 | 972 | 51.2 | 570 | 53.8 | 2574 | 53.3 | 938 | 7.7 (17%) |
| [250,260] | 47.2 | 13 | 49.4 | 17 | 53.5 | 715 | 53.9 | 454 | 55.8 | 1550 | 55.2 | 630 | 8.0 (17%) |
| [260,270] | 50.5 | 2 * | 52.1 | 4 * | 55.4 | 451 | 55.6 | 233 | 57.3 | 650 | 56.6 | 184 | 6.1 (12%) * |
| [270,280] | 56.7 | 110 | 58.4 | 64 | 58.5 | 93 | 57.9 | 33 | - | ||||
References
- Zhang, L.; Wang, J.; Duan, Q. Estimation for Fish Mass Using Image Analysis and Neural Network. Comput. Electron. Agric. 2020, 173, 105439. [Google Scholar] [CrossRef]
- Zion, B. The Use of Computer Vision Technologies in Aquaculture—A Review. Comput. Electron. Agric. 2012, 88, 125–132. [Google Scholar] [CrossRef]
- Saberioon, M.; Císař, P. Automated within Tank Fish Mass Estimation Using Infrared Reflection System. Comput. Electron. Agric. 2018, 150, 484–492. [Google Scholar] [CrossRef]
- Sture, Ø.; Øye, E.R.; Skavhaug, A.; Mathiassen, J.R. A 3D Machine Vision System for Quality Grading of Atlantic Salmon. Comput. Electron. Agric. 2016, 123, 142–148. [Google Scholar] [CrossRef]
- Abe, S.; Takagi, T.; Torisawa, S.; Abe, K.; Habe, H.; Iguchi, N.; Takehara, K.; Masuma, S.; Yagi, H.; Yamaguchi, T.; et al. Development of Fish Spatio-Temporal Identifying Technology Using SegNet in Aquaculture Net Cages. Aquac. Eng. 2021, 93, 102146. [Google Scholar] [CrossRef]
- Phillips, K.; Rodriguez, V.B.; Harvey, E.; Ellis, D.; Seager, J.; Begg, G.; Hender, J. Assessing the Operational Feasibility of Stereo-Video and Evaluating Monitoring Options for the Southern Bluefin Tuna Fishery Ranch Sector. Fish. Res. Dev. Corp. Bur. Rural. Sci. Aust. 2009, 44, 46. [Google Scholar]
- Shieh, A.C.R.; Petrell, R.J. Measurement of Fish Size in Atlantic Salmon (Salmo Salar L.) Cages Using Stereographic Video Techniques. Aquac. Eng. 1998, 17, 29–43. [Google Scholar] [CrossRef]
- Shortis, M.R.; Ravanbakhsh, M.; Shafait, F.; Mian, A. Progress in the Automated Identification, Measurement, and Counting of Fish in Underwater Image Sequences. Mar. Technol. Soc. J. 2016, 50, 4–16. [Google Scholar] [CrossRef]
- Shafait, F.; Harvey, E.S.; Shortis, M.R.; Mian, A.; Ravanbakhsh, M.; Seager, J.W.; Culverhouse, P.F.; Cline, D.E.; Edgington, D.R. Towards Automating Underwater Measurement of Fish Length: A Comparison of Semi-Automatic and Manual Stereo-Video Measurements. ICES J. Mar. Sci. 2017, 74, 1690–1701. [Google Scholar] [CrossRef]
- Deguara, S.; Gordoa, A.; Cort, J.L.; Zarrad, R.; Abid, N.; Lino, P.G.; Karakulak, S.; Katavic, I.; Grubisic, L.; Gatt, M.; et al. Determination of a Length-Weight Equation Applicable to Atlantic Bluefin Tuna (Thunnus thynnus) during the Purse Seine Fishing Season in the Mediterranean. Sci. Pap. ICCAT 2017, 73, 2324–2332. [Google Scholar]
- Puig-Pons, V.; Estruch, V.D.; Espinosa, V.; De La Gándara, F.; Melich, B.; Cort, J.L. Relationship between Weight and Linear Dimensions of Bluefin Tuna (Thunnus thynnus) Following Fattening on Western Mediterranean Farms. PLoS ONE 2018, 13, e0200406. [Google Scholar] [CrossRef] [PubMed]
- Puig-Pons, V.; Estruch, V.D.; Espinosa, V.; De la Gándara, F.; Melich, B.; Cort, J.L. Correction: Relationship between Weight and Linear Dimensions of Bluefin Tuna (Thunnus thynnus) Following Fattening on Western Mediterranean Farms. PLoS ONE 2021, 16, e0259437. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-Benavent, P.; Andreu-García, G.; Valiente-González, J.M.; Atienza-Vanacloig, V.; Puig-Pons, V.; Espinosa, V. Automatic Bluefin Tuna Sizing Using a Stereoscopic Vision System. ICES J. Mar. Sci. 2018, 75, 390–401. [Google Scholar] [CrossRef]
- Muñoz-Benavent, P.; Andreu-García, G.; Valiente-González, J.M.; Atienza-Vanacloig, V.; Puig-Pons, V.; Espinosa, V. Enhanced Fish Bending Model for Automatic Tuna Sizing Using Computer Vision. Comput. Electron. Agric. 2018, 150, 52–61. [Google Scholar] [CrossRef]
- Muñoz-Benavent, P.; Puig-Pons, V.; Morillo-Faro, A.; Andreu-García, G.; Espinosa, V.; Pérez-Arjona, I. Short Term Contract for BFT Growth in Farms Pilot Study (Final Report). Available online: https://www.iccat.int/GBYP/DOCS/Biological_Studies_Phase_10_Growth_Farms_UPV.pdf (accessed on 19 December 2023).
- Tičina, V.; Katavić, I.; Grubišić, L. Growth Indices of Small Northern Bluefin Tuna (Thunnus thynnus, L.) in Growth-out Rearing Cages. Aquaculture 2007, 269, 538–543. [Google Scholar] [CrossRef]
- Heikkila, J.; Silven, O. A Four-Step Camera Calibration Procedure with Implicit Image Correction. In Proceedings of the 1997 Conference on Computer Vision and Pattern Recognition (CVPR ’97), San Juan, Puerto Rico, 17–19 June 1997; IEEE Computer Society: Washington, DC, USA, 1997; p. 1106. [Google Scholar]
- Zhang, Z. A Flexible New Technique for Camera Calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Petrou, M.; Petrou, C. Image Segmentation and Edge Detection. In Image Processing: The Fundamentals; John Wiley & Sons, Ltd.: Chichester, UK, 2011; pp. 527–668. ISBN 9781119994398. [Google Scholar]
- Williams, K.; Lauffenburger, N. Automated Measurements of Fish within a Trawl Using Stereo Images from a Camera-Trawl Device (CamTrawl). Methods Oceanogr. 2016, 17, 138–152. [Google Scholar] [CrossRef]
- Atienza-Vanacloig, V.; Andreu-García, G.; López-García, F.; Valiente-Gonzólez, J.M.; Puig-Pons, V. Vision-Based Discrimination of Tuna Individuals in Grow-out Cages through a Fish Bending Model. Comput. Electron. Agric. 2016, 130, 142–150. [Google Scholar] [CrossRef]
- Sparre, P.; Venema, S.C. Introduction to Tropical Fish Stock Assessment. Pt. 1: Manual. FAO Fish. Tech. Paper 1998, 306, 1–407. [Google Scholar]
- Bhattacharya, C.G. A Simple Method of Resolution of a Distribution into Gaussian Components. Biometrics 1967, 23, 115–135. [Google Scholar] [CrossRef]
- Gayanilo, F.; Sparre, P.; Pauly, D. FAO-ICLARM Stock Assessment Tools II: User’s Guide; FAO: Rome, Italy, 2005. [Google Scholar]
- Cort, J.L.; Arregui, I.; Estruch, V.D.; Deguara, S. Validation of the Growth Equation Applicable to the Eastern Atlantic Bluefin Tuna, Thunnus thynnus (L.), Using Lmax, Tag-Recapture, and First Dorsal Spine Analysis. Rev. Fish. Sci. Aquac. 2014, 22, 239–255. [Google Scholar] [CrossRef]
- Cort, J.L. Age and Growth of Bluefin Tuna (Thunnus thynnus L.) of the Northwest Atlantic. Collect. Vol. Sci. Pap. ICCAT 1991, 35, 213–230. [Google Scholar]
- Landa, J.; Rodriguez-Marin, E.; Luque, P.L.; Ruiz, M.; Quelle, P. Growth of Bluefin Tuna (Thunnus Thynnus) in the North-Eastern Atlantic and Mediterranean Based on Back-Calculation of Dorsal Fin Spine Annuli. Fish. Res. 2015, 170, 190–198. [Google Scholar] [CrossRef]
- Milatou, N.; Megalofonou, P. Age Structure and Growth of Bluefin Tuna (Thunnus thynnus, L.) in the Capture-Based Aquaculture in the Mediterranean Sea. Aquaculture 2014, 424–425, 35–44. [Google Scholar] [CrossRef]
- Rodríguez-Marín, E.; Luque, P.L.; Busawon, D.; Campana, S.; Golet, W.; Koob, E.; Neilson, J.; Quelle, P.; Ruiz, M. An Attempt of Validation of Atlantic Bluefin Tuna (Thunnus thynnus) Ageing Using Dorsal Fin Spines. In Proceedings of the Report of the 2013 Bluefin Tuna Meeting on Biological Parameters Review, Tenerife, Spain, 7–13 May 2013; pp. 11–12. [Google Scholar]
- Rodríguez-Marín, E.; Luque, P.L.; Quelle, P.; Ruiz, M.; Perez, B.; Macias, D.; Karakulak, S. Age Determination Analyses of Atlantic Bluefin Tuna (Thunnus thynnus) within the Biological and Genetic Sampling and Analysis Contract (GBYP). Collect. Vol. Sci. Pap. ICCAT 2014, 70, 321–331. [Google Scholar]
- Santamaria, N.; Bello, G.; Corriero, A.; Deflorio, M.; Vassallo-Agius, R.; Bök, T.; De Metrio, G. Age and Growth of Atlantic Bluefin Tuna, Thunnus thynnus (Osteichthyes: Thunnidae), in the Mediterranean Sea. J. Appl. Ichthyol. 2009, 25, 38–45. [Google Scholar] [CrossRef]
- Deguara, S. Preliminary Investigation Using Stereocamera Technology to Look at the Changes Occurring in the Straight Fork Lengths of Farmed Atlantic Bluefin Tuna (Thunnus thynnus) between Caging and Harvesting. Collect. Vol. Sci. Pap. ICCAT 2016, 72, 1842–1847. [Google Scholar]
- Deguara, S.; Caruana, S.; Agius, C. Results of the First Growth Trial Carried Out in Malta with 60 kg Farmed Atlantic Bluefin Tuna (Thunnus thynnus L.). Collect. Vol. Sci. Pap. ICCAT 2010, 65, 782–786. [Google Scholar]
- Katavic, I.; Grubisic, L.; Ticina, V.; Mislov Jelavic, K.; Franicevic, M.; Skakelja, N. Growth Performances of the Bluefin Tuna (Thunnus thynnus) Farmed in the Croatian Waters of Eastern Adriatic. SCRS 2009, 120, 1–8. [Google Scholar]
- Restrepo, V.R.; Diaz, G.A.; Walter, J.F.; Neilson, J.D.; Campana, S.E.; Secor, D.; Wingate, R.L. Updated Estimate of the Growth Curve of Western Atlantic Bluefin Tuna. Aquat. Living Resour. 2010, 23, 335–342. [Google Scholar] [CrossRef]
- Ailloud, L.E.; Lauretta, M.V.; Hanke, A.R.; Golet, W.J.; Allman, R.J.; Siskey, M.R.; Secor, D.H.; Hoenig, J.M. Improving Growth Estimates for Western Atlantic Bluefin Tuna Using an Integrated Modeling Approach. Fish. Res. 2017, 191, 17–24. [Google Scholar] [CrossRef]



| Year 2020 | 28–29 July | 8–11 August | 23–26 September | 10–14 October | 31 October–3 November | 15–19 November | 6–8 December | 15–18 December |
| Year 2021 | 21–22 January | 15 February | 24–26 March | 5–7 May | 21–23 May |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muñoz-Benavent, P.; Andreu-García, G.; Martínez-Peiró, J.; Puig-Pons, V.; Morillo-Faro, A.; Ordóñez-Cebrián, P.; Atienza-Vanacloig, V.; Pérez-Arjona, I.; Espinosa, V.; Alemany, F. Automated Monitoring of Bluefin Tuna Growth in Cages Using a Cohort-Based Approach. Fishes 2024, 9, 46. https://doi.org/10.3390/fishes9020046
Muñoz-Benavent P, Andreu-García G, Martínez-Peiró J, Puig-Pons V, Morillo-Faro A, Ordóñez-Cebrián P, Atienza-Vanacloig V, Pérez-Arjona I, Espinosa V, Alemany F. Automated Monitoring of Bluefin Tuna Growth in Cages Using a Cohort-Based Approach. Fishes. 2024; 9(2):46. https://doi.org/10.3390/fishes9020046
Chicago/Turabian StyleMuñoz-Benavent, Pau, Gabriela Andreu-García, Joaquín Martínez-Peiró, Vicente Puig-Pons, Andrés Morillo-Faro, Patricia Ordóñez-Cebrián, Vicente Atienza-Vanacloig, Isabel Pérez-Arjona, Víctor Espinosa, and Francisco Alemany. 2024. "Automated Monitoring of Bluefin Tuna Growth in Cages Using a Cohort-Based Approach" Fishes 9, no. 2: 46. https://doi.org/10.3390/fishes9020046
APA StyleMuñoz-Benavent, P., Andreu-García, G., Martínez-Peiró, J., Puig-Pons, V., Morillo-Faro, A., Ordóñez-Cebrián, P., Atienza-Vanacloig, V., Pérez-Arjona, I., Espinosa, V., & Alemany, F. (2024). Automated Monitoring of Bluefin Tuna Growth in Cages Using a Cohort-Based Approach. Fishes, 9(2), 46. https://doi.org/10.3390/fishes9020046







