Abstract
The assessment of fish stocks is often limited by a lack of comprehensive data. Therefore, catch-based methods are increasingly being used because of the availability of more catch data. However, catch-based models may perform differently for species with different traits and fishing histories. In this study, we investigated the performance of catch-based models for species with different life history traits, fishing histories, and under different length selections. We compared simulated biomass with estimated stock status from three widely used catch-based models (Catch-MSY model [CMSY]; catch-only model-sampling importance resampling model [COM-SIR]; state-space catch-only model [SSCOM]) under three fishing history scenarios (constant, increasing then decreasing, and continuously increasing fishing mortality) and three length selectivity scenarios (no selectivity, preferring smaller individuals, preferring larger individuals). Our results showed that CMSY performed the best, particularly when fishing mortality remained constant. Catch-based models performed better for opportunistic species that had larger individuals selected for fishing and equilibrium species that had smaller individuals selected. However, the models tended to overestimate stock status when fishing mortality continued to increase. Therefore, caution should be exercised when applying catch-based methods to data-poor stocks with diverse life history traits, fishing history, and those sensitive to selective fishing.
Keywords:
catch-based model; selective fishing; stock synthesis; data-poor fisheries; diverse life history traits Key Contribution:
This study provided the first evaluation on how fishing selectivity affects the performance of catch-based data-limited models for species with different life history traits and fishing dynamics, using simulated size-structured populations.
1. Introduction
Assessing stock status is a critical step for sound fishery management; however, the majority of fish stocks remain unassessed because of data limitations [1]. While there is increasing attention on the sustainable use of fishery resources, only 20% of the global catch comes from assessed stocks [2]. In other words, there is insufficient information and/or capacity to assess the status of most commercially exploited species. Costello et al. (2012) [3] indicated that 64% of unassessed fisheries may be exploited stocks whose biomass (B) is below the level of the maximum sustainable yield (Bmsy), and that 18% of the unassessed stocks are considered to be collapsed (i.e., B/Bmsy < 0.2). While most of the unassessed fisheries were in developing countries and were small-scale fisheries [4], simple and cost-effective assessment methods are urgently needed to assess the stock status of these fisheries [5].
Data-limited assessment models (DLMs) have been developed to provide alternative assessment methods for species with limited data. Depending on the information required by the models, the DLMs can be broadly divided into length-based and catch-based models. Both types of methods have been used to estimate the stock status of species and to develop feasible fishery management. Examples of applying DLMs in stock assessment range from developed countries to developing countries [6,7,8,9]. Zhou et al. (2017) [7] even pointed out that DLMs can provide estimates similar to comprehensive stock assessments.
The catch-based models mainly rely on catch data to estimate stock status and other reference points for fishery management. Catch data are often the most available data for data-poor stocks, and can therefore be used as important information on stock status. For example, catch has been found to be correlated with biomass at the maximum sustainable yield (Bmsy) [3,7]. Catch data have also been used to estimate the depletion rates in population dynamics [10,11,12]. However, it has been argued that catch is not only correlated with population abundance, but can be affected by factors such as fishing effort [13], catchability [14,15], selectivity [16], and fishery management [14]. Therefore, these effects should be carefully considered when applying catch-based models [15].
Catch-based models may perform differently under different fishing conditions or for species with different life history traits. However, few studies have systematically analyzed the effects of life history traits and fishing mortality history on the performance of catch-based models. Hilborn et al. (2020) [4] showed that there can be complicated interactions between species biomass, fishing mortality, and catches. Carruthers et al. (2012) [17] used two catch-based models [18,19] to assess categorical stock status (e.g., developing or fully exploited), and found that the models had different classification biases for stock status under different effort trend assumptions. Free et al. (2020) [17] showed that the catch-based models had different biases under different exploitation rates and for species with different traits. However, while some studies have investigated the effects of fishing history and life history traits on the performance of catch-based models [8,17], the interactions between fishing and the life history traits of a stock have not been explored.
Selective fishing causes the distribution of the length/age composition of the catch to be skewed in a particular direction [20]. Selective fishing may occur for several reasons, including: (1) fishing gear and method—the mesh or hook targets a specific size of individuals or excludes smaller individuals; (2) fishing area and season—fishing may occur in a specific area and during the feeding or spawning ground/season, resulting in catching a specific size range of a population; (3) fishery management or the market—the government or market encourages catching large individuals. Long-term and highly selective fishing can the alter life history traits of a population [21], limit the reproductive potential of the population [22], and increase population fluctuation [23]. Given that selectivity has a profound effect on the stability of a population, it should be taken into account when estimating stock status. Catch-based models usually only consider the total weight of the catch and neglect the size/age structure of the catch. The impact of size or age selectivity on the performance of catch-based models has not been thoroughly explored.
In this study, we aim to investigate how length-selective fishing and changes in fishing mortality can affect the performance of catch-based models, considering species with different life history traits. We simulated the stock dynamics in thirty-six different scenarios, considering four types of life history strategies, three types of fishing trends, and three types of length selectivity. Our systematic investigation of the drivers of the performance of catch-based models will shed light on the application of DLMs for data-limited stock assessment.
2. Materials and Methods
2.1. Operation Model for Simulating Population Dynamics and Catch Time Series
The operation model (OM) used in this study was an age-structured model with deterministic processes considering survival rate, growth rate, maturity, fecundity, and recruitment over a simulated time period [24]. The details on the population dynamics model can be found in Appendix A of Methot and Wetzel (2013) [25]. We tested various sets of life history trait inputs to represent species with different life histories, then categorized the species into four life strategists (see details in 2.2 Simulation scenarios). Parameters of life history traits were collected from the literature for the representative species of each group (Table S1). The distribution of the variation of recruitment was assumed to be the same for all groups (a lognormal distribution with was between 0 and 1). We simulated a 100-year population dynamic time series with recruitment process errors. We then calculated the total biomass (By) across all ages for each year, y, as follows:
where A is the maximum age of the stock, is the mean weight of individuals at a certain age, a, in a given year, y, while is the number of fishes at a certain age (a) in a given year (y).
After simulating the time series of the population’s biomass, we further produced the time series of the catch using the Baranov catch equation (Methot et al., 2020) [26]:
where is the catch of an age class (a) in a year (y) is the biomass of the age class (a) in the year (y), is the fishing mortality in the year, y, is the selectivity of the age class (a), is the total mortality of the age class (a) in the year (y). We determined the fishing selectivity (S) based on different selectivity scenarios (see Section 2.2 Scenarios).
The unit of the total biomass and the catch was metric tons. The operation model was conducted using the “ss3sim” package [24] in R program (version 4.0.0) for 10 iterations, then we calculated the mean and standard error of the simulated biomass for all iterations for each year.
2.2. Simulation Scenarios
In this study, we simulated population dynamics for 36 scenarios, including combinations of four life history strategies, three fishing history dynamics, and three fishing selectivity types.
Firstly, we collected life history trait information for 42 species described in [27], including length at 50% maturity, maximum length, growth coefficient, fecundity, egg size, and maximum age (Table S1). The information was used to classify the different life history trait strategies [27], as well as being used to construct the operation model for each species. We followed [27], using principal component analysis (PCA) to classify the 42 species into five strategy groups: the opportunistic strategy (OPP), equilibrium strategy (EQU), periodic strategy (PER), salmonic strategy (SAL), and intermediate strategy (INT) (Figure S1). In this study, to compare the life history strategists with more distinct traits, we excluded the intermediate strategists. Eventually, 27 species were analyzed in this study (Table S1). After constructing OM for species in each group, we compared the assessment results among the four strategy groups.
To test the effects of fishing mortality (F) dynamics, we defined three scenarios to reflect different fishing histories (Figure 1): (i) scenario F1, where fishing mortality was constant at all times; (ii) scenario F2, where fishing mortality gradually increased and then gradually decreased; (iii) scenario F3, where fishing mortality increased continuously. The mean F over all tested years (100 years) was the same for all three scenarios (Figure 1). However, the mean F was set differently for each of the life history trait groups. This is because species with different life history traits can tolerate different levels of F before being overfished. Therefore, to evaluate the performance of the data-limited assessment models for populations of different statuses (from not overfished to overfished), we need to consider the different magnitudes of fishing mortality for different life history trait groups. Random noise () was added from a normal distribution to the fishing mortality at each time step:
where is the mean fishing mortality for the whole fishing period, and is the fishing mortality of a year, t.
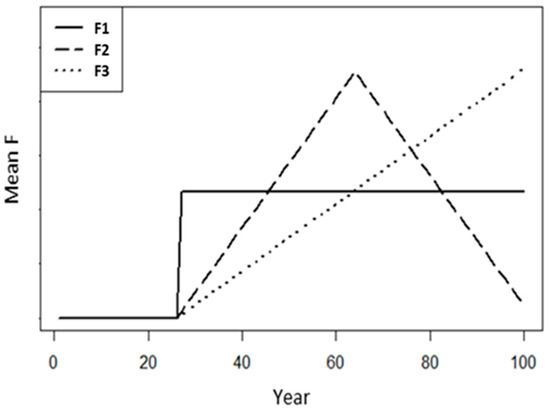
Figure 1.
The simulated fishing mortality dynamics of the three F scenarios (F1, F2, and F3): F1, where fishing started in the 27th year and then remained constant (solid line); F2, where fishing started in the 27th year, increased until the 64th year, and then decreased afterwards (dashed line); F3, where fishing started in the 27th year and continuously increased (dotted line). Note that the mean F was the same for the three scenarios for the same species, but that the mean F may be different between species.
We also tested whether catches from selective fisheries affect the performance of catch-based models. Since selective fishing is typically based on length rather than age in practice, we simulated length selection in this study. In other words, we assumed that a selection of length was equivalent to a selection of age for fishes [28]. We simulated three different length selectivity scenarios (S). The first scenario, S0, represented a non-selective fishery, where the chance of being caught was constant across all length classes. The second scenario, S1, simulated a fishery where smaller individuals had a greater probability of being caught. The third scenario, S2, represented a fishery where larger individuals had a greater probability of being caught (see an example in Figure 2). We used the method of double normal distribution with plateau to determine the probability of selecting individuals in each length class. To determine the peaks of selectivity, we defined the length with the highest selection probability for S1 (S1top) and S2 (S2top) for each species using the following rules: S1top = Lmin + (Lmax − Lmin)/9*3, S2top = Lmin + (Lmax − Lmin)/9*6, where Lmin is the minimum length and Lmax is the maximum length of a species (Table S1). The Lmin is the length at t0 of the von Bertalanffy growth function (VBGF) of the species, collected from Fishbase. The selectivity was between 0 and 1, and the mean of S across all lengths was set as identical for all three scenarios of each species.
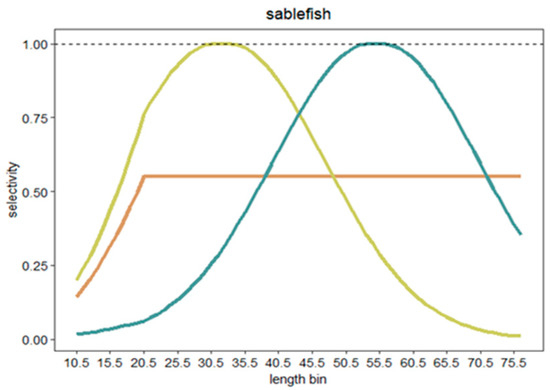
Figure 2.
An example of the simulated three length selectivity scenarios (S0, S1, S2) for sablefish (Anoplopoma fimbria). S0 represents a non-selective fishery (orange); S1 is where smaller individuals had a greater probability of being caught (yellow); S2 is where larger individuals had a greater probability of being caught (green).
Overall, there were nine scenarios of fishing conditions (3 F-scenarios × 3 S-scenarios) for twenty-seven species belonging to four life history strategy groups.
2.3. Catch-Based Models
For each species under each scenario, three catch-based assessment models were applied to the simulated catch data to evaluate model performance. The catch-based models used in this study include the Catch-MSY model [CMSY] [10], catch-only model-sampling importance resampling model [COM-SIR] [11], and state-space catch-only model [SSCOM] [12]. The parameters used in the catch-based models for each species were listed in Table S1. The analyses were conducted by the “datalimited” package [29] in R program (version 4.0.0).
The CMSY [10] required six types of input data, including catch time-series, resilience (r), natural mortality (M), carrying capacity (K), and the range of the depletion rate for the first and the final year. We determined that the priors of r and K were from uniform distributions, and we used the Bernoulli distribution as the likelihood function for viable r–K pairs. To obtain enough pairs of the viable r–K combinations (those with which the population would not collapse or be over the carrying capacity, as defined in [10]), we assumed the maximum value of K as 100 times the maximum catch and the minimum value of r as 0.05. The depletion rate was a default value that was derived from the catch at year 0 and the last year divided by the maximum catch (following [10]). The same prior settings of the range of r and K were also used for the COM-SIR and SSCOM, but the prior distributions were assumed to be normal and lognormal in the COM-SIR and SSCOM, respectively.
For the COM-SIR [11], we assumed the harvest rate as a logistic function that was controlled by the parameters a (the bioeconomic equilibrium as a proportion of K) and x (the intrinsic rate of effort change). We defined the prior probability distribution for each of the parameters as a~U(0, 1) and x~U(0.000001, 1).
For the SSCOM [12], we defined the prior distribution for the model parameters also as uniform distributions: a~U(0, 2) and x~U(0.01, 0.5). Since the SSCOM considers the stochasticity of the population dynamics, effort dynamics, and catch efficiency using a Bayesian state-space framework, we also defined the process errors of effort, biomass, and catchability as ~U (0.01, 1).
2.4. Evaluating the Performance of the Catch-Based Models
In order to examine the performance of catch-based models in estimating stock status under different fishing scenarios, we calculated the relative error (RE) between the model-estimated and the simulated stock biomass (B) proportional to the Bmsy (BBmsy):
where is the estimated value from the catch-based model and is the BBmsy value calculated from the operating model.
3. Results
3.1. Simulation Outputs by Life History Traits and Fishing Strategy
The trends in simulated biomass varied among the F scenarios, life history trait strategies, and S scenarios (Figure S2). In general, species biomass remained stable at constant fishing mortality (F1) after a drop in the first year of fishing. In contrast, for scenario F2, species biomass decreased with increasing fishing mortality and increased with a time lag as fishing mortality decreased. In the scenario where the fishing mortality increased continuously (F3), the species biomass continuously decreased.
The biomass of species with different life history trait strategies had different responses to length selectivity (Figure S2). For the OPP strategists, fishing that favored larger individuals (S2) generally resulted in higher species biomass. In contrast, for the EQU strategists, a preference for smaller individuals (S1) resulted in a greater species biomass. For the SAL and PER strategists, the biomass was not affected by length selectivity.
Catch changed positively with the level of fishing mortality, but often decreased when the fishing mortality reached a certain level and did not increase again even when F decreased in the F2 scenario (Figure 3). For all life history trait strategies, greater selectivity for larger individuals (S2) resulted in higher catches than the scenario that favored smaller individuals (S1) (Figure 3).
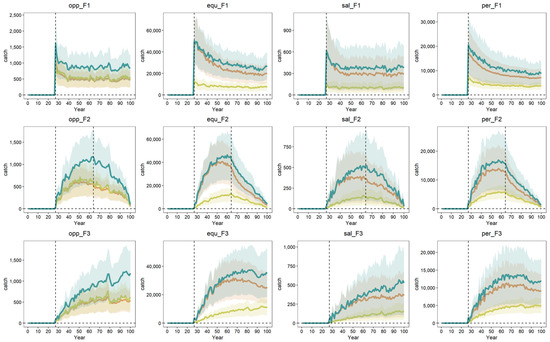
Figure 3.
The simulated catch time series (unit: Mt) of four life history strategy groups (OPP, EQU, SAL, and PER) under three F scenarios (F1, upper panel; F2, middle panel; F3, bottom panel) and three S scenarios (S0, orange; S1, yellow; S2, green). The line is the mean catch of all species of each life history strategy, with the standard errors as the shaded areas.
3.2. Evaluating the Performance of the Catch-Based Models
The relative errors between the catch-based model and the operational model outputs were the smallest for CMSY (Figure 4). In addition, our results showed that the catch-based models had different performances under different fishing selectivity, especially for the OPP and EQU species (Figure 4). We found that for the OPP species, catch-based models performed better (i.e., with a lower RE) under scenario S2, where fishing targeted the larger individuals (Figure 4a). In contrast, for the EQU species, the catch-based models performed better when fishing targeted the smaller individuals (scenario S1) (Figure 4b). REs were generally not significantly different between the S scenarios for the SAL and PER species (Figure 4c,d).
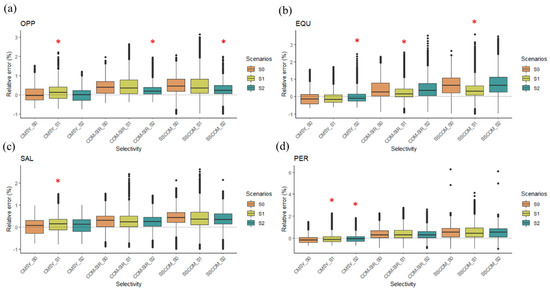
Figure 4.
The boxplots show the relative errors between the estimates of the catch-based models and the simulated true BBmsy for (a) oppertunistic species (OPP), (b) equalibrium species (EQU), (c) salmonic species (SAL), and (d) periodic speices (PER). The red star indicates the significant difference between the scenario and S0.
When comparing them among scenarios with different fishing histories, our results showed that the catch-based models generally performed the best under the F2 scenario (increasing then decreasing fishing). However, the model estimates lagged in reflecting biomass recovery when the fishing mortality was decreasing in the later part of F2 (Figure 5). For the constant fishing mortality scenario (F1), the catch-based models performed better for the OPP and SAL species compared to the EQU and PER species (Figure 5). In addition, the REs of the CMSY remained stable throughout the time series for all life history strategies, whereas the COM-SIR and SSCOM produced increasing REs for the OPP and SAL strategies (Figure 5). For the continuously increasing fishing scenario (F3), the estimated BBmsy values were increasingly over-estimated by the three catch-based models, while the biomass actually decreased, resulting in an increasing RE over time (Figure 5). Overall, the CMSY performed the best among the three models for all F scenarios.
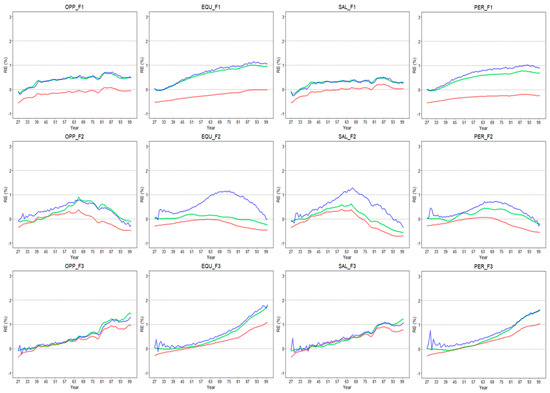
Figure 5.
The relative errors from the 27th year to 100th year of the four life history strategy groups (OPP, EQU, SAL, and PER) under the three F-scenarios (F1, F2, and F3). Red represents the REs estimated from the CMSY; green represents theREs estimated from the COM-SIR; blue represents the REs estimated from the SSCOM.
4. Discussion
We found that the CMSY performed the best for species with different life history traits and under different fishing scenarios among the three commonly used catch-based assessment methods. Such results support previous studies that suggest that CMSY estimates deviate less from the true or assessed biomass status for the comprehensive models than for many other data-limited models [8,30,31]. We also found that catch-based models performed differently with respect to fishing selectivity, with different responses for species with different life history traits. This is the first study examining the effects of selective fishing on the performance of catch-based models. The catch-based models generally had more stable performance at constant fishing mortality, as these models struggled to reflect biomass recovery and overestimated stock status especially when fishing mortality continued to increase. Our results have important implications for the use of catch-based models in the assessment of data-poor fisheries, in particular highlighting the importance of accounting for fishing selectivity and life history traits of species.
Our research indicates that the selective fishing of opportunistic and equilibrium species can impact the performance of catch-based models. This suggests that when using catch-based DLMs, the size and age structure of the stock should be taken into consideration. We found that the three catch-based models performed better when fishing favored larger individuals for opportunistic species and when it favored smaller individuals for equilibrium species. For opportunistic strategists, the extraction of larger individuals would be less damaging to the size structure of the population, given their high resilience [32]. The population under scenario S2 could therefore have had a higher biomass, which would result in a smaller difference in the optimistic estimate than that of catch-based models. In contrast, for equilibrium strategists, the selection of larger individuals would have a greater impact on the stability of the population biomass [23]. The stock status estimated by catch-based models would therefore be overestimated.
Of the three catch-based models tested, the CMSY was found to perform best and to be stable, although all three models showed increasing REs as the fishing mortality continued to increase. Our finding that the CMSY had the best performance was consistent with that of previous studies comparing the CMSY with many other data-limited models [8,30,31]. When the fishing mortality remained constant (scenario F1), the REs of the CMSY remained the smallest and the most stable over the entire simulation period for all life history strategies. In contrast, the COM-SIR and SSCOM produced increasing REs for the OPP and SAL strategies. The stable errors between the years provided opportunities to apply these methods in the stock assessment, as the bias could be easily corrected and interannual comparisons could be made, as also demonstrated by Pons et al. (2020) [8]. In scenario F2 (where fishing mortality decreased after increasing), we found that only the CMSY could detect biomass recovery for all life-history strategies. Our results support the assertion that for the COM-SIR and SSCOM, the effort dynamics should be modelled separately before and after the fishery management is involved [12]. In F3 (which had increasing fishing mortality), the REs of the three catch-based models increased over time, indicating that the catch-based models failed to capture the increasingly exploited state of the stocks. However, we note that a prior study discovered that all catch-based models currently in use encountered challenges when attempting to produce reliable outcomes that aligned with traditional stock assessment methods, despite having access to extensive data [17]. This indicates that catch-based models should still be used with caution.
The differences in the performance of catch-based models for different types of life history traits have been identified in our results. The results of our study support that the life history traits of a species not only directly affect the predictability of catch-based models [17,33], but that the traits also correspond to fishing selectivity in terms of the effect on the performance of DLMs. Given the effects of life history traits, the choice of priors for traits relevant to population growth rate and life span (e.g., r and K) would be critical in the application of these models [10,11,12]. Martell and Froese (2013) [10] therefore suggested that the best available knowledge should be used to decide the priors for r and K, including a consideration of expert opinion and the use of meta-analysis to estimate these values [34].
We note that the assessment results of some catch-based models should be interpreted with caution, as the assessed biomass may be highly correlated with the catch but not with the true biomass dynamics. For example, in our results, the BBmsy estimated by the SSCOM was more similar to the annual variation of catch than to the biomass. Thorson et al. (2013) [12] also pointed out that the SSCOM is highly dependent on the catch time series. Considering that catch data can be affected by many factors in addition to stock biomass, such as market shifts and changes in fishing regulations, the trend of the catch time series could deviate from the biomass [35,36]. We therefore recommend that catch-based models should be applied more carefully to avoid mis-estimating stock status [37].
The development of data-limited methods should not prevent the government from continuously collecting information for comprehensive assessments. Because catch-based models are sensitive to fishing history and strategy [30], as our results showed, we recommend that the history of changes in fishing efforts are considered based on expert opinion or the literature when applying catch-based models. In addition, if the age/length composition of the population is sensitive to length-selective fishing, we should consider the selectivity when applying catch-based models. In a data-limited situation, stock assessment should ideally be carried out under separate fishery management and regulatory phases. While the data-limited models could provide a rapid assessment for management decisions, it should be noted that our use of these methods involved simple hypotheses and often provided biased estimates of fishery status [17]. It is recommended that the management bodies continue to monitor stock status to implement comprehensive fishery management under the regulation of the harvest control rule (HCR) and management strategy evaluation (MSE) framework [31,38].
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/fishes8030130/s1, Table S1, the life-history parameters used for simulating the population dynamics of the 27 species in the four life history strategy groups [27,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73]; Figure S1, the results of the cluster analysis of the 42 fish species in King & McFarlane (2003); Figure S2, the time series of the simulated B/Bmsy of the four life history strategists (OPP, EQU, SAL, and PER) in the three F scenarios (F1, F2, and F3) and three S scenarios (S0, S1, and S2).
Author Contributions
Conceptualization, T.-C.K.; methodology, T.-C.K. and C.-C.C.; validation, T.-C.K.; formal analysis, C.-C.C.; investigation, C.-C.C.; resources, T.-C.K.; writing—original draft preparation, C.-C.C.; writing—review and editing, T.-C.K. and N.-J.S.; visualization, C.-C.C.; supervision, T.-C.K.; project administration, T.-C.K.; funding acquisition, T.-C.K. and N.-J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science and Technology Council, Taiwan, with the grant number MOST110-2636-B-019-001.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Data available upon request.
Acknowledgments
This work was financially supported by National Science and Technology Council in Taiwan, under Grant MOST110-2636-B-019-001. We also thank for the support from the Intelligent Maritime Research Center, National Taiwan Ocean University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pilling, G.; Apostolaki, P.; Science, P.F. Assessment and Management of Data-Poor Fisheries. In Advances in Fisheries Science: 50 Years on From Beverton and Holt; Payne, A.I.L., Cotter, J., Potter, T., Eds.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Worm, B.; Barbier, E.B.; Beaumont, N.; Duffy, J.E.; Folke, C.; Halpern, B.S.; Jackson, J.B.C.; Lotze, H.K.; Micheli, F.; Palumbi, S.R.; et al. Impacts of Biodiversity Loss on Ocean Ecosystem Services. Science 2006, 314, 787–790. [Google Scholar] [CrossRef] [PubMed]
- Costello, C.; Ovando, D.; Hilborn, R.; Gaines, S.D.; Deschenes, O.; Lester, S.E. Status and Solutions for the World’s Unassessed Fisheries. Science 2012, 338, 517–521. [Google Scholar] [CrossRef] [PubMed]
- Hilborn, R.; Amoroso, R.O.; Anderson, C.M.; Baum, J.K.; Branch, T.A.; Costello, C.; De Moor, C.L.; Faraj, A.; Hively, D.; Jensen, O.P.; et al. Effective Fisheries Management Instrumental in Improving Fish Stock Status. Proc. Natl. Acad. Sci. USA 2020, 117, 2218–2224. [Google Scholar] [CrossRef] [PubMed]
- Pita, C.; Villasante, S.; Pascual-Fernández, J.J. Managing Small-Scale Fisheries under Data Poor Scenarios: Lessons from around the World. Mar. Policy 2019, 101, 154–157. [Google Scholar] [CrossRef]
- Sagarese, S.R.; Rios, A.B.; Cass-Calay, S.L.; Cummings, N.J.; Bryan, M.D.; Stevens, M.H.; Harford, W.J.; McCarthy, K.J.; Matter, V.M. Working towards a Framework for Stock Evaluations in Data-Limited Fisheries. N. Am. J. Fish. Manag. 2018, 38, 507–537. [Google Scholar] [CrossRef]
- Zhou, S.; Punt, A.E.; Ye, Y.; Ellis, N.; Dichmont, C.M.; Haddon, M.; Smith, D.C.; Smith, A.D. Estimating Stock Depletion Level from Patterns of Catch History. Fish Fish. 2017, 18, 742–751. [Google Scholar] [CrossRef]
- Pons, M.; Cope, J.M.; Kell, L.T. Comparing Performance of Catch-Based and Length-Based Stock Assessment Methods in Data-Limited Fisheries. Can. J. Fish. Aquat. Sci. 2020, 77, 1026–1037. [Google Scholar] [CrossRef]
- van Gemert, R.; Koemle, D.; Winkler, H.; Arlinghaus, R. Data-Poor Stock Assessment of Fish Stocks Co-Exploited by Commercial and Recreational Fisheries: Applications to Pike Esox Lucius in the Western Baltic Sea. Fish. Manag. Ecol. 2022, 29, 16–28. [Google Scholar] [CrossRef]
- Martell, S.; Froese, R. A Simple Method for Estimating MSY from Catch and Resilience. Fish Fish. 2013, 14, 504–514. [Google Scholar] [CrossRef]
- Vasconcellos, M.; Cochrane, K. Overview of World Status of Data-Limited Fisheries: Inferences from Landings Statistics. In Fisheries Assessment and Management in Data-Limited Situations; Krus, G.H., Gall, V.F., Hay, D.E., Perry, R.I., Peterman, R.M., Shirley, T.C., Spencer, P.D., Wilson, B., Woodby, D., Eds.; Alaska Sea Grant, Univ.: Fairbanks, AK, USA, 2005; pp. 1–20. [Google Scholar]
- Thorson, J.T.; Minto, C.; Minte-Vera, C.V.; Kleisner, K.M.; Longo, C. A New Role for Effort Dynamics in the Theory of Harvested Populations and Data-Poor Stock Assessment. Can. J. Fish. Aquat. Sci. 2013, 70, 1829–1844. [Google Scholar] [CrossRef]
- Harley, S.J.; Myers, R.A.; Dunn, A. Is Catch-per-Unit-Effort Proportional to Abundance? Can. J. Fish. Aquat. Sci. 2001, 58, 1760–1772. [Google Scholar] [CrossRef]
- Macusi, E.D.; Morales, I.D.G.; Macusi, E.S.; Pancho, A.; Digal, L.N. Impact of Closed Fishing Season on Supply, Catch, Price and the Fisheries Market Chain. Mar. Policy 2022, 138, 105008. [Google Scholar] [CrossRef]
- Langlois, T.J.; Newman, S.J.; Cappo, M.; Harvey, E.S.; Rome, B.M.; Skepper, C.L.; Wakefield, C.B. Length Selectivity of Commercial Fish Traps Assessed from in Situ Comparisons with Stereo-Video: Is There Evidence of Sampling Bias? Fish. Res. 2015, 161, 145–155. [Google Scholar] [CrossRef]
- Carruthers, T.R.; Walters, C.J.; McAllister, M.K. Evaluating Methods That Classify Fisheries Stock Status Using Only Fisheries Catch Data. Fish. Res. 2012, 119–120, 66–79. [Google Scholar] [CrossRef]
- Free, C.M.; Jensen, O.P.; Anderson, S.C.; Gutierrez, N.L.; Kleisner, K.M.; Longo, C.; Minto, C.; Osio, G.C.; Walsh, J.C. Blood from a Stone: Performance of Catch-Only Methods in Estimating Stock Biomass Status. Fish. Res. 2020, 223, 105452. [Google Scholar] [CrossRef]
- Kleisner, K.; Pauly, D. Stock-Status Plots for Fisheries for Regional Seas. In The State of Biodiversity and Fisheries in Regional Seas, Fisheries Centre Research Reports 19(3); Christensen, V., Lai, S., Palomares, M.L.D., Zeller, D., Pauly, D., Eds.; Fisheries Centre, University of British Columbia: Vancouver, BC, Canada, 2011. [Google Scholar]
- Froese, R.; Kesner-Reyes, K. Impact of Fishing on the Abundance of Marine Species; ICES: Copenhagen, Denmark, 2002. [Google Scholar]
- Piet, G.J.; Rijnsdorp, A.D. Changes in the Demersal Fish Assemblage in the South-Eastern North Sea Following the Establishment of a Protected Area (“Plaice Box”). ICES J. Mar. Sci. 1998, 55, 420–429. [Google Scholar] [CrossRef]
- Fenberg, P.B.; Roy, K. Ecological and Evolutionary Consequences of Size-Selective Harvesting: How Much Do We Know? Mol. Ecol. 2008, 17, 209–220. [Google Scholar] [CrossRef]
- Birkeland, C.; Dayton, P.K. The Importance in Fishery Management of Leaving the Big Ones. Trends Ecol. Evol. 2005, 20, 356–358. [Google Scholar] [CrossRef]
- Hsieh, C.H.; Reiss, C.S.; Hunter, J.R.; Beddington, J.R.; May, R.M.; Sugihara, G. Fishing Elevates Variability in the Abundance of Exploited Species. Nature 2006, 443, 859–862. [Google Scholar] [CrossRef]
- Anderson, S.C.; Monnahan, C.C.; Johnson, K.F.; Ono, K.; Valero, J.L. Ss3sim: An R Package for Fisheries Stock Assessment Simulation with Stock Synthesis. PLoS ONE 2014, 9, e92725. [Google Scholar] [CrossRef]
- Methot, R.D.; Wetzel, C.R. Stock Synthesis: A Biological and Statistical Framework for Fish Stock Assessment and Fishery Management. Fish. Res. 2013, 142, 86–99. [Google Scholar] [CrossRef]
- Methot, R.D., Jr.; Wetzel, C.R.; Taylor, I.G.; Doering, K. Stock Synthesis User Manual Version 3.30.15. U.S. Department of Commerce, NOAA Processed Report NMFS-NWFSC-PR-2020-05; Northwest Fisheries Science Center: Seattle, WA, USA, 2020.
- King, J.R.; McFarlane, G.A. Marine Fish Life History Strategies: Applications to Fishery Management. Fish. Manag. Ecol. 2003, 10, 249–264. [Google Scholar] [CrossRef]
- Ricker, W.E. Handbook of Computations for Biological Statistics of Fish Populations. Bull. Fish. Res. Board Can. 1958, 119, 1–300. [Google Scholar]
- Anderson, S.C.; Afflerbach, J.; Cooper, A.B.; Dickey-Collas, M.; Jensen, O.P.; Kleisner, K.M.; Longo, C.; Osio, G.C.; Ovando, D.; Minte-Vera, C.; et al. Datalimited: Stock Assessment Methods for Data-Limited Fisheries. R Package Version 0.1.0. 2016. Available online: https://github.com/datalimited/datalimited (accessed on 17 February 2023).
- Rosenberg, A.A.; Fogarty, M.J.; Cooper, A.B.; Dickey-Collas, M.; Fulton, E.A.; Gutiérrez, N.L.; Hyde, K.J.W.; Kleisner, K.M.; Kristiansen, T.; Longo, C.; et al. Developing New Approaches to Global Stock Status Assessment and Fishery Production Potential of the Seas. FAO Fish. Aquac. Circ. 2014, 1086, 175. [Google Scholar]
- Walsh, J.C.; Minto, C.; Jardim, E.; Anderson, S.C.; Jensen, O.P.; Afflerbach, J.; Dickey-Collas, M.; Kleisner, K.M.; Longo, C.; Osio, G.C.; et al. Trade-Offs for Data-Limited Fisheries When Using Harvest Strategies Based on Catch-Only Models. Fish Fish. 2018, 19, 1130–1146. [Google Scholar] [CrossRef]
- Juan-Jordá, M.J.; Mosqueira, I.; Freire, J.; Dulvy, N.K. Population Declines of Tuna and Relatives Depend on Their Speed of Life. Proc. R. Soc. B Biol. Sci. 2015, 282, 20150322. [Google Scholar] [CrossRef]
- Rosenberg, A.A.; Kleisner, K.M.; Afflerbach, J.; Anderson, S.C.; Dickey-Collas, M.; Cooper, A.B.; Fogarty, M.J.; Fulton, E.A.; Gutiérrez, N.L.; Hyde, K.J.W.; et al. Applying a New Ensemble Approach to Estimating Stock Status of Marine Fisheries around the World. Conserv. Lett. 2018, 11, e12363. [Google Scholar] [CrossRef]
- Punt, A.E.; Hilborn, R. Bayesian Stock Assessment Methods in Fisheries-User’s Manual; Food and Agriculture Organization: Rome, Italy, 2001.
- Branch, T.A.; Jensen, O.P.; Ricard, D.; Ye, Y.; Hilborn, R. Contrasting Global Trends in Marine Fishery Status Obtained from Catches and from Stock Assessments. Conserv. Biol. 2011, 25, 777–786. [Google Scholar] [CrossRef]
- Froese, R.; Zeller, D.; Kleisner, K.; Pauly, D. What Catch Data Can Tell Us about the Status of Global Fisheries. Mar. Biol. 2012, 159, 1283–1292. [Google Scholar] [CrossRef]
- Hilborn, R.; Branch, T.A. Fisheries: Does Catch Reflect Abundance? Nature 2013, 494, 303–306. [Google Scholar]
- Hordyk, A.R.; Loneragan, N.R.; Prince, J.D. An Evaluation of an Iterative Harvest Strategy for Data-Poor Fisheries Using the Length-Based Spawning Potential Ratio Assessment Methodology. Fish. Res. 2015, 171, 20–32. [Google Scholar] [CrossRef]
- Sassa, C.; Ohshimo, S.; Tanaka, H.; Tsukamoto, Y. Reproductive Biology of Benthosema Pterotum (Teleostei: Myctophidae) in the Shelf Region of the East China Sea. J. Mar. Biol. Assoc. U. K. 2014, 94, 423–433. [Google Scholar] [CrossRef]
- Garcia Seoane, E. Ecology of the Glacier Lanternfish Benthosema Glaciale (Reinhardt,1837) with Focus on the Flemish Cap; University of Vigo: Vigo, Spain, 2013. [Google Scholar]
- Brand, E.J.; Kaplan, I.C.; Harvey, C.J.; Levin, P.S.; Fulton, E.A.; Hermann, A.J.; Field, J.C. A Spatially Explicit Ecosystem Model of the California Current’s Food Web and Oceanography. NOAA Tech. Memo. NMFS-NWFSC 2007, 84, 145. [Google Scholar]
- Liang, Y.; Sui, X.; Chen, Y.; Jia, Y.; He, D. Life History Traits of the Chinese Minnow Rhynchocypris Oxycephalus in the Upper Branch of Yangtze River, China. Zool. Stud. 2014, 53, 1–10. [Google Scholar] [CrossRef]
- Hay, D.E.; Mccarter, P.B. Status of the Eulachon (Thaleichthys pacificus) in Canada. Can. Stock Assess. Res. Doc. 2000, 92. [Google Scholar]
- Nelson, G.A.; Ross, M.R. Biology and Population Changes of Northern Sand Lance (Ammodytes dubius) from the Gulf of Maine to the Middle Atlantic Bight. J. Northwest Atl. Fish. Sci. 1991, 11, 11–27. [Google Scholar] [CrossRef]
- Griffith, D.A.; Lo, N.C.H.; Jolla, L.; Griffith, D.A. Spawning Biomass of Pacific Sardine (Sardinops sagax), from 1994–2004 off California. CalCOFI Rep 2005, 46. [Google Scholar]
- Galindo-Cortes, G.; De Anda-Montañez, J.A.; Arreguín-Sánchez, F.; Salas, S.; Balart, E.F. How Do Environmental Factors Affect the Stock-Recruitment Relationship? The Case of the Pacific Sardine (Sardinops sagax) of the Northeastern Pacific Ocean. Fish. Res. 2010, 102, 173–183. [Google Scholar] [CrossRef]
- Haist, V.; Stocker, M. Growth and Maturation of Pacific Herring (Clupea harengus pallasi) in the Strait of Georgia. Can. J. Fish. Aquat. Sci. 1985, 42, 138–146. [Google Scholar] [CrossRef]
- Burd, A.C.; Howlett, G.J. Fecundity Studies on North Sea Herring. ICES J. Mar. Sci. 1974, 35, 107–120. [Google Scholar] [CrossRef]
- Nash, R.D.M.; Dickey-Collas, M.; Kell, L.T. Stock and Recruitment in North Sea Herring (Clupea harengus); Compensation and Depensation in the Population Dynamics. Fish. Res. 2009, 95, 88–97. [Google Scholar] [CrossRef]
- Holden, M.J. The Fecundity of Raja clavata in British Waters. ICES J. Mar. Sci. 1975, 36, 110–118. [Google Scholar] [CrossRef]
- Ebert, D.A.; Smith, W.D.; Cailliet, G.M. Reproductive Biology of Two Commercially Exploited Skates, Raja binoculata and R. rhina, in the Western Gulf of Alaska. Fish. Res. 2008, 94, 48–57. [Google Scholar] [CrossRef]
- Drew, M.; White, W.T.; Dharmadi; Harry, A.V.; Huveneers, C. Age, Growth and Maturity of the Pelagic thresher Alopias pelagicus and the Scalloped hammerhead Sphyrna lewini. J. Fish Biol. 2015, 86, 333–354. [Google Scholar] [CrossRef] [PubMed]
- Hsu, H.; Joung, S.J.; Lyu, G.T.; Liu, K.M.; Huang, C.C. Age and Growth of the Blue Shark, Prionace glauca, in the Northwest Pacific. In Proceedings of the Shark Working Group Workshop ISC/11/SHARKWG-2/, La Jolla, CA, USA, 28 November–6 December 2011; p. 22. [Google Scholar]
- King, J.R.; McPhie, R.P. Preliminary Age, Growth and Maturity Estimates of Spotted Ratfish (Hydrolagus colliei) in British Columbia. Deep. Res. Part II Top. Stud. Oceanogr. 2015, 115, 55–63. [Google Scholar] [CrossRef]
- Dutton, J.; Gioia, K.A. Fecundity and Embryonic Development of Spiny Dogfish in the Northwest Atlantic Ocean. Trans. Am. Fish. Soc. 2019, 148, 48–57. [Google Scholar] [CrossRef]
- Kwain, W.H. Spawning Behavior and Early Life History of Pink Salmon (Oncorhynchus gorbuscha) in the Great Lakes (Lake superior). Can. J. Fish. Aquat. Sci. 1982, 39, 1353–1360. [Google Scholar] [CrossRef]
- Godbout, L.; Fu, C.H.; Irvine, J.R. Evaluation of Chum Salmon Fishery Performance Using Ricker and Beverton-Holt Stock Recruitment Approaches in a Bayesian Framework. Reconciling Fish. with Conserv. Vols I Ii 2008, 49, 1417–1433. [Google Scholar]
- Beacham, T.D. Fecundity of Coho Salmon (Oncorhynchus kisutch) and Chum Salmon (Oncorhynchus keta) in the Northeast Pacific Ocean. Can. J. Zool. 1982, 60, 1463–1469. [Google Scholar] [CrossRef]
- Hartman, W.L.; Conkle, C.Y. Fecundity of Red Salmon at Brooks and Karluk Lakes, Alaska. Fish. Bull. Fish Wildl. Serv. 1960, 61, 53–60. [Google Scholar]
- Kerns, J.A.; Rogers, M.W.; Bunnell, D.B.; Claramunt, R.M.; Collingsworth, P.D. Comparing Life History Characteristics of Lake Michigan’s Naturalized and Stocked Chinook Salmon. N. Am. J. Fish. Manag. 2016, 36, 1106–1118. [Google Scholar] [CrossRef]
- Echeverria, T.W. Thirty-Four Species of California Rockfishes: Maturity and Seasonality of Reproduction. Fish. Bull. 1988, 85, 229–250. [Google Scholar]
- Haigh, R.; Starr, P. A Review of Yellowmouth Rockfish Sebastes reedi along the Pacific Coast of Canada: Biology, Distribution, and Abundance Trends. CSAS Res. Doc. 2008, 3848, 105. [Google Scholar]
- Stanley, R.D.; Kronlund, A.R. Life History Characteristics for Silvergray Rockfish (Sebastes brevispinis) in British Columbia Waters and the Implications for Stock Assessment and Management. Fish. Bull. 2005, 103, 670–684. [Google Scholar]
- Conrath, C.L.; Knoth, B. Reproductive Biology of Pacific Ocean Perch in the Gulf of Alaska. Mar. Coast. Fish. 2013, 5, 21–27. [Google Scholar] [CrossRef]
- Love, M.S.; Morris, P.; McCrae, M.; Colins, R. Life History Aspects of 19 Rockfish Species (Scorpaenidae: Sebastes) from the Southern California Bight. NOAA Tech. Rep. NMFS 87 1990. [Google Scholar]
- Beyer, S.G.; Sogard, S.M.; Harvey, C.J.; Field, J.C. Variability in Rockfish (Sebastes spp.) Fecundity: Species Contrasts, Maternal Size Effects, and Spatial Differences. Environ. Biol. Fishes 2015, 98, 81–100. [Google Scholar] [CrossRef]
- Schmitt, C.; St-Pierre, G. Evaluation of Two Methods to Determine Maturity of Pacific Halibut; International Pacific Halibut Commission: Seattle, WA, USA, 1997; pp. 1–24. [Google Scholar]
- Haug, T.; Gulliksen, B. Fecundity and Oocyte Sizes in Ovaries of Female Atlantic Halibut, Hippoglossus hippoglossus (L.). Sarsia 1988, 73, 259–261. [Google Scholar] [CrossRef]
- Head, M.A.; Keller, A.A.; Bradburn, M. Maturity and Growth of Sablefish, Anoplopoma fimbria, along the U.S. West Coast. Fish. Res. 2014, 159, 56–67. [Google Scholar] [CrossRef]
- Hunter, J.R.; Macewicz, B.J.; Kimbrell, C.A. Fecundity and Other Aspects of the Reproduction of Sablefish, Anoplopoma fimbria, in Central California Waters. CalCOFI Rep 1989, 30, 61–72. [Google Scholar]
- Schirripa, M.J.; Goodyear, C.P.; Methot, R.M. Testing Different Methods of Incorporating Climate Data into the Assessment of US West Coast Sablefish. ICES J. Mar. Sci. 2009, 66, 1605–1613. [Google Scholar] [CrossRef]
- Pearson, K.E.; Gunderson, D.R. Reproductive Biology and Ecology of Shortspine Thornyhead Rockfish, Sebastolobus alascanus, and Longspine Thornyhead Rockfish, S. altivelis, from the Northeastern Pacific Ocean. Environ. Biol. Fishes 2003, 67, 117–136. [Google Scholar] [CrossRef]
- Cooper, D.W.; Pearson, K.E.; Gunderson, D.R. Fecundity of Shortspine Thornyhead (Sebastolobus alascanus) and Longspine Thornyhead (S. altivelis) (Scorpaenidae) from the Northeastern Pacific Ocean, Determined by Stereological and Gravimetric Techniques. Fish. Bull. 2005, 103, 15–22. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).